The Enantiomers of 4-Amino-3-fluorobutanoic Acid as Substrates for γ-Aminobutyric Acid Aminotransferase. Conformational Probes for GABA Binding

Abstract

γ-Aminobutyric acid aminotransferase (GABA-AT), a pyridoxal 5’-phosphate dependent enzyme, catalyzes the degradation of the inhibitory neurotransmitter γ-aminobutyric acid (GABA) to succinic semialdehyde with concomitant conversion of pyridoxal 5’-phosphate (PLP) to pyridoxamine 5’-phosphate (PMP). The enzyme then catalyzes the conversion of α-ketoglutarate to the excitatory neurotransmitter L-glutamate. Racemic 4-amino-3-fluorobutanoic acid (3-F-GABA) was shown previously to act as a substrate for GABA-AT, not for transamination, but for HF elimination. Here we report studies of the reaction catalyzed by GABA-AT on (R)- and (S)-3-F-GABA. Neither enantiomer is a substrate for transamination. Very little elimination from the (S)-enantiomer was detected using a coupled enzyme assay; The rate of elimination of HF from the (R)-enantiomer is at least 10 times greater than that for the (S)-enantiomer. The (R)-enantiomer is about 20 times more efficient as a substrate for GABA-AT catalyzed HF elimination than GABA is a substrate for transamination. The (R)-enantiomer also inhibits the transamination of GABA 10 times more effectively than the (S)-enantiomer. Using a combination of computer modeling and the knowledge that vicinal C-F and C-NH₃⁺ bonds have a strong preference to align gauche rather than anti to each other, it is concluded that on binding of free 3-F-GABA to GABA-AT the optimal conformation places the C-NH₃⁺ and C-F bonds gauche in the (R)-enantiomer but anti in the (S)-enantiomer. Furthermore, the dynamic binding process and the bioactive conformation of GABA bound to GABA-AT have been inferred based on the different biological behavior of the two enantiomers of 3-F-GABA when they bind to the enzyme. The present study suggests that the C-F bond can be utilized as a conformational probe to explore the dynamic binding process and provide insight into the bioactive conformation of substrates, which cannot be easily determined by other biophysical approaches.

γ-Aminobutyric acid aminotransferase (1, 2) (GABA-AT, E.C. 2.6.1.19) is a pyridoxal-5’-phosphate (PLP) dependent enzyme responsible for the degradation of the major inhibitory neurotransmitter, γ-aminobutyric acid (GABA, 1) (3), in the mammalian central nervous system to succinic semialdehyde. Inhibition of this enzyme causes an increase in the concentration of GABA in the brain, which could have therapeutic applications in neurological disorders including epilepsy (4, 5), Parkinson’s disease (6), Huntington’s chorea (7), and Alzheimer’s disease (8, 9). It has also been found that an increase in the availability of GABA can block the effects of drug addiction (10, 11).

Because of its potential importance in neuropharmacology, a variety of GABA analogues have been synthesized and studied (12, 13). Over the years, we have synthesized numerous halogenated analogues of GABA as inactivators and inhibitors of GABA-AT (14 – 30). In 1981 we investigated the activity of 4-amino-3-fluorobutanoic acid (3-F-GABA, 2) as a potential inactivator of GABA-AT and found that, although it was not an inactivator, it was a substrate for GABA-AT but without conversion of the PLP to PMP (31). The enzyme catalyzed the elimination of HF from the substrate, converting it to succinic semialdehyde, the same product obtained by GABA-AT catalyzed oxidation of GABA. Fluorine is the next largest atom to hydrogen that can be covalently bound to carbon, and it is often explored as a hydrogen mimic in medicinal chemistry. However, a fluorine for hydrogen exchange can substantially change the electronic profile of a molecule and in this case results in a mechanistic deviation driven by HF elimination. It is well known that in protonated β-fluoroamines there is a strong preference for the C-NH₃⁺ and C-F bonds to align gauche rather than anti to each other, such that the fluorine and nitrogen atoms move close to each other because of an electrostatic attraction. This has been observed in 2-fluoroethylammonium and related structures (32, 33), including the amino acids 3-amino-2-fluoropropionic acid (34), 4-fluoroprolines (35), and 3-fluoropiperidinium rings (36 – 38); the anti-gauche energy differences are around 5.0 kcal·mol⁻¹ (~20 kJ·mol⁻¹). The origin of this effect appears to lie in a favorable charge-dipole interaction between the charge of the R-⁺NH₃ group and the dipole of the C-F bond (36 – 38). In the context of 3-F-GABA it became evident that this effect may differentially influence the conformation, and therefore the binding, of the enantiomers of 3-F-GABA to GABA-AT and could reveal some insights on the preferred binding mode of the amino acid to the enzyme. Also, it was anticipated that the elimination of hydrogen fluoride from each of the enantiomers of 3-F-GABA, (R)-2 and (S)-2 after transamination to PLP may be subject to stereoelectronic control, and each enantiomer may show a different propensity to act as an elimination substrate. This paper reports the binding kinetics and rates of hydrogen fluoride (fluoride ion) elimination for (R)-2 relative to (S)-2 and draws conclusions regarding the mode of binding of 1 to GABA-AT.

Experimental Methods

Syntheses of (R)-2 and (S)-2

Full details of the asymmetric syntheses, stereochemical analysis, and characterization of these compounds has recently been published (39).

Purification of GABA-AT from Pig Brain

GABA-AT was isolated and purified from pig brain by a modified procedure (40). The purified GABA-AT used in these experiments was found to have a concentration of 9.81 mg/mL with a specific activity of 0.89 units/mg.

Substrate Activity of (R)- and (S)-4-amino-3-fluorobutanoic acids with GABA-AT (2)

Enantiomers (R)-2 and (S)-2 were tested as substrates for GABA-AT using two different substrate assay methods. A coupled assay with succinic semialdehyde dehydrogenase as the secondary enzyme was used to monitor conversion of GABA to succinic semialdehyde as previously described (31). The compounds were further assayed by monitoring the conversion of [U-¹⁴C]-α-ketoglutarate to [¹⁴C]-L-glutamic acid as a measure of the rate of PLP reduction to PMP, which in turn corresponds to the rate of GABA oxidation to succinic semialdehyde as described earlier (31) but with the following modifications: The total assay volume was reduced to 100 µL in pyrophosphate buffer (50 mM, pH 8.5), and all reactions were quenched after a 15 min incubation period at room temperature via the addition of 20% aq. trichloroacetic acid (30 µL). The quenched reactions were transferred to columns containing Bio-Rad AG 50W-X8 cation exchange resin (proton form, 1.0 g). Columns were eluted with water (6 × 1.0 mL) followed by 2 M NH₄OH (6 × 1.0 mL). The water eluants were found to contain all of the [U-¹⁴C]-α-ketoglutarate, and the NH₄OH eluant was found to contain all of the [U-¹⁴C]-L-glutamic acid. Variable GABA concentrations (500 µM to 2.0 mM) and 3-F-GABA concentrations (both enantiomers, 500 µM to 1.0 mM) were used for the determination of kinetic constants associated with the inhibition GABA transamination. The concentration of [U-¹⁴C]-α-ketoglutarate (3.52 mM, 88.58 µCi/mmole) was maintained in all experiments. Ultima Gold (Packard) scintillation fluid (15 mL) was added to each fraction containing 2.0 mL eluant prior to scintillation counting. No [U-¹⁴C]-L-glutamic acid was detected in the absence of enzyme.

Fluoride Ion Elimination from (R)- and (S)-4-amino-3-fluorobutanoic acids

Enzyme reactions were prepared as solutions containing pyrophosphate buffer (50 mM, pH 8.5), α-ketoglutarate (3.06 mM in pyrophosphate buffer, pH 8.5), and GABA-AT (0.487 mg/mL). Reactions were initiated by addition of (R)-2 and (S)-2 (1.0 mM final concentration). In control experiments, the GABA-AT was replaced with pyrophosphate buffer to monitor any nonenzymatic fluoride ion elimination. At 5, 10, 20, and 30 min periods 100 µL aliquots of each of the solutions (the experimental and control solutions for each enantiomer) were removed and quenched by addition to a buffer containing one part low level Total Ionic Strength Adjustment Buffer (TISAB; prepared as described in the Orion electrode manual), one part pyrophosphate buffer, and a concentration of NaF (Orion standard solution) such that the overall fluoride concentration in any sample in the absence of any fluoride ion elimination would be 5 µM; this background reduces experimental error. The total volume of this solution after the addition of the experimental or control solution was 2.00 mL. The electric potential across the electrode (Thermo Electron Corporation, Orion Ion Plus Fluoride Electrode 96-09) in each solution was then measured. These potentials were converted to fluoride ion concentrations using a curve generated as described in the electrode manual (low level measurement). It was found that in the absence of GABA-AT no increase in electric potential was observed over time; therefore, nonenzymatic elimination does not occur.

Computer Modeling

FlexX (incremental construction algorithm) (41) and AutoDock 3.0 (Lamarckian genetic algorithm) (42), were employed to perform the docking calculations. FlexX docking was performed using SYBYL molecular modeling software 6.9 (43) operating under IRIX 6.5. FlexX performs flexible docking using an incremental fragment construction method to place a flexible ligand into a rigid protein structure. The receptor structure used was the X-ray crystal structure of two homodimers of pig liver GABA-AT in complex with vigabatrin (4-vinyl-GABA) (PDB code: 1OHW) (44). Water molecules were removed as they were found not to be located within the active site region. Hydrogens were not displayed in the receptor structure. The ligand binding site was defined as all residues within 6.5 Å from the PLP-vigabatrin adduct of monomer A in the crystal structure (PDB code: 1OHW). The PLP-vigabatrin adduct was deleted from the crystal structure, and the PLP-(R)-2 or PLP-(S)-2 adducts were built; appropriate atom types were specified and labeled for physiological conditions. The PLP-(R)-2 or PLP-(S)-2 adducts were then docked into the vacant ligand binding site with hydrogens present. The FlexX default parameters were used in the docking calculation, and the top 50 scoring docking solutions were saved.

The Lamarckian genetic algorithm of AutoDock 3.0 was also used to dock PLP-(R)-2 or PLP-(S)-2 adducts into the active site of pig liver GABA-AT. The protein crystal structure was the same as the one used in the FlexX docking. The protein was treated using the united-atom approximation, and only the polar hydrogen atoms were added to the protein. Kollman united-atom partial charges were assigned, and all hydrogen atoms were added to the crystallographic water molecules, the ligand vigabatrin, and cofactor PLP. The partial atom charge calculations were carried out by the Gasteiger-Marsili method (45). The nonpolar hydrogen atoms of the ligand and PLP were deleted, and the partial atom charges of the deleted hydrogen atoms were merged with the charges of the corresponding carbon atoms to which they were bonded. Energy minimizations were then performed to assign the optimal orientation of the added hydrogen atoms, especially the side chain hydrogen atoms of tyrosine, threonine, and serine residues. Atomic solvation parameters and fragmental volumes were then assigned to the protein atoms using the AutoDock utility AddSol. All crystallographic water molecules were removed in the docking calculation. The PLP-(R)-2 or PLP-(S)-2 adducts were built in the same way as the ones used in FlexX docking. All hydrogens were added, and partial atomic charges were calculated using the Gasteiger-Marsili method. The rotatable bonds in the molecule were defined using an AutoDock utility, AutoTors, which also unites the nonpolar hydrogens added by Sybyl for the partial atomic charge calculation. The grid maps were calculated using AutoGrid. The definition of ligand binding site is the same as that in the FlexX calculation. The dimensions of the grid box were 18.5 × 19 × 19.5 Å with a grid-point spacing of 0.375 Å. Parameters for the docking experiments were as follows: initial population size of 200; random starting position and conformation; maximal mutation of 0.2 Å in translation and 5° in orientation and rotation; elitism of 5; mutation rate of 0.02 and crossover rate of 0.8; local search rate of 0.06 and maximal iteration per local search of 300. Simulations were performed with a maximum of 1.5 × 10⁶ energy evaluations and a maximum of 27,000 generations. Other parameters of AutoDock calculations were the default value. One hundred docked conformations were obtained, and the binding affinity of the inhibitors to the protein was then evaluated by the total AutoDock docking energies and further rescored using the CScore module of Sybyl 6.9, which comprises the following scoring functions: F_Score, D_Score, PMF_Score, G_Score and ChemScore. A visual comparison of the superposition of the backbone calculated conformations and that of vigabatrin served as a preliminary identification of appropriate structures. Conformations were then further evaluated based on their total docking energies.

Results

3-F-GABA (2) as a substrate for GABA-AT catalyzed transamination

Previously, it was noted that racemic 3-F-GABA (2) underwent exclusive HF elimination with no detectable transamination (conversion of the PLP cofactor to PMP) by GABA-AT (31). This was demonstrated using racemic 2 as a substrate for GABA-AT in the presence of radiolabeled α-ketoglutarate (α-KG). Oxidation of the amine would result in the conversion of the PLP cofactor of GABA-AT to PMP, which is subsequently oxidized with concomitant reduction of [¹⁴C]-α-KG to [¹⁴C]-L-glutamate. For every molecule of substrate that is oxidized, one molecule of α-KG is reduced. The amount of α-KG that is converted to L-glutamate is representative of the amount of 3-F-GABA (the substrate) that is converted to the corresponding aldehyde. No conversion from [¹⁴C]-α-KG to [¹⁴C]-L-glutamate was observed in the present study when either (R)-2 or (S)-2 was incubated with GABA-AT, consistent with the previous findings using the racemic mixture (31).

Determination of the K_m and V_max values for conversion of (R)-2 and (S)-2 amino-3-fluorobutanoic acids to succinic semialdehyde using a coupled enzyme assay

In the case of the (R)-2 enantiomer significant succinic seminaldehyde production was observed, which facilitated the determination of the kinetic constants. The results are summarized in Table 1. In the case of the (S)-2 enantiomer, succinic semialdehyde production was observed at a much slower rate. The rate of elimination from the (S)-2 enantiomer appeared to be more than an order of magnitude lower than the rate of elimination observed with the (R)-2 enantiomer. The rate of succinic semialdehyde production from (S)-2 was so slow that determination of the kinetic constants for this reaction proved to be too unreliable using this methodology.

Table 1.

Results from the coupled enzyme assay using (R)-2 as the substrate for GABA-AT. Previous data regarding the kinetic constants for GABA and racemic 3-F-GABA (1) are also shown.

Substrate	Km (mM)	Vmax (µmol/min*mg)	Vmax/Km (L/min*mg)
GABA	2.6a [2.1]b	8.9 [12.1]	0.0034 [0.0058]
(±) 3-F-GABA-1c	0.045 [0.063]	1.3 [1.4]	0.0289 [0.0222]
(R)-2	0.059 [0.050]	4.93 [5.28]	0.0836 [0.1056]
(S)-2	Could not be determinedd	Could not be determinedd	Could not be determinedd

^aKinetic constants not in brackets were determined using a Hanes-Woolf plot.

^bKinetic constants shown in brackets were determined using a Lineweaver-Burk plot.

^cSee reference 31.

^dThe rate was too slow for an accurate measurement.

Rate of HF elimination from (R)-2 and (S)-2 3-F-GABA measured with a fluoride ion electrode

The rates of HF elimination from (R)-2 and (S)-2 were also assessed using a more sensitive fluoride ion detection method, a fluoride ion electrode to determine whether the (R)-2 or (S)-2 undergoes the HF elimination reaction when it was incubated with GABA-AT. For every fluoride ion detected in solution, one molecule of 3-F-GABA has undergone HF elimination. The relative rates of HF elimination from (R)-2 and (S)-2 were determined by measuring [F⁻] with time, which is equivalent to the relative rate of succinic semialdehyde formation (see Supporting Information). Enantiomer (R)-2 underwent fluoride ion elimination at a rate of 6.63 × 10⁻² µmoles/min·mg whereas (S)-2 underwent fluoride ion elimination at a rate of 6.26 × 10⁻³ µmoles/min·mg. The rate of HF elimination from (R)-2 is an order of magnitude greater than that from (S)-2. No fluoride ion release was detected for either isomer in the absence of enzyme.

(R)-2 and (S)-2 3-F-GABA enantiomers as inhibitors of GABA transamination

To determine if both enantiomers of 3-F-GABA are able to bind to the active site of GABA-AT, the compounds were tested as inhibitors of GABA transamination using the radiolabeled α-KG assay. It was found that the (R)-enantiomer of 2 showed substantial inhibition of GABA transamination, whereas, the (S)-enantiomer showed no significant inhibition of GABA transamination using this method (Table 2).

Table 2.

Inhibition of GABA transamination as measured by a reduction in the rate of conversion of [U-¹⁴C]-α-KG to [U-¹⁴C]-Glu over 15 min.

[(R)-2 or (S)-2] (mM)	% α-KG converted to Glu/unit time
	(R)-2	(S)-2
0.000	6.79	6.79
0.050	6.97	7.28
0.250	3.89	7.00
0.500	1.87	7.23
1.000	0.97	6.74

The data in Table 2 suggest that the (S)-2 does not bind to the active site of GABA-AT, as such binding would inhibit the transamination of GABA, resulting in a reduction in the rate of Glu production; only the (R)-2 caused inhibition of transamination at these concentrations and clearly this enantiomer binds more efficiently to the enzyme. The type of inhibition of GABA transamination by (R)-2 was determined by a kinetic analysis using radiolabeled α-KG at variable concentrations of GABA and (R)-2. The data were collected and used to construct Dixon and Cornish-Bowden plots (Supporting Information). The fact that the Cornish-Bowden plot shows that all concentrations of GABA give the same rate of change of [GABA]/ν with respect to [(R)-2] indicates that (R)-2 acts as a competitive inhibitor of GABA transamination. The K_i value for (R)-2 determined from the Dixon plot is 49 µM.

The inhibition of GABA transamination by 3-F-GABA 2 was only observed in the case of the (R)-enantiomer, suggesting that the (S)-enantiomer does not bind well to the active site of GABA-AT. To verify this result, the compounds were tested as inhibitors of GABA transamination using the coupled enzyme assay described above. It emerges again that the (R)-enantiomer is a much better competitive inhibitor of GABA transamination than the (S)-enantiomer, although there appears to be some inhibition by the (S)-enantiomer in this case (Table 3). However, because of the complexity of the competing elimination reactions, these results may not be as accurate as those from the radioactive α-KG coupled assay results described above. Taken together, it appears that the (S)-enantiomer is not a proficient substrate for GABA-AT because it binds poorly to the active site of the enzyme.

Table 3.

Inhibition of GABA transamination by the enantiomers of 3-F-GABA (2) using the coupled enzyme assay. Succinic semialdehyde production via turnover of 3-F-GABA was accounted for by subtracting the rate of succinic semialdehyde production for each 3-F-GABA enantiomer from the observed rate of GABA transamination in the presence of that enantiomer.

Reaction	Rate (change in abs/min)	% activity remaining
GABA (1)	0.142	100
GABA + 1 mM (R)-2	0.012	8
GABA + 1 mM (S)-2	0.122	86

Computer modeling

Two different automated flexible docking approaches, AutoDock 3.0 (Lamarckian genetic algorithm) and FlexX (incremental construction algorithm), were employed to perform the docking calculations. The overall docking orientations of (R)-2 and (S)-2 are very similar to each other and also similar to the binding conformations of vigabatrin (3; 4-amino-5-hexenoic acid) and 4-amino-5-hexynoic acid (4) observed from X-ray crystallographic analysis.20 The PLP adducts of both (R)- and (S)- 3-F-GABA were used as the docking ligands. The docking models of the FlexX calculations are representative of the results and are shown in Figure 1.

Figure 1.

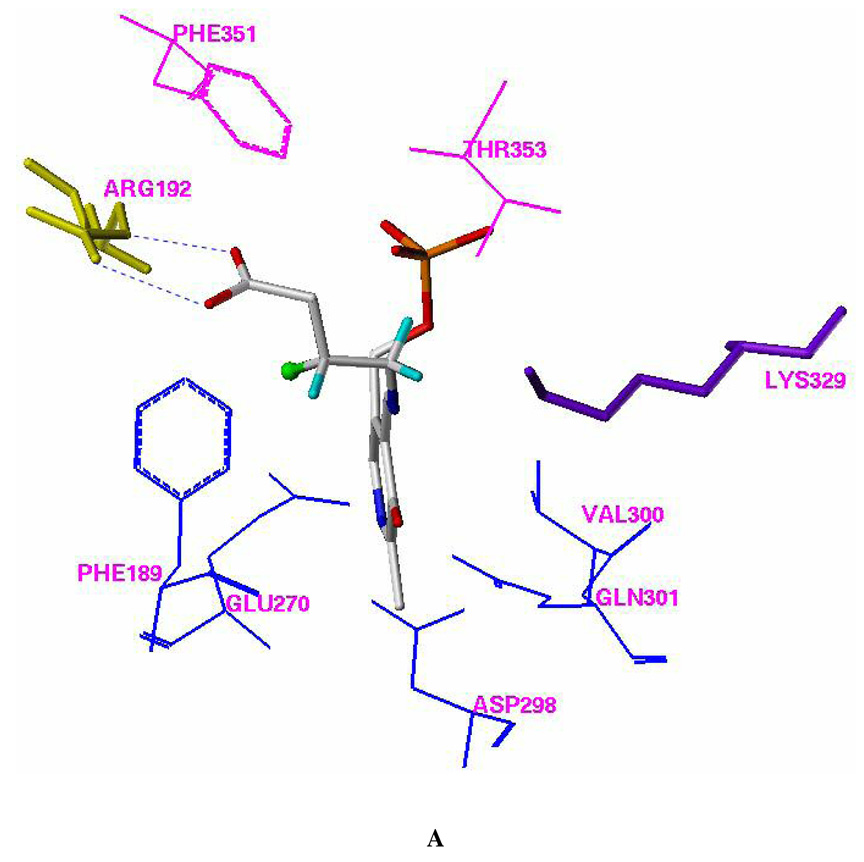
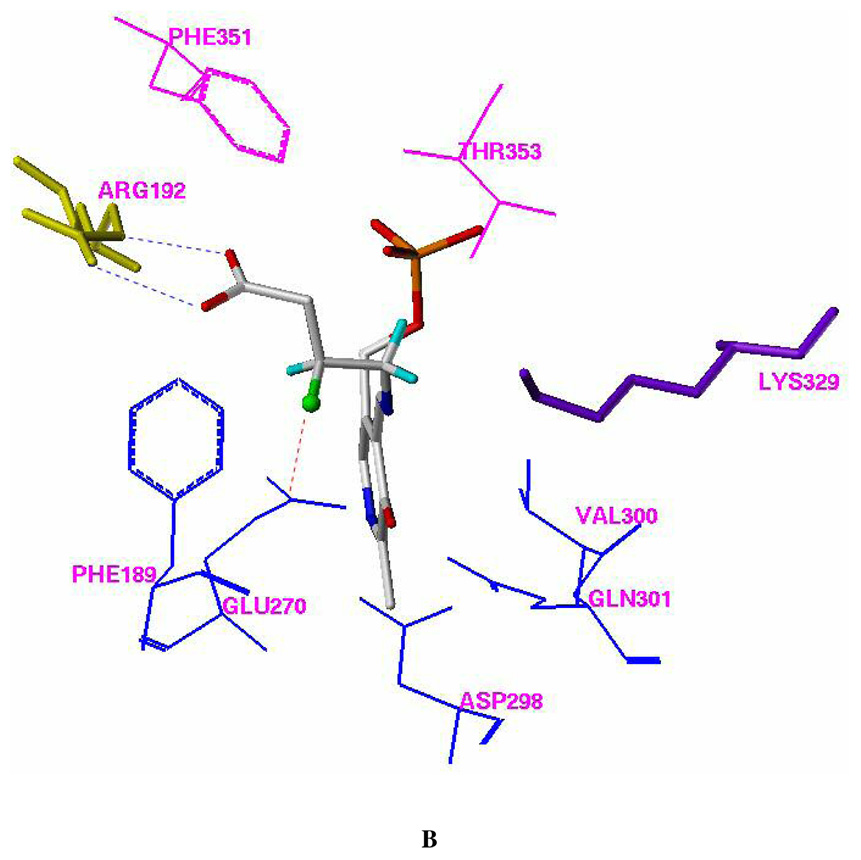
Docking models of (R)-2 (A) and (S)-2 (B) with pig liver GABA-AT (FlexX model). Residues Phe351 and Thr353, which are from the other monomer of the homodimer, are shown in magenta. All of the hydrogen atoms except those attached to C-3 and C-4 of (R)-2 and (S)-2 were omitted for clarity. The fluorine atom is presented in a ball and stick model. The putative H-bonds between Arg 492 and the carboxylic group of (R)-2 or (S)-2 are shown in blue. The putative dipole-dipole interaction (C ^δ+-F^δ−…C^δ+-O⁻) between the side chain of Glu270 and the C-F group of (S)-2 is shown in red.

The 3-fluoro substituent in (R)-2 is close to the side chain of Phe189 and forms a van der Waals contact with the phenyl ring (Figure 3A). The 3-fluoro

substituent in (S)-2 is close to the side chain of Glu270 and forms van der Waals contacts with the carboxylic acid and the methylene groups of this residue (Figure 3B). The docking interaction energies for (R)-2 and (S)-2 are similar to each other (Table 4).

Figure 3.

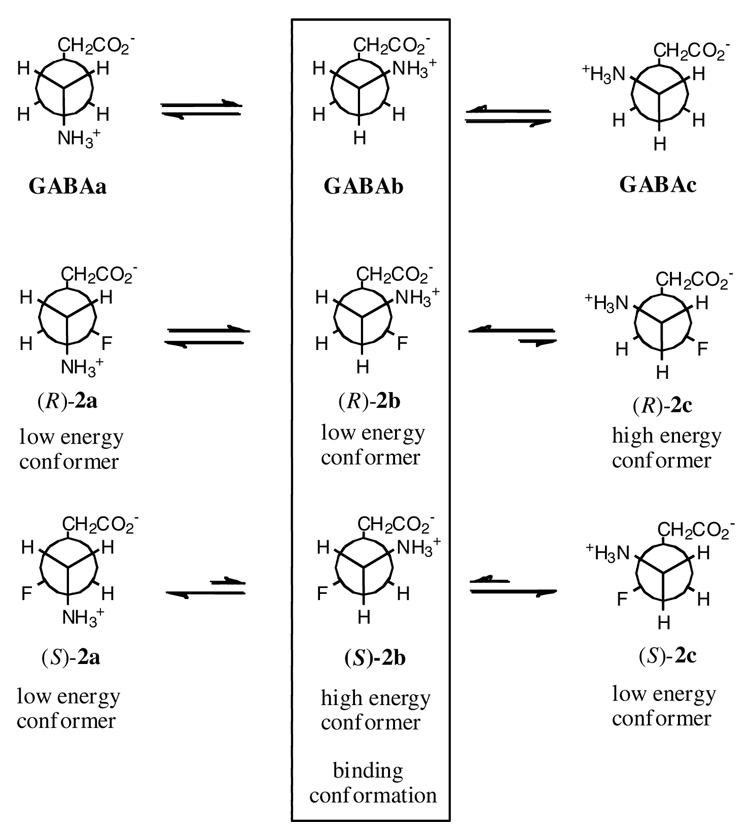
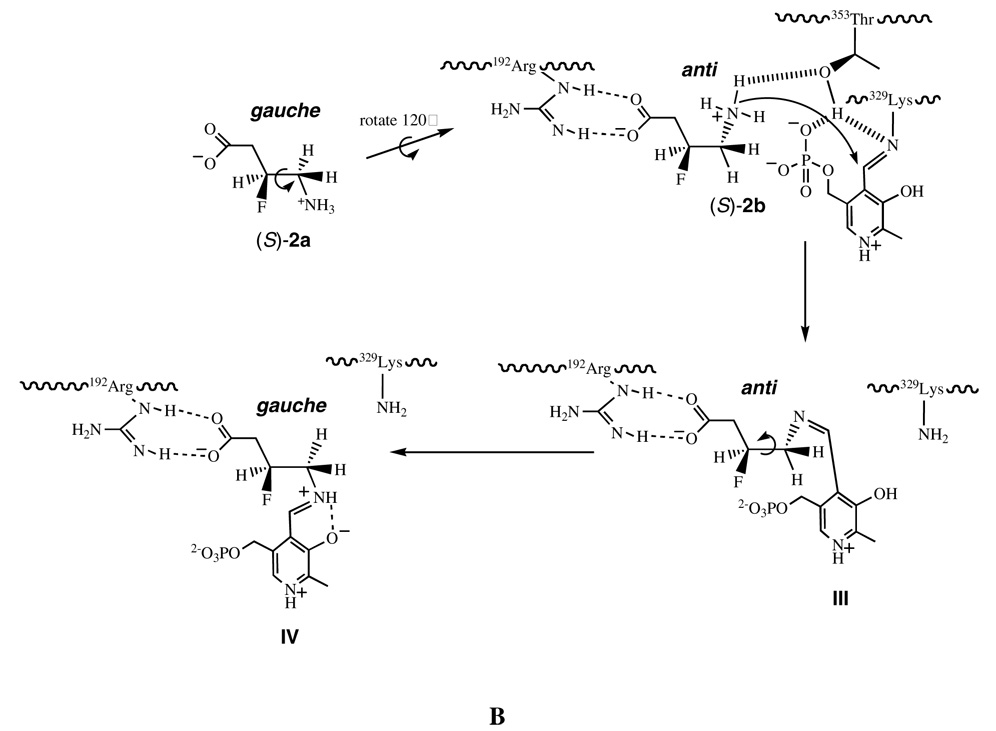
Topological description of the staggered conformations around C3–C4 and the preferred binding modes of GABA and the enantiomers (R)-2 and (S)-2 for GABA-AT. Gauche conformations of C-F and C-NH₃⁺ are low in energy, and anti conformations are high in energy. Only the GABAb conformation satisfies the experimental data from (R)-2 and (S)-2 with GABA-AT.

Table 4.

Predicted binding free energies (kcal/mol) for (R)-2- and (S)-2- PLP adducts with GABA-AT using PMF, Gold, AutoDock, ChemScore, Dock, and FlexX scoring functions.

3F-GABA-PLP adduct	PMF	Gold	E-docked	ChemScore	Dock	FlexX
(R-2)	−106.22	−291.21	−11.93	−28.88	−239.16	−41.41
(S-2)	−114.06	−293.80	−12.22	−28.88	−239.16	−40.90

Discussion

Previously, racemic 3-F-GABA (2) was found to undergo elimination of HF followed by enamine-imine tautomerization and finally hydrolysis, ultimately resulting in the formation of succinic semialdehyde, the normal product of GABA transamination by GABA-AT (31). Additionally, it was noted that this compound did not undergo oxidation to the corresponding aldehyde, as evidenced by the inability of racemic 3-F-GABA to reduce the PLP cofactor of GABA-AT (31).

The ability of enantiomers (R)-2 and (S)-2 to undergo GABA-AT catalyzed transamination was measured using a radioactive α-KG assay. If transamination occurs, the PLP is converted to PMP, which in the presence of [¹⁴C]-α-KG is converted back to PLP with concomitant conversion of the [¹⁴C]-α-KG to [¹⁴C]-glutamate. [¹⁴C]-Glutamate was not detected after incubation of either (R)-2 or (S)-2 with GABA-AT, giving no evidence for transamination and confirming our previous observation for the racemate (31).

However, either one or both of (R)-2 and (S)-2 are candidate substrates for HF elimination, because the racemate is susceptible to HF loss (31). The kinetic parameters (V_max and K_m) for racemic 3-F-GABA were determined using a coupled enzyme assay in which GABA-AT catalyzes the elimination of HF from 3-F-GABA with the ultimate formation of succinic semialdehyde. This is also the product of GABA transamination. The succinic semialdehyde is then oxidized to succinic acid in the presence of excess succinic semialdehyde dehydrogenase with concomitant reduction of NADP⁺ to NADPH. The rate of this reduction can be assessed by measuring the rate of production of NADPH as a change in UV absorption over time. The dehydrogenase and NADP⁺ cofactor are used in excess, so the rate of NADP⁺ reduction corresponds to the rate of succinic semialdehyde formation. The V_max/K_m value for the (R)-enantiomer is 18–25 times greater than that for the natural substrate GABA and 3–5 times greater than the racemate (Table 1), indicating that (R)-2 is a more efficient substrate for HF elimination than GABA is for transamination. The rate of HF elimination, as measured by the coupled assay, from the (S)-2 enantiomer was so slow that it could not be quantified accurately.

In another attempt to determine whether or not the HF elimination reaction had taken place with GABA-AT, a more sensitive assay, which measures fluoride ion release, was carried out. It was found that an accurate measurement could only be made at high enantiomer concentrations because of the instability of the enzyme, possibly as a result of the formation of HF generated by the elimination reaction. The solution became acidic at high concentrations of the enantiomers, which destroyed the enzyme, and increasing the ionic strength of the buffer interfered with the fluoride ion electrode analysis. Accordingly only one concentration of the enantiomers was used (1.0 mM), which is saturating for (R)-2. It was found that at that concentration, the (R)-enantiomer eliminated HF at a rate greater than 10 times that for the (S)-enantiomer, although the (S)-enantiomer did appear to undergo some elimination. However, because, at the concentration used, the (R)-isomer is at saturation and the (S)-isomer is not, this rate difference represents a lower limit.

The fact that (S)-2 undergoes a much slower rate of elimination than (R)-2 has several possible origins. One possibility is that the (S)-enantiomer binds to GABA-AT but then undergoes slow conversion to succinic semialdehyde (a V_max effect). Alternatively, the (S)-enantiomer may simply be less efficient at binding to the enzyme (a K_m effect). Thirdly, its poorer performance could be a combination of both of these effects. In an attempt to differentiate between these V_max and K_m effects the inhibition of GABA turnover by (R)-2 and (S)-2 was determined. Using the radioactive α-KG assay for measuring GABA turnover, it was found that (R)-2 was a good inhibitor of the enzyme; Dixon and Cornish-Bowden plots indicated competitive inhibition with a K_i value of 49 µM. The (S)-enantiomer exhibited no inhibition up to 1.0 mM concentration. Inhibition of GABA-AT using the coupled spectrophotometric assay was also explored with each enantiomer. However, the results of this experiment are complicated by the fact that (R)-2 undergoes GABA-AT catalyzed HF elimination although (S)-2 does so only poorly, and the elimination reaction with (R)-2 is more efficient than the transamination reaction with GABA. Consequently, inhibition of GABA transamination using these compounds was observed only at high concentrations (1.0 mM), as shown in Table 3, and the rate of succinic semialdehyde production from GABA is greatly inhibited by (R)-2, whereas (S)-2 shows minimal inhibition. Nonetheless, this experiment suggests that (R)-2 inhibits GABA-AT at least 10 times more effectively than (S)-2, again suggesting an improved competitive binding effect for (R)-2 over (S)-2.

Modeling of the 3-F-GABA enantiomers into the active site as PLP adducts reveals identical structures except for the orientation of the C-F bond (Figure 1). The C-F and C-N-PLP bonds, although oriented in different directions, are gauche for both enantiomers. In each case, the C-F fluorine orientation is dictated by the overall conformation of the GABA framework within the active site, which is controlled by covalent imine bond formation to the cofactor at one end, and by electrostatic and/or hydrogen bonding interactions between the GABA carboxylate and Arg-192, at the other end of the molecule. For (R)-2 the C-F bond is close to the phenyl group of Phe189 (Figure 1A), although it is difficult to argue a particular stabilizing/destabilizing interaction between the C-F bond and the phenyl ring. For (S)-2 the C-F bond forms a close contact (3.4 Å) to the carbonyl carbon of the carboxylic acid side chain of Glu270 (Figure 1B). Again it is difficult to ascribe particular significance to this interaction, although such an orientation may result in some dipole-dipole stabilization (C^δ+-F^δ−…C^δ+-O⁻; Figure 1), as has been proposed by other groups for the interactions of C-F bonds with amide carbonyls in inhibitor-receptor interactions (46 – 48) or with carboxylic acids in small-molecule crystallographic analysis (49).

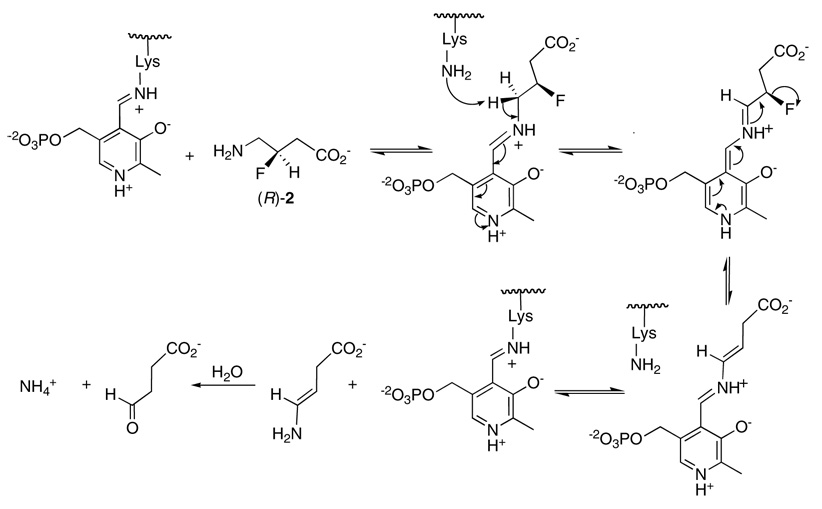
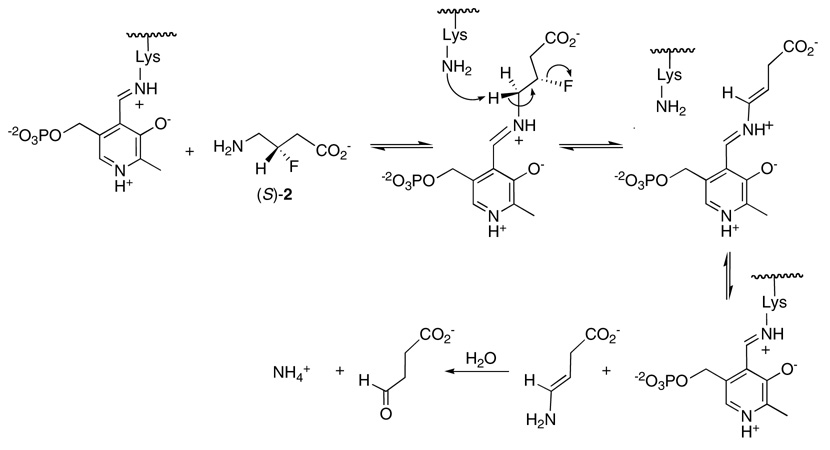
The different orientations of the C-F bond could have, however, differential consequences for the elimination of HF, particularly if the mechanism has a strict stereoelectronic requirement. There are two general elimination mechanisms that can be considered for the conversion of (R)-2 and (S)-2 into their metabolic product, succinic semialdehyde as shown in Scheme 1 and Scheme 2. These are a concerted E2, or a non-concerted E1cb type elimination. Lys329 is the candidate base for the elimination, and modelling suggests that it abstracts the (S)-γ proton from (R)-2 or (S)-2, as is known from labeling studies (50). A concerted E2 mechanism requires an antiperiplanar relationship between the eliminating H and F atoms. Combined experimental and theoretical studies by Alunni et al. (51, 52) have demonstrated that with fluoride as the leaving group, an E1cb mechanism is generally favored over an E2 mechanism, as the electron withdrawing power of the fluorine promotes β-anion stability. Looking at Scheme 1 and Scheme 2 it can be seen that substrate (R)-2 does not conform to an antiperiplanar arrangement of the eliminating substituents and can only achieve an E1cb mode of elimination, whereas substrate (S)-2 can satisfy either mechanism because the eliminating substituents are anti to each other. Given the ability of (R)-2 to undergo a more rapid elimination than (S)-2 we conclude that these eliminations are E1cb in character, most probably in both cases, and that in the case of (R)-2 there is no inherent stereoelectronic impediment to HF elimination. Thus, we conclude that the poorer performance of the (S)-enantiomer as a substrate arises from a K_m and not to a k_cat or V_max effect.

Scheme 1.

E1cb mechanism for elimination of HF from (R)-2

Scheme 2.

E2 mechanism for elimination of HF from (S)-2

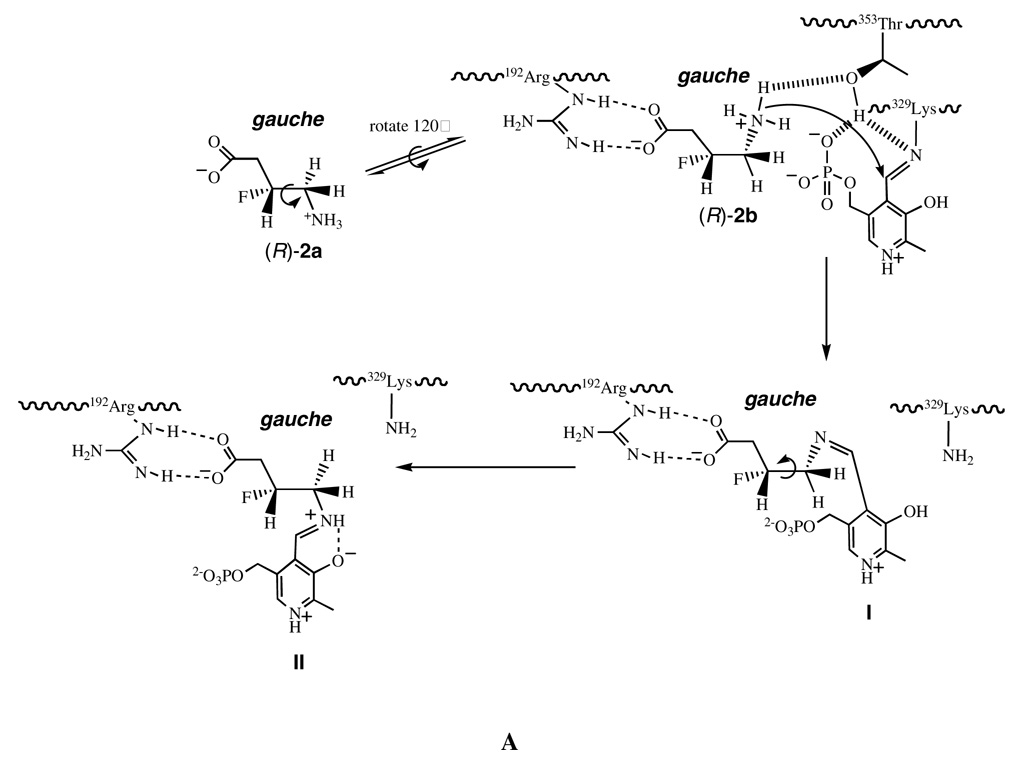
This suggests that the conformation of (R)-2 is more optimal for binding to the enzyme as a zwitterion than (S)-2. One explanation for these observations is that the GABA-AT binding process of (R)-2 or (S)-2 from its solution conformation to its bioactive conformation is different, as illustrated in Figure 2. For (R)-2, the low energy conformations in solution are probably (R)-2a or (R)-2b (Figure 2A), consistent with the solution conformation of 2 (39) and the calculated favored solution conformations of GABA (53). The C3–C4 single bond of conformer (R)-2a requires a clockwise rotation by 60° to conformer (R)-2b to allow contact between the ammonium group and the Thr353 hydroxyl group. The energy penalty in this step is relatively small as both (R)-2a and (R)-2b are low energy conformers with the C-⁺NH₃ and C-F bonds gauche with respect to each other (Figure 2A). The favored solution conformers for the (S)-enantiomer are probably (S)-2a and (S)-2c (again, so that the C-F and C-NH₃⁺ bonds are gauche); deprotonation requires a 60° rotation around C3–C4 to access conformer (S)-2b (Figure 2B). The energy penalty in going from (S)-2a or (S)-2c to conformer (S)-2b is predicted to be high (~4.0–5.0 kcal mol⁻¹) because the C-⁺NH₃ and C-F bonds are required to adopt an anti conformation in (S)-2b; therefore, the conformational equilibrium is unfavorable for the generation of (S)-2b. However, the substrate-binding site of GABA-AT requires (R)-2 and (S)-2 to adopt specific conformers (R)-2b and (S)-2b, respectively, for their catalytic reaction. Therefore, conformer (R)-2b is in a relatively high concentration in solution, whereas conformer (S)-2b is in a relatively low concentration, and conversion from the solution conformation to the bioactive conformation is a lower energy process for (R)-2 than for (S)-2. This difference in the concentration of active conformers may account for the difference in the kinetics for the two isomers.

Figure 2.

Illustration of the dynamic binding process of (R)-2 (A) and (S)-2 (B) from their solution conformations to their bioactive conformations.

After entering the substrate-binding site of GABA-AT a cascade of reactions will follow initiated by deprotonation, followed by a Burgi-Dunitz (54) trajectory attack of the resultant amine on the Lys329-PLP imine, to form the PLP-ligand adduct. As implied in Figure 1 and shown in Figure 2, amine attack is required at the top side of the imine. Based on the crystal structure of the active site, a likely candidate for deprotonation of the substrate ammonium ion is Thr353 (PDB code 1OHV; SYBYL Molecular Modeling Package, version 6.9, Tripos; St. Louis, MO, 2002. http://www.tripos.com), but a threonine hydroxyl group is not sufficiently basic for ammonium ion deprotonation. However, the distance between the hydroxyl group oxygen of Thr353 and the phosphate group of the PLP is only 2.6Å (see Supporting Information Figure 4); the PLP phosphate may initiate the deprotonation of Thr353. Another possibility is Lys329, bound as a Schiff base to the PLP, which is 3.8Å from the hydroxyl group oxygen of Thr353, close enough to assist in the initial deprotonation of Thr353, which could, in turn, deprotonate the ammonium ion of (R)- or (S)-2. A catalytic diad between the active site threonine and lysine residues (in this case a lysine bound as a Schiff base, which needs to be protonated for activation) has been proposed for urate oxidase (43).

Subsequent to the formation of the initial PLP-ligand adduct (I or III, Figure 2A or 2B, respectively), rotation around C3–C4 will generate the bound conformation predicted from the docking experiments (II or IV), most probably to accommodate the cofactor-substrate adduct, a conformation of the GABA framework that does not necessarily reflect the initial binding conformation. Therefore this study with the 3-F-GABA enantiomers can be used to illuminate the preferred conformation of GABA when binding to GABA-AT. Figure 3 illustrates the three staggered conformations (a, b and c) for GABA (1) and 3-F-GABA (2) by rotation around the C3–C4 bond. Conformers b and c are enantiomeric. The high energy conformers (R)-2c and (S)-2b have the C-F and C-NH₃⁺ bonds anti to each other; the remaining low energy conformers have these bonds aligned gauche. The experimentally observed difference in binding of the (R)-2 and (S)-2 enantiomers of 3-F-GABA to GABA-AT suggests that the extended binding conformation, GABAa, is not relevant, as both enantiomers should be able to accommodate this conformer equally well, but they do not. The GABAb conformer emerges as the most likely approximation of the binding conformer because the gauche C-F/C-⁺NH₃ relationship in the (R)-2b conformer is stabilizing, whereas the anti C-F/C-⁺NH₃ relationship in (S)-2b is destabilizing, consistent with the enhanced activity of (R)-2 over (S)-2. If the GABAc conformer were relevant, then the reverse of the experimental outcomes for (R)-2 and (S)-2 would be predicted.

As the major inhibitory neurotransmitter in the mammalian central nervous system (CNS), GABA plays a vital role in maintaining normal neuronal activity by regulating the equilibrium between neuronal excitation and inhibition. It is clear that knowledge of the bioactive conformation of GABA will facilitate the design and development of drugs targeting GABA receptors. GABA is known to exist as a zwitterion in aqueous solution (54, 55), and it has been concluded (54, 56 – 60) that the extended zwitterion conformers are more stable in solution than the folded zwitterions; however, this does not necessarily reflect the biologically active conformation, which may also vary among receptor types. In fact, as a substrate of GABA-AT, it is impossible to determine the real bioactive conformation of GABA and/or its dynamic binding process to its receptor by biophysical approaches such as X-ray crystallography or multiple NMR spectroscopy because of rapid catalytic turnover upon binding to the enzyme. This study illustrates that 3-F-GABA enantiomers (R)-2 and (S)-2 can provide insights into such binding modes.

Conclusions

Neither (R)-2- or (S)-2- 3-F-GABA is a substrate for transamination by GABA-AT. However, enantiomer (R)-2 is an excellent substrate for GABA-AT catalyzed elimination of HF, whereas enantiomer (S)-2 is poor at best. Furthermore, the (R)-2 enantiomer binds at least 10 times better than (S)-2, as evidenced by their relative K_m values and their respective abilities to inhibit GABA transamination. The fluorine atom is only slightly larger than hydrogen, and it is not anticipated to introduce a significant steric perturbation on binding to the enzyme. However, it has important electronic consequences and results in a mechanistic deviation, giving an exclusive elimination reaction. In this study the C-F bond emerges as a novel conformational probe. The strong tendency for the C-F bond to lie gauche rather than anti to the C-NH₃⁺ bond in enantiomers (R)-2 and (S)-2 and to accommodate a stabilizing charge-dipole interaction (32) places a conformational bias on both (R)-2 and (S)-2 in solution. This study reveals that GABA has a preferred binding mode (GABAb, Figure 3) when binding to GABA-AT, and this emerges because only (R)-2, and not (S)-2, can easily access this binding mode in solution. Using the C-F bond as a conformational probe in this way and comparing the efficacy of (R)- and (S)-2 with its target protein, opens up prospects for further conformational studies of GABA with various GABA receptor types.

Supplementary Material

1File002. Supporting Information Available.

Plots of the increase in [F⁻] (as determined from the electric potential across a calibrated electrode) as a function of time for (R)-2 and (S)-2; Dixon and Cornish-Bowden plots for the inhibition of GABA-AT by (R)-2; crystal structure of active site of GABA-AT to show distances of various groups from Thr353. This material is available free of charge via the Internet at http://pubs.acs.org.turing.library.northwestern.edu

Abbreviations

GABA

γ-aminobutyric acid

GABA-AT

γ-aminobutyric acid aminotransferase

α-KG

α-ketoglutarate

PLP

pyridoxal 5’-phosphate

PMP

pyridoxamine 5’-phosphate

3-F-GABA

4-amino-3-fluorobutanoic acid