Abstract
Study Design
In vitro biomechanical study on rat caudal motion segments to evaluate association between compressive loading and water content under static and cyclic conditions.
Objective
To test hypotheses: 1) there is no difference in height loss and fluid (volume) loss of discs loaded in compression under cyclic (0.15–1.0 MPa) and static conditions with the same root-mean-square (RMS) magnitudes (0.575 MPa); and 2) after initial disc bulge, tissue water loss is directly proportional to height loss under static loading.
Summary of Background Data
Disc degeneration affects water content, elastic and viscoelastic behaviors. There is limited understanding of the association between transient water loss and viscoelastic creep in a controlled in vitro environment where inferences may be made regarding mechanisms of viscoelasticity.
Methods
A total of 126 caudal motion segments from 21 Wistar rats were tested in compression using 1 of 6 protocols: Static loading at 1.0 MPa for 9, 90, and 900 minutes, Cyclic loading at 0.15 to 1.0 MPa/1 Hz for 90 minutes, Mid-Static loading at 0.575 MPa for 90 minutes, and control. Water content was then measured in anulus and nucleus regions.
Results
Percent water loss was significantly greater in nucleus than anulus regions, suggesting some water redistribution, with average values under 1 MPa static loading of 23.0% and 14.9% after 90 minutes and 26.9% and 17.6% after 900 minutes, respectively. Cyclic loading resulted in significantly greater height loss (0.506 ± 0.108 mm) than static loading with the same RMS value (0.402 ± 0.096 mm), but not significantly less than static loading at peak value (0.539 ± 0.122 mm). Significant and strong correlations were found between percent water loss and disc height loss, suggesting water was lost through volume decrease.
Conclusion
Peak magnitude of cyclic compression and not RMS value was most important in determining height change and water loss, likely due to differences between disc creep and recovery rates. Water redistribution from nucleus to anulus occurred under loading consistent with an initial elastic compression (and associated disc bulge) followed by a reduction in disc volume over time.
Keywords: intervertebral disc, biomechanics, motion segment, axial compression, water content, hydration, viscoelastic, dynamic loading
The intervertebral disc plays the essential biomechanical roles of supporting load and permitting motion in the spine.1 The disc is a heterogeneous structure composed of a central nucleus pulposus surrounded by a highly organized fiber-reinforced anulus fibrosus. The nucleus pulposus is a hydrated gelatinous tissue composed of negatively charged glycosaminoglycans, collagens, and noncollagenous proteins.2,3 The glycosaminoglycan-associated negative charges in the nucleus pulposus produce a swelling force.4,5 Degeneration of the disc results in a loss of both water and proteoglycan contents2,3 as well as alterations in its elastic and viscoelastic behaviors.1,6
The hydration of the disc varies according to the condition of loading; fluid is expelled when the disc is loaded over its baseline swelling pressure and absorbed when it is unloaded.7–10 Several in vivo magnetic resonance imaging studies have indicated load-induced changes in the water content of the disc.11–14 Loading conditions on the motion segment affect the degree of hydration of the intervertebral disc and, in particular of the nucleus pulposus, under loading, and alterations in hydration subsequently also affect the elastic and viscoelastic mechanical behaviors of the intervertebral disc.1,7,15–17
There is a limited understanding of the time-dependent association between water loss and viscoelastic creep in the disc, and this requires additional experiments in a controlled in vitro environment that permits inferences regarding volume loss and mechanisms of viscoelasticity. There are very few studies on effects of cyclic loading on fundamental motion segment creep and hydration and improved understanding of the motion segment behaviors under cyclic or repetitive loading conditions is a priority for defining safe loading regimens. A clear understanding of the unique interaction between the solid porous matrix and the fluid can only be obtained using appropriate analytical models along with in vitro and in vivo experimental methods.18
The purpose of this study is to investigate the effects of variations in the load duration, load magnitude, and loading mode (i.e., cyclic or static) on rat caudal motion segment height and water loss in the nucleus and anulus. These data have implications for mechanobiology studies, and are important for improved understanding of mechanisms of viscoelasticity. It was hypothesized that:
There is no difference in height loss and fluid (volume) loss of motion segments loaded in compression under cyclic (0.15–1.0 MPa) and static conditions with the same time average magnitudes (0.57 MPa).
After initial disc bulge, tissue water loss is directly proportional to height loss under static loading.
Materials and Methods
A total of 126 caudal motion segments from 21 16-week-old female Wistar rats were used in this experiment. Rats were obtained within a half hour of being killed for another purpose, which would not impact the results of the present study. Skin and soft tissues were removed from the tails, and 6 adjacent motion segments were harvested using methods similar to those previously described.19 Briefly, the vertebral bodies of each motion segment were potted in aluminum tubes using cyanoacrylate. Potted motion segments were then frozen in liquid nitrogen, wrapped in phosphate-buffered saline soaked gauze, double-wrapped in plastic, and stored at −20°C for 3 to 7 days until testing.
Specimens underwent a force-controlled test protocol using an axial testing machine (Enduratec ELF-3200, Bose Corp., Minnetonka, MN) and custom grips previously described (Figure 1).19 Motion segments were systematically assigned to 1 of 6 groups in a manner that would average out any potential effects of disc level on measured parameters. Before applying the main loading condition, a preconditioning load (static, 0.15 MPa for 900 seconds) was applied to each motion segment that also served to restore any possible loss of water content due to specimen preparation and freezing. This resting stress of 0.15 MPa was chosen based on the resting stress obtained in an in vivo study.20 After preconditioning loading, each specimen was subjected to its assigned main loading protocol, and force, displacement, and time data were stored for subsequent analysis. The height loss of the disc was calculated as difference between the displacement at the end of the loading protocol and the displacement at the end of the preloading period.
Figure 1.
a, Experimental loading apparatus with custom specimen grips, fluid chamber, and 2 axis positioning stage. b, Detail of motion segment and clamping system.
All specimens underwent 1 of 6 loading protocols (Table 1). To test hypothesis 1 on the effects of the different loading modes on the motion segment creep and water content, the 3 90-minute duration loading groups were compared: Static II, Cyclic, and Midstatic. The Static II and Midstatic groups had magnitudes equal to the peak and root mean square (RMS) values of the Cyclic loading group, respectively. To test hypothesis 2 on the effects of load duration on motion segment creep and water content, 4 loading groups were compared: Static I, Static II, Static III, and Control.
Table 1.
Loading Groups
| Group | Control | Static I | Static II | Static III | Cyclic | Mid-Static |
|---|---|---|---|---|---|---|
| Preload | 0.15 MPa | 0.15 MPa | 0.15 MPa | 0.15 MPa | 0.15 MPa | 0.15 MPa |
| 15 min | 15 min | 15 min | 15 min | 15 min | 15 min | |
| Load | 1.0 MPa | 1.0 MPa | 1.0 MPa | 0.15–1.0 MPa | 1.0 MPa | |
| 9 min | 90 min | 900 min | 90 min | 9 min |
Each motion segment was subjected to a preload of 0.15 MPa static loading for 15 minutes and then assigned to one of the loading groups.
After loading, samples were removed from the phosphate-buffered saline bath, surface dried, and immediately frozen using liquid nitrogen in order to minimize loss of hydration or the gelatinous nucleus tissue during subsequent handling. Each frozen tail disc was separated into nucleus pulposus and anulus fibrosus section using a scalpel and biopsy punches (2.0 and 4.0 mm diameter, Miltex Instrument Co., Inc., Lake Success, NY). Tissue sections were immediately placed in preweighed vials and wet tissue weights were measured. Specimens were subsequently lyophilized for 24 hours to obtain dry tissue weights. The percent water content (%H2O) of each anulus and nucleus section was calculated from the wet (Weightwet) and dry (Weightdry) weight of each tissue section (See equation below). The percent loss in water due to mechanical loading (%loss) was calculated as the relative difference in %H2O between the loaded groups (%H2Oloaded) and the control group (%H2Ocontrol) (See equation below).
In order to provide an average time history of each group, the creep behavior of the motion segment was fitted using the stretched exponential model, as previously described19
where d0 and d∞ are the initial and equilibrium displacements, and τ and β are the time constant and stretch parameter, respectively. The value (d∞ − d0) corresponds to the predicted value for equilibrium height loss, τ is a measure of the time it takes to reach equilibrium, and β (0 < β ≤ 1) describes the relative complexity of the mechanical behavior where β =1 corresponds to behavior that can be described by a single exponential. The curve-fit was performed using code written in MATLAB (Mathworks, Natick, MA).
All results were analyzed using a repeated measures ANOVA with Fisher PLSD used as a post hoc test to compare each group and P values less than 0.05 considered significant. Correlations between motion segment height loss and % water loss in the anulus and nucleus were calculated. All statistical analyses were performed with Statview software (SAS Institute, Cary, NC).
Results
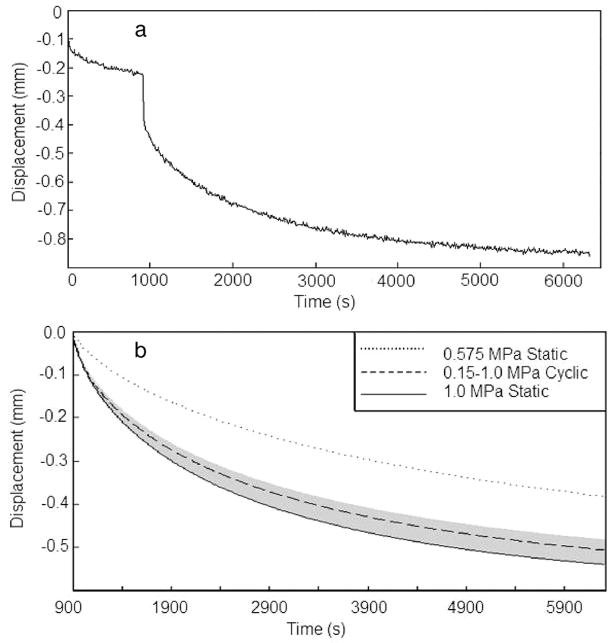
The results from 3 of the 126 motion segments tested in this study were omitted because of technical errors in the experiments. Visible damage was not detected in any remaining specimens after loading. All motion segments exhibited viscoelastic behavior that was well described by the stretched-exponential model (Figure 2, model parameters in Table 2). Both motion segment height loss (Figure 3) and water loss (Figure 4) were time-dependent until equilibrium level was achieved under static compressive loading within 900 minutes.
Figure 2.
Typical displacement data from creep experiment (a) and average stretched exponential fits (b). Shaded area in b bounds the average peak and valley displacements of the cyclic group.
Table 2.
Stretched Exponential Curve Fit Parameters
| Group | d∞ − d0 | τ | β |
|---|---|---|---|
| Static I | 0.4890 ± 0.1134 | 821 ± 334 | 0.7657 ± 0.0601 |
| Static II | 0.6145 ± 0.1532 | 1755 ± 591 | 0.6882 ± 0.0573 |
| Static III | 0.7712 ± 0.1961 | 1834 ± 928 | 0.5552 ± 0.1262 |
| Cyclic | 0.5849 ± 0.1608 | 1849 ± 599 | 0.6903 ± 0.1130 |
| Mid-static | 0.5591 ± 0.2053 | 4367 ± 5355 | 0.7139 ± 0.0790 |
Values are mean ± SD.
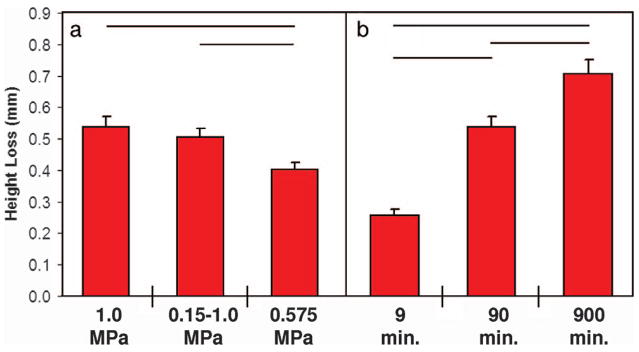
Figure 3.
Height loss (mean ± SEM) in the motion segment calculated as the difference in displacement from the end of preloading period to the end of the testing period for (a) groups of 90 minutes duration and (b) groups of 1.0 MPa magnitude. Bars denote significant differences (P < 0.05).
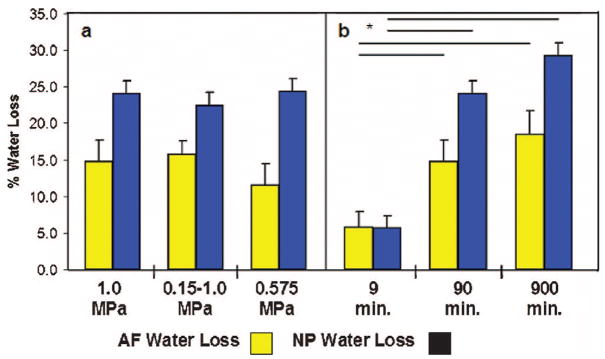
Figure 4.
The % water loss (mean ± SEM) relative to control for (a) groups of 90 minutes duration and (b) groups of 1.0 MPa magnitude. Bars denote significant differences (P < 0.05).
Among the 90-minute duration groups (Figure 3a), Cyclic loading resulted in height loss that was significantly greater than Mid-Static (P < 0.01), but not significantly less than Static II loading at 1.0 MPa (P > 0.2). The model results demonstrate this same trend for the for the entire time period with average displacement for Cyclic loading being higher than the Mid-Static condition (Figure 2b). In addition, peak displacement of the cyclic tests were nearly equal to the creep displacement of the 1.0 MPa static condition. The experimentally determined decrease in motion segment height with time was significant between the three 1.0 MPa static loading groups (Figure 3b) (P < 0.01).
Nucleus and anulus water contents for the control group averaged 83.5% and 70.4%, respectively. For the loaded groups, average nucleus and anulus water contents ranged from 60.8% to 78.8% and 58.3% to 66.4%, respectively. There were no significant differences in water loss between the three 90-minute groups (Figure 4a), but Cyclic loading resulted in greater anulus fibrous water loss than Mid-Static loading (P = 0.03). Water content decreased over time under compressive static loading at 1.0 MPa, although groups having ≥90 minutes loading duration were not significantly different. Relative water loss was significantly larger for nucleus than anulus tissue for loading durations of ≥90 minutes (Figure 4b).
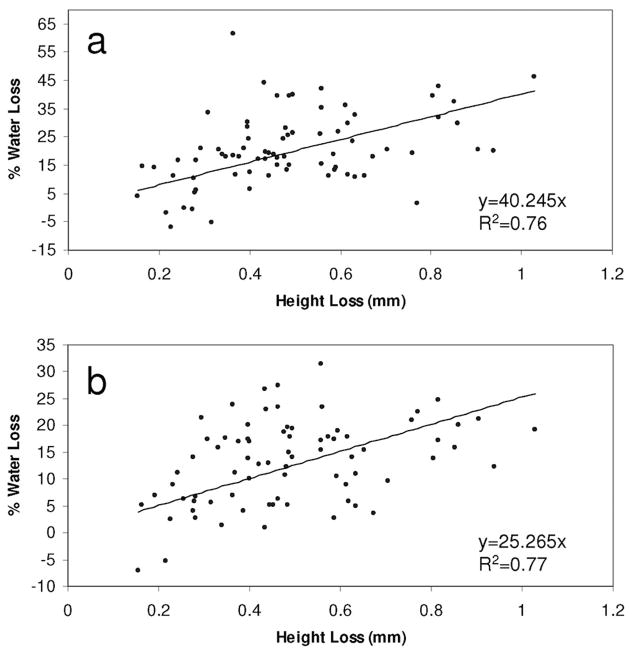
The water content of anulus and nucleus regions both monotonically decreased with increasing creep deformation, and the change in motion segment height significantly correlated with water loss in the anulus and nucleus (Figure 5).
Figure 5.
Correlations of motion segment height loss with % water loss (relative to control) in the (a) nucleus and (b) anulus regions.
Discussion
This study investigated how the compressive loading magnitude, mode (static vs. cyclic), and duration (9–900 minutes) affects rat intervertebral motion segment creep behaviors and water content. Rat caudal motion segments were subjected to 6 distinct loading protocols, and creep displacement and water contents were measured in order to test 2 hypotheses concerning their response to static versus cyclic loading.
Contrary to our first hypothesis, cyclic loading resulted in a loss in motion segment height and anulus fibrous water content that was similar to static loading at 1 MPa but significantly greater than static loading at the root mean square value (0.575 MPa, Mid-Static group). Consequently, the most important finding of this study was that peak value of cyclic compressive loading at a frequency of 1 Hz (and not the time average magnitude) was most important in determining height change and water loss. We infer that this finding is associated with differences in creep and recovery rates of the disc, since time constants previously reported for recovery are substantially longer than for creep time, as reported previously for rat caudal motion segments.19
In agreement with our second hypothesis, a significant correlation and nearly linear relationships between motion segment height loss and water loss (Figure 5, R2 = 0.76 and 0.77 for nucleus and anulus regions, respectively) suggested that creep was the result of volume change (water loss). Interestingly, more water was lost relative to the height change in the nucleus than in the anulus, suggesting a redistribution of water, but the relative loss was only significant for load durations of ≥90 minutes. The strong correlations between creep deformation and water loss in anulus and nucleus regions along with the apparent linearity of the relationships suggest that volume change is at least partly responsible for creep in compression, especially because it is expected that the time constants would be different for intrinsic and flow-dependent viscoelasticity. We therefore conclude that some water redistribution occurred under compressive load but that water loss after our first measurement at 9 minutes was consistent with the findings of an initial elastic compression (and associated disc bulge) followed by a reduction in disc volume with time.
It is generally accepted that the balance between external load, osmotic pressure, and elastic stiffness control the fluid content of the intervertebral disc.5,21 Fluid exchange may also play an important role in transport of large solutes in the intervertebral disc22,23 and disc water content is known to affect whole disc mechanical behaviors and failure mechanisms.16,24 All specimens were frozen before testing to improve quality control and uniformity during all testing and analysis procedures. Under a given compressive load, the equilibrium hydration of a bathed disc was reported to be independent of its hydration history.25 Because measuring hydration changes in response to loading was an essential feature in this study, our methods included an equilibration period in a fluid bath where the specimen could rehydrate under a consistent and physiologically relevant preload. The effects of freezing on intervertebral discs has been the subject of several published studies, and the literature demonstrates there is no effect of freezing on stiffness, creep, hysteresis, and water content when such methods are used.25–29
The linear association between motion segment height loss and water loss suggests that, at long time scales, creep of the intervertebral disc was associated with volume changes and not radial disc bulging. This is in direct agreement with magnetic resonance imaging measurements reporting relatively small amounts of radial bulging of the outer layer of the anulus fibrosus, indicating that the majority of volume loss was associated with loss in disc height.30,31 However, in vitro testing on human cadaveric discs under similar relative compression loads (i.e., force normalized by cross-sectional area) resulted in a lower loss of hydration (18% loss) and less relative creep (~2 mm) relative to human disc height21 than in the present study, which is to be expected because of the relatively large “toe-region” reported for caudal motion segments as compared with lumbar regions.32 The finding of greater water loss in the nucleus than the anulus is generally consistent with the steady state fluid shift reported under axial compressive loading at long times in the magnetic resonance imaging study by Kusaka et al,31 although some differences were present for transient fluid patterns. These differences may be associated with T1 times being affected by more factors than water content alone as previously reported,33 or with differences in time constants for bovine and rat caudal discs.
Rat caudal motion segments were used in this study because the geometric simplicity and lack of sagittal curvature allowed a more direct association between loading conditions and disc hydration in order to test the specific hypotheses. Differences in size and loading conditions of rat caudal models relative to the human spine are a limitation, yet there is enough relevance to the model to allow some general applicability of the findings. For example, caudal motion segments have similar compressive and torsional stiffness in the linear region as human lumbar motion segments once normalized for geometry.32 Furthermore, while caudal motion segments are not weight-bearing, they have resting stresses20 that are similar to values in lumbar disc levels (in both rat and human). Finally, this study provides in vitro mechanical and water content data that may be used for comparison with the growing numbers of in vivo and organ culture studies using rat lumbar and caudal models.6,7,10,12,13,15–17,19,27,29 A quantitative association of relative contributions of disc bulging and volume loss would require a 3-dimensional multiphasic finite element model with intrinsic solid phase viscoelasticity, which is beyond the scope of this manuscript, although some similar models on human lumbar disc exist.34
The quantitative demonstration that cyclic loading amplitude is most important in determining the creep behaviors of caudal motion segments, while needing validation on a human lumbar model, has important implications in the definition of safe loading protocols for the disc. This finding also has important implications for mechanobiology studies of the disc that apply controlled mechanical loading conditions to caudal and other intervertebral discs using animal models and organ culture. Results provide a quantitative demonstration that water redistribution and volume change occur under compressive loading in the rat caudal model.
Key Points
This study investigated how compressive loading magnitude, mode (static vs. cyclic) and duration (9–900 minutes) affected motion segment creep behaviors and water content using a rat tail model.
The amplitude of cyclic compressive loading (at 1 Hz frequency), and not the time average magnitude, was most important in determining height change and water loss. This finding was likely due to differences between disc creep and recovery rates and has implications in the definition of safe loading protocols for the disc.
Under compressive loading, water redistribution (from nucleus to anulus) and water loss occurred in the disc.
The correlation between height loss and water loss was consistent with an initial elastic compression (and associated disc bulge) followed by a reduction in disc volume over time.
Acknowledgments
Supported by National Institutes of Health Grant Nos. R01AR051146 and R01AR049370.
Federal and Institutional funds were received in support of this work.
Footnotes
The manuscript submitted does not contain information about medical device(s)/drug(s).
No benefits in any form have been or will be received from a commercial party related directly or indirectly to the subject of this manuscript.
References
- 1.Adams MA, Dolan P. Spine biomechanics. J Biomech. 2005;38:1972–83. doi: 10.1016/j.jbiomech.2005.03.028. [DOI] [PubMed] [Google Scholar]
- 2.Antoniou J, Steffen T, Nelson F, et al. The human lumbar intervertebral disc: evidence for changes in the biosynthesis and denaturation of the extracellular matrix with growth, maturation, ageing, and degeneration. J Clin Invest. 1996;98:996–1003. doi: 10.1172/JCI118884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Roughley PJ. Biology of intervertebral disc aging and degeneration: involvement of the extracellular matrix. Spine. 2004;29:2691–9. doi: 10.1097/01.brs.0000146101.53784.b1. [DOI] [PubMed] [Google Scholar]
- 4.Nachemson A, Morris JM. In vivo measurements of intradiscal pressure: discometry, a method for the determination of pressure in the lower lumbar discs. J Bone Joint Surg Am. 1964;46:1077–92. [PubMed] [Google Scholar]
- 5.Urban JP, McMullin JF. Swelling pressure of the lumbar intervertebral discs: influence of age, spinal level, composition, and degeneration. Spine. 1988;13:179–87. doi: 10.1097/00007632-198802000-00009. [DOI] [PubMed] [Google Scholar]
- 6.Stokes IA, Iatridis JC. Mechanical conditions that accelerate intervertebral disc degeneration: overload versus immobilization. Spine. 2004;29:2724–32. doi: 10.1097/01.brs.0000146049.52152.da. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Adams MA, Hutton WC. The effect of posture on the fluid content of lumbar intervertebral discs. Spine. 1983;8:665–71. doi: 10.1097/00007632-198309000-00013. [DOI] [PubMed] [Google Scholar]
- 8.Iatridis JC, Laible JP, Krag MH. Influence of fixed charge density magnitude and distribution on the intervertebral disc: applications of a poroelastic and chemical electric (PEACE) model. J Biomech Eng. 2003;125:12–24. doi: 10.1115/1.1537190. [DOI] [PubMed] [Google Scholar]
- 9.Natarajan RN, Williams JR, Andersson GB. Modeling changes in intervertebral disc mechanics with degeneration. J Bone Joint Surg Am. 2006;88(suppl 2):36–40. doi: 10.2106/JBJS.F.00002. [DOI] [PubMed] [Google Scholar]
- 10.Urban JP, Maroudas A. Swelling of the intervertebral disc in vitro. Connect Tissue Res. 1981;9:1–10. doi: 10.3109/03008208109160234. [DOI] [PubMed] [Google Scholar]
- 11.Boos N, Wallin A, Gbedegbegnon T, et al. Quantitative MR imaging of lumbar intervertebral disks and vertebral bodies: influence of diurnal water content variations. Radiology. 1993;188:351–4. doi: 10.1148/radiology.188.2.8327677. [DOI] [PubMed] [Google Scholar]
- 12.Malko JA, Hutton WC, Fajman WA. An in vivo magnetic resonance imaging study of changes in the volume (and fluid content) of the lumbar intervertebral discs during a simulated diurnal load cycle. Spine. 1999;24:1015–22. doi: 10.1097/00007632-199905150-00016. [DOI] [PubMed] [Google Scholar]
- 13.Malko JA, Hutton WC, Fajman WA. An in vivo MRI study of the changes in volume (and fluid content) of the lumbar intervertebral disc after overnight bed rest and during an 8-hour walking protocol. J Spinal Disord Tech. 2002;15:157–63. doi: 10.1097/00024720-200204000-00012. [DOI] [PubMed] [Google Scholar]
- 14.Roberts N, Hogg D, Whitehouse GH, et al. Quantitative analysis of diurnal variation in volume and water content of lumbar intervertebral discs. Clin Anat. 1998;11:1–8. doi: 10.1002/(SICI)1098-2353(1998)11:1<1::AID-CA1>3.0.CO;2-Z. [DOI] [PubMed] [Google Scholar]
- 15.Johannessen W, Vresilovic EJ, Wright AC, et al. Intervertebral disc mechanics are restored following cyclic loading and unloaded recovery. Ann Biomed Eng. 2004;32:70–6. doi: 10.1023/b:abme.0000007792.19071.8c. [DOI] [PubMed] [Google Scholar]
- 16.Perie DS, Maclean JJ, Owen JP, et al. Correlating material properties with tissue composition in enzymatically digested bovine annulus fibrosus and nucleus pulposus tissue. Ann Biomed Eng. 2006;34:769–77. doi: 10.1007/s10439-006-9091-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Yao H, Justiz MA, Flagler D, et al. Effects of swelling pressure and hydraulic permeability on dynamic compressive behavior of lumbar annulus fibrosus. Ann Biomed Eng. 2002;30:1234–41. doi: 10.1114/1.1523920. [DOI] [PubMed] [Google Scholar]
- 18.Natarajan RN, Williams JR, Andersson GB. Recent advances in analytical modeling of lumbar disc degeneration. Spine. 2004;29:2733–41. doi: 10.1097/01.brs.0000146471.59052.e6. [DOI] [PubMed] [Google Scholar]
- 19.Maclean JJ, Owen JP, Iatridis JC. Role of endplates in contributing to compression behaviors of motion segments and intervertebral discs. J Biomech. 2006;40:55–63. doi: 10.1016/j.jbiomech.2005.11.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.MacLean JJ, Lee CR, Alini M, et al. The effects of short-term load duration on anabolic and catabolic gene expression in the rat tail intervertebral disc. J Orthop Res. 2005;23:1120–7. doi: 10.1016/j.orthres.2005.01.020. [DOI] [PubMed] [Google Scholar]
- 21.McMillan DW, Garbutt G, Adams MA. Effect of sustained loading on the water content of intervertebral discs: implications for disc metabolism. Ann Rheum Dis. 1996;55:880–7. doi: 10.1136/ard.55.12.880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ferguson SJ, Ito K, Nolte LP. Fluid flow and convective transport of solutes within the intervertebral disc. J Biomech. 2004;37:213–21. doi: 10.1016/s0021-9290(03)00250-1. [DOI] [PubMed] [Google Scholar]
- 23.Urban JP, Smith S, Fairbank JC. Nutrition of the intervertebral disc. Spine. 2004;29:2700–9. doi: 10.1097/01.brs.0000146499.97948.52. [DOI] [PubMed] [Google Scholar]
- 24.Race A, Broom ND, Robertson P. Effect of loading rate and hydration on the mechanical properties of the disc. Spine. 2000;25:662–9. doi: 10.1097/00007632-200003150-00003. [DOI] [PubMed] [Google Scholar]
- 25.Pflaster DS, Krag MH, Johnson CC, et al. Effect of test environment on intervertebral disc hydration. Spine. 1997;22:133–9. doi: 10.1097/00007632-199701150-00003. [DOI] [PubMed] [Google Scholar]
- 26.Smeathers JE, Joanes DN. Dynamic compressive properties of human lumbar intervertebral joints: a comparison between fresh and thawed specimens. J Biomech. 1988;21:425–33. doi: 10.1016/0021-9290(88)90148-0. [DOI] [PubMed] [Google Scholar]
- 27.Gleizes V, Viguier E, Feron JM, et al. Effects of freezing on the biomechanics of the intervertebral disc. Surg Radiol Anat. 1998;20:403–7. doi: 10.1007/BF01653130. [DOI] [PubMed] [Google Scholar]
- 28.Dhillon N, Bass EC, Lotz JC. Effect of frozen storage on the creep behavior of human intervertebral discs. Spine. 2001;26:883–8. doi: 10.1097/00007632-200104150-00011. [DOI] [PubMed] [Google Scholar]
- 29.Flynn J, Rudert MJ, Olson E, et al. The effects of freezing or freeze-drying on the biomechanical properties of the canine intervertebral disc. Spine. 1990;15:567–70. doi: 10.1097/00007632-199006000-00025. [DOI] [PubMed] [Google Scholar]
- 30.Botsford DJ, Esses SI, Ogilvie-Harris DJ. In vivo diurnal variation in intervertebral disc volume and morphology. Spine. 1994;19:935–40. doi: 10.1097/00007632-199404150-00012. [DOI] [PubMed] [Google Scholar]
- 31.Kusaka Y, Nakajima S, Uemura O, et al. Intradiscal solid phase displacement as a determinant of the centripetal fluid shift in the loaded intervertebral disc. Spine. 2001;26:E174–81. doi: 10.1097/00007632-200105010-00009. [DOI] [PubMed] [Google Scholar]
- 32.Elliott DM, Sarver JJ. Young investigator award winner: validation of the mouse and rat disc as mechanical models of the human lumbar disc. Spine. 2004;29:713–22. doi: 10.1097/01.brs.0000116982.19331.ea. [DOI] [PubMed] [Google Scholar]
- 33.Perie D, Iatridis JC, Demers CN, et al. Assessment of compressive modulus, hydraulic permeability and matrix content of trypsin-treated nucleus pulposus using quantitative MRI. J Biomech. 2006;39:1392–400. doi: 10.1016/j.jbiomech.2005.04.015. [DOI] [PubMed] [Google Scholar]
- 34.Schroeder Y, Wilson W, Huyghe JM, et al. Osmoviscoelastic finite element model of the intervertebral disc. Eur Spine J. 2006;15(suppl 3):361–71. doi: 10.1007/s00586-006-0110-3. [DOI] [PMC free article] [PubMed] [Google Scholar]