Facilitation, complexity growth, mode coupling, and activated dynamics in supercooled liquids

Abstract

In low-temperature-supercooled liquids, below the ideal mode-coupling theory transition temperature, hopping and continuous diffusion are seen to coexist. Here, we present a theory that shows explicitly the interplay between the two processes and shows that activated hopping facilitates continuous diffusion in the otherwise frozen liquid. Several universal features arise from nonlinear interactions between the continuous diffusive dynamics described here by the mode coupling theory (MCT)] and the activated hopping (described here by the random first-order transition theory). We apply the theory to a specific system, Salol, to show that the theory correctly predicts the temperature dependence of the nonexponential stretching parameter, β, and the primary α relaxation timescale, τ. The study explains why, even below the mean field ergodic to nonergodic transition, the dynamics is well described by MCT. The nonlinear coupling between the two dynamical processes modifies the relaxation behavior of the structural relaxation from what would be predicted by a theory with a complete static Gaussian barrier distribution in a manner that may be described as a facilitation effect. Furthermore, the theory correctly predicts the observed variation of the stretching exponent β with the fragility parameter, D. These two predictions also allow the complexity growth to be predicted, in good agreement with the results of Capaccioli et al. [Capaccioli S, Ruocco G, Zamponi F (2008) J Phys Chem B 112:10652-10658].

The glass transition is characterized by a number of interesting kinetic phenomena. Very slow and simultaneously nonexponential relaxation of time correlation functions over large time windows is one such important phenomenon. This relaxation is often approximated by the stretched exponential, Kohlrausch–William–Watts (KWW) formula, ø(t) = exp(−(t/τ))^β, with both β and τ exhibiting nontrivial temperature dependence. The origin of the stretching is usually attributed to the presence of dynamic heterogeneity in the system (1, 2). The temperature dependence of the typical relaxation time can be described by the the Vogel–Fulcher–Tamman (VFT) expression, τ = τ_VFT exp(DT_o/(T−T_o)), where τ_VFT is the high-temperature relaxation time, T_o is the VFT temperature, and D is the fragility index. The fragility index, D, determines the degree of deviation from the Arrhenius law that is appropriate for simple activated events. Experimental and theoretical model studies have shown that β and D are correlated (3–5). The temperature dependence of τ has also been described by phenomenological mode coupling theory (MCT) expression, τ ∼ [(T−T_c^fit)/T_c^fit]^−γ, (γ > 0), but this ultimately breaks down at low temperature. T_c^fit is referred to as the MCT transition temperature. Above T_c^fit, MCT is found to explain many experimental results (6–9), and below T_c^fit, the MCT picture of continuous diffusion fails eventually. It is conjectured that this breakdown is due to the ergodic to nonergodic transition in the dynamics and below T_c^fit activated dynamics becomes a dominant mode of transport. However in an elegant work, Brumer and Reichman (10) (BR) have recently shown that the idealized MCT using microscopic input breaks down at a much higher temperature, T_c⁰, which corresponds to the temperature, T_L, where the landscape properties show a sharp change. Kob et al. (11) have shown that the structural MCT predicts the proper dynamics till very close to T_c^fit but needs static inputs to be calculated at a higher effective temperature. Stevenson et al. (12, 13) have shown that below the ergodic to nonergodic transition but before the predicted crossover to the activated dynamics, string or fractal excitations drive the dynamics and that this qualitatively describes the crossover temperature as occurring at a specific value of the configurational entropy.

Computer simulation studies seem to show the coexistence of continuous diffusion and hopping as mechanism of mass transport at temperatures much above T_c^fit (14–17). These studies show that individual hopping events are often followed by enhanced continuous diffusion or more hops of the surrounding atoms or molecules (14, 15, 18). Simulations have also shown that a single hopping event relaxes the local stress (16), hence, it is expected that hopping events are followed by continuous diffusive dynamics. From BR study we know the temperature at which the ergodic to nonergodic transition takes place (T_c⁰ = T_L) (10). However, there is no clear theoretical understanding of the dynamics in the range, T_c^fit < T < T_c⁰. Furthermore, we need to understand, why, below T_c⁰, the MCT still seems to explain the form of the dynamics rather well and, finally, what happens at T_c^fit that leads to the breakdown of the MCT as far as the temperature dependence is concerned. In an earlier work it was shown that the full dynamics is a synergetic effect of continuous diffusive motion and activated dynamics (19). Here, we show how the coupling between these two dynamical processes influences each other. The coupling leads to hopping-induced diffusive motion below T_c⁰ and thus explains the validity of MCT below T_c⁰. The study also explains the origin of the apparent breakdown of MCT at T₀^fit. The crucial result of the present study is that the coupling renormalizes the distribution of hopping barriers which participates in the dynamics. This provides a formal treatment of the facilitation effect discussed by Xia and Wolynes (4, 5) in their theory of the stretching exponent.

The present work uses a scheme of calculation similar to the one presented earlier (19) with a few modifications. For describing the diffusive motion we use the schematic F₁₂ model of the MCT (20–22) but the activated hopping dynamics now have a static barrier height distribution (4, 5). The equation of motion for the total intermediate scattering function is written as,

In describing the activated dynamics we consider that there is a distribution of the hopping barriers in the system arising from the entropy fluctuation (4, 5). Thus, the total contribution from the multiple-barrier hopping events is written as,

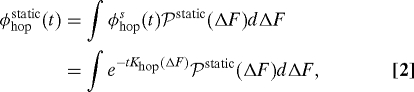where ℘^static(ΔF) is taken to be Gaussian,

We call this distribution, the static barrier height distribution. Here, ø_hop^s = e^{–tK_hop(ΔF)} describes the activated hopping dynamics for a single hopping barrier. K_hop(ΔF) = ℱ(q)P_hop(ΔF). The expression for ℱ(q) is given by $ℱ(q)=\frac{v_0}{v_P}(1-G(q))$.^¶ For the present work the q dependence of ℱ(q) will be neglected and ℱ(q) will be set to unity. P_hop(ΔF) is the average hopping rate, which is a function of the free-energy barrier height, ΔF, and is given by $P_{\text{hop}}(\Delta F)=\frac{1}{{\tau }_0}\exp (-\Delta F/k_{B}T)$ (23).

The equation of motion for the MCT part of the intermediate scattering function, ø_MCT(t), is written as,

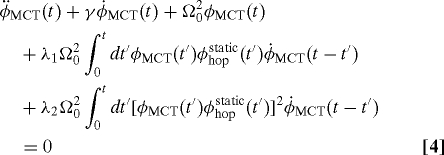Now, the MCT part of the intermediate scattering function, ø_MCT(t) is self-consistently calculated with the full scattering function, ø(t). In describing the dynamics with schematic MCT the coupling between the different wave vectors is neglected and the contribution from the static and dynamic quantities is calculated at a single wavenumber q = q_m (q_m is the wave number where the peak of the structure factor appears) which is known to provide the dominant contribution. In the present formalism it is assumed that hopping opens up multiple relaxation channels for the otherwise frozen MCT dynamics.

Eqs. 1 and 4 together describe the full dynamics, which is similar in spirit to the extended MCT (21) and other recent approaches (24). The similarity of the present scheme to the extended MCT of Gotze and Sjogren was elaborately analyzed in our earlier work (19).

As in our earlier work (19), the values of Ω_o and γ are kept fixed at unity, neglecting their temperature dependence, and the scaling time is taken as 1 ps. ${\lambda }_1=\frac{(2\lambda -1)}{{\lambda }^2}+\varepsilon \frac{\lambda }{(1+{(1-\lambda )}^2)}$ and ${\lambda }_2=\frac{1}{{\lambda }^2}+\varepsilon \frac{\lambda (1-\lambda )}{(1+{(1-\lambda )}^2)}$ (21, 22). The MCT formalism predicts a relationship between λ and β_MCT as β_MCT = −log(2)/log(1−λ) (22). ɛ is a measure of the distance from the ergodic to nonergodic transition temperature of the ideal MCT, T_C⁰, thus $\varepsilon =\frac{T_c^0-T}{T_c^0}$. To calculate the MCT part of the relaxation we need to estimate λ and T_c⁰. These quantities can be calculated for systems where the static quantities (like static structure factor) are known, but for realistic systems, because of the unavailability of the static quantities, the estimation becomes difficult. We thus use the following methods to estimate λ and T_c⁰. The ergodic to nonergodic transition is found to take place at T_L where the energy landscape properties first change (10), thus we set T_c⁰ = T_L. T_L is also the temperature where the stretching parameter starts falling (25). From experimental studies we know that for the Salol system the stretching parameter starts falling at T = 278 K (7). Thus, we estimate that T_c⁰ = T_L = 278 K. Now, to estimate λ in this schematic MCT equation, we again make use of experimental results. MCT is expected to explain the dynamics above T_c⁰; thus, the stretching parameter above T_c⁰ should be equal to β_MCT = 0.84 (7). We have also mentioned that λ and β_MCT are related. Thus, λ is fixed in such a way that, above T_c⁰, we get the correct β_MCT.

Next, we discuss the hopping dynamics for the Salol system as predicted from random first-order transition (RFOT) theory. According to the RFOT theory, the free-energy cost, F(r), which is used to calculate the mean barrier height, can be written as $F(r)=\frac{{\Gamma }_K(r){\Gamma }_A(r)}{{\Gamma }_K(r)+{\Gamma }_A(r)}-\frac{4\pi }{3}{r}^{3}T{s}_c$, where Γ_K(r) and Γ_A(r) are the surface energy terms at T_K (Kauzmann temperature) and T_A (temperature where hopping barrier disappears), respectively (19, 23). The temperature dependence of the configurational entropy can also be given by an empirical formula (26), s_c = s_fit(1−T_K/T), where s_fit is a system dependent parameter which is also related to the specific heat jump at the Kauzmann temperature (Δ̄c_p(T)=s_fit(T_K)/T)). For the Salol system s_fit = 2.65, T_K = 175 K and T_A = 333 K. With these values of the parameters the mean barrier height and the critical nucleus radius are calculated. We find that at T = 280 K, the size of the critical nucleus is above unity. Thus, although T_A = 333 K, for all practical purposes T = 280 K should be considered as the temperature where activated events start, which, as found in simulations, is close to T_c⁰ (17). The value of τ_o is fixed in such a way that at T = 280 K, both the MCT and the hopping dynamics together predict a relaxation time that is close to that obtained in the experiment (8). Thus, for Salol the fitting gives τ₀ = 2400 ps. A more microscopic treatment of the barrier height can be found by treating the shape of the nucleating region as a fuzzy sphere (12). The distribution of barrier heights arises due to the fluctuation in entropy density, which can be related to the specific heat according to the Landau formula, 〈(ΔS)²〉 = k_BC_p (27), where ΔS is the entropy fluctuation and C_P is the specific heat. This expression can be rewritten in terms of configurational entropy fluctuation per bead δs_c and heat capacity jump per bead Δ̄c_p(T) as, $\delta s_c=\sqrt{\frac{k_{\text{B}}\overline{\Delta }{c}_p(T)}{\frac{4\pi }{3}{(r*/a)}^3}}$ and $\frac{\delta s_c}{\langle s_c\rangle }=\sqrt{\frac{3k_{\text{B}}T{T}_K}{4\pi s_{\text{fit}}{(T-T_K)}^2{(r*/a)}^3}}$. Here, r* is the droplet radius determined by using F(r*) = 0. a is the length of the bead. We can also relate the entropy fluctuation to the width of the barrier height distribution, $\frac{\delta \Delta F}{\Delta F_o}\simeq \frac{\frac{\delta s_c}{\langle s_c\rangle }}{1+\frac{\delta s_c}{\langle s_c\rangle }}$, and thus define the width of the static barrier height distribution in terms of entropy fluctuation and specific heat.

Combining the static RFOT and MCT, we solve Eqs. 1 and 4 numerically.^‖ We use a numerical method presented earlier (28) with a minor modification (29). The total relaxation time, τ_total, and the stretching parameter, β_total, are obtained from the coupled dynamics by fitting the long time part of ø(t) (obtained from Eq. 1) to a KWW stretched exponential function, ø(t) = A exp(−(t/τ_total))^β_total. Similarly from ø_MCT(t) we obtain the MCT relaxation time, τ_MCT, and the corresponding stretching parameter, β_MCT.

Hopping-Induced Continuous Diffusion

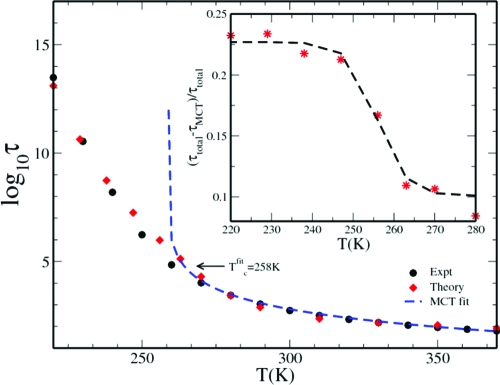
The plot for the relaxation time τ_total is given in Fig. 1, where we have also shown the experimental results (for Salol) and the fit to the MCT phenomenological expression. Already the temperature dependence of τ_total reveals several interesting physics. The τ_total compares well with the experimental results (8) and predicts the correct glass transition temperature, T_g = 220 K. Recall that in our calculation the ergodic to nonergodic transition takes place at T_c⁰ = 278 K where the activated dynamics also becomes significant. Thus, we know that the idealized MCT prediction breaks down at T = 278 K and below this temperature, its validity as such is unclear. However, when we fit the relaxation time to MCT expression (τ ∼ [(T−T_c^fit)/T_c^fit]^−γ) we obtain a value, T_c^fit = 258 K, which is in excellent agreement with the experimental fits (6, 8, 9).

Fig. 1.

Temperature dependence of the α relaxation timescale for Salol–hopping-induced diffusive dynamics. The timescale for the longtime part of the total structural relaxation, ø(t), obtained from experiments (8) (black circles) and that calculated from the present coupled theory, τ_total (red diamonds) are plotted against temperature. We fit the τ_total to the MCT phenomenological expression, τ_total ∼ [(T−T_c^fit/T_c^fit]^−γ (blue dashed line), we obtain T_c^fit = 258 K. (Inset) We plot (τ_MCT−τ_total)/τ_total as obtained from the theory (red stars). The black dashed line is a guide to the eye. The function shows a jump at approximately T = 258 K. We find that across this temperature the hopping dynamics changes its role and below T_c^fit = 258 K it plays a direct role in the dynamics. The scaling times is 1 ps.

The advantage of the present scheme of calculation is that, in addition to addressing the coupling between the continuous diffusion and the hopping motion, we can separately analyze their relative contributions to the total dynamics and explore the origin of the apparent validity of the MCT below T_c⁰. Due to the nonlinear coupling in Eqs. 1 and 4, the activated dynamics plays both a “direct” and a “hidden” role in the total relaxation. The direct role is the direct relaxation of ø via ø_hop^static. However, if we analyze the structure of Eq. 4, we find that the activated dynamics also acts to soften the growth of the longitudinal viscosity, which finally leads to the relaxation of the otherwise frozen ø_MCT. Thus ø_hop^static plays a hidden role in the relaxation by helping ø_MCT to relax. Earlier simulation studies of Bhattacharyya and Bagchi have already observed this hidden role of hopping in relaxing the local stress (16). We now analyze these two different roles of the hopping dynamics and their effect on the total relaxation.

The present study shows that both continuous and activated dynamics change continuously across T_c^fit. However, when we plot (τ_MCT − τ_total)/τ_total against T (in Fig. 1 Inset) this quantity is seen to undergo a rapid increase in the temperature range of the phenomenological MCT transition temperature T_c^fit. This implies that although below T_c^fit the continuous diffusion still remains the dominant mode of relaxation, there is an increased contribution from the activated dynamics. This plot suggests that in the range, T_c^fit < T < T_c⁰, where direct hopping contribution is small, the activated dynamics plays only an important hidden role, whereas below T_c^fit, it also plays a direct role in the relaxation process.

One important observation is that although idealized MCT breaks down at T_c⁰ = 278 K, the functional form of MCT continues to describe the dynamical characteristics until 258 K. The latter is a widely known result, usually obtained from fitting the MCT functional forms to the experimental data (6, 8, 9). Thus, our study provides an explanation of this intriguing result in terms of the interaction between the MCT and activated dynamics, which leads to hopping-induced continuous diffusive motion. This also quantitatively explains the observations reported by Kob et al. (11). The authors find that until close to T_c^fit the dynamics can be described via MCT, although the static inputs need to be calculated at a higher effective temperature. The present study further shows that as we progressively lower the temperature below T_c^fit, although the continuous diffusive dynamics continues to play an important role in the relaxation, the increased contribution from the activated dynamics finally leads to the breakdown of the MCT predictions.

Renormalized Barrier Height Distribution

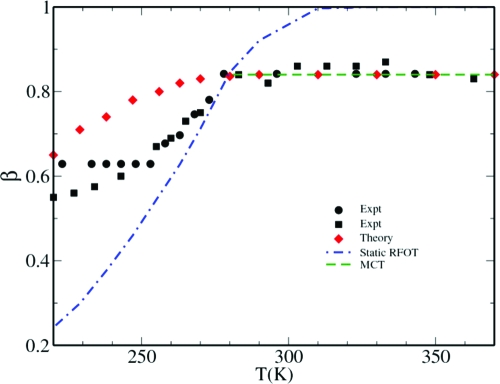
In Fig. 2 we plot the calculated temperature dependence of the stretching parameter β_total. In the same figure we also plot β_MCT and β_hop^static as predicted by the MCT and the static RFOT theory^†† (by using static barrier height distribution), respectively. The experimental results on Salol are also plotted in the same figure (6, 7). It is clear that neither the MCT nor the static RFOT distribution can alone describe the proper temperature dependence of the stretching parameter. However, the coupled theory predicts a temperature dependence of β_total which is qualitatively similar to that found in experiments. The stretching parameter is known to provide a measure of the heterogeneity in the system. In our study the heterogeneity arises from the distribution of hopping barriers. However, below T_c⁰, β_total is larger than β_hop^static, which means that the barrier height distribution that participates in the dynamics (dynamic barrier height distribution) is narrower than the initial assumption of distribution (static barrier height distribution). This modification of the barrier height distribution (or heterogeneity) takes place because of the coupling between the diffusive and the activated dynamics. The timescale analysis reveals that the smaller barriers contribute to the dynamics, which implies that, in the presence of the quasi-static dynamic heterogeneity, the coupling leads to a facilitation effect. Regions that would be slow are relaxed by their neighbors.

Fig. 2.

Temperature dependence of the stretching parameter for Salol. The stretching parameter for the longtime part of the total structural relaxation, ø(t), obtained from experiments (6) (black squares) and (7) (black circle) and that calculated from the present coupled theory, β_total (red diamonds), are plotted against temperature. In the same plot we also present the stretching parameter predicted by the RFOT theory by using the static barrier height distribution, β_hop^static (blue dashed-dot line) and the MCT, β_MCT (green dashed line) (which shows no temperature dependence).

To quantify these points, we carry out the following analysis. Nonexponential relaxation in the system can be considered as arising from superposition of exponentials,

It is now possible to find an effective distribution function of the relaxation times ℘^dynamic(τ) by Laplace inverting the stretched exponential. Once we obtain the distribution of relaxation times we can convert it into the distribution of barrier heights by using, ℘^dynamic(ΔF)dΔF = ℘^dynamic(τ)dτ, provided τ can be expressed in terms of ΔF. The details are presented in Materials and Methods. Note that it is possible to find an analytical relation between τ and ΔF only when the individual dynamics are exponential. Hence, we do this analysis considering only exponential MCT relaxation (i.e., for this analysis we choose λ such that β_MCT = 1.0). We now analyze the dependence of ℘^dynamic(ΔF) on the MCT relaxation time and show that ℘^dynamic(ΔF) not only depends on ℘^static(ΔF), but also depends on the MCT relaxation time τ_MCT = K_MCT⁻¹. We fix the ℘^static(ΔF) and change the τ_MCT by calculating the MCT dynamics [which is coupled to ℘^static(ΔF)] at different temperatures. The results are presented in Fig. 3.

Fig. 3.

Temperature dependence of the probability distribution of barrier heights which participate in the dynamics, ℘^dynamics(ΔF). In this figure we plot the static barrier height distribution, ℘^static(ΔF), which is used in the calculation of the total dynamics (black solid curve). From the total dynamics we again estimate the barrier height distribution that actually participates in the dynamics (colored dashed line). This has been done for different MCT relaxation time scale by changing the temperature of the MCT part of the dynamics (T = 240 K, 230 K, 200 K, and 175 K). As the temperature is lowered, the barrier height distribution becomes broader.

At high temperatures, where MCT dynamics is fast, ℘^dynamic(ΔF) is narrow (β_total is large), and the position of the maximum, ΔF_max, is shifted to smaller ΔF (Fig. 3). We also find that, as the MCT dynamics slows down, the distribution becomes broader and more non-Gaussian (β_total also becomes smaller), larger barriers contribute to the dynamics, and ΔF_max shifts to higher values (though it always remains smaller than ΔF_o). Thus, we find, in accord with the literature, that as the temperature is lowered (or the dynamics becomes slower) there is a growth in dynamic heterogeneity. We may say that ℘^dynamic(ΔF) provides a mean field estimation of the dynamic heterogeneity. Note that ℘^dynamic(ΔF) is always narrower than ℘^static(ΔF) and overlaps with it only in the low barrier side. Xia and Wolynes (4) have given a physical interpretation of this exclusion of the higher barriers from the dynamics by using the picture of dynamic mosaic structure. Because the exclusion of higher barriers hastens the hopping dynamics this can be described as a “facilitation effect.” The present theoretical model does not explicitly treat the spatial structure of the dynamical mosaic. However, we find that the presence of the continuous dynamics and its coupling to the activated dynamics does lead to such a facilitation effect. Note that the facilitation is strongest when the MCT dynamics is exponential and should be weaker when we have stretching in the MCT dynamics.

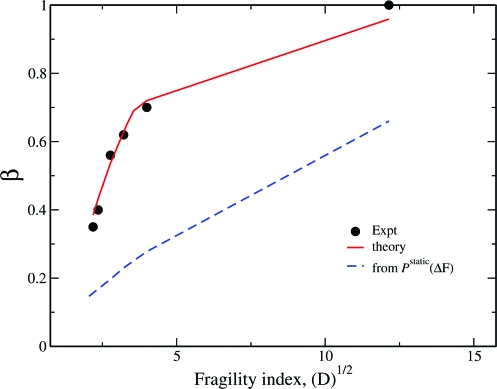
The MCT modification of the static barrier height distribution, as predicted by the present theory, plays a key role in describing the proper relationship between the fragility index, D, and the stretching parameter, β. The study of Bohmer et al. (3) finds a relationship between the fragility index, D, and the stretching parameter, β, at T = T_g. As discussed in ref. 4, β_hop^static is related to the width of the static Gaussian distribution of the barrier heights δΔF. δΔF can be related to the fragility, D, $\frac{\delta \Delta F}{\Delta F_o}\simeq \frac{1}{2\sqrt{D}}$. Thus, β_hop^static can be related to the fragility (4), ${\beta }_{\text{hop}}^{\text{static}}={[1+{(\Delta F_o/2k_{\text{B}}T\sqrt{D})}^2]}^{-1/2}$. However, it was found that this expression alone (with the full static barrier height distribution) does not describe the correct relationship between β and D (4).

The details of the calculation are presented in Materials and Methods. In Fig. 4 we plot the relationship between β_total and D as predicted by the present calculation. In the same plot we also show the experimental results (3). We find that the present theory captures the correct trend. This is to be contrasted with the predictions obtained from the static distribution of barrier heights. Note that, in all the cases, β_total > β_hop^static, which implies that ℘^dynamic(ΔF) is always narrower than ℘^static(ΔF). Earlier we showed that ℘^dynamic(ΔF) overlaps with ℘^static(ΔF) only on the low barrier side. Thus, the higher barriers do not participate in the dynamics leading to facilitation effect. Hence, for a wide range of systems the theory predicts a proper modification of the barrier height distribution. Note that Xia and Wolynes (4) showed that the static barrier height distribution should have a cutoff to describe the relationship between β and D. The authors gave a physical explanation of this “cutoff” by using the picture of dynamic mosaic structure.

Fig. 4.

Fragility dependence of the stretching parameter. The stretching parameter for the total structural relaxation, ø(t), obtained from experiments β_expt (3) (black circles) and that calculated from the present coupled theory, β_total (red solid line) are plotted against the square root of fragility index D. As D decreases, the fragility of the system increases. In the same plot we also present the stretching parameter predicted by the full static barrier height distribution (blue dashed line). The experimental and the theoretical values are at the glass transition temperature T = T_g.

The combination of distributed activated hopping and mode coupling facilitation also explains some recent exciting experimental observations of Capaccioli et al. (31). These authors recognized that, in those theories of glassy dynamics based on an underlying entropy crisis, the complexity of a dynamically correlated region is a key quantity. They also used earlier insights (32, 33) to show how this quantity can be roughly inferred from experiment. This inference is independent of chemical details, such as bead count, which have previously been used for comparisons of RFOT theory with experiment.

The complexity, α_CRR (the logarithm of the number of accessible states in a cooperatively rearranging region) is obtained by combining the configurational entropy density, S_c, inferred from calorimetry, with the temperature dependence of dynamics as reflected in the alpha relaxation time, τ_α(T), and stretching exponent of dielectric relaxation or viscosity, β(T) (31).

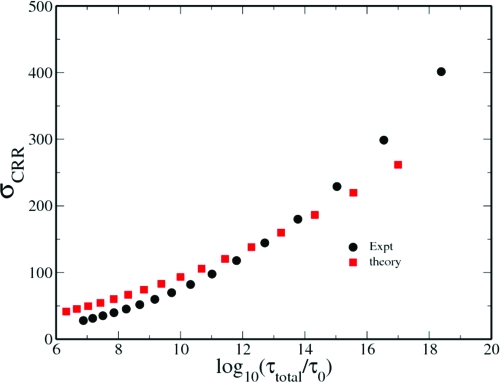
In those purely kinetic models of the glass transition that are based on the facilitation concept but have trivial underlying thermodynamics (34), one would not expect this inferred complexity to be a universal function of the relaxation time. However, according to the Adam–Gibbs argument, the complexity should be a constant for all values of the relaxation time but could depend on substance. The static RFOT theory predicts that the logarithm of the relaxation timescales should be a universal function of the complexity of the dynamically reconfiguring regions for all glass formers. In contrast to the expectations from thermodynamically trivial kinetic models, Capaccioli et al. (31) showed a very strong data collapse of this complexity, σ_CRR versus log₁₀(τ_α) for many substances. The Adam–Gibbs prediction of a constant value is not borne out, however. In contrast also to static RFOT, which predicts an asymptotically linear relation, the experimental data show a distinct curvature.

In Fig. 5 we show the prediction of σ_CRR versus log₁₀(τ_total/τ₀) that is obtained from the present calculation^‡‡ for Salol using the analysis of Capaccioli et al. along with their results (31). In harmony with the experimental observation we see that the combined MCT/activated RFOT mechanism does give a curvature. The universal curve obtained experimentally was fit by an assumed scaling form containing several adjustable exponents. The present calculations suggest that the true asymptotic region may not yet have been reached experimentally. At the same time, we must be clear that the present calculation is still a low-order one. It is conceivable that a renormalization group treatment, in which the static RFOT barriers themselves are modified by the MCT effects that occur on shorter-length scales, could ultimately give anomalous scaling even in the ultimate asymptotic regime.

Fig. 5.

Relation between alpha relaxation timescale and complexity of dynamically reconfiguring regions. σ_CRR calculated from the present theory (see footnote ‡‡) (red squares) is plotted against log₁₀ (τ_total/τ₀) for Salol by using the analysis of Capaccioli et al. (31). This τ₀ is the relaxation time at high temperature and different from the τ₀ used to describe the activated dynamics. We also plot the results presented by Capaccioli et al. (31) that they obtained from experimental data (black circles).

The present study enriches our understanding of the dynamics below the ergodic to nonergodic transition temperature, T_c⁰. It predicts the presence of hopping-induced diffusive dynamics below T_c⁰. It also predicts that this diffusive dynamics continues to exist even below T_c^fit and provides a dominant contribution to the total dynamics. However, in this temperature range there is an increased contribution from the activated dynamics that leads to the breakdown of the MCT. The diffusive dynamics is found to modify the activated dynamics by redefining the barrier height distribution of the hopping events in a way such that the higher barriers are excluded from the total dynamics. Thus, we find that in this unified theory the two dynamical processes do not just act as parallel channels of relaxation, but they interact with each other and modify each other's behavior, which leads to the facilitation of the total dynamics.

Materials and Methods

Relationship Between τ_total and ΔF.

According to the present theory, ${\tau }_{\text{total}}=\frac{1}{K_{\text{MCT}}+K_{\text{hop}}}$, where $K_{\text{hop}}=\frac{1}{{\tau }_0}exp(-\Delta F/k_{\text{B}}T)$. Even for the simple exponential MCT relaxation the relationship between K_MCT and ΔF is nontrivial (29). However, in the low-temperature limit we can write $K_{\text{MCT}}=\frac{2K_{\text{hop}}}{{\lambda }_2{A}^2+2{\lambda }_{1}A-1}=\alpha K_{\text{hop}}$, where $\alpha =\frac{2}{{\lambda }_2{A}^2+2{\lambda }_{1}A-1}$. A is the Debye–Waller factor or the form factor (height of the plateau), thus, ${\tau }_{\text{total}}=\frac{1}{(\alpha +1)K_{\text{hop}}}$. ΔF_o, is calculated at T = T_g, by using Salol parameters. δΔF is related to β_hop^static [by β_hop^static = [1+(δΔF/k_BT)²]^−1/2 (4, 30)] and it is taken in such a way that it gives β_hop^static = 0.5. We calculate the total relaxation and fit it to a stretched exponential. From the fitting we obtain τ_total and β_total. This is now fed into Eq. 5 to obtain ℘^dynamic(ΔF).

Fragility Dependence of β_total.

The mean barrier height depends on the configurational entropy and is almost independent of the system; thus, for all the systems (12), we calculate ΔF_o by using Salol parameters (s_fit = 2.65, T_K = 175 K, T_c⁰ = 278 K). δΔF is fixed according to the value of D, which is taken from Bohmer et al. (3). For the Salol system τ_o is used as a fitting parameter to describe the proper timescale of the dynamics. In this calculation we also vary τ_o for each system in such a way that at T = T_g the relaxation time is of the order of 100 s. We find that, for a more fragile system, we need a larger value of τ_o.

Above T_c^fit, the dynamics is expected to be described completely by the MCT. Thus, the β_total above T_c⁰ should be equal to the β_MCT value. For the systems like Salol (6), Glycerol (35), and Silica [Silica is known to be a strong liquid with β ≃ 1.] where the value of β_MCT at high temperatures is known, we use these values to define β_MCT. For the systems where β_expt at high temperatures are not known, we use a reasonable value [definitely larger than β_expt(T = T_g)] and also vary it in small amounts along with τ_o to get the proper relaxation timescale at T_g. T_c⁰ is kept same as that for the Salol system. So, our only constraint is that the timescale should be of the order of 100 s at T_g.