Abstract
The transient receptor potential vanilloid 1 (TRPV1) nonselective cationic channel is a polymodal receptor that activates in response to a wide variety of stimuli. To date, little structural information about this channel is available. Here, we used quaternary ammonium ions (QAs) of different sizes in an effort to gain some insight into the nature and dimensions of the pore of TRPV1. We found that all four QAs used, tetraethylammonium (TEA), tetrapropylammonium (TPrA), tetrabutylammonium, and tetrapentylammonium, block the TRPV1 channel from the intracellular face of the channel in a voltage-dependent manner, and that block by these molecules occurs with different kinetics, with the bigger molecules becoming slower blockers. We also found that TPrA and the larger QAs can only block the channel in the open state, and that they interfere with the channel's activation gate upon closing, which is observed as a slowing of tail current kinetics. TEA does not interfere with the activation gate, indicating that this molecule can reside in its blocking site even when the channel is closed. The dependence of the rate constants on the size of the blocker suggests a size of around 10 Å for the inner pore of TRPV1 channels.
INTRODUCTION
The transient receptor potential vanilloid 1 (TRPV1) channel is a nonselective cation channel primarily expressed in sensory C and Aδ fibers and in neurons from the dorsal root and trigeminal ganglia (Szolcsanyi et al., 1990, 1991; Szallasi et al., 1993, 1995; Caterina et al., 1997; Szallasi and Blumberg, 1999). Being a polymodal receptor, TRPV1 is activated by diverse stimuli such as voltage (Piper et al., 1999; Gunthorpe et al., 2000), temperature (>43°C), protons (pH, <5.4) (Caterina et al., 1997; Tominaga et al., 1998), and several naturally occurring pungent compounds such as capsaicin from chili peppers (Caterina et al., 1997) and allicin from garlic (Macpherson et al., 2005; Salazar et al., 2008).
Accumulating evidence points to a role of the TRPV1 channel in inflammatory processes and the pain pathway, being one of the key signal transducers mediating inflammatory pain detection and hyperalgesia (Hwang et al., 2000; Premkumar and Ahern, 2000; Chuang et al., 2001; Tominaga et al., 2001; Bhave et al., 2002; Moriyama et al., 2003; Numazaki and Tominaga, 2004; Premkumar et al., 2004; Price et al., 2004; Zhang et al., 2005; Cortright et al., 2007; Szallasi et al., 2007).
Despite the numerous physiological processes in which this channel is involved, we currently have little knowledge of the structural characteristics and basic biophysical properties of TRPV1. The available information points to structural conservation between TRP channels and the voltage-dependent potassium channels in regard to overall channel topology and the general structure of the pore domain (Ferrer-Montiel et al., 2004; Voets et al., 2004; Tominaga and Tominaga, 2005; Owsianik et al., 2006). Several lines of evidence indicate that the functional TRPV1 channel is a tetramer with each subunit formed by six transmembrane segments with the pore domain formed by the S5, S6, and the loop between them (Kedei et al., 2001; Cheng et al., 2007). A recent study has provided information regarding the structure of the pore and indicated that it is formed by α-helices that might be forming a bundle crossing, as has been observed for voltage-activated K+ channels (Susankova et al., 2007). Additionally, TRP channels possess multi-ion permeation properties, as do several potassium channels (Owsianik et al., 2006; Oseguera et al., 2007).
Mutagenesis experiments have revealed that several point mutations in the putative S5-S6 loop alter the permeation properties of the channel, in accordance with this region being the selectivity filter (Garcia-Martinez et al., 2000; Mohapatra et al., 2003).
Pore blocker molecules constitute a helpful tool in our understanding of the general architecture of the permeation pathway and the gating properties of ion channels. Quaternary ammonium ions (QAs), in particular, are a family of potassium channel blockers that have been successfully used in structure–function studies, providing information about the properties and dimensions of the pore (French and Shoukimas, 1981, 1985; Guo and Lu, 2001), as well as the first description of an activation gate in a voltage-activated K+ channel (Armstrong, 1971; Armstrong and Hille, 1972; Bezanilla and Armstrong, 1972).
Here, we showed that QA derivatives are also pore blockers of TRPV1 channels and performed experiments to probe their mechanism of action. We have previously reported that tetrabutylammonium (TBA) blocks open TRPV1 channels and interferes with closing of a gate (Oseguera et al., 2007). We extended this previous study and found that all QAs tested act as voltage-dependent pore blockers that can produce blockade in a manner that depends on the channel being in the open state. Channels that were blocked by tetrapropylammonium (TPrA), TBA, and tetrapentylammonium (TPA) showed considerable slowing of the closure kinetics, consistent with a state-dependent block mechanism and “foot-in-the-door”–like effects on closure as described for Kv channels. Even though TEA also blocks the channel, it does not interfere with the gating mechanism, suggesting that a TEA molecule can reside in its blocking site even when the channel is closed and that the channel pore is large enough to accommodate this small ion.
MATERIALS AND METHODS
Mammalian Cell Culture and Recording
Methods are similar to those described in Oseguera et al. (2007). Recordings were performed using HEK 293 cells expressing large T antigen. Cells were transfected with Lipofectamine (Invitrogen) according to the manufacturer's instructions. The rTRPV1-pCDNA3 plasmid (provided by D. Julius, University of California, San Francisco, San Francisco, CA) was cotransfected with pIRES-GFP (BD Biosciences) to fluorescently visualize transfected cells. Cells plated in coverslips were used for recording 1 d after transfection. Bath and pipette low divalent solutions consisted of 130 mM NaCl, 3 mM HEPES, pH 7.2, and 1 mM EDTA for Ca2+-free conditions, unless otherwise indicated. 4 mM capsaicin (Sigma-Aldrich) stocks were prepared in ethanol and diluted to the desired concentrations in recording solution.
TEA, TPrA, and TPA were purchased from Sigma-Aldrich. TBA was obtained from Fluka. Stock solutions were prepared using the low divalent solution described above and diluted to their final concentrations in the presence of capsaicin. Intracellular solutions in inside-out patches were changed using an RSC-200 rapid solution changer (Biological).
Macroscopic and single-channel currents were low-pass filtered at 2.5 kHz and sampled at 10 kHz with an EPC 10 amplifier and acquired and analyzed with PULSE data acquisition software (HEKA Elektronik GMBH). For macroscopic current recordings, the following voltage protocol was used: Patches were held at 0 mV and given a prepulse of −120 mV for 30 ms. Voltage was then stepped from −150 to 150 mV in 10-mV increments for 100 ms and then stepped back to −120 mV for 30 ms. Steady-state current measurements were taken as the average of the last 30 ms of the test pulse. Channel closure kinetics were measured using a tail current protocol in which the voltage was stepped to −120 mV for 20 ms, and then to 60 mV for 100 ms followed by pulses starting from −220 to 0 mV in 20-mV steps for 100 ms. All tail current recordings are the average of three current traces to reduce noise. Pipettes for recording were pulled from borosilicate glass, covered in Q-Dope (GC Electronics), and had a resistance of 2–4 MΩ. All recordings were performed at room temperature (19°C). For leak subtraction, currents in the absence of capsaicin were subtracted from currents in the presence of capsaicin. This procedure does not influence the shape or size of currents because the voltage-activated TRPV1 currents in the absence of capsaicin at this temperature are negligible (the open probability at 100 mV is 0.01).
Data Analysis
Blocker dose–response relations were obtained from current measurements in the same patch using voltage steps from −120 to 100 mV in 20-mV increments for 200 ms, first in the absence and then in the presence of varying concentrations of blocker. The fraction of current blocked (FB) was calculated as:
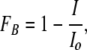 |
where I is the current in the presence of blocker and Io is the current in the absence of blocker. For each QA, the apparent dissociation constant, KD, was obtained at a given voltage by fitting FB as a function of blocker concentration with the Hill equation:
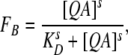 |
(1) |
where s is the steepness factor and [QA] is the quaternary ammonium concentration. The voltage dependence of KD was obtained by plotting the value obtained from the Hill equation fit as a function of voltage.
Burst analysis was performed on single-channel openings in inside-out patches containing multiple channels recorded at low capsaicin concentrations using the same solutions as for macroscopic current recordings. A burst of openings was defined as in Oseguera et al. (2007), using the criterion of Colquhoun and Sakmann (1985). Event detection was performed with the 50% threshold crossing technique. Dwell times were logarithmically binned and exponential probability density functions were fitted with a maximum likelihood method (Sigworth and Sine, 1987; Colquhoun and Sigworth, 1995).
Determination of Blocking Rates Using the β Distribution
Block induced by TEA and TPrA is too fast to be resolved in single-channel recordings. To determine the rates of blocker association (on-rate) and dissociation (off-rate), we made use of the β distribution (Fitzhugh, 1983) to fit amplitude histograms from single-channel openings. As discussed by Yellen (1984), this method was analytically derived for a simple RC filter, but it can be used with modification for data filtered with a multi-pole Bessel filter. As a Gaussian filter is a good numerical approximation to a Bessel filter, we wanted to determine if this method could also be reliably applied to Gaussian-filtered data. A two-state process filtered by a single-pole filter has a probability density function given by:
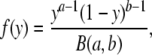 |
(2) |
with a = ατ, b = βτ, and
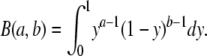 |
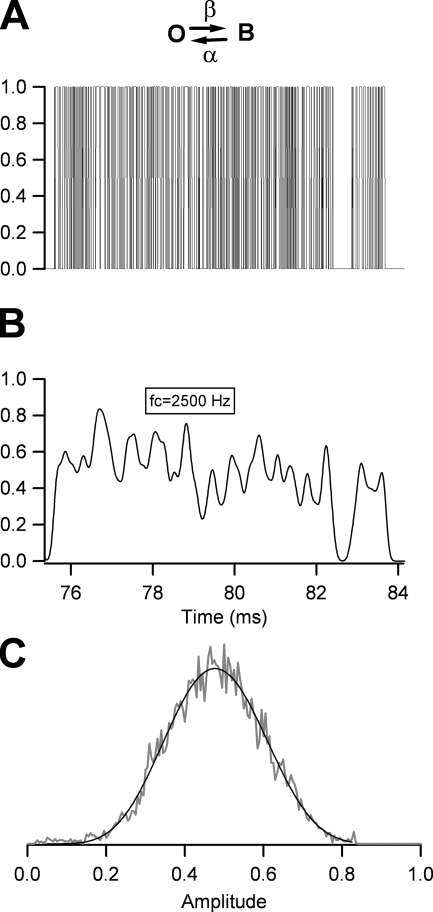
In these equations, τ is the single-pole filter time constant, α is the blocker dissociation rate constant, β is the association rate constant, and B(a,b) is the β function, used as a normalization factor. We simulated a noiseless two-state Markov process with a Monte-Carlo algorithm and filtered the data at 2,500 Hz, which is the filter cutoff frequency used in our experiments. The simulation was performed with the two states, identified as blocked and open, having amplitudes of 0 and 1, respectively (Fig. 1 A). Data were simulated with rates α and β = 51,000 s−1. The same data after Gaussian filtering and its corresponding amplitude distribution is shown in Fig. 1 (B and C). To fit Eq. 2 to the amplitude distribution, the single-pole filter time constant, τ, is corrected by a factor ε/fc, where fc is the Gaussian corner frequency. The term ε can be determined from fits of Eq. 2 to amplitude distributions derived from simulated data, by holding α and β = 51,000 s−1. We determined a value for ε = 0.418 and thus τ = 0.418/ fc. This value of τ provided the best fits to the amplitude distribution of simulated data over a wide range of values for α and β. All-points histograms collected from individual openings or bursts of openings were scaled in such a way that zero corresponds to the closed channel current level and one is the open-channel amplitude in the absence of blocker. The closed events were subtracted from the histograms to obtain only the open event distribution. Histograms were then normalized so that the area under the curve would be equal to one. To fit the amplitude histograms, β distributions were convolved with a Gaussian function that represents the added noise observed when the channel was fully closed. All data analysis was performed with programs written in Igor Pro (Wavemetrics Inc.).
Figure 1.
Analysis of a fast two-state process with amplitude histograms and the β distribution. (A) Monte-Carlo simulation of the process with blocking rate β and unblocking rate α = 51,000 s−1. The simulation is set so that the amplitudes of the states in the scheme are O (open) = 1 and B (blocked) = 0. (B) The simulated data in A after filtering with a Gaussian filter with corner frequency, fc, of 2500 Hz. The data becomes smeared and the amplitude is reduced. (C) Amplitude histogram compiled from all the points from the trace in B (gray trace). The black trace is the fit of the β distribution to the data (Eq. 2) with parameters β = 51,200 s−1, α = 50,950 s−1, and τ = 0.418/fc.
RESULTS
Quaternary Ammonium Block of TRPV1 Channels Is Voltage Dependent
Here, we have examined some fundamental properties of the effects of QAs on TRPV1 channels. We used TEA, TPrA, TBA, and TPA to determine how block of TRPV1 channels is affected by the different sizes of these QAs and to obtain information on the state dependence of block of TRPV1 channels by these compounds.
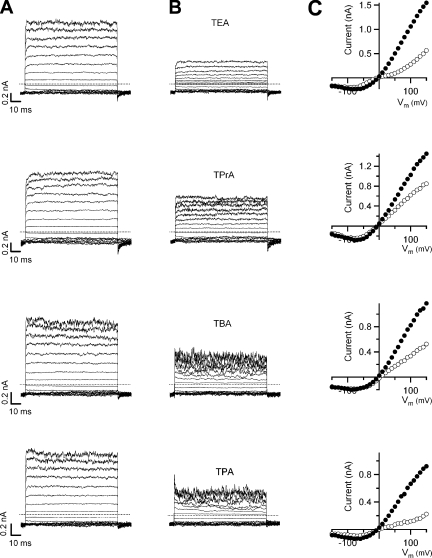
Intracellular application of all four QAs readily blocked currents through TRPV1. Fig. 2 A shows macroscopic TRPV1 currents activated by voltage pulses in the presence of saturating 4 μM capsaicin recorded from inside-out patches in the absence of blocker. The addition of QAs effectively induced current block (Fig. 2 B). Fig. 2 C shows the steady-state current to voltage relations obtained from the traces in A and B. The outward rectifying character of the TRPV1 channel can be clearly seen and block seems to be voltage dependent, with QAs blocking with higher affinity at positive membrane potentials. The reversal potential lies near zero mV, as expected under isometric sodium conditions.
Figure 2.
Block of TRPV1 currents by intracellular QAs. Current traces without blockers (A) and with blockers (B). The currents were elicited by stepping membrane voltage from a 0-mV holding potential to −120 mV, and then to various test potentials from −150 to 150 mV in 10-mV increments. For clarity, only the traces at every 20 mV are shown. All current traces in B were obtained after applying the corresponding QA to the patch in A and corrected for leak current in the absence of agonist. The blocker concentrations used are: 10 mM TEA, 0.9 mM TPrA, 250 μM TBA, and 40 μM TPA. The dotted lines identify the zero current levels. (C) Steady-state current to voltage relations obtained from the traces in A (closed symbols) and B (open symbols).
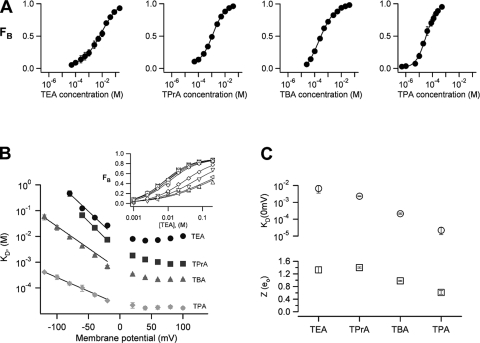
Fig. 3 A shows the dose-response curves for the various QAs obtained at 100 mV. Blockade was dose dependent with the apparent dissociation constant, KD, decreasing with blocker size, indicating an increase in affinity. The steepness of the Hill equation used to fit the data is close to one, suggesting that only a molecule of blocker can bind to the channel at a time (Fig. 3 A). A plot of the apparent dissociation constant, KD, versus voltage indicates that block is clearly voltage dependent; however, contrary to the expectation from a Woodhull-type model (Woodhull, 1973), the value of KD for all blockers reaches an asymptotic value at positive potentials (Fig. 3, B and inset). This apparent relief of block has been explained in other types of ion channels by several different mechanisms, including a permeant blocker mechanism (Guo and Lu, 2000), diffusion limitation of the on-rate at positive voltages (Blaustein and Finkelstein, 1990b), and permeant–ion interactions with the blocker in the conduction pathway (Heginbotham and Kutluay, 2004). For TBA, we have previously shown that relief of block can be explained by the latter mechanism (Oseguera et al., 2007), and it is very likely that the same is true for the rest of QA blockers used here. At negative voltages, the KD does behave as an exponential function of voltage, and we can estimate the valence of the blocking reaction at voltages more negative than 0 mV by fitting Eq. 3 to the data:
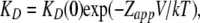 |
(3) |
where KD(0) is the value of KD at zero mV and Zapp is the apparent charge associated with the blocking reaction. These parameters are shown in Fig. 3 C for each blocker. Similar to observations in voltage-dependent potassium channels (Choi et al., 1993), the apparent affinity of the blocker increases with the size and hydrophobicity of the QA derivative (Fig. 3 C). It can also be appreciated that the voltage dependence of TEA, TPrA, and TBA, represented by the value of Zapp (Fig. 3 C), is higher than or near a value of one. A similar observation of high apparent valences of blockers in potassium-permeable channels has been shown to be due to the coupling of permeant ion movement with blocker occupancy (French and Shoukimas, 1985; Spassova and Lu, 1998), and we have shown previously that in the case of TBA, a large fraction of this voltage dependence is due to movement of Na+ ions in the selectivity filter of the TRPV1 channel, which is coupled to blocker occupancy, and not due to the blocker traversing a large fraction of the transmembrane voltage (Oseguera et al., 2007).
Figure 3.
Voltage dependence and steady-state block at negative voltages. (A) Dose-response curves for the different QAs measured at a voltage of 100 mV. The solid lines represent fits to the Hill equation. The parameters are: TEA, KD = 8.7 ± 0.7 mM, s = 0.77 ± 0.08 (n = 5); TPrA, KD = 940 ± 60 μM, s = 0.79 ± 0.04 (n = 6); TBA, KD = 327 ± 25 μM, s = 0.88 ± 0.02 (n = 9); TPA, KD = 36 ± 8 μM, s = 1.15 ± 0.12 (n = 3). All recordings were performed in the presence of 4 μM capsaicin. (B) The apparent dissociation constant, KD, derived from data as in A at different voltages. The inset shows a complete dataset for TEA for voltages from −80 to 100 mV. Voltage dependence of block was determined at negative voltages by fitting Eq. 3 to the data in B up to −20 mV. (C) The parameters obtained from the fit are plotted as a function of the size of the blocker. KD at 0 mV (in units of M; top): TEA, 6.65 × 10−3 ± 3.10−3 (n = 4); TPrA, 2.31 × 10−3 ± 0.11 × 10−3 (n = 4); TBA, 21.3 × 10−5 ± 1.7 × 10−5 (n = 6); TPA, 2.2 × 10−5 ± 10−5 (n = 5). The values of Z (bottom) are (in units of eo): TEA, 1.32 ± 0.097; TPrA, 1.4 ± 0.02; TBA, 0.98 ± 0.02; TPA, 0.61 ± 0.06. The affinity of the channel for the blockers increases with blocker size. Group data are presented as mean ± SEM.
Kinetics of Block by TEA
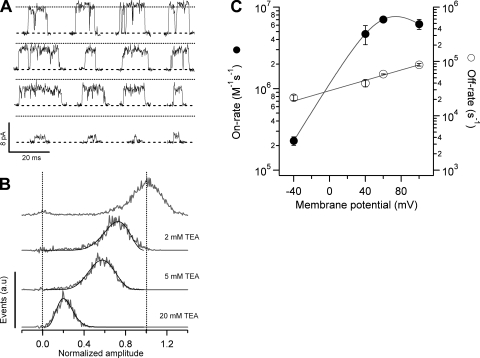
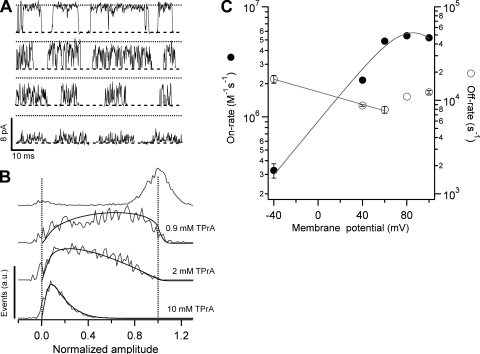
Block of TRPV1 by TEA is a very fast process. The individual blocking events are so short-lived that they are smeared by the filter and, as a result, block appears as an apparent reduction of the single-channel conductance. For this reason and to estimate the kinetic parameters of the blocking reaction, we used an approach to analyze the all-points amplitude histogram from bursts of openings, which makes use of the β distribution. As discussed in Materials and methods, we showed that this approximation can describe a two-state process filtered by a Gaussian filter with reasonable accuracy. Fig. 4 A shows representative single-channel openings in the absence and presence of increasing concentrations of TEA obtained at 60 mV. It is apparent that the effect of the blocker is a reduction of the single channel current. Fig. 4 B shows amplitude histograms for channel openings obtained from traces as in Fig. 4 A and constructed as indicated in Materials and methods. Superimposed on the histograms are fits to Eq. 2 convolved with a Gaussian function, which describes the current amplitude distribution of the closed level in the absence of blocker.
Figure 4.
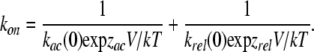 |
The β distribution provides an excellent description of the data, and blocker association and dissociation rates can be readily extracted. To obtain the pseudo first order on-rate constant, the rate obtained from the β distribution fit was plotted as a function of blocker concentration and the slope was used as an estimate of the association rate constant. The off-rate constant did not depend on the blocker concentration, and the dissociation rate constant was obtained as the zero intercept of the line fitted to the data (not depicted).
The voltage dependence of both the on- and off-rates is shown in Fig. 4 C. There are some striking features of these data. First, the on-rate constant is not a monotonic function of voltage. At voltages between −40 and 40 mV it increases exponentially with an equivalent valence of 0.94 eo, but at more positive voltages it approaches a maximum asymptotic value. As the estimated on-rate is very fast, a possible explanation for this is that at voltages more positive than 60 mV, the rate is limited by diffusion of the blocker to its binding site, as has been shown to occur for block of Anthrax toxin channels by QAs and in BK channels by Na+ (Yellen, 1984; Blaustein and Finkelstein, 1990a). A rough estimate of the expected diffusion-limited on-rate for a spherical blocker the size of TEA (8 Å diameter) and an absorbing disk of radius 6 Å, yields a value of 2.5 × 108 M−1s−1, which is more than an order of magnitude higher than the observed on-rate of 6.2 × 106 M−1s−1 at 100 mV. This result suggests that the plateauing on-rate is not due to diffusion limitation, and thus another mechanism should explain this observation, as will be shown for TPrA.
The other striking feature of the TEA kinetic data is that the off-rate increases with positive voltages. The off-rate cannot be estimated by the amplitude method at negative potentials because, due to the strong outward rectification of the single-channel I-V curve, currents at voltages more negative than −40 mV, even in the absence of blocker, are very small and difficult to separate from the recording noise. Nevertheless, given an overall voltage dependence of block at negative voltages of 1.5 eo (Fig. 3) and the voltage dependence of the on-rate constant, we estimated that the off-rate constant should have a valence of ∼−0.5 eo.
Both the saturation of the on-rate constant and the increase of the off-rate constant of TEA at positive voltages are responsible for the observed steady-state relief of block. These two observations seem counterintuitive, as the exit rate for a positively charged blocker is expected to increase at negative voltages and the entry rate to increase at positive potentials. We will come back to this point when we discuss block by TPrA.
Kinetics of Block by TPrA
Just as in the case of TEA, blockade by TPrA is exceedingly fast, and the individual blocking events are not well resolved at our recording bandwidth (Fig. 5). For this reason, we also applied the β distribution approach to estimate the rate constants of TPrA block of TRPV1. Fig. 5 A shows single-channel traces in the absence and presence of TPrA at the concentrations indicated in Fig. 5 B. All-point amplitude histograms derived from single-channel openings can be well described by the β distribution (Eq. 2), and on- and off-rate constants can be derived (Fig. 5, B and C). As with TEA, the on-rate constant for TPrA block saturates at positive potentials, and this happens at a value near 5 × 106 M−1s−1, well below the estimated diffusion-limited on-rate of 1.7 × 108 M−1s−1 for TPrA (9 Å diameter), which was calculated as for TEA. The voltage dependence of the on-rate constant is exponential at voltages below 40 mV, with a valence of 0.7 eo. In this same range of voltages, the off-rate constant increases with hyperpolarization with a valence of −0.19 eo, but, as for TEA block, the off-rate constant also increases at voltages more positive than 40 mV, instead of monotonically decreasing, and this behavior accounts for the marked relief of block at positive potentials that is also observed with TPrA.
Figure 5.
Kinetics of TPrA block. (A) Single-channel openings in the absence (top-most trace) and presence of 0.9, 2, and 10 mM TPrA obtained at 60 mV. The current amplitude decreases as the TPrA concentration is increased, as expected for a fast blocker. The dashed line represents the closed-channel current level, and the dotted line is the mean open-channel level in the absence of TPrA. (B) Normalized amplitude histograms obtained from traces as in A. Solid lines are fits to the β distribution with parameters: 0.9 mM, β = 8,571.7 s−1, α = 7,315.9 s−1; 2 mM, β = 8,563 s−1, α = 12,193 s−1; 10 mM, β = 11,198 s−1, α = 49,061 s−1. (C) Blocking rate constants obtained from the fits to the β distribution as in B in three different patches at several voltages and blocker concentrations. The on-rate increases with voltage and reaches a plateau. The off-rate decreases with increasing voltages but starts to increase at voltages more positive than 60 mV. The solid line is a fit to a double exponential as in Fig. 4. The values of kon and koff at 0 mV were estimated from an exponential fit to the data between −40 and 60 mV, and the parameters of the fit are: kon(0) = 8.6 × 105 M−1 s−1; z = 0.69 eo; koff(0) = 1.23 × 104 s−1; z = −0.19 eo. Group data are presented as mean ± SEM.
Ion Interactions and TPrA Blocker Kinetics
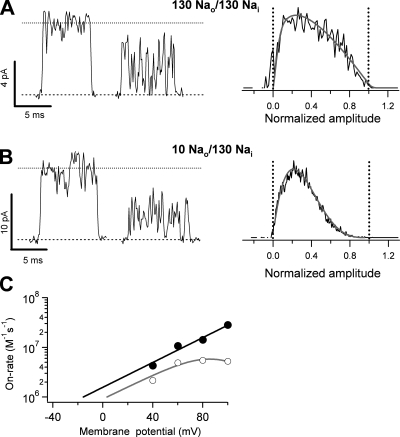
What is the origin of the saturation of the on-rate constant for TEA and TPrA? Given the observation that saturation occurs at rates below the expected diffusion-limited rate, we sought to investigate which other mechanism may be responsible for this effect. As mentioned earlier, we have observed that the voltage dependence of TBA blockade of TRPV1 channels can be explained by the coupled movement of permeant ions and blocker occupancy (Oseguera et al., 2007). This led us to suspect that a similar mechanism may be at work for TPrA and may be responsible for the voltage dependence of the kon at positive voltages. It has been observed that the coupling between permeant ions and the blocker occurs partially due to electrostatic interactions (Spassova and Lu, 1998). In our experimental conditions, we expect that repulsion of Na+ by TPrA into the selectivity filter may cause the charge displacement that is manifested as a large valence of the on-rate constant; at the same time, this electrostatic repulsion between the Na+ ion and TPrA molecule will tend to reduce the entry rate of TPrA to its blocking site and may be responsible for the observed saturation of the on-rate. To test this hypothesis, we performed measurements of the on-rate of TPrA under conditions of reduced extracellular Na+ concentration. We hypothesized that this maneuver would have the effect of reducing Na+ occupancy of the pore, causing a reduction of the possible interactions between the permeant ions and TPrA.
The data in Fig. 6 shows that, as expected, blockade of TRPV1 by TPrA is more effective in the low extracellular Na+ (10 mM; Fig. 6 B) experiments than in the isometric (130 mM) Na+ concentration experiments (Fig. 6 A), as indicated by the larger reduction of current amplitude produced by TPrA under low extracellular sodium conditions. This reduced current amplitude translates into larger values for the on-rate constant. In addition, the on-rate constant no longer saturates at positive voltages and behaves as an exponential function of voltage for the entire range of voltages tested. The corresponding valence of this exponential is 0.7 eo (Fig. 6 C), which is the same as that measured at negative potentials under isometric 130 mM Na+ conditions.
Figure 6.
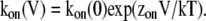 |
These data support our hypothesis that the entry rate of TPrA is limited at positive voltages by its interaction with the permeant ion. This interaction with Na+ also suggests that QA blockers bind to an intracellular site in the pore of TRPV1 channels, allowing us to use these molecules as probes for obtaining information about the pore properties of this channel protein.
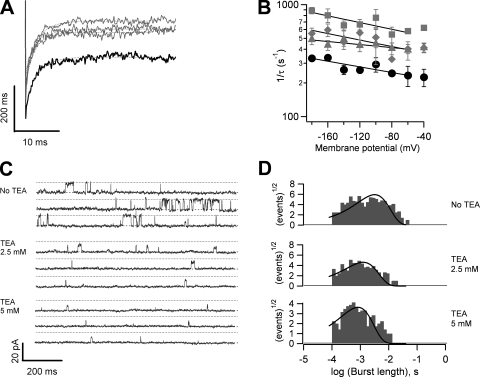
Block Kinetics of Slower Blockers: TBA and TPA
It has been shown that the kinetics of TRPV1 block by TBA are sufficiently slow to be observed in macroscopic current recordings as an exponential relaxation of current during depolarizing pulses (Oseguera et al., 2007). We observed that TPA is also a slower blocker than TEA and TPrA. In single-channel recordings, TPA does not affect the single-channel conductance, and blocking events can be well resolved (Fig. 7 A). When dwell-time histograms are compiled, blockade is observed as an increase in the number of long-duration events in the closed-time histogram (Fig. 7 B). The voltage-dependent blocking kinetics of TPA can also be observed in macroscopic recordings as a current relaxation during positive voltage steps (Fig. 7 C). This relaxation can be fitted with an exponential function (Fig. 7 C, top). During repolarizing voltage pulses, the channel seems to no longer be able to deactivate and instead the tail current increases with a rate that is voltage dependent. This behavior of the tail current reflects the time course of TPA leaving its binding site in the channel, and an estimate of this rate can be obtained from the inverse of the time constant of an exponential function fitted to the tail current relaxation (Fig. 7 C, bottom). The summarized data for on- and off-rate constants of block by TPA, obtained from macroscopic current recordings, is presented in Fig. 7 D. Both rates are exponential functions of voltage.
Figure 7.
Kinetics of block by TPA. (A) Single-channel traces in the absence (top trace) and presence of 80 μM TPA (bottom trace). (B) Closed time histograms from multiple traces as in A fitted with three exponential components. (C; top) Macroscopic kinetics of block during depolarizing voltage pulses ranging from 40 to 160 mV in the presence of 40 μM TPA. The onset of block can be seen as an exponential decay of the initial current, as expected for a slower blocker. (Bottom) Blocker dissociation observed during tail current experiments. Traces were obtained in the presence of 80 μM TPA at −20, −40, −60, −80, and −100 mV. Blocker dissociation can be seen as an exponential increase in the current. The off-rates were obtained from fits to an exponential (solid lines). (D) The on- and off-rates obtained from traces as in C, plotted as a function of voltage. Both rates are voltage dependent and have the following values estimated from an exponential fit to the data: koff(0 mV) = 10.73 s−1 (n = 3); zoff = 0.45 eo; kon(0 mV) = 1.03 × 105 M−1s−1 (n = 5); zon = 0.68 eo. Group data are presented as mean ± SEM.
Table I summarizes the results of kinetic analysis for all four blockers. The main observation is that as the size of the blocker increases, so does its apparent affinity. When one compares the smaller blocker, TEA, to the bigger one, TPA, it is observed that the increase in apparent affinity as a function of blocker size is accomplished by a >1,000-fold decrease in the off-rate and only a 10-fold decrease in the on-rate constant.
TABLE I.
Summary of Kinetic Parameters for QA Block of TRPV1a
| Blocker | Association rate constant kon(0 mV), (M−1s−1) |
Dissociation rate constant koff (0 mV), (s−1) |
zon (eo) | zoff (eo) |
|---|---|---|---|---|
| TEA (n = 3) | 1.04 × 106 ± 4.8 × 105 | 2.89 × 104 ± 3.2 × 103 | 0.94 ± 0.13 | 0.27 ± 0.03 |
| TPrA (n = 3) | 8.59 × 105 ± 1.5 × 105 | 1.23 × 104 ± 186 | 0.69 ± 0.14 | −0.19 ± 0.01 |
| TBA (n = 6) | 2.5 × 105 ± 2.9 × 104 | 83.76 ± 10 | 0.93 ± 0.03 | −0.63 ± 0.03 |
| TPA (n = 5) | 1.03 × 105 ± 4 × 104 | 10.73 ± 0.95 | 0.68 ± 0.06 | −0.45 ± 0.02 |
The table summarizes the on- and off-rates for the four blockers used in this study and their associated valence.
Data are mean ± SEM.
Closure Kinetics in the Presence of Blockers
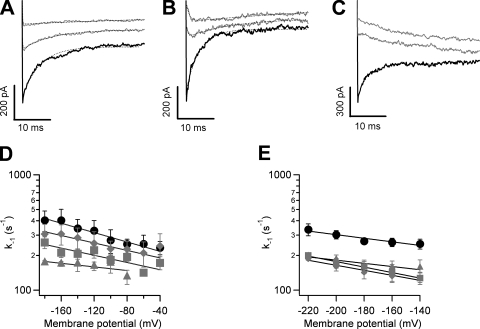
The kinetics of channel closure in the presence of a blocker molecule can reflect some aspects of the nature of the gating mechanism. It has been shown that if the blocker is able to only reach its binding site when the channel is open, the time course of channel closure should be slowed down because the blocker needs to leave the open channel before the activation gate can close (Armstrong, 1971; Choi et al., 1993; Li and Aldrich, 2004). To understand the relationship between blocker occupancy and gating, we examined channel closure kinetics with tail current protocols, both in unblocked channels and when channels were blocked by the fast blockers, TEA and TPrA, and by the slow blockers, TBA and TPA. The voltage dependence of deactivation of TRPV1 channels is small (z−1, ∼0.1 eo; Figs. 8 B and 9, D and E) when compared with Kv channels, and as a result the channels cannot be completely closed upon repolarization to the voltages we used; nevertheless, tail currents can be reliably recorded at negative voltages.
Figure 8.
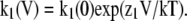 |
Figure 9.
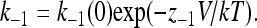 |
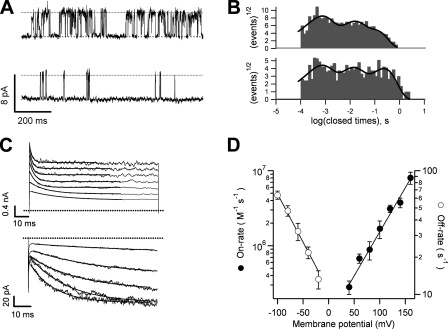
Block of TRPV1 channels by TEA is more voltage dependent than that produced by the other blockers used in this study, and when this blocker is applied to inside-out patches, tail currents were in fact accelerated, as if TEA made closing easier. The magnitude of the tail current in the presence of TEA is decreased, reflecting steady-state block at the depolarizing prepulse. Tail currents in the absence and presence of blocker could be fitted to an exponential time course (Fig. 8 A). A plot of the inverse of the time constant of this exponential as a function of voltage reveals a weak voltage dependence for channel closure. In the absence of TEA, the channels close with a rate at 0 mV of 196 s−1 and a valence of 0.07 eo, a rather modest voltage dependence. When TEA is present, the closing rate increases up to approximately threefold at 80 mM TEA over all voltages, indicating that channel closure is in fact faster when the channel is blocked by TEA (Fig. 8 B).
This observation can be explained by a model in which the channels are able to close with TEA in the pore or, alternatively, by assuming that TEA can gain access to channels in the closed state. In both cases, one expects an acceleration of the closing rate because the closed blocked states provide a second closing pathway. Another indication that TEA may remain in its binding site when the channel is closed is provided by the observation that the duration of bursts of openings is shorter in the presence of TEA (Fig. 8, C and D). The shortening of burst lengths can again be explained by considering a mechanism that allows occupation of closed states by TEA.
The blocking behavior of TPrA differs from that of TEA. Tail currents of TRPV1 in the presence of TPrA show significant differences in time course when compared with currents in the absence of blocker. Tails were significantly slower in the presence of the blocker (Fig. 9 A).Moreover, tail currents in the presence of TPrA develop a characteristic “hook” indicative of the blocker having to exit the channel before it can close, as has been described in Na and Kv channels (Yeh and Narahashi, 1977; Clay, 1995).
Tail current kinetics behaves in a similar fashion when TBA is present. That is, a significant slowing of closure is obtained and there is a marked appearance of hooks in the tail currents (Fig. 9 B).
Because tail current experiments with TPrA and TBA are consistent with a “foot-in-the-door” mechanism, quantitation of the slowing of tail currents by these blockers was performed in the framework of this mechanism as follows: After a depolarizing step in the presence of a blocker, the channels are mostly in an open but blocked state. During hyperpolarization, the blocker will first leave the channel with rate koff and then channel closure occurs, with rate k−1, according to Scheme 1.
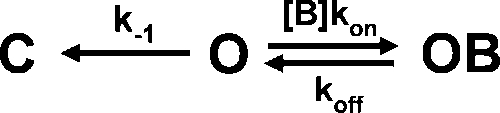 |
(SCHEME 1) |
At negative voltages the blocking rate ([B]kon) and the reopening rate are small, and thus the time course of the occupancy of the open state is approximately given by:
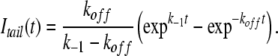 |
(4) |
The tail currents are proportional to the probability of being in state O, so tail currents were fitted to Eq. 4, and k−1 was plotted as a function of voltage to serve as an index of the channel's closing rate. This was compared with the closing rate in the absence of blockers. Fig. 9 compares the voltage dependence of the apparent closing rate (k−1) as the concentrations of TPrA and TBA are increased. We observed that these two blockers behave in similar fashion and markedly slow the closing rate of TRPV1 channels (Fig. 9, D and E).
When TPA is used, the off-rate of the blocker is so slow that the channels close much more slowly than the duration of the hyperpolarizing pulse and, as explained earlier (Fig. 7), only a slow increase in current that is produced by the slow exit of TPA from the channel can be observed (Fig. 9 C). Nevertheless, the results of tail current experiments with TPrA, TBA, and TPA suggest that these blockers occupy a binding site accessible through the intracellular mouth of the channel pore and that these molecules occupy the open state and leave the binding site before channel closure can occur, that is, the blocker acts as a foot in the door (Scheme 1). Mechanistically, these observations of the effects of TPrA, TBA, and TPA on tail current kinetics are consistent with an open-state block mechanism, and suggest that these blockers gain access to a binding site located after a cytoplasmic gate, as has been observed in voltage-dependent potassium channels (Armstrong, 1971; Choi et al., 1993; Li and Aldrich, 2004).
DISCUSSION
The results presented here indicate that the quaternary ammoniums TPrA, TEA, TBA, and TPA interact with TRPV1 channels through different mechanisms, depending on the size of the blocker. Similar to what happens in potassium-selective channels, an increase of the size of the blocker and its hydrophobic character produces a corresponding increase in the affinity of the blocker for the channel. In the case of Shaker potassium channels, it has been shown that the affinities of Qn-TEA blockers increase with size in a manner that is consistent with the expectation that each methylene group should add 1.2 RT units to the absolute value of the apparent binding energy of the blocker (Choi et al., 1993). A similar analysis of our data shows that this energy is larger, in the order of 2 RT. This value is remarkably close to what is expected from the energy of hydration of the blocker molecules using the Born theory of ion solvation (Hille, 2001). This similarity probably arises from the fact that hydrophobic interactions are the main determinants of the interaction of the blockers with the channel pore. Our experiments show that the kinetic reason for the increase in apparent affinity with increasing blocker size is mainly the result of a decrease in the rate at which the blocker leaves the channel, with the smaller size blockers TEA and TPrA having dissociation rates at 0 mV in the order of 105 and 104 s−1, respectively, whereas TBA and TPA have dissociation rates of 84 and 10 s−1, respectively.
Voltage Dependence of Block
All four blockers produce a blockade that is clearly voltage dependent, although they show some differences from the block they induce in other voltage-gated channels. The main difference is the presence of reduced block at positive voltages, which may be explained by a permeant blocker mechanism. A recent paper (Chung et al., 2008) suggests that the permeability of TRPV1 to large cations is increased upon prolonged activation by capsaicin and modulation by PKC, and this is manifested as a time-dependent shift of the reversal potential when Na+ is only present in the inside and a large cation is in the outside of the membrane. We have not observed shifts of reversal potential in the presence of large concentrations of intracellular blockers, nor changes in the single-channel current size through the duration of the experiment. We suspect that our recording conditions are sufficiently different to explain these observations. In our experiments, Na+ ions are always present in both the intracellular and extracellular media. Of course, there may still be a fraction of current carried by the blockers, which may contribute to relief of block, but it is too small to be measured as a shift in reversal potential in our experiments.
Kinetics of Block by Small Blockers
To be able to measure the kinetics of the fast blockers TEA and TPrA, we have applied an analysis method that has been shown to work well with similarly fast blockers in BK channels, Ca2+ channels, and Na+ channels (Yellen, 1984; Franco et al., 1991; Winegar et al., 1991; Kimbrough and Gingrich, 2000). To use this method, we had to address two fundamental issues: First, this method was previously applied to Bessel-filtered data, whereas our data were filtered with a Gaussian filter. The validation method we used was to numerically simulate a random two-state process, which is then filtered by a Gaussian filter. We sought to determine if the β distribution can provide a good estimate of the rate constants used to simulate the data. This approach was able to determine rate constants with an error of <1%. The second issue had to do with the validity of considering the blockade observed here a two-state process, where the blocked state has a nominally zero conductance. The evidence we have for this is that at elevated TEA and TPrA concentrations there is no residual current flowing though TRPV1 channels. This is also true when we examined the slower blockers, TBA and TPA, at the single-channel level. Here, the blocking events can readily be observed and the blocker produces a blocked state with conductance indistinguishable from that of the closed-channel noise level.
A very interesting observation is the fact that the blocker association rates (on-rates) for TEA and TPrA are so fast that blockade is manifested as a reduction of the single-channel current. Fast blocker kinetics indicates that there is a small energy barrier to the entrance and exit of the blocker molecule. An estimate of the blocker association rate constant using the β distribution method indicates that these rates are on the order of 106 M−1s−1 at 0 mV for both blockers. These on-rates are similar to rates observed for other QAs in voltage-dependent potassium channels (Choi et al., 1993; Kutluay et al., 2005; Faraldo-Gomez et al., 2007). The blocker dissociation rate constant (off-rate) is also very fast, on the order of 105 s−1 for TEA and 104 s−1 for TPrA. These very fast off-rate constants are responsible for the observed fast block and are many orders of magnitude faster than those observed in inward rectifier potassium channels (Guo and Lu, 2001), although they are similar to TEA off-rates reported for the RCK2 voltage-dependent K+ channel (Kirsch et al., 1991) and the KcSA channel (Kutluay et al., 2005).
The blocker association constant shows saturation at voltages more positive than 60 mV. A similar phenomenon has been observed in the blockade by QAs of the Anthrax toxin channel. In that case, it was shown that the saturation occurred at the value of blocker association rate predicted by diffusion and that indeed the on-rate constant was diffusion limited (Blaustein and Finkelstein, 1990a; Blaustein et al., 1990). In the present experiments, saturation of the on-rate of TEA and TPrA occurs at a value well below the calculated diffusion-limited rate constant for association of a blocker molecule with an absorbing disc of 6 Å diameter (Berg, 1983). This is a simplified calculation that assumes that the TEA and TPrA molecules are spherically symmetric and provides a lower bound for the value of the on-rate constant.
In the case of TPrA, our experiments using low concentrations of extracellular Na+ clearly show that the rate of TPrA association increases exponentially with voltage, reaching values almost an order of magnitude larger at 100 mV than at high extracellular Na+ concentrations, and not showing evidence of saturation with voltage. We interpret this result as an indication that, indeed, the entry of positively charged blocker molecules to the inner pore of TRPV1 is limited by interactions with the permeant ion, in this case Na+. This is analogous to the knockoff effect observed in potassium channels, where increasing the extracellular concentration of permeant ions decreases the affinity of the blocker molecule (Armstrong, 1971; Hille and Schwarz, 1978). These results are also consistent with previous data indicating ion–blocker interactions in the pore of TRPV1 between Na+ and TBA, and indicate that the permeation pathway of TRPV1 channels has multi-ion pore characteristics.
Both for TEA and TPrA, most of the voltage dependence of the blocking reactions is related to the association rate (kon), with zon values of 0.94 and 0.69, respectively. These very high valences cannot be explained by the traditional interpretation that relates them to the voltage drop across the inner channel pore. It has been shown that for the open potassium channels, the voltage drop across this region is at most 15% (Jiang et al., 2002). If this is also the case for TRPV1 channels, the very high apparent blocking valences may be the result of coupling between blocker binding and charge movement in the selectivity filter (Spassova and Lu, 1998).
The fact that most of the voltage dependence is associated with the blocker on-rate constant can be understood if the energy barrier for entry of TEA and TPrA is highly asymmetrical and may reflect the fact that the charge displacement due to permeant ions occurs when the blocker first enters the pore and subsequent exit of the blocker is not accompanied by a strictly coupled rearrangement of permeant ions. In contrast with TEA and TPrA, block by TBA and TPA is less voltage dependent and this voltage dependence is observed both in the blocker association as well as in the dissociation rate constants (Table I).
Closure Kinetics in the Presence of Blockers
Our experiments measuring the effects of blockers on closure kinetics provide evidence that the mechanism of channel block is different for each blocker and that it depends on the size of the blocker. The bigger blockers, like TBA and TPA, very clearly affect the kinetics of tail currents at negative voltages in a manner that is consistent with a state-dependent mechanism. The tail currents become slower and the kinetics can be explained with a model in which the channel has to let the blocker dissociate before it can close (Scheme 1), an effect that has been previously observed with open-state block of potassium channels, particularly by QAs (Armstrong, 1971; Choi et al., 1993; Clay, 1995). The smaller blocker TPrA produces a less dramatic effect on the shape of the tail current, but it still slows tail currents as is observed with TBA and TPA. This indicates that TPrA is able to occupy its binding site in the open channel and interferes with channel closure.
For TEA, the mechanism of block is clearly different from the other QAs. Tail currents in the presence of TEA were not slowed down, and in fact the channels were able to close faster with TEA in the pore. This kinetic effect can be also observed in single-channel burst kinetics as a progressive shortening of the burst length with increasing TEA concentrations. In spite of the very fast dissociation rates of TEA, we know that the channels are blocked at the beginning of the hyperpolarizing pulse because the amplitude of the tail current is reduced with respect to the tail current in the absence of TEA (Fig. 8 A). The fact that channels remain blocked by this fast blocker at negative potentials and that they are able to close with faster kinetics suggests that TRPV1 can close with TEA still in its binding site.
A mechanism in which the blocker can only access its binding site when the channel is open, but becomes trapped upon channel deactivation, has been demonstrated in Kv and HCN potassium channels (Holmgren et al., 1997; Shin et al., 2001). Alternatively, the faster closing kinetics with TEA can be explained if this blocker is able to gain access to closed channels as well as open channels. To differentiate between these possibilities, we attempted to measure trapping of TEA, TBA, or TPA, but two problems prevented us from achieving this goal. TRPV1 channels cannot be completely opened or closed with voltage alone. We measured a ligand-independent open probability in the order of 0.01 at 100 mV, and this is reduced to ∼0.005 at −140 mV (not depicted). Second, removal of capsaicin cannot be achieved fast enough to close channels in this manner, so we suspect that TEA can leave the open channels before they can be closed by capsaicin washout. However, both possible mechanisms for TEA block require that the channel can accommodate this QA ion in the closed state. The fact that TEA may be able to reside in the closed channel, combined with the observation that TPrA interferes with channel closure, suggests that the inner pore cavity of TRPV1 can comfortably accommodate an ion of ∼8 Å in the closed state, but not a 9-Å molecule.
Significance for the Structure of the Gate and the Dimensions of the Inner Pore
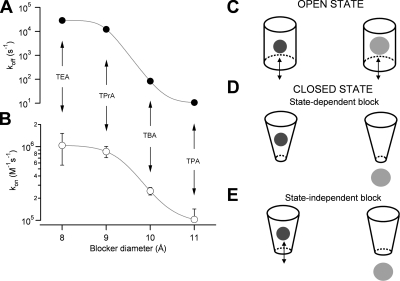
What do these experiments tell us about the probable structure of the inner pore of TRPV1 channels? In principle, probing the channel with varying sizes of blocker molecules should provide us with a way to size the pore in an analogous manner to what was achieved for Na+ channels (Hille, 1971). We observed that both the association and dissociation rate constants decrease in a monotonic fashion as a function of the blocker size (Fig. 10, A and B). Based on the shape of this relationship, it could be argued that the inner pore of an open channel has an admission cutoff size between the size of TPrA and TBA, with 9 and 10 Å, respectively, which corresponds to the region where the association and dissociation rates have their largest reduction. This does not mean that larger organic compounds cannot enter the inner pore. In fact, TPA is able to block TRPV1, and we have observed that QAs as large as tetraoctylammonium (14 Å) can also block this channel (not depicted). This approximate size of the inner pore of open TRPV1 is consistent with the size of the inner pore of the open MthK potassium channel, which is 12 Å (Jiang et al., 2002).
Figure 10.
Dependence of the on- and off-rates of QA blockers on their size. The blocker dissociation (A) or association rates (B) are plotted as a function of their ionic radii. The continuous lines are drawn as a visual guide and have no theoretical significance. The decrease of the rates as a function of size is monotonic and there is not a clear cut-off size. Data are mean ± SEM of five to six experiments. (C–E) Cartoon depicting the possible ways in which the QAs may interact with the channel pore. (C) Cartoon of the open-channel pore with a blocker the size of TEA (right) or TPrA (left). (D) A model in which all QAs are only able to access the blocking site when the channel is in the open state, but TEA can reside inside the closed channel (left), whereas larger QAs cannot (right). (E) Alternative model in which the TEA molecule can block the channel in a state-independent manner, whereas the rest of the QAs can only access the blocking site when the channel is open, and hence interact with channel gating. In any way, TEA can reside in its blocking site when the channel is closed, whereas the other QAs do not.
Our observation that TEA may remain in the closed channel, but TPrA already interferes with channel deactivation, would also suggest that the inner pore becomes smaller than 9 Å when the channel is closed. The structure of the closed KcsA channel suggests that the inner pore in this conformation has dimensions from 12 to 14 Å, so that depending on how deep the QA binding site is in TRPV1 channels, it may not be able to accommodate TPrA in the closed state.
The possibility that the closed TPRV1 channel can accommodate TEA but not TPrA is not surprising. It has been shown that wild-type Shaker K+ channels cannot trap TEA, but the mutant I470C, which presumably has a larger pore, is able to do it (Holmgren et al., 1997; Melishchuk and Armstrong, 2001). This would suggest that the main determinant of trapping may be the pore size (or blocker size), and a size difference of just a few angstroms is all that is needed for the closed pore to accommodate a blocker molecule. Fig. 10 (C–E) shows a cartoon of the ways in which the blockers may be interacting with the channel and affecting channel gating. Fig. 10 D represents the case in which all blocker molecules, including TEA, can only access their binding site when the channel is in the open state; however, TEA can become trapped inside the channel when it closes. The other possibility (Fig. 10 D) is that the TEA molecule can block the channel in a state-independent manner, whereas the rest of the QAs can only access their blocking site when the channel is open.
Interestingly, the blocking characteristics of these molecules suggest the existence of an intracellular gate that may or may not be a gate for permeant ions. It remains to be seen if the gate of these channels is like that of the voltage-gated potassium channels (Holmgren et al., 1998; Yellen, 2002) or more like the pore gate in CNG-activated channels (Contreras et al., 2008), or the bacterial-nonselective channels, which apparently are closer to TRP channels in their pore sequence and probable structure.
Acknowledgments
We thank Félix Sierra, Laura Ongay, Sergio Rojas, Juan Manuel Barbosa, Ivette Rosas, Adrián Aguilera Jiménez, and Aurey Galván at Instituto de Fisiología Celular of UNAM for valuable technical support. We are grateful to Miguel Holmgren at the National Institutes of Health for invaluable discussions of this manuscript.
This study was supported by CONACyT grants 48990 (to L.D. Islas) and 46004 (to T. Rosenbaum), and DGAPA (PAPIIT) grants IN201705 (to T. Rosenbaum) and IN202006-3 (to L.D. Islas).
Angus C. Nairn served as editor.
Abbreviations used in this paper: QA, quaternary ammonium ion; TBA, tetrabutylammonium; TPA, tetrapentylammonium; TPrA, tetrapropylammonium; TRPV1, transient receptor potential vanilloid 1.
References
- Armstrong, C.M. 1971. Interaction of tetraethylammonium ion derivatives with the potassium channels of giant axons. J. Gen. Physiol. 58:413–437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armstrong, C.M., and B. Hille. 1972. The inner quaternary ammonium ion receptor in potassium channels of the node of Ranvier. J. Gen. Physiol. 59:388–400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berg, H.C. 1983. Random Walks in Biology. Princeton University Press, Princeton, NJ. 142 pp.
- Bezanilla, F., and C.M. Armstrong. 1972. Negative conductance caused by entry of sodium and cesium ions into the potassium channels of squid axons. J. Gen. Physiol. 60:588–608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhave, G., W. Zhu, H. Wang, D.J. Brasier, G.S. Oxford, and R.W. Gereau. 2002. cAMP-dependent protein kinase regulates desensitization of the capsaicin receptor (VR1) by direct phosphorylation. Neuron. 35:721–731. [DOI] [PubMed] [Google Scholar]
- Blaustein, R.O., and A. Finkelstein. 1990. a. Diffusion limitation in the block by symmetric tetraalkylammonium ions of anthrax toxin channels in planar phospholipid bilayer membranes. J. Gen. Physiol. 96:943–957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blaustein, R.O., and A. Finkelstein. 1990. b. Voltage-dependent block of anthrax toxin channels in planar phospholipid bilayer membranes by symmetric tetraalkylammonium ions. Effects on macroscopic conductance. J. Gen. Physiol. 96:905–919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blaustein, R.O., E.J. Lea, and A. Finkelstein. 1990. Voltage-dependent block of anthrax toxin channels in planar phospholipid bilayer membranes by symmetric tetraalkylammonium ions. Single-channel analysis. J. Gen. Physiol. 96:921–942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caterina, M.J., M.A. Schumacher, M. Tominaga, T.A. Rosen, J.D. Levine, and D. Julius. 1997. The capsaicin receptor: a heat-activated ion channel in the pain pathway. Nature. 389:816–824. [DOI] [PubMed] [Google Scholar]
- Cheng, W., F. Yang, C.L. Takanishi, and J. Zheng. 2007. Thermosensitive TRPV channel subunits coassemble into heteromeric channels with intermediate conductance and gating properties. J. Gen. Physiol. 129:191–207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi, K.L., C. Mossman, J. Aube, and G. Yellen. 1993. The internal quaternary ammonium receptor site of Shaker potassium channels. Neuron. 10:533–541. [DOI] [PubMed] [Google Scholar]
- Chuang, H.H., E.D. Prescott, H. Kong, S. Shields, S.E. Jordt, A.I. Basbaum, M.V. Chao, and D. Julius. 2001. Bradykinin and nerve growth factor release the capsaicin receptor from PtdIns(4,5)P2-mediated inhibition. Nature. 411:957–962. [DOI] [PubMed] [Google Scholar]
- Chung, M.K., A.D. Guler, and M.J. Caterina. 2008. TRPV1 shows dynamic ionic selectivity during agonist stimulation. Nat. Neurosci. 11:555–564. [DOI] [PubMed] [Google Scholar]
- Clay, J.R. 1995. Quaternary ammonium ion blockade of IK in nerve axons revisited. Open channel block vs. state independent block. J. Membr. Biol. 147:23–34. [DOI] [PubMed] [Google Scholar]
- Colquhoun, D., and B. Sakmann. 1985. Fast events in single-channel currents activated by acetylcholine and its analogues at the frog muscle end-plate. J. Physiol. 369:501–557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colquhoun, D., and F. Sigworth. 1995. Fitting and statistical analysis of single-channel records. In Single-channel Recording. B. Sakmann and E. Neher, editors. Plenum Press, New York. 483–587.
- Contreras, J.E., D. Srikumar, and M. Holmgren. 2008. Gating at the selectivity filter in cyclic nucleotide-gated channels. Proc. Natl. Acad. Sci. USA. 105:3310–3314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cortright, D.N., J.E. Krause, and D.C. Broom. 2007. TRP channels and pain. Biochim. Biophys. Acta. 1772:978–988. [DOI] [PubMed] [Google Scholar]
- Faraldo-Gomez, J.D., E. Kutluay, V. Jogini, Y. Zhao, L. Heginbotham, and B. Roux. 2007. Mechanism of intracellular block of the KcsA K+ channel by tetrabutylammonium: insights from X-ray crystallography, electrophysiology and replica-exchange molecular dynamics simulations. J. Mol. Biol. 365:649–662. [DOI] [PubMed] [Google Scholar]
- Ferrer-Montiel, A., C. Garcia-Martinez, C. Morenilla-Palao, N. Garcia-Sanz, A. Fernandez-Carvajal, G. Fernandez-Ballester, and R. Planells-Cases. 2004. Molecular architecture of the vanilloid receptor. Insights for drug design. Eur. J. Biochem. 271:1820–1826. [DOI] [PubMed] [Google Scholar]
- Fitzhugh, R. 1983. Statistical properties of the asymmetric random telegraph signal, with applications to single-channel analysis. Math. Biosci. 64:75–89. [Google Scholar]
- Franco, A. Jr., B.D. Winegar, and J.B. Lansman. 1991. Open channel block by gadolinium ion of the stretch-inactivated ion channel in mdx myotubes. Biophys. J. 59:1164–1170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- French, R.J., and J.J. Shoukimas. 1981. Blockage of squid axon potassium conductance by internal tetra-N-alkylammonium ions of various sizes. Biophys. J. 34:271–291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- French, R.J., and J.J. Shoukimas. 1985. An ion's view of the potassium channel. The structure of the permeation pathway as sensed by a variety of blocking ions. J. Gen. Physiol. 85:669–698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garcia-Martinez, C., C. Morenilla-Palao, R. Planells-Cases, J.M. Merino, and A. Ferrer-Montiel. 2000. Identification of an aspartic residue in the P-loop of the vanilloid receptor that modulates pore properties. J. Biol. Chem. 275:32552–32558. [DOI] [PubMed] [Google Scholar]
- Gunthorpe, M.J., M.H. Harries, R.K. Prinjha, J.B. Davis, and A. Randall. 2000. Voltage- and time-dependent properties of the recombinant rat vanilloid receptor (rVR1). J. Physiol. 525:747–759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo, D., and Z. Lu. 2000. Mechanism of IRK1 channel block by intracellular polyamines. J. Gen. Physiol. 115:799–814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo, D., and Z. Lu. 2001. Kinetics of inward-rectifier K+ channel block by quaternary alkylammonium ions. Dimension and properties of the inner pore. J. Gen. Physiol. 117:395–406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heginbotham, L., and E. Kutluay. 2004. Revisiting voltage-dependent relief of block in ion channels: a mechanism independent of punchthrough. Biophys. J. 86:3663–3670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hille, B. 1971. The permeability of the sodium channel to organic cations in myelinated nerve. J. Gen. Physiol. 58:599–619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hille, B. 2001. Ion Channels of Excitable Membranes. Sinauer, Sunderland, MA. 814 pp.
- Hille, B., and W. Schwarz. 1978. Potassium channels as multi-ion single-file pores. J. Gen. Physiol. 72:409–442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmgren, M., P.L. Smith, and G. Yellen. 1997. Trapping of organic blockers by closing of voltage-dependent K+ channels: evidence for a trap door mechanism of activation gating. J. Gen. Physiol. 109:527–535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmgren, M., K.S. Shin, and G. Yellen. 1998. The activation gate of a voltage-gated K+ channel can be trapped in the open state by an intersubunit metal bridge. Neuron. 21:617–621. [DOI] [PubMed] [Google Scholar]
- Hwang, S.W., H. Cho, J. Kwak, S.Y. Lee, C.J. Kang, J. Jung, S. Cho, K.H. Min, Y.G. Suh, D. Kim, and U. Oh. 2000. Direct activation of capsaicin receptors by products of lipoxygenases: endogenous capsaicin-like substances. Proc. Natl. Acad. Sci. USA. 97:6155–6160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang, Y., A. Lee, J. Chen, M. Cadene, B.T. Chait, and R. MacKinnon. 2002. The open pore conformation of potassium channels. Nature. 417:523–526. [DOI] [PubMed] [Google Scholar]
- Kedei, N., T. Szabo, J.D. Lile, J.J. Treanor, Z. Olah, M.J. Iadarola, and P.M. Blumberg. 2001. Analysis of the native quaternary structure of vanilloid receptor 1. J. Biol. Chem. 276:28613–28619. [DOI] [PubMed] [Google Scholar]
- Kimbrough, J.T., and K.J. Gingrich. 2000. Quaternary ammonium block of mutant Na+ channels lacking inactivation: features of a transition-intermediate mechanism. J. Physiol. 529:93–106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirsch, G.E., M. Taglialatela, and A.M. Brown. 1991. Internal and external TEA block in single cloned K+ channels. Am. J. Physiol. 261:C583–C590. [DOI] [PubMed] [Google Scholar]
- Kutluay, E., B. Roux, and L. Heginbotham. 2005. Rapid intracellular TEA block of the KcsA potassium channel. Biophys. J. 88:1018–1029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, W., and R.W. Aldrich. 2004. Unique inner pore properties of BK channels revealed by quaternary ammonium block. J. Gen. Physiol. 124:43–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macpherson, L.J., B.H. Geierstanger, V. Viswanath, M. Bandell, S.R. Eid, S. Hwang, and A. Patapoutian. 2005. The pungency of garlic: activation of TRPA1 and TRPV1 in response to allicin. Curr. Biol. 15:929–934. [DOI] [PubMed] [Google Scholar]
- Melishchuk, A., and C.M. Armstrong. 2001. Mechanism underlying slow kinetics of the OFF gating current in Shaker potassium channel. Biophys. J. 80:2167–2175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mohapatra, D.P., S.Y. Wang, G.K. Wang, and C. Nau. 2003. A tyrosine residue in TM6 of the Vanilloid Receptor TRPV1 involved in desensitization and calcium permeability of capsaicin-activated currents. Mol. Cell. Neurosci. 23:314–324. [DOI] [PubMed] [Google Scholar]
- Moriyama, T., T. Iida, K. Kobayashi, T. Higashi, T. Fukuoka, H. Tsumura, C. Leon, N. Suzuki, K. Inoue, C. Gachet, et al. 2003. Possible involvement of P2Y2 metabotropic receptors in ATP-induced transient receptor potential vanilloid receptor 1-mediated thermal hypersensitivity. J. Neurosci. 23:6058–6062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Numazaki, M., and M. Tominaga. 2004. Nociception and TRP channels. Curr. Drug Target. CNS Neurol. Disord. 3:479–485. [DOI] [PubMed] [Google Scholar]
- Oseguera, A.J., L.D. Islas, R. Garcia-Villegas, and T. Rosenbaum. 2007. On the mechanism of TBA block of the TRPV1 channel. Biophys. J. 92:3901–3914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Owsianik, G., K. Talavera, T. Voets, and B. Nilius. 2006. Permeation and selectivity of TRP channels. Annu. Rev. Physiol. 68:685–717. [DOI] [PubMed] [Google Scholar]
- Piper, A.S., J.C. Yeats, S. Bevan, and R.J. Docherty. 1999. A study of the voltage dependence of capsaicin-activated membrane currents in rat sensory neurones before and after acute desensitization. J. Physiol. 518:721–733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Premkumar, L.S., and G.P. Ahern. 2000. Induction of vanilloid receptor channel activity by protein kinase C. Nature. 408:985–990. [DOI] [PubMed] [Google Scholar]
- Premkumar, L.S., Z.H. Qi, J. Van Buren, and M. Raisinghani. 2004. Enhancement of potency and efficacy of NADA by PKC-mediated phosphorylation of vanilloid receptor. J. Neurophysiol. 91:1442–1449. [DOI] [PubMed] [Google Scholar]
- Price, T.J., A. Patwardhan, A.N. Akopian, K.M. Hargreaves, and C.M. Flores. 2004. Modulation of trigeminal sensory neuron activity by the dual cannabinoid-vanilloid agonists anandamide, N-arachidonoyl-dopamine and arachidonyl-2-chloroethylamide. Br. J. Pharmacol. 141:1118–1130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salazar, H., I. Llorente, A. Jara-Oseguera, R. Garcia-Villegas, M. Munari, S.E. Gordon, L.D. Islas, and T. Rosenbaum. 2008. A single N-terminal cysteine in TRPV1 determines activation by pungent compounds from onion and garlic. Nat. Neurosci. 11:255–261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shin, K.S., B.S. Rothberg, and G. Yellen. 2001. Blocker state dependence and trapping in hyperpolarization-activated cation channels: evidence for an intracellular activation gate. J. Gen. Physiol. 117:91–101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigworth, F.J., and S.M. Sine. 1987. Data transformations for improved display and fitting of single-channel dwell time histograms. Biophys. J. 52:1047–1054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spassova, M., and Z. Lu. 1998. Coupled ion movement underlies rectification in an inward-rectifier K+ channel. J. Gen. Physiol. 112:211–221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Susankova, K., R. Ettrich, L. Vyklicky, J. Teisinger, and V. Vlachova. 2007. Contribution of the putative inner-pore region to the gating of the transient receptor potential vanilloid subtype 1 channel (TRPV1). J. Neurosci. 27:7578–7585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szallasi, A., and P.M. Blumberg. 1999. Vanilloid (Capsaicin) receptors and mechanisms. Pharmacol. Rev. 51:159–212. [PubMed] [Google Scholar]
- Szallasi, A., B. Conte, C. Goso, P.M. Blumberg, and S. Manzini. 1993. Characterization of a peripheral vanilloid (capsaicin) receptor in the urinary bladder of the rat. Life Sci. 52:PL221–PL226. [DOI] [PubMed] [Google Scholar]
- Szallasi, A., S. Nilsson, T. Farkas-Szallasi, P.M. Blumberg, T. Hokfelt, and J.M. Lundberg. 1995. Vanilloid (capsaicin) receptors in the rat: distribution in the brain, regional differences in the spinal cord, axonal transport to the periphery, and depletion by systemic vanilloid treatment. Brain Res. 703:175–183. [DOI] [PubMed] [Google Scholar]
- Szallasi, A., D.N. Cortright, C.A. Blum, and S.R. Eid. 2007. The vanilloid receptor TRPV1: 10 years from channel cloning to antagonist proof-of-concept. Nat. Rev. Drug Discov. 6:357–372. [DOI] [PubMed] [Google Scholar]
- Szolcsanyi, J., A. Szallasi, Z. Szallasi, F. Joo, and P.M. Blumberg. 1990. Resiniferatoxin: an ultrapotent selective modulator of capsaicin-sensitive primary afferent neurons. J. Pharmacol. Exp. Ther. 255:923–928. [PubMed] [Google Scholar]
- Szolcsanyi, J., A. Szallasi, Z. Szallasi, F. Joo, and P.M. Blumberg. 1991. Resiniferatoxin. An ultrapotent neurotoxin of capsaicin-sensitive primary afferent neurons. Ann. NY Acad. Sci. 632:473–475. [DOI] [PubMed] [Google Scholar]
- Tominaga, M., and T. Tominaga. 2005. Structure and function of TRPV1. Pflugers Arch. 451:143–150. [DOI] [PubMed] [Google Scholar]
- Tominaga, M., M.J. Caterina, A.B. Malmberg, T.A. Rosen, H. Gilbert, K. Skinner, B.E. Raumann, A.I. Basbaum, and D. Julius. 1998. The cloned capsaicin receptor integrates multiple pain-producing stimuli. Neuron. 21:531–543. [DOI] [PubMed] [Google Scholar]
- Tominaga, M., M. Wada, and M. Masu. 2001. Potentiation of capsaicin receptor activity by metabotropic ATP receptors as a possible mechanism for ATP-evoked pain and hyperalgesia. Proc. Natl. Acad. Sci. USA. 98:6951–6956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voets, T., G. Droogmans, U. Wissenbach, A. Janssens, V. Flockerzi, and B. Nilius. 2004. The principle of temperature-dependent gating in cold- and heat-sensitive TRP channels. Nature. 430:748–754. [DOI] [PubMed] [Google Scholar]
- Winegar, B.D., R. Kelly, and J.B. Lansman. 1991. Block of current through single calcium channels by Fe, Co, and Ni. Location of the transition metal binding site in the pore. J. Gen. Physiol. 97:351–367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woodhull, A.M. 1973. Ionic blockage of sodium channels in nerve. J. Gen. Physiol. 61:687–708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeh, J.Z., and T. Narahashi. 1977. Kinetic analysis of pancuronium interaction with sodium channels in squid axon membranes. J. Gen. Physiol. 69:293–323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yellen, G. 1984. Ionic permeation and blockade in Ca2+-activated K+ channels of bovine chromaffin cells. J. Gen. Physiol. 84:157–186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yellen, G. 2002. The voltage-gated potassium channels and their relatives. Nature. 419:35–42. [DOI] [PubMed] [Google Scholar]
- Zhang, N., S. Inan, A. Cowan, R. Sun, J.M. Wang, T.J. Rogers, M. Caterina, and J.J. Oppenheim. 2005. A proinflammatory chemokine, CCL3, sensitizes the heat- and capsaicin-gated ion channel TRPV1. Proc. Natl. Acad. Sci. USA. 102:4536–4541. [DOI] [PMC free article] [PubMed] [Google Scholar]