Dynamics of Positional Enrichment: Theoretical Development and Application to Carbon Labeling in Zymomonas mobilis

Abstract

Positional enrichment analysis has become an important technique for assessing detailed flux distributions and the fates of specific atoms in metabolic pathway systems. The typical approach to positional enrichment analysis is performed by supplying specifically labeled substrate to a cell system, letting the system reach steady state, and measuring where label had arrived and accumulated. The data are then evaluated mathematically with the help of a linear stoichiometric flux distribution model. While this procedure has proven to yield new and valuable insights, it does not address the transient dynamics between providing label and its ultimate steady-state distribution, which is often of great interest to the experimentalist (pulse labeling experiments). We show here that an extension of a recent mathematical method for dynamic labeling analysis is able to shed light on these transitions, thereby revealing insights not obtained with traditional positional enrichment analyses. The method traces the dynamics of one or more carbons through fully regulated metabolic pathways, which, in principle, may be arbitrarily complex. After a brief review of the earlier method and description of the theoretical extension, we illustrate the method with an analysis of the pentose phosphate pathway in Zymomonas mobilis, which has been used for traditional positional enrichment analyses in the past. We show how different labeling schemes result in distinctly different transients, which nevertheless eventually lead to a steady-state labeling profile that coincides exactly with the corresponding profile from traditional analysis. Thus, over the domain of commonality, the proposed method leads to results equivalent to those from state-of-the-art existing methods. However, these steady-state results constitute only a small portion of the insights obtainable with the proposed method. Our method can also be used as an “inverse” technique for elucidating the topology and regulation of pathway systems, if appropriate time series data are available. While such dynamic data are still rather rare, they are now being generated with increasing frequency and we believe it is desirable, and indeed necessary, to accompany this trend with an adequate, rigorous method of analysis.

1. Introduction

Isotopomers are molecules consisting of the same atomic structures but differing in the positions of isotopic substitutions. Radioactive labeling in specific positions and novel sophisticated tracking techniques have made it possible to customize isotopomers and use them to determine the fates of individual atoms during metabolic processes (e.g.,[1; 2; 3]). For instance, using glucose input that is labeled in one specific position, it has become possible to determine exactly how the hexose is split into trioses during glycolysis and how specific carbon atoms move through the citric acid cycle. For a molecule of n isotopic positions, the complete isotopomer set contains 2ⁿ possible labeling states if two isotopes such as ¹²C and ¹³C are considered. If complex pathways are considered, the number of “labeling states” grows quickly and becomes an impediment to experimental and theoretical studies alike, rendering specific tracking tasks in vivo complicated. Nonetheless, great strides have been made, at least for analyses of metabolic systems that are allowed to reach steady state. On the experimental side, nuclear magnetic resonance (e.g., [4]) and mass spectrometry (e.g.,[5]) have proven to be very effective.

Dictated primarily by the complexity of mathematically representing general dynamic labeling processes, theoretical analyses have mostly focused on the distribution of fluxes in stoichiometric network models at steady state [1; 3; 6; 7; 8]. Nonetheless, the potential benefit of dynamic analyses has been acknowledged and addressed in rudimentary form (e.g.,[9]), for instance, for kinetic investigations of individual enzymes (e.g., [10; 11]) and in the analysis of secondary metabolism (e.g., [12]). In fact, early studies that described the rate of change in metabolites with differential equations and multiplied the fluxes with appropriate tracer-to-tracee ratios [9; 13]; see also [14; 15; 16; 17; 18] may be seen as the foundation of a general formulation of the mathematical tracking problem, as it is proposed here.

The advantages of extending analyses beyond the steady state are clear. First, the steady-state distribution of fluxes does not provide any information about the speed with which material distributes throughout the system. In fact, given only one measurement of the flux distribution, it is not clear whether the system even has reached steady state so that present methods are valid. From a biochemical point of view, steady-state analysis is useful for evaluating levels of metabolites as well as degradation/clearance rates. On the other hand, pulse labeling studies provide unique information on rates of synthesis and incorporation. For these and other reasons, many biochemists prefer pulse labeling and combination studies over exclusive steady-state analyses. Second, a dynamic analysis allows a much refined exploration of control and regulation in the system. This exploration may be achieved through simulation studies or, at least in principle, through nonlinear regression in cases where experimental time series measurements are available. In particular, if former experimentation had concluded that a pathway could be organized in one of two ways, a targeted experiment, evaluated with the method proposed here, could permit the final determination. Third, the proposed method allows a true evaluation and interpretation of positional labeling experiments, if they are executed as time series, which is not possible with traditional steady-state analysis. Fourth, in some situations, only the labeling dynamics yields true insight, as is the case for CO₂ assimilation during autotrophic photosynthesis [19]. In other cases, such as batch cultures, where continuous labeling may be intractable or impractical, the system may not even reach a steady state. Fifth, further complications with traditional methods arise if the system contains flux cycles, if ubiquitous metabolites like ATP or NADH are involved in the labeling process, or if the pathway simply becomes too complex [19]. Recently, Wiechert and collaborators proposed an approach called Instationary Metabolic Flux Analysis [20; 21; 22], which allows to some degree the tracking of isotopomer dynamics of metabolites during transitions. This approach is not generally applicable, though, because it requires that the fractions of labeled metabolites are in a (pseudo)-steady state and that the input label pulse does not modify the internal metabolite levels. Sixth, given good data, the method can be used to explore the connectivity and regulation of pathway systems, by virtue of inverse engineering and the matching of simulated labeling results computed for hypothesized model structures against observation data. In this mode, the method not only elucidates flux rates and flux split ratios, but has the potential of discovering the full dynamics of the system. In fact, since our method involves several sets of equations, but no more parameters than a simple pathway model, this inverse task is not any more complicated than other reverse engineering tasks that have been discussed widely in the recent literature [23; 24; 25; 26; 27].

Pursuing a different and more general strategy, we proposed a mathematical method for following a radioactive label throughout a fully dynamic metabolic pathway system [28]. The method combined probabilistic arguments with kinetic modeling based on Generalized Mass Action (GMA) equations and predicted the likely distributions of labeled and unlabeled molecules within each metabolite pool throughout the experimental period of time. The method was shown not to require assumptions on metabolic effects of the input pulse, the size of the pulse, or the structure or complexity of the system. We tested the method first with artificial data and subsequently through simulations of yeast sphingolipid metabolism, where we predicted the dynamics and fate of a labeled palmitate substrate [29]. Validation experiments showed a high degree of semi-quantitative concordance with the model predictions.

Our earlier approach to assessing the dynamics of label was designed to characterize how much of a given metabolite pool is labeled at a given point in time. However, this method does not allow a distinction between different degrees of labeling within a given molecule or between labels at different atomic positions. This latter distinction is at the core of positional enrichment (also referred to as atom positional labeling or fractional enrichment) analysis and the topic of the model extension presented here. As in the original paper, the method is independent of a particular kinetic modeling framework, and we will illustrate it with “canonical” GMA models within Biochemical Systems Theory (BST; [30; 31; 32; 33]). In these models, each flux is represented as a product of power-law functions that contains all variables contributing to the dynamics of this flux, along with a rate constant. The variables are raised to powers, called kinetic orders, whose signs indicate whether their effect is augmenting (positive sign) or diminishing (negative sign). The repertoire of dynamic responses that can be captured by GMA models is vast [34], and GMA models have been used successfully in many contexts, within and outside metabolic pathway analysis. The wide applicability and flexibility of these models is important, because, as Ratcliffe and Shachar-Hill [9] remarked in the recent review: “Dynamic labeling has not seen such rapid progress as steady-state labeling [22], and it still suffers from inherent limitations in complex networks [19].”

In the following, we first describe the extension of the previous method to the dynamics of positional enrichment and subsequently illustrate the method with the pentose phosphate pathway of Zymomonas mobilis, as presented in Wiechert and de Graaf (1997) [35]. This system has particular appeal because the authors characterized it well and analyzed its steady state after positional enrichment, thereby affording us with direct data for comparison at least for some aspects of our method. Secondly, the pathway contains several splitting reactions that are the drivers of distributed atom positions. Finally, kinetic information characterizing this system was recently made available [36].

The purpose of our proposed method is quite different from conventional methods of isotopomer or atom position analysis that are based on stoichiometric models. The traditional methods are typically used to determine flux distribution patterns in a system that has reached its steady state after the application of a label. For this currently prevalent type of analysis, a linear approach is adequate, and this approach requires considerably less information than what we require. Our method does not attempt to compete with (or improve on) this current approach. Instead, our method elucidates the entire transient response between administration of the label and the system’s return to steady state. This elucidation is obviously tied closely to the dynamics of the system and therefore requires information about the regulatory features of the system in addition to information on flux distributions. This increased information requirement is achievable with modern methods of experimental biochemistry and computational systems analysis and analyzed in the Discussion.

2. Model Assumptions

As is typical in labeling analyses, we assume that enzymes do not differentiate in their catalytic activity between unlabeled or differently labeled metabolites. Moreover, it, is not necessary to make assumptions about isotope mass effects or isotope fractionations [37]. Also, we do not need to assume that the amount of labeled material is negligibly small. Here any amount of label is admissible.

In contrast to traditional positional labeling analyses, which merely require knowledge of the connectivity of the system, we must assume here that a kinetic model, including all relevant enzymatic conversions and regulatory signals, is known. Clearly, this information requirement is much higher than in the traditional approach. It is the price to be paid for gaining insight into transient responses. Stoichiometric and kinetic details required for our Zymomonas mobilis illustration are presented in Tables 1 - 3

Table 1.

Fate of carbon atoms for each reaction step within the pentose phosphate pathway in Zymomonas mobilis. Upper and lower case characters are used to indicate source and target positions. Data obtained from [35].

Enzyme	:	Substrate 1	+	Substrate 2	→	Product 1	+	Product 2
Upt (X8):	:	Xyl (X7) #ABCDE			→ →	P5P (X1) #ABCDE
PP4 (X11)	:	P5P (X1) #ABCDE	+ +	E4P (X4) #abcd	→ →	GAP (X3) #CDE	+ +	F6P (X5) #ABabcd
PP2 (X9)	:	P5P (X1) #ABCDE	+ +	P5P (X1) #abcde	→ →	S7P (X2) #ABabcde	+	GAP (X3) #CDE
PP3 (X10)	:	S7P (X2) #abcdefg	+ +	GAP (X3) #ABC	→ →	E4P (X4) #defg	+ +	F6P (X5) #abcABC
Gly2 (X12)	:	F6P (X5) #ABCDEF			→ →	GAP (X3) #CBA	+ +	GAP (X3) #DEF
Gly3 (X13)	:	GAP (X3) #ABC			→ →	Pyr #ABC
Gly1 (X14)	:	F6P (X5) #ABCDEF			→ →	G6P (X6) #ABCDEF
PP1 (X15)	:	G6P (X6) #ABCDEF			→ →	CO2 #A	+ +	P5P (X1) #BCDEF

Table 3.

Specific activities and kinetic parameters for the pentose phosphate pathway in Zymomonas mobilis.

Enzyme	Symbol in the Model	Specific Activity(†)	Kinetics Parameters	Comments	References
Xylose Uptake (Upt)	X8	29509 U/mg			[36]
			Km = 92-148 mM (Xylose)	Glucose facilitator (glf)	[45]
			Km = 40mM (Xylose) Vmax = 115 nmol min-1 mg[dry wt]-1 (*)		[46]
Transketolase-a(α) (PPP2)	X9	120 U/mg			[36]
		9.7 U/mg	Km = 160 μM (Xy5P) Km = 1400 μM (Rib5P)		[47]. Tables 2 and 5
Transketolase-(PPP3)	X10	34.29 U/mg	Km = 9950 μM (S7P) Km = 8690 μM (GAP)		[36]
		2.7 U/mg		At 29 hr. Xylose as carbon source	[38]. Table 10
Transketolase-b(α) (PPP4)	X11	120 U/mg	Km = 160 μM (Xy5P) Km = 90 μM (E4P)		[36]
		2.5 U/mg		At 29 h. Xylose as carbon source	[38]. Table 10
		12.7 U/mg	Km = 90 μM (E4P) Km = 31000 μM (Rib5P)	E. coli	[48]. Table 1 and 2
			Km = 18 μM (E4P)	Yeast	[48]. Table 2
Transaldolase (Gly2)	X12	60 U/mg	Km = 1040 μM (F6P)		[36]
Glyceraldehyde-3-Phosphate Dehydrogenase (Gly3)	X13	25 U/mg			[36]
			Km = 29 μM(GAP)	Celery leaves. No data for Z. mobilis	[49]
Phosphoglucose isomerase (α) (Gly1)	X14	228 U/mg	Km = 200 μM (F6P)		[36]
		1.2 U/mg		At 29 h. Xylose as carbon source	[38]. Table 10
6-phosphogluconate dehydrogenase (PPP1)	X15		Km = 25 μM (6PG)		[36]
		245 U/mg	Km = 40 μM (6-phosphogluconate) Ki = 400 μM (DL-alpha-glycerophosphate)		[50]

^(†)U/mg = μM min^-1 mg protein^-1

^(*)Parameters in bold were used in the model

^(α)Enzyme kinetics from [36]. Table II

3. Methods

The proposed method for dynamic atom position analysis is a direct extension of a prior dynamic labeling method [28]. The concepts of this method are illustrated with the simple artificial pathway in Fig. 1a. Consider the dynamics of X₁, which is governed by inputs from X₂ and X₃ and one efflux leaving the system. The describing GMA is

Fig 1.

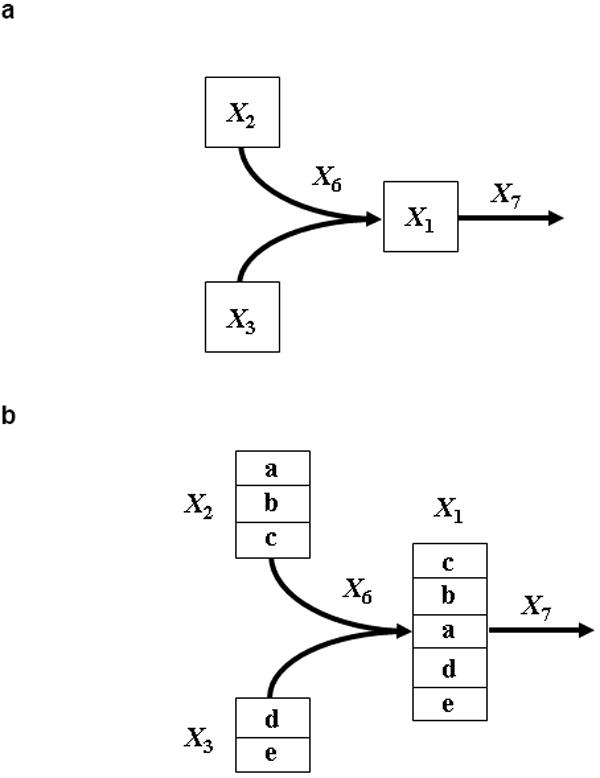
1a. Generic enzyme catalyzed reaction with two substrates.

1b. Bimolecular reaction with explicit description of the fate of each atom.

$${\mathit{dX}}_1/\mathit{dt}={\gamma }_{2,1}{X}_2^{f_{2,1,1}}{X}_3^{f_{2,1,3}}{X}_6^{f_{2,1,6}}-{\gamma }_{1,0}{X}_1^{f_{1,0,1}}{X}_7^{f_{1,0,7}}$$ (1)

To account for the distinction between labeled an unlabeled molecules in the pool of X₁, Eq. (1) is augmented by two similar equations, one describing the labeled sub-pool L₁ and the other one describing the unlabeled sub-pool U₁. Allowing for the fact that label could come from either X₂, X₃, or both, the equations for these sub-pools are composed of the same terms as in Eq. (1), which, however, are weighted by the degree of labeling in X₁, X₂ and X₃. Thus,

$${\mathit{dL}}_1/\mathit{dt}=((L_2\cdot U_3+U_2\cdot L_3+L_2\cdot L_3)/(X_2\cdot X_3))\cdot {\gamma }_{2,1}{X}_2^{f_{2,1,1}}{X}_3^{f_{2,1,3}}{X}_6^{f_{2,1,6}}-(L_1/X_1)\cdot {\gamma }_{1,0}{X}_1^{f_{1,0,1}}{X}_7^{f_{1,0,7}},$$

$$d{\mathrm{U}}_1/\mathit{dt}=(U_2\cdot U_3/(X_2\cdot X_3))\cdot {\gamma }_{2,1}{X}_2^{f_{2,1,1}}{X}_3^{f_{2,1,3}}{X}_6^{f_{2,1,6}}-(U_1/X_1)\cdot {\gamma }_{1,0}{X}_1^{f_{1,0,1}}{X}_7^{f_{1,0,7}}.$$ (2)

It is easy to confirm that the two equations in (2) add up to the equation in (1). In other words, the equations in (2) split the dynamics of the total pool in Eq. (1) into labeled and unlabeled fractions while satisfying mass conservation for all time points, including the initial time 0, namely

$$X_1(t)=L_1(t)+U_1(t)\mathrm{for\; all}t.$$ (3)

The basic idea for extending this approach to positional enrichment consists of describing each atom that could potentially be labeled within each metabolite as a dependent variable. This requires that the dynamics of each atom is represented by a separate differential equation, whose structure is directly derived from the kinetic description of the total pool, as in Eq. (1). Thus, instead of splitting the pool into two sub-pools, as above, the pool is split into twice the number of possibly labeled atoms in the molecule.

Continuing the former illustration, suppose the pathway in Fig. 1a describes the formation of a pentose, X₁, and we account explicitly for each carbon atom, as shown in Fig. 1b. Specifically, we do not just want to describe how many molecules in X₁ are unlabeled or “somewhere labeled,” but characterize all the transient positional labeling states by tracking which carbon in the pentose could be labeled or unlabeled. This requires one equation each for the fractions of labeled and unlabeled atoms in positions 1 through 5. Focusing on pool X₁, these ten differential equations thus represent, in obvious nomenclature: L_1a, L_1b, L_1c, L_1d, L_1e and U_1a, U_1b, U_1c, U_1d, U_1e.

It is convenient to begin by formulating equations for the dynamics of the total sub-pools X_1a, X_1b, X_1c, X_1d, X_1e, where X_1k = L_1k + U_1k, k = a, …, e. The first two equations in this set are

$${\mathit{dX}}_{1a}/\mathit{dt}={\gamma }_{2,1}{X}_2^{f_{2,1,1}}{X}_3^{f_{2,1,3}}{X}_6^{f_{2,1,6}}-{\gamma }_{1,0}{X}_1^{f_{1,0,1}}{X}_7^{f_{1,0,7}}$$

$${\mathit{dX}}_{1b}/\mathit{dt}={\gamma }_{2,1}{X}_2^{f_{2,1,1}}{X}_3^{f_{2,1,3}}{X}_6^{f_{2,1,6}}-{\gamma }_{1,0}{X}_1^{f_{1,0,1}}{X}_7^{f_{1,0,7}}$$ (4)

Their right-hand sides are equivalent, because all atom positions are subject to the same reaction and therefore have the same dynamics. The initial values are set as equal fractions of the total initial mass, divided by the number of carbons in the molecule X_1k(t₀) = 1/5 X₁(t₀), k = a, …, e.

Thus, carbon labeling within the X₁-pool consists of five differential equations that are structurally equivalent to those of the total masses, but weighted by the fraction of enrichment that affects any one of the carbon atoms as the consequence of the specific enzymatic action. For instance, in Fig 1b, if X₃ were labeled, but X₂ not, there would be no possibility for positive quantities L_1a, L_1b, and L_1c. In general terms, allowing for all combinations, the five equations for labeled carbons are

$${\mathit{dL}}_{1a}/\mathit{dt}=(L_{2c}/X_{2c})\cdot {\gamma }_{2,1}{X}_2^{f_{2,1,2}}{X}_3^{f_{2,1,3}}{X}_6^{f_{2,1,6}}-(L_{1a}/X_{1a})\cdot {\gamma }_{1,0}{X}_1^{f_{1,0,1}}{X}_7^{f_{1,0,7}}$$

$${\mathit{dL}}_{1b}/\mathit{dt}=(L_{2b}/X_{2b})\cdot {\gamma }_{2,1}{X}_2^{f_{2,1,2}}{X}_3^{f_{2,1,3}}{X}_6^{f_{2,1,6}}-(L_{1b}/X_{1b})\cdot {\gamma }_{1,0}{X}_1^{f_{1,0,1}}{X}_7^{f_{1,0,7}}$$

$${\mathit{dL}}_{1c}/\mathit{dt}=(L_{2a}/X_{2a})\cdot {\gamma }_{2,1}{X}_2^{f_{2,1,2}}{X}_3^{f_{2,1,3}}{X}_6^{f_{2,1,6}}-(L_{1c}/X_{1c})\cdot {\gamma }_{1,0}{X}_1^{f_{1,0,1}}{X}_7^{f_{1,0,7}}$$

$${\mathit{dL}}_{1d}/\mathit{dt}=(L_{2d}/X_{2d})\cdot {\gamma }_{2,1}{X}_2^{f_{2,1,2}}{X}_3^{f_{2,1,3}}{X}_6^{f_{2,1,6}}-(L_{1d}/X_{1d})\cdot {\gamma }_{1,0}{X}_1^{f_{1,0,1}}{X}_7^{f_{1,0,7}}$$

$${\mathit{dL}}_{1e}/\mathit{dt}=(L_{2e}/X_{2e})\cdot {\gamma }_{2,1}{X}_2^{f_{2,1,2}}{X}_3^{f_{2,1,3}}{X}_6^{f_{2,1,6}}-(L_{1e}/X_{1e})\cdot {\gamma }_{1,0}{X}_1^{f_{1,0,1}}{X}_7^{f_{1,0,7}}$$ (5)

At the beginning of the experiment, where no label had been available before, the initial values associated with these equations are typically zero.

Similarly, equations are formulated for the unlabeled fractions, namely:

$${\mathit{dU}}_{1a}/\mathit{dt}=(U_{2c}/X_{2c})\cdot {\gamma }_{2,1}{X}_2^{f_{2,1,2}}{X}_3^{f_{2,1,3}}{X}_6^{f_{2,1,6}}-(U_{1a}/X_{1a})\cdot {\gamma }_{1,0}{X}_1^{f_{1,0,1}}{X}_7^{f_{1,0,7}}$$

$${\mathit{dU}}_{1b}/\mathit{dt}=(U_{2b}/X_{2b})\cdot {\gamma }_{2,1}{X}_2^{f_{2,1,2}}{X}_3^{f_{2,1,3}}{X}_6^{f_{2,1,6}}-(U_{1b}/X_{1b})\cdot {\gamma }_{1,0}{X}_1^{f_{1,0,1}}{X}_7^{f_{1,0,7}}$$

$${\mathit{dU}}_{1c}/\mathit{dt}=(U_{2a}/X_{2a})\cdot {\gamma }_{2,1}{X}_2^{f_{2,1,2}}{X}_3^{f_{2,1,3}}{X}_6^{f_{2,1,6}}-(U_{1c}/X_{1c})\cdot {\gamma }_{1,0}{X}_1^{f_{1,0,1}}{X}_7^{f_{1,0,7}}$$

$${\mathit{dU}}_{1d}/\mathit{dt}=(U_{2d}/X_{2d})\cdot {\gamma }_{2,1}{X}_2^{f_{2,1,2}}{X}_3^{f_{2,1,3}}{X}_6^{f_{2,1,6}}-(U_{1d}/X_{1d})\cdot {\gamma }_{1,0}{X}_1^{f_{1,0,1}}{X}_7^{f_{1,0,7}}$$

$${\mathit{dU}}_{1e}/\mathit{dt}=(U_{2e}/X_{2e})\cdot {\gamma }_{2,1}{X}_2^{f_{2,1,2}}{X}_3^{f_{2,1,3}}{X}_6^{f_{2,1,6}}-(U_{1e}/X_{1e})\cdot {\gamma }_{1,0}{X}_1^{f_{1,0,1}}{X}_7^{f_{1,0,7}}$$ (6)

with typical initial values X_{1k =}U_1k. Among the three sets of equations, for total, labeled, and unlabeled pools, two sets of equations are to be formulated, while the third is simply convenient but may also be obtained from the other two, be virtue of X_1k = L_1k + U_1k , k = a, …, e.

Reversible reactions should typically not be replaced with “net fluxes,” because label may flow back and forth. Instead, reversible reactions should be split into forward and reverse steps. As an example, consider the pathway in Fig 2. Splitting the reversible reaction in two different terms, V_C,B and V_B,C, the total mass equations for the first positions are

Fig 2.

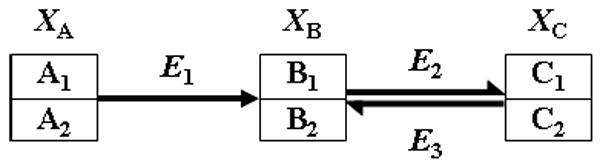
Generic reversible reaction with indication of differently positioned atoms.

$${\mathit{dX}}_{A1}/\mathit{dt}=-V_{A,B},X_{A1}(0)=X_A(0)/2,$$

$${\mathit{dX}}_{B1}/\mathit{dt}=V_{A,B}+V_{C,B}-V_{B,C},X_{B1}(0)=X_B(0)/2,$$

$${\mathit{dX}}_{C1}/\mathit{dt}=V_{B,C}-V_{C,B},X_{C1}(0)=X_C(0)/2,$$ (7)

where the fluxes in GMA implementation are given as

$$V_{A,B}={\gamma }_{A,B}{X}_A^{f_A}{E}_1^{f_{E1}}$$

$$V_{C,B}={\gamma }_{C,B}{X}_C^{f_C}{E}_3^{f_{E3}}$$

$$V_{B,C}={\gamma }_{B,C}{X}_B^{f_B}{E}_2^{f_{E2}}$$ (8)

Using the same arguments as before, the equation for labeled atom L_B1 are, for instance,

$${\mathit{dL}}_{B1}/\mathit{dt}=(L_{A1}/X_{A1})\cdot V_{A,B}+(L_{C2}/X_{C2})\cdot V_{C,B}-(L_{B1}/X_{B1})\cdot V_{B,C},L_{B1}(0)=0,$$ (9)

and the corresponding equation for the unlabeled atom U_B1 is

$${\mathit{dU}}_{B1}/\mathit{dt}=(U_{A1}/X_{A1})\cdot V_{A,B}+(U_{C2}/X_{C2})\cdot V_{C,B}-(U_{B1}/X_{B1})\cdot V_{B,C},U_{B1}(0)=X_B(0)/2.$$ (10)

Analogous equations are to be developed for atoms A₁, C₁, A₂, B₂, and C₂ in the same fashion.

The generic examples above render it evident that the proposed strategy for assessing the dynamics of positional labeling states primarily constitutes a very large bookkeeping task, where all candidate atoms and all reactions have to be taken into consideration and the initial conditions must be set to reflect a particular labeling scenario. Clearly, the number of equations grows quite rapidly, but one has to keep in mind that, given the kinetic model for the overall dynamics, all other equations are created quite mechanically and that only minimal information (such as the initial state of the system) needs to be known in addition to the original model. We will demonstrate this now with the pentose pathway in Zymomonas mobilis.

4. Analysis of the pentose phosphate pathway in Zymomonas mobilis

In a seminal paper on ¹³C positional enrichments, Wiechert and Graaf [35] analyzed the cyclic pentose phosphate pathway in a mutant strain of Zymomonas mobilis. The pathway is redrawn in Fig. 3. It constitutes a particularly useful illustration of our proposed method, for several reasons. First, the original analysis provides carbon labeling enrichment results at steady-state that we can use for a partial comparison with the proposed method. Second, the pathway includes four bi-product reactions, which are the most interesting in positional enrichment analysis. Third, the fates of all carbon atoms are described in the appendix of Wiechert and Graaf’s article [35]. Finally, most of the kinetic rate equations, metabolite concentrations and enzyme activities are available from a recent paper of Altintas [36] (see also Tables 2 and 3). Table 4 presents the fluxes used in the model; they were established from the relationships presented in Wiechert and de Graaf’s paper [35], with values scaled according to xylose uptake information [38]. One might consider it a disadvantage that the authors used simulations and not actual data. However, this is an advantage for our comparative analysis here, because the simulated results are guaranteed to be consistent in themselves and without experimental noise or uncertainty. It is noted that recent work [39] suggests that transketolase and transaldolase might better be modeled as half reactions. In order to permit comparisons with the results of Wiechert and de Graaf, we retain the reaction kinetics of their paper here.

Fig 3.

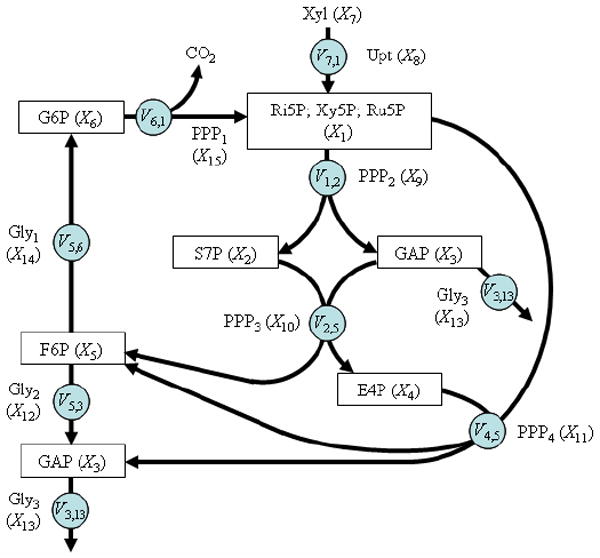
Cyclic pentose phosphate pathway in a mutant strain of Zymomonas mobilis. Redrawn from Wiechert and de Graaf (1997) [35]. Boxes indicate dependent system variables; other variables, indicating input, uptake, and enzyme catalyzed reactions, are independent. Fluxes are presented in circles. Symbol names X_i correspond to the representation in the GMA model. Note that GAP (X₃) is represented in two locations for clarity.

Abbreviations: Dependent variables: Ri5P, Ribose-5-phosphate; Xy5P, Xylulose-5-phosphate; Ru5P, Ribulose-5-phosphate; S7P, Sedoheptulose 7-phosphate; GAP, Glyceraldehyde 3-phosphate; E4P, Erythrose 4-phosphate; F6P, Fructose-6-Phosphate; G6P, 6-Phosphogluconate and Glucose-6-Phosphate; Independent variables: Xyl, Xylose; Upt, Xylose Uptake; PPP₂, Transketolase-a; PPP₃, Transaldolase; PPP₄, Transketolase-b; Gly₂, Transaldolase; Gly₃, Glyceraldehyde-3-Phosphate Dehydrogenase; Gly₁, Phosphoglucose isomerase; PPP₁, 6-phosphogluconate dehydrogenase.

Table 2.

Metabolite concentrations of external xylose and of the internal (dependent) variables of the pentose phosphate pathway in Zymomonas mobilis.

Metabolite	Symbol	Symbol in Model	Concentration (μm)	Reference
Pentose-phosphate pool consisting of Ri5P, Xy5P, and Ru5P	P5P	X1	113.6	[1]
Sedoheptulose 7-phosphate	S7P	X2	3609	[1]
Glyceraldehyde 3-phosphate	GAP	X3	0.97	[1]
Erythrose 4-phosphate	E4P	X4	5.68	[1]
Fructose-6-phosphate	F6P	X5	30.31	[1]
6-Phosphogluconate (3)	G6P	X6	0.19	[1]
Xylose	Xyl	X7	29509 (*)	[1]
			466000	[2]

¹[36]

²[38]

³Glucose-6-phosphate is first converted into 6-phosphogluconate and then degraded by 6- phosphogluconate dehydrogenase to form Ru5P and CO₂

^(*)value used in the model

Table 4.

Stochiometric relationships and fluxes of the pentose phosphate pathway in Zymomonas mobilis.

Individual fluxes	Flux route	Flux values (*)
V7,1	Xyl → P5P	36.72
V1,2	P5P → S7P	72.36
V2,5	S7P → F6P GAP → F6P	72.36
V4,5	E4P → F6P P5P → F6P	72.36
V5,3	F6P → GAP	36.72
V3,13	GAP → Gly3	109.8
V5,6	F6P → G6P	108
V6,1	G6P → P5P	108

^(*)Based on a xylose uptake flux of 108 μmol (g dry weight)^-1 min^-1 reported in [38]. Table 9

Wiechert and de Graaf’s pathway model consists of six dependent variables (metabolites) and nine independent variables (enzyme activities). All enzymatic reactions are considered unidirectional, which simplifies our analysis by not necessitating the splitting into forward and reverse reactions. Details of the model are shown in the Appendix, and we focus here, as an illustration, merely on the first dependent variable of the model, X₁, which represents the metabolite pool “P5P” consisting of Ri5P, Xy5P, and Ru5P with two influxes and two effluxes:

$${\mathit{dX}}_1/\mathit{dt}=V_{7,1}+V_{6,1}-V_{4,5}-V_{1,2}$$ (11)

Because the pentoses in X₁ consist of five carbons, we define a group of five identical differential equations, one for each carbon, such as

$${\mathit{dX}}_{1a}/\mathit{dt}=V_{7,1}+V_{6,1}-V_{4,5}-V_{1,2},X_{1a}(0)=1/5\cdot X_1(0).$$ (12)

Similar equations are formulated for X_1b, X_1c, X_1d, and X_1e. Following the conventions of BST, the reaction steps are formulated as power-law functions,

$$V_{7,1}=0.022X_7^{0.871}{X}_8$$

$$V_{6,1}=2.2912X_6^{0.992}{X}_{15}$$

$$V_{4,5}=0.00369X_4^{0.940}{X}_1^{0.731}{X}_{11}$$

$$V_{1,2}=0.03529X_1^{0.599}{X}_9$$ (13)

where the numerical values of the kinetic orders and rate constants are computed from the information in Tables 2 and 3 with methods shown in the literature many times (e.g.,[33]). We assume, as natural default, that the experiment begins free of label, so that the initial values for both total mass and unlabeled material equal the initial mass divided by the number of carbons, as described before. Any other initial state could be chosen without difficulty, if deemed appropriate.

To formulate equations for the various atom positions, we follow the fate of each carbon atom, according to Table I, and refer to different carbon labeling positions as #A, #B, etc. For instance, the material in pool L_1a consists of carbon #A of the P5P pool. This labeled material potentially derives from two sources, namely from carbon #A of Xyl (L_7a) and/or from carbon #B of G6P (L_6b). The dynamics of the L_1a pool is thus given as

$${\mathit{dL}}_{1a}/\mathit{dt}=V_{7,1}\cdot (L_{7a}/X_{7a})+V_{6,1}\cdot (L_{6b}/X_{6b})-V_{4,5}\cdot (L_{1a}/X_{1a})-V_{1,2}\cdot (L_{1a}/X_{1a})$$ (14)

and we set L_1a(t₀) = 0 for the beginning of the experiment. Similarly, the complementary sub-pool of unlabeled mass is

$${\mathit{dU}}_{1a}/\mathit{dt}=V_{7,1}\cdot (U_{7a}/X_{7a})+V_{6,1}\cdot (U_{6b}/X_{6b})-V_{4,5}\cdot (U_{1a}/X_{1a})-V_{1,2}\cdot (U_{1a}/X_{1a})$$ (15)

with initial concentration U_1a(t₀) = U₁(t₀) / 5. In this fashion, equations are formulated for each carbon atom in each involved metabolite.

Fig. 4 exhibits the carbon labeling dynamics in response to a sustained supply of xylose labeled at carbon #A that first becomes available at time 0. This perturbation does not alter the external total xylose concentration. After some transient phase, the pathway reaches a new steady state, where sugar influx equals the production of pyruvate and CO₂, which both leave the system. The responses in labeled carbons are qualitatively similar; they all rise monotonically from 0 to their respective final values. However, the speed of these responses is quite different. In particular, L_1a jumps up rapidly, which is understandable because it is the direct recipient of labeled xylose, whereas L_4a rises much more slowly (Fig. 4b). The unlabeled components (Fig. 4c,d) also change dynamically because they are being replaced by labeled material.

Fig. 4.

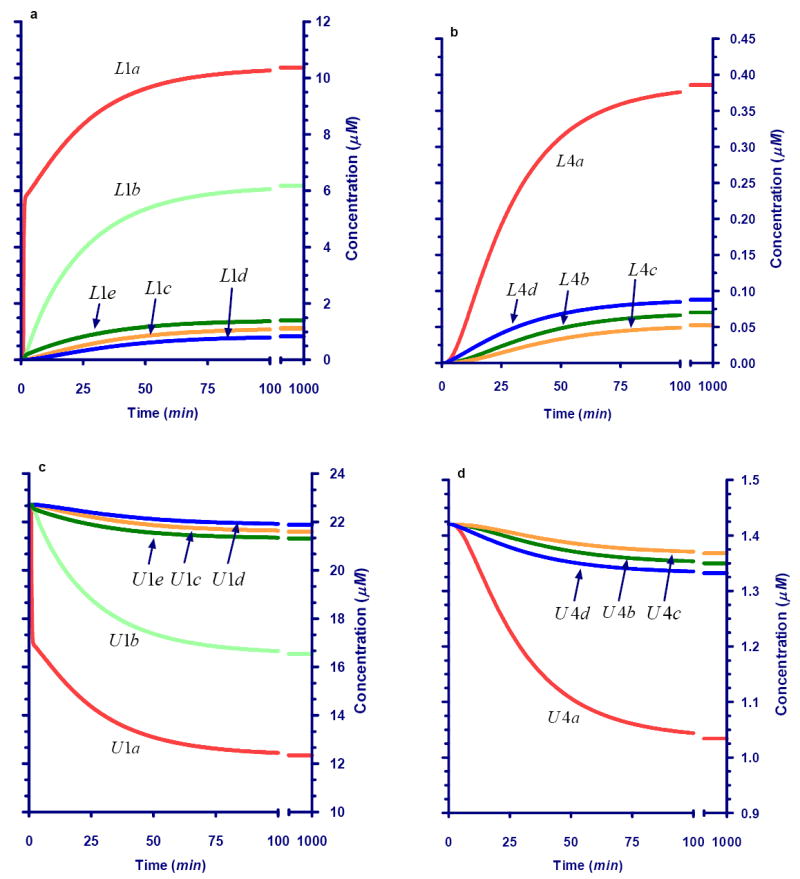
Dynamics for Ri5P, Xy5P, and Ru5P pool (X₁) isotopes in response to sustained availability of xylose labeled in #A position under conditions of isomolarity. Panel a: Dynamics of carbon isotopes of Ri5P, Xy5P, and Ru5P labeled in #A position (L₁ pool). Panel b: Dynamics of carbon isotopes of Ri5P, Xy5P, and Ru5P not labeled in #A position (U₁ pool).

The most interesting result is the observation that the original label at carbon #A eventually occupies all other positions as well. This is due to the sequence of conversions between two pentoses into a heptose and a triose, then into a hexose and tetrose, and finally from a hexose into a pentose and CO₂. These conversions during the pentose cycle “shift” the labeled carbon into different positions. It is also interesting to note that not all #A in the P5P is ultimately replaced by labeled atoms. This is so because unlabeled atoms for instance from position #B in the xylose molecule eventually become #A atoms in P5P.

Although no data exist to confirm these results directly, they are quantitatively consistent with the steady-state carbon labeling fractions reported by Wiechert and de Graaf [35], who also show that the label eventually occupies different positions with different prevalences. In fact, even though these authors’ results and our own results were obtained with distinctly different methods, they are exactly the same over the domain where they are comparable, namely at the steady state (Fig. 5 and Table. 5). This consistency shows that our approach is in some sense a generalization of the method of Wiechert and de Graaf [35] with the distinct advantage that it is now possible to track the entire dynamics of the system.

Fig 5.

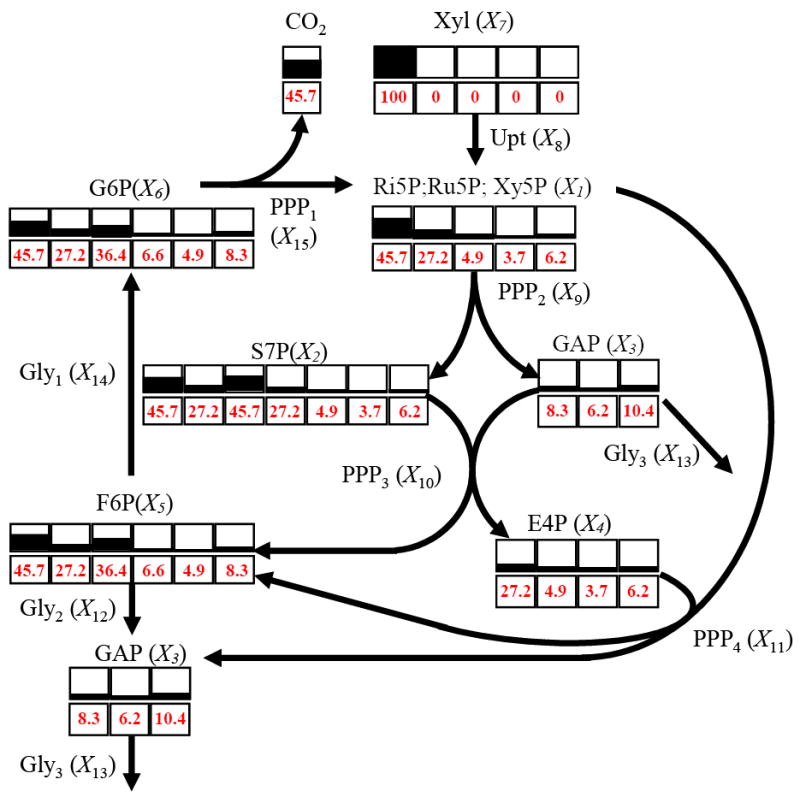
Atom positional enrichment in the dynamic model reaches the same steady state as obtained with the method of Wiechert and de Graf [35]. In this simulation, the input consisted of xylose labeled in #A position (L7a). Partially shaded blocks are redrawn from Wiechert and de Graf. Numbers in boxes are steady-state percentages of label in each position, computed with the method proposed here.

Table 5.

Steady-states carbon enrichment (in percent) after input of xylose labeled in #A position (L7a). Results obtained with the traditional method of Wiechert and de Graf [35] and the dynamic approach presented in this paper.

	Enrichment (%)
	[35], Fig 4b	This paper
E1a	45.65217	45.6522
E1b	27.17391	27.1739
E1c	4.934017	4.9340
E1d	3.682102	3.6821
E1e	6.185931	6.1859
E2a	45.65217	45.6522
E2b	27.17391	27.1739
E2c	45.65217	45.6522
E2d	27.17391	27.1739
E2e	4.934017	4.9340
E2f	3.682102	3.6821
E2g	6.185931	6.1859
E3a	8.289148	8.2891
E3b	6.185931	6.1859
E3c	10.39236	10.3924
E4a	27.17391	27.1739
E4b	4.934017	4.9340
E4c	3.682102	3.6821
E4d	6.185931	6.1859
E5a	45.65217	45.6522
E5b	27.17391	27.1739
E5c	36.41304	36.4130
E5d	6.611582	6.6116
E5e	4.934017	4.9340
E5f	8.289148	8.2891
E6a	45.65217	45.6522
E6b	27.17391	27.1739
E6c	36.41304	36.4130
E6d	6.611582	6.6116
E6e	4.934017	4.9340
E6f	8.289148	8.2891

Figure 6 shows various aspects of the carbon labeling dynamics that result from the addition of a bolus of xylose, labeled at #A, to the system at steady state. Experimentally, this situation could result from moving cells from normal growth medium into labeled medium. Before we describe details, it is worth emphasizing that the dynamic responses depend significantly on the position of the labeled carbon atom within the xylose molecule. For instance, labeling carbon #A eventually causes all metabolite pools to be labeled to some degree in all positions, whereas a label in position #C never reaches some positions in some of the metabolites, primarily because the #C carbon enters GAP, from where it exits the system.

Fig 6.

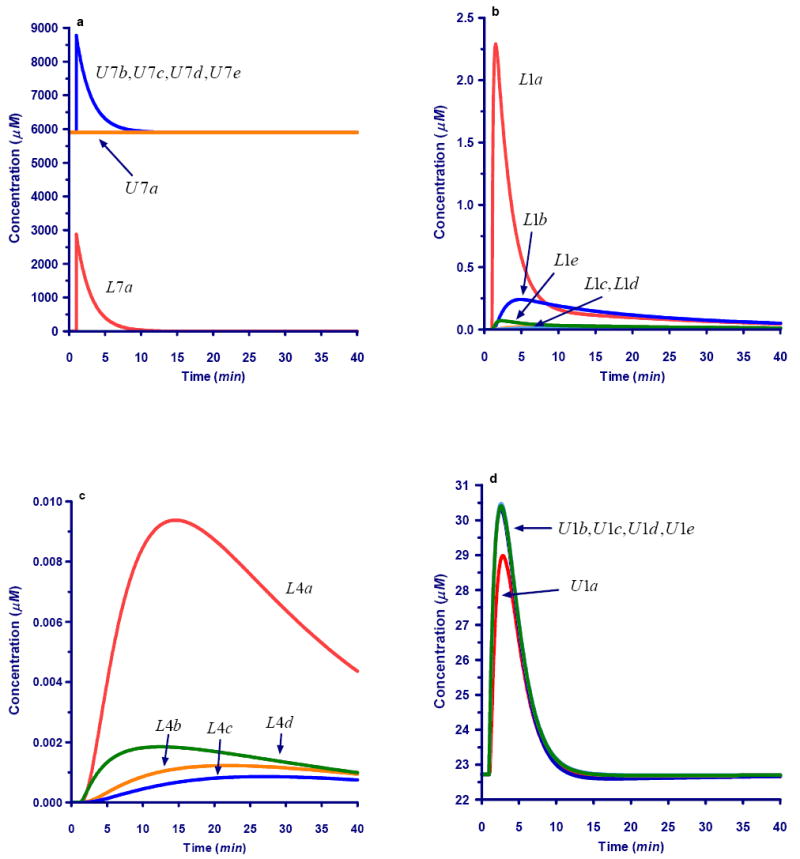
Dynamics of selected carbons after a bolus perturbation of xylose labeled in #A position.

6a. Decrease in external xylose after perturbation with label in #A position. Yellow: Unlabeled carbon #A (U_7a); Red: Labeled carbon #A (L_7a). Green: Unlabeled carbon in other positions (U_7b, U_7c, U_7d, and U_7e). Total carbon pools (X_7b, X_7c, X_7d, and X_7e) for the various positions are equivalent to U_7b to U_7e profiles (not shown).

6b. Dynamics of labeled carbons for the combined Ri5P, Xy5P, and Ru5P pool (L₁).

6c. Dynamics of labeled carbons within the E4P pool (L₄)

6d. Dynamics of unlabeled carbons for the combined Ri5P, Xy5P, and Ru5P pool (U₁)

6e. Dynamics of unlabeled carbons within the E4P pool (U₄)

Fig 6a represents the situation where at minute 1 a bolus with 100% #A-labeled carbon is added to the system, which had been at steady state. Mimicking the typical experimental situation, the addition of labeled material adds corresponding amounts to the unlabeled pools in positions #B-#E, because whole xylose molecules are added. The labeled bolus is rapidly taken up and distributes throughout the system. Since unlabeled xylose continues to flow into the system, the labeled materials would eventually be purged from the system (a chase situation), but completion of this process requires a long time. Stopping the experiment at 40 minutes, one sees that the dynamics of the different carbons is quite different (e.g., Figs. 6b and c).

It is interesting to mention that not only the labeled, but also the unlabeled pools are changing in concentration over time. Most noticeably, some of the unlabeled mass is pushed out of position #A of the P5P pool but “recovers” quickly, as label is only supplied as a one-time bolus (Fig. 6d). Other unlabeled positions at first receive unlabeled material, then labeled material in later cycles, and ultimately return to their original steady state (Fig. 6e).

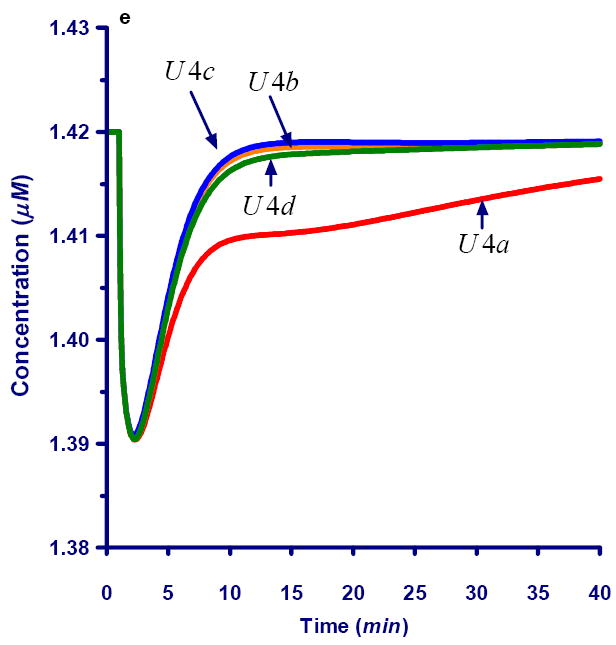
Figure 7 exhibits dynamic responses in carbons following a bolus of added xylose #C-labeled carbon. These figures are to be compared with the corresponding graphs in Figure 6, where the label was positioned at the #A carbon. Although only the position of the label is altered, the responses are distinctly different. In particular, some atom positions, such as #A of the P5P pool never receive the label. This is due to the structure of the pathway and the specific enzymatic action, which causes #C of P5P to reach only particular positions. Specifically, L_1c (#C of P5P) moves to L_2e (#E of S7P) and L_3a (#A of GAP). A fraction of the L_3a material leaves the system via pyruvate (Pyr), while the rest moves toward L_5d (#D of F6P) and then to L_6d (#D of G6P), from where it returns to #C of the P5P, thereby beginning a new cycle. The labeled carbon atom of S7P, L_2e, becomes L_4b (#B of E4P), which moves toward L_5d (#D of F6P) and like L_3a eventually returns to L_1c (#C of P5P) and begins a new cycle (Table I). The responses of the labeled atoms are shown in Figures 7a-c, grouped by amounts. All other carbons remain unlabeled throughout the experiment (results shown in Appendix Figures A1-A6). Eventually, all label disappears, because only a one-time bolus was given.

Fig. 7.

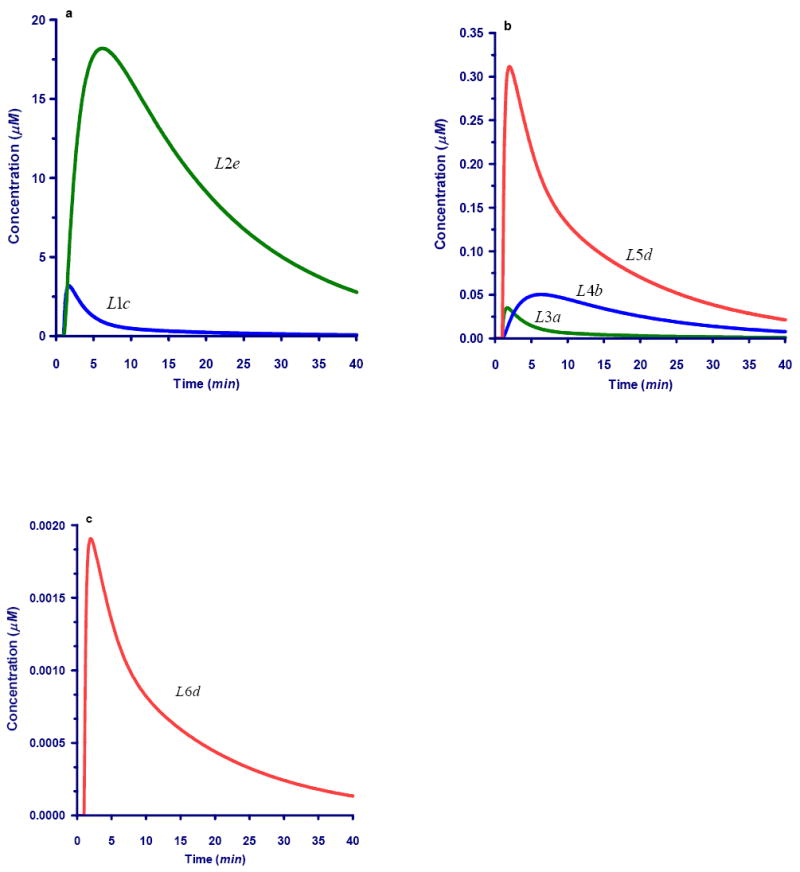
Dynamics for selected carbons following a bolus perturbation with xylose labeled in #C position. Carbons not shown are not affected by the perturbation. Compare time courses with Figure 6. The dynamics of unlabeled carbons is shown in Fig. A of the Appendix.

7a. Dynamics of #C and #E within the xylose-P pool and sedoheptulose-7- phosphate (L1c and L2e, respectively).

7b. Labeling dynamics for #A within the GAP pool (L3a), #B within the E4P pool (L4b), and #D within the F6P pool (L5d).

7c. Dynamics for C4 within the G6P pool (L6d).

Fig. A.

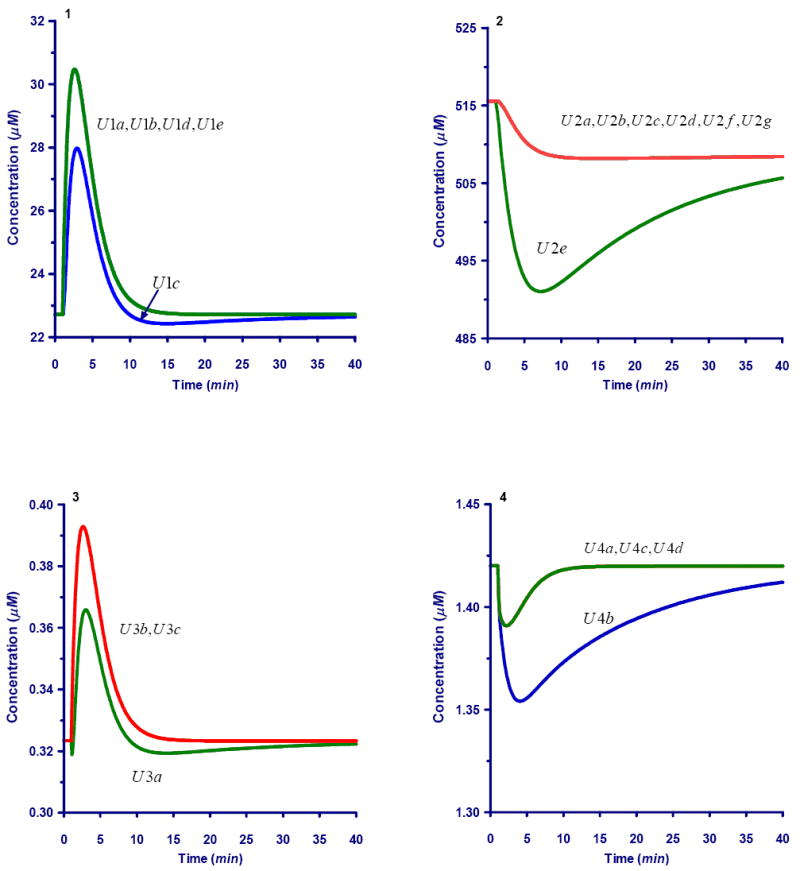
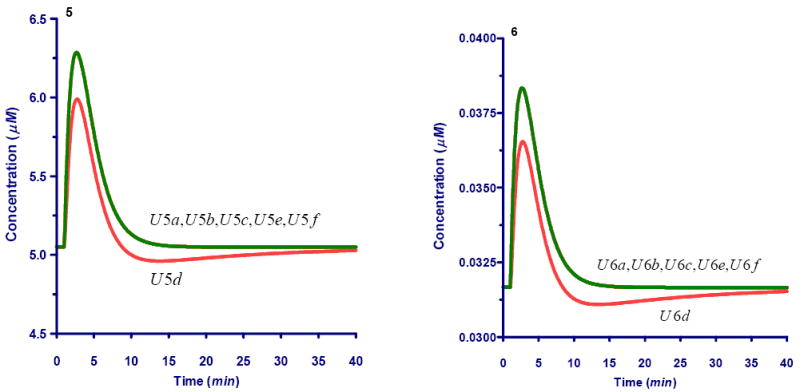
Dynamics for Ri5P unlabeled carbons following a bolus perturbation at #C of external xylose. The label carbon dynamics is show in Fig. 7

A1. Dynamics of unlabeled carbons within the pentose phsophate pool (X₁)

A2. Dynamics of unlabeled carbons within the sedoheptulose-7-phosphate pool (X₂)

A3. Dynamics of unlabeled carbons within the glyceraldehyde-3-phosphate pool (X₃)

A4. Dynamics of unlabeled carbons within the erythrose-4-phosphate pool (X₄)

A5. Dynamics of unlabeled carbons within the fructose-6-phosphate pool (X₅)

A6. Dynamics of unlabeled carbons within the 6-phosphogluconate pool (X₆)

The simulations presented in Figs. 6 and 7 show the potential of dynamic atom positional analysis for complex pathways. The simulations also make it clear that dynamic responses to inputs with label in several or all positions are easily modeled with the same method. The Appendix contains additional simulation results.

As a concluding note regarding this example, we should emphasize that the purpose of our case study is clearly not to interpret the physiology of a specific organism or to suggest new insights into the functioning of Z. mobilis. Instead, it is used to demonstrate the proposed method with independent data outside our control and to show that over the range of commonality (namely the steady state flux distribution) our method leads to exactly the same conclusion as standard methods, even though our method computes the steady-state flux distribution in an entirely different fashion than Wiechert and Graaf have done [35]. The chances that one proven method and a new, incorrect, method would yield the same, complex result are very small, suggesting from yet a different angle that our proposed model is reasonable.

It would be desirable to validate not only the steady state aspects of our analysis, but the entire time course with de novo data. While such data are presently not available to us, there is no principal problem generating them with today’s experimental techniques. In fact, it may be likely that such data have not been published because no efficacious method of analysis was available so far. Although we have no direct comparative data for a comprehensive model validation, we have shown previously that the simpler case of dynamic labeling without consideration of atom positions was adequately represented by a method that is conceptually very similar to the method presented here [28]. Because the mathematics of the method proposed here is a direct derivative of the former method, we are confident that our conclusions are justified on mathematical grounds.

5. Discussion

For practical reasons, both on the experimental and the mathematical-analytical side, positional enrichment analysis has so far almost exclusively focused on steady states. Thus, specifically labeled substrate or precursor was supplied to a metabolic system, and after some while, which was deemed long enough to lead to a new steady state, the metabolites were analyzed with respect to their labeling status. This procedure has been yielding a variety of new insights (cf. [9]).

It is well known from theoretical studies—and not intuitively surprising—that much more information can be gained if not only the steady state, but also the transients are studied, starting at the time when the label is supplied. Mathematically, this type of analysis was recently made possible by a method for characterizing the dynamics of labels moving through a metabolic system [28]. However, this method only addressed the binary (yes or no) labeling status of a given metabolite at a given time. This resolution was insufficient for transient positional enrichment analyses, thus prompting us to develop an extension that is capable of following every atom position that could potentially become labeled. Beyond the common results that reflect the final state of the system, the new method elucidates all details of the transients following the initiation of labeling. The insights gained are often not intuitive, and there appears to exist no other method to characterize this dynamics. The method characterizes the speed with which particular positions receive label, works for small or large amounts of label, and does not depend on the system assuming a steady state. Most interesting are probably the comparisons between responses to labeling at different positions (Figs. 6 and 7), which can be distinctly different. The case presented in Figure 7 is extreme in a sense that some atom pools never receive label due to the structure of the pathway and the splitting of molecules. In other cases (similar to Fig 6), the label may eventually reach all pools, but in different quantities, depending on the original labeling position.

In comparison to traditional positional enrichment analysis and our earlier dynamic labeling method, the approach presented here may appear to be overly complicated, because even for a moderately small pathway the number of equations grows rapidly and may seem overwhelming. There is no doubt that setting up the “kinetic master model” requires considerably more effort than the comparatively simple flux distribution analysis in a steady-state enrichment analyses, but that is the price one has to pay for insights into the dynamic responses, in addition to a steady-state distribution pattern. Once a kinetic model describing the overall dynamics of the pathway is established, all further equations related to the atoms of a given metabolite have essentially the same structure, and no additional kinetic information is needed to construct the dynamic positional enrichment model. Indeed, given the kinetic model, the construction of the dynamic positional enrichment model is rather mechanical and could be automated, using computer algebra software. It follows simple rules that weigh the contributions of labeled and unlabeled atoms to a newly produced metabolite and determine the initial values for each equation. This richness of the method and its results becomes evident in the comparison of the published analysis of Zymomonas mobilis data with our assessment, which includes the published results completely and exactly as a natural special case, but offers much greater insight.

There is no doubt that our method requires more information on metabolites, enzymes, and fluxes than the existing stoichiometric methods. This need is directly associated with the fact that we are investigating regulation and dynamics, in addition to the steady-state flux distribution. In other words, the insights that can be gained with our method do not come for free. While the input requirements are thus higher, many modelers have shown with concrete examples that it is indeed possible to construct fully dynamic, regulated kinetic models. As one example, our recent sphingolipid model [40] contains several dozen variables, and its responses have been validated with de novo experiments [29]. Furthermore, modern methods of mass spectrometry and in vivo nuclear magnetic resonance promise to yield information that can be extracted for the parameterization of such models [41; 42]. The recent literature contains numerous rudimentary experimental and computational methods for such analyses, so that the methods proposed here will certainly gain in potential applicability. Also aiding our need for input information, we have recently shown in diverse examples that the modeling framework of Biochemical Systems Theory is in many cases robust enough to allow the utilization of default parameters in cases where specific information is unavailable or imprecise.

The proposed method has significant advantage of existing methods. The main advance is our greatly expanded focus, which is no longer limited to pathway systems at their steady state but accounts for the entire (or partial) trajectory between application of label and later time points in the development of the system, possibly all the way to its reaching the steady state. By addressing the full dynamics of the system, our method is able to trace where and when specific atoms become labeled and when molecules lose their label. This type of insight is categorically excluded from all other presently existing methods and allows much richer comparisons with labeling data that are available in the form of time series. As a side issue, the method shows whether a system will even approach a steady state and how quickly this might occur. Thus, in contrast to all other current approaches, our method does not require us to assume that the system has reached steady state but shows all details of the time courses of all system variables following the input of label, whether or not the system reaches a steady state and even if material leaves the system, for instance in the form of CO₂. Our method also functions properly and without any adaptations if the pathway system contains parallel reactions or substrate cycles, situations that are known to cause notorious problems in the present methods.

While dynamic atom position data are still rather rare to date, they are now being generated with increased frequency and accuracy [43; 44]. It is therefore desirable, and indeed necessary, to accompany this trend with an adequate, rigorous method of analysis. Such an analysis may target the comparison between data and an alleged model or have the purpose of discovering unknown features of an ill-defined pathway system. Specifically, if time series data following a labeled input are available, the method can be used to explore the connectivity and regulation of not fully characterized pathway systems. This type of analysis is possible by virtue of inverse engineering and the matching of simulated labeling results computed for hypothesized model structures against observation data. In this mode, the method not only elucidates flux rates and flux split ratios, but has the potential of discovering the full dynamics of the system. The complexity of this inverse process is almost entirely driven by the number of unknown parameters (rather than the number of variables or equations), and this number is the same for the extended set of equations of our proposed method as it is for the underlying “master model.” Thus, the inverse task with atom positioning equations is of a complexity comparable with other reverse engineering tasks that have been discussed widely in the recent literature (e.g., [23; 26] and references therein). The fact that such inverse tasks are beginning to be approachable from a computational point of view suggests that positional enrichment experiments may gain additional appeal as the basis for characterizing pathway regulation with increased sophistication.

5. Conclusions

Positional enrichment analysis has become an important tool for pathway identification [43]. By labeling specific atoms on precursor molecules, the method makes it possible to determine precisely how metabolic materials are distributed throughout a pathway and, for instance, which carbons of a hexose ring ultimately enter specific trioses, pentoses, other sugars, or CO₂.

In terms of mathematics, the method proposed here constitutes a large bookkeeping task that keeps track of the dynamics of metabolites and their potentially labeled atoms. The dynamics in this task is based on a metabolic “master” model that describes with ordinary differential equations the overall kinetics of the pathway. This model is combined with arguments that determine how much label is distributed into which atom position of the next metabolite through the action of enzymes. For linear pathways, the results are rather similar to our earlier dynamic labeling method [28], but as soon as splitting reactions are involved, the method proposed here fills gaps in the earlier method.

Our analysis of the pentose pathway demonstrates that the results of this method include as special cases those of traditional carbon enrichment analysis. Specifically, the dynamic model created here approaches the steady-state carbon labeling distribution that is obtained from the traditional analysis.

The proposed method can be used in principle for inverse tasks, in which time series labeling data are assessed with the goal of identifying structural or regulatory elements in ill-defined pathway systems.

Appendix

GMA model for positional enrichment dynamics in the pentose phosphate pathway of Zymomonas mobilis

The diagram in Figure 1 is readily formulated as

$${\mathit{dX}}_1/\mathit{dt}=V_{7,1}+V_{6,1}-V_{4,5}-V_{1,2}$$

$${\mathit{dX}}_2/\mathit{dt}=V_{1,2}-V_{2,5}$$

$${\mathit{dX}}_3/\mathit{dt}=V_{4,5}+V_{5,3}+V_{1,2}-V_{3,13}-V_{2,5}$$

$${\mathit{dX}}_4/\mathit{dt}=V_{2,5}-V_{4,5}$$

$${\mathit{dX}}_5/\mathit{dt}=V_{4,5}+V_{2,5}-V_{5,6}-V_{5,3}$$

$${\mathit{dX}}_6/\mathit{dt}=V_{5,6}-V_{6,1}$$ (A1)

Here, the flux term V_7,1 corresponds to the input to the system, calculated with X₇/5, accounting for the five carbon atoms of xylose. For the GMA representation, the flux terms V_i,j are set up as power law equations, whose parameters are computed from information in Tables 1-3 with well-established methods (see [33]). The result is

$$V_{1,2}=0.03529X_1^{0.599}{X}_9$$

$$V_{2,5}=2.078X_2^{0.0055}{X}_3{X}_{10}$$

$$V_{3,13}=4.4937X_3^{0.967}{X}_{13}$$

$$V_{4,5}=0.00369X_4^{0.940}{X}_1^{0.731}{X}_{11}$$

$$V_{5,3}=0.0214X_5^{0.973}{X}_{12}$$

$$V_{5,6}=0.02446X_5^{0.868}{X}_{14}$$

$$V_{6,1}=2.2912X_6^{0.992}{X}_{15}$$

$$V_{7,1}=0.022X_7^{0.871}{X}_8$$ (A2)

Substituting these terms into the above mass balance equations yields a model for the total masses of all carbons. Within each metabolite, the equations for each atom are identical:

$${\mathit{dX}}_{1k}/\mathit{dt}=V_{7,1}+V_{6,1}-V_{4,5}-V_{1,2},X_{1k}(0)=1/5\cdot X_{1}k=a,\dots ,e$$

$${\mathit{dX}}_{2k}/\mathit{dt}=V_{1,2}-V_{2,5},X_{2k}(0)=1/7\cdot X_{2}k=a,\dots ,g$$

$${\mathit{dX}}_{3k}/\mathit{dt}=V_{4,5}+V_{5,3}+V_{1,2}-V_{3,13}-V_{2,5},X_{3k}(0)=1/3\cdot X_{3}k=a,\dots ,c$$

$${\mathit{dX}}_{4k}/\mathit{dt}=V_{2,5}-V_{4,5},X_{4k}(0)=1/4\cdot X_{4}k=a,\dots ,d$$

$${\mathit{dX}}_{5k}/\mathit{dt}=V_{4,5}+V_{2,5}-V_{5,6}-V_{5,3},X_{5k}(0)=1/6\cdot X_{5}k=a,\dots ,f$$

$${\mathit{dX}}_{6k}/\mathit{dt}=V_{5,6}-V_{6,1},X_{6k}(0)=1/6\cdot X_{6}k=a,\dots ,f$$ (A3)

Equations for labeled and unlabeled carbons are derived from these “master equations” by applying appropriate weights to all fluxes. Each weight reflects the probability of receiving a labeled or unlabeled atom through a given flux. Thus, one obtains for the labeled atoms of the first metabolite (P5P):

$${\mathit{dL}}_{1a}/\mathit{dt}=V_{7,1}·(L_{7a}/X_{7a})+V_{6,1}·(L_{6b}/X_{6b})-V_{4,5}·(L_{1a}/X_{1a})-V_{1,2}·(L_{1a}/X_{1a}),L_{1a}(0)=0$$

$${\mathit{dL}}_{1b}/\mathit{dt}=V_{7,1}·(L_{7b}/X_{7b})+V_{6,1}·(L_{6c}/X_{6c})-V_{4,5}·(L_{1b}/X_{1b})-V_{1,2}·(L_{1b}/X_{1b}),L_{1b}(0)=0$$

$${\mathit{dL}}_{1c}/\mathit{dt}=V_{7,1}·(L_{7c}/X_{7c})+V_{6,1}·(L_{6d}/X_{6d})-V_{4,5}·(L_{1c}/X_{1c})-V_{1,2}·(L_{1c}/X_{1c}),L_{1c}(0)=0$$

$${\mathit{dL}}_{1d}/\mathit{dt}=V_{7,1}·(L_{7d}/X_{7d})+V_{6,1}·(L_{6e}/X_{6e})-V_{4,5}·(L_{1d}/X_{1d})-V_{1,2}·(L_{1d}/X_{1d}),L_{1d}(0)=0$$

$${\mathit{dL}}_{1e}/\mathit{dt}=V_{7,1}·(L_{7e}/X_{7e})+V_{6,1}·(L_{6f}/X_{6f})-V_{4,5}·(L_{1e}/X_{1e})-V_{1,2}·(L_{1e}/X_{1e}),L_{1e}(0)=0$$ (A4)

The unlabeled complements are formulated in the same fashion, with the initial mass divided equally among them. For instance,

$${\mathit{dU}}_{1c}/\mathit{dt}=V_{7,1}·(U_{7c}/X_{7c})+V_{6,1}·(U_{6d}/X_{6d})-V_{4,5}·(U_{1c}/X_{1c})-V_{1,2}·(U_{1c}/X_{1c}),U_{1c}(0)=1/5·U_1$$ (A5)

The remainder of the system is constructed in the same fashion. Hence, we obtain for the labeled fractions:

$${\mathit{dL}}_{2a}/\mathit{dt}=V_{1,2}·(L_{1a}/X_{1a})-V_{2,5}·(L_{2a}/X_{2a}),L_{2a}(0)=0$$

$${\mathit{dL}}_{2b}/\mathit{dt}=V_{1,2}·(L_{1b}/X_{1b})-V_{2,5}·(L_{2b}/X_{2b}),L_{2b}(0)=0$$

$${\mathit{dL}}_{2c}/\mathit{dt}=V_{1,2}·(L_{1a}/X_{1a})-V_{2,5}·(L_{2c}/X_{2c}),L_{2c}(0)=0$$

$${\mathit{dL}}_{2d}/\mathit{dt}=V_{1,2}·(L_{1b}/X_{1b})-V_{2,5}·(L_{2d}/X_{2d}),L_{2d}(0)=0$$

$${\mathit{dL}}_{2e}/\mathit{dt}=V_{1,2}·(L_{1c}/X_{1c})-V_{2,5}·(L_{2e}/X_{2e}),L_{2e}(0)=0$$

$${\mathit{dL}}_{2f}/\mathit{dt}=V_{1,2}·(L_{1d}/X_{1d})-V_{2,5}·(L_{2f}/X_{2f}),L_{2f}(0)=0$$

$${\mathit{dL}}_{2g}/\mathit{dt}=V_{1,2}·(L_{1e}/X_{1e})-V_{2,5}·(L_{2g}/X_{2g}),L_{2g}(0)=0$$ (A6)

$${\mathit{dL}}_{3a}/\mathit{dt}=V_{4,5}·(L_{1c}/X_{1c})+V_{5,3}·\left(\right[L_{5c}+L_{5d}]/[X_{5c}+X_{5d}\left]\right)+V_{1,2}·(L_{1c}/X_{1c})-V_{3,13}·(L_{3a}/X_{3a})-V_{2,5}·(L_{3a}/X_{3a}),L_{3a}(0)=0$$

$${\mathit{dL}}_{3b}/\mathit{dt}=V_{4,5}·(L_{1d}/X_{1d})+V_{5,3}·\left(\right[L_{5b}+L_{5e}]/[X_{5b}+X_{5e}\left]\right)+V_{1,2}·(L_{1d}/X_{1d})-V_{3,13}·(L_{3b}/X_{3b})-V_{2,5}·(L_{3b}/X_{3b}),L_{3b}(0)=0$$

$${\mathit{dL}}_{3c}/\mathit{dt}=V_{4,5}·(L_{1e}/X_{1e})+V_{5,3}·\left(\right[L_{5a}+L_{5f}]/[X_{5a}+X_{5f}\left]\right)+V_{1,2}·(L_{1e}/X_{1e})-V_{3,13}·(L_{3c}/X_{3c})-V_{2,5}·(L_{3c}/X_{3c}),L_{3c}(0)=0$$ (A7)

$${\mathit{dL}}_{4a}/\mathit{dt}=V_{2,5}\cdot (L_{2d}/X_{2d})-V_{4,5}\cdot (L_{4a}/X_{4a}),L_{4a}(0)=0$$

$${\mathit{dL}}_{4b}/\mathit{dt}=V_{2,5}\cdot (L_{2e}/X_{2e})-V_{4,5}\cdot (L_{4b}/X_{4b}),L_{4b}(0)=0$$

$${\mathit{dL}}_{4c}/\mathit{dt}=V_{2,5}\cdot (L_{2f}/X_{2f})-V_{4,5}\cdot (L_{4c}/X_{4c}),L_{4c}(0)=0$$

$${\mathit{dL}}_{4d}/\mathit{dt}=V_{2,5}\cdot (L_{2g}/X_{2g})-V_{4,5}\cdot (L_{4d}/X_{4d}),L_{4d}(0)=0$$ (A8)

$${\mathit{dL}}_{5a}/\mathit{dt}=V_{4,5}\cdot (L_{1a}/X_{1a})+V_{2,5}\cdot (L_{2a}/X_{2a})-V_{5,6}\cdot (L_{5a}/X_{5a})-V_{5,3}\cdot (L_{5a}/X_{5a}),L_{5a}(0)=0$$

$${\mathit{dL}}_{5b}/\mathit{dt}=V_{4,5}\cdot (L_{1b}/X_{1b})+V_{2,5}\cdot (L_{2b}/X_{2b})-V_{5,6}\cdot (L_{5b}/X_{5b})-V_{5,3}\cdot (L_{5b}/X_{5b}),L_{5b}(0)=0$$

$${\mathit{dL}}_{5c}/dt=V_{4,5}\cdot (L_{1a}/X_{1a})+V_{2,5}\cdot (L_{2c}/X_{2c})-V_{5,6}\cdot (L_{5c}/X_{5c})-V_{5,3}\cdot (L_{5c}/X_{5c}),L_{5c}(0)=0$$

$${\mathit{dL}}_{5d}/\mathit{dt}=V_{4,5}\cdot (L_{1b}/X_{1b})+V_{2,5}\cdot (L_{2a}/X_{2a})-V_{5,6}\cdot (L_{5d}/X_{5d})-V_{5,3}\cdot (L_{5d}/X_{5d}),L_{5d}(0)=0$$

$${\mathit{dL}}_{5e}/\mathit{dt}=V_{4,5}\cdot (L_{1c}/X_{1c})+V_{2,5}\cdot (L_{2b}/X_{2b})-V_{5,6}\cdot (L_{5e}/X_{5e})-V_{5,3}\cdot (L_{5e}/X_{5e}),L_{5e}(0)=0$$

$${\mathit{dL}}_{5f}/\mathit{dt}=V_{4,5}\cdot (L_{1d}/X_{1d})+V_{2,5}\cdot (L_{2c}/X_{2c})-V_{5,6}\cdot (L_{5f}/X_{5f})-V_{5,3}\cdot (L_{5f}/X_{5f}),L_{5f}(0)=0$$ (A9)

$${\mathit{dL}}_{6a}/\mathit{dt}=V_{5,6}\cdot (L_{5a}/X_{5a})-V_{6,1}\cdot (L_{6a}/X_{6a}),L_{6a}(0)=0$$

$${\mathit{dL}}_{6b}/\mathit{dt}=V_{5,6}\cdot (L_{5b}/X_{5b})-V_{6,1}\cdot (L_{6b}/X_{6b}),L_{6b}(0)=0$$

$${\mathit{dL}}_{6c}/\mathit{dt}=V_{5,6}\cdot (L_{5c}/X_{5c})-V_{6,1}\cdot (L_{6c}/X_{6c}),L_{6c}(0)=0$$

$${\mathit{dL}}_{6d}/\mathit{dt}=V_{5,6}\cdot (L_{5d}/X_{5d})-V_{6,1}\cdot (L_{6d}/X_{6d}),L_{6d}(0)=0$$

$${\mathit{dL}}_{6e}/\mathit{dt}=V_{5,6}\cdot (L_{5e}/X_{5e})-V_{6,1}\cdot (L_{6e}/X_{6e}),L_{6e}(0)=0$$

$${\mathit{dL}}_{6f}/\mathit{dt}=V_{5,6}\cdot (L_{5f}/X_{5f})-V_{6,1}\cdot (L_{6f}/X_{6f}),L_{6f}(0)=0$$ (A10)

Examples of the unlabeled fractions are:

$${\mathit{dU}}_{2a}/\mathit{dt}=V_{1,2}\cdot (U_{1a}/X_{1a})-V_{2,5}\cdot (U_{2a}/X_{2a}),U_{2a}(0)=1/7\cdot U_2$$

$${\mathit{dU}}_{3a}/\mathit{dt}=V_{4,5}\cdot (U_{1c}/X_{1c})+V_{5,3}\cdot ([U_{5c}+U_{5d}]/[X_{5c}+X_{5d}])+V_{1,2}\cdot (U_{1c}/X_{1c})-V_{3,13}\cdot (U_{3a}/X_{3a})-V_{2,5}\cdot (U_{3a}/X_{3a}),U_{3a}(0)=1/3\cdot U_3$$

$${\mathit{dU}}_{4a}/\mathit{dt}=V_{2,5}\cdot (U_{2d}/X_{2d})-V_{4,5}\cdot (U_{4a}/X_{4a}),U_{4a}(0)=1/4\cdot U_4$$

$${\mathit{dU}}_{5a}/\mathit{dt}=V_{4,5}\cdot (U_{1a}/X_{1a})+V_{2,5}\cdot (U_{2a}/X_{2a})-V_{5,6}\cdot (U_{5a}/X_{5a})-V_{5,3}\cdot (U_{5a}/X_{5a}),U_{5a}(0)=1/6\cdot U_5$$

$${\mathit{dU}}_{6a}/\mathit{dt}=V_{5,6}\cdot (U_{5a}/X_{5a})-V_{6,1}\cdot (U_{6a}/X_{6a}),U_{6a}(0)=1/6\cdot U_6$$ (A11)

Total molecular masses of labeled and unlabeled carbons are directly computed by summing, such as L₁ = L_1a + L_1b + L_1c + L_1d + L_1e and U₁ = U_1a + U_1b + U_1c + U_1d + U_1e. Finally, the xylose input is represented through sub-fractions are equal in magnitude, such as U_7k = 1/ 5 · U₇, L_7k = 1/ 5 · L₇, and X_7k = U_7k + L_7k (k = a, …, f).

Simulations

Sustained availability of labeled #A-carbon xylose is implemented with the initial conditions

$$L_{7k}=0;k=a,\dots ,e$$

$$U_{7k}=1/5\cdot U_7;k=a,\dots ,e$$

$$X_{7k}=1/5\cdot X_7;k=a,\dots ,e$$ (A12)

For bolus labeling, the substrate is formulated as an additional set of differential equations. As an example, a bolus of #C-carbon labeled xylose is implemented at time t by defining an uptake rate and perturbation, such as

$${\mathit{rate}}_7=0.4884$$

$$\mathit{Bolus}=X_7/5$$ (A13)

and decay equations, which in the simplest case may be

$${\mathit{dSL}}_{7k}/\mathit{dt}=-X_7/5\cdot {\mathit{rate}}_7;k=a,\dots ,e$$

$${\mathit{dL}}_{7k}/\mathit{dt}={\mathit{rate}}_7\cdot {\mathit{SL}}_{7k};L_{7k}(t)=\mathit{Bolus};k=a$$ (A14)