Can laser speckle flowmetry be made a quantitative tool?

Abstract

The ultimate objective of laser speckle flowmetry (and a host of specific implementations such as laser speckle contrast analysis, LASCA or LSCA; laser speckle spatial contrast analysis, LSSCA; laser speckle temporal contrast analysis, LSTCA; etc.) is to infer flow velocity from the observed speckle contrast. Despite numerous demonstrations over the past 25 years of such a qualitative relationship, no convincing quantitative relationship has been proven. One reason is a persistent mathematical error that has been propagated by a host of workers; another is a misconception about the proper autocorrelation function for ordered flow. Still another hindrance has been uncertainty in the specific relationship between decorrelation time and local flow velocity. Herein we attempt to dispel some of these errors and misconceptions with the intent of turning laser speckle flowmetry into a quantitative tool. Specifically we review the underlying theory, explore the impact of various analytic models for relating measured intensity fluctuations to scatterer motion, and address some of the practical issues associated with the measurement and subsequent data processing.

1. INTRODUCTION

Over 25 years ago, Fercher and Briers [1] put forth the idea of estimating flow velocity based on the contrast of laser speckle. The concept was to infer a temporal correlation time constant from the observed speckle contrast and subsequently to relate this time constant to the flow velocity. Since that time, various researchers [2–4] have demonstrated this qualitative relationship, yet no convincing quantitative relationship has been shown. One reason is a persistent mathematical error that has been propagated by a host of workers. Another is a misconception about the proper statistical relationship between motion of the scatterers and the resulting spatial and temporal speckle contrast. Many researchers use the Lorentzian model for such a relationship. In fact, the Lorentzian is a homogeneous line profile appropriate only for Brownian motion. In such a case, the dynamics of a single particle are representative of the ensemble. The other extreme is an inhomogeneous (Gaussian) profile that corresponds to a process in which the dynamics are particular to the individual scatterers. The proper model for complex motion such as blood flow is undoubtedly intermediate between these two extremes. Still another hindrance to the development of laser speckle flowmetry as a quantitative tool has been an unsubstantiated proposed relationship between decorrelation time and local flow velocity. Herein we address each of these three general issues. The intention is the realization of this measurement concept as a quantitative tool for full-field flow assessment.

2. THEORY AND RESULTS

Here we review the theory of laser speckle contrast imaging for the assessment of flow and discuss a number of issues that have impeded its becoming a quantitative tool. Specifically we address persistent mathematical errors, discuss various mathematical correlation functions, and finally treat the issue of interpretation of the data inferred from a typical measurement.

A. Persistent Mathematical Error

The concept of laser speckle flowmetry relies on the association between speckle contrast and camera integration time. This is expressed at a fundamental level by the relationship between the instantaneous intensity i(r̄,t) and its corresponding measured intensity,

$$I(\overline{r},t)=\frac{1}{T}{\int }_{-\infty }^{\infty }d{t}^{\prime }i(\overline{r},t^{\prime })\text{rect}\left(\frac{t-t^{\prime }}{T}\right),$$ (1a)

where T is the camera integration time, the integration window is defined as

$$\text{rect}(x)\equiv \{\begin{array}{ll}1\hfill & \mid x\mid \le 1/2\hfill \\ 0\hfill & \text{else}\hfill \end{array},$$ (1b)

and dependence on the spatial coordinate r̄ is denoted explicitly. Contrast is typically defined as the quotient of the mean and standard deviation of the measured intensity,

$$K(\overline{r})\equiv \frac{{\sigma }_1(\overline{r})}{{\mu }_1(\overline{r})}.$$ (2)

We are specifically interested in the imaging condition. In such a situation, subject motion, or flow, is reflected as a boiling of the speckle pattern rather than a translation. Experimentally a combination of boiling and translation is observed in the vicinity of the image plane, and pure boiling only at the precise focus [5]. Note that ordered motion results in a translating speckle pattern only for the condition of misfocus. Under these conditions, the speckle motion and object motion are related through the misfocus distance (and the direction from focus) and the image magnification.

From Eq. (1) it is easily shown that the first-order statistics of the integrated intensity in Eq. (2) are given by

$$E\{I(\overline{r},t)\}\equiv {\mu }_1(\overline{r})=\frac{1}{T}{\int }_{-\infty }^{\infty }\text{d}{t}^{\prime }E\{i(\overline{r},t^{\prime })\}\text{rect}\left(\frac{t-t^{\prime }}{T}\right)={\mu }_{\text{i}}(\overline{r})$$ (3a)

and

$${\sigma }_{\text{I}}^2(\overline{r})=\frac{1}{T}{\int }_0^T\text{d}\tau C_i(\overline{r},\tau )[2(1-\tau /T)],$$ (3b)

where E denotes expectation and C_i is the covariance of the instantaneous intensity. Note that the term in square brackets in Eq. (3b) was missing in the original publication by Fercher and Briers [1] and although this omission has been pointed out by numerous authors [6–8], the incorrect formula persists in the literature [9, 10].

Note that the variance of the integrated intensity in Eq. (3b), which is a first-order statistic, requires knowledge of the second-order statistic of the instantaneous intensity. The covariance of the instantaneous intensity in terms of its autocorrelation is

$$C_i(\overline{r},\tau )+{\mu }_{\text{i}}^2(\overline{r})=R_{\text{i}}(\overline{r},\tau )=\langle i(\overline{r},t)i(\overline{r},t+\tau )\rangle .$$ (4)

Under the assumption that the instantaneous intensity is due to scatter from a large number of particles, one can argue that the field is a complex circular Gaussian process. As such, one can invoke the complex Gaussian moment theorem [11] that expresses the fourth-order statistical moment in terms of products of second-order moments with the result that

$$R_{\text{i}}(\overline{r},\tau )={\mu }_{\text{i}}^2(\overline{r})+\mid R_{\text{E}}(\overline{r},\tau ){\mid }^2.$$ (5)

This association between the correlation function for the intensity and that of the field (denoted by the subscript E) is known as the Siegert relation [12]. At this point, the usual practice is to assume that the scattering particles are undergoing Brownian motion with the result that the correlation function for the particle velocity (and thus the field) takes the form [13]

$$R_{\text{E}}(\overline{r},\tau )={\mu }_{\text{i}}(\overline{r})exp\{-\mid \tau \mid /{\tau }_{\text{c}}\},$$ (6)

where τ_c is a characteristic correlation time depending on the mass of the particle and the frictional forces in its environment. From this relationship we have for the covariance of the instantaneous intensity

$$C_{\text{i}}(\overline{r},\tau )={\mu }_{\text{i}}^2(\overline{r})exp\{-2\mid \tau \mid /{\tau }_{\text{c}}\},$$ (7)

and thus for the contrast [Eqs. (2), (3), and (7)],

$$K(\overline{r})={\left\{\frac{{\tau }_{\text{c}}}{2T}\left[2-\frac{{\tau }_{\text{c}}}{T}(1-e^{-2T/{\tau }_{\text{c}}})\right]\right\}}^{1/2}.$$ (8a)

The corresponding result as given by Fercher and Briers [1] without inclusion of the triangular window in Eq. (3b) is

$$K(\overline{r})={\left\{\frac{{\tau }_{\text{c}}}{2T}(1-e^{-2T/{\tau }_{\text{c}}})\right\}}^{1/2}.$$ (8b)

Equations (8a) and (8b) are plotted in Fig. 1, thus illustrating the importance of including the triangular window. One may argue that operation in the long-exposure regime, where the effect of this triangular window is minimal, renders this distinction academic [14]. In the past, limitations imposed by video rate cameras indeed have forced operation in the long-exposure regime. However, with recent advances in CCD and CMOS technologies, this is no longer the case. A more general formulation is now relevant, as data acquisition using shorter integration times has some distinct advantages.

Fig. 1.

(Color online) Historical result due to Fercher and Briers [1] and correction.

B. Proper Statistical Model

As originally proposed by Fercher and Briers [1], the relationship of Eq. (8b) could be used in a single exposure (photograph) to assess flow velocity. This argument relies on the relative values of the correlation time τ_c and the camera integration time T. The idea further assumes that the correlation time is inversely proportional to the velocity of the scatterers. Thus if the camera integration time is long compared to the correlation time, the motion of the scatterers will blur the speckle and the contrast will be reduced. On the other hand, if the integration time is short with respect to the correlation time, the speckle motion will be effectively frozen and the contrast will remain high. In the intermediate regime, the contrast should bear a functional dependence on the ratio T/τ_c. The difficulty with this argument is that there are multiple characteristic correlation times. One is associated with the ordered flow τ_c=τ_F, while another is associated with the unordered Brownian motion τ_c=τ_B. The desired behavior is observed only if τ_F <τ_B. Otherwise, the speckle motion associated with the random Brownian motion destroys the contrast.

Another fundamental problem with this approach is that it is often assumed that the exponential correlation function associated with Brownian motion is appropriate for organized motion. As pointed out by Fercher and Briers [1], the exponential correlation function corresponds to a Lorentzian line shape, which in the nomenclature of laser engineering is referred to as a homogeneously broadened line or spectral feature [15]. Such a correlation law describes a collection of scatterers with identical dynamic behavior. As an alternative viewpoint, one might view organized flow as a totally inhomogeneous broadening phenomenon. For this process, the dynamic behavior is particular to the individual scatterers. In this case the line shape for an ensemble of scatterers is Gaussian and as a result, so too is the correlation function. Such a phenomenon is often referred to as Doppler broadening. If we adopt such a Gaussian model for the covariance of instantaneous intensity [16]

$$C_i(\overline{r},\tau )={\mu }_i^2(\overline{r})exp\{-2{(\tau /{\tau }_{\text{c}})}^2\},$$ (9)

then the measured contrast is given by

$$K(\overline{r})={\left\{\frac{{\tau }_{\text{c}}}{2T}\left[\sqrt{2\pi }\text{erf}\left(\frac{\sqrt{2}T}{{\tau }_{\text{c}}}\right)-\frac{{\tau }_{\text{c}}}{T}(1-e^{-2{(T/{\tau }_{\text{c}})}^2})\right]\right\}}^{1/2}.$$ (10)

The substantial differences between the resulting contrasts for the Lorentzian [Eq. (8a)] and Gaussian [Eq. (10)] line shapes are shown in Fig. 2. We view these two results as limiting behaviors. Undoubtedly the actual correlation behavior is some mixture of the two statistically independent processes. In such a case the true model would be given by the convolution of the two line shapes, Lorentzian and Gaussian, i.e., a Voigt profile [15]. Historically, the distinction between these two behaviors was academic because typical camera integration times were so long that only the asymptotic (large T/τ_c) behavior was of interest. In this regime we find $K\sim a/\sqrt{T/t_{\text{c}}}$, where a is of the order of unity for each of these two limiting behaviors. The factor T/τ_c is the expected reduction in the variance due to the number of independent samples.

Fig. 2.

(Color online) Speckle contrast as a function of relative integration time for Lorentzian and Gaussian autocorrelation functions.

Note that in the above discussion we have referred to the convolution of the two line shapes. While it is obvious through the Wiener–Khinchin theorem [13] that the exponential and Lorentzian functions form a Fourier transform pair (as do the Gaussian and Gaussian), it is often not appreciated that these “line spectra” are actually the first-order probability-density functions (PDFs) of the corresponding stochastic processes [13]. Further recall that for addition of statistically independent random variables, the PDF of the sum is the convolution of the respective PDFs. By the convolution theorem, therefore, the net correlation function for a combined process involving ordered and unordered motion is the simple product of the Gaussian and exponential correlation functions [17].

In the absence of any a priori knowledge of the proper correlation behavior, therefore, the inferred ratio τ_c/T for a measured contrast K will display an uncertainty as shown in Fig. 3. As seen in this figure, even for operation in the asymptotic regime, the uncertainties are substantial.

Fig. 3.

(Color online) Fractional uncertainty in decorrelation time due to uncertainty in proper correlation model.

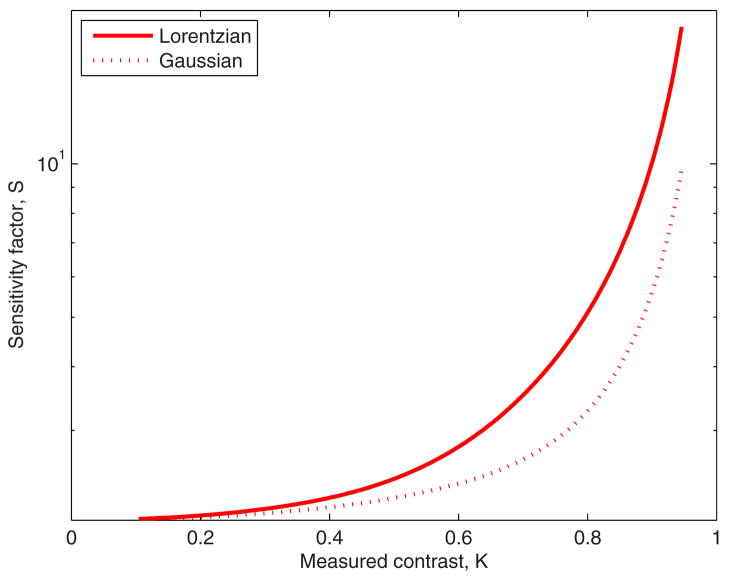
Finally, one must address the issue of the sensitivity of the measurement. We define this sensitivity factor as the fractional change in the inferred time constant for a fractional change in the measured contrast

$$S=\frac{\partial {\tau }_{\text{c}}/{\tau }_{\text{c}}}{\partial K/K}$$ (11)

Note that the definition of sensitivity in Eq. (11) differs from that of Yuan et al. [18] because it is the decorrelation time that is of ultimate interest, not the contrast. As shown in Fig. 4 the sensitivity factors for these two limiting correlation laws are essentially constant in the asymptotic regime. These results predict, for example, that within the asymptotic regime, a 2% change in measured contrast results in a 4% change in the inferred time constant. The slopes of the curves in Fig. 4 further illustrate that operating in this asymptotic region (i.e., where T/τ_c is large) is a poor choice for discriminating between regions that exhibit similar flows, as the sensitivity to different flow velocities is very low. If operation in the (long-exposure) asymptotic regime is unavoidable due to equipment limitations, then a means of obviating the issue of the proper correlation law is to adopt a common definition of the correlation law such as in Ramirez-San-Juan et al. [14]. These authors make the point that a common definition of coherence time of the speckle intensity [19],

$${\tau }_{\text{c}}={\int }_{-\infty }^{\infty }\mid C_i(\overline{r},\tau )/{\mu }_i^2(\overline{r})\mid \text{d}\tau ,$$ (12)

renders the asymptotic behavior of the contrast for the Lorentzian and Gaussian models identical. This concordance, however, does not make it possible to discriminate between random and ordered flows. In fact, because the objective is to assess ordered flows, it is highly desirable to be able to distinguish between random and ordered flows.

Fig. 4.

(Color online) Sensitivity factors for two limiting correlation behaviors.

C. Data Acquisition and Processing Issues

A data acquisition issue that is often treated in an ad hoc fashion is the limiting form of the speckle contrast. This issue comes about because heretofore all the statistical relationships discussed have been analytic ones. Specifically, it is often pointed out, e.g., [6], that the intensity may be measured over an extended spatial domain (rather than by a point sensor), and as a result, the speckle contrast is reduced. Commonly this effect is expressed in terms of the contrast relationship

$$K^2(T)=\frac{1}{T}{\int }_0^T\text{d}\tau \beta \mid g_1(\tau ){\mid }^2[2(1-\tau /T)],$$ (13)

where β≤1 is a parameter that accounts for the reduction in the measured contrast due to averaging (by the detector) over uncorrelated speckles [20], and g₁(τ) is the field autocorrelation coefficient. The parameter β is sometimes called a “coherence factor” that depends on the detection optics [7], but is actually the inverse of Goodman’s integrated speckle parameter ℳ[21]. Unfortunately, the nomenclature “coherence factor” is sufficiently similar to the “complex coherence factor” of Mandel and Wolf [22] to cause confusion. Further, the nomenclature “coherence factor” may suggest that it is related to the (temporal) coherence of the source [23]; under practical measurement configurations, it is not. To see this, one need only consider the vastly different time scales of the typical source coherence time and the motion correlation time.

As suggested by the preceding discussion, the mathematical foundations of quasi-elastic light scatter (QLS) [12] and LSCA are sufficiently similar, that it is often assumed that the measurement requirements are identical. Specifically, it appears to be a foregone conclusion that for LSCA measurements, the acquisition geometry should be chosen such that the speckle size matches the detector pixel size, e.g., [18]. This has been demonstrated as optimum for QLS measurements in order to maximize the signal [6]. That this matching condition violates the (spatial) Nyquist sampling requirement is usually ignored. Further, the data processing for LSCA and QLS are substantially different. In particular, subsequent to LSCA data acquisition, one must calculate a local speckle contrast from the appropriate sample statistics. Implicit in the use of these sample statistics is the assumption that the initial speckle image(s) as acquired by the camera faithfully represent(s) the speckle field. This can be so only if the sampling is at or above the Nyquist rate, i.e., the smallest speckle is at least twice the size of the pixel. This is most easily accomplished by a reduction of the f-stop of the lens [21]. While violation of this sampling criterion technically does not result in aliasing, because the integration over the individual detector elements is effectively a spatial low-pass filtering operation [21], the spatial structure of the speckle pattern under the matching condition is not preserved.

Calculation of the local speckle contrast subsequently uses the sample statistics for the mean and variance. Specifically, the local contrast is given by the following:

$$\begin{array}{c}K=\frac{S}{M},\\ M=\frac{1}{N_{\text{s}}}\sum _{i=1}^{N_{\text{s}}}{I}_{\text{i}},S^2=\frac{1}{N_{\text{s}}-1}\sum _{i=1}^{N_{\text{s}}}{(I_{\text{i}}-M)}^2,\end{array}$$ (14)

where the region in question is N_s=L×W pixels. Subsequently one could invert the relationship of Eq. (8a) or Eq. (10) to obtain an estimate of the correlation time. Note, however, as demonstrated by Duncan et al. [24], the local contrast computed as in Eq. (11) displays a probability distribution function depending on the size of the local neighborhood and the speckle size with respect to the pixel. These local contrast values, even for a fully developed, polarized speckle pattern can depart substantially from the theoretical value of unity. Thus one could attach error bounds to the correlation times inferred through such a process.

The sample statistics of Eq. (14) are explicitly for the local spatial contrast within a single image. Extension of the definition of these statistics into the temporal direction is possible as in the temporal LASCA (tLASCA) [9], modified laser speckle imaging (mLSI) [25], or quantitative temporal speckle contrast imaging (qTSCI) [26] concepts. Such temporal statistics are effective for dealing with scatter from stationary structures. Local neighborhoods encompassing both spatial and temporal domains can prove useful as well [24].

D. Interpretation of Inferred Correlation Time

In addition to the uncertainties associated with a proper choice of correlation behavior and statistical distribution of the sample statistics for local contrast is the problem of the relationship between the inferred time constant τ_c and the velocity V. It has been assumed that τ_c and V are inversely related, however, a specific relationship remains elusive. One suggested relationship [27] is

$${\tau }_{\text{c}}=\frac{\lambda /2\pi }{V},$$ (15)

that is, the correlation time is the quotient of a physical length scale (in this case the wavelength) and the local velocity. The authors [27] admit that this relationship is speculative and give no first principles argument as to its veracity. Nevertheless this relationship has entered the literature as fact [9]. A more physically realistic relationship, however, can be found from the expression for the normalized intensity covariance due to Goodman [19]:

$$\frac{C_{\text{i}}(\overline{r},\tau )}{{\mu }_{\text{i}}^2(\overline{r})}={\left[\frac{2J_1\left(\frac{\pi DV\tau }{\lambda z}\right)}{\left(\frac{\pi DV\tau }{\lambda z}\right)}\right]}^2,$$ (16)

where D is the pupil diameter. This result is based on a phase screen model of the object motion and predicts decorrelation for a physical length scale of the order of the point-spread function (PSF), which, for a circular pupil as assumed here, is a simple Airy function [28]. Contrast as a function of integration time for this model is compared to the Brownian and Gaussian forms in Fig. 5. Clearly this behavior is intermediate between these two limiting forms, more closely resembling the Lorentzian results for long-time exposures and the Gaussian for short-time exposures [16]. This effect could easily account for the nonlinear relationship between time constant and velocity as observed by Parthasarathy et al. [29]. Consistent with the correlation functions previously discussed, it is easily shown that in the asymptotic regime, the contrast is $K\sim a/\sqrt{T/{\tau }_{\text{c}}}$.

Fig. 5.

(Color online) Speckle contrast as a function of integration time for various intensity correlation laws.

Finally, from Eq. (16), we obtain the decorrelation time

$${\tau }_{\text{c}}=\frac{\omega }{V},$$ (17a)

where ω is the characteristic width of the Airy function

$$\omega =\frac{\lambda z}{D},$$ (17b)

and the velocity V and PSF are referred to a common plane. This result makes physical sense; once the volume of scatters moves a distance of the order of ω, it is replaced by a new volume containing scatterers that are un-correlated with those in the previous volume element. Again note that if the velocity is defined within the object plane, the PSF must be referred to the object plane as well.

3. DISCUSSION AND CONCLUSIONS

We have highlighted a number of issues that have hindered the concept of LSCA becoming a quantitative tool for the estimation of flow:

1. a persistent erroneous formula expressing contrast as a function of integrated instantaneous covariance of intensity;

2. the inappropriate use of the Lorentzian field correlation relationship;

3. a tendency to operate in the long-exposure asymptotic regime and the subsequent lack of sensitivity;

4. a common assumption that the requirements of QLS and LCSA measurements are the same; and

5. the oft-cited, nonphysical association between the decorrelation time and its associated flow velocity. In particular, we emphasize that association of the exponential correlation model with any ordered motion is patently inconsistent, as such a model is valid only for completely nonordered motion.

The situation for multiple scattering is equally challenging. In this regime one must consider the absorption and scatter “coefficients” μ_a and μ_s in relation to the dimensions of the structures being probed. As example, for whole blood at the He–Ne wavelength of 633 nm, 1/μ_s ~3 μm [30], so that for any vessel of this order or larger, one must consider the possibility of higher-order effects. Based on the previous discussions, it is clear that the correlation function for an nth-order process is simply the nth power of the correlation function (appropriately weighted by the probability of the higher-order effects [31]). For example a second-order exponential process has an effective correlation time that is half that of the first-order process. In the limit of diffusing wave spectroscopy (DWS), motions of the order of $\lambda /\sqrt{n}$ are sufficient for decorrelation [32]. Higher-order scatter has the effect of shifting the contrast curves to the right. Interpretation of the speckle contrast of such higher-order process in terms of a first-order process would thus have the effect of overestimating the true first-order correlation time.

On the other hand there are approaches for mitigating the effects of these higher-order scatter processes. One is to employ linearly polarized illumination and to assess the contrast of only the co-polarized backscatter component. The cross-polarized component (if there is one) is undoubtedly associated with a higher-order scatter event. Of course a separate measurement of any cross-polarized component can give valuable clues as to the existence of these higher-order scatter events. Other discrimination methods include the use of multiple illumination wavelengths or multiple detectors viewing the same scatter volume from different perspectives [32].

Substantial challenges remain if LSCA is to become a quantitative tool for assessing flow. The proper correlation law undoubtedly lies between the Lorentzian and Gaussian limits. A plausible correlation law based on rigid-body motion has been hypothesized, but remains to be verified experimentally. An advantage of this rigid-body model is that it offers a compelling physical link between the decorrelation time constant and the local velocity. However, this too must be verified experimentally.

Much effort remains in linking the uncertainties in the estimated local velocities to the measured contrast, taking into account the probability distributions of the sample statistics. Note that one important parameter in the distribution of the sample statistics of speckle contrast is the relationship between speckle size, detector size, and processing neighborhood. In particular, the proper relationship between speckle and detector sizes is an important issue to be addressed. It is often assumed that the matching condition [18], which has been demonstrated as optimum by researchers in the field of QLS [6], should be applied to LSCA measurements. That this condition violates the Nyquist (spatial) sampling requirement is usually ignored.

Finally, the issue of optimum integration time with respect to the decorrelation time needs to be resolved. One way to proceed would be to acquire data at much higher frame rates and to subsequently explore this relationship numerically, after detection. This approach was indeed chosen by Yuan et al. [18], but their conclusions suffered from a number of the errors and misconceptions cited herein.

Much effort is required before LSCA can be claimed to be a quantitative tool for flow assessment. The issue is not whether there is an answer (i.e., a quantitative link between speckle contrast and local velocity), but rather that there are many answers, each dependent on specific assumptions about the relationships between particle dynamics and light scatter.