Inferring brain variability from diffeomorphic deformations of currents: an integrative approach

Abstract

In the context of computational anatomy, one aims at understanding and modelling the anatomy of the brain and its variations across a population. This geometrical variability is often measured from precisely defined anatomical landmarks such as sulcal lines or meshes of brain structures. This requires (1) to compare geometrical objects without introducing too many non realistic priors and (2) to retrieve the variability of the whole brain from the variability of the landmarks.

We propose, in this paper, to infer a statistical brain model from the consistent integration of variability of sulcal lines. The similarity between two sets of lines is measured by a distance on currents that does not assume any type of point correspondences and it is not sensitive to the sampling of lines. This shape similarity measure is used in a diffeomorphic registrations which retrieves a single deformation of the whole 3D space. This diffeomorphism integrates the variability of all lines in a as spatially consistent manner as possible.

Based on repeated pairwise registrations on a large database, we learn how the mean anatomy varies in a population by computing statistics on diffeomorphisms. Whereas usual methods lead to descriptive measures of variability, such as variability maps or statistical tests, our model is generative: we can simulate new observations according to the learned probability law on deformations. In practice, this variability captured by the model is synthesized in the principal modes of deformations. As a deformation is dense, we can also apply it to other anatomical structures defined in the template space. This is illustrated the action of the principal modes of deformations to a mean cortical surface.

Eventually, our current-based diffeomorphic registration (CDR) approach is carefully compared to a pointwise line correspondences (PLC) method. Variability measures are computed with both methods on the same dataset of sulcal lines. The results suggest that we retrieve more variability with CDR than with PLC, especially in the direction of the lines. Other differences also appear which highlight the different methodological assumptions each method is based on.

1. Introduction

From the ever growing databases of medical images, there is considerable interest in extracting the most relevant information to characterize normal anatomical variability within a group of subjects as well as between different groups, to detect anatomical abnormalities, to classify new images according to their pathologies, and for understanding disease progression. However, modeling the individual anatomy and its normal variability across a population is difficult as there are commonly no physical models for comparing different subjects, and anatomical shapes are complex and require large number of degrees of freedom to model adequately. Moreover, anatomical landmarks such as curves or surfaces embedded in ℝ³ as well as deformations of the 3D space do not belong to usual vector spaces. Defining statistical models is therefore difficult and specific tools have to be developed to accurately measure anatomical variations. If anatomic variation were better understood, tools encoding these variations could have a significant impact in neuroscience to minimize the influence of the anatomical variability in functional group analysis, and in clinical medical image analysis to better drive the personalization of generic models of the anatomy (called also template, atlas or prototype in the literature).

Instead of analyzing the anatomical variability directly in the 3D intensity space, it is often preferable to extract precisely defined anatomical land marks such as sulcal lines (Thompson et al., 1996a; Mangin et al., 2004), cortical surface models (Fischl et al., 2001; Tosun and Prince, 2005), or models of some sub-cortical structures (Hazlett et al., 2005; Vaillant et al., 2007). The data to be analyzed are thus curves, surfaces or volumes represented by structured or unstructured point sets. The first attempts to compare such shapes was based on defining correspondences between points (Zhang, 1994; Chui and Rangarajan, 2003). However, the sampling of two different geometric subjects can be so different that such a correspondence assumption introduces a bias that often hides the “real” underlying geometrical variability. To overcome this difficulty, some authors proposed to measure variations of some features extracted a priori such as length, area, volume, complexity, principal modes of variation of the cloud of sampled points, etc. See Paus et al. (2001) for instance. Although these approaches, that derive scalar measures from structure models, are relatively easy to set up from a computational point of view, they fail to capture fine geometrical variations between subjects like for instance a twisting of the extremity of a sulcus, which cannot be readily described by a set of a priori selected features. Also, data analysis often proceed by computing dense displacement fields that encode variations in shape and volume among individuals, often based on deformable registration of shapes. The deformation that maps one shape onto another has been proved to be useful for measuring significant anatomical variability among different subjects (Fillard et al., 2007a; Vaillant et al., 2007; Ashburner and al, 1998; Durrleman et al., 2007). Due to the presence of noise and of sampling effects, it may be advantageous to allow a trade off between the regularity of the deformation and the precision of the matching, instead of exact matching. This raises the need to develop a consistent deformation framework and a shape similarity measure that does not rely on point correspondences nor on features selected a priori.

In this perspective, one interesting framework consists of modeling geometrical primitives as currents (Vaillant and Glaunès, 2005; Vaillant et al., 2007; Durrleman et al., 2007). The idea is to characterize shapes via vector fields, which are used to probe them. For instance, a surface is characterized by the flux of any vector field through it, a line by the path integral of any vector field along it. Conversely, associating a flux to any vector field specifies an object which is more general than a surface or a curve and which is called a current. This way of embedding shapes in a Hilbert space allows one to define algebraic operations such as addition or averaging, and to measure distance between geometrical primitives via an inner product that does not assume a specific type of point correspondence. Discrete and continuous objects are handled in the same setting, offering a way to measure the sampling quality and to guarantee numerical stability. This framework has been used to compute and visualize mean lines and surfaces, and to perform principal component analysis on datasets of such primitives, suggesting the efficiency and generality of the approach (Durrleman et al., 2008).

However this similarity measure is too weak to capture the broad range of possible differences between shapes: it is beneficial to couple it with a deformation framework. The large deformation diffeomorphic metric mapping (LDDMM) framework (Trouvé, 1998; Grenander and Miller, 1998; Dupuis et al., 1998; Miller et al., 2002, 2006) is ideal for this task as shown in Vaillant and Glaunès (2005) and Glaunès and Joshi (2006) although it might be possible to adapt other diffeomorphism registrations method proposed for images (e.g. Ashburner and Friston (2003); Avants et al. (2006)). The deformation that matches a pair of shapes is sought within a group of regular diffeomorphisms in order to optimize a trade-off between the regularity of the deformation and matching accuracy, as measured by the dissimilarity measure on currents (Vaillant and Glaunès, 2005; Durrleman et al., 2007). As a result, the registration decomposes the differences between two shapes into (1) a deformation that captures a “global” misalignment and (2) a residual term (representing the difference between the registered shape and the target shape) that contains possible non-diffeomorphic variations as well as physical and numerical noise. In the approach followed here, we perform our statistical analysis of shape on the deformation term only. Our results on a dataset of sulcal lines show that this method can be used to detect and characterize anatomical variability within a group of subjects.

Moreover, this diffeomorphic framework enables to register multiple objects in a spatially consistent way. Indeed, a dataset of anatomical landmarks often consists of a set of several shapes (e.g. a set of sulcal lines or set of meshes representing different sub-cortical structures for instance (Mangin et al., 2004; Duchesnay et al., 2007; Gorczowski et al., 2007). If one set of manifolds, such as a distributed set of sulcal landmark curves, is embedded in another manifold which also varies, such as the cortical surface, one often aims to measure the variability not only of the embedded landmarks but also of the whole underlying brain surface or 3D brain volume. The framework based on currents enables precisely to define a distance between multiple objects sets even if they are not labeled or if all subjects have not the same number of objects. (In these cases the distance will just be less precise than for labeled objects). The diffeomorphic framework in turn finds a single deformation of the underlying image domain that integrates the variability of all objects in as consistent manner as possible. By contrast, several methods such as in Fillard et al. (2007a) analyze the variability of each shape individually; there is a need for an extrinsic extrapolation scheme to retrieve a variability in the space between the objects. The approach proposed in Hellier and Barillot (2003); Cachier et al. (2001) makes a model of deformation that has constraints on sulci, cortex, and whole brain, all within a single optimization framework. Earlier work like Thompson and Toga (1996) just used the matching of low order manifolds first, and used these as hard constraints or boundary conditions on subsequent mappings one dimension higher. Altough there are many other registration frameworks in the literature, we focus in this paper on the current-based diffeomorphic registrations (CDR) to build brain variability models.

This paper aims to present and discuss such a framework, based on diffeomorphic registration of currents, in the case of curves. We apply the method on a dataset of labeled sulcal lines to infer the variability of the brain surface within a population. In Section 2, we explain the framework for registration of sulcal lines. How this differs from the pointwise line correspondence (PLC) approach, proposed in Fillard et al. (2007a), is discussed in depth from a methodological point of view. In Section 3, we perform a statistical analysis of the underlying brain surface based on these registrations. This allows us to measure and visualize how the brain surface varies in a population. A comparison with the results obtained in Fillard et al. (2007a) on the same database illustrates some of the different methodological assumptions each method is based on.

2. Registering Sets of 3D Curves

Registering a set of 3D curves L₀ onto another set of 3D curves L₁ can be formulated as the task of looking for the most regular deformation ø that transports all curves of L₀ and best matches the curves of L₁. We follow here the approach introduced in Glaunès (2005): the unknown deformation is sought in a subgroup of diffeomorphisms and its regularity is measured based its distance to the identity (i.e. no deformation), the similarity measure is computed by embedding the curves into a space of currents. As it is common practice in deformable image registration, we find the registrations by minimizing a cost function that balances the regularity of the deformation against the matching fidelity.

2.1. Non-parametric Representation of Curves as Currents

The space of currents is a vector space that may be equipped with a norm that measures geometrical similarity between curves. In this space, curves could be discrete or continuous and may consist of several different parts. All these objects are handled in the same setting and inherit many interesting mathematical properties: linear operations, distance, convergence, etc. Moreover, this definition of distance between curves does not make any assumption about point correspondences, even implicitly. This framework differs therefore from usual methods such as that in Joshi and Miller (2000) where landmark matchings are performed or those in Chui and Rangarajan (2003); Granger and Pennec (2002); Cachier et al. (2001) where curves are considered as unstructured point sets and different kind of “fuzzy” correspondences are assumed. We recall here how to build a space of currents and how to compute explicitly a similarity measure on curves. For more details on the theory we refer the reader to Vaillant and Glaunès (2005); Glaunès (2005); Durrleman et al. (2008) and references therein.

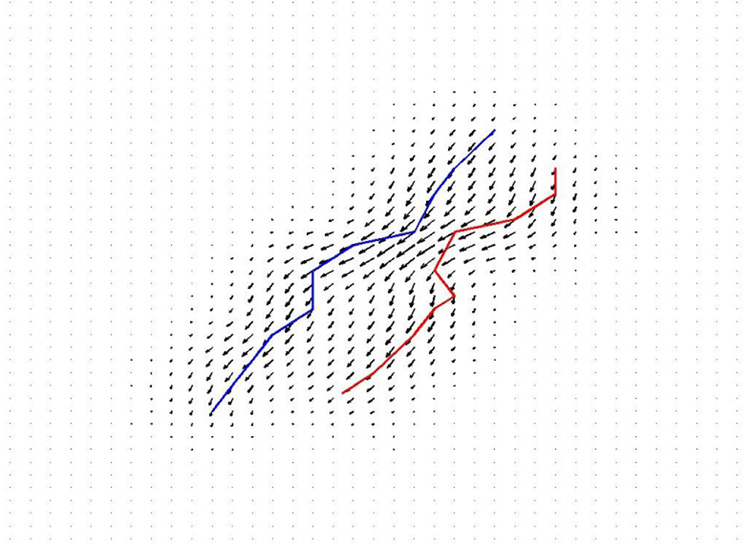
In the framework of currents, curves are seen via the way they integrate vector fields. Any continuous curves or any finite set of polygonal lines (denoted here generally L) can be characterized by the path integral of any vector field ω along it:

$$\forall \omega \in W,L:\omega \to {\displaystyle {\int }_L}<\omega (\mathit{l}),\tau (\mathit{l}){>}_{{ℝ}^3}dl$$ (1)

where τ (l) is the unit tangent vector (defined almost everywhere) of L at point l and W is a test space of smooth vector fields (See Fig.1). More generally, a current L is defined as a continuous linear mapping from the test space W to ℝ. As a set of mappings, the space of current (denoted W*) is a vector space: (L₁+L₂)(ω) = L₁(ω)+L₂(ω) and (λL)(ω) = λ(L(ω)). For curves, this means that the path integral along two curves is the sum of the path integral along each curve: the addition corresponds therefore to the union of the two curves. Scaling a curve means scaling the path integral along the curve.

Figure 1.

Measure of dissimilarity between lines modeled as currents: given two lines L and L′ (in red and blue) we compute the difference between the path integral of a vector field ω (here drawn in black) along both lines. The maximum difference obtained when ω varies among all possible regular vector fields (i.e. ∥ω∥_W ≤ 1) is a measure of the geometrical dissimilarity between the two lines. In this way, we define a distance between shapes without assuming point correspondences. The more we allow the test vector fields ω to have high spatial frequencies, the more finely we measure geometrical differences. In this application, manual delineation of the sulci is typically accurate to within a 1–2 mm Hausdorff distance to a gold standard developed from multiple raters, so the matching of features at a slightly coarser scale than this is empirically reasonable.

Suppose now, that we can provide the test space W with a norm (∥.∥_W) that measures the regularity of the vector fields in W. We can define then a norm of a current L as the supremum path integral of any regular vector field (i.e. ∥ω∥_W ≤ 1) along $L:\parallel L\parallel {}_{W*}^2=Su{p}_{\parallel \omega {\parallel }_W\le 1}|L(\omega )|.$ The distance between two curves $(\parallel L-L\prime {\parallel }_{W*}^2={\sup }_{\parallel \omega {\parallel }_W\le 1}|L(\omega )-L\prime (\omega )|)$ is therefore obtained for the vector field that best separate the two lines, in the sense that the difference between the path integrals along both curves is the largest possible. This distance between curves is geometric: it does not depend on how curves are parametrized and does not assume any point-correspondences between curves.

For computational purposes, we suppose, from now onward, that W is a reproducible kernel Hilbert space (r.k.h.s.) with kernel K^W (see Aronszajn (1950); Saitoh (1988) for details): vector fields in W are convolutions between any square-integrable vector fields and the kernel. This framework is general and includes for instance radial basis functions. In this setting, the vector space of currents is a dense span of the set of all delta Dirac currents ${\delta }_x^{\alpha },$ which is defined by: ${\delta }_x^{\alpha }(\omega )={\langle \omega (x),\alpha \rangle }_{{ℝ}^3}$ for any ω ∈ W. A Dirac current may be seen as an oriented segment α entirely concentrated at one point x. Although a curve has an infinite set tangents, polygonal lines may be approximated in the space of currents by a finite sum ${\displaystyle {\sum }_k{\delta }_{C_k}^{T_k}.}$ where c_k is the center of the k^th segment and T_k the tangent of the line at c_k.

In this setting, it has been shown (Vaillant and Glaunès, 2005; Glaunès, 2005) that the norm on W* comes from an inner product 〈.,.〉_W* =. On basis elements, this inner product is ${\langle {\delta }_x^{\alpha },{\delta }_y^{\beta }\rangle }_{W*}={\alpha }^t{K}^W(x,y)\beta .$ The inner product between two polygonal lines $L={\displaystyle {\sum }_{i=1}^n{\delta }_{C_i}^{T_i}}\text{and}L\prime ={\displaystyle {\sum }_{j=1}^m{\delta }_{C{\prime }_j}^{T{\prime }_j}}$ (where n is not necessarily equal to m) is therefore given by:

$${\langle L,L\prime \rangle }_{W*}={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^m{(T_i)}^t{K}^W(c_i,c_j^{\prime })}}{T}_j^{\prime }$$ (2)

This enables to compute explicitly the distance between two curves:

$$d^2(L,L\prime )=\parallel L\prime -L{\parallel }_{W*}^2=\parallel L{\parallel }_{W*}^2+\parallel L\prime {\parallel }_{W*}^2-2{\langle L,L\prime \rangle }_{W*}$$ (3)

. In our applications, we choose K^W to be isotropic and Gaussian: for all points $x,y\in {ℝ}^3,K^W(x,y)=\exp (-\parallel x-y{\parallel }^2/{\lambda }_W^2)Id.$

We observe that the distance between two curves (Eq.3), induced by the Hilbertian inner product Eq.2, measures geometrical differences both in pose and shape (See Fig.1). If the points on one curve are at a distance much larger than λW from the points on the other curve, then curves are considered as orthogonal (〈L, L′〉_W* ~ 0) and their distance is large whatever their respective shapes are. By contrast, if two parts of the curves are located within an area of size λ_W, local alignment of the tangent vectors is taken into account by the inner product within the sums in Eq.2, thus measuring shape variations. Furthermore within this area, variations at a scale much smaller than λ_W are not taken into account thanks to the smoothing effect of the kernel. Such variations are considered as noise. Finally, this distance captures first misalignment and then shape dissimilarities until a noise level quantified by λ_W is reached. Used as a data fidelity term, this distance integrates a denoising process, to some extent, into the modeling, preventing systematically overfitted registrations.

2.2. Diffeomorphic Registration

We use here the large deformation framework founded in the paradigm of Grenander’s group action approach for modeling objects (see Grenander (1994); Miller et al. (2006); Glaunès and Joshi (2006); Marsland and Twining (2004)). This framework enables to find a globally consistent deformation of the underlying space that best matches the sets of lines. This differs from Fillard et al. (2007a) where each line is registered individually without assuming spatial consistency of the displacement field between lines.

We build our deformations as diffeomorphisms ${\varphi }_1^v,$ solutions at time t = 1 of the flow equation:

$$\frac{\partial {\varphi }_t(x)}{\partial t}={\upsilon }_t({\varphi }_t(x))$$ (4)

with initial condition ϕ₀ = id_ℝ³ (i.e., ϕ0(x) = x: no deformation). The time-varying vector field v = (v_t)_t∈[0,1] is the speed field in the Lagrangian coordinates. We suppose, from now onwards, that at every time t, v_t belongs to a r.k.h.s. V with kernelK^V. We denote ∥.∥_V the norm on this space that measure the spatial regularity of the vector field. To measure the regularity of the final diffeomorphism, we integrate the regularity of this speed field along time (Grenander and Miller, 1998; Miller et al., 2002): $\upsilon \in L^2([0,1],V):\parallel \upsilon {\parallel }_{L^2([0,1],V)}^2={\int }_0^1\parallel {\upsilon }_t{\parallel }_V^{2}dt.$

Our registration problem is to map a set of n labeled sulcal lines $L_0={\cup }_{i=1}^n{L}_{0,i},$ to another labeled set $L_1={\cup }_{i=1}^n{L}_{1,i}.$ We must find therefore a time varying vector fields (v_t)_t∈[0,1] that minimizes the following cost function J:

$$J(\upsilon )=\gamma \parallel \upsilon {\parallel }_{L^2([0,1],V)}^2+{\displaystyle \sum _{i=1}^n\parallel {\varphi }_1^{\upsilon }.L_{0,i}-L_{1,i}{\parallel }_{W*}^2}$$ (5)

where γ is a trade-off between the regularity of the deformation and the fidelity to data.

ϕ.L represents the geometrical transportation of the curve L by the deformation ϕ. This formulation is compatible with our framework based on currents. The path integral of ω along a deformed curve ϕ(L) equals the path integral along L of the pulled-back vector field: ϕ ★ ω (x) = (d_x ϕ)^t ω(ϕ(x)). This is a change of variables formula within Eq.1, from which we deduce a general action of diffeomorphism on any currents: ϕ.L(ω) = L(ϕ ★ ω). In particular, on basis element, this gives: $\varphi .{\delta }_x^{\alpha }={\delta }_{\varphi (x)}^{d_x\varphi (\alpha )}$: an infinitesimal segment α at point x is transported into ϕ(x) and deformed by the Jacobian matrix: d_xϕ. Combined with Eq.2 and Eq.3, this makes computable the fidelity to data term in Eq.5, once a deformation is given.

To minimize the cost function in Eq.5, we take advantage of a dimensionality reduction property. Although the vector fields v_t are dense, it has been shown (for instance in Miller et al. (2002); Vaillant and Glaunès (2005)) that, in case of discrete curves, $L_0={\displaystyle {\sum }_{i=1}^N{\delta }_{c_i}^{T_i}},$ the minimum of Eq.5 is achieved for a vector field v_t which interpolates the trajectories of the points of L₀:

$$\forall x\in {ℝ}^3,{\upsilon }_t(x)={\displaystyle \sum _{i=1}^N{K}^V}(x,c_i(t)){\alpha }_i(t)$$ (6)

where the momenta (α_i(t)) is a set of N vectors (in 3D) for each time t and c_i(t) = ϕ_t(c_i) are the trajectories of the points of L₀. Based on Eq.4 evaluated at x = ci, these trajectories depend only on the momenta α_i(t). This means that the minimizing dense vector field v_t is entirely determined by a set of 3 * N parameters for each time t. Once the time interval [0, 1] is discretized, the cost function Eq.5 depends on a finite set a parameters and may be therefore minimized by a standard gradient descent scheme. All computational details of this gradient descent can be found in Vaillant and Glaunès (2005); Glaunès (2005).

For K^V we choose an isotropic and Gaussian kernel with standard deviation λ_V. This parameter controls the regularity of the speed vector field v_t at each time t and hence the regularity of the final diffeomorphism. λ_V defines roughly the scale of the difffeomorphism’s spatial consistency (called also rigidity). This is then the scale at which the underlying deformation tries to integrate the geometrical information. If λ_V is much smaller than the distance between lines, the final deformation can vary dramatically in space, each piece of lines are then matched almost independently and the deformation is negligible outside the data. On the contrary, the greater λ_V, the more consistently the deformation tries to explain the variation of each lines, jointly with less and less precise matching.

2.3. Registration Results

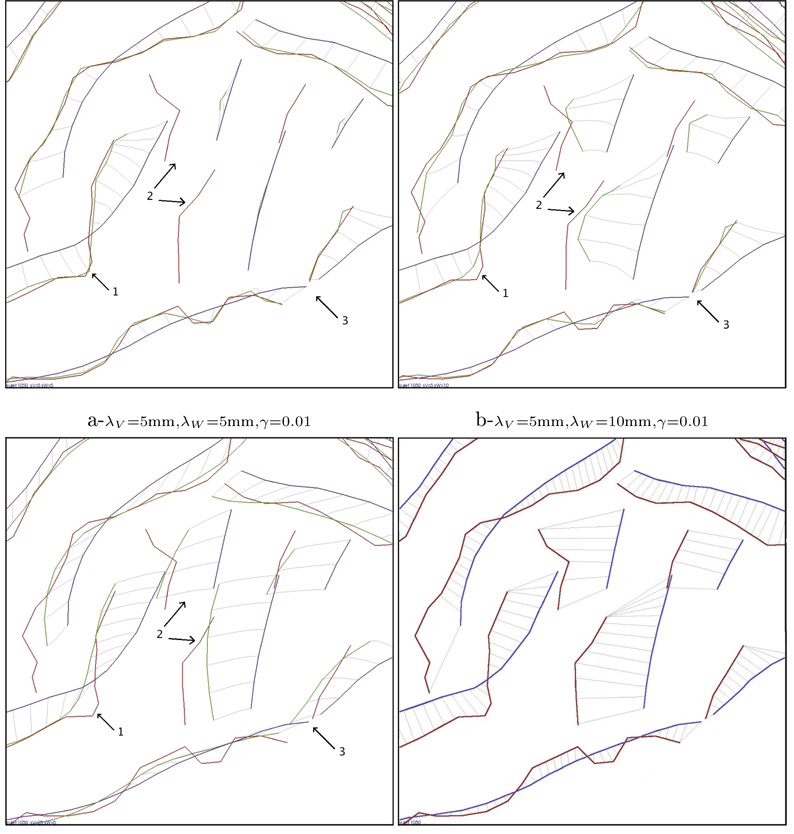
As part of a collaborative project involving the Asclepios-LONI associated team Brain-Atlas, we used a dataset consisting of cortical sulcal landmarks (72 per brain) delineated in a large number of subjects scanned with 3D MRI (age: 51.8 +/− 6.2 years). In order to compare our measures of variability with the ones of Fillard et al. (2007a), we used the same set of 72 mean lines that the authors of Fillard et al. (2007a) computed from the same dataset. For 34 subjects in the database, we register this set of mean lines onto every individual subject’s set of sulcal lines. The registrations were computed by J. Glaunès’ algorithm detailed in Glaunès (2005). This algorithm depends on the 3 parameters: λ_V, λ_W and γ. To understand the impact of these parameters and the specificity of this current-based diffeomorphic registrations (CDR) with respect to a pointwise line correspondence (PLC) method (Fillard et al., 2007a), we ran the registration algorithm for several different sets of parameters.

Figure 3-a,b and c show for different parameter values the registrations in the superior temporal area of the cortex in the right hemisphere (view from inside), the brain faces to the left of this figure, and region surrounding the Sylvian fissure, on the lateral surface of the right hemisphere, is magnified. From 3-a to 3-b, λ_W is doubled: greater variations are considered as noise and the matching is less precise (area 1). However, when λ_W is too small, lines with few sampled points are not matched correctly (area 2). Small curves have small weight in the data fidelity term and matching them is not worth the cost of the deformation: the algorithm is locally in a minimum. Greater λ_W makes distance loss larger due to the curve’s motion to its target. The local minimum issue is avoided. In both cases (a and b), the deformation kernel’s size is very small: λ_V = 5mm whereas the diameter of the brain is about 120mm. The speed vector field is highly irregular and each curve is matched almost independently. This is particularly obvious in area 3, which is close to the supramarginal and angular gyri of the temporo-parietal cortex, where the speed vector field varies dramatically between two close points that belong to two different curves. There is almost no deformation between the curves. By contrast, in figure 3-c, λ_V = 25mm and the deformation tends to explain the sulcal lines variability with a consistent deformation of the underlying space. This makes the speed vector field more regular, as in area 3. Whereas λ_W is the same as in figure 3-a, small curves are now matched since they are ”pushed“ by the large curves in the surroundings. To match the larger curves, the space must deform consistently in this area with the effect of moving small curves to their target. This global constraint also leads to larger residual matching errors than in figure 3-a (area 1). Such residual errors contain both geometrical noise on lines (quantified by λ_W) and some variability that cannot be explained consistently with other curves in a neighborhood of size λ_V , which is regarded as noise in the model. Besides λ_V and λ_W, γ refines the compromise between the regularity of the deformation and the precision of the matching.

Figure 3.

Registration of the same subject for three different sets of parameters (a,b,c) and with a pointwise line correspondences approach (d). In these figures, the superior temporal area of the cortex is magnified (arrow 1 points the extremity of the Sylvian Fissure). The parameters influence the precision of the matching (like in area 1), the regularity of the deformation field (area 3) and the way the deformation integrates geometrical information (area 2).

Figure 3−d shows, in the same anatomical region, how a pointwise line correspondence method (PLC) set up in Fillard et al. (2007a) handles the same data. Lines are registered individually and point correspondences are assumed between source and target lines. Extremal points are supposed to be matched. In between points are matched via a closest neighbor procedure after B-spline smoothing and resampling. As no correlations between curves are assumed and no correspondence field computed outside the data, this matching can be seen as an approximation of our registrations when λ_V tends to zero. Since the correspondences between points do not take noise into account, it is also the limit as λ_W tends to zero but avoiding the local minimum issue. The different way that PLC handles lines matching have important consequences. For instance, the tangential variation of two curves is mainly captured at the extremities of the curves, and minimized elsewhere. With the current approach, these variations are captured more geometrically all along the curves. Moreover, the PLC approach does not take noise into account (in the sense that noisy point correspondence field computed from the manual traces is regarded as true), and does not model any deformation of the space between the curves. As we will see in the next section, PLC approach needs afterwards to handle two additional processing, denoising and extrapolation of the variability measures, to compute brain shape statistics. This method consists therefore of 3 distinct processing steps: matching, denoising, extrapolation, each with its own assumptions and parameters. By contrast, the approach proposed here based on currents’ diffeomorphic registrations (CDR) integrates denoising, matching and extrapolation within a single consistent framework. Matching based on currents avoids the need to define a principle for enforcing specific point correspondences. Denoising is performed jointly with the matching while minimizing the cost function. Extrapolation is performed on the basis of a deformation of the underlying biological material. The whole framework is explicitly controlled by 3 parameters λ_V , λ_W and γ that effect a compromise between the different processing steps. This method, however, discounts variability that is not compatible with the modeling. Residual matching errors may hide non-diffeomorphic variations between subjects although one would like to take them into account. Setting the 3 parameters is difficult since they are not independent and determine jointly the final residual matching errors. After extensive experiments, we choose the typical coherence scale of diffeomorphisms λ_V = 25mm, the typical noise scale on lines λ_W = 5mm and the tradeoff γ = 0.01 by visually inspecting the results. Changing these parameters would smoothly affect the typical correlation size of the following variability maps. These values highlight the specificity of our framework, that will explain, in turn, the different variability maps retrieved by our CDR method and the PLC approach on the same dataset as in Fillard et al. (2007a).

3. Statistics on Deformations

3.1. Tangent-space Representation of Diffeomorphisms

To compute statistics on deformations, we take advantage of an additional property of the minimizing diffeomorphisms. It has been shown (in Miller et al. (2006) for instance) that the diffeomorphism retrieved by the minimization of Eq.5 is geodesic: among all time-varying vector-fields that enables to go from Id to ϕ₁, the minimizer of Eq5 has the smallest norm in L²([0, 1], V ). As a consequence, the momenta (α_i(t))_i solve the Euler-Lagrange equations (Miller et al., 2002, 2006): they are entirely determined by their initial values:α_i(0). This is the usual tangent-space representation as highlighted in Vaillant et al. (2004) or in Pennec et al. (2006) for finite dimensional manifolds. This representation enables to generate randomly deformations of L₀: given any set of N vectors ${\alpha }_i^0,$ we can solve the Euler-Lagrange equations (partial differential equations) to give the momenta at every time: α_i(t).We deduce then from Eq.6 evaluated at every x = c_i, the speed of the trajectories of the points c_i of L₀: v_t(c_i). Integrating the flow equation Eq.4 enables then to compute the whole trajectories ϕ_t(c_i). The generated deformation does not act only on the line L₀ but it is a diffeomorphism of the whole 3D space. Based on the interpolation property Eq.6, we can compute the speed (and then the trajectory by Eq.4) of any point x of the space, thus computing the entire diffeomorphism. The purpose of our forthcoming statistical estimations is to learn a law on the momenta ${\alpha }_i^0,$ so that diffeomorphisms simulated according to this law model the variability within the studied population.

From the previous 34 registrations of the mean lines to each subject’s lines, we store 34 sets of initial momenta: $({\alpha }_i^{\mathrm{s}})$ for i = 1 … N and s = 1 … 34 where N is the total number of points c_i within the set of mean lines: $L_0={\displaystyle {\sum }_{i=1}^N{\delta }_{c_i}^{T_i}}.$ We define an inner product (resp. a norm) on this space of momenta as the inner product (resp. norm) of its associated dense vector field ${\upsilon }_0(x)={\displaystyle {\sum }_{i=1}^N{K}^V}(x,c_i){\alpha }_i(0)$ based on Eq.6. Since V is a r.k.h.s. with kernel K^V, the inner product between two sets of 3N momenta (from the registration of two different subjects) ${({\alpha }_i^p)}_i\text{and}{({\alpha }_i^q)}_i\text{is equals to}{\displaystyle {\sum }_{i,j=1}^N{({\alpha }_i^p)}^t{K}^V(c_i,c_j){\alpha }_j^q.}$ In the sequel, we denote this inner product between two vectors in ℝ^3N: 〈α^p, α^q〉_V*. Our statistics on diffeomorphisms are then reduced to statistics in ℝ^3N provided by this inner product.

3.2. Mean of Deformations

Since the mean lines we used as a template were obtained in Fillard et al. (2007a), they are not consistent with our registration framework. The deformations are not centered around the identity (i.e. no deformation), so the vectors in ℝ^3N do not have zero-mean. To measure the induced bias, we compute the mean of the initial momenta at each sample: ${\overline{\alpha }}_i=\frac{1}{34}{\displaystyle {\sum }_{s=1}^{34}{\alpha }_i^s}.$ The norm of this bias is given by $\parallel \overline{\alpha }{\parallel }_{V*}^2={\displaystyle {\sum }_{i,j=1}^N{\overline{\alpha }}_i}{K}^V(c_i,c_j){\overline{\alpha }}_j.$ Numerically we find in our experiments: $\parallel \overline{\alpha }{\parallel }_{V*}/\sqrt{\frac{1}{34}{\displaystyle {\sum }_{s=1}^{34}\parallel {\alpha }^s-\overline{\alpha }{\parallel }_{V*}^2}=0.39}.$ This means that the bias is less than 0.4 times the standard deviation, far below the usual 3σ threshold to decide a statistical significance.¹

We now substract the mean field to each subject’s field so that the analyzed data are centered for the following computations of second order statistics.

3.3. A Gaussian Model on Deformations

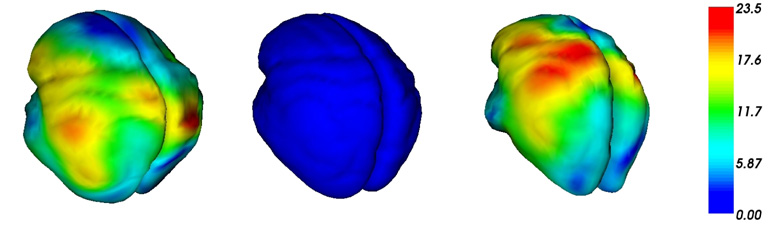
To compute the covariance structure of the set of deformations, we perform a Principal Component Analysis (PCA) on the set of vectors α^s ∈ ℝ^3N for each subject s. For this purpose, we build the 34 × 34 symmetric matrix whose coeffcients are 〈α^p, α^q〉_V*. If V¹ ∈ ℝ³⁴ is the first eigenvector of this matrix, the first mode of initial momenta is given by: $m_i={\displaystyle {\sum }_{s=1}^{34}{V}_s^1{\alpha }_i^s}$ (the normalization factor has been set to 1 so that $\parallel m{\parallel }_{V*}^2={\lambda }_1,$ i.e. the eigenvalue corresponding to V¹). Given this first mode of initial momenta m, we follow the procedure explained in section 3.1, to generate the diffeomorphism determined by m. We call this deformation, the first mode of deformation. It illustrates, to the first order, how the mean anatomy varies within the population. Since the diffeomorphism is dense, we can apply it not only on the mean lines points but also on a mean cortical surface to which the mean lines are close (Fig. 4-middle). This deformation shows the variability between 0 and σ (Fig. 4-right). Repeating the procedure for -α give the first mode of deformation between 0 and -σ (Fig. 4-left). Complete movie of the first deformation mode is available at first author’s webpage². This illustrates the generative property of the modelling: the lines and surfaces build by this procedure do not belong to the original database.

Figure 4.

First mode of deformation obtained by a PCA on the initial vector speed fields. Original mean brain surface (Center) and its deformation at −σ (Left) and +σ (Right). Colors measure the displacement of each point along the deformation process (in mm).

These results show that we learn here a complete statistical model of the whole brain surface deformation constrained by the sulcal lines. This differs from other methods that measure only the variability of the sulcal lines. This is possible due to integrative power of the proposed approach: the dif feomorphisms integrate the information of all sulcal constraints to find the most acceptable deformation of the brain volume. As for the modes of deformation, this enables to generate new observations (new brain surfaces) according to the learned probability law on deformations. This determine at least visually how these new observations compare with the original data and therefore understand the variability that the model captured. For this reason, such models are called generative models: we not only learn how to factorize an observation into a deformation and residual noise, but also how to reconstruct it. Such models offer an approach to classify new subjects according to characteristics such as gender, handedness, pathologies, etc., and identify systematic differences in anatomy that correlate with these features. Given a previously unseen individual anatomy, we can decompose it into a global deformation driven by its sulcal lines position and a residual noise. Our statistical model tells us how probable such a deformation may be within a given population. Other methods try to retrieve similar correlations but with descriptive statistics such as statistical test for instance (Narr et al., 2007; Hamilton et al., 2007; Luders et al., 2004). In the PLC approach (Fillard et al., 2007a) no deformation is computed outside the lines. In this framework, the lines variability is computed from the displacement field at each mean lines samples positions. Then an extrinsic extrapolation scheme enables to retrieve a variability measure on the whole brain surface. In this aspect, the link between the observations and the mean surface is broken by the succession of distinct processing: the statistical model is learned on the lines only and the extrapolation scheme does not directly infer a probability model on the brain surface. PLC approach deduces from the observations variability maps on the brain surface (see next section) but the way to reconstruct surfaces from these maps is missing. There are other methods that exrapolate sulcal line deformations to a full cortical surface, based on covariant partial differential equations that are invariant to the surface parametrization (Thompson et al., 2002), based on harmonic mappings that minimize a surface-to-surface deformation energy (Shi et al., 2007; Wang et al., 2005) Some of these methods even extend the surface deformation to the full volume, using interpolation (Thompson and Toga, 1996). In each of these cases, the differential operator governing the mapping may be regarded, after suitable normalization, as the exponent of a Bayesian prior on the space of allowable deformations, so in a sense there is an assumed probability law that captures the variability and spatial covariance of the mappings in between the explicitly defined landmarks, even when a partial differential equation or variational method is used to interpolate the mappings.

3.4. Comparison of Variability Maps

To compare our CDR-based variability measures with those computed with a PLC approach on the same database we create variability maps similar to those in Fillard et al. (2007a): in absence of generative models, PLC approach performs such descriptive statistics. At each point x of the mean surface, we computed the covariance matrix of the 34 initial speed vectors v₀(x), computed with Eq.6 for each set of initial momenta. These 3 x 3 matrices (called also tensors) show how locally one point is varying among the studied population, as proposed in Thompson et al. (1996b, 1998). We notice that this variance contains less information than the former principal component analysis. Here each point are considered independently whereas the PCA takes into account the correlations of all points’ motion together. Moreover, due to the diffeomorphic approach, the initial vector field is dense and no extrinsic extrapolation scheme is required to compute the covariance matrices at each point of the mean surface. By contrast, PLC approach computes these 3 × 3 matrices from the correspondence fields at the mean lines samples. These tensors are then extrapolated to the whole brain surface using a log-Euclidean framework (Pennec et al., 2006; Arsigny et al., 2006) without any guarantee that the obtained variability measures are compatible with an underlying deformation of the brain surface. This gives an aggregated measure at the population level that is not based on individual deformation mappings. The two approaches are based on radically different assumptions and the following variability maps show how these different models influence the results. Differences stem from the different way lines are matched, noise is removed and variability is extrapolated to the brain surface.

3.4.1. Regularity of the Variability

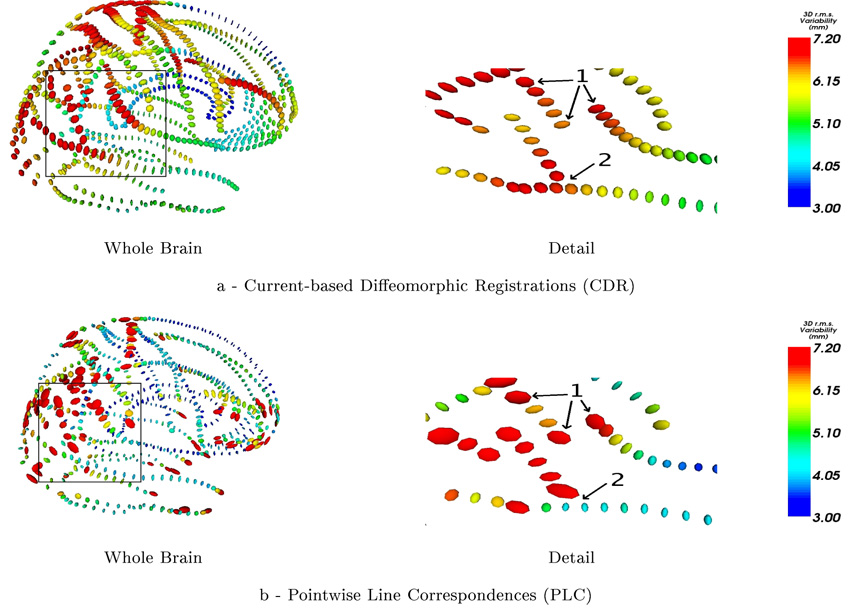
The figure 5 shows the covariance matrices built from the initial vector speed at the mean lines points (c_i) in our Current-based Diffeomorphic Registrations (CDR) (Fig.5-a) and from the correspondence field in the PLC approach (Fig.5-b). We notice that the point matching method leads to irregular tensor fields at extremities of the lines and between lines, whereas the global regularity constraint of the difffeomorphism in CDR imposes the retrieved variability to be spatially smoother. CDR thus discounts any variability contained in the residual matching errors, which is considered here as noise. In PLC, the tensor field is denoised separately by removing “unreliable” large tensors at the end of lines before the extrapolation step.

Figure 5.

At each sampling point, ellipsoids represent the square root of the empirical covariance matrix of the initial speed vectors (left hand side) or displacement field (right hand side). With PLC method, extremal points are supposed to be matched: this induces a high variability at the extremities of lines (area 1, right). This is avoided by the current approach (area 1, left). With PLC, each line is registered individually: the variance can vary dramatically where lines cross (area 2, right). This situation can occur where a sulcus has a branch, in ”Y“-shape configuration, and the junction may not be considered by the PLC approach. The global regularity constraint of CDR leads to smoother results (area 2, left).

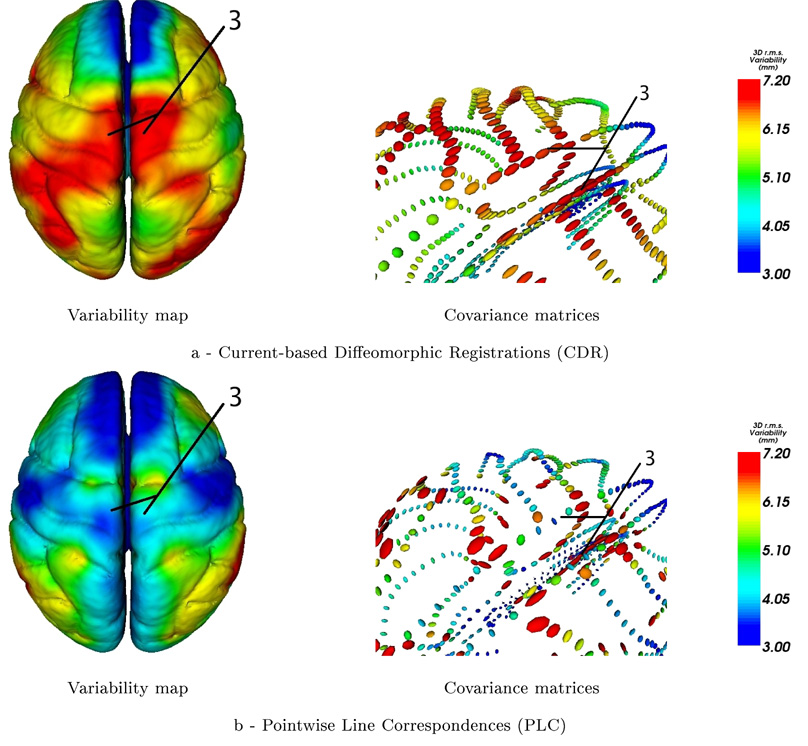
3.4.2. Variability in the Direction of the Lines

One drawback of PLC’s method as underlined in Fillard et al. (2007a) is the fact that it systematically under-estimates the variability in the direction of the lines. This variability is indeed essentially captured at the extremities of the lines and minimized in between. As a pragmatic solution, in the PLC approach, the large extremal tensors were removed before extrapolating the variability, and the final measures minimize the variability in the direction of the lines. This aperture problem is particularly visible on the top of the brain as shown in figure 6. By contrast, the models based on currents (CDR) manage to represent a larger part of this variability. This effect is of particular importance since this tangential variation is one of the major variation trends within the population as shown in Fig.4. Anatomically, any lateral splaying of the central and pre-central sulci (at the top of the brain) is usually a sign atrophy, consistent with widening of the interhemispheric fissure. If this variation is discounted, for example by discarding tensors at the extreme points of sulci, any future registration approach that uses the tensor fields to model variation will underestimate the true anatomic variation in these areas. Otherwise, the variability which is orthogonal to the direction of the lines is in good agreement for the most part.

Figure 6.

In the variability maps, a variability in the direction of the lines is retrieved in area 3 (extremities of central sulci) by CDR and not by PLC. The covariance matrices in this region show that the variability is mainly longitudinal. Since, in PLC method, large tensors at the endpoints of the sulcal lines are removed before the extrapolation, the variability in the direction of the lines is missed and the total variability is unreasonably small.

3.4.3. Distinction between correlated and anticorrelated motions

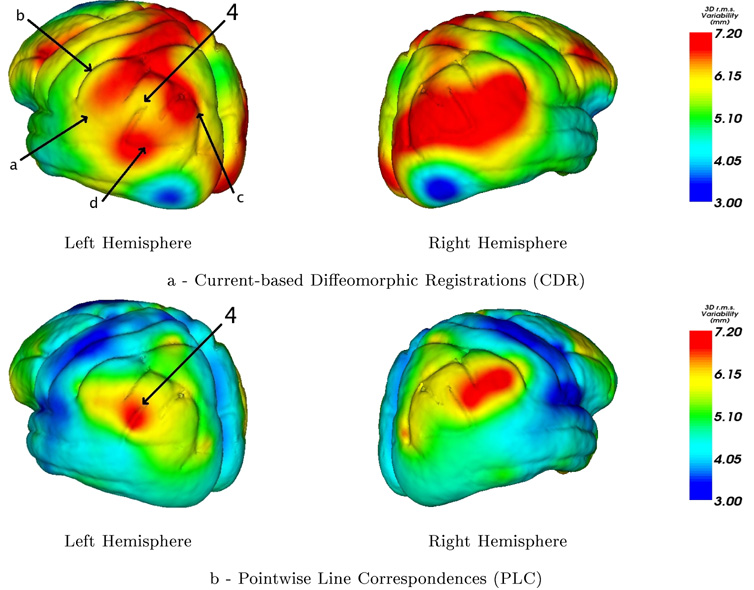
In our CDR framework the tensors at every points of the mean surface are computed from the initial speed vectors at these points that are interpolations of the initial speed vectors at the mean lines samples (see Eq.6): the interpolation is performed before computing the variability measures. By contrast, in the PLC method the covariance are computed on the mean samples and then extrapolated to the brain surface. As shown figure 9 this difference theoretically enables CDR to distinguish between areas where points are deviating from the mean anatomy in a correlated or anti-correlated manner. This is a possible explanation of the different variability maps retrieved in area 4 of figure 8.

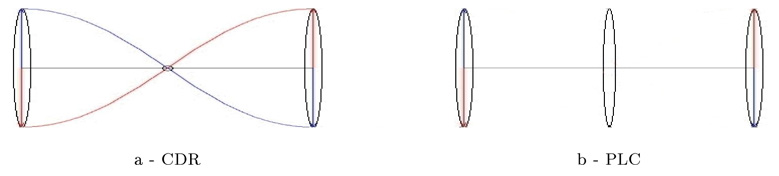
Figure 9.

Extrapolation schemes in the simple case of anti-correlated vectors. Right: In PLC framework the tensors are computed at the sample points and then extrapolated in the middle point: the tensor in the middle is similar to the two others. Left: In CDR approach one first extrapolates the vector field and then computes at each point the covariance matrix. Since the vectors are anti-correlated, the field is close to zero at the center and the variability measured at this point is negligible.

Figure 8.

Area 4 is surrounded by 4 major sulci: the Sylvian fssure (a), postcentral sulcus (b), intraparietal sulcus (c) and superior temporal sulcus (d). In the left hemisphere the first two vary, with respect to the sample mean, mostly in a decorrelated manner with respect to the last two sulci whereas their respective motions are much more correlated on the right hemisphere. The CDR approach tries to combine the motion of all lines and therefore leads to a small variability in area 4 (the perisylvian cortex) in the left hemisphere and to a large one in the right hemisphere. In these perisylvian areas, the variability is likely to differ by hemisphere as the right hemisphere perisylvian sulci are torqued forward and at a higher angle of elevation than their counterparts in the left hemisphere (Thompson et al., 1998). With PLC method this asymmetry in the magnitude of anatomical variability is not retrieved directly.

4. Discussion and Conclusion

In this paper we present a methodological framework to build global brain shape statistics by measuring and consistently integrating the variability of anatomical constraints such as sulcal lines. This framework is based on two methodological tools: lines are modeled as currents, and multiple object sets are matched by a single diffeomorphic deformation. By modeling lines as currents, we are able to measure geometrical dissimilarity between curves without assuming point correspondences between objects. Discrete and continuous lines are handled in the same setting, thus guaranteeing numerical stability and nice convergence properties. This distance is also robust to noise, preventing small perturbations of lines from hiding true underlying geometrical differences. On the other hand, the diffeomorphic framework consistently integrates the geometrical variations of a set of currents into a single deffformation. We avoid modeling the variability of each objects independently. On the contrary, we try to explain the variability of the sulcal constraints by a global deformation of the underlying image domain. By inferring a Gaussian model on such deformations, we can define a generative statistical model that roots the variability measures into a rigorous model for individuals. Principal trends of variations within the database can be highlighted by looking at the deformation of a mean brain surface. Such statistical models offer an approach for classifying new observations according to their pathologies, gender,etc. The synthesis of the geometrical variations into principal modes of variations may also make it easier to identify spatially correlated anatomical patterns and may lead to new scientific findings.

This framework however raises several questions. Our statistical modeling focuses on the deformation term whereas there is obviously no ground truth regarding anatomical homology between brains. Even so, a diffeomorphism can capture a large part of the geometrical variability between shapes and sets of shapes. It is clear that some of the ”true“ underlying variability is not captured by the diffeomorphism and remains unmodeled in the residual matching errors. These residuals contain numerical and physical noise, possible non-diffeomorphic variations (changes in topology or folding patterns for instance) as well as variations that are not compatible with the variations of other objects in the surroundings. Our statistical model focuses here on the deformation term only and our results indicate that it can model a great part of the variability. However, a more complete statistical framework would take into account the matching residuals as well. A given observation would be therefore decomposed into a deformation and residuals and the statistical model would say how probable such a decomposition might be. Building such a statistical framework is beyond the scope of the present paper, but it must be the topic of further investigation.

Some comment is also necessary regarding whether the norm on currents is appropriate for the data, as this model does not take explicitly curvature into account and every points on lines play the same role. When anatomical curves are matched using a smooth registration field, Leow et al. (2005) have previously explored the case where the curves are modeled as level sets of an implicit functions, and no explicit point correspondence is enforced, allowing the mapping to relax along sulcal lines. They investigated the matching of anatomic structures by directly constructing their implicit level set representations and the proposed matching cost functionals were shown to be closely related to the Hausdorff metric. With this type of mapping, brain structural variability was reduced by 10% in most regions and up to 40% in other regions; greatest reduction was observed in the temporal and frontal lobes, while a lesser reduction was observed in areas with greatest anatomic variability. Arguably, this results in mappings that have less distortion while still matching homologous gyral anatomy in detail from one subject to another. Contrary to some other norms that explicitly take into account surface curvature (Fischl et al., 2004), or differential invariants within a curve (such as torsion) derived from the Frenet frames of the curves being matched (Guéziec and Ayache, 1994), our norm in this paper, and the one in the paper by Leow et al. (2005) do not consider that there are particular points of anatomical interest along the curves that can be identified as reliable landmarks. With some minor exceptions (such as the genu of the central sulcus (Vaillant and Davatzikos, 1999; Goualher et al., 2000), curvature, at least at the finer scale of indentations within sulci, is not a reliable guide to functional or structural homology in the human cortex, and using points of maximum curvature to guide correspondence may be problematic. Our approach is somewhat more agnostic in regard to point matching. At least for the human cortex, details visible on MRI along the length of a sulcus would not be reliable features for anatomical matching, although this does not preclude their identification in future, e.g. using other modalities such as DTI.

The third issue concerns the choice of sulcal lines as constraints to retrieve the global variability of the brain. The question of the anatomical significance of the sulcal lines is often raised in the literature (Toga and Thompson, 2007; Thompson and Toga, 2003). The sulci that we use here as topological constraints for cortical matching are essentially those which have been chosen to have functional significance, occur consistently in large numbers of normal individuals, and are not so variable in their incidence and relation to other sulci that it would preclude their reliable identification in large numbers of subjects. Moreover, the sulcal lines are labeled and supposed to be in a single part. However, the framework based on currents is not limited to such databases: lines could be discontinuous and consists of several parts, which may indeed be more accommodating of interrupted sulci, which are known to occur (Mangin et al., 2004; Duchesnay et al., 2007). Even if the lines are not labeled, a matching based on currents is still possible: we then consider all the lines as a single current. Preliminary experiments on the bottom lines of the sulci automatically extracted from a few subjects Rivière et al. (2002) raises however several problems. The geometry of the lines can be so complex that it is not possible to define a global orientation of the sulci. The variability is too high to retrieve sensible correspondences in the absence of any priors on sulcal labels. The quality of the lines extraction (and possibly the quality of the labeling itself) does not enable to find reasonable matchings between subjects. The geometry of the sulci depends actually on the process of extraction (whatever it is manual or automatic). In order to better constrain the registrations, one needs to account for more information than only the most probable lines. One would like for instance to use probability maps of the presence of the sulci in order to account for variability of the extraction itself. Sulcal ribbons could also contain more reliable geometrical information. A similar framework (but that does note require orientation of lines) has been used in Auzias et al. (2008) with the sulci of Rivière et al. (2002). In the future, alternative cortical landmarks, including perhaps the endpoints of fiber paths inferred from DTI, may also supplant or partially replace the reliance on sulci as a guide to anatomical homology in the human cortex (Cathier and Mangin, 2006).

The comparison with a pointwise line correspondence (PLC) method is also difficult to interpret. The comparison remains here largely qualitative and at a methodological level. Even so, it is clear that each result is biased by the assumptions on which the variability measures are based. Each approach reveals new features from the database such as the principal modes of deformation, or unexpected patterns of anatomical correlation at distant points (Fillard et al., 2007b). A fair comparison between both methods would rely on objective statistical performance metrics, such as their respective predictive power for instance. In future, we will design studies that aim to predict extrinsic information about the subjects (e.g. sex, handedness, disease subtype, prognosis), from the information encoded in the cortical deformations. In a sense, the best model of anatomical variability is one that allows most reliable inferences and predictions regarding population. However, such a deep comparison is beyond the scope of this paper. Our purpose was here to present a general framework to compute statistics of brain shapes, to highlight its strength and limitations and finally to show its feasibility and relevance for addressing a range of statistical problems in the field of computational anatomy.

Figure 2.

Registration of the mean lines set (in blue) towards one subject’s lines set (in red). A unique deformation transports all the mean blue lines to the registered green lines. The spatial consistency constraint as well as the smoothing effect of the norm of currents prevents overfitted registrations from occurring. The residuals (i.e., the difference between the registered green lines and target’s red lines) contains physical and numerical noise as well as possible non-diffeomorphic variations. They are considered here as noise: the statistics on brain shape will rely only on the diffeomorphism. A movie of this deformation can be seen at first author webpage: www-sop.inria.fr/asclepios/personnel/Stanley.Durrleman.

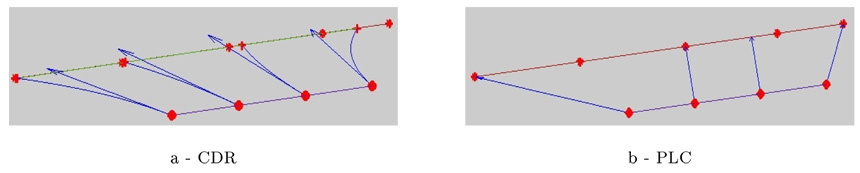
Figure 7.

The registration method influences the way tangential variability is taken into account. With point correspondences the tangential variability is mainly captured at the endpoints of the lines and minimized in between. The approach based on current (CDR) retrieves a tangential component of variability all along the lines.