Prediction of Error Associated with False Positive Rate Determination for Peptide Identification in Large-Scale Proteomics Experiments Using a Combined Reverse and Forward Peptide Sequence Database Strategy

Abstract

In recent years a variety of approaches have been developed using decoy databases to empirically assess the error associated with peptide identifications from large scale proteomics experiments. We have developed an approach for calculating the expected uncertainty associated with false positive rate determination using concatenated reverse and forward protein sequence databases. After explaining the theoretical basis of our model, we compare predicted error with the results of experiments characterizing a series of mixtures containing known proteins. In general, results from characterization of known proteins show good agreement with our predictions. Finally, we consider how these approaches may be applied to more complicated datasets, as when peptides are separated by charge state prior to false positive determination.

Introduction

In recent years great strides have been made in the development of techniques for high-throughput peptide analysis via mass spectrometry, most importantly the development of a variety of algorithms for the automated identification of peptides based on their intact masses and fragmentation patterns. Some of the more commonly used programs include Sequest¹, Mascot², and OMSSA³, among others. While these algorithms differ in many details of their function, they are generally founded on the same basic concept: because peptides tend to fragment in predictable ways based on their amino acid sequence, one can predict the fragmentation pattern that any peptide will produce with a high degree of accuracy. In practice these algorithms compare an observed MS/MS fragmentation pattern from an unknown peptide with those fragmentation patterns predicted for all peptides of equivalent mass within a given protein database and return the peptide sequence whose predicted fragmentation pattern best matches the observed spectrum.

One consequence of this database approach for peptide identification is the possibility for false positive peptide identifications. Because these programs return the best peptide match for each MS/MS spectrum within a given database, which may not necessarily be a perfect match, a portion of these identifications will be incorrect peptide sequence assignments due to coincidental similarity in MS/MS fragmentation patterns⁴. In large scale proteomics experiments these spurious assignments can account for a very large portion of identified spectra⁵. To differentiate among true and false peptide identifications, all algorithms for peptide identification provide scores for each peptide assignment intended to reflect the likelihood that it occurred by chance. Typically those peptides identified with scores above a certain threshold are accepted while those with lower scores are rejected. In practice this means that some correct peptide identifications will be rejected (false negatives) while a hopefully small and defined number of incorrect peptide identifications (false positives) will be accepted.

A number of factors influence the likelihood of incorrect peptide identifications, including the number of peptide sequences considered (database size), the types of variable modifications considered, the mass accuracy and resolution of MS and MS/MS spectra, and the nature of the sample itself^6,7. While peptide identification algorithms generally consider these factors when assigning scores and setting thresholds for peptide identification, they may not completely account for their effects. Furthermore, experimental conditions and instrumental biases may not be considered. Finally, because each algorithm uses different methods for assessing the quality of its peptide assignments, direct comparison of peptide identifications obtained from different search engines can be misleading. For all these reasons, independent methods for assessing the quality of peptide identifications from large scale datasets across a variety of platforms, search engines and experimental conditions are essential.

One empirical approach for estimating the false positive rate within a given dataset involves the use of a composite peptide sequence database containing all possible protein and peptide sequences from a given organism as well as an equivalent number of nonsense protein and peptide sequences that should not be present in the sample to be analyzed⁸. These nonsense sequences are often generated by randomly scrambling or reversing the sequences within the original database. While all true peptide sequence matches will be to the unaltered portions of the combined database, those matches that occur randomly should be made against the unaltered and nonsense sequences with equal frequency. Thus the number of peptide assignments made against the nonsense portion of the database should reflect the number of coincidental peptide identifications drawn from the sequences of real proteins. For its ease of implementation and applicability across platforms, search engines and experimental conditions, the use of combined forward and reversed protein databases for assessment of false positive rates has become commonplace^{4, 8, 9}.

To date the reversed database strategy has been shown to be an effective means of estimating false positive rates, especially when applied to large datasets⁸. However, as this approach is used with more diverse datasets, one must consider under what conditions it may be appropriately applied. Two important questions are, how accurate will the reversed database approach be, and how will its accuracy vary as the number of peptide observations is varied? Though recent improvements in instrumentation have simplified collection of large datasets, some experimental techniques resulting in relatively simple protein mixtures such as immunoprecipitations will tend to produce smaller datasets regardless of instrumentation. Furthermore, peptides may be separated by a variety of properties such as charge state prior to false positive rate determination, potentially leading to small sample sizes. Thus sample size will remain an issue for determination of false positive rates.

To address this issue, we present a statistical analysis of how well the reversed database approach can be expected to match the actual false positive rate for datasets of varying sizes. In particular, we define the error associated with false positive estimation as a function of the number of reversed peptide identifications within a given dataset. Additionally, we compare our predictions with the error rates seen in the analysis of known control proteins. Finally, we consider how this knowledge can be applied in practice for typical proteomics experiments.

Materials and Methods

Unless otherwise stated, all purified proteins and reagents were purchased from Sigma (St. Louis).

Calculation of Distributions

All calculations were performed using Mathematica 5.2 (Wolfram Research). To calculate the probability distribution function describing the number of incorrect hits to the forward database (a) given a particular number of hits to the reversed database (n) the binomial distribution was used, with the assumption that random matches were equally likely to be made against either the forward or reversed database. For n hits to the reversed database, Equation 1 was evaluated, varying the possible number of random hits to the forward database a from 1 to 500. All values were then divided by their sum for normalization. In turn these distributions were calculated varying n from 1 to 100.

$$F(a|n)=\left(\frac{(a+n)!}{a!n!}\right){(0.5)}^a{(0.5)}^n$$ (1)

Preparation of Control Proteins

Twenty-one proteins including cytochrome C (horse heart), lactoferrin (bovine), hemoglobin (bovine), myoglobin (equine), ribonuclease A (bovine pancreas), carbonic anhydrase (bovine erthrocytes), amyloglucosidase (Aspergillus niger), alcohol dehydrogenase (Saccharomyces cerevisiae), beta glucuronidase (E. coli), alpha glucosidase (S. cerevisiae), serum albumin (human), alpha lactalbumin (bovine), transferrin (human), alpha casein (bovine), alpha amylase (porcine pancreas), catalase (bovine), lysozyme (chicken egg white), glucose oxidase (A. niger), conalbumin (chicken), lactoglobulin (bovine), and lipase (Candida cylindracea) were dissolved individually in 8M urea, 50 mM ammonium bicarbonate, 5 mM DTT. These stock solutions were then mixed to form nine groups of 2-5 proteins each. The mixed samples were then diluted with 50 mM ammonium bicarbonate, 5 mM DTT to a final concentration of 1 M urea and 1 mg/mL total protein. The individual proteins were present in equal amounts by mass in each mixture. All fractions were digested overnight at room temperature using porcine modified trypsin (Promega, Madison, WI) at a ratio of 1:20 by mass. Prior to analysis, all digested mixtures were brought to 5% formic acid and extracted using SPEC C18 solid phase extraction pipette tips (Varian).

Mass Spectrometric Analysis

Approximately 10 μg of each protein mixture was analyzed via nano LC-MS/MS on a Micromass QTOF II with an Agilent 1100 Series HPLC. All LC separations were performed using a Zorbax Eclipse XDB-C18 column (100 μm i.d.) prepared in-house. Each sample was analyzed in triplicate, using MS methods designed to favor sequencing of either singly, doubly, or triply charged peptides, respectively. After sample loading, peptides were eluted with a gradient from 95% Buffer A (0.1% formic acid in water) and 5% Buffer B (0.1% formic acid in 95% acetonitrile) to 50% Buffer B in 105 minutes. Then over 5 minutes Buffer B was raised to 60%, with a final increase to 100% Buffer B over an additional 5 minutes. Protein Lynx Global Server 2.1.5 was used for peak extraction, with normal background subtraction (35% threshold, 1^st order polynomial) and 2 iterations of Savitsky-Golay smoothing for MS scans. MS/MS scans were subject to adaptive background subtraction and 2 iterations of Savitsky-Golay smoothing with no deisotoping.

Peptide Identification

Peptides were identified using a local Mascot server (version 2.0, Matrix Science) and the following search parameters: +/- 0.2 Da mass tolerances for MS and MS/MS, full tryptic digestion, up to 2 missed cleavages, 1+, 2+, 3+ ions, variable Met oxidation and N-acetylation (Protein), monoisotopic mass, and AUTO number of responses. Methods provided in the msParser toolkit (1.2.2, Matrix Science) were used within scripts prepared in-house using Java (Sun Microsystems) to parse Mascot results files. A composite database containing protein sequences from the complete Arabidopsis genome (Version 4, The Institute for Genomic Research) in forward and reverse as well as the sequences of multiple isoforms of all control proteins downloaded from NCBI and of common contaminants such as trypsin and human keratin was used for all searches. The Arabidopsis genome was chosen for this study because its size (ca. 29,000 sequences) is similar to human and other databases often used for proteomics, yet Arabidopsis not closely related to the organisms from which control proteins were obtained, minimizing the effects of homology. Sequences of all peptides matched to non-control proteins were compared with the control protein sequences to ensure that they could not be assigned to both. Only peptides longer than seven amino acids were considered for false positive rate determination, and for peptides of this minimum length no possible conflicts were found.

Results and Discussion

Calculation of Predicted Distributions

The principle behind many peptide identification algorithms including Mascot and Sequest is the automated comparison of theoretical fragmentation patterns derived from peptides in a specified database with an observed fragmentation pattern to identify the best match. At some level these matches will occur due to chance, leading to spurious identifications. When searches are performed against a composite database containing both forward and reversed sequences these random matches should occur against both the forward and reversed sequences with equal frequency, allowing estimation of the false positive rate in an empirical way. The underlying assumption for this approach is that the numbers of random matches against the forward and reversed sequences will be essentially the same. This has been demonstrated previously using fairly large datasets, showing only small variation due to chance^4,8,9. However, as datasets decrease in size, stochastic effects will lead to greater variation between the true and estimated false positive rates. Knowing the error associated with estimation of false positive rates by this approach is essential for application to datasets of varying sizes.

Each random match will be made against either a forward or reversed sequence. Since there are only two possible outcomes for each match, the likelihood of particular combinations of matches can be described by the binomial distribution (Equation 2), where n is the total number of items in a group from which k are selected.

$$\text{Bin}(n,k)=\left(\frac{n!}{k!(n-k)!}\right)p^k{(1-P)}^{n-k}$$ (2)

If we assume that random matches are equally likely to occur against either a forward or reversed sequence since they represent equal fractions of the overall database, then we can calculate the probabilities associated with any combination of forward and reverse random matches, denoted a and n, respectively (Equation 3).

$$F(a|n)=\left(\frac{(a+n)!}{a!n!}\right){(0.5)}^a{(0.5)}^n$$ (3)

As an example, consider a dataset with 3 hits against the reversed database. There could be 0,1,2, … forward incorrect hits (a) in the same dataset. Using Equation 3 above, we calculate the relative likelihood for each of these values, given that there are 3 reversed hits (n). When normalized so that the total area is 1.0, the result is a probability distribution function representing the likelihood of each possible number of forward incorrect identifications (Figure 1). By then repeating this process for a range of numbers of reverse hits, we define similar distributions for any number of reverse matches.

Figure 1. Distribution of Forward Incorrect Identifications.

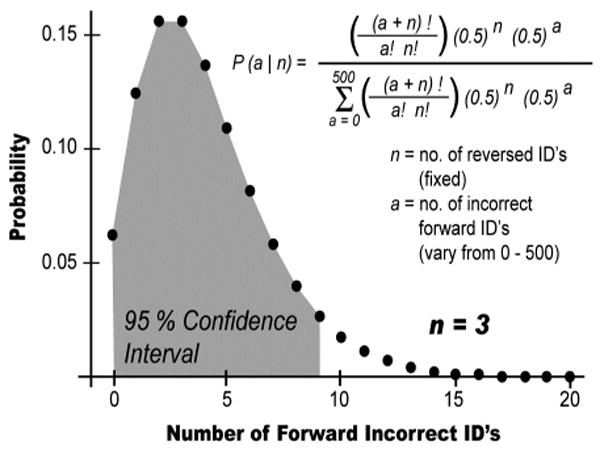
The equation listed above expresses the probability of there being a incorrect forward identifications in a particular dataset, given that n reversed peptides were identified. When this equation is solved for a range of possible values for a, a probability distribution is defined. Plotted above is the probability distribution observed for the case where 3 reversed peptide identifications have been made. The 95% confidence interval is shaded in gray.

Once we have calculated these distributions, we can define reasonable limits for the numbers of forward incorrect identifications in the dataset. When the size of the entire dataset is considered we can define these limits in terms of false positive rate. Given in Table 1 are the expected minimum and maximum numbers of forward incorrect identifications at the 95% confidence level as the number of reversed peptide identifications varies from 1 to 30. Also listed are the expected minimum and maximum false positive rates when the number of reversed peptide identifications is set to a particular target false positive rate. Note that as the number of reverse identifications increases, the range of likely numbers of forward incorrect identifications also increases. Yet when the size of the total dataset is considered, the range of likely accurate false positive rates narrows considerably and begins to center on the false positive rate predicted by the reverse peptide identifications. For a more extensive table covering from 1-100 reverse identifications, see Supplementary Table 1.

Table 1. Predicted Variation Between Reversed and Forward Incorrect Peptide Identifications.

Number Reversed ID's	Predicted Distribution		95% Confidence Intervals		0.1% False Positive			1% False Positive			2% False Positive
	Mean	Standard Deviation	Minimum Number Forward	Maximum Number Forward	Min	Max	Total ID's	Min	Max	Total ID's	Min	Max	Total ID's
0	1	1.41	0	4	*	*	*	*	*	*	*	*	*
1	2	2.00	0	6	0.00	0.60	1000	0.00	6.00	100	0.00	12.00	50
2	3	2.45	0	8	0.00	0.40	2000	0.00	4.00	200	0.00	8.00	100
3	4	2.83	0	9	0.00	0.30	3000	0.00	3.00	300	0.00	6.00	150
4	5	3.16	0	11	0.00	0.28	4000	0.00	2.75	400	0.00	5.50	200
5	6	3.46	0	12	0.00	0.24	5000	0.00	2.40	500	0.00	4.80	250
6	7	3.74	0	14	0.00	0.23	6000	0.00	2.33	600	0.00	4.67	300
7	8	4.00	0	15	0.00	0.21	7000	0.00	2.14	700	0.00	4.29	350
8	9	4.24	0	17	0.00	0.21	8000	0.00	2.13	800	0.00	4.25	400
9	10	4.47	0	18	0.00	0.20	9000	0.00	2.00	900	0.00	4.00	450
10	11	4.69	1	19	0.01	0.19	10000	0.10	1.90	1000	0.20	3.80	500
11	12	4.90	1	21	0.01	0.19	11000	0.09	1.91	1100	0.18	3.82	550
12	13	5.10	2	22	0.02	0.18	12000	0.17	1.83	1200	0.33	3.67	600
13	14	5.29	2	23	0.02	0.18	13000	0.15	1.77	1300	0.31	3 54	650
14	15	5.48	3	25	0.02	0.18	14000	0.21	1.79	1400	0.43	3.57	700
15	16	5.66	4	26	0.03	0.17	15000	0.27	1.73	1500	0.53	3.47	750
16	17	5.83	4	27	0.03	0.17	16000	0.25	1.69	1600	0.50	3.38	800
17	18	6.00	5	29	0.03	0.17	17000	0.29	1.71	1700	0.59	3.41	850
18	19	6.16	6	30	0.03	0.17	18000	0.33	1.67	1800	0.67	3.33	900
19	20	6.32	6	31	0.03	0.16	19000	0.32	1.63	1900	0.63	3.26	950
20	21	6.48	7	33	0.04	0.17	20000	0.35	1.65	2000	0.70	3.30	1000
21	22	6.63	8	34	0.04	0.16	21000	0.38	1.62	2100	0.76	3.24	1050
22	23	6.78	9	35	0.04	0.16	22000	0.41	1.59	2200	0.82	3.18	1100
23	24	6.93	9	36	0.04	0.16	23000	0.39	1.57	2300	0.78	3.13	1150
24	25	7.07	10	38	0.04	0.16	24000	0.42	1.58	2400	0.83	3.17	1200
25	26	7.21	11	39	0.04	0.16	25000	0.44	1.56	2500	0.88	3.12	1250
26	27	7.35	11	40	0.04	0.15	26000	0.42	1.54	2600	0.85	3.08	1300
27	28	7.48	12	42	0.04	0.16	27000	0.44	1.56	2700	0.89	3.11	1350
28	29	7.62	13	43	0.05	0.15	28000	0.46	1.54	2800	0.93	3.07	1400
29	30	7.75	14	44	0.05	0.15	29000	0.48	1.52	2900	0.97	3.03	1450
30	31	7.87	14	45	0.05	0.15	30000	0.47	1.50	3000	0.93	3.00	1500

^*These values are undefined for the case where the number of reversed peptide identifications equals zero.

It is worth noting that this estimate represents the minimum error associated with the false positive rate given a particular sample size, having only considered the effects of chance on the distribution of random peptide identifications across a combined forward/reverse database. In practice deviations from the assumption that incorrect matches will distribute evenly across both forward and reverse sequences may tend to skew errors in one direction or the other. Such an error may occur in cases where an incomplete database is used for peptide identifications. Additionally, some bias toward forward incorrect peptide identifications may be seen due to sequence homology between the true parent protein and the protein to which the peptide was assigned. Although accounting for these issues is difficult in practice, knowing the minimum error associated with a given false positive estimate can still be useful for evaluation of experimental results.

Validation of Predictions

In order to test this model for experimental error associated with false positive determination, a series of nine mixtures of known proteins were analyzed in triplicate, varying charge state preferences for data dependent MS/MS acquisition to improve coverage. Each mixture contained 2-5 proteins, for a total of 21 proteins overall. The resulting MS/MS spectra from these analyses were searched using Mascot against a composite database containing the forward and reversed protein sequences from Arabidopsis, chosen for its typical size and low homology with readily available control proteins, with sequences of all control proteins as well as common contaminants appended. Because the proteins present in each sample are known, forward correct and forward incorrect peptide assignments may be easily distinguished and compared with numbers of reverse incorrect peptide assignments. Thus the predicted and actual false positive rates may be compared for all runs individually as the number of observed reverse peptide identifications varies. This analysis was also repeated for all runs combined one by one in random order to achieve different sized datasets.

Plotted in Figure 2 are the numbers of forward incorrect peptide identifications predicted by our model, as a function of the observed number of forward incorrect peptide identifications. Each prediction is represented by a circle representing the mean value of the distribution specified by the number of observed reversed peptide identifications, with error bars representing +/- one standard deviation. Values for individual analyses are represented by white circles, while values for combinations of analyses combined in random order are represented by black circles. Ideally the predicted numbers of incorrect forward peptide identifications would exactly match the numbers observed; this is represented by the line plotted with slope = 1.0 and intercept = 0. While the predictions drift somewhat around the ideal, essentially all pass within one standard deviation. Thus this model provides reasonable predictions of numbers of incorrect forward peptide identifications, while also providing a reasonable estimate of error.

Figure 2. Number of Incorrect Forward Peptide Identifications: Predicted versus Observed.

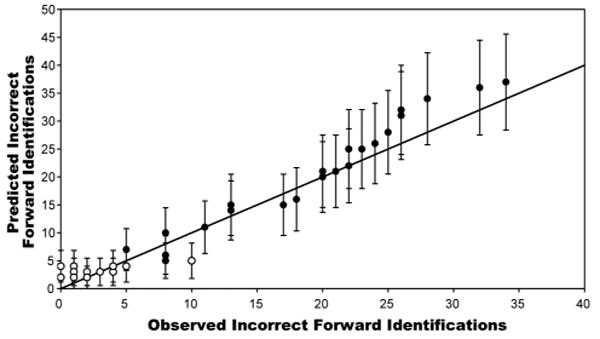
Each of several mixtures of control proteins were analyzed via mass spectrometry and peptides were identified by searching a composite database containing the forward and reversed sequences of all proteins in Arabidopsis, as well as the sequences for the selected control proteins. Numbers of incorrect peptide identifications against both the forward and reversed protein sequences were determined at an estimated 1% false positive rate based on numbers of reversed peptide identifications. The number of reversed peptide identifications was then used to predict the number of forward incorrect peptide identifications, using the equation in Figure 1. Plotted above are the predicted numbers of incorrect forward peptide identifications, as a function of the number of incorrect forward peptide identifications that were actually observed. Circles represent the average, while error bars represent +/- one standard deviation, as determined by the appropriate probability distribution. White circles represent each of several separate analyses of control proteins, while the black circles represent the peptide identifications from these same analyses, combined in random order to generate datasets of varying sizes. The diagonal line represents the ideal case where the predicted number of incorrect forward peptide identifications exactly equals the observed number of incorrect forward identifications.

Plotted in Figure 3 are the results of the individual and combined control protein analyses, along with the predicted 95% confidence limits for the accurate false positive rate as a function of the total number of reverse peptide identifications. All files are displayed at an estimated 1% false positive rate based on reversed peptide identifications. The inset displays a cross-section of this plot for the case of 3 reversed peptide identifications to give an indication of topology. Note that at low numbers of reverse peptide matches, the 95% confidence limits are very broad and the underlying distribution is skewed. However, as the number of reverse peptide matches increases, the 95% confidence limits narrow and the underlying distribution becomes more symmetrical about the target false positive rate. Also, note the slightly jagged appearance of the curves describing the confidence limits. This is because the numbers of reverse and forward identifications are both discrete functions. Thus the true confidence level reflected by the curve is a minimum of 95%, may drift upward slightly for some integer values due to the shape of the corresponding probability distribution. As can be seen in the graph, this effect is most pronounced for low integer values.

Figure 3. Comparison of Predicted versus Actual False Positive Rates.

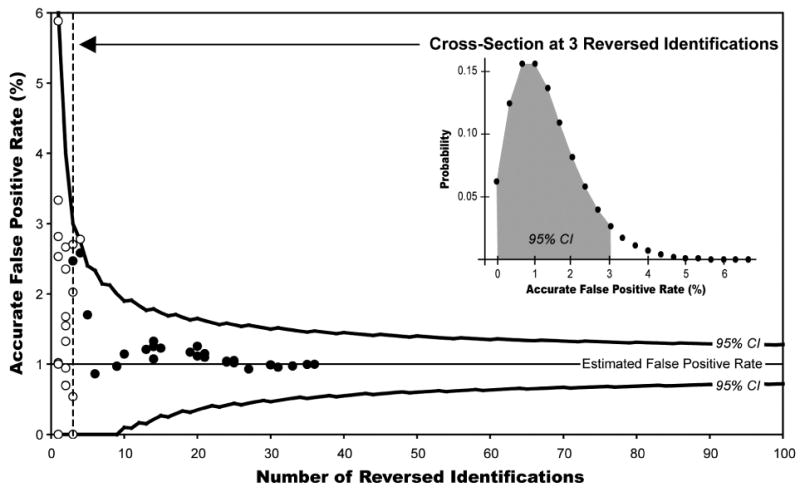
Plotted above is the actual false positive rate as a function of the number of reversed peptide identifications. The solid lines indicate upper and lower boundaries of the 95% confidence intervals (CI) for 1-100 reversed peptide identifications, assuming an estimated 1% false positive rate. A cross-section of for 3 reversed peptide identifications (dotted line) is included as an inset. Also plotted are the actual false positive rates as a function of numbers of reversed peptide identifications at a 1% estimated false positive rate for several analyses of control proteins individually (white circles) and when added in random order to generate datasets of varying sizes (black circles).

Also plotted in Figure 3 are the actual false positive rates as a function of total numbers of reverse peptide identifications for all files analyzed individually and when combined. When these files are considered as individual populations of spectra (white circles), the true false positive rates show wide dispersion, which is consistent for the relatively small numbers of identifications considered. However, when these individual files are combined one by one in random order to generate progressively larger datasets (black circles), the accurate false positive rate quickly converges on the predicted false positive rate (1%). Overall, the distribution of experimental data is consistent with the confidence limits presented.

In practice, the information derived from the theoretical calculations described above can be used to assess the accuracy of FP rate for datasets of any size. For example, consider the combination of all control protein analyses (Table 2). A total of 35 reverse ID's were seen out of 3418 total forward identifications (correct and incorrect). At the 95% confidence level, the true number of forward incorrect identifications is expected to be between 18 and 51 (as taken from Table 1), corresponding to a false positive rate between 0.53 and 1.51% when these values are divided by the total number of forward identifications. This is consistent with the actual false positive rate among forward identifications, which was 1.08%.

Table 2. Effects of Charge State Separation on Error in False Positive Estimation.

Charge State	MASCOT Cutoff	False Positive Rates		Number of Peptides			95% Confidence Intervals
		Predicted	Accurate	Forward	Reversed	Forward, Incorrect	No. Peptides		FP Rate
1	34	4.17	0.00	24	1	0	0	6	0.00	25.00
2	23	1.03	1.49	1920	20	29	7	33	0.36	1.72
3	16	1.08	0.65	1374	15	9	4	26	0.29	1.89
4	< 10	0.00	1.29	230	0	3	0	4	0.00	1.74
Combined (1,2,3,4+)		1.01	1.16	3548	36	41	21	56	0.59	1.58
Ignore Charge State	22	1.02	1.08	3381	35	37	18	51	0.53	1.51

Error Rates upon Separation by Charge State

These previous analyses have involved setting false positive thresholds while considering all peptide identifications as a single group. However, it has been shown that a variety of peptide characteristics, especially charge state can have significant effects on the confidence of its identification⁷. Thus to minimize the number of false negative identifications it is beneficial to determine separate false positive thresholds for peptides depending on their charge state. In practice this can lead to dramatically different threshold scores for various charge states, using the same search engine (Table 2). Also, there are significant differences in the numbers of peptides for each charge state. Thus although all charge states have been set to a predicted 1% false positive rate, the associated error rate with this prediction varies greatly. This raises the question, what is the true error rate for the dataset as a whole when false positive thresholds are set for each charge state individually? By combining estimates of error associated with each individual charge state as described above we can calculate this error.

To address this issue the first step is to calculate distributions describing the error expected for false positive determination for each charge state individually based on the number of reverse peptide identifications observed. The boundaries associated with the 95% confidence intervals for these populations are given in Table 2. As can be seen, there is considerable variation in error associated with each charge state. Notably, the error is especially large for singly and quadruply charged peptides due to the small small dataset size and resulting numbers of reversed peptide identifications, just as our model would predict. The false positive estimate for singly charged peptides is especially suspect. To determine the error associated with the false positive rate of the entire dataset we must now combine these error distributions for all charge states. Viewing the errors in false positive rates as being independent across charge states, we multiply the distributions together in pairs, and then sum the components of the resulting two-dimensional matrix according to the total number of reversed peptide identifications to obtain a composite error distribution (see Supplementary Data for a detailed description of these calculations). This process is repeated until all charge states have been considered. The boundaries of the 95% confidence interval defined for this distribution are given in Table 2 for the combination of all charge states (1-4). They can be compared with the boundaries of the 95% confidence interval determined for the same population of peptides when a 1% false positive threshold is set for the entire population as a whole without separation by charge state.

Comparison of results from the control protein experiment given in Table 2 suggests that separating peptides by charge state prior to setting false positive thresholds leads to a similar degree of uncertainty in the predicted false positive rate as would be seen without separation with respect to charge state. However, there is a slight shift to higher false positive values when peptides are separated by charge state. This is consistent with the slight increase in true false positive value we observed with separation by charge state. As expected, when peptides were separated by charge state we observed more peptides at a comparable false positive rate. Interestingly, although relatively imprecise false positive estimates were incorporated for some charge states, these did not have significant adverse effects on false positive rate for the overall dataset.

Conclusions

As a variety of decoy database strategies become applied more frequently as an empirical measure of the quality of peptide identifications for proteomics experiments, it is important to consider the error associated with these approaches. We have devised a method of predicting the error associated with use of a combined forward/reverse database to determine false positive rates for peptide identifications. In particular, this has allowed us to assess the accuracy of false positive estimates depending on the size of the individual dataset and the number of reversed peptide identification observed. Through comparison with results from analysis of mixtures of known standard proteins, this statistical model seems to fit the experimental data well. Furthermore, this model can be extended for analysis of false positive rates for more complex data sets, as when peptides have been separated by charge state. By understanding the error associated with the combined reverse/forward database approach for false positive estimation we will be able to apply it with greater confidence and understanding to a variety of datasets of varying sizes.

Supplementary Material

1si20061006_04. Supporting Information Available.

An expanded version of Table 1 encompassing from 1 to 100 reverse peptide identifications is provided as supporting information. A list of all peptide assignments with Mascot scores greater than 10 (correct, as well as forward and reverse incorrect identifications) from the control protein analyses is provided as well. Finally, a detailed description of how the 95% confidence limits were calculated in Table 2 for combined charge states is provided.