Cues for masked amplitude-modulation detection

Abstract

The ability of psychoacoustic models to predict listeners’ performance depends on two key stages: preprocessing and the generation of a decision variable. The goal of the current study was to determine the perceptually relevant decision variables in masked amplitude-modulation detection tasks in which the modulation depth of the masker was systematically varied. Potential cues were made unreliable by roving the overall modulation depth from trial to trial or were reduced in salience by equalizing the envelope energy of the standard and target after the signal was added. Listeners’ performance was significantly degraded in both paradigms compared to the baseline (fixed-level modulation masker) condition, which was similar to those used in previous studies of masking in the envelope-frequency domain. Although this observation was broadly consistent with a simple long-term envelope power-spectrum model, there were several aspects of the data that were not. For example, the steep rate of change in threshold with masker depth and the fact that an optimal amount of envelope noise could enhance performance were not predicted by decision variables calculated directly from the stimulus envelope. A physiologically based processing model suggested a realistic nonlinear mechanism that could give rise to these second-order features of the data.

I. INTRODUCTION

Behaviorally relevant acoustic stimuli such as speech cannot be defined solely by their long-term audio-frequency composition. Temporal variations in a signal’s spectrum and interactions between individual spectral components result in amplitude-modulated (AM) sounds. Viemeister (1979) used concepts from linear systems analysis as a framework to determine the effective temporal modulation transfer function (MTF) of the auditory system by measuring the just-noticeable modulation depth of a sinusoidally amplitude-modulated (SAM) noise for a range of modulation frequencies (f_m). Viemeister’s approach has proven highly valuable as a first-order approximation of the system’s (low-pass) properties and as a starting point for many other studies. For example, the modulation filter-bank model structure (e.g., Dau et al., 1997a), which assumes that the envelope of the output of each audio-frequency channel passes through a bank of bandpass filters (broadly) tuned to f_m, is able to account for several perceptual findings that a low-pass pre-processor cannot explain (i.e., Dau et al., 1997a, b, 1999; Ewert and Dau, 2000).

To predict psychophysical thresholds, the output of any model must be concisely quantified with some decision variable (DV). And while the preprocessing model structures are fundamentally different for the two models mentioned earlier, both the Viemeister (1979) model and the most recent implementations of the Dau model [the envelope power-spectrum model, Ewert and Dau, 2000; Ewert et al., 2002; Ewert and Dau, 2004] assume an average rms DV at the output of their envelope-filtering process. This assumption has been shown to be reasonable for many types of AM-detection tasks, but it is not clear whether decision statistics that rely on local temporal envelope features (instead of average or long-term features) would be equally successful as quantifications of the model outputs.

The broad goal of the current set of experiments was to further elucidate which features of AM stimuli are perceptually salient and used by listeners in modulation detection tasks. To accomplish this, empirical data are presented that provide critical tests for various DVs. Paradigms from the audio-frequency tone-in-noise (TIN) detection literature that highlight shortcomings of long-term decision statistics in the spectral-frequency domain (roving-level and energy-equalized TIN detection) were translated into the modulation-frequency domain. Because the stimuli had envelope-frequency bandwidths smaller than the presumed modulation filter widths, the internal representation of the stimulus envelope was similar for the low-pass (Viemeister) model and the bandpass (Dau) model. An alternative model, developed to predict responses of inferior colliculus (IC) neurons to AM signals (Nelson and Carney, 2004), was tested alongside the previously proposed psychophysical (signal-processing) models. The working hypothesis was that a physiologically motivated model structure would shape the internal representation of the stimulus more like the real system than “effective” signal-processing models.

There are two reasons to consider a masked AM-detection task (instead of pure, or unmasked, AM detection) to test our hypotheses. First, several reasonable techniques can be used to adjust a given model’s unmasked detection abilities, which makes it difficult to dismiss one competing decision statistic over another. A more interesting reason is that real-world sounds have complex modulation spectra, so it is useful to consider envelope detection abilities and limitations for stimuli other than pure sinusoidal AM. Previous studies of masked-AM detection have focused on the effects of varying the frequencies of the signal and/or masker modulation (Houtgast, 1989; Bacon and Grantham, 1989; Strick-land and Viemeister, 1996; Dau et al., 1997a; Ewert and Dau, 2000; Ewert et al., 2002). Here, masker level (or masker modulation depth) was the only systematically manipulated stimulus dimension. Predicted signal-detection thresholds based on a battery of potentially relevant DVs were compared to the masked thresholds measured psychophysically. Because several decision devices predicted statistically similar thresholds, a more detailed analysis of the relationships between DVs and listener responses on a trial-by-trial basis was also carried out.

A subset of the potential perceptually relevant decision devices investigated in the present study can be introduced in the context of previous work. Perhaps the most influential and straightforward DV assumed in previous AM-coding work is the long-term rms energy measured at the output of some envelope-filtering process. Such a statistic can explain the shape of the temporal modulation transfer function (with low-pass preprocessing: Viemeister, 1979; Strickland and Viemeister, 1996) and the envelope-frequency selectivity observed in experiments measuring sinusoidal AM-detection thresholds in the presence of a narrowband-noise masker modulation applied to the same carrier (with bandpass preprocessing: Ewert and Dau, 2000; Ewert et al., 2002). Moore and Sek (2000) measured detection thresholds for stimuli with three AM-frequency components for three different phase configurations, and found no dependence of thresholds on the components’ relative phases. This finding is also consistent with predictions of an average (rms) envelope statistic. Note that any local temporal structure present in the stimulus (or its internal representation) is discarded with an average (rms) metric.

Strickland and Viemeister (1996) concluded that the ratio of the maximum value to the minimum value of the envelope (max/min) was the best predictor of listeners’ thresholds in a tone-on-tone modulation masking experiment. In contrast to the rms statistic, which averages over the entire temporal waveform, max/min makes decisions based on only two points in the envelope representation. Crest factor (ratio of maximum envelope value to the envelope rms) represents a compromise in some sense: a single value of the waveform is normalized by an averaged value. Lorenzi et al. (1999) accounted for performance in a (supra-threshold) modulation component phase discrimination task by basing decisions on the crest factor of a low-pass filtered version of the envelope of their stimuli. DVs based on the higher-order moments of envelope amplitude distributions have also been tested in various envelope-processing tasks (i.e., skewness: Lorenzi et al., 1999; kurtosis: Strickland and Viemeister, 1996).

Another aspect of a signal with a complex modulation spectrum is its venelope, or second-order envelope (Shofner et al., 1996; Ewert et al., 2002; Lorenzi et al., 2001a, b). Venelope cues could potentially be used in modulation masking experiments, especially in conditions with tonal maskers and noise signals (Ewert et al., 2002). This line of reasoning parallels results from audio-frequency tone and noise masking experiments in which envelope cues have been shown to have various effects on detection performance, depending on the masker-signal configuration (i.e., the asymmetry of masking; see Derleth and Dau, 2000). It is reasonable to hypothesize that venelope fluctuations may also provide a detection cue for conditions with sinusoidal signals and random maskers (as measured in the present study), especially when first-order envelope cues are made unreliable or completely removed.

As an alternative to signal-processing-based DVs, threshold predictions were also made based on a physiologically motivated model for neural responses to AM tones (Nelson and Carney, 2004). The average firing rate of model inferior colliculus cells was tested as a physiologically realistic DV, alongside several of the signal statistics described earlier. In the model cells, firing rate increases monotonically with signal modulation depth. Interactions between strong inhibitory and weaker excitatory inputs result in a “hard” threshold modulation depth that limits the model’s detection performance even in the absence of internal or external (stimulus-induced) noise sources. Model-cell rate MTFs are bandpass, with Q values (measured at the half-maximal-rate points) of approximately 1. This broad tuning is realized in the physiological model by assuming different time courses in the effective low-pass filtering properties of inhibition and excitation. The Q values are consistent with the signal-processing modulation filters derived recently by Dau and co-workers to predict several aspects of psychophysical envelope coding (Dau et al., 1997a; Ewert and Dau, 2000; Ewert et al., 2002). For the band-limited stimuli used in the present study, the filtering properties of the IC model cells have little effect on shaping the internal representation of the envelope. Again, the focus is on understanding the perceptually salient quantifications of the internally represented envelope (as opposed to testing the validity of a bandpass modulation filter versus a “smoothing” or low-pass modulation filter).

Independent of the chosen DV, simulations of psychophysical experiments must include some mechanism to limit model performance in the detection and discrimination of deterministic stimuli (without external noise). The most common way to do this is to add some amount of internal noise, either to the internal representation, or to the final value of the decision statistic in each interval. Ewert and Dau (2004) have provided some insight into the appropriate statistical description of the internal noise relevant to envelope-processing tasks. They measured AM depth-discrimination thresholds for a wide range of standard depths, and found the Weber fraction for sinusoidal carriers to be independent of standard depth, as long as the standard was well above threshold. This can be accounted for in a model by assuming a constant ratio between the DVs in the target and standard interval at threshold, or by including an internal noise whose variance is proportional to the value of the assumed decision statistic. For low standard depths (i.e., -28 and -23 dB in 20 log m, where m is linear modulation depth), the situation was different. In this range, a constant increase in modulation depth was required to reach discrimination threshold (independent of the standard depth). This can be thought of as arising from a second type of internal noise process—one with a fixed variance, which dominates threshold measurements at low modulation depths. We will address Ewert and Dau’s (2004) findings, but we will also consider model predictions with a fixed-variance noise only, as a “best-case scenario” for the various decision statistics (i.e., if a decision statistic predicts higher thresholds than the listeners’ performance with the fixed-variance noise alone, it would certainly not be able to account for thresholds if the constant-ratio noise, or Weber-fraction noise, were also included).

Two specific paradigms that have been used in the audio-frequency domain to test the power spectrum model of masking were translated into the envelope-frequency domain in the current study: roving-level and equal-energy TIN detection. A within-trial rove in overall energy renders long-term rms cues unreliable, and models based on energy cues predict higher thresholds in a roving-level situation. The absolute amount of increase over fixed-level conditions depends on the rove range (Green, 1983). Kidd et al. (1989) found that roving the overall level by 32 dB in an audio-frequency TIN detection task did not have a significant effect on thresholds (for noise bandwidths greater than one-third of the psychophysically measured auditory-filter bandwidth). In another paradigm that challenges energy-based audio-frequency models of masking, Richards and Nekrich (1993) measured the detectability of tones in narrow bands of masking noise after the energy in the two observation intervals was equalized. Pure long-term energy models predict that such a task would be impossible (for subcritical bandwidths), but listeners performed the task reliably. Richards and Nekrich (1993) attributed their results to differences in the envelopes of the noise-alone and tone-plus-noise stimuli.

With this body of previous work in mind, we present here psychophysical masked-AM detection data and predicted thresholds based on a diverse set of decision statistics. Measured and simulated thresholds in roving-level and equal-energy conditions are compared to those from a baseline fixed-level masker condition, over a wide range of masker modulation depths.

II. PSYCHOPHYSICAL EXPERIMENT

A. Methods

1. Subjects and procedure

Four listeners with normal hearing participated in the experiment. Pure-tone thresholds for all of the subjects were less than 15 dB HL at octave frequencies between 500 Hz and 8 kHz. The authors served as two of the subjects (S2 and S3) and had experience in psychoacoustic measurements. The remaining two listeners had no previous experience. A training period, typically lasting three or more 1.5-h sessions, was provided in which masked and absolute modulation thresholds were estimated using procedures similar to those described in the following. Further training was provided for the roving-level and equal-envelope-energy (EEE) conditions (see the following). Data collection began when thresholds for a subject stabilized; there were typically no learning effects observed after four to five tracks on a given condition. The listeners became familiar with the different stimulus conditions, and were aware of the particular condition prior to the start of a track.

Masked SAM detection thresholds were obtained using an adaptive two-interval, two-alternative forced-choice (2I, 2AFC) procedure with a two-down, one-up stepping rule that estimated the modulation depth necessary for 70.7% correct detection (Levitt, 1971). This combination of parameters resulted in a threshold estimate that corresponded to a d’ of about 0.8. In the randomly chosen target interval, the signal modulation was imposed along with a masker modulation on the tone carrier. The standard interval contained only the masker modulation. The signal modulation depth m at the beginning of a track was set well above threshold, and was varied initially by 3-dB steps (in 20 log m), and in steps of 1.5 dB after the first two reversals. The tracking procedure was run until 16 reversals were obtained; threshold for a given track was taken as the mean modulation depth of the last ten reversals. For each stimulus condition, thresholds presented here are the mean of four such estimates. Only tracks in which the standard deviation of the last ten reversals was less than 3 dB were included in further analysis. Across-subject average data are presented as the mean and standard deviation of the 16 threshold estimates (4 listeners×4 tracks per condition).

2. Apparatus and stimuli

Subjects listened diotically through calibrated Sennheiser HD 580 headphones while seated in a sound-treated booth. Stimuli were digitally generated at a sampling rate of 48.828 kHz and converted to analog signals via the TDT System III two-channel real-time processor (RP2.1) digital-to-analog converter and the TDT System III headphone buffer (HB7), with its gain set to -27 dB (to eliminate back-ground noise). Signals were generated and presented with visual feedback using matlab. Noise waveforms were saved for both intervals on every trial (by recording random-number-generator seeds) so that the exact stimuli could be reconstructed for post hoc analysis (see Sec. III A 3).

The two intervals were each 600 ms in duration including 50-ms cos² ramps, and were presented with a 500-ms interstimulus interval. Both the sinusoidal signal (always in sine phase) and the narrow-band Gaussian-noise masker modulation were applied to the envelope of a 2800-Hz tone carrier for the entire duration of the stimulus. The signal frequency was 64 Hz; the masker was centered on the signal frequency and had a bandwidth of 32 Hz. These parameters were chosen to satisfy several specific constraints. First, the modulation frequencies were low enough to avoid the introduction of audio-frequency spectral resolution cues that arise when the sidebands generated by modulation are remote from the carrier frequency component. In addition, the band-width of the masker was wide enough to allow for the slower second-order (venelope) fluctuations to fall within a range that could potentially be detected in a 600-ms duration signal (the venelope energy was concentrated around 10 Hz). The AM signal and masker parameters were also influenced by modeling considerations, as described below.

Two statistically independent realizations of the masker were generated for the standard and target intervals. An additive approach, as opposed to the multiplicative one used in several related studies (Ewert and Dau, 2000; Ewert et al., 2002; Houtgast, 1989), was used to combine the signal and masker. This allowed for more careful control of the envelope-frequency domain magnitude spectrum (i.e., addition of time-domain waveforms results in the addition of their frequency-domain spectra, whereas multiplication of time waveforms is equivalent to a convolution of their frequency spectra). The equation for the stimuli in both intervals is

$$s\left(t\right)=c\left\{\sin \left(2\pi f_{c}t\right)[1+m\sin \left(2\pi f_{m}t\right)+M\left(t\right)]\right\},$$

where f_c is the carrier frequency, m is the stimulus modulation depth (zero in the standard interval), f_m is the signal modulation frequency, and M(t) is the masker waveform (zero when measuring absolute thresholds). Masker level was defined in terms of the rms of M(t). The compensation factor c was included so the overall power in both intervals was equivalent to that of a 65-dB SPL pure tone. Every stimulus was checked for over modulation caused by the stochastic nature of the narrow-band maskers; no envelope with a modulation index greater than one was presented to the listeners.

3. Conditions

The acoustic stimuli used in this experiment were similar to those described in Ewert et al. (2002). Different parameter variations, as well as minor procedural modifications, distinguish the two studies. Ewert et al. (2002) focused on frequency effects (of both signal and masker). Here, we explicitly considered the effect of masker level (i.e., the masker rms modulation depth) and the consequences of systematically controlling the availability of envelope-detection cues. Thresholds for three conditions were measured: (1) SAM detection with a fixed-level modulation masker, (2) SAM detection with a random 10-dB within-trial rove in masker level, and (3) SAM detection with EEE in the standard and target intervals (after the signal was added). The roving-level condition effectively made envelope energy an unreliable cue; the EEE condition strongly attenuated first-order envelope energy differences as a cue for detection. Thresholds from the fixed-level condition provided a baseline for evaluating the consequences of these two manipulations. Note that the fixed-level condition was comparable to those of previous studies (i.e., Ewert et al., 2002).

B. Results and discussion

1. Fixed-level modulation masker

General trends in the results were similar across the four listeners, but individual sensitivity varied considerably in the masked-AM detection task. Both individual (upper panel) and mean thresholds (lower panel) are shown in Fig. 1 for the detection of a 64-Hz sinusoidal modulation in the presence of an additional masker modulation. The masker had a bandwidth of 32 Hz, and was always centered on the signal frequency. Signal thresholds are shown for a 10-dB range of masker modulation depths.

FIG. 1.

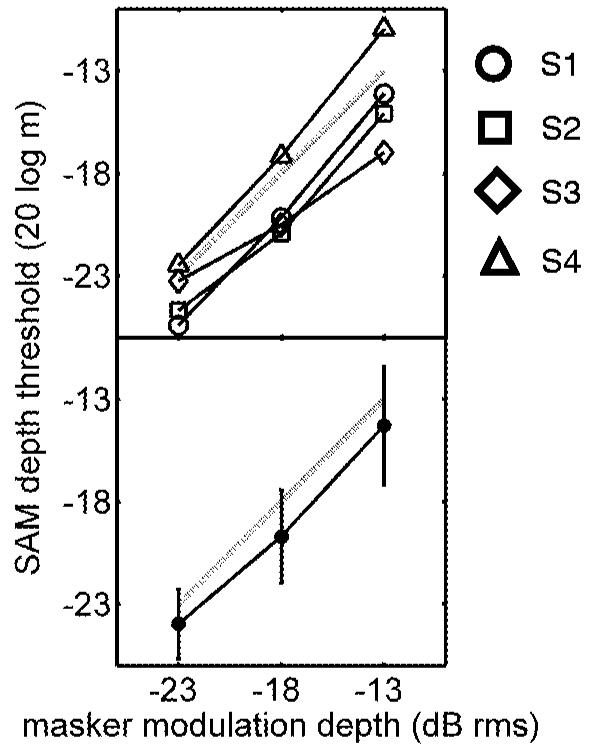
Individual (top panel) and mean (bottom panel) masked-SAM detection sensitivity. Thresholds at these supra-threshold masker depths increased at a rate of about 1 dB (20 log m) per 1 dB (masker rms); the dashed lines in the two panels serve as a reference with a 1 dB/dB slope. Signal f_m=64 Hz; masker bandwidth=32 Hz, centered on signal frequency; SPL=65 dB; carrier f_c=2800 Hz; duration=600 ms. Standard deviations of individual listener threshold estimates were between 2 and 4 dB (error bars omitted for clarity).

Thresholds increased monotonically as the masker level increased over this range of masker depths. Listener S4 was less sensitive than the other three subjects, while the thresholds of Subject S3 increased at a rate less than 1 dB/dB. Mean thresholds were 1-2 dB (20 log m) lower than the masker modulation depth (dB rms), and increased with a slope of 1 dB/dB. These results are consistent with those of Houtgast (1989), who measured detection thresholds for an 8-Hz sinusoidal signal modulation in the presence of a 2.8 -Hz bandwidth masker modulation. In contrast with the present study, Houtgast (1989) combined the signal and masker multiplicatively and imposed them on a noise carrier.

Somewhat less intuitive are the patterns of thresholds measured for lower-level maskers. In efforts to map out the entire range of masker modulation depths that produced masking while still avoiding overmodulation, for the purpose of the roving-level experiment (to follow), it became clear that some of the listeners’ masked thresholds were lower than their pure AM-detection thresholds. This “facilitation” is illustrated in Fig. 2 in the form of nonmonotonic threshold versus masker level functions for two of the four listeners (S2 and S3). The thresholds for the three right-most points in each function are replotted from Fig. 1. Unmasked detection thresholds ranged from -25 to -30 dB (masker level=-99 dB rms; left-most point on each plot), and were consistent with previously reported pure-tone SAM detection thresholds for comparable f_c, f_m, and SPL (i.e., Kohlrausch et al., 2000). The external variability of the noise maskers began to influence thresholds between -40 and -30 dB rms. The presence of the region of facilitation was not related to absolute sensitivity to AM; the two subjects that exhibited the clearest facilitation had the lowest (S2) and highest (S3) thresholds in unmasked AM detection. In addition, the masker level that resulted in the most facilitation was the same for both listeners (-28 dB rms).

FIG. 2.

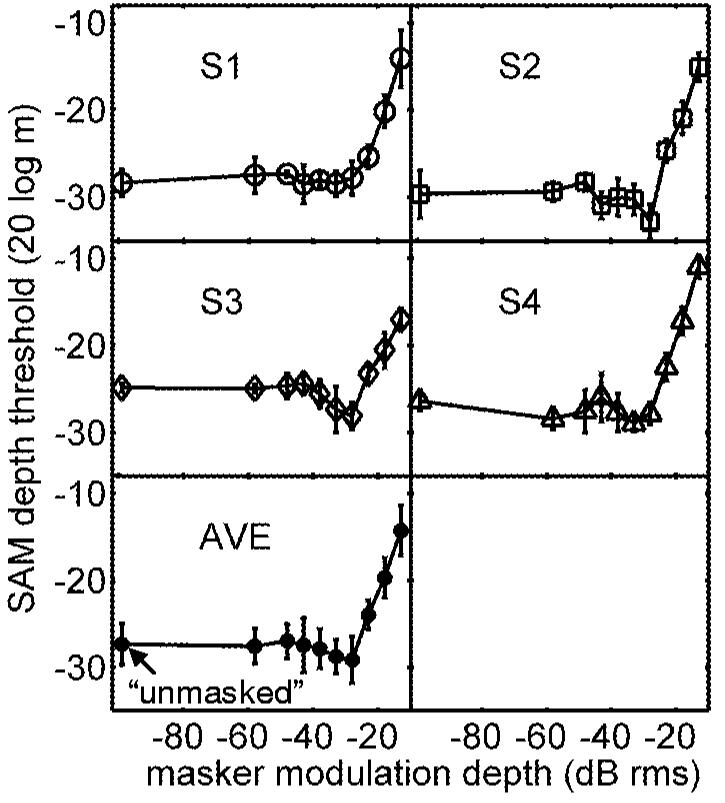
Masked-detection thresholds for a wide range of masker modulation depths. Two of the listeners (S2 and S3) exhibited a nonmonotonic dependence of sensitivity on masker level; their thresholds were lower for a masker level of -28 dB than in the unmasked condition. The three right-most points in each panel are replotted from Fig. 1; these masker levels consistently caused “positive” masking without causing overmodulation.

Strickland and Viemeister (1996) and Bacon and Grantham (1989) reported facilitation in some of their tone-on-tone modulation masking conditions, when the frequency of the masker was well below that of the signal. They accounted for this type of negative masking by assuming that their listeners were able to attend to the valleys of the masker when its fluctuations were slow enough, resulting in a temporally localized larger effective modulation depth. The facilitation illustrated in Fig. 2 is fundamentally different: the masker and signal occupy the same frequency region, and inherent fluctuations in the narrow-band masker made the timing of its valleys unpredictable to our listeners. Also, the negative masking effects in previous studies increased as the masker modulation depth increased; the effect observed in the current study is only measurable at very low masker depths (near or even below detection thresholds). Potential mechanisms underlying on-frequency, low-level noise-masker facilitation will be evaluated in Sec. III.

2. Roving-level modulation masker

The effect of introducing a random 10-dB within-trial rove in masker level on listeners’ thresholds is shown in Fig. 3. Because the masker modulation depth was different in every interval, it was necessary to track on the level of the signal with respect to the level of the noise (i.e., the difference between the two in dB). Detection thresholds are plotted for a fixed-level (-18 dB rms) noise masker (filled bars) and for the roving level (uniformly distributed from -23 to -13 dB rms) noise masker (open bars). Individual and across-subject average thresholds are included in the figure.

FIG. 3.

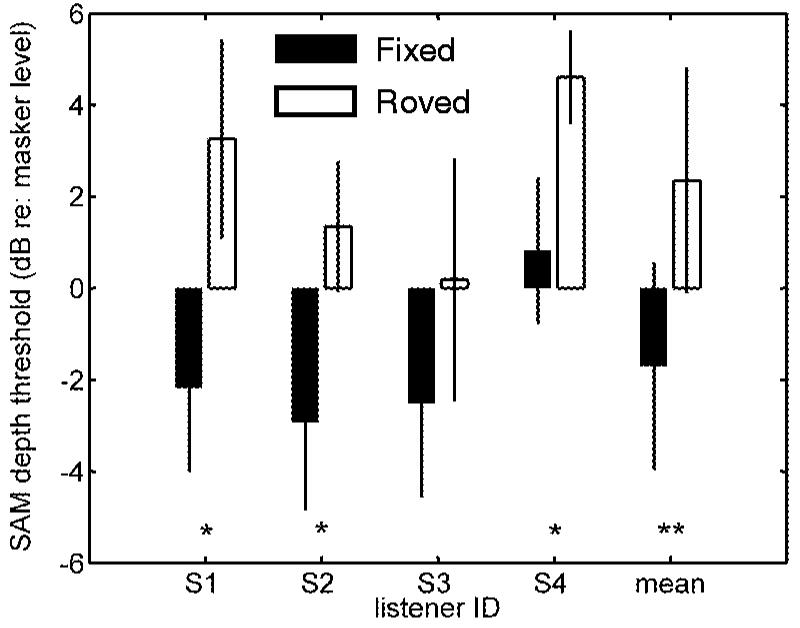
Comparison of fixed-level thresholds at a masker depth of -18 dB (closed bars) and roving-level thresholds, where the masker depth was randomly chosen from a uniformly distributed 10-dB range centered on -18 dB (open bars). Asterisks indicate cases where the difference between the fixed- and roving-level thresholds was significant (*p<0.02; **p<0.0001).

In general, thresholds in the roving-level condition were 3-5 dB higher than those in the fixed-level case. The effect was significant (t-test, p<0.02) for three of the four individual listeners, and highly significant (p<0.0001) when the across-subject mean and variance was considered. The 10-dB rove in masker level increased the mean thresholds by 4 dB. Unfortunately, the small dynamic range of AM maskers precluded the use of larger rove ranges in the present study (i.e., the masker must be intense enough to cause masking, but not so strong as to result in overmodulation, especially in the signal interval). Despite the limitations, the significant effect of this relatively small rove range contrasts with results from audio-frequency TIN detection experiments, where even a 32-dB rove in masker level did not significantly affect listeners’ thresholds (except at the narrowest bandwidth tested, Kidd et al., 1989). The convincing results of Kidd et al. (1989) provide a critical test that challenges the power spectrum model of masking in the audio-frequency domain. Qualitatively, models which assume the long-term energy of the (ac-coupled) envelope as the perceptually relevant quantity (e.g., Viemeister, 1979; Ewert and Dau, 2002) are not seriously challenged by the current results obtained with the roving-level modulation masker. A more careful analysis of this general statement is provided in Sec. III.

3. Equalized-envelope-energy modulation masker

As an alternative approach to test energy-based models, (long-term) first-order envelope cues were removed by forcing the rms modulation depth of the standard and target intervals to be the same, regardless of the level of the signal (in 20 log m). The task was the same as in the fixed-level and roving-level condition: listeners chose the interval containing the sinusoidal signal modulation. Pure long-term energy decision statistics did not provide any cues for detection in this paradigm (as long as the masker bandwidth was within the passband of the envelope-filtering process). Overmodulation was not an issue in the EEE condition: the average depth in both standard and target intervals was determined by the depth of the masker-alone modulation. Qualitatively, the signal-interval envelope fluctuations became more sinusoidal as m increased (but the overall rms modulation depth was the same in both the standard and target envelopes).

Example waveforms for a -13-dB rms standard depth are illustrated in Fig. 4(a) along with individual listener and mean thresholds for a 10-dB range of masker-alone modulation depths [Fig. 4(b)]. Note that absolute thresholds are not plotted in Fig. 4; instead, increases in threshold over the corresponding fixed-level masker condition are shown. The key result illustrated in Fig. 4 is that the listeners were able to perform the task, although measured thresholds were about 10 dB worse on average than in the fixed-level condition (in which the overall rms modulation depth was allowed to naturally vary across intervals). Perhaps the most striking aspect of the individual thresholds is the high variability both within and across listeners (note the expanded scale of the y axis). Anecdotally, the task became considerably more difficult in the EEE condition, and listeners reported the use of a very different strategy compared to that employed in the fixed-level case. The following sections quantitatively explore potential cues that could explain thresholds in all three masker configurations (fixed-level, roving-level, and EEE).

FIG. 4.

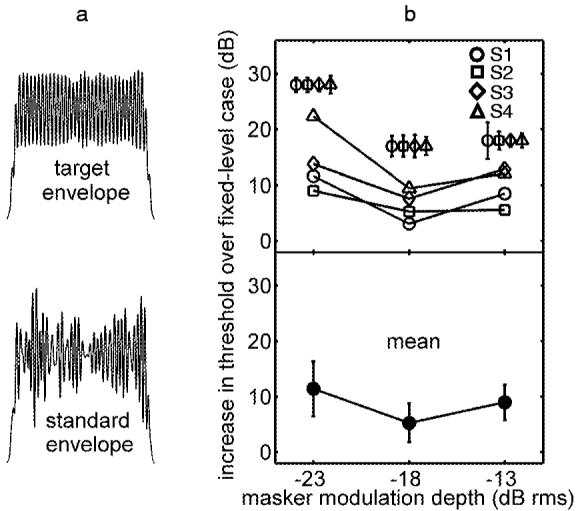
Effect of equalizing the overall modulation depth in the two observation intervals after the signal was added. (a) Example wave forms: masker depth=-13 dB rms; signal added to target interval masker at a +20 dB SNR. (b) Increases in thresholds over comparable fixed-level conditions (absolute thresholds are shown along with model predictions in Fig. 7). Individual listener standard deviations are shown above the corresponding means [(b), top panel].

III. MODELING

A. Methods

1. Simulating threshold runs

Masked-detection thresholds were determined for each assumed DV using the same procedure, stimuli, and conditions as described in the psychophysical methods. The mean and standard deviation of 16 estimates were obtained (for comparison to the 4 subjects×4 repetitions measured psychophysically). Only the steady-state portion of the envelope (the central 500 ms) was used to compute decision statistics.

Several DVs were calculated from the Hilbert envelopes of the stimuli and used in simulated tracking procedures: (1) rms ac-coupled envelope energy, (2) average local modulation depth, (3) average rate of model IC cell, (4) crest factor, (5) maximum local modulation depth, and (6) max/min ratio. The first three DVs can be considered “long-term,” as they are based on an integrated representation of the entire steady-state envelope. The remaining three statistics assume that short-term fluctuations are salient perceptual cues in the masked modulation-detection task.

DVs based on local modulation depths [(2) and (5) in the list above] were calculated from a running ratio of the ac to dc envelope energy in each cycle of the signal modulation. More specifically, the max/min ratio was computed for every cycle of the steady-state envelope, and divided by the mean value of the envelope for that same time period. From the resulting 32 points (500 ms of a 64-Hz signal), an average value was computed (in the case of the average local depth DV), or the maximum value was extracted (for the maximum local depth DV).

Because the envelope-frequency spectra of the stimuli were always within the passband of a 64-Hz modulation bandpass filter and a modulation low-pass filter with a cutoff frequency of 150 Hz, there was no filtering applied to the Hilbert envelopes before determining the signal-based decision statistics. In this respect, predictions based on the model IC cell average rate are different from the others: rate MTFs of simulated IC neurons are bandpass. Again, this difference has very limited consequence for the stimuli presented in this study (but see EEE predictions). Only the cell tuned to the signal frequency (64 Hz) was considered. Implementation details for the physiological model were the same as in Nelson and Carney (2004), except the convolution of alpha functions and instantaneous rate functions was carried out in the frequency domain for computational reasons (see website for code: web.syr.edu/~lacarney). Model parameters were matched to those describing the cell in Figs. 8(c), 9-11 in Nelson and Carney (2004), except the auditory-nerve (AN) characteristic frequency (CF) was set to the stimulus carrier frequency (f_c=2800 Hz), and the strength of inhibition (re: excitation) at the level of the IC model cells (S_IC,INH) was set to 1.1. Also, the stimulus presentation level was set to 24 dB SPL for simulations with the model IC cells. This SPL resulted in near-maximal synchrony at the level of model AN fibers (compared to responses at other SPLs), which translates into higher rates in model IC cell responses. Similar responses would be expected from off-CF AN fibers for stimuli presented at higher SPLs [e.g., Joris and Yin (1992), their Fig. 8(c)]. The decision to use low-SPL stimuli as inputs to the physiological model carries with it an assumption that the central nervous system is able to weight responses from peripheral channels that are least affected by saturation and/or compression. Such assumptions are at least indirectly supported by psychophysical work that shows improvements in modulation detection performance as the overall SPL is increased (i.e., Kohlrausch et al., 2000) despite the fact that saturation and compression are likely to be affecting near-CF responses.

FIG. 8.

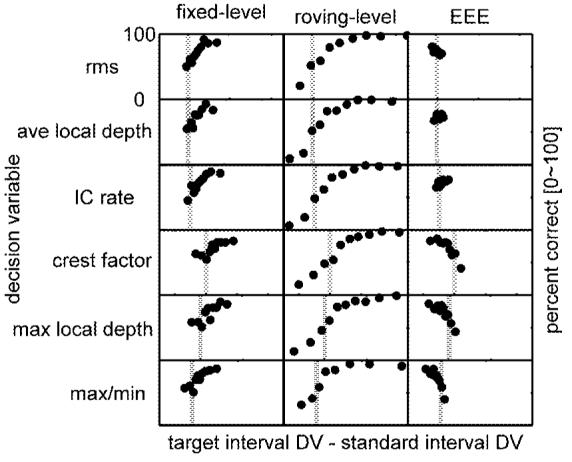
Decision-variable-reconstructed psychometric functions for six DVs and three key masker configurations: fixed-level (-18-dB masker depth; left column), roving-level (masker depths randomly chosen from a 10-dB range centered at -18 dB; middle column), and equal-envelope-energy (-18-dB standard-interval masker depth). The range of differences plotted for each DV was determined by the range covered in the roving-level conditions. The ranges were: envelope rms: [-0.07 0.23]; average local depth: [-0.004 0.013]; model IC cell rate: [-6 18]; crest factor: [-0.3 0.5]; maximum local depth: [-0.01 0.02]; max/min ratio: [-1.46 4.00]. Vertical dashed lines indicate the zero-difference point on the x axis.

Since the stimuli were deterministic, it was necessary to limit model performance in conditions without a masker (pure AM detection, or a masker level of -99 dB) by adding a Gaussian random variable to the final values of the decision statistics in each interval. The variance of this noise was adjusted to yield pure SAM detection thresholds of about -27 dB, and was held constant for all of the experimental conditions once it was determined.

2. Ruling out some potential cues

Several DVs were unable to predict trends or absolute thresholds comparable to those of the listeners in any of the masked-AM detection conditions (except at the lowest masker depths, where the task is essentially pure AM detection). Because of their poor performance in general, simulations based on skewness (the third central moment of the envelope amplitude distribution), kurtosis (the fourth moment), and venelope fluctuations are not included in the figures presented here. Predicted thresholds based on these three DVs were too high, often immeasurable, and also highly variable across the 16 estimates. The skewness of the point-by-point envelope distribution did not reliably change when the sinusoidal signal was added for any of the noise levels in this task. Values of venelope standard deviation and kurtosis consistently decreased when the tone was added, but only at modulation depths much higher than the listeners’ thresholds.

Another decision statistic that was unable to predict performance in the current set of experiments was one based on a quantification of the instantaneous frequency (IF) of the envelope time waveform. A noise-alone modulated carrier would be expected to have higher variability in its envelope IF than that of a tone-plus-noise-modulated carrier. The bandwidth of the modulation maskers (32 Hz), along with external stimulus variability and the use of relatively low modulation depths, made envelope IF an unreliable cue for SAM detection in the present study. Tracking simulations based on a target-interval drop in envelope IF variance resulted in predicted thresholds that were highly variable across tracks and higher than the listeners’ thresholds.

Several recent studies have used a cross-correlation calculation between a template response derived at some suprathreshold signal level and the “current” stimulus representation as a method to quantify model responses and predict psychophysical thresholds (i.e., Dau et al., 1997a, b; Ewert and Dau, 2004). This technique is optimal in the sense that the signal is assumed to be known exactly, both in terms of its magnitude and phase, and has been shown to reasonably predict performance in a wide variety of psychoacoustical experiments, including modulation detection and modulation masking (Dau et al., 1997a, b; 1999). Accounting for performance with such an optimal strategy comes at the expense of being able to identify the specific perceptually relevant features of the stimulus or response. As such, a correlation-based DV is fundamentally different from the other DVs considered in this study. It is interesting to point out that a template-based approach predicts no effect of masker-depth-roving or energy-equalization (simulations not shown). Furthermore, the templates for all three masker conditions (averaged over many noise tokens) are essentially identical: the sinusoidal signal is the only portion of the stimulus that remains after averaging many repetitions of the signal-plus-noise waveform. This aspect of the cross-correlation model contrasts with the tracking simulations and qualitative listener comments that all point to the use of a different cue in the EEE conditions as compared to the fixed-level and roving-level masker conditions.

3. Trial-by-trial response analysis: Decision-variable-reconstructed psychometric functions

The ability of a given decision statistic to track on realistic detection thresholds is necessary but not sufficient as a requirement for concluding that listeners are using the cue on a trial-by-trial basis. To further test each potential cue, several key conditions were analyzed by comparing the values of different DVs that were derived from the exact stimuli presented to the listeners during the tracking procedure. The first step in this analysis (which required no additional time of the listeners) was to save the standard and target interval waveforms as the listeners performed the 2I,2AFC task (in practice, only the MATLAB random number generator seeds were saved). To recreate the stimuli presented during the track, the only other variables needed were the modulation depths of the signal and masker in both intervals, and the masker-level configuration (i.e., fixed, roved, or equal-energy).

The logic behind the decision-variable-reconstructed psychometric (DVRP) functions was as follows: if listeners were using the assumed DV as a primary cue, then their performance should have systematically depended on the magnitude of the difference between the DVs calculated from the two intervals. If there was no difference, performance should have been at chance; for big differences, performance should have been near 100% correct. When percent correct was plotted as a function of the difference in DVs (target interval DV-standard interval DV), two shapes of the DVRP function were possible if the DV was salient and being consistently used by the listeners: monotonically increasing with high values of percent correct at large positive differences, and monotonically decreasing with the best performance when the difference between the target and standard DV was negative (i.e., the presence of the tone modulation was consistently signaled by a lower value of the DV). In general, the sign of the slope of the function indicated whether the signal interval corresponded to the higher or lower value of the DV.

Three representative masker conditions were analyzed with DVRP functions: (1) fixed-level masker (-18 dB rms), (2) roving-level masker (chosen from a uniform distribution from -23 to -13 dB rms, and (3) EEE masker (masker-alone depth of -18 dB rms). To generate each function, responses were combined across the four listeners and four tracks per condition. This resulted in approximately 80 observations per point in each function [16 tracks×∼50 trials per track/10 points (bins) per function]. The spacing of consecutive points was not fixed; instead, a fixed number of responses were placed into unevenly spaced bins. There was no internal noise introduced to construct the DVRP functions; external stimulus variability was the only random factor included.

B. Results and discussion

1. Fixed-level modulation masker

Predictions for each of the decision statistics along with the average listener thresholds for the fixed-level masker condition are shown in Fig. 5. The solid horizontal line in each panel indicates the listeners’ mean threshold with no masker. Dashed lines without symbols in Fig. 5 show corresponding unmasked detection performance for each tested cue, which was determined in the simulations by a fixed-variance noise added to the DVs.

FIG. 5.

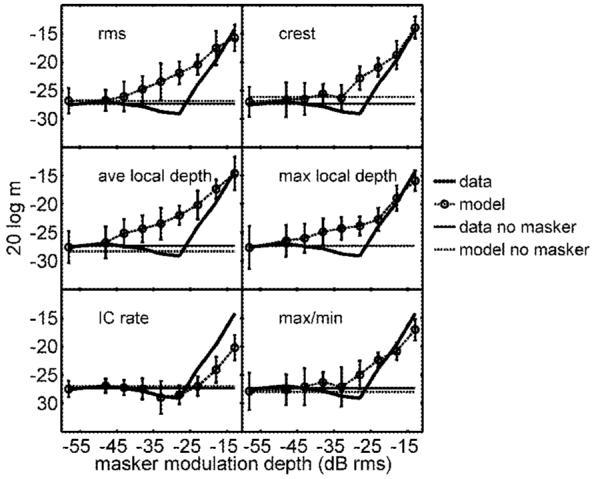
Model thresholds from simulated tracks based on six DVs (o), along with the listeners’ fixed-level data from Fig. 2 (solid lines, no symbols). Unmasked (pure) SAM detection thresholds are shown with the solid horizontal lines. Unmasked model thresholds (thick dashed lines) were set by adding a fixed-variance internal noise to the DV in each interval. Predictions based on long-term DVs are shown in the left column; local temporal features were included in the simulations summarized in the right column.

First, consider the simulated thresholds in the left column of Fig. 5. These DVs (envelope rms, average local modulation depth, and IC cell average rate) make up the subset of the “long-term” statistics that predict performance broadly consistent with that of the listeners. However, each of them has shortcomings, even in this straightforward fixed-masker-level task (in which no detection cues have been manipulated). Average local depth and rms thresholds were almost identical (this is also true for the roving-level and equal-energy conditions), and suffered the same inconsistencies with the data. Specifically, the external variability of the stimulus caused increases in threshold at masker depths considerably lower than in the data. As a result, predicted thresholds based on envelope rms and average local depth were higher than the listeners’ thresholds in the observed “dip” around -30 dB rms. Because the slope of the function was lower in the rms and average depth predictions than it was in the data, the curves reconverged at the highest masker levels tested.

Thresholds based on the average firing rate of a model IC cell are shown in the bottom row of the left column in Fig. 5. This threshold-masker level function distinguishes itself from any of the signal-based DV predictions in two important respects. First, the IC model correctly predicted a nonmonotonic dependence of signal sensitivity on masker modulation depth. Second, simulated thresholds were lower than the data at masker depths above -23 dB. The nonmonotonic shape was a direct result of the “hard” modulation-depth threshold that arises from the strong inhibitory inputs present in the model cell. In the absence of any internal noise or external signal variability, the model IC cell did not respond until the signal modulation depth was above ∼-32 dB. This value was set by the strength of inhibition relative to the excitation: stronger inhibition results in higher thresholds. When an appropriate amount of noise was added to the sinusoidal signal (i.e., at a masker modulation depth of -28 dB rms), the instantaneous modulation depth rose above this hard threshold more often than it did with an equal-amplitude signal in “quiet,” resulting in lower detection thresholds and a pronounced dip in the threshold-masker level function. At higher masker modulation depths (>-23 dB rms), the external variability of the masker swamped out this subtle effect. The fact that the absolute values of thresholds at these higher masker levels were lower in the simulations than in the data does not represent a fatal flaw. In fact, the inclusion of a Weber-fraction-type noise (i.e., one that is proportional to the stimulus or its response, see Ewert and Dau, 2004) would improve the match between model and data at these masker depths. The fit between other DVs and the data would not be improved by including this multiplicative type of internal noise because they predicted thresholds higher than the data, even with “fixed-variance” internal noise alone.

Local temporal features were incorporated in the simulated thresholds shown in the right column of Fig. 5. In general, the fit to the data was slightly better for these DVs than the other signal-based statistics: the overestimation of thresholds in the data’s shallow notch was less severe, especially for the crest factor and max/min DVs. In a sense, it was surprising that predictions based on only two points of the modulating waveform (i.e., the max/min statistic) were more consistent with the listeners’ performance than traditional long-term (rms) measures. Ewert and Dau (2002) showed that a pure long-term cue could account for several trends in the frequency effects of modulation masking, using a masker modulation depth of -10 dB rms. Interestingly, at comparable masker levels in the present study, long-term and local feature cues were all reasonable predictors of modulation detection thresholds (i.e., model thresholds were either similar to or lower than the data). From the thresholds measured here across the range of low masker depths, it seems fair to conclude that predicted performance based on DVs that incorporated temporally local features were as consistent with the listeners’ performance as rms (time-averaged) cues. Implementation of the physiological model suggested a mechanism (namely, a modulation-depth threshold nonlinearity) that could be incorporated into models for envelope processing to account for the nonmonotonicity observed in the listeners’ threshold-masker level functions.

2. Roving-level modulation masker

When the masker modulation depth was randomly chosen from a 10-dB uniformly distributed range of values centered at -18 dB rms on a trial-by-trial basis, mean psychophysical thresholds increased by about 4 dB over the -18-dB fixed-level condition (Fig. 3). We can ask the simple question: how much are thresholds based on these different DVs affected by the same manipulation? Figure 6 answers this question by comparing the fixed-level and roving-level thresholds for each DV (the listeners’ mean data are replotted from Fig. 3 at the far left). The simulated thresholds for fixed-level conditions in Fig. 6 are identical to those illustrated in Fig. 5 at a masker modulation depth of -18 dB rms, but replotted as a signal-to-noise ratio (SNR) for direct comparison to the roving-level condition, where the SNR was the tracking variable. Simulations using long-term DVs are represented in the first three columns to the right of the mean data. Thresholds with various combinations of local features included are shown in the last three pairs of bars.

FIG. 6.

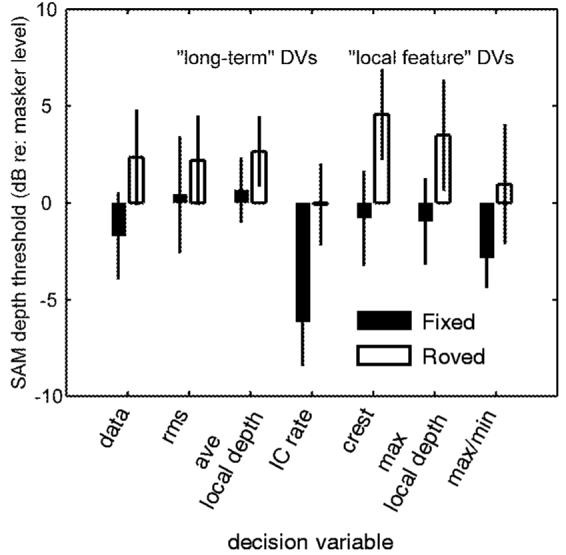
Roving-level masker simulations and comparison with listeners’ mean data. The format is the same as Fig. 3, but the thresholds of different DVs are shown instead of the performance of different listeners.

Two aspects of the simulations are worth noting. First, all six of the tested DVs were affected by an amount that was consistent with the effect seen in the data: thresholds were increased by 2-6 dB when the masker level was roved. Also, thresholds based on the model IC cell’s average firing rate were lower than those obtained with the signal-based statistics. Again, this is not a serious failure of the physiological model. The inclusion of a second noise source, proportional to the magnitude of the stimulus or response fluctuations, would increase thresholds at these (relatively high) masker modulation depths, while maintaining the difference between the fixed-level and roving-level conditions. The other DVs would not benefit from such a modification (with the possible exception of the max/min statistic), as their predicted thresholds were at or above the actual data with a fixed-variance noise source alone.

Despite the subtle differences between the effects predicted by the different DVs, the variability of the threshold estimates with respect to the small observed threshold elevation does not allow for strong conclusions supporting or disputing the validity of a specific DV in the roving-level task. The use of a larger rove range would have potentially produced more pronounced effects that could have critically tested the different DVs; unfortunately, the limited dynamic range that was available in the amplitude-modulation domain for this manipulation did not allow for definitive answers to these questions. In our paradigm, only masker modulation depths that clearly caused masking while also avoiding over-modulation were used.

3. Equalized-envelope-energy modulation masker

Predictions based on each of the tested DVs for the EEE conditions are compared to listeners’ thresholds in Fig. 7 (dashed lines). The fixed-level thresholds are also replotted (solid lines) to provide a baseline for comparison to the EEE thresholds. Actual data are shown in each panel without symbols or error bars; DV predictions are shown with symbols and error bars (◇=EEE; ○=fixed-level). By definition, rms and average-local-depth metrics were unable to track on thresholds in the EEE conditions (the signal-plus-noise modulation depth was adjusted to have the same long-term rms depth as the corresponding noise-alone interval).

FIG. 7.

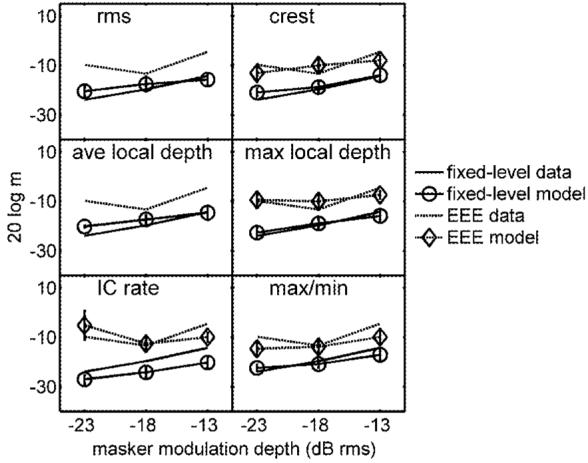
Comparison of measured thresholds (lines with no symbols) and predicted thresholds (connected symbols with error bars) for EEE (dashed lines) and fixed-level conditions (solid lines). DVs are arranged as in Fig. 5. If a given combination of DV and masker condition resulted in overmodulation or tracks that did not converge, simulated thresholds were not plotted (this occurred with the rms and average local depth DVs in EEE conditions).

The only long-term DV that was able to consistently track on a reasonable signal level at threshold was the firing rate of a model IC cell. The predictions of the physiological IC model were comparable to the listeners’ thresholds at masker depths of -18 and -13 dB rms. However, the IC model predicted that the difference between fixed-level and EEE thresholds should decrease with masker depth. This was not observed in the data. The fact that the IC rate DV could predict EEE thresholds at all was a result of the effective bandpass envelope filtering that preceded the decision device. Although the bandwidth of the stimuli was within the passband of the filter (the half-rate Q value is about 1, corresponding to a 64-Hz passband for the cell tuned to the signal modulation frequency), the resulting output spectra were nevertheless shaped by the cell’s modulation-tuning properties. There was less attenuation of the energy concentrated near the peak of the modulation filter, so target-interval stimuli in the EEE conditions could elicit a larger response (higher firing rate) than the standard-interval stimuli. A similar effect would be expected for a rms DV following any realistic envelope bandpass filtering process. Still, such a cue did not predict the appropriate variation in EEE thresholds with masker depth, and the absolute difference between fixed-level and EEE thresholds was higher than observed in the data. The use of an invariant cue across all conditions was also not consistent with listeners’ anecdotal reports suggesting that their strategy was very different between the fixed-level and equal-energy conditions.

The DVs that were the best predictors of the listeners’ EEE data were those based on local temporal envelope features (Fig. 7, right column). Max/min, crest factor, and max local depth all accounted reasonably well for the difference in performance between the fixed-level and EEE thresholds as well as the absolute values of the thresholds and the higher variability associated with the EEE data. Importantly, the decision rule had to be switched for these three statistics: simulations selected the interval with the larger value of the DV in fixed-level conditions and the interval with the smaller value in EEE conditions as the target interval. This signflipping was qualitatively consistent with subjective accounts from the listeners that they had developed a different strategy (based on feedback) in the EEE paradigm: often the “smoother” or “more regular” envelope was reportedly chosen as the signal interval. Given this, the success of the local feature statistics in predicting the data was somewhat surprising, since the calculations were all heavily weighted by a small temporal portion of the envelope waveform. Nevertheless, the match to the data was quite good, and it was clear that the most straightforward way to account for the listeners’ performance in the EEE conditions was to incorporate information about local fluctuations into the decision device. The finding that local temporal features were crucial for explaining the EEE data was different than the conclusions drawn from analogous audio-frequency energy-equalized TIN detection tasks (i.e., Richards and Nekrich, 1993), in which the overall flattening of the (long-term) envelope when a tone was added could explain performance consistent with that of the listeners. The corollary cue in the current experiment would be a drop in the (long-term) venelope energy, which we determined to be incapable of predicting performance consistent with the listeners.

4. Decision-variable-reconstructed psychometric functions

As an alternative method to compare and contrast different DVs (beyond predicting thresholds), we analyzed trial-by-trial decisions made by the listeners and considered how those choices correlated with the magnitude and direction of variation in each DV between the two stimuli presented to the listener. Figure 8 shows DVRP functions for three masker conditions and six DVs. The masker modulation depth for all of the conditions shown was nominally -18 dB rms (note that this value was randomly chosen from a 10-dB range in the roving-level conditions, and was effectively attenuated in the target interval for the EEE conditions). Fixed-level results are contained in the first column; rovinglevel and EEE analyses are shown in the second and third columns, respectively. The vertical dashed line in each panel indicates the point where the target and standard DVs were the same (i.e., their difference was zero). The ordinate limits are set at 0 and 100% correct in each panel. The x axes are fixed for each DV; they were determined by the largest range of variation observed across the three conditions (usually the roving-level case; see the figure caption for exact values).

DVRP functions for the fixed-level condition (left column) can be placed in one of two categories. The first three DVs (ac-coupled envelope rms, average local depth, and IC rate) all showed a consistent increase in percent correct as the target interval DV became larger than the DV measured in the corresponding standard interval. Also, these three cues were typically not “confused” by the task: the vast majority of the trials resulted in a positive difference between target and standard DV.

The second group of statistics is made up of DVs based on local temporal features (crest factor, max local depth, and max/min ratio). Listeners’ percent correct increased for positive differences (target DV>standard DV) as they did for the long-term statistics in the top three rows, but a higher proportion of trials resulted in standard-interval DVs that were larger than the target-interval DVs (>20%; represented by points to the left of the vertical dashed line). This confusion suggested that long-term DVs may have been more reliable cues in the fixed-level masker conditions, because they were less susceptible to changes in local features caused entirely by the stochastic nature of the maskers.

Roving-level masker DVRP functions (Fig. 8, middle column) spanned a wider range of DV differences than fixed-level or EEE-masker conditions, as expected. Because the roving-level DVRP functions were qualitatively similar, none of the six DVs (Fig. 8, middle column) can be considered more or less consistent than any of the others in this paradigm. In about one-quarter of the trials, percent correct dropped below chance (50%) when the cue in the standard interval was bigger than that in the target interval for all six of the tested DVs. It would be possible for the functions to be symmetric about zero if the listeners recognized conditions where the level-roving caused such a reversal in cue direction. This was not seen in any of the DVRP functions; the listeners tended to choose the interval with the larger DV value, regardless of the particular random combination of standard and target masker level. The similarity of the DVRP functions for the roving-level results makes it difficult to point out one DV as being more consistent with the data. Similar conclusions were made with the roving-level threshold-tracking simulations (Fig. 6).

The target-interval rms modulation depth was normalized to match that of the standard interval in the EEE conditions. DVRP functions for a -18-dB EEE masker are shown in the right column of Fig. 8. Compared to the fixed- and roving-level cases, the spread of DV differences is highly compressed for rms, average local depth, and IC rate decision statistics (Fig. 8, top three panels, right column). This reflects the stimulus manipulation; the fact that there was any spread in the rms DVRP was because only the steady-state portion (the central 500 ms) of the stimulus was used to compute the DVs, while the entire duration of modulation was equalized in the stimuli presented to the listeners (including the onset and offset ramps). Still, there were no strong trends in the upper three EEE DVRP functions of Fig. 8: percent correct was nearly independent of the DV difference, which was always close to zero. The situation was different for the local-feature-based DVs (bottom-right three panels in Fig. 8). High signal modulation depths resulted in low values of crest factor, max local depth, and max/min ratio. The tracking simulations (Fig. 7) and DVRP functions suggested that listeners were using a drop in the value of a DV that incorporated some local feature; max/min ratio predicted absolute thresholds that were slightly closer to the listeners’ thresholds than crest factor or max local depth.

Analysis of DVRP functions provided a different angle on the same question that was addressed with the tracking simulations; the consistency between the two approaches is reassuring. The technique is promising for pulling apart decision statistics in other psychophysical tasks that include external stimulus variability, especially those with competing DVs that are weakly correlated with one another. The procedure requires no assumptions to be made about internal noise, and no additional time from the listeners. Analysis of adaptive tracking procedure responses has previously been validated as an efficient and accurate way to extract psychometric functions (Dai, 1995); the current implementation simply considered statistics based on the actual stimuli presented, instead of the signal level, or modulation depth, presented in each trial. In the context of the current simulations, two specific and important pieces of information are reinforced with the DVRP functions. First, they reiterate the notion that the sign or direction of the cue flips in EEE conditions for the local-feature DVs with respect to the direction of the cue in fixed- and roving-level masker conditions. Second, the proportion of DV calculations that elicit a larger value in the standard interval in the fixed-level conditions is higher for the short-term DVs than for the long-term DVs.

IV. GENERAL DISCUSSION

The remainder of this article is divided into three parts. In the first section, potential mechanisms underlying specific features of the fixed-level results are further discussed. Directions for future work are then detailed. Finally, the key psychophysical and modeling results are summarized.

A. Negative masking

The nonmonotonic relationship between sensitivity and noise level apparent in two of the four listeners in the fixed-level masker condition (Fig. 2) can be interpreted as stochastic resonance (for a recent review, see Wiesenfeld and Jaramillo, 1998). There are (at least) two straightforward mechanisms that could underlie such an effect. One possible explanation is that the listeners used a nonoptimal criterion that remained constant across noise level [see Tougaard (2000) for an analysis of such an assumption]. This interpretation is less than satisfying for several reasons. First, the presence of the nonmonotonicity is not related to the listeners’ pure AM-detection thresholds (with no masker). If the effect was simply an epiphenomenon of poor criterion placement, the two listeners whose data suggest stochastic resonance should have been less sensitive than the other listeners at low masker depths. Another problem with the poor-criterion explanation is related to the types of mistakes that such a mechanism would predict. In low-masker-level conditions, the fixed DV criterion is never reached, and as a result, the signal is never “perceived” as being present. The opposite is true for the high masker levels, where even the noise-alone DV distribution lies above the fixed criterion: the above explanation suggests that the signal should sound as though it is present on every trial. These bias-related observations are also inconsistent with subjective impressions given by the listeners, and they suggest that some other mechanism may underlie the stochastic resonance effects.

Another mechanism that can explain the nonmonotonicity in our data is based on a combination of weak signals and a threshold nonlinearity (i.e., Ward et al. 2002). If a system does not respond to a subthreshold periodic stimulus, the addition of noise may push the input amplitude above threshold at a mean frequency related to the periodicity of the weak signal. An example of such a system with an envelope (modulation-depth) threshold is the physiological model tested here (Nelson and Carney, 2004). The ability of such a simple model to account for the effect highlights the potential advantages of using physiologically motivated model front-ends when predicting psychophysics to gain insight into underlying mechanisms. In addition to modeling work, there is also direct physiological evidence suggesting that central auditory neurons respond in a way consistent with a modulation-depth threshold device. Adding a low-level noise modulation to a sinusoidal AM can both enhance neural synchronization to the tone and increase average firing rate over responses to the SAM tone alone in the frog auditory midbrain (Bibikov, 2002). The negative masking effects observed in the current study are also likely related to similar psychophysical measures in cochlear implant listeners of masked (electrically stimulated) modulation detection thresholds (e.g., Chatterjee and Robert, 2001).

B. Future directions

A main focus of future work will be to quantitatively relate actual (as opposed to modeled) midbrain physiological responses to psychophysical performance in AM detection tasks. To date, the relative roles of timing (i.e., synchronization to the envelope) and average rate information as neural substrates for AM perception at low modulation depths (near behavioral thresholds) remain unclear. The rate versus timing debate can be thought of as a discussion of underlying neural DVs, similar to the classifications of signal-based DVs as long-term or local-feature-containing. It is typically assumed that information about AM is largely transformed into an average-rate-based scheme by the level of the IC (which is one reason we only considered the rate responses of our model IC cell here), but the majority of the data supporting that view comes from stimuli with high modulation depths (for a review, see Joris et al., 2004). The fact that our listeners could perform the EEE task suggests that the local temporal structure of AM stimuli is available as a cue under certain conditions. To reconcile these inconsistencies, we are currently recording responses in the awake rabbit IC to both pure SAM and noise-masked SAM across a wide range of modulation depths (from -35 to 0 dB in 20 log m).

Another issue that deserves further study is the effect of including a “Weber-fraction noise,” along with the fixed-variance internal noise that was used here to limit performance with deterministic stimuli. Existing data suggest that tone-carrier AM-depth discrimination sensitivities may be determined by a fixed-variance noise at low modulation depths and a noise that is proportional to the elicited response at high modulation depths (i.e., Ewert and Dau, 2004). Assuming that the listeners were using an overall depth-related cue, then the fixed-level masker SAM detection paradigm can be thought of as depth discrimination task, with both external and internal noise processes playing a role. At the highest masker depths tested (-13 dB rms), most of the DV-derived thresholds are at or below the listeners’ data (Fig. 5), suggesting the need for an additional source of noise at high modulation depths. This is consistent with the findings from the AM-depth discrimination literature. To better account for all of the data presented here, it seems necessary to implement a model with a modulation depth threshold, along with some form of local feature detection and two types of internal noise (fixed-variance and Weber-fraction).

C. Summary

1. SAM depth thresholds in an on-frequency masked AM-detection task were influenced by external stimulus variability at very low masker modulation depths (i.e., -40 to -30 dB rms). Negative masking, or stochastic resonance, was observed in two of the four listeners at masker levels around -30 dB rms (Fig. 2).

2. Roving the overall modulation depth (Fig. 3) or equalizing the long-term envelope energies (Fig. 4) from trial to trial both resulted in significant increases in threshold. These findings contrast with observations in comparable TIN detection tasks in the audio-frequency domain.

3. Tracking simulations showed that several competing DVs were able to qualitatively account for performance for the fixed-level (baseline) and roving-level masker conditions (Fig. 5).

4. Reconstruction of psychometric functions based on a variety of DVs revealed that long-term statistics (averaged across the entire stimulus duration) may have been more robust cues in the fixed-level condition than statistics based on local temporal features. This was inferred because of the larger proportion of trials that resulted in the standard interval DV being larger than the corresponding target interval DV when local features were assumed to be the primary detection cues (Fig. 8).

5. Thresholds in the EEE conditions could only be accounted for with a “local feature” DV, as long-term cues were minimized by equalizing the overall energy of the standard and target envelopes, after the sinusoidal signal was added. Listeners apparently chose the interval with a lower max/min ratio, crest factor, maximum local depth, or some other local feature cue in these conditions (Fig. 7).

6. Implementing a physiologically motivated model structure and comparing predictions based on its rate responses to the fixed-level data showed that a hard modulation-depth threshold mechanism can predict negative masking at low masker depths. This suggests that such a nonlinearity could be included (along with an internal noise source) to limit performance in the absence of external variability in a more complete model of envelope processing (Fig. 5).