Robust dynamic classes revealed by measuring the response function of a social system

Abstract

We study the relaxation response of a social system after endogenous and exogenous bursts of activity using the time series of daily views for nearly 5 million videos on YouTube. We find that most activity can be described accurately as a Poisson process. However, we also find hundreds of thousands of examples in which a burst of activity is followed by an ubiquitous power-law relaxation governing the timing of views. We find that these relaxation exponents cluster into three distinct classes and allow for the classification of collective human dynamics. This is consistent with an epidemic model on a social network containing two ingredients: a power-law distribution of waiting times between cause and action and an epidemic cascade of actions becoming the cause of future actions. This model is a conceptual extension of the fluctuation-dissipation theorem to social systems [Ruelle, D (2004) Phys Today 57:48–53] and [Roehner BM, et al., (2004) Int J Mod Phys C 15:809–834], and provides a unique framework for the investigation of timing in complex systems.

Uncovering rules governing collective human behavior is a difficult task because of the myriad of factors that influence an individual's decision to take action. Investigations into the timing of individual activity, as a basis for understanding more complex collective behavior, have reported statistical evidence that human actions range from random (1) to highly correlated (2). Although most of the time, the aggregated dynamics of our individual activities create seasonal trends or simple patterns, sometimes our collective action results in blockbusters, best sellers, and other large-scale trends in financial and cultural markets.

Here, we attempt to understand this nontrivial herding by investigating how the distribution of waiting times describing individuals' activity (3) is modified by the combination of interactions (4) and external influences in a social network. This is achieved by measuring the response function of a social system (5) and distinguishing whether a burst of activity was the result of a cumulative effect of small endogenous factors or, instead, the response to a large exogenous perturbation. Looking for endogenous and exogenous signatures in complex systems provides a useful framework for understanding many complex systems and has been successfully applied in several other contexts (6).

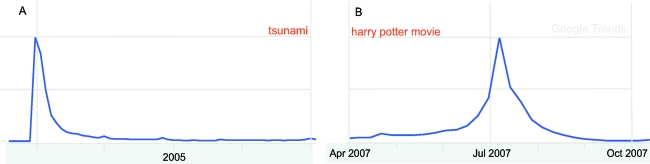
As an illustration of this distinction in a social system, consider the example of trends in queries on internet search engines (http://trends.google.com) in Fig. 1, which shows the remarkable differences in the dynamic response of a social network to major social events. For the “exogenous” catastrophic Asian tsunami of December 26th, 2004, we see that the social network responded suddenly. In contrast, the search activity surrounding the release of a Harry Potter movie has the more “endogenous” signature generated by word of mouth, with significant precursory growth and an almost symmetric decay of interest after the release. In both “endo” and “exo” cases, there is a significant burst of activity. However, we expect to be able to distinguish the post peak relaxation dynamics on account of the very different processes that resulted in the bursts. Furthermore, we expect the relaxation process to depend on the interest of the population because this will influence the ease with which the activity can be spread from generation to generation.

Fig. 1.

Search queries as a proxy for collective human attention. (A) The volume of searches for the word “tsunami” in the aftermath of the catastrophic Asian tsunami. The sudden peak and relatively rapid relaxation illustrates the typical signature of an “exogenous” burst of activity. (B) The volume of search queries for “Harry Potter movie.” The significant growth preceding the release of the film and symmetric relaxation is characteristic of an “endogenous” burst of activity.

To translate this qualitative distinction into quantitative results, we describe a model of epidemic spreading on a social network (7) and validate it with a dataset that is naturally structured to facilitate the separation of this endo/exo dichotomy. Our data consist of nearly 5 million time series of human activity collected subdaily over 8 months from the fourth most visited web site [YouTube (http://youtube.com., according to Alexa.com)]. At the simplest level, viewing activity can occur one of three ways: randomly, exogenously (when a video is featured), or endogenously (when a video is shared). This provides us with a natural laboratory for distinguishing the effects that various impacts have and allows us to measure the social “response function.”

The Model

Various factors may lead to viewing a video, which include chance, triggering from email, linking from external websites, discussion on blogs, newspapers, and television, and from social influences. The epidemic model we apply to the dynamics of viewing behavior on YouTube uses two ingredients whose interplay captures these effects.

The first ingredient is a power law distribution of waiting times describing human activity (2,3,8) that expresses the latent impact of these various factors by using a response function, which, on the basis of previous work (9,10,11), we take to be a long-memory process of the form

By definition, the memory kernel φ(t) describes the distribution of waiting times between “cause” and “action” for an individual. The cause can be any of the above mentioned factors. The action is for the individual to view the video in question after a time t since she was first subjected to the cause without any other influences between 0 and t, corresponding to a direct (or first-generation) effect. In other words, φ(t) is the “bare” memory kernel or propagator, describing the direct influence of a factor that triggers the individual to view the video in question. Here, the exponent θ is the key parameter of the theory that will be determined empirically from the data.

The second ingredient is an epidemic branching process that describes the cascade of influences on the social network. This process captures how previous attention from one individual can spread to others and become the cause that triggers their future attention (12). In a highly connected network of individuals whose interests make them susceptible to the given video content, a given factor may trigger action through a cascade of intermediate steps. Such an epidemic process can be conveniently modeled by the so-called self-excited Hawkes conditional Poisson process (13). This gives the instantaneous rate of views λ(t) as

where μ_i is the number of potential viewers who will be influenced directly over all future times after t_i by person i who viewed a video at timet_i. Thus, the existence of well connected individuals can be accounted for with large values of μ_i. Lastly, V(t) is the exogenous source, which captures all spontaneous views that are not triggered by epidemic effects on the network.

Predictions of the Model: Dynamic Classes

According to our model, the aggregated dynamics can be classified by a combination of the type of disturbance (endo/exo) and the ability of individuals to influence others to action (critical/subcritical), all of which is linked by a common value of θ. The following classification of behaviors emerges from the interplay of the bare long-memory kernel φ(t) given by Eq. 1 and the epidemic influences across the network modeled by the Hawkes process Eq. 2.

• Exogenous Subcritical. When the network is not “ripe” (that is, when connectivity and spreading propensity are relatively small), corresponding to the case when the mean value 〈μ_i〉 is <1, then the activity generated by an exogenous event at time t_c does not cascade beyond the first few generations, and the activity is proportional to the direct (or “bare”) memory function φ(t − t_c):

  
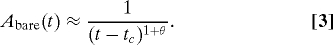
• Exogenous Critical. If instead, the network is ripe for a particular video, i.e., 〈μ_i〉 is close to 1, then the bare response is renormalized as the spreading is propagated through many generations of viewers influencing viewers influencing viewers and so on, and the theory predicts the activity to be described by ref. 7:

  
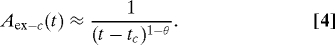
• Endogenous Critical. If in addition to being ripe, the burst of activity is not the result of an exogenous event, but is instead fueled by endogenous (word-of-mouth) growth, the bare response is renormalized giving the following time dependence for the view count before and after the peak of activity (7):

  
• Endogenous Subcritical. Here, the response is largely driven by fluctuations and not bursts of activity. We expect that many time series in this class will obey a simple stochastic process.

  

  where η(t) is a noise process.

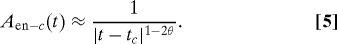
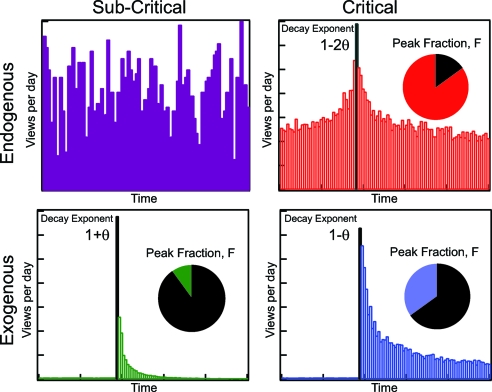
The dynamics described by the above classifications are illustrated in Fig. 2.

Fig. 2.

A schematic view of the four categories described by our models: Endogenous-subcritical (Upper Left), Endogenous-critical (Upper Right), Exogenous-subcritical (Lower Left), and Exogenous-critical (Lower Right). The theory predicts the slope of the response function conditioned on the class of the disturbance (exogenous/endogenous) and the susceptibility of the network (critical/subcritical). Also shown schematically in the pie chart is the fraction of views contained in the main peak relative to the total number of views for each category. This is used as a simple basis for sorting the time series into three distinct groups for further analysis of the exponents.

Predictions of the Model: Peak Fraction

In addition to these dynamic classes, the model predicts, by construction, a relationship between the fraction of views observed on the peak day compared with the total cumulative views (Fig. 2 Inset), henceforth referred to as “peak fraction” or F. This simple observation turns out to be a useful metric for grouping time series into categories based on whether they are endogenous or exogenous. For the exogenous subcritical class, the absence of precursory growth and fast relaxation following a peak imply that close to 100% of the views are contained in the peak. For the exogenous critical class, the fractional views in the peak should be smaller than the previous case on account of the content penetrating the network resulting in a slower relaxation. Finally, for the endogenous critical class, significant precursory growth followed by a slow decay imply that the fractional weight of this peak is very small compared with the total view count.

Results

We find that most videos' dynamics (≈90%) either do not experience much activity or can be described statistically as a Poisson process (verified using a Chi-Squared test). This large set of data is consistent with the endo-subcritical classification. For the remaining 10% (≈500,000 videos), we find nontrivial herding behavior that accurately obeys the three power-law relations described above. Characteristic examples of endogenous and exogenous dynamics are shown in Fig. 3.

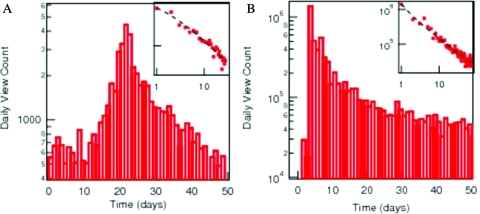
Fig. 3.

An illustration of the typical response found in hundreds of thousands of time series on YouTube. (A) The endogenous-critical class is marked by significant precursory growth followed by an almost symmetric relaxation. (B) The exogenous-critical class is marked by a sudden burst of activity followed by a power-law relaxation. (Inset) The post~peak relaxation on log–log scale, revealing the power-law behavior that lasts over months for both classes.

For these videos that experience bursts, we extract the relaxation exponents using a least-squares fit on the logarithm of the data over a window of 10 days after the peak. This procedure is repeated for all possible window sizes ranging from 10 to 224 days. The “best” window is then chosen to be the largest number of days over which one can assume that the residuals of the percent deviation from the best fit are normally distributed. Once this assumption is violated at the 1% level, which occurs when the dynamics are no longer governed by Eqs. 3, 4, or 5, the fit is stopped. Although estimation of scaling laws is a subtle and controversial issue (13,14), this procedure has been extensively tested by using synthetic data and is able to sufficiently recover exponents with an accuracy of ±0.1.

An unconditional examination of the distribution of these exponents (Fig. 4, black line, large dashes) reveals the existence of a bimodal distribution with one peak near 0.2 and a second broader peak between 0.5 and 0.6, suggesting the existence of at least two dynamic classes. In order to obtain a more detailed test of the predictions of our model, we calculate the fraction F of views on the most active day compared with the total count as described above and sort the time series into three classes:

1. Class 1 is defined by 80% ≤ F ≤ 100 %.

2. Class 2 is defined by 20% < F < 80%.

3. Class 3 is defined by 0% ≤ F ≤ 20%.

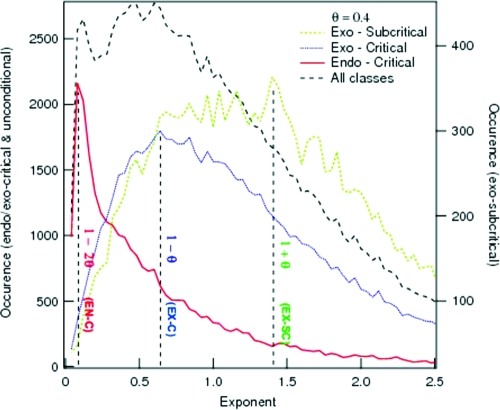
Fig. 4.

Histogram of all of the exponents of the power-law relaxation ∼ 1/t^p of the view counts following a peak (black dashed line). The bimodal distribution provides evidence of the existence of at least two dynamic classes in the absence of conditioning. A more refined analysis based on the peak fraction F reveals three distinct distributions belonging respectively to Class 1 (dashed green line), Class 2 (dotted blue line) and Class 3 (continuous red line). The predicted values for the exogenous subcritical class (Eq. 3), exogenous critical class (Eq. 4) and for the endogenous critical class (Eq. 5) are shown by the vertical dashed lines with their quantitative values determined with the choice θ = 0.4.

Should our model have any informative power, we should find a correspondence

• Class 1 ↔ Exogenous subcritical

• Class 2 ↔ Exogenous critical

• Class 3 ↔ Endogenous critical.

Based on this simple classification, we show in Fig. 4 the histogram of exponents characterizing the power law relaxation ≈ 1/t^p. The exponents in these classes cluster into three distinct groups with the most probable exponent in each class given respectively by p ≈ 1.4, 0.6, and 0.2. These values are compatible with the predictions Eqs. 3–5 of the epidemic model with a unique value of θ = 0.4 ± 0.1.

The existence of the exogenous critical (Class 2) and endogenous critical (Class 3) are unaffected by the choice of class boundaries, as one can see by examining the unconditional distribution of exponents in Fig. 4. However, the question of existence of a distinct exogenous-subcritical class requires more attention, because this class has a very poorly defined peak in its distribution (Fig. 4, small green dashes). To this end, we have examined the stability of this distribution with respect to changes in F. We find that although this distribution is very broad, the weight of the distribution is concentrated between p=1.0 and p=1.5—much higher than the exogenous-critical class—and the bulk features are insensitive to changes once F is >70%. As the lower boundary of F for Class 1 is increased further toward 100%, the weight of the distribution continues to shift toward larger exponents and always maintains its most probable value (i.e. peak in its distribution) between 1.25 < p < 1.40, in good agreement with the predictions of the model.

As a further test of whether the exponents actually cluster into distinct classes or are instead only negatively correlated with F, we have performed a fuzzy clustering analysis following ref. 16 in the 2D plane (F, p) and find the centroids of the three main clusters at exponent values of 0.22 (with F=6.5%), 0.58 (with F=45%), and 1.42 (with F=56%), a result that is also visible to the naked eye (data not shown). That the clustering analysis recovers exactly the results found by a much simpler analysis based on the simple classification on the peak fraction F (0% ≤ F ≤ 20%, 20% < F < 80%, 80% ≤ F ≤ 100 %) provides additional support for the existence of the dynamic classes proposed by our model.

Having empirically extracted a value for the key parameter θ of the model and having verified the existence of three main classes with interesting structured relaxations, we can further test the model with the last distinctive property not yet exploited, namely the preshock dynamics. We check this by performing a peak-centered, aggregate sum for all videos with exponents near 1.4, 0.6, or 0.2, with the intent of visualizing the characteristic time evolution of each class. Each time series is first normalized to 1 to avoid a single video from dominating the sum, and the final result is divided by the number of videos in each set so we can compare the three classes. The model predicts, and we indeed observe in Fig. 5, that videos whose post peak dynamics are governed by small exponents have significantly more precursory growth. One also sees very little precursory growth for the two exogenous classes. Because, by construction, our selection of videos was based on the exponent characterizing the relaxation after the peaks, this test on the precursory behavior before the peaks provides a remarkable independent validation of the epidemic model.

Fig. 5.

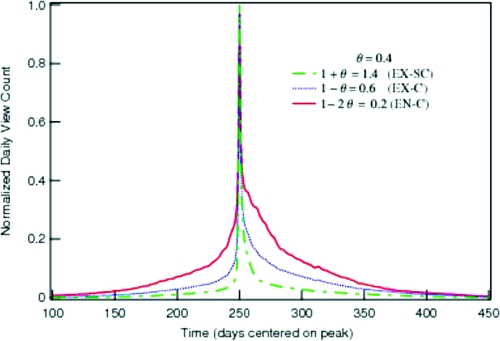
Test of the precursory dynamics. The (endogenous/exogenous) and (critical/subcritical) classification is based on measuring the exponent governing the relaxation after a peak. However, the epidemic branching model also predicts significant precursory growth before a peak for the endogenous class with p centered on 1 − 2θ≈ 0.2 and no precursory growth for the two exogenous classes. The figure shows the peak-centered, aggregate sum for all videos with exponents near either 1.4 (ex-sc), 0.6 (ex-c), or 0.2 (en-c). We observe that videos classified as endogenous-critical (continuous red line) on the basis of their relaxation exponent, indeed have significantly more precursory growth. We also see very little precursory growth for the two exogenous classes.

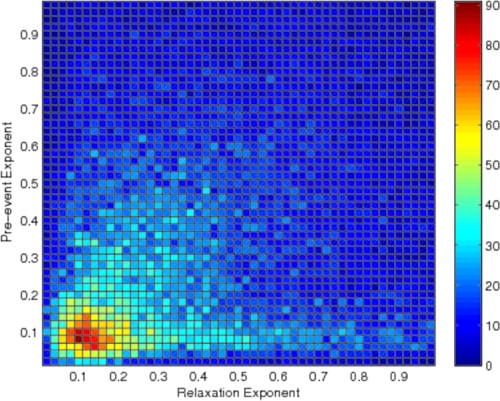
The model goes further and predicts that the precursory acceleration of views culminating in an endogenous critical peak should be also a power law with the same exponent 1 − 2 θ as the relaxation after the peak. Fig. 6 shows a plot of pre-event exponent versus relaxation exponent for all time series. Although the test of whether the pre-event and post-event exponents are identical is, according to the model, applicable only to the videos in the endogenous-critical class, we have performed the analysis of the pre-event exponents on the full dataset to avoid any selection bias in analyzing the data. We find that the highest density of exponents cluster around p ≈ 0.15 for both the pre- and post-peak exponent. This result provides support that p ≈ 0.15 is correctly associated with the endogenous-critical class, independent of our previous methods of analysis, because this class has the largest number of videos satisfying the predicted exponent equality. An additional result of this analysis is that our algorithm failed to measure an exponent very often for time series classified as exogenous (i.e. having a relaxation exponent p > 0.6). There were two common reasons that our algorithm failed to extract a pre-event exponent. The first was a result of not having enough data preceeding an event. This is consistent with videos in the exogenous class because their peaks often occur shortly after the videos are uploaded to the site. The second reason was a result of not being able to fit an exponent to the data, which occurs when the data are not of the form 1/t^p, again consistent with the definition of an exogenous peak.

Fig. 6.

2D Histogram of the pre-event and relaxation exponents for the 54,312 time-series whose preevent exponent is defined. The highest density of points cluster near p = 0.15. This not only provides evidence that the preevent and relaxation exponents are equal within the precision of our analysis algorithm, but provides independent support that we have correctly identified the endogenous-critical class, since this class has the largest number of videos satisfying the predicted exponent equality.

Discussion

These results provide direct evidence that collective human dynamics can be robustly classified by epidemic models and understood as the transformation of the distribution of individual waiting times by collective cascades propagating through word-of-mouth. One of the strong points validating the proposed epidemic model of social influence is that the various classes are related by a single common parameter θ. Its numerical value determined here (θ = 0.4 ± 0.1) is close to what has been found in other studies (12), suggesting a common origin, perhaps in the psychology of time perception in humans (17).^‡ From the view point of the epidemic word-of-mouth model, θ controls the persistence of external perturbations both at the individual and collective level. Paradoxically, when the social network is at criticality, the faster the individual response function to an external shock (larger θ within the interval 0 ≤ θ < 1), the slower and more persistent is the collective response.

In addition to these results, understanding collective human dynamics opens the possibility for a number of tantalizing applications. It is natural to suggest a qualitative labeling that is quantitatively consistent with the three classes derived from the model: viral, quality, and junk videos. Viral videos are those with precursory word-of-mouth growth resulting from epidemic-like propagation through a social network and correspond to the endogenous critical class with an exponent 1 − 2θ. Quality videos are similar to viral videos but experience a sudden burst of activity rather than a bottom-up growth. Because of the “quality” of their content, they subsequently trigger an epidemic cascade through the social network. These correspond to the exogenous critical class, relaxing with an exponent 1 − θ. Last, junk videos are those that experience a burst of activity for some reason (spam, chance, etc.) but do not spread through the social network. Therefore, their activity is determined largely by the first generation of viewers, corresponding to the exogenous subcritical class, and they should relax as 1/t^1+θ. Although one might argue that these labels are inherently subjective, they reflect the objective measure contained in the collective response to events and information. This is further supported by the average number of total views in each class, which is largest for “viral” (33,693 views) and smallest for “junk” (16,524 views), as one would expect for these arguments.

Although the above description applies to videos, one could extend this technique to the realm of books (9,12), movies, and other commercial products, perhaps using sales as a proxy for measuring the relaxation of individual activity. The proposed method for classifying content has the important advantage of robustness because it does not rely on qualitative judgment, using information revealed by the dynamics of the human activity as the referee. More importantly, the method does not rely on the magnitude of the response because of the scale-free nature of the relaxation dynamics. This implies that identification of relevance—or lack of relevance—can be made for content that has mass appeal, along with that which appeals to more specialized communities. Furthermore, this framework could be used to provide a quantitative measure of the effectiveness of marketing campaigns by measuring the sales response to an exogenous marketing event.

A tenant of complex systems theory is that many seemingly disparate and unrelated systems actually share an underlying universal behavior. In the digital age, we now have access to unprecedented stores of data on human activity. This data is usually almost trivial to acquire—in both time and money—when compared with “traditional” measurements. If the complex behavior in social systems is shared by other complex systems, then our approach, which disentangles the individual response from the collective, may provide a useful framework for the study of their dynamics.