WND-CHARM: Multi-purpose image classification using compound image transforms

Abstract

We describe a multi-purpose image classifier that can be applied to a wide variety of image classification tasks without modifications or fine-tuning, and yet provide classification accuracy comparable to state-of-the-art task-specific image classifiers. The proposed image classifier first extracts a large set of 1025 image features including polynomial decompositions, high contrast features, pixel statistics, and textures. These features are computed on the raw image, transforms of the image, and transforms of transforms of the image. The feature values are then used to classify test images into a set of pre-defined image classes. This classifier was tested on several different problems including biological image classification and face recognition. Although we cannot make a claim of universality, our experimental results show that this classifier performs as well or better than classifiers developed specifically for these image classification tasks. Our classifier’s high performance on a variety of classification problems is attributed to (i) a large set of features extracted from images; and (ii) an effective feature selection and weighting algorithm sensitive to specific image classification problems. The algorithms are available for free download from openmicroscopy.org.

1. Introduction

The increasing use of digital imagery in many fields of science and engineering introduces a demand for accurate image analysis and classification. Applications include remote sensing (Smith & Li, 1999), face recognition (Shen & Bai, 2006; Jing & Zhang, 2004; Pentland & Choudhury, 2000) and biological and medical image classification (Boland & Murphy, 2001; Awate et al., 2006; Cocosco, Zijden-bos & Evans, 2004; Ranzato et al., 2007). Although attracting considerable attention in the past few years, image classification is still considered a challenging problem in machine learning due to the very complex nature of the subjects in real-life images, making quantitative similarity measures difficult.

A common approach to quantitatively measure similarity between images is to extract and analyze a set of low-level image features (Heidmann, 2005; Gurevich & Koryabkina, 2006). These can include color (Stricker & Orengo, 1995; Funt & Finlayson, 1995; Tieu & Viola, 2004), texture (Smith & Chang, 1994, 1996; Livens et al., 1996; Ferro & Warner, 1995), shape (Mohanty et al., 2005), histograms (Flickner et al., 1995; Chapelle, Haffner & Vapnik, 1999; Qiu, Feng & Fang, 2004) and more. However, image features perform differently depending on the image classification problem (Gurevich & Koryabkina, 2006), making the accuracy of a task-specific image classifier limited when applied to a different imaging task.

The performance of task-specific classifiers in problems they were not originally designed for can often be inadequate, introducing a significant barrier to using automated image classification in science and engineering. New image classification problems are continually emerging in these fields, requiring the continual development and optimization of new image classifiers to specifically address these problems. The knowledge and experience needed to successfully implement such vision systems are not typically available to an experimentalist or application developer who does not specialize in image analysis or pattern recognition.

The proliferation of imaging problems and classifiers to address them is acute in the field of Cell Biology. The range of instrumentation and imaging modes available for capturing images of cells multiplexed with the variety of morphologies exhibited by cells and tissues preclude a standard protocol for constructing problem-specific classifiers. There are very few “standard problems” in Cell Biology: Identification of specific sub-cellular organelles is an important exception, but the vast majority of experiments where image classification would be an invaluable tool do not fall into standard problem types. The advent of High Content Screening (HCS) where the goal is to search through tens of thousands of images for a specific target morphology requires a flexible classification tool that allows any morphology to be used as a target. Since the variety of target morphologies is vast, a general image classification tool is required to fully exploit the potential offered by HCS.

Here we describe a multi-purpose image classifier and its application to a wide variety of image classification problems without the sacrifice of classification accuracy. Although the classifier was initially developed to address High Content Screening, it was found surprisingly effective in image classification tasks outside the scope of Cell Biology. In Section 2 we describe the features extracted from training and test images, in Section 3 we discuss the high dimensionality classifier that computes similarities between the test and training images, and in Section 4 we present experimental results demonstrating the efficacy of the proposed algorithm in several test cases along with comparisons to previously proposed task-specific classifiers.

2. Image Feature Extraction

The first step in generalized image classification is to represent the image content as a set of numeric values (features). Due to the wide range of possible tasks performed by generalized image classifiers, the number of features computed during training is far greater than in task-specific classifiers. The types of features used by the image classifier described in this paper fall into four categories: polynomial decompositions, high contrast features, pixel statistics, and textures. In polynomial decomposition, a polynomial is generated that approximates the image to some fidelity, and the coefficients of this polynomial are used as descriptors of the image content. Texture features report on the inter-pixel variation in intensity for several directions and resolutions. High contrast features, such as edges and objects, comprise statistics about object number, spatial distribution, size, shape, etc. Pixel statistics are based on the distribution of pixel intensities within the image, and includes histograms and moments. In addition to calculating these features for the raw image, we subject the image pixels to several standard transforms (Fourier, wavelet, Chebyshev), and calculate features on these transforms, as well as some transform combinations. As will be discussed in Section 4, the discriminating power of these features in many of the tested image sets is greater than features computed from raw pixels.

Together, the feature vector comprises 1025 variables, each of which reports on a different aspect of image content. All features are based on grayscale images, so color information is not currently used. Since we have made no attempt to normalize this variable space, many of these features may be interdependent and cannot be considered orthogonal. Furthermore, we make no claim that this feature set is complete in any way. In fact, it is expected that new types of features will be added, which will make this classification approach more accurate, more general or both.

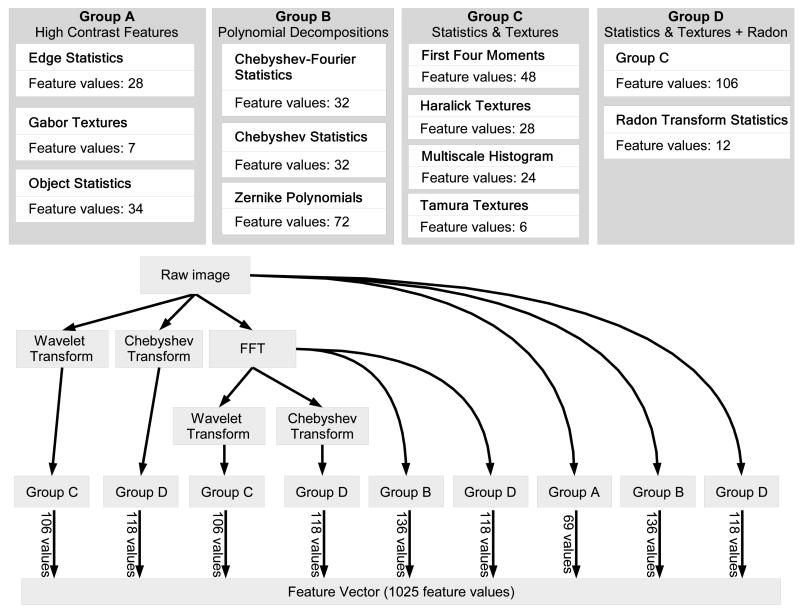
Figure 1 illustrates the construction of the feature vector by computing different groups of image features on the raw image and on the image transforms (Fourier, wavelet, Chebyshev) and transform combinations. As can be seen in the figure, not all features are computed for each image transform. For instance, object statistics are computed only on the original image, while Zernike polynomials are computed on the original image and its FFT transform, but not on the other transforms. Multiscale histograms, on the other hand, are computed for the raw image and all of its transforms. The permutations of feature algorithms and image transforms was selected intuitively to be a useful subset of the full set of permutations. Evaluation of this subset has established that this combinatorial approach yields additional valuable signals (see Figure 6). It is quite likely that further valuable signals could be obtained by calculating a more complete set of permutations.

Fig. 1.

The construction of the feature vector.

Fig. 6.

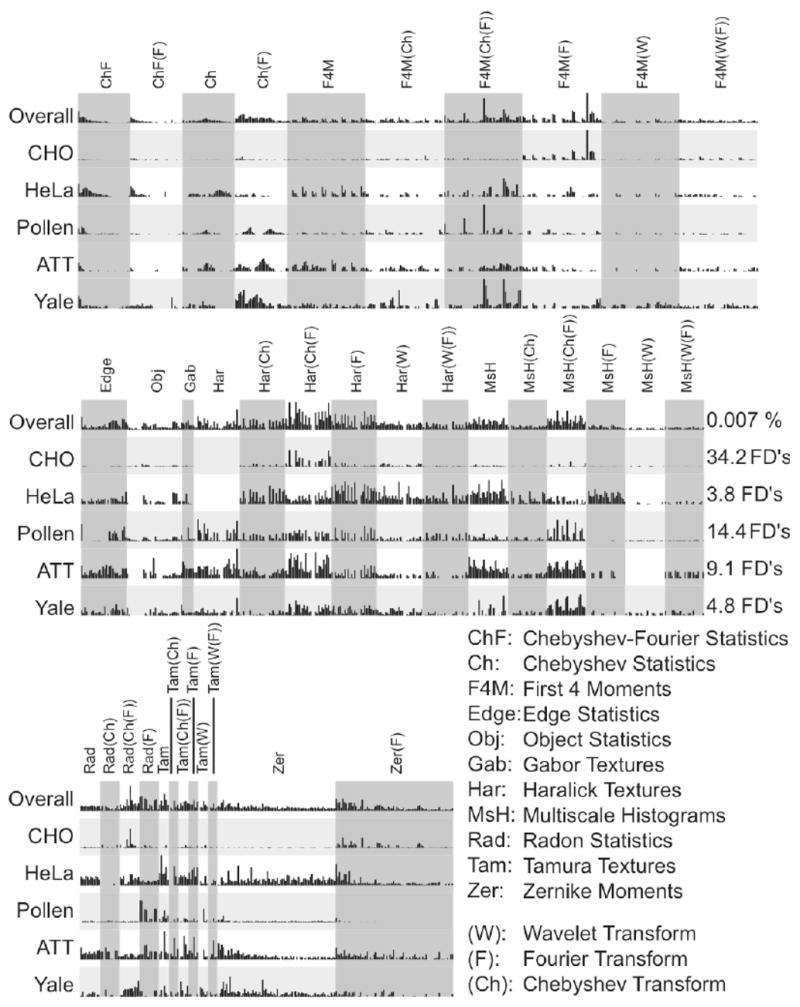
Comparison of Fisher scores assigned to the 1025 features in different image classification problems

2.1. Basic image transforms

Image features can be extracted not only from the raw image, but also from its transforms (Rodenacker & Bengtsson, 2003; Gurevich & Koryabkina, 2006; Orlov et al., 2006). Re-using feature extraction algorithms on image transforms leads to a large expansion of the feature space, with a corresponding increase in the variety of image content descriptors, but without a corresponding increase in algorithm complexity. For Fourier transform we used the FFTW (Frigo & Johnson, 2005) implementation of the Fourier transform. This transform results in complex-valued plane, of which only absolute values were used. For the wavelet transform, the standard MATLAB Wavelet toolbox functions were used to compute a Symlet 5, level 1 two-dimensional wavelet decomposition of the image. The Chebyshev transform was implemented by our group and is described in Section 2.2. Transform algorithms can also be chained together to produce compound transforms. In this work we also generated Chebyshev and wavelet transforms of the Fourier transform of the image. As will be described in Section 4, image content extracted from transforms of the image is a key contributor to the accuracy of the proposed image classifier.

2.2. Image features based on Chebyshev transform

Chebyshev polynomials T_n(x) = cos(n·arccos(x)) (Gradshtein & Ryzhik, 1994) are widely used for approximation purposes. For any given smooth function, one can generate its Chebyshev approximant such as $f(x)\simeq {\sum }_{n=0}^N{\alpha }_n{T}_n(x)$, where T_n is a polynomial of degree n, and α is the expansion coefficient. Since Chebyshev polynomials are orthogonal (with a weight) (Gradshtein & Ryzhik, 1994), the expansion coefficients α_n can be expressed via the scalar product α_n = 〈f(x),T_n(x)〉. For a given image I, its two-dimensional approximation through the Chebyshev polynomials is $I_{ij}=I(x_i,y_i)\simeq {\sum }_{n,m=0}^N{\alpha }_{nm}{T}_n(x_i)T_m(y_j)$. The fast algorithm that was used in the transform computation takes two consequent 1D transforms, first for rows of the image, then for the columns of the resulting matrix, similarly to the implementation of 2D FFT.

Chebyshev is used by the proposed image classifier both as a transform (with orders matching the image dimensions) and as a set of statistics. For the statistics, the maximum transform order does not exceed N = 20, so that the resulting coefficient vector has dimensions (1 × 400). The image features are the 32-bin histogram of the 400 coefficients. Since the Chebyshev features are computed on the raw image and on the Fourier-transformed image, the total number of image descriptors added to the feature vector is 64.

2.3. Image features based on Chebyshev-Fourier transform

The Chebyshev-Fourier 2D transform is defined in polar coordinates, and uses two different kinds of orthogonal transforms for its two variables: distance and angle. The distance is approximated with Chebyshev polynomials, and the angle is deduced by Fourier harmonics, as described by Equation 1.

$${\mathrm{\Omega }}_{nm}(r,\phi )=T_n(\frac{2r}{R}-1)e^{im\phi },0\le r\le R$$ (1)

For the given image I, the transform is described by Equation 2.

$$I_{ij}\Rightarrow I(r_k,{\phi }_l)\simeq \sum _{m=-\frac{N}{2}}^{\frac{N}{2}}\sum _{n=0}^N{\beta }_{nm}{\mathrm{\Omega }}_{nm}(r_k,{\phi }_l)$$ (2)

In the proposed image classifier, image descriptors are based on the coefficients β_nm of the Chebyshev-Fourier transform, and absolute values of complex coefficients are used for image description (Orlov et al., 2006). The purpose of the descriptors based on Equation 2 is to capture low-frequency components (large-scale areas with smooth intensity transitions) of the image content. The highest order of polynomial used is N = 23, and the coefficient vector is then reduced by binning to 1 × 32 length. Since Chebyshev-Fourier features are computed on the raw image and on the Fourier-transformed image, this algorithm contributes 64 image descriptors to the feature vector.

2.4. Image features based on Gabor wavelets

Gabor wavelets (Gabor, 1946) are used to construct spectral filters for segmentation or detection of certain image texture and periodicity characteristics. Gabor filters are based on Gabor wavelets, and the Gabor transform of an image I in frequency f is defined by Equation 3.

$$GT(x,y,f)={\int }_{w_x}{\int }_{w_y}(x-w_x,y-w_y)G(w_x,w_y,f)d{w}_{x}d{w}_y$$ (3)

where the kernel G(w_x,w_y,f) takes the form of a convolution with a Gaussian harmonic function (Gregorescu, Petkov & Kruizinga, 2002), as described by Equation 5.

$$\begin{array}{l}G(w_x{w}_y;f_0)=e^{-\frac{X^2+\gamma Y^2}{2{\alpha }^2}}·e^{i(f_{0}X+\phi )}\\ X=w_{x}cos(\theta )+w_{y}sin(\theta )\\ Y=-w_{x}sin(\theta )+w_{y}cos(\theta )\end{array}$$ (4)

The parameters of the transform are θ (rotation), γ (ellipticity), f₀ (frequency), and α (bandwidth). As proposed by (Gregorescu, Petkov & Kruizinga, 2002), the parameter γ is set to 0.5, and α is set to $0.56\times \frac{2\pi }{f_0}$. The Gabor features (GF) used in the proposed image classifier are defined as the area occupied by the Gabor-transformed image, as defined by Equation 5.

$$GF(f_0)=\frac{1}{G_L}{\int }_x{\int }_{y}GT(x,y,f_0)\mathit{dxdy}.$$ (5)

To minimize the frequency bias, these features are computed in a frequency range ( $f_0\in {\{f_k\}}_{k=1}^K$) and normalized with the low frequency component G_L = GF(f_L). The frequency values that are used in the proposed image classifier are f_L = 0.1 and f₀ = [1, 2,…, 7]. This results in seven image descriptors, one for each frequency value that corresponds to high spectral frequencies, especially grid-like textures. Gabor filters are computed only for the raw image, and therefore seven feature values are added to the feature vector.

2.5. Image features based on Radon transform

The Radon transform (Lim, 1990) computes a projection of pixel intensities onto a radial line from the image center at a specified angle. The transform is typically used for extracting spatial information where pixels are correlated to a specific angle. In the proposed image classifier, the Radon features are computed by a series of Radon transforms for angles 0, 45, 90, and 135. Each of the resulting series values are then convolved into a 3-bin histogram, so that the resulting vector totals 12 entries.

The Radon transform is computed for the raw image, the Chebyshev transform of the image, the Fourier transform of the image, and the Chebyshev transform of the Fourier transform. The Radon transform provides 12 feature values each time it is applied, so the total number of features contributed to the feature vector is 48.

2.6. Multi-scale histograms

This set of features computes histograms with varying numbers of bins (3, 5, 7, and 9), as proposed by (Hadjidementriou, Grossberg & Nayar, 2001). Each frequency range best corresponds to a different histogram, and thus variable binning allows measuring content in a large frequency range. The maximum number of counts is used to normalize the resulting feature vector, which has 1 × 24 elements.

Multi-scale histograms are applied to the raw image, the Fourier-transformed image, the Chebyshev-transformed image, Wavelet-transformed image, and the Wavelet and Chebyshev transforms of the Fourier transform. Since each multi-scale histogram has 24 bins, the total number of feature elements is 6 × 24 = 144.

2.7. Four-way oriented filters for first four moments

For this set of features, the image is subdivided into a set of “stripes” in four different orientations (0°, 90°, +45° and −45°). The first four moments (mean, variance, skewness, and kurtosis) are computed for each stripe and each set of stripes is sampled as a 3-bin histogram. Four moments in four directions with 3-bin histograms results in a 48-element feature vector.

Like the multi-scale histograms, the four moments are also computed for the raw image, the three transforms and the two compound transforms, resulting in 6 × 48 = 288 feature values.

2.8. Tamura features

Three basic Tamura textural properties of an image are contrast, coarseness, and directionality (Tamura, Mori & Yamavaki, 1978). Coarseness measures the scale of the texture, contrast estimates the dynamic range of the pixel intensities, and directionality indicates whether the image favors a certain direction. For the image features we use the contrast, directionality, coarseness sum, and the 3-bin coarseness histogram, totaling six feature values for this group.

Tamura features are computed for the raw image and the five transforms (three transforms plus two compound transforms), so that the total number of feature values contributed to the feature vector is 36.

2.9. Edge Statistics

Edge statistics are computed on the image’s Prewitt gradient (Prewitt, 1970), and include the mean, median, variance, and 8-bin histogram of both the magnitude and the direction components. Other edge features are the total number of edge pixels (normalized to the size of the image) and the direction homogeneity (Murphy et al., 2001), which is measured by the fraction of edge pixels that are in the first two bins of the direction histogram. Additionally, the edge direction difference is measured as the difference amongst direction histogram bins at a certain angle α and α + π, and is recorded in a four-bin histogram. Together, these contribute 28 values to the feature vector.

2.10. Object Statistics

Object statistics are calculated from a binary mask of the image resulting from applying a the Otsu global threshold (Otsu, 1979), and then finding all 8-connected objects in the resulting binary mask. Basic statistics about the segmented objects are then extracted, which include Euler Number (Gray, 1971) (the number of objects in the region minus the number of holes in those objects), and image centroids (x and y). Additionally, minimum, maximum, mean, median, variance, and a 10-bin histogram are calculated on both the objects areas and distances from objects centroids to the image centroid. These statistics are calculated only on the original image, and contribute 34 values to the feature vector.

2.11. Zernike and Haralick features

Zernike features (Teague, 1980) are the coefficients of the Zernike polynomial approximation of the image, and Haralick features (Haralick, Shanmugam & Dinstein, 1973) are statistics computed on the image’s co-occurrence matrix. While Zernike coefficients are complex-valued, absolute values are used as image descriptors. A detailed description of how these features are computed and used in the proposed classifier can be found at (Murphy et al., 2001).

The number of values computed by Zernike and Haralick features are 72 and 28, respectively. While Haralick features are computed for the raw image and the five image transforms, Zernike features are computed only on the raw image and its Fourier transform. Therefore, the total number of feature values added by Zernike and Haralick features is 6 × 28 + 2 × 72 = 312.

3. Feature Value Classification

Due to the high dimensionality of the feature set, some of the features computed on a given image dataset are expected to represent noise. Therefore, selecting an informative feature sub-space by rejecting noisy features is a required step. In task-specific image classification, selection of relevant image features is often manual. For general image classification, however, feature selection (or dimensionality reduction) and weighting must be accomplished in an automated way.

There are two different approaches of handling a large set of features; hard thresholding, in which a subset of the most informative features are selected from the pool of features, and soft thresholding, in which each feature is assigned a weight that corresponds to its informativeness. In the proposed classifier, we combine the two approaches by calculating weights for each feature, rejecting the least informative features, and using the remaining weighted features for classification.

In the proposed implementation, the feature weight W_f of feature f is a simple Fisher Discriminant score (Bishop, 2006) described by

$$W_f=\frac{{\sum }_{c=1}^N{(\overline{T_f}-\overline{T_{f,c}})}^2}{{\sum }_{c=1}^N{\sigma }_{f,c}^2}·\frac{N}{N-1}$$ (6)

where W_f is the Fisher Score, N is the total number of classes, $\overline{T_f}$ is the mean of the values of feature fin the entire dataset, $\overline{T_{f,c}}$ is the mean of the values of feature f in the class c, and ${\sigma }_{f,c}^2$ is the variance of feature f among all samples of class c. The Fisher Score can be conceptualized as the ratio of variance of class means from the pooled mean to the mean of within-class variances. The multiplier factor of $\frac{N}{N-1}$ is a consequence of this original meaning. All variances used in the equation are computed after the values of feature f are normalized to the interval [0,1]. This weighting method was found to be simple, fast and effective for this classifier. After Fisher scores are assigned to the features, the weakest 35% of the features (with the lowest Fisher scores) are rejected. This number was selected empirically, based on our observations with several classification problems indicating that the classification accuracy reaches its peak when 45% of the strongest features are used. Since the accuracy is essentially unaffected in this wide range, we set the threshold in the middle of it. The resulting number of features used by this classifier is still significantly larger than most other image classifiers such as (Yavlinsky, Heesch & Ruger, 2006; Heller & Ghahramani, 2006; Rodenacker & Bengtsson, 2003), that use 120 to 240 different image content descriptors.

These reduced and weighted features are used in a variation of nearest neighbor classification we named Weighted Neighbor Distances (WND-5). For feature vector x computed from a test image, the distance of the sample from a certain class c is measured by using

$$d(x,c)=\frac{{\sum }_{t\in T_c}{\left[{\sum }_{f=1}^{\mid x\mid }{W}_f^2{(x_f-t_f)}^2\right]}^p}{\mid T_c\mid }$$ (7)

where T is the training set, T_c is the training set of class c, t is a feature vector from T_c, |x| is the length of the feature vector x, x_f is the value of image feature f W_f is the Fisher score of feature f, |T_c| is the number of training samples of class c, d(x, c) is the computed distance from a given sample x to class c, and p is the exponent, which is set to −5. That is, the distance between a feature vector and a certain class is the mean of all weighted distances (in the power of p) from that feature vector to any feature vector that belongs to that class. After the distances from sample x to all classes are computed, the class that has the shortest distance from the given sample is the classification result.

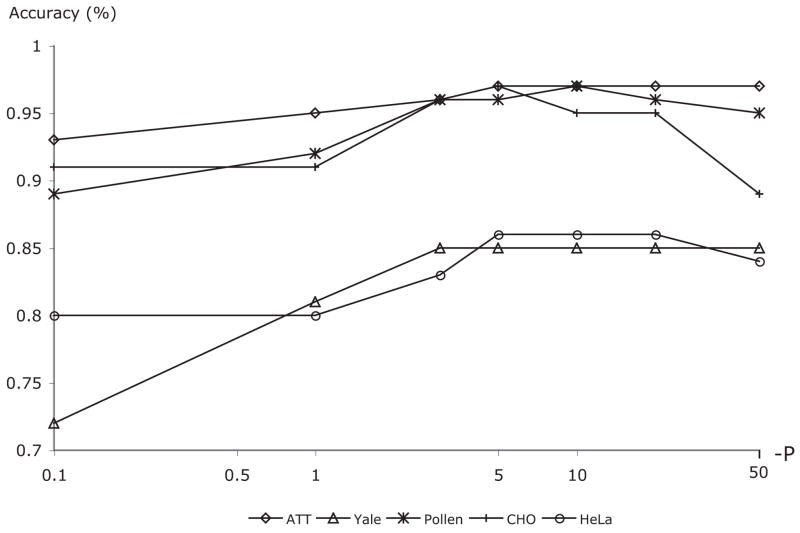
While in simple Nearest Neighbor (Duda, Hart & Stork, 2000) only the closest (or k closest) training samples determine the class of the given test sample, WND-5 measures the weighted distances from the test sample to all training samples of each class, so that each sample in the training set can effect the classification result. The exponent (p) dampens the contribution of training samples that have a relatively large distance from the test sample. This value was determined empirically, and observations suggest that classification accuracy is not extremely sensitive to it. Figure 2 shows how the performance of several image classification problems (described in Section 4) respond to changes in the value of the exponent. As can be seen in the plot, a broad range of p between −20 and −4 gives comparable accuracies.

Fig. 2.

The effect of the exponent value – p on the accuracy of five image classification problems.

This modification of the traditional NN approach provided us with the most accurate classification, as will be demonstrated in Section 4. The combination of the feature extraction algorithms with the WND-5 classifier was named WND-CHARM (Weighted Neighbor Distances using a Compound Hierarchy of Algorithms Representing Morphology).

4. Experimental Results

The performance of WND-CHARM was evaluated using several datasets from different types of image classification problems. For each dataset evaluated, the performance of the algorithm described in this paper was compared with the performance of previously proposed application-specific algorithms that were developed exclusively for that dataset. For biological images we used the HeLa dataset (Boland & Murphy, 2001), consisting of fluorescence microscopy images of HeLa cells using 10 different labels, the Pollen dataset (Duller et al., 1999), which shows geometric features of pollen grains, and the CHO dataset (Boland, Markey & Murphy, 1998), consisting of fluorescence microscopy images of different sub-cellular compartments. For face classification we used the AT&T dataset (Samaria & Harter, 1994) that includes a total of 400 images of 40 individuals with different facial expressions, and the Yale dataset (Georghiades, Belhumeur & Kriegman, 2001) that contains 165 images of 15 individuals with different expressions and lightning conditions. Other experiments included the Brodatz (Brodatz, 1966) texture dataset and COIL-20 (Nene, Nayar & Murase, 1996), which is a set of images of 20 objects in different orientations. The sizes of the training sets, test sets, and the number of classes in each dataset are similar to those used for the evaluation of the reported task-specific classifiers, and are listed in Table 1.

Table 1.

Datasets used for accuracy comparison

Dataset	No. of classes	No. of training images	No. of test images
Hela	10	590	272
Pollen	7	490	140
CHO	5	80	262
Brodatz	112	896	896
COIL-20	20	1080	360
AT'T	40	200	200
Yale	15	90	75

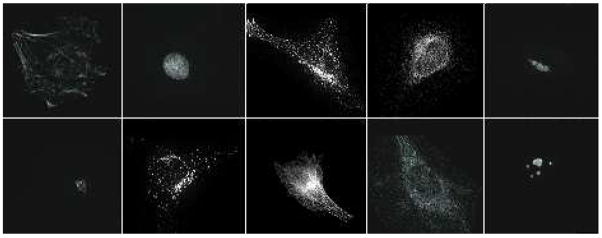
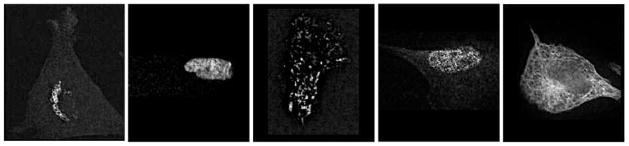
The classification accuracy of the HeLa dataset was compared with the performance of a backpropagation neural network reported by Murphy (2004), CHO was compared with with the work of Boland, Markey & Murphy (1998), and for the Pollen dataset we compared WND-CHARM with the application-specific algorithm described by France et al. (1997). Figures 3, 4 and 5 are examples of the different images in the HeLa, Pollen, and CHO datasets, respectively. Each dataset was randomly partitioned 50 times into a training set and a test set, and the classification algorithm was applied to each partition. The reported classification accuracy is the average accuracy of these 50 runs (see Table 2). The accuracies reported for task-specific algorithms are as published - we did not perform these tests again ourselves. As can be learned from the table, the accuracy of WND-CHARM is greater than the benchmark accuracy of algorithms that were designed and developed specifically for these datasets.

Fig. 3.

Typical images of the 10 classes of the HeLa dataset

Fig. 4.

Typical images of pollen grains of the 7 classes of the Pollen dataset

Fig. 5.

Typical images of the 5 classes of the CHO dataset (giant, hoechst, lamp2, nop4, tubulin)

Table 2.

Comparison of the accuracy (%) of WND-CHARM with application-specific classifiers

Dataset	Benchmark algorithm	Benchmark No. of features used	Benchmark accuracy	Accuracy of WND-CHARM
Hela	(Murphy, 2004)	37	83	86
Pollen	(France et al., 1997)	8	79	96
CHO	(Boland, Markey' Murphy, 1998)	37	87	95

AT&T and Yale face recognition datasets were compared with the accuracy of Eigenface (Turk & Pentland, 1991), Fisherface (Belhumeur, Hespanha & Kriegman, 1997), DLDA (Yu & Yang, 2001), discriminant wavelength (Chien & Wu, 2002), and discriminant DCT (Jing & Zhang, 2004), as reported by (Jing & Zhang, 2004). The accuracy measures are listed in Table 3. As the table shows, the accuracy of WND-CHARM for both datasets was comparable with the other methods.

Table 3.

Comparison of the accuracy (%) of WND-CHARM to application-specific classifiers on face recognition datasets

Dataset	Eigenface	Fisherface	DLDA	Discriminant wavelength	Discriminant DCT	WND-CHARM
AT'T	90	82.5	89	94.5	97.5	97
Yale	91	80	88	85.5	98	83

The full (112 textures) Brodatz dataset (Brodatz, 1966) was compared using several different algorithms as reported in (Do & Vetterli , 2002), and showed good classification accuracy as can be seen in Table 4.

Table 4.

Comparison of the accuracy (%) of WND-CHARM to application-specific classifiers on the Brodatz dataset

Method	Accuracy
L1+L2 (Manjunath ' Ma, 1996)	64.83
GCD (Do ' Vetterli , 2000)	75.73
scalar WD-HMM (Grouse, Nowak ' Baraniuk, 1998)	76.51
vector WD-HMM (Do ' Vetterli , 2002)	80.05
WND-CHARM	90.3

The Brodatz dataset was also used to test the rotational and scale invariance of the proposed method. This test was performed using the rotated subset of Brodatz dataset used by (Do & Vetterli , 2002), which included the textures bark, sand, pigskin, bubbles, grass, leather, wool, raffia, weave, water, wood,straw, brick. The performance was evaluated using the method described in (Manjunath & Ma, 1996), and (Do & Vetterli , 2002) (percentage of relevant images among the top 15 retrieved images). The results were compared with the performance several other algorithms as described in (Do & Vetterli , 2002), as listed in Table 5.

Table 5.

Retrieval rate (%) of WND-CHARM compared to the application-specific classifiers described in (Do ' Vetterli , 2002) on rotated Brodatz images

Method	Retrieval rate
w/o rotation invariance	52
w/ rotation invariance	87
WND-CHARM	79

The same data and settings were used to evaluate the scale invariance of the proposed image classifier, but instead of rotating the images by different angles, the images were scaled by four different factors, ranging from 0.6 to 0.9 with a 0.1 interval. The results were compared with the performance of the Steer Pyramid approaches M-SPyd (Montoya-Zegarra, Leite & Torres, 2007) and C-SPyd (Simoncelli & Freeman., 1995), and Gabor Wavelets (Han & Ma, 2007), as described in Table 6.

Table 6.

Retrieval rate (%) of WND-CHARM compared to application-specific classifiers on scaled Brodatz images

Method	Retrieval rate
M-Spyd	86.5
C-SPyd	80.5
Gabor Wavelets	60.7
WND-CHARM	73.5

As can be seen in Tables 5 and 6, the proposed method was less effective than algorithms designed specifically for texture classification in different rotations or scales. However, compared to an algorithm for texture classification that was not designed for rotation invariance, the proposed image classifier recorded a significantly higher accuracy, and also performed better than Gabor Wavelets on scale-variant textures. These results indicate that the method described in this paper can handle a certain degree of rotational and scale invariance, but may be less effective than application-specific algorithms.

An additional experiment on rotational invariance was performed using the COIL-20 image dataset, and was compared to Max-tree and S.E. BV algorithms described in (Urbach, Roerdink & Wilkinson, 2007). The results are reported in Table 7, and show that the proposed method is favorably comparable to previously proposed algorithms.

Table 7.

Comparison of classification accuracy (%) on the COIL-20 dataset

Method	Accuracy
Max-tree	98.9
S.E. BV	99.0
WND-CHARM	99.7

Each of the tested image classification problems makes use of a different set of image features. The features used are assigned different weights for each dataset, according to their ability to discriminate between different image classes. Figure 6 is a bar graph comparing Fisher Discriminant (FD) scores for every image feature used in several of the tested datasets. The raw FD scores for each dataset were normalized to facilitate comparison. The vertical scale in each row is the percentage of the feature’s FD score compared to the highest-scoring feature in a given dataset. The highest FD score is also reported on the right for comparison. An aggregate score for each feature over all datasets was also computed in order to compare the features overall usefulness. We first calculated the percent contribution of each feature to each problem by dividing its FD score by the sum of the FD scores for all features in a given dataset. The average percent contribution of each feature for all datasets was used as the overall score for that feature.

As can be seen in Figure 6, in some datasets (e.g. CHO), a small number of image features contribute disproportionately to classification (first four moments, Haralick textures and Radon transforms). In other datasets (e.g. AT&T), a much larger number of image features contribute relatively equally to the classification. Comparing the FD scales between CHO and AT&T indicates that CHO’s few features are highly discriminative, while all of AT'T's features are relatively less informative.

The efficacy of the WND classifier described in Section 3 was tested by comparing it to the performance that was achieved when using Weighted NN and the Bayesian Network implementation of Murphy (2001) with feature selection using greedy hill climbing (Kohavi ' John, 1997) and the value discretization method of Dougherty, Kohavi ' Sahami (1995). The resulting performance figures are listed in Table 8.

Table 8.

Comparison of classification accuracies (%) when using WND, WNN and Bayesian Network classifiers

Dataset	Bayesian Network	WNN	WND
Hela	69	85	86
CHO	78	94	95
Pollen	78	96	96
AT'T	65	97	97
Yale	58	81	83

As the table shows, the performance of the Bayesian network was significantly lower than WND-5, which also outperformed WNN for the tested datasets. This experiment demonstrates the effectiveness of WND when the number of features is high.

4.1. Image Features of Transforms and Compound Transforms

An important aspect of the described method is the use of image features computed on image transforms and image compound transforms. The image transforms used in the proposed method are non-linear mappings of the original image content into non-physical spaces. Although the image transforms look drastically different visually than the original image, the actual image content remains the same, but represented in a different form where pixels make different patterns, and pixel associations obey different rules. This allows to significantly expand the image content descriptors, and extract more information from each image. A simple example is multi-frequency features, which may be hidden when working with the raw pixels, but can easily be extracted from their Fourier domain.

Figure 6 shows that features computed on transforms and compound transforms of the image are in many cases more informative than the same features derived from the image itself. For instance, in the tested datasets Chebyshev Statistics computed on the Fourier transform are overall more informative than Chebyshev Statistics computed on the raw image. Haralick texture features computed on the Chebyshev transform of the Fourier transform are overall more informative than either Haralick features computed on the Fourier transform, on the Chebyshev transform or on the raw image.

The contribution of image features computed on image transforms and image compound transforms is described in Table 9, which shows a comparison of the classification accuracies of the tested datasets when using image features computed only on the raw images, raw images + image transforms, and raw images + compound transforms.

Table 9.

Comparison of classification accuracy (%) with and without transforms and compound transforms

Dataset	Raw pixels	Raw pixel + image transforms	Raw pixels + image transforms + compound transforms
Hela	81	84	86
CHO	82	95	95
Pollen	91	93	96
AT'T	94	94	97
Yale	75	77	83

As Table 9 shows, computing image features on image transforms has a dramatic effect on the classification accuracy in most cases, while compound transforms also contribute significantly to the performance of the image classifier.

4.2. Computational Complexity

Perhaps the major downside of the proposed algorithm is its computational complexity. With a MAT-LAB implementation of the described method, computing all image features of a 100 × 100 image requires ~2 seconds using a system equipped with an Intel processor at 2GHz and 1GB of RAM. This number grows approximately linearly with the image size, resulting in poor performance in terms of computational complexity, making this method unsuitable for real-time or other types of applications in which speed is a primary concern. For example, the execution time required for training the different image classifiers for AT'T and Yale datasets are listed in Table 10.

Table 10.

Comparison of the training time (in seconds, using a 1.4 GHZ Pentium processor) of different image classifiers

Dataset	Eigenface	Fisherface	DLDA	Discriminant wavelength	Discriminant DCT	WND-CHARM
AT'T	23.7	26.4	22.1	28.5	24.9	9220
Yale	14.3	14.9	13.1	15.2	14.8	12950

In order to compute image features for large datasets, we used two levels of parallelism to take advantage of modern multi-core, multi-CPU platforms. Because image features are computed for each image independently, feature computation on different images can be easily paralleled. Another level of parallelism used is computing several different sets of features on the same image at the same time. E.g., while Haralick textures are computed by one processor, another processor can extract the Zernike features of the same image. These two levels of parallelism have been implemented by our group, and the software is available as part of the OME (Swedlow et al., 2003) open source package. More details describing the parallelism and the algorithm execution are provided at (Macura et al., 2008).

Another viable approach for improving the execution time is the use of FPGAs (Field Programmable Gate Arrays). Because the proposed method performs well on many different image classification problems, it is a good candidate for an FPGA implementation to improve execution time. Similar algorithms have already been implemented for common image processing tasks such as FFT or Convolution, and we are currently considering implementation of the proposed method on these platforms.

5. Conclusion

We described an image classification algorithm that can address a wide variety of image classification problems without modifications or parameter adjustments, and can provide accuracy favorably comparable to previously proposed application-specific classifiers. WND-CHARM is based on computing a very large set of image features. Since different groups of image features are more informative for different image classification problems, the large set of features used by this method can provide a sufficient pool of features for an unknown image classification task. We encourage scientists and engineers who face new image classification tasks to try WND-CHARM before developing their own task-specific image classifiers. The MATLAB code is part of the OME (Swedlow et al, 2003) software suite, which is available for download at http://www.openmicroscopy.org