Estimating Motion From MRI Data

Abstract

Invited Paper

Magnetic resonance imaging (MRI) is an ideal imaging modality to measure blood flow and tissue motion. It provides excellent contrast between soft tissues, and images can be acquired at positions and orientations freely defined by the user. From a temporal sequence of MR images, boundaries and edges of tissues can be tracked by image processing techniques. Additionally, MRI permits the source of the image signal to be manipulated. For example, temporary magnetic tags displaying a pattern of variable brightness may be placed in the object using MR saturation techniques, giving the user a known pattern to detect for motion tracking. The MRI signal is a modulated complex quantity, being derived from a rotating magnetic field in the form of an induced current. Well-defined patterns can also be introduced into the phase of the magnetization, and could be thought of as generalized tags. If the phase of each pixel is preserved during image reconstruction, relative phase shifts can be used to directly encode displacement, velocity and acceleration. New methods for modeling motion fields from MRI have now found application in cardiovascular and other soft tissue imaging. In this review, we shall describe the methods used for encoding, imaging, and modeling motion fields with MRI.

I. Introduction

There are two main driving forces behind the research in motion analysis using magnetic resonance imaging (MRI): 1) the quantitative measurement of blood flow,; and 2) the analysis of heart and other tissue motion (tongue, lung, upper airway, bones, and connective tissues at a joint and skeletal muscle). For direct application to medicine, the measurement of myocardial function is tremendously important; cardiovascular diseases are the primary cause of mortality in developed countries [1]. Development of better functional cardiac imaging techniques in the hope of achieving early diagnosis and better patient follow-up is therefore a very active research area. Our focus in this paper is the assessment of tissue motion using MRI; special emphasis will be cardiac applications. Due to space limitations, we had to leave out two topics: MR elastography [2] imaging and MR diffusion imaging [3].

Although this paper focuses on the heart, there are several other organ systems where such a detailed motion analysis can be very helpful and has been pursued. Examples are: 1) dynamic imaging of the musculoskeletal system; 2) investigation of other soft tissue (tongue, chest wall, and lung) motion; and 3) detailed motion analysis of internal organs during certain exercises.

In the next section we will give a brief background on MRI and several motion analysis techniques. These are: tagged MRI (TMRI), phase contrast MRI (PCMRI), displacement encoding with stimulated echoes (DENSE), and harmonic phase imaging (HARP). Examples are given for each technique in the third section. Comparative analysis, advantages and disadvantages of each technique, hardware issues, technical challenges, and a brief look into the future can be found in the final section.

II. Background and Theoretical Development

In this section we start with a brief introduction to MRI. The aim is to introduce only the basics of MRI that are necessary to understand the main principles of the different imaging techniques that will be presented in the following subsections. For introductory material on MRI, the reader is referred to [4] and [5]; more theoretical material on cardiac motion analysis with a detailed survey of current physical and mathematical models and postprocessing techniques for cardiac MRI can be found in [6].

A. An Introduction to Magnetic Resonance Imaging

MRI [7] is based on exciting magnetic dipoles, mainly protons of water molecules within the body, and observing the subsequent effects. In MRI, the subject is first introduced into a high magnetic field B₀ with a commonly used field strength of 1.5 T for clinical imaging (compare it to earth's magnetic field strength of 40–70 μT). Ensembles of protons align themselves very quickly with the main field. In the semiclassical vector model, the ensembles can be regarded as magnetization vectors that behave like spinning tops rotating with a frequency proportional to the strength of the local magnetic field ω = γB, known as the Larmor frequency. The constant γ is known as the gyromagnetic ratio and is approximately 42.58 MHz/T for protons.

The magnetization can be disturbed (excited, tipped, or flipped) from its aligned equilibrium state by the brief application of a second magnetic field B₁ oriented perpendicularly to the main field and tuned to the Larmor frequency. Since this frequency is approximately 64 MHz for protons at 1.5 T, the applied pulse is often referred to as a radio frequency (RF) pulse and can be generated using a tuned coil driven by an RF amplifier. The effect of the RF pulse is to tip the magnetization vectors out of alignment with the main B₀ field, providing a transverse component M_xy = M₀ sin(α) orthogonal to the main field and a longitudinal component M_z = M₀ cos(α) parallel to it, where M₀ is the initial equilibrium longitudinal magnetization and α is the flip angle given by α = γ ∫ B₁ dt. The excited magnetization precesses, rotating around the main field at the Larmor frequency like a spinning top rotates around the vertical gravitational field. The rotating transverse component of the magnetization M_xy induces electromotive force (EMF) in a conducting RF receiver coil placed near the subject (this could be the same coil as used for the B₁ excitation pulse), which is measured as the MR signal by the MRI scanner.

After excitation, the magnetization vectors gradually return to their equilibrium positions, aligned with the main magnetic field B₀ by processes which can be characterized using simple first-order kinetics of the two orthogonal components of magnetization. The longitudinal magnetization component M_z recovers exponentially with a rate constant of T₁, known as the longitudinal or spin-lattice relaxation time, toward the equilibrium state magnetization M₀ according to

$$\begin{array}{cc}\hfill M_z\left(t\right)& =M_0-(M_0-M_z\left(0\right))e^{-t∕T_1}\hfill \\ \hfill & =M_z\left(0\right)e^{-t∕T_1}+M_0(1-e^{-t∕T_1}).\hfill \end{array}$$ (1)

The transverse magnetization component M_xy decays exponentially with a rate constant of T₂, known as the transverse or spin-spin relaxation time, according to

$$M_{\mathit{xy}}\left(t\right)=M_{\mathit{xy}}\left(0\right)e^{-t∕T_2}.$$ (2)

Various types of tissues (e.g., muscle, fat, blood) often have different relaxation times, providing a source of contrast in MR images. Generally, T₂ < T₁, but in practice, the MR signal appears to decay with an even shorter rate constant of $T_2^{\ast }$. This latter decay time constant arises primarily from the dephasing effects of magnetic field inhomogeneities (for example, due to susceptibility differences between tissues) over the region of interest. These cause the various magnetization vectors to dephase with respect to one another, resulting in signal attenuation due to destructive interference. Techniques exist for generating the so-called spin echoes and stimulated echoes [8] that can reverse much of the effects of this inhomogeneous decay, in which case the more fundamental decay rate T₂ is revealed. The T₁ and T₂ relaxation parameters are effective measures of the ability of the magnetization to act as a memory and retain information. Patterns (such as tags for motion tracking) encoded at t = t₀ in the longitudinal M_z(t₀) and transverse magnetization M_xy(t₀) are lost with rate constants T₁ and T₂, respectively.

Magnetic field gradients are of great importance for both the formation of MR images and motion encoding. Gradients provide the means for performing spatially specific operations. The gradient field is a small magnetic field with linear spatial variation that can be superposed on the main field under scanner control. Writing the main field as B = B₀k, the gradient magnetic field is given by

$$\mathbf{G}=\nabla B_0={\left(\frac{\partial B_0}{\partial x},\frac{\partial B_0}{\partial y},\frac{\partial B_0}{\partial z}\right)}^T.$$ (3)

Physically, the gradient field is generated by three sets of coil windings providing linear field variation in each of the physical X, Y, and Z directions. Gradient fields in any arbitrary direction r are obtained by applying combinations of the three primary gradients in the ratio of the direction cosines of r. In the presence of the gradient field, the magnetization precessing according to the Larmor equation will have a frequency offset directly proportional to the component of its position in the direction of the magnetic field variation given by

$$B\left(\mathbf{r}\right)=B_0+\mathbf{G}\cdot \mathbf{r}\Rightarrow \omega \left(\mathbf{r}\right)=\gamma (B_0+\mathbf{G}\cdot \mathbf{r})={\omega }_0+\gamma \mathbf{G}\cdot \mathbf{r}.$$ (4)

Thus, frequency selective operations can be made spatially selective through the use of gradients. It is most common to work in a rotating frame of reference so that frequency offsets are measured relative to the Larmor frequency. Thus, the influence of a gradient can be written as

$$\omega \left(\mathbf{r}\right)=\gamma \mathbf{G}\cdot \mathbf{r}.$$ (5)

Slice selection is achieved through the simultaneous application of an RF pulse and gradient field [9]. The RF pulse is modulated so that it is band limited and, consequently, excites the magnetization within a specific, limited range of frequencies. The gradient field is applied such that it varies linearly in the desired slice selection direction: thus, only the magnetization vectors within a planar slab are excited. The slice profile is determined by the duration and modulation of the RF pulse, while its position in the slice gradient direction can be adjusted by modifying the RF pulse frequency band. The slab thickness and orientation are controlled by adjusting the amplitude and direction of the slice selection gradient.

After excitation, the imposition of further gradient fields will cause the magnetization in different regions of the slice to precess with a spectrum of frequencies determined by the spatial positions of the magnetization vectors in accordance with (4). This spectrum can be found by acquiring the MR signal and performing a Fourier transformation on it, thereby providing a one-dimensional (1-D) spatial profile of the subject.

More generally, an arbitrary time varying gradient G(t) applied after excitation causes transverse magnetization vectors to dephase according to the equation ω(r, t) = γG(t)·r, so that the total phase accumulation at time t is

$$\theta (\mathbf{r},t)=\gamma \left({\int }_0^t\mathbf{G}\left(t^{\prime }\right){\mathit{dt}}^{\prime }\right)\cdot \mathbf{r}.$$ (6)

Integrating the signal over the volume of interest in the subject, we obtain

$$S(\mathbf{G},t)=A{\int }_V\rho \left(\mathbf{r}\right)\exp \left[i\gamma \left({\int }_0^t\mathbf{G}\left(t^{\prime }\right){\mathit{dt}}^{\prime }\right)\cdot \mathbf{r}\right]d^3\mathbf{r}$$ (7)

where A is a constant for coil and electronics-related parameters, and ρ(r) is the proton density. Now, introduce the so-called k-space conjugate variables [10] by defining

$$\mathbf{k}\left(t\right)=\frac{\gamma }{2\pi }{\int }_0^t\mathbf{G}\left(t^{\prime }\right){\mathit{dt}}^{\prime }$$ (8)

and dropping the constant A makes the Fourier transform (FT) relationship between data acquisition and image reconstruction for MRI clear, as follows:

$$\begin{array}{cc}\hfill S\left(\mathbf{k}\right)& ={\int }_V\rho \left(\mathbf{r}\right)\exp (i2\pi \mathbf{k}\cdot \mathbf{r})d^3\mathbf{r}\hfill \\ \hfill \rho \left(\mathbf{r}\right)& ={\int }_{{\Re }^3}S\left(\mathbf{k}\right)\exp (-i2\pi \mathbf{k}\cdot \mathbf{r})d^3\mathbf{k}.\hfill \end{array}$$ (9)

A map of the spatial distribution of magnetization (i.e., an image) can be obtained from a map of the conjugate spatial domain S(k). Equation (9) shows how MRI gradient pulse sequences can be designed to obtain sufficient data from k-space locations for image reconstruction via an inverse FT.

The availability of the fast FT (FFT) favors the collection of data with a regular pattern in k-space: e.g., a two-dimensional (2-D) Cartesian grid where, typically, one row of the k-space data matrix is acquired at a time, and the process is repeated over all such rows. Images are then reconstructed using the 2-D FFT. Data collected in a polar sampling scheme can be reconstructed by a 1-D FT followed by filtered back-projection. More general acquisition schemes (e.g., spiral sampling) can be reconstructed by regridding the samples onto a regular Cartesian grid and applying the 2-D FFT.

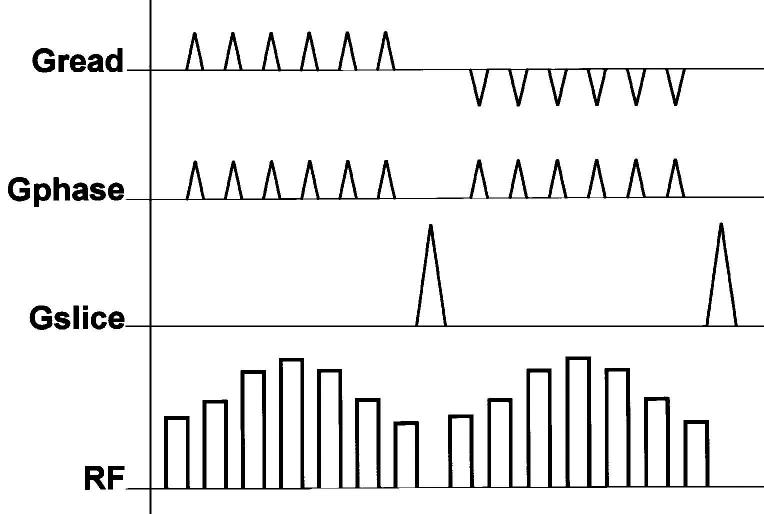
A pulse sequence diagram displays the timing of all these gradients (see Fig. 1), RF pulses and acquisition of induced signals, or echoes. Readers who wish to get a quick introduction to MR scanner hardware and some further MRI terminology, and familiarize themselves with hardware requirements of cardiac MRI, are referred to [11]. In one of the major modes of MR imaging, spoiled gradient echo imaging, a sequence of short low-amplitude RF (small flip angle) slice-selective excitation pulses is played at a rate of up to 400 pulses/s, and the MR signal is acquired in an approximately 1–4-ms window after each RF pulse (see Fig. 1). Spatial encoding is achieved as for the 2-D Cartesian grid given previously: a gradient is applied in the read direction during the acquisition window; encoding in the orthogonal phase encoding direction is accomplished by repeating this acquisition step multiple times with phase encoding gradient pulses of increasing amplitudes used to offset the data acquisition k-space line.

Fig. 1.

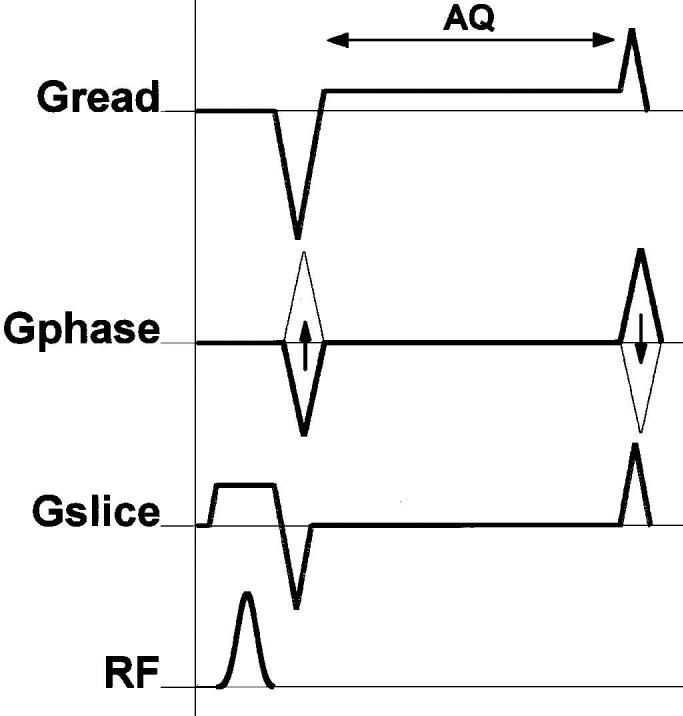
A pulse sequence diagram of spoiled gradient echo imaging displaying the timing of all major events during imaging. These are slice selective (Gslice), phase encoding (Gphase), and readout (Gread) gradients, applied RF pulses for excitation (RF), and acquisition (AQ) of induced signals, or echoes. Spatial encoding is for a 2-D Cartesian grid: Gread is on during the acquisition window; encoding in the orthogonal, phase encoding direction is accomplished by repeating this acquisition step multiple times with phase encode gradient pulses of increasing amplitudes.

The length of this pulse sequence repeat unit in Fig. 1 defines TR (repetition time), and the time from the center of the excitation RF pulse to the center of the acquisition window defines TE (echo time). The contrast between the various tissues arises from the pulse sequence parameters (notably TR and TE), as well as tissue proton (i.e., ¹H nuclei) content, the tissue-specific magnetic relaxation properties T₁, T₂, and $T_2^{\ast }$.

The expression for the MR signal obtained during a spoiled gradient echo sequence, such as the one presented in Fig. 1, is shown at the bottom of this page in (10), where k ≡ k (t) is the k-space trajectory, typically covering a rectangular grid, one line per TR, and α is the RF flip angle. Note that the term

$$M_{\mathit{ss}}=\frac{1-e^{-TR∕T_1}}{1-\cos \left(\alpha \right)e^{-TR∕T_1}}$$ (11)

is the longitudinal steady-state magnetization resulting from the repeated flipping and spoiling of the magnetization, sin(α) represents the transverse component of the tipped magnetization, and $e^{-t∕T_2^{\ast }}$ represents attenuation due to signal decay during data acquisition.

It is the transverse magnetization that excites the current in the receiver coil. The transverse magnetization has both an amplitude (size of the vector in the transverse plane) and a phase (location of the vector in the plane). The phase of the transverse magnetization can be manipulated by changing the rate of precession of the magnetization with the applied field gradients. It is this information that is used to perform the spatial encoding to form the MR image. Each pixel in the final MR image is in fact a complex number representing both the magnitude and the phase of the transverse magnetization at time TE.

Neglecting relaxation effects, the signal-to-noise ratio (SNR) ratio for MRI is in proportion to the voxel volume and the square root of the total acquisition time for the image. In practice, the need to allow for some longitudinal recovery of the magnetization may limit the minimum repeat time TR. Similarly, the effects of $T_2^{\ast }$ signal decay limits the duration of the acquisition readout window. Thus, MRI is essentially a constant optimization exercise with several imaging parameters, preparation pulses, and gradients to get the desired image with adequate contrast and SNR in a reasonable acquisition time.

Imaging the heart presents the additional challenge of dealing with cardiac motion during the image acquisition process. One approach to meet this challenge is to acquire consecutive images as rapidly as possible, by using as short a TR as possible. Images acquired in this fashion generally have limited spatial resolution (due to the limited number of k-space lines that can be acquired), and poor temporal resolution (150–300 ms). Improvements can be achieved by using echo-planar techniques (i.e., collecting several k-space lines per TR by modulating the gradients) [12]-[14] or by using longer k-space readout trajectories [15], [16] in each TR. More recently, techniques known as parallel imaging have provided the possibility for accelerating the imaging process further via the use of multiple receiver coils [17], [18], albeit with some SNR penalty. The adoption of these techniques may make the direct acquisition of cardiac images with high spatial and temporal resolution feasible in the near future.

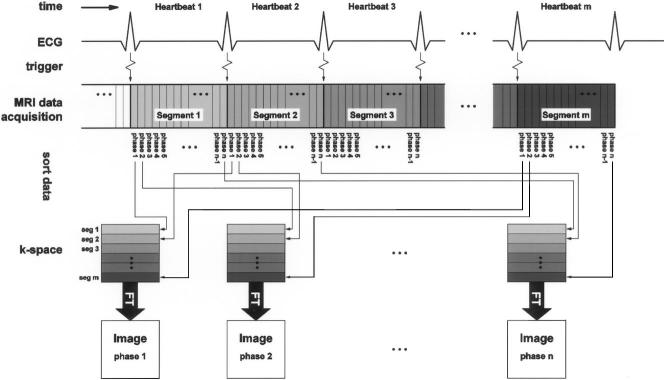
Segmented k-space imaging is an alternative approach permitting the acquisition of a set of images at multiple cardiac phases over the course of several heartbeats in a single ECG-gated, breathheld scan. This is achieved by partitioning the k-space data matrix into several so-called segments. The region corresponding to each k-space segment is acquired repeatedly for the duration of a heartbeat, providing multiple cardiac phases, and the successive segments are acquired in successive heartbeats. The set of segments for each cardiac phase is then assembled and reconstructed into an image, as shown in Fig. 2. The temporal resolution can be improved by reducing the segment size (i.e., by reducing the number of k-space lines in a segment), but note that this is at the price of an increased total imaging and, therefore, breath-hold time. Segmented k-space imaging techniques can be improved by using interpolation techniques to adjust for slight variations in the cardiac cycle [19]. The acquisition times for segmented k-space imaging can also be reduced through the use of echo-planar, spiral, and parallel imaging techniques. For further reading, several review articles exist for a general introduction to these different imaging techniques with a focus on their cardiac implementations [20], [21].

Fig. 2.

In segmented k-space cardiac imaging data acquisition is synchronized, gated, with EKG. After each heartbeat same spatial encoding gradients for a specific k-space segment is acquired repeatedly, each is subsequently assigned to different images, providing multiple snapshots of cardiac activity. The segments within each image are acquired in successive heartbeats. Please note that each segment may contain multiple k-space lines.

B. Overview of Different Techniques for Motion Tracking

The standard method of kinematics is to follow objects using temporal sequence of 2-D and three-dimensional (3-D) data sets. From these images, boundaries and edges of desired tissue is first identified by tissue segmentation techniques and subsequently tracked using object registration methods. Several imaging modalities can be utilized for this depending on the application. If the moving organ can be observed directly (e.g., whole arm or foot), special markers for landmarks, or active or passive stereo computer vision techniques, can be employed. A rich literature already exists in this type of applications (e.g., gait analysis). Our focus here is imaging of moving tissues inside the body.

One of the methods for in vivo motion imaging is 3-D X-Ray stereophotogrammetry, which requires insertion of metallic balls into the bones [22]. This overcomes the limitations of working with 2-D radiographic projections but cannot be used as a routine tool. Computerized tomography (CT) can also be utilized [23], although X-ray dose becomes critical when multiple 3-D datasets are needed.

MRI has several advantages, since it provides excellent contrast between soft tissues, and images can be acquired at positions and orientations freely defined by the user without the use of ionizing radiation. As an example, the 3-D motion characteristics of peritalar joint complex is analyzed in vivo using 3-D datasets acquired during the foot motion ranging from extreme pronation to extreme supination at eight positions [24], [25]. Similarly, shoulder kinematics is examined using sequential increments of arm rotation and acquisition and comparison of 3-D models of glenoid and humerus [26].

MRI can do much more than providing detailed anatomic images as was the case in the previously mentioned kinematics studies. Specific MRI techniques have the ability to track tissue or give more quantitative motion data directly. These are: 1) TMRI; 2) PCMRI; and 3) pulse field gradient-based MRI methods (HARP and DENSE).

TMRI modulates the underlying image intensity with the help of a specific presaturation technique. This essentially produces a pattern of dark lines, or so-called tags, on the image. Deformation of these temporary lines is analyzed to derive a motion model of the underlying tissue. In contrast, PCMRI uses phase shifts induced in the transverse magnetization with “instantaneous” velocity encoding pulses for measuring motion; the phase of the signal is directly related to the velocity of the material within each voxel at the time of velocity encoding. The velocity field can then be integrated to get the displacement. In DENSE and HARP, a uniform pattern of phase modulation is encoded into the tissue at a chosen time, and the deformation of that pattern is detected at a later time and utilized to estimate the motion.

This is a rapidly evolving area in MRI research; the latest technical refinements or detailed explanation of each technique is not the scope of this paper. In the following subsections we will introduce and describe each technique briefly, and their examples will be given in the next section.

C. Tagged Magnetic Resonance Imaging

In MRI, temporary magnetic fiducial markers, or tags, can be created within the tissues. Subsequently, when the same tissue is imaged after a certain time, the shape changes of the tags reflect the underlying tissue motion (see Fig. 3). The principle for tagging can be traced back to techniques for the measurement of bulk flow [27]; over the past decade it has been developed extensively for measuring cardiac motion. Several types of tagging approaches have been proposed in the literature [29]-[32]. For detailed information on tagging, the reader is referred elsewhere [33], [34]. The parallel plane stripe pattern and the combination of two orthogonal plane tags forming a grid are the most common types. Basic tag sequences of this type are now integrated within the pulse sequence libraries of all clinical MRI machines.

Fig. 3.

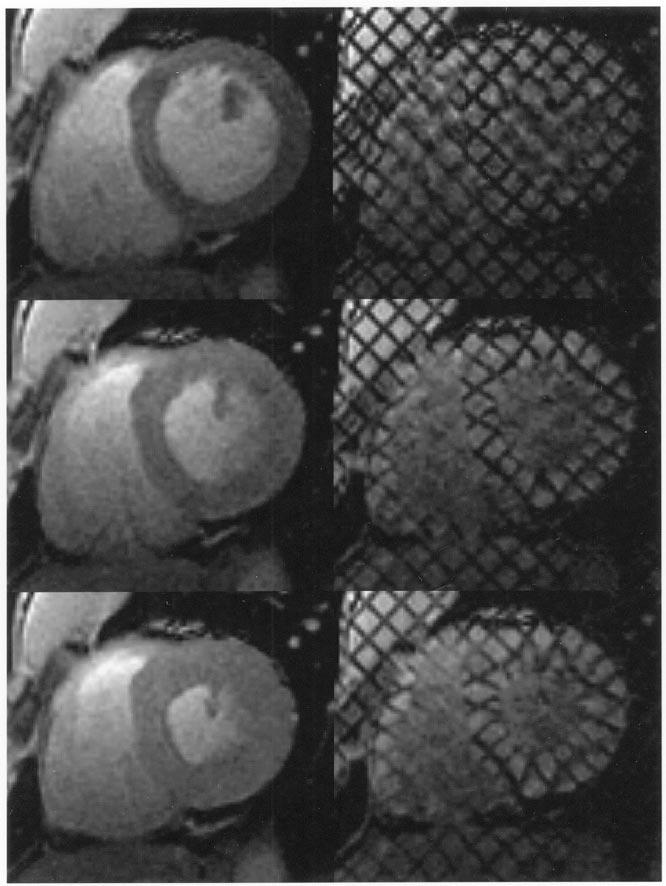
Left: standard cardiac MR images. Right: for the same heart, location, and cardiac phase, the corresponding tagged MR images. Top: at end-diastole, when the ventricular cavity is at its maximum filling, right after tagging. Middle: At mid-systole, when the heart is contracting. Bottom: at end-systole, when the maximum amount of blood has been ejected and the heart muscle is at its maximum contraction.

The tagging operation may be considered to be a spatially selective excitation involving the combined use of RF pulses and gradients. However, compared to slice selection (discussed previously) in which only a single plane of magnetization was excited, it is desired to excite multiple planes of magnetization for saturation tagging. The excited magnetization is then spoiled, i.e., dephased using gradient pulses, so that it makes no significant contribution to the subsequently acquired images. The effect of the tagging excitation and spoiling is to leave null regions in the remaining longitudinal magnetization that will appear as corresponding nulls in the images at the tagged locations.

A number of preparation modules have been developed to perform the tagging operation. While some highly specialized tagging methods have been developed to effect arbitrary spatial tagging patterns, we limit the discussion here to the generation of tagging patterns that comprise regularly spaced parallel lines or grids, and that use the FT approximation to model the effects of RF pulses.

The DANTE RF pulse scheme, which comprises a train of very short RF pulses, is a useful basis upon which MRI tagging procedures can be developed. An idealized DANTE pulse can be denoted mathematically as

$$f_{\mathrm{DANTE}}\left(t\right)={\delta }_{\Delta t}\left(t\right)=\sum _{n=-\infty }^{\infty }\delta (t-n\Delta t)$$ (12)

for which FT theory shows that the frequency spectrum comprises a comb with spacing Δν = 1/Δt. Practical implementation of the sequence must employ a finite length comb with RF pulses of nonzero duration and finite amplitude

$$f_{\mathrm{DANTE}}\left(t\right)=m\left(t\right)({\delta }_{\Delta t}\ast p)\left(t\right)$$ (13)

where p(t) denotes the shape of a single RF pulse and m(t) is the amplitude envelope of the comb. The response function is now

$$S\left(\nu \right)=[M\ast \left({\delta }_{\Delta \nu }P\right)]\left(\nu \right)$$ (14)

where M(ν) and P(ν) are the FTs of m(t) and p(t), respectively. Hence, the width of the tagged comb will increase as p(t) decreases and the shape of the excited tags is controlled by m(t). As with slice selection, the frequency selective DANTE pulse is made spatially selective by the simultaneous application of a gradient while the comb of RF tagging pulses is being played.

Tagging using the DANTE pulse sequence [31], [35] is effective on small (e.g., animal) imaging systems, where relatively short high-amplitude RF pulses can be achieved. On larger, whole body systems, however, the ability to play arbitrarily short but intense RF pulses is limited. For these systems, it is more common to turn the gradient off during the transmission of each RF pulse in the comb of RF pulses, yielding the SPAtial Modulation of Magnetization (SPAMM) tagging procedure [30]. This modification renders the individual RF excitations nonspatially selective, eliminating the requirement that the RF pulses be short to avoid excessive modulation of the response by P(ν).

Between the RF pulses, the gradient pulse causes the magnetization vectors to acquire phase in proportion to their position in the tagging direction. Those vectors that acquire a phase of 2πK radians (for integer K) from each gradient pulse will experience the full, combined flipping effect of all the RF pulses. However, for other vectors, the effect of the RF pulses is generally much less coherent, and the combined effect over many RF pulses is negligible.

In practice, the tag spacing must be chosen such that tag pairs can be resolved by image processing, requiring 5–7-pixel separation between tags. Doubling the tagging density to improve the spatial resolution of the motion data generally requires a doubling in image resolution, which results in lower SNR. A method to overcome this is to perform the original tagging procedure twice, with the tags shifted by half the tag spacing. Multiplication of these images together provides an image with half the original tag spacing [36].

A typical SPAMM tagging pulse scheme is shown in Fig. 4. The scheme to create a single set of parallel stripe tags involves the application of 5 to 7 400-μs RF pulses to tag each spatial direction, sufficient to achieve a combined flip angle of 90°–180°. The tagging gradient is blipped (i.e., a quick gradient on and off) between each successive RF pulse in the comb; the time integral of each blip determines the inverse tagging separation. After the comb is played out, a large spoiler gradient is played in a direction orthogonal to the tags to dephase the excited fingers of magnetization. Grid tags are created by the successive creation of two sets of parallel stripe tags with tagging gradient pulses oriented orthogonal to each other.

Fig. 4.

A typical SPAMM tagging pulse scheme to create a grid from two sets of parallel stripe tags at 45° and 135° angles on the imaging plane. For each tagging direction, a series of RF pulses that are separated by tagging gradient blips are used. After each set, a spoiler gradient is played to dephase the residual horizontal magnetization. After these tagging pulses, standard imaging pulse sequences will follow.

Once created, the encoded tagging pattern decays over time as the magnetization recovers by longitudinal relaxation with time constant T₁, as discussed previously. The myocardium has a T₁ of approximately 850 ms, so that potentially, tag contrast can persist throughout an entire cardiac cycle. In practice, the imaging process further accelerates this rate of tag fading. In each successive TR, a α-flip angle RF excitation pulse samples the tagged component of the magnetization, reducing it by a factor cos(α): the available contrast is, therefore, rapidly depleted during the early cardiac phases. In addition to depleting the tagging pattern, longitudinal relaxation causes regrowth of the untagged image term, producing an apparent gradual increase in the signal at the tagged locations over the cardiac cycle, complicating the identification of the tags in late diastolic images. The complementary SPAMM (CSPAMM) method [37] provides an effective method to even out the sampling of the tagged magnetization, so that the tagging contrast remains constant throughout the cardiac cycle. In CSPAMM, two successive 1–1 SPAMM imaging procedures are performed with a phase cycling of the second tagging RF pulse. Subtraction of the two sets of images eliminates the relaxed/untagged term, providing tagged images in which the tags remain nulled throughout the cardiac cycle. CSPAMM also employs a scheme of ramped imaging flip angles [38] tuned to the tissue T₁ which are contrived to sample the tagged magnetization in such a way that the contrast between the tags and myocardium is constant throughout the cardiac cycle. Compared to nonramp-flipped imaging, tag contrast is reduced in the early systolic phases and enhanced in the later diastolic phases.

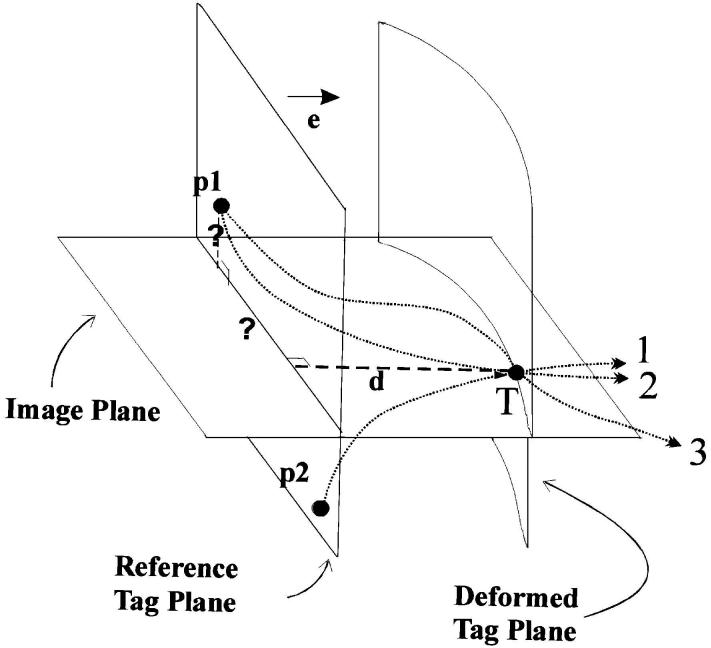
The measured tag deformation at a single tag point contains only a unidirectional component of its past motion, from tagging to imaging time (see Fig. 5). In order to achieve a full 3-D tracking of any point through time, the information coming from different tagging sets has to be combined and interpolated in space and time. The classical analysis of TMRI contains three steps: 1) segmentation of the myocardium by drawing endo- and epicardial contours which is routinely done interactively [39] or semiautomatically [40]; 2) detection of the tag points for each slice, tag orientation, and cardiac time frame; and 3) fitting a motion field (or tissue model) using three (or two for 2-D analysis) orthogonal 1-D displacement information coming from all the tag detected points.

Fig. 5.

The tag point displacement d, which is measured at the tag point T at a given time, gives only one component of the past trajectory, so it cannot be mapped back uniquely. For example, point T might originate from p1, or from p2. The correct matching point p1 at the undeformed state (at tagging time) can only be found by incorporating the tag displacement information coming from other tag planes. Using all tags at a given time frame, we can locate point p1, but we cannot be sure of its trajectory (lines 2 and 3 are two of the many possible paths). Using the matching points at every time frame, we calculate a final forward motion field and find the correct trajectory.

Several approaches have been taken for the various steps in the past. For the myocardial contour detection and tag analysis, we can name the approach of Guttman et al. [40], [41] or the approach of Axel et al. [42], [43], which also includes finite element-based cardiac modeling tools. Most of the differences in the various techniques come from the underlying motion model once the tag points are identified [44]. Some of them rely on specific geometry of the chambers and utilize a specific coordinate system: e.g., prolate spheroidal [45] or planospherical-based approaches [46] for the left ventricle (LV). Other techniques rely on finite element models. In the work of O'Donnell et al. [47], volumic superquadric with parametric offsets; in the approach of Part et al. [47], volumic deformable superquadric; and in Young's work [49], 16-element cubic polynomials provide the model for the finite element bases. In a completely different approach, the myocardial wall is decomposed into a finely spaced mesh and displacement at each node is constrained via finite difference analysis [50]. This method has been recently improved to give unsupervised strain reconstruction on the LV [51].

B-spline-based methods have been proposed because they provide several attractive properties like parametric continuity, compact representation of the information, local support, and differentiability [52]. Several B-spline-based techniques have been employed in the past to describe deformed tags: Moulton et al. [53] utilized them to describe the deformed tag planes as surfaces, but they used a global polynomial basis function expansion for the final forward tracking. In the first approach of Amini et al. [54], tags were segmented using a 2-D coupled B-snake grid; they later extended their approach to 3-D [55]. A step-by-step derivation of a B-spline-based four-dimensional (4-D) (3-D plus time) motion field [tagged tissue tracker (TTT)] is also proposed and evaluated in vivo [56]-[58]. Examples of tag strain (E) analysis (TEA) and TTT analysis are given in Section III-A.

Most of the methods proposed in the literature for TMRI-based motion analysis separate tag detection and motion field fitting, but several combined approaches have also been proposed [59], [60]. The recently developed harmonic phase imaging (HARP) technique has the potential of rapidly detecting tag locations without the need for myocardial segmentation [61]-[64]. HARP derives the motion information from the noncentral spectral peaks in the frequency domain. When tagged images are Fourier transformed, the resulting k-space reveals multiple spectral peaks. When the first peak is isolated and inverse Fourier transformed, the phase contours in the resulting complex valued image behave similarly to a conventional tagging pattern, tracking the underlying motion. At a user defined region, this approach can yield close to real-time strain analysis. A myocardial segmentation method with a high degree of automation has also been proposed for HARP making a more automated myocardial motion analysis feasible [65]. The HARP approach can also be used to acquire faster motion encoded images by tailoring the MR pulse sequence. The acquisition approach of HARP (FastHARP) will be covered more in Section II-F.

D. Phase Contrast Magnetic Resonance Imaging

A different approach to motion analysis is based on the sensitivity of the phase of the MR signal to motion. It was intended initially for blood flow measurements [65]-[67], but it is now used to obtain strain measurements of the myocardium [68]-[73].

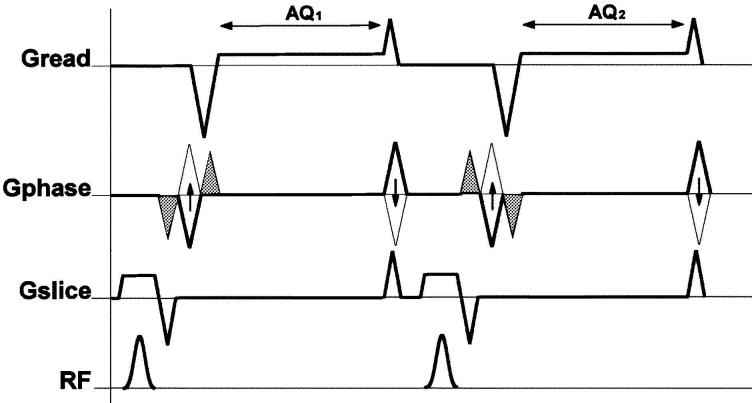
This technique gives pixel-by-pixel value for the underlying tissue's velocity. The basic principle is to acquire two datasets with two different velocity encoding gradients but otherwise identical acquisition parameters and to subtract the two phase images (see Fig. 6). The resulting difference image will be proportional to the flow (or tissue motion) if the solution (or underlying tissue) can be assumed to have a constant velocity during the acquisition window.

Fig. 6.

Basic pulse sequence diagram unit of a conventional PCMRI. For each line of k-space acquired, two scans are acquired. Velocity encoding gradient in the phase encoding direction is indicated here by the solid bipolar gradient pair.

Velocity encoding gradients are bipolar, so they do not affect stationary protons but impart phase shifts to moving protons. The equation describing the magnetization at TE for this pulse sequence is

$$M_{\mathit{xy}}\left(\mathbf{r}\right)=\rho \left(\mathbf{r}\right)\exp (i2\pi \mathbf{v}\left(\mathbf{r}\right)\cdot {\mathbf{V}}_{\mathrm{enc}})$$ (15)

where V_enc is the velocity sensitivity of the velocity encoding bipolar gradient pulse.

In order to eliminate the phase effects of sources other than flow or motion, a reference scan is acquired. Since velocity information can be obtained only in one direction at a time, four independent measurements should be obtained to obtain a 3-D dataset. Whether imaging flow or tissue motion, careful planning of the velocity encoding gradients is necessary to eliminate aliasing or unintentional signal cancellation.

For deriving myocardial strain in PCMRI, as with the case of TMRI, there are several different numerical approaches. Van Wedeen et al. [68] calculated the strain rate tensor directly from the velocity data. Zhu et al. [71], [72] obtained a displacement field from the velocity data and then used this field to calculate the strain tensor.

E. Introduction to Pulsed Field Gradient Methods

The inherent motion sensitivity of MR was recognized shortly after the discovery of the MR phenomenon [74]-[76]. Remarkably, proposals employing the use of magnetic field gradients and FT methods for the measurement of velocity distributions [77], [78] were made even before the advent of MR imaging. Since that time, many techniques have been developed employing a common motion encoding mechanism: a pair of pulsed field gradients (PFGs). A major advantage of the PFG schemes is that they provide a direct measure of the tissue displacement, greatly simplifying image postprocessing requirements compared to either time of flight and inflow enhancement methods.

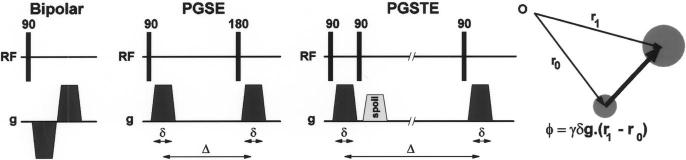
Referring to Fig. 7, the first pulsed field gradient of amplitude −g and duration δ causes the magnetization vectors to rotate with an additional frequency proportional to their instantaneous location, causing a phase accumulation θ = −γδg · r. After an evolution period Δ during which the tissue can move to a new location r(t + Δ), a second gradient pulse, logically opposite to the first, is applied. After the second pulse, the net phase accumulation is θ = γδg. [r(t + Δ) − r(t)], thus encoding the displacement that occurred during the motion evolution interval in the phase of the magnetization. By combining PFG methods with MR imaging sequences, maps of displacement can be directly obtained: the displacement is proportional to the phase of the complex-valued sample at each image pixel. The precision of the motion measurement obtainable with PFG methods is determined by the area δg of the pulsed gradients, and is independent of the spatial resolution of the image. However, it should be noted that the measured value represents a superposition of all the signals from the whole voxel, and so is an average of the motion taken over the whole voxel. Also, since the motion information is encoded as phase, the possibility of aliasing must be considered either by restricting the range of phase evolution to −π < θ < π, or by obtaining additional measurements to assist in resolving the ambiguity.

Fig. 7.

A simple PFG sequence, where two opposing gradients which are separated by a certain duration causes the magnetization vectors to first rotate and later return to their original phase value for stationary protons, causing a net phase accumulation only for nonstationary protons. Two variants of this simple PFG pulse sequence are also given: pulsed gradient spin-echo (PGSE) sequence with the introduction of a spin echo and the pulsed gradient stimulated echo (PGSTE) sequence, which stores one component of the magnetization along longitudinal magnetization (see Section II-E for details).

The phase contrast velocity encoding mechanism (described previously) can be viewed as a PFG technique in which the assumption of uniform velocity during the motion evolution period Δ (which is kept small) is made. More generally, where longer motion evolution periods are employed, uniform, bulk displacements of the magnetization produce signal phase shifts in proportion to the PFG area and interval Δ. Simultaneously, dispersive motions (diffusion, sheer, compression, and rotations) occurring in a given voxel will cause signal attenuation due to destructive interference caused by the reduction in phase coherence [77].

In practice, variants of the simple PFG pulse sequence are generally preferred. The bipolar encoding sequence is not well-suited to cardiac motion encoding because the signal: 1) decays rapidly with $T_2^{\ast }$ and 2) suffers phase distortions due to local main field inhomogeneities ΔB₀. The introduction of a spin echo yields the pulsed gradient spin-echo (PGSE) sequence, reducing attention to the effects of T₂ and refocuses inhomogeneities. The pulsed gradient stimulated echo (PGSTE) sequence [79] reduces attention to T₁ by storing one component of the magnetization along M_z, permitting even longer motion encoding periods. Recently, methods known as DENSE [80] and HARP [81] have been proposed for imaging myocardial function, which employ a stimulated echo encoding technique.

A single motion encoded sample generally does not provide sufficient information to recover the actual displacements due to the presence of additional sources (e.g., B₀ inhomogeneity, RF coil phase) of phase in the MRI signal. Fortunately, these spurious effects can largely be canceled though the use of reference scans (in which different PFGs are employed) and phase cycling schemes. These sensitivities permit the use of PFG methods to obtain measures of displacements and evaluate derivative measurements for velocity, strain, and elasticity.

F. DENSE: Displacement Encoding With Stimulated Echoes

Aletras et al. [80], [82], [83] have recently proposed a family of highly sensitive motion-encoding schemes, collectively termed DENSE, to obtain cardiac strain maps. The DENSE methods are implementations of the PFG motion encoding sequence, employing a cardiac gated PGSTE encoding scheme with increasingly complex strategies to reduce imaging time and eliminate spurious sources of artifact and error.

The original proposal [80] comprises a direct implementation of the PFG sequence with respiratory and cardiac gated gradient echo imaging (see Fig. 8). Four values of the motion encoding gradient were employed to provide a reference and sensitivity to motion in all three spatial directions in a scan time of approximately 20 min. While inefficient from an imaging standpoint, just one k-space line was collected per respiratory cycle, and the sequence demonstrated proof of concept for the technique yielding convincing maps of myocardial displacement and strain. Subsequent versions of DENSE, known as FastDENSE [82] and MetaDENSE [83], address the inefficiency of the data sampling strategy to make DENSE methods more clinically relevant.

Fig. 8.

The basic pulse sequence unit of DENSE, which employs a cardiac and respiratory gated PGSTE encoding scheme. Four values of the motion encoding gradient are needed to provide a reference and sensitivity to motion in all three spatial directions. For FastDENSE and MetaDENSE, see Section II-F.

FastDENSE employs a STEAM [84], [85] imaging method with an echotrain readout that repeatedly samples the PFG encoded magnetization during a relatively quiet point in the cardiac cycle to improve acquisition efficiency. FastDENSE permits in-plane displacement maps and related strain maps to be obtained in a single, 24-heartbeat breath-hold time duration.

G. FastHARP: An MR Acquisition Scheme Optimized for HARP Analysis

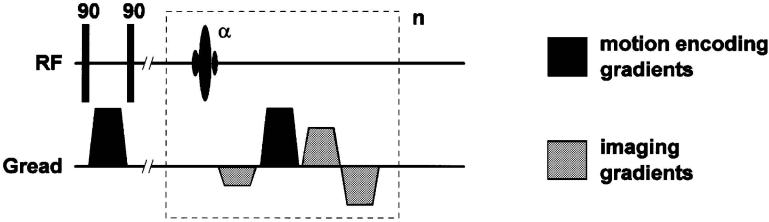
The HARP technique [61]-[64], introduced in Section II-C, was originally proposed as a postprocessing method to quantify in-plane motion from tagged MR images. The HARP method involved the acquisition of conventional SPAMM tagged images from which a single spectral peak corresponding to the fundamental tagging spatial frequency was isolated by band-pass filtering. The FastHARP pulse sequence [81] is intended to directly acquire the small region of k-space data required for HARP processing rather than acquiring a full k-space dataset.

Tagging in FastHARP is performed using the simplest tagging sequence, 1–1 SPAMM, which comprises just two 90° RF pulses. The 1–1 SPAMM sequence generates a sinusoidal tagging pattern corresponding to two tagging spectral peaks offset symmetrically from the k-space origin. Generally it is desirable to generate as few tagging spectral peaks as possible in order to maximize the SNR of the subsequent FastHARP images. This simple tagging scheme is efficient because the available signal energy is divided between only two tagging spectral peaks, maximizing the signal that is collected. Data acquisition is offset in k-space so that only a small region centered on one of these tagging spectral peaks is acquired.

A schematic of the FastHARP pulse sequence is shown in Fig. 9. The FastHARP sequence can now be related to a stimulated echo PFG motion-encoding scheme (PGSTE). The 1–1 SPAMM tagging preparation is identical to the initial PFG premotion evolution encoding pulses. For FastHARP, the data acquisition must be offset in k-space to center it on one of the tagging spectral peaks. In practice, this is achieved by modifying the prereadout dephaser gradient, by adding a gradient area to cause the desired k-space offset. The additional area required is precisely equal to that used in the SPAMM tagging procedure, i.e., the first PFG gradient pulse. Thus, the prereadout gradient pulse is a combination of a standard imaging read dephaser plus the second PFG motion encoding gradient pulse. It is clear that the stimulated echo PFG and FastHARP employ essentially identical physical principles in their motion encoding mechanisms.

Fig. 9.

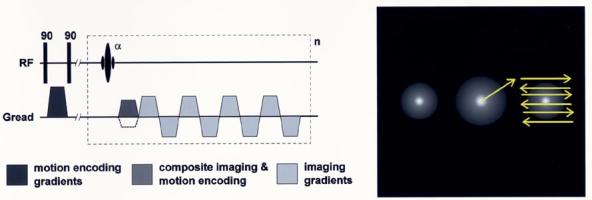
A schematic of the FastHARP pulse sequence. It starts as a 1–1 SPAMM tagging pulse, followed by a gradient, which is needed to center the k-space on one of the tagging spectral peaks. It ends with an echo-planar type of acquisition to further speed things up. If the acquisition is gated and the whole k-space is acquired in a single shot, repeating this sequence unit n times within a cardiac cycle, would yield n cardiac frames.

The method, however, faces a number of challenges. The SNR of the HARP images is limited because the available encoded magnetization must be divided among the multiple cardiac phases that are to be imaged in each cardiac cycle. Also, the regrowth of longitudinal magnetization by relaxation is a source of confounding signals in FastHARP images. Recently, an imaging scheme employing ramped flip angles and CSPAMM-like phase cycling of the second SPAMM RF pulse (albeit with a doubling of the effective imaging time) has been demonstrated [86] to address these issues. More generally, to produce datasets without breath holding, imaging must be completed for each encoding direction in just one to two heartbeats. This limits the degree of segmentation of k-space that can be performed, which in turn limits the size of the data matrix that can be acquired for a given temporal resolution, and encourages the use of highly efficient imaging methods.

Since the data processing for PFG methods is straightforward and does not require operator attention, FastHARP potentially provides a method for real-time strain monitoring of cardiac function without patient breath holding.

III. Application Examples

Here we present several applications of motion analysis techniques. We will mainly focus on cardiac implementations, finishing with an example of tongue motion analysis at the end.

A. Regional Myocardial Motion Analysis Using TMRI

MR tagging is the only imaging modality to date that has been able to quantify local contraction over the entire heart [87], [88]. A database of systolic 3-D strain patterns has been developed for the LV in healthy subjects [89]. This is a very active research area; detailed mechanical analysis of the LV has been performed to quantify changes due to ischemia [90] or pressure overload [91], to describe the effects of or recovery from surgical procedures [92], [93] and effects of drug treatments [94]. We will start next with two quick examples of LV strain analysis and later present a more detailed example of a detailed biventricular motion analysis.

Our first example for tag motion analysis is detailed strain analysis over a canine LV in various pacing conditions in a canine model [95]. Tagged MR images are analyzed with the help of a LV-specific method TEA [45] after obtaining the tags using the Findtags program [41]. Strain images in a single canine heart for two pacing conditions are shown in Fig. 10. When the ventricle is paced from the right ventricle (RV) free wall, the contraction begins at the pacing site and spreads around the LV. There is significant prestretch on the heart wall opposite to the pacing site. When the heart is paced from the LV free wall, the pattern is the same, but the origin of the contraction wave is moved to the new pacing site (not shown). When paced simultaneously at both RV and LV pacing sides, resulting electrical excitation produces a more coherent contraction pattern both in space and time (see Fig. 10). This pattern is similar to normal physiology when the electrical signal originates at the right atrium and spreads concurrently to both ventricles through a specialized conduction system.

Fig. 10.

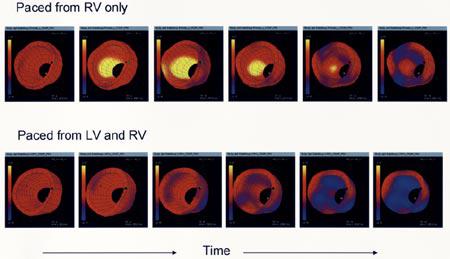
Strain images in a single canine heart for three pacing conditions. Contraction is shown as blue, stretching is yellow, and pacing site is shown with an asterisk. Evolution of strain over the LV is shown for atrium (physiological) and two ventricle-originated pacing protocols.

An important research area is devising custom designed pacing protocols for ischemic and dilated cardiac diseases [96]. In Fig. 11, a comparison of myocardial strain images from a normal and a dilated heart (dilated cardiomyopathy) is made. In the patient, an early contraction of the septum (9 o'clock) is evident, with a late contraction of the LV free wall (3 o'clock). Techniques such as these can be used to evaluate the remodeling of the heart after the onset of ischemic pathologies or during pacing [97].

Fig. 11.

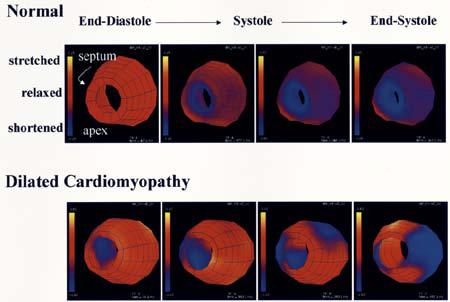
Comparison of myocardial strain images from a normal LV (top row) and an LV of a patient with dilated cardiomyopathy (bottom row).

We will now present activation time analysis using the local time-strain relationship. Data presented in this section were obtained from MRI recordings of a canine heart, which was paced from the atrium or the right ventricle (RV) by using a GE Signa 1.5 T scanner with segmented k-space acquisitions with breath-hold periods. The scanning parameters used were a 28–32-cm field of view, time to repetition of 6.5 ms, time to echo of 2.1 ms, 256 × 96 acquisition matrix, ±32-kHz bandwidth, two to three readouts per movie frame, in-plane spatial resolution of 1.25 × 3 mm, and slice thickness of 6–7 mm. We employed a motion analysis method based on a 4-D B-Spline tensor representation [56], [57]. Local deformation gradients were obtained by using this parametric model, and 3-D strain values were estimated by using finite strain tensor analysis computed over a mesh located at mid myocardium of the RVs and LVs. The motion field and activation time calculations are done automatically once the tags have been detected. Two ventricles are modeled differently; the LV was modeled as a deformed cylinder, and the RV as a deformed half cylinder. A mesh is defined on these cylinders, and from the motion analysis, we obtain the time series of strain on each mesh point (see Fig. 12). These graphs are subsampled dramatically in both directions for display purposes. We have opted to use circumferential strain (Ecc) values in our analysis because the orientation of the major muscle fibers in mid-myocardium are known to be in that direction [98].

Fig. 12.

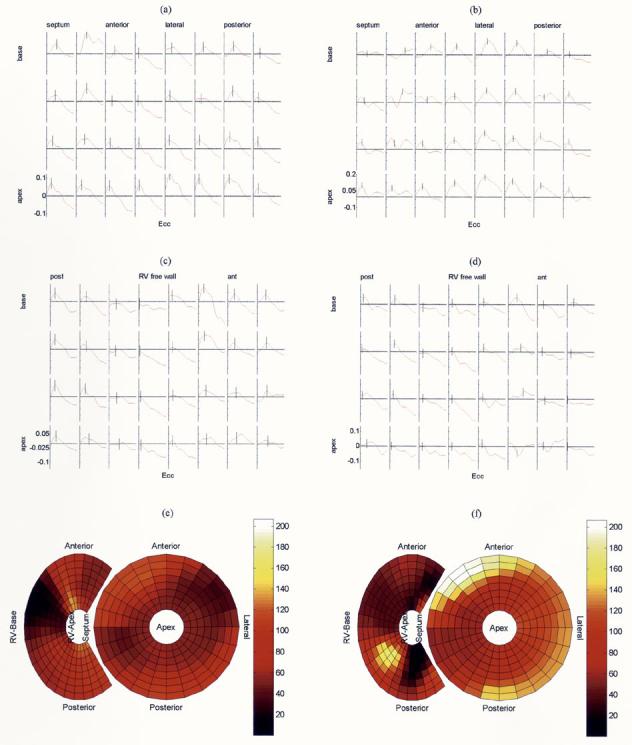
Strain values over the LV during systole of a canine heart for: (a) atrial excitation and (b) RV excitation. Y -axis represents strain; −0.1 means 10% shortening; positive values represent stretching. Calculated activation times for each location are displayed on the small strain evolution graphs with a small vertical line. The small plots in each row represents mesh points arranged circularly in a short axis cut of the heart. Coming down on each column represents moving from the base of the heart toward its apex. Strain values over the RV during systole of a canine heart and calculated activation times are displayed in the middle again for: (c) atrial excitation and (d) RV excitation. (e) and (f) Corresponding biventricular bulls-eye plots of activation times are shown. Note that the widened activation time scale (in milliseconds) and propagation of activation from right to left for RV pacing [see Fig. 12(f)].

The activation time has been chosen as the time of peak Ecc strain value. When no peak is present, neighborhood-based correlation is employed as in [95]. The calculated activation time values are further scanned for local activation wave direction inconsistencies to eliminate velocity computation at sink or source locations. RV and LV analyses are done independently.

If we compare the time-strain plots for both pacing conditions [see Fig. 12(a)-(d)], for atrial pacing, we obtain similar local strain time graphs over the LV and RV. Strains decrease almost linearly during ventricular systole. On the other hand, for ventricular pacing, we observe double peaks due to initial or delayed stretch; definitely a more complex time-strain pattern is observed with the start of contraction delayed at certain locations.

Another helpful display method for showing the activation times over both ventricles is the bulls-eye graph [see Fig. 12(e) and (f)]. In this graph, apex of the LV is the central ring, and the basal part is the most outer ring. RV is shown on the right side with partial rings; color represents the activation time from a reference time in imaging. It provides a quick display of the overall activation pattern of the heart.

In bulls-eye plots, for atrial activation, we see relatively small activation time range (134 ms) over both ventricles. Mechanical activation seems to start at several locations at once and proceeds in various directions. Some of the basal portion of the LV is activated last. These findings are compatible with the known physiological excitation patterns through the Purkinje system. This is also supported mostly by higher propagation speed than ventricular pacing (not shown). However, we should note that a definite distinction between propagation over the Purkinje system or myocardium itself cannot be made definitely using this data. On the ventricular paced heart, clearly, a propagation wave can be identified, starting from the RV and proceeding toward the LV. This, and slower speed of activation wave propagation, results in a higher range of the activation times for the LV (206 ms).

B. Ventricular Blood Flow Analysis Using PCMRI

Our PCMRI examples come from the work of Thompson et al. [99]. In this study, a high temporal resolution PC technique is employed. Improvement by a factor of two in the temporal resolution was achieved by acquiring the differentially flow-encoded images in separate breath-holds. Additionally, a multiecho readout was incorporated into the PC experiment to acquire more views per unit time than is possible with the single gradient-echo technique. A complete set of images containing velocity data in all three directions was acquired in four breath-holds on normal volunteers, with a temporal resolution of 11.2 ms and an in-plane spatial resolution of 2 mm × 2 mm. For the measurement of all three velocity components, phase-difference images were calculated using velocity encoded data. Sample velocity images in three logical axes (V_x, V_y, V_z) and a magnitude image on a mid-cardiac short axis plane are shown in Fig. 13. Horizontal and vertical gradients can be observed for V_x and V_y images over the myocardial wall of the LV, since it predominantly contracts toward its center. On the other hand, there is a uniform through-plane motion of the myocardium for this slice, which is displayed nicely on the V_z image.

Fig. 13.

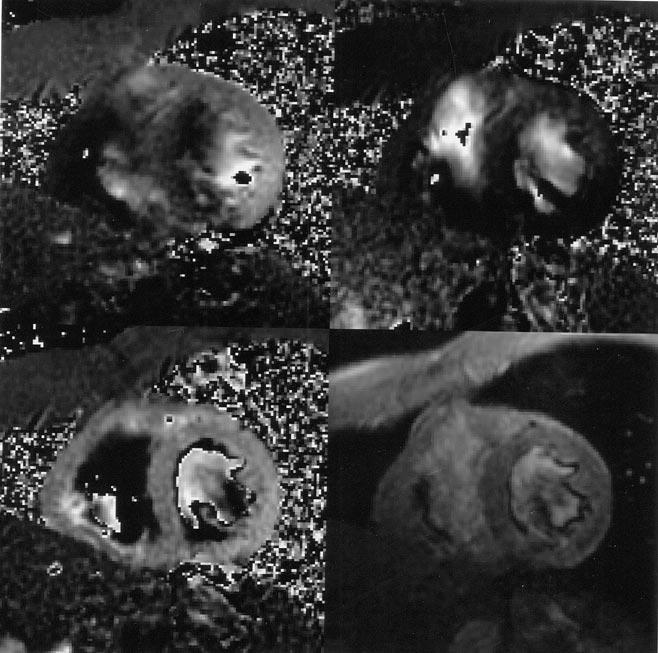
Cardiac velocity images in all three directions at end systole. Top left: V_x, velocity in the horizontal direction. Top right: V_y. Bottom left: V_z. Bottom right: magnitude image. The in-plane resolution is 2.0 mm × 2.0 mm for both the magnitude image and all the vector images. (Images are courtesy of R. Thompson, National Institutes of Health, National Heart, Lung, and Blood Institute, Bethesda, MD).

The finer details of myocardial motion, like twisting, require combined vector analysis of the velocity images. For example, vector analysis at this high frame rate can also be used to analyze fine details of blood motion patterns (see Fig. 14).

Fig. 14.

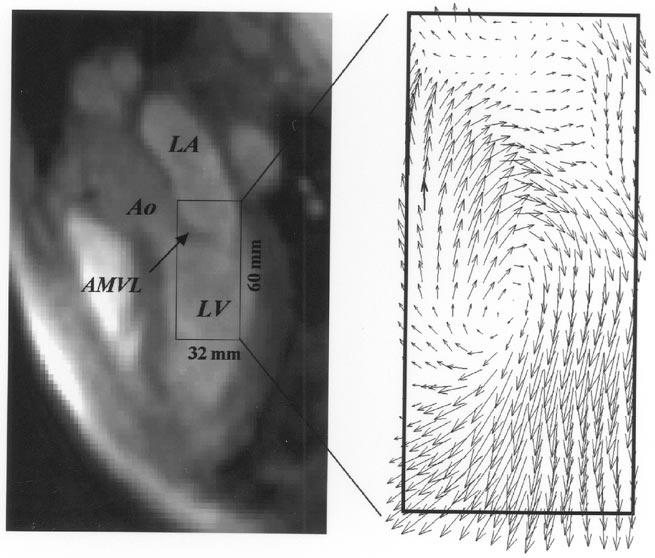
Left: a single three-chamber image (frame 59) from 100 frames reconstructed from a multiecho, multibreath-hold PC acquisition from a healthy volunteer. Right: a velocity vector plot calculated from the in-plane velocities, from the image plane shown on the left, for a 32- × 60-mm rectangular region of interest. The in-plane resolution is 2.0 × 2.0 mm for both the magnitude image and the vector field image. LA = left atrium; Ao = aorta; LV = left ventricle; AMVL = anterior mitral valve leaflet. (Images are courtesy of R. Thompson, National Institutes of Health, National Heart, Lung, and Blood Institute, Bethesda, MD).

C. DENSE and Cardiac Motion Analysis

To date, DENSE methods have concentrated on obtaining high precision and high-resolution measurements. To maximize the available SNR and permit high-resolution imaging, the sequences acquire an image only at one phase of the cardiac cycle. Strain measurements are then obtained for the total systolic contraction.

FastDENSE acquisitions have been initially reported with a 128 × 96 acquisition matrix, 2.5-mm spatial resolution, and acquiring a single cardiac phase (26-ms temporal resolution) with a total imaging (i.e., breath-hold) time of 24 heartbeats [82]. The MetaDENSE methodology reduced the breath-holding time for a similarly specified scan to just 12 heartbeats. MetaDENSE [83] improves the image acquisition efficiency, by utilizing a train of 180° refocusing pulses resembling a fast-spin-echo (FSE) readout, instead of the STEAM-EPI-based scheme. The FSE readout employed in DENSE is long (∼ 100 ms), and so must be performed during a quiescent period of the heart cycle. In addition, the sequence incorporates several features to reduce artifacts and associated errors in the displacement encoded data. The sequence employs a 180° inverting RF pulse approximately half way through the motion encoding interval in order to effectively nullify the (nonmotion encoded) signals from tissue that relaxed during the evolution period. In effect, this inverting RF pulse serves the same purpose as the RF pulse phase-cycling scheme in CSPAMM without doubling the image acquisition time, but can only nullify the signal for a particular T1 species (e.g., myocardium), and cardiac phase.

Fig. 15 shows the results of a typical MetaDENSE study of a mid-ventricular short axis slice from a normal volunteer. The superimposed vectors represent the direction of principal strains, which corresponds to local circumferential and radial strains. These two different types of strain patterns can be identified by the negative and positive eigenvalues, which are used in the color-coding of line segments in Fig. 15. In a normal myocardium during systole, a uniform circumferential shortening is observed due to myocardial fiber orientation. The myocardial volume is kept almost constant; therefore, circumferential shortening is accompanied by a similarly uniform radial thickening in normal individuals.

Fig. 15.

Sample meta-DENSE-based 2-D strain analysis results from a normal volunteer overlaid on the corresponding a mid-ventricular short axis slice. The superimposed lines represent the direction of the principle strains with colors representing their eigenvalues. (Images are courtesy of A. Aletras, National Institutes of Health, National Heart, Lung, and Blood Institute, Bethesda, MD).

D. Example HARP Analysis for Cardiac Motion

Development of FastHARP has been focused toward rapid imaging for the real-time monitoring during cardiac stress function testing where conventionally tagged imaging suffers from several drawbacks due to the requirement for repeated breath-holding and the lengthy time required for image postprocessing. FastHARP currently employs an interleaved, 8-echo echotrain (EPI) acquisition to collect a 32 × 32 matrix at 9 mm spatial resolution. Although this resolution is low compared to conventional anatomical imaging, it is comparable to the resolution of the motion data (i.e., the tag spacing) in a conventionally tagged image.

In each heartbeat, the sequence yields 12–20 cardiac phases (46-ms temporal resolution) of motion-encoded data, with one in-plane spatial direction being encoded. Two heartbeats are required for complete displacement and strain mapping, because, as with other PFG methods, reference scans are required to suppress spurious sources of phase in the images. These can be either acquired at the beginning of scanning, or interleaved with the real-time cardiac strain mapping. Nonbreathheld and breathheld examples of acquisition are given in Fig. 16 along with corresponding standard SPAMM images for comparison. The displayed FastHARP images have been reconstructed from original data with synthetic tags to make comparison easier.

Fig. 16.

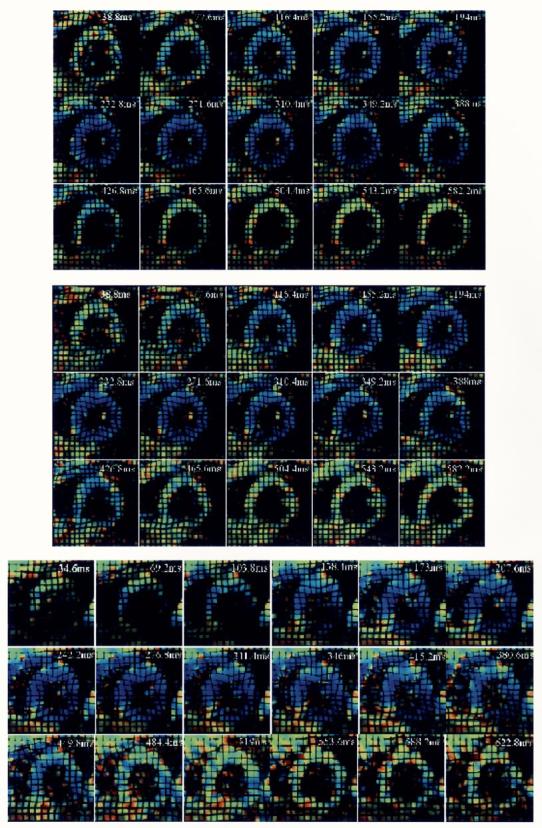
(Top) Nonbreathheld and (middle) breathheld examples of fastHARP acquisition. Both image sets are acquired in two heartbeats. These images have been reconstructed from original data with synthetic tags to resemble (bottom) the equivalent tagged image data set. They are also colored displaying contraction (blue) and relaxation patterns all around the ventricle wall in a normal volunteer. (Images are courtesy of S. Sampath, Johns Hopkins University, Baltimore, MD).

E. Motion Analysis of the Tongue

As an example of the motion analysis of a noncardiac tissue, we provide here an example of the analysis of tongue motion. Such an analysis can give important clues about speech control and causes of various speech pathologies. Imaging the movement of the tongue is challenging because the selected technique must image without interfering normal tongue motion and must be capable of recording its rapid motion. Different research groups have used different techniques, including X-ray [100], X-ray micro-beam [101], electropalatography [102], electromagnetic articulography [103], electromyography [104], [105], ultrasound (US) [106], and MRI [107]-[109], the MRI being our current focus.

For the speech material a consonant-to-vowel syllable (“sha”) was chosen due to its large tongue motions and short durations (see Fig. 17). Here, a modified gated multiecho SPGR sequence in a 1.5-T GE Signa cardiac scanner is used (TR 11.3 ms, TE 1.5 ms, FA 10, ETL 8, NVP 40, BW 125, 128 × 96 matrix, NEX 0.8, FOV 30 × 15 cm, ST 7 mm, tag spacing 5 mm). For these images, only one syllable repetition per slice is used, in contrast to the work of Dick et al. [110] where a segmented k-space acquisition was used. A gating input was provided to the scanner in sync with the cue. During 1 s, 16 images are acquired for a given slice. The acquisition is repeated for all the slices. For the full 4-D (space and time) displacement and strain analysis [57], three sagittal and eight axial slices, with grid tagging, are obtained. Previously, a preliminary 2-D surface deformation analysis was done for all four syllables [111]; here we present the first 4-D tongue motion analysis as an example of noncardiac tissue motion tracking. Fig. 18 displays a 4-D compression-expansion analysis of the internal points of the tongue for tagged MR images during the utterance of the syllable “sha.”

Fig. 17.

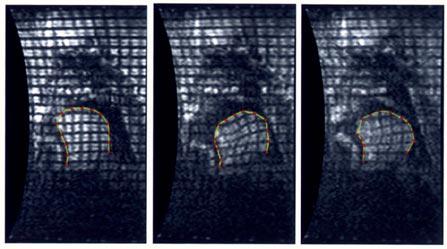
Real-time, tagged MRI images of the tongue during the syllables “sha” at 164, 350, and 600 ms. Intersection of the tags with the tongue surface are also displayed at each time frame.

Fig. 18.

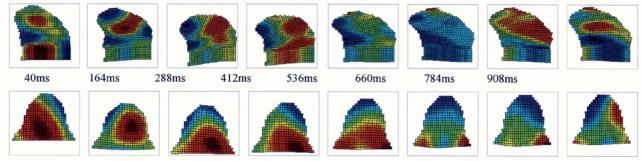
Four-dimensional compression-expansion analysis of the tongue during the utterance of syllable “sha.” Top row: we observe two compression regions in sagittal view at the first time frame: one in the upper-center and the other in the bottom-left part of the tongue. The compression region seen at the first time frame disappears later and we observe a huge compression region at the back of the tongue in the end. Bottom row: for the axial images, we observe compression in the middle-back and expansion in the front regions of the tongue in the first time frame. Compression in the middle-back region observed in “sha” at the first time frame, moves to the back of the tongue and disappears in the last time frames. At the end of the utterance “sha,” expansion is observed in the tip.

IV. Discussion

It is known for a long time that myocardial ischemia due to lack of adequate blood supply to the heart muscle causes myocardial wall motion abnormalities [112], [113]. Actually, local motion abnormalities are shown to be one of the earliest signs of the ischemic disease, when most of the global measures are kept normal by compensating mechanisms in other regions of the heart [114], [115]. Precise and accurate methods for measuring myocardial motion can be helpful in the early diagnosis and accurate staging of diseases and quantitative evaluation of new treatment modalities.

In this paper, we reviewed several techniques that are unique to MRI to measure precise tissue motion, with a special emphasis on the heart. Various imaging techniques allow the acquisition of dynamic sequences of 3-D (4-D) heart images: various nuclear medicine techniques (like gated SPECT), X-ray CT, and US. There are several advantages of MRI over others: high spatial resolution, excellent soft tissue contrast, intrinsic 3-D acquisition, ability to acquire images from any arbitrary plane, and absence of ionizing radiation.

Although we have focused on unique methods for MRI, classical motion analysis approaches can also be applied to MR derived images. These techniques utilize 4-D datasets (surfaces or volumes) and are essentially similar among all imaging modalities (e.g., CT, US). Due to high tissue contrast and resolution, which is significantly improved with the reintroduction of balanced gradient imaging techniques [116], such approaches are usually much easier to implement for MR. Historically, cardiac motion analysis, especially of the LV, has been the main focus of such approaches. Generic deformable surface models [117]-[119], models exploiting curvature information [120]-[123], 4-D models [124], or models with temporal constraints [125], [126] have been previously described for cardiac motion analysis, and they are all based on surface tracking.

The major shortcomings of surface-based approaches are the inability to display transmyocardial strain differences and the difficulty in describing the rotational component of cardiac motion. The clockwise and counterclockwise twisting of the LV during contraction and relaxation has received significant attention in recent studies, and disturbances in these complex motion parameters are being investigated as early signs in various pathologies [127], [128].

The methods that are described in this paper (TMRI, PCMRI, DENSE, and HARP) are unique to MRI because they allow the tissue motion to be measured more directly. A summary and side-by-side comparison of these techniques is presented in Table 1. In TMRI, temporary markers are put within the tissue and then followed over time. In PCMRI, DENSE, and PCMRI, we essentially get a velocity or displacement image. These are in sharp contrast with the inferred motion, which is derived from surface or volume matching techniques.

Table 1.

A Quick Comparison of Different Motion Analysis Techniques That Are Unique to MRI

Feature	Phase Contrast MRI (PCMRI)	MR Tagging	Pulse Field Gradient (PFG) Methods: HARP, DENSE
Time Resolution	- Velocity-encoding pulses require 4ms in current scanners. - Phase difference calculation required (at least two acquisitions). - Time integration required for desplacement estimate.	- Simple tagging pulses take ∼3 ms in each direction. - Time resolution set by imaging method. - Tag pattern detection is very insensitive to motion.	- HARP: Multiphase acquisition is possible, time resolution is set by imaging method. - DENSE: Currently implemented only for a single phase.
Spatial Resolution	- Resolution is determined by the dimensiion of the derivative operator (two pixel) minimum and the SNR of the velocity induced phase shift.	- Limited by the density of tagging pattern.	- Limited by the spatial resolution of imagging method. - In general, higher spatial resolution with DENSE.
Acqusition Time	- Four acquisitions required for 3D deformations.	- Depends on method used: 1-3 acquisitions required for 3D deformation.	- Depends on method used: 1-3 acquisitions required for 3D deformation.
MRI Physics	- Phase shifts from other processes can interfere with velocity encoding. - Steady state must be maintained during acquisition. - Motion estimated can be obtained over the entire heart cycle.	- Tag fading from T1 recovery limits duration of motion tracking. - Tagging pattern detection is very robust to image artifacts. - Any imaging method can be used.	- T1 recovery limits the duration of motion tracking. - Dispersive effects of intravoxel dephasing are the main limitation.
Quantification and Visualization	- No segmentation required for quantitative estimates. - Strain cannot be viewed directly from the raw images. - Strain-rate computed directly from spatial gradients of velocity.	- 2D myocardial strain can be observed directly from the deformation patterns on the images.	- Allows direct quantification of displacement. - Segmentation not necessary. - Synthetic tags can be used.

Of course, the surface-based tracking techniques and methods based on TMRI (or other MR specific methods) are not mutually exclusive. For the tag-based motion analysis of the whole heart, a combined approach is needed, because tagging is not possible on the relatively thin walls of the atria. Even for the ventricles, using both techniques together in combined optimization has been proposed but has not been fully developed [129].

Detailed mechanical analysis of the heart is certainly an important research tool. Tagged MRI has shown to produce mechanical activation maps that are closely correlated with the corresponding electrical activation maps for the LV [130], [131]. Generating electrical activation times requires an invasive approach and can be obtained only on the endocardial surface using specialized catheters, or accessible pericardial surfaces. As explained in Section III-A (also in Figs. 10-12), a detailed mechanical analysis can be performed for both ventricles, and combined mechanical activation maps can be created [132], [133].

Comparative analysis between these different approaches of motion tracking in MR is rare in the MR literature, because most of the methods remained experimental and restricted to certain labs (and to certain type of scanners). Declerck et al. [44] proposed a platform for the comparison of the different techniques for TMRI and did a detailed comparison of four approaches: 1) TEA [45]; 2) discrete model-free (DMF) method [50]; 3) 4-D tag strain (E) analysis (FTEA) [46]; and 4) TTT [57]. All of these methods need the segmented tag points as inputs and provide different approaches to motion field fitting: continuous (TEA, FTEA, TTT) or discrete (DMF) in space, using LV specific (TEA, FTEA) or the standard Cartesian coordinate system (TTT, DMF). These methods have been compared using synthetic, experimental animal and human data, and their performance has been quantified. They conclude that the choice of a specific method has to be based on the individual requirements for noise sensitivity and spatial resolution, which has been quantitatively classified. For example: DMF uses the least amount of smoothing; therefore, it has the highest spatial resolution, but the highest noise sensitivity. FTEA uses more smoothing than the other three and is the least noise sensitive, but it has the lowest spatial resolution. Despite these small differences, they concluded that all four methods produce strain maps that are useful for characterizing myocardial function with great precision [44].

Recently, Aletras et al. [134] compared the results of TMRI with DENSE in six normal volunteers. Displacement and circumferential shortening measurements were found to be very similar between the two methods. On the other hand, radial thickening measurements of the LV were significantly different. He suggested that the overestimation in TMRI was possibly due to the undersampling of motion along the radial direction. A disadvantage of the tagging techniques is the fact that the spatial resolution of the functional myocardium compared to the anatomic resolution of the underlying images is reduced by a factor of three to five in linear dimensions due to the need to be able to resolve the tags in the images. On the other hand, tagging can provide a time series of images through the cardiac cycle, which may aid in the identification of abnormal contraction. The DENSE methods currently provide only a single measure of overall systolic contraction. Further comparative research is certainly needed among different techniques.

Although FastHARP was developed based on the framework of magnitude tagging, further analysis reveals that it is, in effect, a variant of the PFG technique. The initial premotion-evolution encoding schemes are identical: an initial nonselective excitation, subsequent encoding with a pulsed gradient, which is followed by z storage of the encoded magnetization by a second nonselective RF pulse (see Fig. 9). After the motion evolution interval, the stored magnetization is reexcited with a slice selective RF pulse. The offset k-space data acquisition is achieved by modifying the prereadout dephaser gradient pulse, adding gradient area equal to that used in the tagging preparation gradient pulse. This additional pulse area is, effectively, the second PFG pulse.

With the improvements of PCMRI techniques [99], it is now possible to achieve adequate resolution appropriate for imaging blood flow within the cardiac chambers, in addition to conventional vessel flow imaging. In the past, such flow patterns due to valve opening and closures, and indirectly pressure gradients, could be examined only by Doppler techniques. PCMRI with both high temporal and spatial resolution can offer some advantages; e.g., it has neither an acoustic window nor a source angle variability problem.

The heart motion is periodical and is well suited for gated MRI techniques. Other moving tissues such as the tongue provide additional challenges for MRI. For example, human tongue has a complicated muscular structure that is not easily explained by the deformation patterns seen on the surface of the tongue during speech. MRI-based motion analysis is shown to provide an important insight into the internal dynamics of the tongue [135], and in Section II-G we provided a preliminary sample result of a 4-D compression analysis of tongue during utterance of “sha” using tagged, real-time MRI.

Other noncardiac applications of tagged MRI is certainly possible; the limitation comes mostly from the tag fading and the difficulties with synchronization of the motion with image acquisition, which requires a special hardware for each application. An interesting example is presented by Huszar et al. [136], where they quantified the chest wall deformation during cardiopulmonary resuscitation (CPR) using tagged MRI. The development of effective CPR machines or techniques, or understanding the effects of external trauma on internal organs, can be effectively examined by the techniques presented here. Lung motion is also examined during normal respiration using MRI tagging [137]. When the flow is relatively slow and uniform, as it is the case for the cerebrospinal fluid, MRI tagging can also be applied directly to quantify fluid motion [138]-[140].

Another set of applications of dynamic MR imaging involves detailed evaluation of certain internal tissue movements that can occur physiologically or under pathological conditions. In these applications, the subject is asked to perform certain maneuvers (e.g., straining) while inside the magnet, and the newly acquired images are compared with the control images. A common target of this type of application is the assessment of pelvic floor defects [141], [142]. Although the initial aim is to confirm the initial diagnosis and evaluate the exact anatomic defect of deeper structures, detailed quantitative analysis using the advanced techniques in this paper can be performed.

Standard 1.5-T closed MR scanners have proven their value in the evaluation of normal tissue anatomy and its integrity in the case of general trauma [143]. Dynamic MR imaging of the musculoskeletal system is usually performed in dedicated or open MR systems. With the advances of imaging technologies, low-field MRI systems claim now specificity and sensitivity that are equal to or better than high-field systems in identifying many musculoskeletal pathologies, e.g., identifying and characterizing meniscal tears [144]. These low-field systems allow a wide range of dynamic studies; these are routinely analyzed only visually or using surface-based motion-tracking techniques.

In musculoskeletal imaging, detailed kinematical models can be built using MRI-derived 3-D structures. Example applications are the analysis of the motion of the spine [145], patella [146], wrist [147], [148], ankle [24], [25], shoulder [26], or building realistic models for general locomotion [149]. Although, these are extremely valuable as a research tool, such dynamic MR-derived models are not yet in routine clinical use.

Faster and faster MRI techniques provide not only better resolution in space and time, but also more and more data available to the clinicians. Efforts should be made to provide physicians with only a small number of relevant parameters necessary to establish a reliable diagnosis or fast staging of a given disease. For cardiac motion analysis, the exact clinical importance of such detailed motion analysis has not been fully answered, requiring extensive long-term studies in this area.

Biographies

Cengizhan Ozturk (Member, IEEE) received the M.D. degree from Marmara School of Medicine, Istanbul, Turkey, in 1990, the specialization in physiology from Cerrahpasa Medical School, Istanbul University, Istanbul, Turkey, in 1994, and the Ph.D. degree from the School of Biomedical Engineering, Science and Health Systems, Drexel University, Philadelphia, PA, in 1997, with a dissertation on the development of a new 3-D computer vision technique (perfect submap based structured light) to acquire 3-D surface images of objects and finding better methods of aligning them.

From 1997 to 2000, he was a Postdoctoral Research Fellow at Medical Imaging Lab, Department of Biomedical Engineering, Johns Hopkins University, Baltimore, MD, where his main research area was the development of new methods for rapid physiologic evaluation and tissue tracking for cardiac MRI images, evaluation of right ventricular function, atrial motion, and development of a four-chamber motion field. Since 2000, he has been an Assistant Professor at the Institute of Biomedical Engineering, Bogazici University, Istanbul, Turkey. He is currently performing research on real-time MRI and magnetic resonance guided medical interventions at the National Institutes of Health, National Heart, Lung, and Blood Institute, Bethesda, MD.

J. Andrew Derbyshire received the B.S. degree in mathematics and the M.S. degree in control engineering from the University of Sheffield, Sheffield, U.K., in 1988 and 1989, respectively, and the Ph.D. degree from University of Cambridge, Cambridge, U.K., in 1995. His Ph.D. research on echo-planar and motion sensitive MRI methods was conducted at the Herchel Smith Laboratory, University of Cambridge, under Dr. T. A. Carpenter and Professor L. D. Hall.

From 1995 to 1998, he was a Postdoctoral Fellow with the Imaging Research Group, Department of Medical Biophysics, University of Toronto, Toronto, ON, Canada, working with Drs. M. Henkelman, S. Hinks, and G. Wright on the development of MRI technologies for surgical intervention, in a joint project with General Electric Medical Systems, Toronto, ON, Canada. From 1998 to 2000, he was an Advanced Development Engineer with General Electric Medical Systems, developing cardiovascular MRI as a clinical product while working as a visiting scientist in the Radiology Department, School of Medicine, Johns Hopkins University, Baltimore, MD. In 2000, he joined Dr. E. McVeigh's group as a Staff Scientist, Laboratory of Cardiac Energetics, National Institutes of Health, National Heart, Lung, and Blood Institute, Bethesda, MD. His research interests include real-time and interactive MR imaging technologies focusing on cardiovascular applications.

Elliot R. McVeigh (Member, IEEE) received the B.Sc. degree in physics and the Ph.D. degree from the University of Toronto, Toronto, ON, Canada, in 1984 and 1988, respectively. He obtained his Ph.D. under the guidance of Drs. Mark Henkelman and Michael Bronskill at the Ontario Cancer Institute, Toronto, ON, Canada, where one of the first in vivo MRI systems in Canada was installed.

From 1988 to 1999, he was with the radiology faculty at Johns Hopkins University School of Medicine, Baltimore, MD, working with Dr. E. Zerhouni developing a research program in cardiac MRI. In 1991, he joined the Department of Biomedical Engineering, Johns Hopkins, to found the Medical Imaging Program. In 1999, he established a laboratory for the development of cardiovascular interventional MRI at the National Institutes of Health, National Heart, Lung, and Blood Institute, Bethesda, MD. He has published over 100 peer-reviewed research papers.