Abstract
The purpose of this study is to couple a cellular bone homeostasis model with the pharmacokinetics (PK) and mechanism of action of denosumab, an inhibitor of receptor activator of nuclear factor-κB ligand, to characterize the time course of serum N-telopeptide (NTX), a bone resorption biomarker, following single escalating doses in multiple myeloma (MM) patients. Mean PK and median serum NTX temporal profiles were extracted from a previously conducted randomized, double-blind, double-dummy, active-controlled, multicenter study including 25 MM patients receiving escalating denosumab doses. Nonlinear denosumab PK profiles were well described by a target-mediated disposition model that includes rapid binding of drug to its pharmacological target. Fixed PK profiles were integrated into a previously reported theoretical cellular model of osteoblast-osteoclast interactions, and the NTX concentrations were linked to a resorbing active osteoclast (AOC) pool by a nonlinear transfer function. Reasonable fits were obtained for the NTX profiles from maximum likelihood estimation using the final model. Transfer function parameters, including the basal NTX level and the AOC concentration producing 50% of maximal NTX production, were estimated with good precision as 5.55nM and 1.88×10−5pM. An indirect response model for inhibition of NTX production by denosumab was also used to characterize the data. Although this model adequately characterized the pharmacodynamic data, simulations conducted with the full model reveal that a cellular model coupled with clinical data has the distinct advantage of not only quantitatively describing data but also providing new testable hypotheses on the role of cellular system variables on drug response.
Introduction
Multiple Myeloma (MM) is the second most prevalent blood cancer after non-Hodgkin’s lymphoma, affecting around 50,000 individuals, with approximately 15,000 new cases reported each year in the United States alone (Hideshima et al., 2003). The disease is characterized by the infiltration of malignant plasma cells in the bone marrow that results in genomic instability and changes in the bone-marrow microenvironment, whereby patients often develop osteolytic lesions that cause fractures and severe bone pain (Kyle and Rajkumar, 2004; Hideshima et al., 2007). These lesions are a result of imbalanced bone remodeling with increased bone degradation and decreased bone formation due to many factors, including the overexpression of receptor activator of nuclear factor-κB ligand (RANKL) and down regulation of its decoy receptor, osteoprotegrin (OPG) (Kyle and Rajkumar, 2004; Matsumoto and Abe, 2006).
The cellular components of bone remodeling are the osteoblasts, derived from the mesenchymal stem cells and responsible for bone formation, and the osteoclasts, derived from hematopoietic stem cells, causing bone degradation/resorption (Filvaroff and Derynck, 1998). The binding of RANKL, a tumor necrosis factor (TNF)-related cytokine expressed on the surface of osteoblasts, to its cognate cell surface receptor (RANK) on osteoclast precursors induces a cascade of signaling events that stimulates the differentiation of precursor cells into mature multinucleated bone degrading osteoclasts and also maintains their viability (Aubin and Bonnelye, 2000; Boyle et al., 2003). As a counterbalance, osteoblasts release another TNF-related cytokine, OPG, that binds RANKL and thus inhibits its function. Besides the key regulatory RANK-RANKL-OPG axis, there are several growth factors, cytokines, and systemic hormones (e.g., TGF-α, TGF-β, TNF-α, IL-1, IL-6, PTH and estrogen) that contribute to bone homeostasis (Roodman, 1999; Hofbauer et al., 2000; Boyle et al., 2003).
Appreciation for the RANK-RANKL-OPG pathway in bone remodeling has provided novel targets for therapeutics. Denosumab (AMG 162; Amgen Inc., Thousands Oaks, CA) is a human IgG2 monoclonal antibody that binds to RANKL with high affinity and specificity inhibiting RANKL-RANK interaction. Initial clinical trials in MM and other bone disorders have demonstrated denosumab to effectively decrease bone resorption rapidly and for a sustained period of time with minimal side effects (Bekker et al., 2004; Body et al., 2006). Currently, denosumab has entered phase III clinical trials for the treatment of bone loss in postmenopausal osteoporosis, prostrate and breast cancer, and multiple myeloma (Schwarz and Ritchlin, 2007).
Limited PK/PD analyses of denosumab using noncompartmental approaches have been reported. Since rodent RANKL is not recognized by this drug, preclinical data have been limited to studies conducted in cynomolgus monkeys (Kostenuik, 2005). Initial phase I studies in MM, breast cancer patients, and postmenopausal women, reveal dose-dependent pharmacokinetics of the drug following subcutaneous (SC) administration (Bekker et al., 2004; Body et al., 2006). The drug exhibited rapid and prolonged absorption with the average maximum serum concentrations occurring between 7 and 21 days post-dose and a relatively long elimination half-life of 33.3 days in MM patients. This study monitored the levels of urine and serum NTX, which represents a bone resorption biomarker derived from N-telopeptide of type I collagen. NTX levels rapidly declined after a single SC dose of denosumab. The onset of drug action was within a day and lasted through 84 days for the higher dose levels (Body et al., 2006).
On the other hand, mathematical models capable of describing various factors controlling bone homeostasis on the cellular level have been developed. A simple model by Komarova and coworkers (2003) describes the autocrine/paracrine regulation of osteoclasts and osteoblasts. Martin and Buckland-Wright (2004) developed a model that includes the RANK-RANKL-OPG pathway; however, its primary purpose is to describe in vitro bone resorption. A model by Lemaire and colleagues (2004), describes the tight coupling between osteoblasts and osteoclasts during the remodeling process and also includes several key regulatory factors including the essential RANK-RANKL-OPG pathway. This cellular bone homeostasis model exhibits good semi-quantitative correlation with experimental data from the literature and can be used to simulate changes associated with disease conditions. This model was subsequently adapted to understand TNF-α induced bone loss in mice (Iqbal et al., 2006).
The purpose of this report is to integrate the denosumab PK with the cellular bone homeostasis model and to incorporate drug effects on the RANK-RANKL-OPG pathway in order to capture the time course of NTX in MM patients. The pharmacokinetics of denosumab is characterized over a range of doses using a target-mediated drug disposition model. The pharmacodynamic data are also characterized by a basic indirect response model with denosumab inhibiting the production of serum NTX.
Methods
Data Source
Mean PK and absolute median PD data were digitized (Graph Digitizer version 1.9) from a previously conducted randomized, double-blind, double-dummy, active-controlled, multicenter study that included 25 MM patients (Body et al., 2006) Patients received either 0.1, 0.3, 1.0 or 3.0 mg/kg of denosumab subcutaneously and blood samples were obtained at 1, 2, 4, 8 and 24 hours after drug administration and then weekly up to 84 days.
Pharmacokinetics
The time-course of serum denosumab concentrations was characterized using a rapid binding model of target-mediated drug disposition (Fig. 1) (Mager and Krzyzanski, 2005). Drug is absorbed into the central compartment (CP, Vc) from the subcutaneous injection site by a first order rate process (ka). In the central compartment, drug reversibly binds to the free ligand to form the drug-ligand complex (RC) which is subsequently internalized (kint). Free drug is also eliminated from the central compartment at a first-order rate (kel). The prolonged absorption phase and the absence of i.v. data allowed for neglecting the distribution of the drug to a non-specific tissue compartment and thus reduced the number of parameters in this model.
Figure 1.
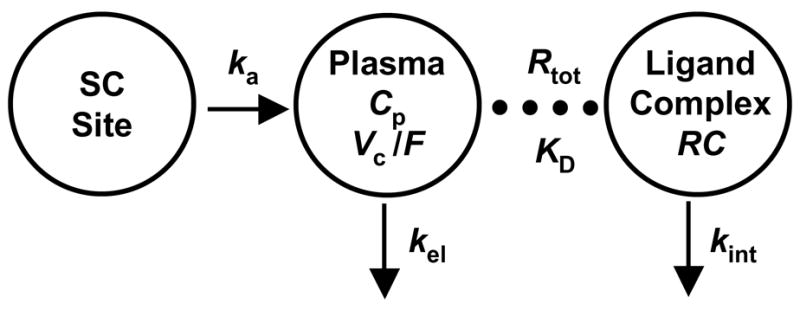
Target-mediated disposition model for denosumab pharmacokinetics. Drug administered subcutaneously gets absorbed (ka) into the plasma compartment (Cp, Vc). Drug can be eliminated (kel) or rapidly bind to the pharmacological target to form a drug-ligand complex (RC). The model also includes the internalization of the drug-ligand complex (kint).
The key feature of this model is that it assumes rapid binding of the drug to its pharmacological target (free ligands) with high affinity. Thus it is assumed that the free drug (Cp), free ligand (R), and drug-ligand complex (RC) are related by R · Cp/RC= koff/kon =KD, where kon and koff are the second- and first-order rates of association and dissociation and KD is the equilibrium dissociation constant. It was also assumed that the total ligand concentration (Rtot) representing the sum of free ligand and drug-ligand complex, Rtot= R + RC, was time-invariant, the validity of which has been discussed previously (Mager and Jusko, 2001). When drug is not present endogenously, Rtot is equal to the steady-state free ligand concentration, Rss. The equations used to describe denosumab pharmacokinetics are as follows:
| (1) |
| (2) |
Where Ctot (= Cp + RC) is the total drug concentration representing the sum of both free drug and the drug-ligand complex, and Vc/F is the volume of the central compartment adjusted for bioavailability. The initial condition for Equation 1 is set to zero.
Pharmacodynamics — Basic Indirect Response Model
A compartmental analysis of the pharmacodynamic data was performed using a well established basic indirect response model (Dayneka et al., 1993; Sharma and Jusko, 1998). This model assumes that denosumab has an inhibitory action on the production rate of the response variable, which is consistent with known mechanism of action of the drug. The rate of change of NTX over time can be represented as:
| (3) |
where kin is the apparent zero-order production rate of the response, kout is the first-order rate of loss of response, Imax is the maximal fractional extent of inhibition, and IC50 is the drug concentration producing 50% of maximal inhibition. The initial condition for Equation 3 was set to the steady state baseline value of NTX (NTXSS), which is the ratio of kin and kout (NTXSS = kin/kout). The median baseline values of NTX for patients in the four dosing groups (0.1, 0.3, 1.0, and 3.0 mg/kg) were 9.8, 9.1, 10.2, and 8.1 nM respectively (Body et al., 2006).
Pharmacodynamics-Cellular Bone Homeostasis Model
The structure of an integrated model incorporating the cellular bone homeostasis model of Lemaire and coworkers (2004) with the action of denosumab and the pharmacodynamic biomarker (serum NTX) is illustrated in Figure 2. The details of the cellular model can be obtained from the original publication (Lemaire et al., 2004) as only key features relevant to our PK/PD analysis are described here.
Figure 2.
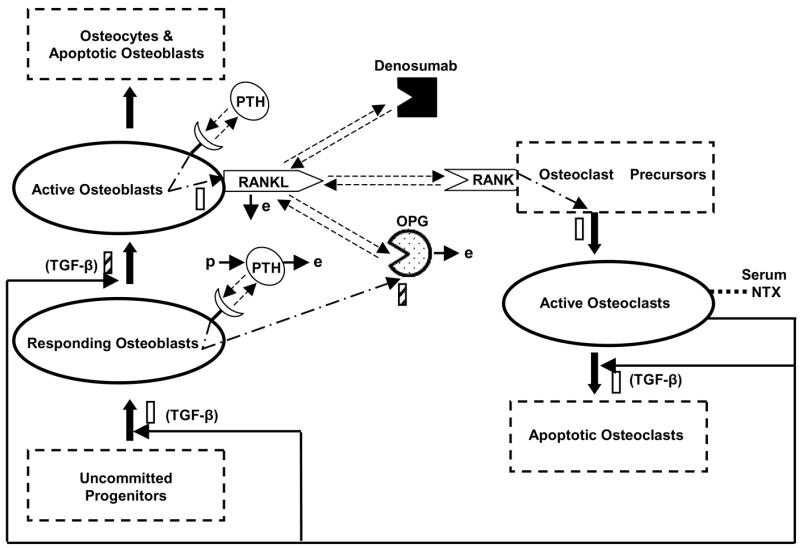
Schematic diagram of the integrated cellular bone homeostasis model. Adapted from Lemaire et. al. (2004). Details of the model are provided in the Methods.
The cellular model accounts for four major differentiation stages of osteoblasts and three stages of osteoclasts. An unlimited supply of uncommitted mesenchymal progenitors capable of differentiating into several cell types (myocytes, adipocytes, osteoblasts) serves as a large source for osteoblasts. Upon the stimulatory action of TGF-β, a portion of these uncommitted progenitors differentiate into cell types having characteristics of osteoblast precursors, the so-called responding osteoblasts (ROB). The ROB further differentiate to active osteoblasts (AOB). The model includes the inhibitory action of TGF-β on this differentiation process. The AOB represent the pool of cells that are responsible for bone formation and ultimately die or transform into osteocytes or lining cells.
Similar to the osteoblastic lineage, it is assumed that there is an unlimited supply of osteoclast precursors which differentiate into active osteoclasts (AOC) upon stimulation of a signaling pathway initiated by RANK-RANKL binding. The AOC represent the pool of cells that degrade bone and eventually transform into apoptotic cells by a process stimulated by TGF-β. Among the several differentiation stages mentioned, the ROB, AOB and AOC are the only state variables in Lemiare’s model.
The tight coupling between the osteoclasts and osteoblasts that result in bone homeostasis has been effectively maintained in this model. The proportion of active osteoclasts is controlled by the active osteoblasts through the RANK-RANKL interaction. It is assumed that RANKL is expressed on the surface of active osteoblasts and thus the amount of RANKL in the system is proportional to the active osteoblasts. The RANK-RANKL interaction is also controlled by OPG which is produced and released by the responding osteoblasts. Similarly the proportion of osteoblasts is controlled by the active osteoclasts through the action of TGF-β which is released from the bone matrix during bone resorption by active osteoclasts.
The influence of PTH on the RANK-RANKL-OPG axis has also been incorporated. PTH receptors are assumed to be present on both active and responding osteoblasts. Binding of PTH to the receptors on active osteoblasts and responding osteoblasts stimulates the production of RANKL and inhibits the production of OPG respectively. The net effect is to enhance the RANK-RANKL interaction and consequently increase the active osteoclast pool.
This paper extends the cellular bone homeostasis model (Lemaire et al., 2004) described above by incorporating the disposition and mechanism of action of denosumab and linking the model to the serum NTX biomarker. The high affinity binding of denosumab with RANKL would inhibit the RANK-RANKL interaction necessary for the differentiation of osteoclast precursors; thus decreasing the active osteoclast pool. This decrease would be reflected as a decrease in the levels of serum NTX, which is a byproduct of bone resorption by active osteoclasts.
The governing equations for the concentration of the state variables, the responding osteoblasts (CROB), the active osteoblasts (CAOB), and the active osteoclasts (CAOC) are as follows:
| (4) |
| (5) |
| (6) |
where DR is the differentiation rate of osteoblast progenitors, DB is a proportionality constant indicating the differentiation rate of responding osteoblasts, kB is the rate of elimination of active osteoblasts, DC is the differentiation rate of osteoclast precursors, and DA is the rate of osteoclast apoptosis. The terms πC and πL are the receptor occupancies of TGF-β and RANK. It is assumed that any cellular behavior in response to receptor-ligand binding is a function of receptor occupancy. The response is proportional to the occupancy when binding results in stimulation of a cellular process. Conversely, it is inversely proportional when binding inhibits a cellular process. Since TGF-β promotes the differentiation of osteoblast progenitors into responding osteoblasts, in Equation 4, the flow of differentiated progenitors entering the responding osteoblast compartment is proportional to the TGF-β occupancy and is given by DRπC. Conversely, since TGF-β inhibits the differentiation of responding osteoblasts into active osteoblasts, the flow of differentiated responding osteoblast leaving the compartment is inversely proportional to the TGF-β occupancy and is given by . Initial conditions for the differential equations (Eqs. 4–6) were fixed to the steady state baseline values of the cellular components. These values for the responding osteoblasts, the active osteoblasts and the active osteoclasts are 7.734 × 10−4, 7.282 × 10−4, and 9.127 × 10−4 pM respectively (Lemaire et al., 2004).
The RANK receptor occupancy in the presence of the drug is dependent on the binding of RANK (K), OPG (O) and denosumab (CP) with RANKL (L) independently. These account for three separate binding reactions as shown in Scheme (1). While the surface density of RANKL was assumed to be constant to obtain the pharmacokinetic profile of denosumab, the production (pL) and elimination (eL) of RANKL is considered in the derivation of RANK occupancy (Lemaire et al., 2004). For simplicity, the internalization of the drug-ligand complex has been ignored. It is assumed that the concentration of RANK receptors is a constant throughout the bone remodeling process as they are present on an undiminished supply of osteoclast precursors. The production (pO) and elimination (eO) of OPG is considered specifically and the production/elimination of denosumab is described by the PK model (Eqs. 1 and 2). The kinetic equations for these binding reactions are provided in Data Supplement (online).
Scheme 1.

Binding reactions in biological systems are usually much faster than the time required for cell populations to change. Thus, the receptors/ligands are considered to be at a pseudo-steady-state during bone remodeling. Applying the pseudo-steady state assumption along with the expressions for the production/elimination of RANKL and OPG, the receptor occupancy of RANK (πL = K·L/K) can be calculated as (online supplemental data):
| (7) |
where rL is the net rate of RANKL production, is the maximum number of RANKL attached on each surface, πP is the occupancy of the PTH receptor, and IL is the rate of increase in RANKL through pathways independent of bone remodeling. External administration would represent one such pathway. The expressions for πP, O, and the receptor occupancy of TGF-β, are listed in Data Supplement (online).
The expression derived for πL (Eq. 7) suggests that increasing doses of denosumab would cause a decrease in πL that would result in a decrease in the active osteoclast pool (Eq. 6). Also in the absence of drug (CP = 0), πL reduces to the derivation presented in the original model (Lemaire et al., 2004).
The active osteoclast is linked with serum NTX concentration using the following non-linear transfer function:
| (8) |
where Eb is the basal NTX concentration corresponding to very low levels of active osteoclasts in the system, NTXSS is the steady state baseline value of NTX, n is the Hill coefficient, and EC50 is the osteoclast concentration producing 50% of the maximal NTX production.
Data Analysis
The rapid binding target-mediated disposition model (Fig. 1; Eqs. 1 and 2) was fitted to the mean denosumab plasma concentration-time profiles. The equilibrium dissociation constant, KD, was fixed to the known literature value (3 × 10−12 M; (Schwarz et al., 2005). The PK parameters to be estimated included: ka, kint, kel, VC/F and RSS.
The cellular bone homeostasis model (Fig. 2; Eqs. 4–8) and the basic indirect response model (Eq. 3) were each fitted separately to the serum NTX profiles. All of the base parameters of the cellular model, with the exception of DA and DC, were fixed to values obtained from the literature (Lemaire et al., 2004). The parameters of the integrated cellular model that were estimated included DA, Eb, EC50 and the Hill-coefficient, n. The initial value of Eb was obtained from the serum NTX concentration following the highest dose at later time points (~70–85 days). DC was calculated in order to maintain the steady-state baseline conditions as:
| (9) |
where the superscript represents the steady state values of the variables.
The initial parameter estimates for the indirect response model were calculated as described elsewhere (Sharma and Jusko, 1998). The estimated parameters for this model included kout, Imax, and IC50. The production rate, kin, was calculated to maintain steady-state baseline conditions (kin = koutNTXSS).
All parameters were estimated using the ADAPT5 (beta-version) computer program (D’Argenio and Schumitzky, 1997) by the maximum likelihood method. Separate variance models were specified for PK and PD outcomes using the following equation:
| (10) |
where VARi is the variance of the ith data point, σ1 and σ2 are the variance parameters, and Yi is the model predicted concentration or response. σ1 was fixed to 0.0001 and 0 for the PK and PD variance models. The goodness of fit for both PK and PD were assessed by system convergence, Akaike Information Criterion, Schwartz Criterion, estimator criterion value for the maximum likelihood method, examination of residuals, and visual inspection of the fitted curves.
Results
Pharmacokinetics
The mean plasma concentration-time profiles of denosumab and fitted curves after single SC administration of four different dose levels in multiple myeloma patients are shown in Figure 3. A conventional noncompartmental analysis revealed non-linear disposition with dose related decrease in apparent clearance (CL/F) and steady state volume of distribution (Vss/F) (Table 1). The terminal slope is observed to be much steeper for the lowest dose suggesting non-linear PK and saturation of a capacity-limited process. A trend of increasing mean residence time (MRT) with increasing dose was also observed; however, the truncated terminal phase might represent one source of bias in assessments of CL/F and MRT. The profiles also show relatively rapid but prolonged absorption of denosumab.
Figure 3.
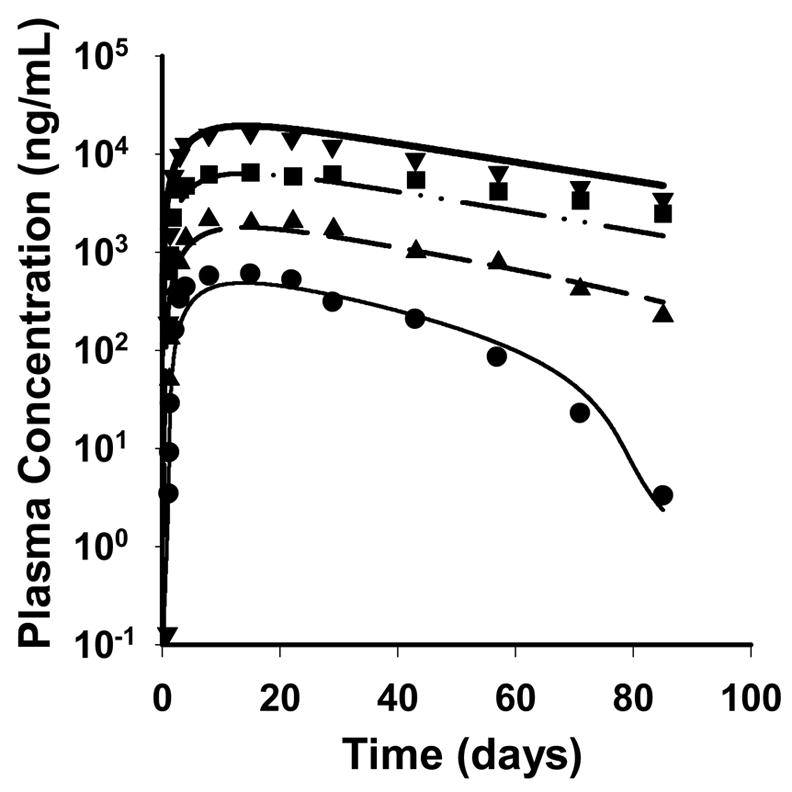
Pharmacokinetic profiles of denosumab after simultaneously fitting the rapid binding target-mediated disposition model to the mean data of four single SC doses of 0.1 (●, thin solid), 0.3 (▲, dashed), 1.0 (■, dash-dotted), and 3.0 mg/kg (▼, thick solid). Symbols represent mean data from the literature (Body et al., 2006) and lines represent the predicted profiles from the model.
Table 1.
Noncompartmental analysis of denosumab pharmacokinetics in multiple myeloma patients
| Dose (mg/kg) | λz (day−1) | AUC (×105ng·day/mL) | CL/F (mL/day/kg) | VSS/F (mL/kg) | MRT (day) |
|---|---|---|---|---|---|
| 0.1 | 0.116 | 0.203 | 4.94 | 119 | 24.2 |
| 0.3 | 0.044 | 1.01 | 2.98 | 104 | 34.9 |
| 1.0 | 0.019 | 5.36 | 1.87 | 116 | 62.3 |
| 3.0 | 0.022 | 9.33 | 3.21 | 158 | 49.2 |
The applied model characterizes the time course of denosumab plasma concentrations reasonably well. The final estimated parameters are listed in Table 2 and low CV% values were obtained. The estimated volume of the central compartment (0.114 L/kg) is approximately double the plasma volume which is typical for large molecules with very specific targets contributing as sites of distribution in the body (Lobo et al., 2004).
Table 2.
Pharmacokinetic parameter estimates for denosumab in patients with multiple myeloma.
| Parameter (units) | Final Estimate | CV% |
|---|---|---|
| ka(day−1) | 0.167 | 17.4 |
| kel (day−1) | 2.12 × 10−2 | 15.8 |
| kint (day−1) | 2.67 × 10−2 | 16.1 |
| Vc/F (L/kg) | 0.114 | 12.4 |
| Rss(nM) | 1.07 | 11.6 |
Pharmacodynamics – Basic Indirect Response Model
The time-course of the absolute median serum NTX concentrations and fitted curves after single SC administration of denosumab is shown in Figure 4. The indirect response model reasonably captures the time-course of NTX concentrations, and low CV% values were obtained for the final estimated parameters. The first-order loss of response, kout was estimated to be 0.572 day−1 (39.3 CV%). The estimated values of the maximum fractional inhibition, Imax, and the IC50 terms were 0.331 (7.37 CV%) and 2.64 nM (40.4 CV%), respectively. Some evidence of bias is shown for the nadir values for the 0.3 to 3 mg/kg doses. Differences in recession slopes are attributed to different baseline values of NTX for the four dose levels.
Figure 4.
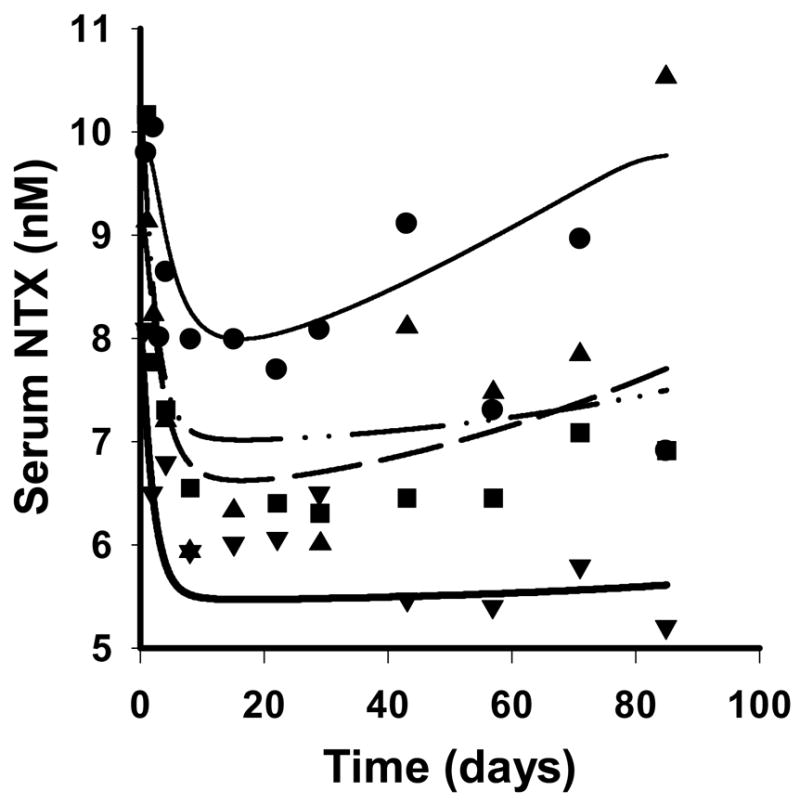
Serum NTX concentration-time profiles after simultaneously fitting the basic indirect response model to the median data for four single SC doses of 0.1 (●, thin solid), 0.3 (▲, dashed), 1.0 (■, dash-dotted), and 3.0 mg/kg (▼, thick solid). Symbols represent data from the literature (Body et al., 2006) and lines represent the predicted profiles from the model.
Pharmacodynamics – Cellular Bone Homeostasis Model
The PD data were also reasonably described by the integrated homeostasis model and the predicted time profiles for NTX concentrations are shown in Figure 5. The final estimated parameters are listed in Table 3, and low CV% values were obtained for all of the fitted parameters. Only one parameter of the base cellular model (Lemaire et al., 2004), DA was estimated and DC was calculated to maintain steady-state conditions. The values for DA and DC obtained from this study (29.8day−1 and 0.0894 pMday−1) are greater than the literature values (0.7 day−1 and 2.1×10−3pMday−1) (Lemaire et al., 2004). Although literature values for in vivo data are not available for comparison, this change is expected as values are likely to fluctuate with changes in the physiological environment under consideration, and the domain for the cellular model is a population of bone remodeling units (BMUs) distributed over a section of bone (Lemaire et al., 2004).
Figure 5.
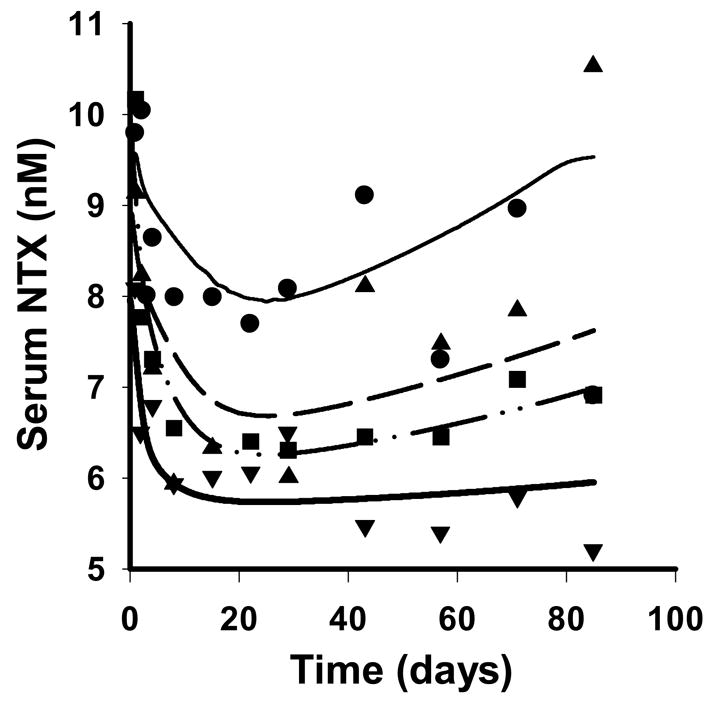
Serum NTX concentration-time profiles after simultaneously fitting the integrated cellular bone homeostasis model to the median data for four single SC doses. Symbols and lines are as defined in Figure 4.
Table 3.
Pharmacodynamic parameter estimates for NTX in MM patients using a cellular bone homeostasis model.
| Parameter (units) | Final Estimate | CV% |
|---|---|---|
| DA(day−1) | 29.8 | 1.48 |
| Eb(nM) | 5.55 | 6.73 |
| EC50(pM) | 1.88 × 10−5 | 40.3 |
| n (dimensionless) | 0.745 | 25.6 |
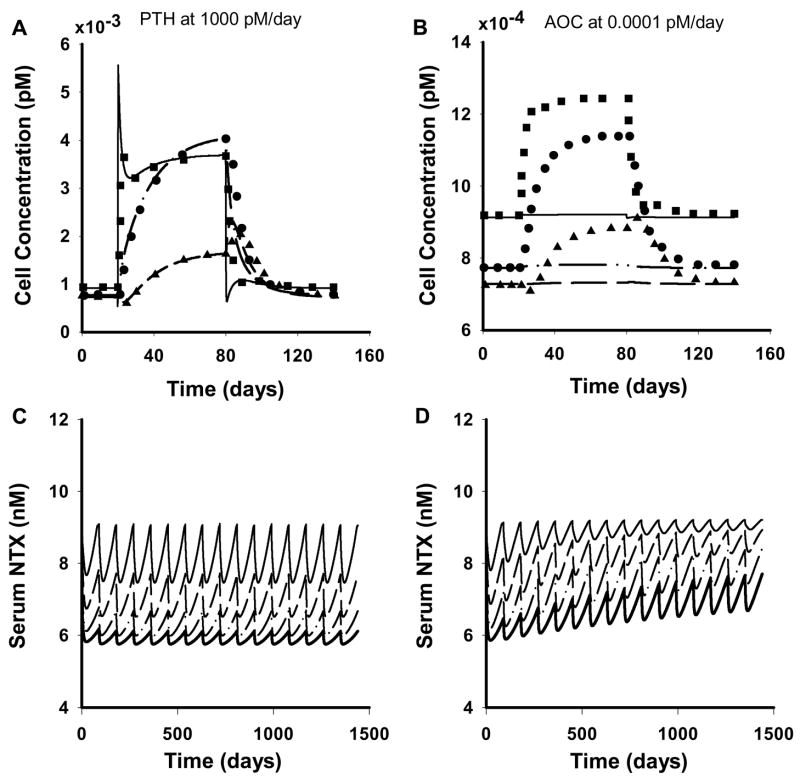
Simulations were performed to test the cellular model performance with the parameters obtained in this study against the original parameters. Lemaire and coworkers (2004) simulated various biological effects of the bone remodeling process, including, the catabolic action of continuous infusion of PTH on bone mass, the increase in bone turnover by OPG administration, and the catabolic action of RANKL and its reversal by OPG. In addition, the tight coupling of osteoclasts and osteoblasts was demonstrated through perturbations of the system by adding or removing cells from specific compartments as zero-order processes. We performed all of these simulations with the new parameter values and obtained similar profiles for a majority of them. One such representative profile on the effect of continuous administration of PTH (1000 pMday−1 for 60 days) to increase the concentrations of active osteoclasts, responding osteoblasts, and active osteoblasts is shown in Figure 6A. This increase is attributed to the increase in RANKL and decrease in OPG in the system due to PTH. In contrast, the cellular concentration-time profiles for the cases of active osteoclast input and depletion obtained in this study were significantly different from the original profiles. The profile for the effect of active osteoclast administration (0.0001pMday−1) is shown in Figure 6B. Simulations with original parameters show a rapid increase in active osteoclasts followed by an increase in responding osteoblasts. This increase in the responding osteoblasts is due to the increase in the levels of TGF-β which stimulates the differentiation of progenitors into responding osteoblasts and inhibits their differentiation into active osteoblasts. The active osteoblasts show an initial decline due to the inhibitory action of TGF-β followed by an increase due to the increase of responding osteoblasts in the system. This effect was not captured with the new parameters and the concentrations remained at their steady-state baseline values (Fig. 6B). While an inflow/outflow of 1.26 × 10−4 pMday−1 to/from the active osteoclast compartment is needed to maintain the level of osteoclasts at steady-state with the original parameter values, a higher inflow/outflow of 5.35 × 10−3 pMday−1 is defined by the new values. Thus, 0.0001pMday−1 of osteoclast input is not sufficient to alter profiles relative to the faster turnover process. Since the choice of the osteoclast input rate is relatively arbitrary, and close agreement with the original model was observed for all other cases, these simulations suggest that the new parameter values do not alter the key features of bone remodeling.
Figure 6.
Simulated predictions of the cellular bone homeostasis model under varying conditions. A) Concentration-time profiles of the bone cells with continuous administration of 1000 pMday−1 of PTH for 60 days. B) Concentration-time profiles of the bone cells with continuous administration of 0.0001 pMday−1 of active osteoclasts for 60 days. Symbols (●, ▲, ■) represent digitized data from simulations conducted by Lemaire et al. (2004) with the value of DA, 0.7 day−1 and lines (dash-dotted, dashed, solid) represent the predicted profiles of the responding osteoblasts, active osteoblasts and the active osteoclasts respectively from this study using a value of DA, 29.8 day−1. C) Serum NTX concentration-time profiles following multiple SC dosing of denosumab every 90 days. D) Serum NTX concentration-time profiles following multiple SC dosing of denosumab with a linear increase in RANKL in the system. The thin solid, dashed, dash-dotted and thick solid lines represent escalating SC doses of 0.1, 0.3, 1.0, and 3.0 mg/kg.
Simulations were performed to assess the effect of multiple-dosing and a theoretical time-dependent increase in RANKL in the system on the pharmacodynamics of denosumab. Subcutaneous dosing every 90 days for the four dose levels (0.1, 0.3, 1.0, 3.0 mg/kg) was considered. Multiple-dosing in the first case revealed a further reduction in the maximum response for the second dosing cycle and attainment of steady-state conditions thereafter (Fig. 6C). The response was dose-dependent and, for the highest dose, the maximum response was close to the value of Eb, suggesting extremely low levels of active osteoclasts in the system. A theoretical disease progression was introduced using a linear time-dependent increase in RANKL (IL(t) = mLt in Eq. 7) for the second case which otherwise was set as zero. This increase in RANKL is reflective of an increase independent of the bone remodeling process. Recent studies have shown myeloma cells to express RANKL which would represent one such pathway for its upregulation (Sezer et al., 2002; Heider et al., 2003). In this multiple dosing scheme, a steady rise in the serum NTX concentration was observed with time for every dosing cycle (Fig. 6D). For the lowest dose the serum concentration seems to asymptotically approach a value of approx. 9 nM, equal to the baseline condition.
Discussion
The primary objective of this study was to demonstrate that a cellular systems model can be effectively linked with the pharmacokinetics and mechanism of action of a drug to characterize the time-course of the pharmacodynamic response. To this end, the pharmacokinetics of denosumab was integrated with a cellular bone homeostasis model (Lemaire et al., 2004) (Fig. 2) and used to characterize the temporal profiles of serum NTX following drug administration in MM patients.
Noncompartmental analysis of the plasma concentration profiles of denosumab showed an apparent trend for decreasing clearance (CL/F) and steady-state volume of distribution (VSS/F) with increasing dose (Table 1). These nonlinear properties might be attributed to saturable binding with RANKL or other factors including ligand down-regulation. Although it was assumed that Rtot (the free and the bound ligand) remained constant, the target-mediated model (Fig. 1) captured the pharmacokinetic profile of denosumab reasonably well (Fig. 3). Denosumab concentrations at later time points were slightly under-predicted (1.0 mg/kg) and over-predicted (3.0 mg/kg) for the higher doses. However, since the primary goal of the PK analysis was to obtain a reasonable driving function for the PD, additional parameters in attempting to describe other pathways (for example, ligand turnover) were not warranted for these minor deviations. Also, the prolonged absorption phase of the drug precluded the assessment of the distribution of the drug to a peripheral tissue compartment, thus reducing the number of parameters to be estimated. However, it is important to note that a tissue compartment would perhaps be needed to characterize intravenous and SC data simultaneously.
Denosumab PK was integrated into the cellular bone homeostasis model (Lemaire et al., 2004) by considering the binding of the drug along with RANK and OPG to RANKL (Eq. 7). These receptors/ligands were assumed to be in a pseudo-steady-state in the current model as binding reactions tend to be much faster relative to bone remodeling processes. However, experimentally derived temporal profiles of RANKL and OPG might be useful for describing transient characteristics of these reactions and facilitate the estimation of in vivo production (pL, pO) and elimination (eL, eO) rates. The active osteoclast compartment of the integrated model was further linked to NTX, a clinical biomarker for bone resorption through a non-linear transfer function (Eq. 8), which accounts for the different baseline conditions for the four dosing groups of patients. While such functions have been commonly used to link the plasma drug concentration to response in traditional PK/PD modeling, we have utilized this technique and linked response to an intermediate physiological compartment, the active osteoclasts. The integrated model (Fig. 2) characterizes the time course of serum NTX in multiple myeloma patients reasonably well (Fig. 5) and the parameters were estimated with good precision (Table 3). There were slight deviations in the predicted pharmacodynamic profiles that may be due to several factors including the variability in NTX concentrations and the use of median data. The time course of serum NTX was also characterized independently by the indirect response model where the production of response is inhibited by the drug (Fig. 4). The fits for both the models (cellular and indirect response) in terms of the residuals, AIC, and Schwarz Criteria were comparable (data not shown).
The cellular pharmacodynamic model, apart from effectively characterizing the clinical data, has the distinct advantage of assessing the role of cellular variables on drug response. A theoretical disease progression was simulated by increasing RANKL independent of the bone remodeling process, revealing a steady increase in serum NTX levels even for the highest dose administered once every 3 months (Fig. 6D), whereas NTX levels were suppressed and maintained around 6 nM when RANKL was not increased (Fig. 6C). RANKL was increased in the system because multiple myeloma patients have an upregulated RANKL (Kyle and Rajkumar, 2004; Matsumoto and Abe, 2006) and myeloma cells also express RANKL (Sezer et al., 2002; Heider et al., 2003). These simulations demonstrate the added value of linking physiological systems with PD models, namely the capability to incorporate disease effects and other factors that may influence short- and long-term responses to a drug. Although data on the long-term clinical effects of denosumab are not yet available, the approach outlined in this study might prove useful in interpreting outcomes and sources of inter-individual variability. Current efforts are underway to link the model to biomarkers from pre-clinical models of MM.
The work we have presented begins to highlight the interdependence of bone biology and endocrine system components (e.g. PTH) to maintain homeostasis. The relationships between cell lines, cytokines either produced by, or implicated in, osteoclast and osteoblast functions, calcium balance requirements to sustain life, the role of PTH, and other organs that mediate calcium balance is complex. Therefore, it is reasonable that models will require increasing levels of complexity if they are going to be able to generalize across diseases and therapeutic interventions. A model aimed at condensing the available literature into a single physiological model for bone was recently presented (Peterson and Riggs, 2007). That model utilized the same cellular concepts as this work described by Lemaire and colleagues (2004), and took a further step of introducing many of the mentioned organ and cytokine components in order to describe bone biology from the perspective of calcium balance, with attention on generalizability and ability to predict certain disease effects. Whether it will present a reasonable construct for exploring disease effects such as those seen in MM remains to be seen. At a minimum it represents an application of systems biology modeling to bone physiology, and supports the approach demonstrated here in this work.
In conclusion, an integrated cellular bone homeostasis model was developed and has been successfully applied to human clinical data. The proposed model is mechanistic in nature, including key cellular variables and the effect of denosumab pharmacokinetics on the RANK-RANKL-OPG pathway. It reflects the processes that are thought to regulate the production of the clinical biomarker, NTX. This cellular model has a clear advantage of assessing the role of physiologically important substances (e.g., RANKL) on drug response and thus providing new testable hypotheses for designing effective therapeutic strategies for multiple myeloma and possibly other osteolytic diseases.
Acknowledgments
a) This study was funded, in part, by an Amgen Postdoctoral Fellowship (to A.M.) and Grant GM57980 from the National Institutes of Health (for D.E.M.).
Abbreviations
- MM
multiple myeloma
- NTX
N-telopeptide
- OPG
osteoprotegrin
- PK
pharmacokinetics
- PD
pharmacodynamics
- RANK
receptor activator of nuclear factor-κB
- RANKL
RANK ligand
- PTH
parathyroid hormone
- SC
subcutaneous
- ROB
responding osteoblast
- AOB
active osteoblast
- AOC
active osteoclast
Footnotes
This research was presented, in part, at the Experimental Biology Annual Meeting in San Diego, CA (April 2008).
Dr. Mark C. Peterson is employed by Amgen, Inc., the manufacturer for denosumab.
References
- Aubin JE, Bonnelye E. Osteoprotegerin and its ligand: a new paradigm for regulation of osteoclastogenesis and bone resorption. Osteoporos Int. 2000;11:905–913. doi: 10.1007/s001980070028. [DOI] [PubMed] [Google Scholar]
- Bekker PJ, Holloway DL, Rasmussen AS, Murphy R, Martin SW, Leese PT, Holmes GB, Dunstan CR, DePaoli AM. A single-dose placebo-controlled study of AMG 162, a fully human monoclonal antibody to RANKL, in postmenopausal women. J Bone Miner Res. 2004;19:1059–1066. doi: 10.1359/JBMR.040305. [DOI] [PubMed] [Google Scholar]
- Body JJ, Facon T, Coleman RE, Lipton A, Geurs F, Fan M, Holloway D, Peterson MC, Bekker PJ. A study of the biological receptor activator of nuclear factor-kappaB ligand inhibitor, denosumab, in patients with multiple myeloma or bone metastases from breast cancer. Clin Cancer Res. 2006;12:1221–1228. doi: 10.1158/1078-0432.CCR-05-1933. [DOI] [PubMed] [Google Scholar]
- Boyle WJ, Simonet WS, Lacey DL. Osteoclast differentiation and activation. Nature. 2003;423:337–342. doi: 10.1038/nature01658. [DOI] [PubMed] [Google Scholar]
- D’Argenio DZ, Schumitzky A. Biomedical Simulation Resource. Los Angeles, California: 1997. ADAPT II User’s Guide. [Google Scholar]
- Dayneka NL, Garg V, Jusko WJ. Comparison of four basic models of indirect pharmacodynamic responses. J Pharmacokinet Biopharm. 1993;21:457–478. doi: 10.1007/BF01061691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Filvaroff E, Derynck R. Bone remodelling: a signalling system for osteoclast regulation. Curr Biol. 1998;8:R679–682. doi: 10.1016/s0960-9822(98)70434-8. [DOI] [PubMed] [Google Scholar]
- Heider U, Langelotz C, Jakob C, Zavrski I, Fleissner C, Eucker J, Possinger K, Hofbauer LC, Sezer O. Expression of receptor activator of nuclear factor kappaB ligand on bone marrow plasma cells correlates with osteolytic bone disease in patients with multiple myeloma. Clin Cancer Res. 2003;9:1436–1440. [PubMed] [Google Scholar]
- Hideshima T, Mitsiades C, Tonon G, Richardson PG, Anderson KC. Understanding multiple myeloma pathogenesis in the bone marrow to identify new therapeutic targets. Nat Rev Cancer. 2007;7:585–598. doi: 10.1038/nrc2189. [DOI] [PubMed] [Google Scholar]
- Hideshima T, Richardson P, Anderson KC. Novel therapeutic approaches for multiple myeloma. Immunol Rev. 2003;194:164–176. doi: 10.1034/j.1600-065x.2003.00053.x. [DOI] [PubMed] [Google Scholar]
- Hofbauer LC, Khosla S, Dunstan CR, Lacey DL, Boyle WJ, Riggs BL. The roles of osteoprotegerin and osteoprotegerin ligand in the paracrine regulation of bone resorption. J Bone Miner Res. 2000;15:2–12. doi: 10.1359/jbmr.2000.15.1.2. [DOI] [PubMed] [Google Scholar]
- Iqbal J, Sun L, Kumar TR, Blair HC, Zaidi M. Follicle-stimulating hormone stimulates TNF production from immune cells to enhance osteoblast and osteoclast formation. Proc Natl Acad Sci U S A. 2006;103:14925–14930. doi: 10.1073/pnas.0606805103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Komarova SV, Smith RJ, Dixon SJ, Sims SM, Wahl LM. Mathematical model predicts a critical role for osteoclast autocrine regulation in the control of bone remodeling. Bone. 2003;33:206–215. doi: 10.1016/s8756-3282(03)00157-1. [DOI] [PubMed] [Google Scholar]
- Kostenuik PJ. Osteoprotegerin and RANKL regulate bone resorption, density, geometry and strength. Curr Opin Pharmacol. 2005;5:618–625. doi: 10.1016/j.coph.2005.06.005. [DOI] [PubMed] [Google Scholar]
- Kyle RA, Rajkumar SV. Multiple myeloma. N Engl J Med. 2004;351:1860–1873. doi: 10.1056/NEJMra041875. [DOI] [PubMed] [Google Scholar]
- Lemaire V, Tobin FL, Greller LD, Cho CR, Suva LJ. Modeling the interactions between osteoblast and osteoclast activities in bone remodeling. J Theor Biol. 2004;229:293–309. doi: 10.1016/j.jtbi.2004.03.023. [DOI] [PubMed] [Google Scholar]
- Lobo ED, Hansen RJ, Balthasar JP. Antibody pharmacokinetics and pharmacodynamics. J Pharm Sci. 2004;93:2645–2668. doi: 10.1002/jps.20178. [DOI] [PubMed] [Google Scholar]
- Mager DE, Jusko WJ. General pharmacokinetic model for drugs exhibiting target-mediated drug disposition. J Pharmacokinet Pharmacodyn. 2001;28:507–532. doi: 10.1023/a:1014414520282. [DOI] [PubMed] [Google Scholar]
- Mager DE, Krzyzanski W. Quasi-equilibrium pharmacokinetic model for drugs exhibiting target-mediated drug disposition. Pharm Res. 2005;22:1589–1596. doi: 10.1007/s11095-005-6650-0. [DOI] [PubMed] [Google Scholar]
- Martin MJ, Buckland-Wright JC. Sensitivity analysis of a novel mathematical model identifies factors determining bone resorption rates. Bone. 2004;35:918–928. doi: 10.1016/j.bone.2004.06.010. [DOI] [PubMed] [Google Scholar]
- Matsumoto T, Abe M. Bone destruction in multiple myeloma. Ann N Y Acad Sci. 2006;1068:319–326. doi: 10.1196/annals.1346.035. [DOI] [PubMed] [Google Scholar]
- Peterson MC, Riggs MM. Calcium homeostasis and bone remodeling: Development of an integrated model for evaluation and simulation of therapeutic responses to bone-related therapies. PAGE Annual Meeting; Copenhagen, Denmark. 2007. [Google Scholar]
- Roodman GD. Cell biology of the osteoclast. Exp Hematol. 1999;27:1229–1241. doi: 10.1016/s0301-472x(99)00061-2. [DOI] [PubMed] [Google Scholar]
- Schwarz EM, Keefe O, Regis J, Lianping X, Looney JR, Ritchlin CT. Receptor activator of nuclear [kappa]B ligand and osteoprotegrin: where are we now and what about future treatment uses? Current Opinion in Orthopedics. 2005;16:370–375. [Google Scholar]
- Schwarz EM, Ritchlin CT. Clinical development of anti-RANKL therapy. Arthritis Res Ther. 2007;9(Suppl 1):S7. doi: 10.1186/ar2171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sezer O, Heider U, Jakob C, Eucker J, Possinger K. Human bone marrow myeloma cells express RANKL. J Clin Oncol. 2002;20:353–354. doi: 10.1200/JCO.2002.20.1.353. [DOI] [PubMed] [Google Scholar]
- Sharma A, Jusko WJ. Characteristics of indirect pharmacodynamic models and applications to clinical drug responses. Br J Clin Pharmacol. 1998;45:229–239. doi: 10.1046/j.1365-2125.1998.00676.x. [DOI] [PMC free article] [PubMed] [Google Scholar]