A Computational Strategy to Analyze Label-Free Temporal Bottom-Up Proteomics Data

Abstract

Biological systems are in a continual state of flux, which necessitates an understanding of the dynamic nature of protein abundances. The study of protein abundance dynamics has become feasible with recent improvements in mass spectrometry-based quantitative proteomics. However, a number of challenges still remain related to how best to extract biological information from dynamic proteomics data, for example, challenges related to extraneous variability, missing abundance values, and the identification of significant temporal patterns. This paper describes a strategy that addresses these issues and demonstrates its values for analyzing temporal bottom-up proteomics data using data from a Rhodobacter sphaeroides 2.4.1 time-course study.

Introduction

Proteomics studies aimed at developing predictive biological models require detailed knowledge of the dynamics of biological systems. While most quantitative proteomics efforts using mass spectrometry have focused on static protein abundance measurements, liquid chromatography coupled with mass spectrometry (LC-MS) based proteomics has recently witnessed considerable progress in instrumentation technology, throughput, and data analysis.¹ Substantial improvements have also been made with regard to quantitation, such as the development of isotopic labeling methods^2-7 and label-free approaches.⁸ With these technological advances, the study of protein abundance dynamics has become feasible.⁹

Nevertheless, the potential benefits from studying proteome dynamics are accompanied with a number of challenges that include how to efficiently analyze the resulting large amounts of data. Among the prominent data analysis challenges are how to handle the extraneous variability and missing abundance values, and how to identify significant temporal patterns. While algorithms designed to attenuate the influence of extraneous variability have been applied to microarray data¹⁰ and have also been adapted for static proteomics data via abundance normalization,^10-12 a new adaptation designed specifically for temporal proteomics data is needed.

Another important consideration is how to handle instances of missing peptide and protein abundance values. This issue is more prominent in proteomics than in gene-array studies due to the nature of the analytical platform and how data is processed. For any method of missing value imputation, the central issue is how to best make use of the information contained in the available data. A number of missing-value imputation approaches have been reported, including Bayesian Principal Component Analysis,¹³ Fixed Rank Approximation Algorithm,¹⁴ the weighted K-nearest neighbors,¹⁰ the least-squares principle,¹⁵ and the local least-squares imputation method.¹⁶ These methods are mostly designed for static microarray data and often draw on relationships among replicates. However, for time-course data, missing values not only can occur among technical and/or biological replicates, but can also be missing across the time series. Therefore, any missing value imputation method for temporal data should take into account temporal relationships.

Protein abundance data can be obtained using both bottom-up and top-down proteomics approaches. While top-down methods measure intact protein abundances directly, bottom-up methods involve the digestion of proteins into peptides, and it is the peptide abundances that are measured by mass spectrometry. Therefore, for quantitative bottom-up proteomics studies, the calculation of protein abundance values from corresponding peptide abundance values is required, and it is critical that this calculation preserve any significant temporal patterns in the peptide-level data.

This article describes an analytical strategy developed specifically to confront data analysis challenges inherent to dynamic bottom-up proteomics studies. To evaluate its utility, this strategy was applied to data from a time-course study of Rhodobacter sphaeroides 2.4.1. Dynamic patterns in the peptide-level data were studied both with and without abundance normalization, and the results showed that normalization is crucial for the reliable extraction of significant dynamic patterns.

Methods

Biological, Experimental, and Data Analysis Framework

The analytical strategy presented herein was applied to data obtained from a quantitative proteomic investigation of R. sphaeroides 2.4.1 as it transitioned from aerobic to photosynthetic metabolism. Cell samples were collected at 10 time points over a period of 18 h. The 10 time points corresponded to 0, 1, 2, 3, 4, 5, 8, 10, 12, and 18 h into the transition. Each sample was analyzed by LC-MS five times (50 analyses total). In the following text, time point 1-10 will be used to denote the temporal order of the sample collection time and time will be used to denote the actual time in hours.

As it was unrealistic to expect the LC-MS instrumentation to be in exactly the same condition throughout all of the LC-MS analyses, cell samples were scheduled (Supplemental Figure 1) for LC-MS analyses such that an entire time series of samples (i.e., samples from the 10 different time points) were placed in the same block of LC-MS analyses, and technical replicates (i.e., replicate LC-MS analyses of a sample) were placed in separate blocks of LC-MS analyses (i.e., there were five blocks total). Within each block, the samples were ordered randomly to undergo consecutive LC-MS analyses. After the LC-MS analyses were finished for all of the samples within the entire block, a different block was analyzed. This setup reduced the effects of slight variations in instrument performance on the measured temporal patterns of peptide abundance values since the average time interval between samples within the same time series is minimized. This blocking feature is taken advantage of in the design of the peptide abundance normalization.

Peptide identification and quantitation were achieved using a label-free, accurate mass and elution time (AMT) tag approach.^1,17-19 An AMT tag database of peptide identifications was generated previously using LC-MS/MS,¹¹ and the resulting data was stored and filtered using an in-house developed data management system²⁰ and discriminant score.²¹ Mass and normalized elution time (NET) features observed from the 50 LC-MS data sets were matched to this database to identify peptides. Matched features were filtered on the uniqueness of the match according to previously developed metrics.^19,22,23 Abundance values of the identified peptides were calculated from the accumulative peak heights of consecutive MS scans (i.e., a peptide is usually observed in multiple consecutive MS scans, and the sum of the peak intensities in these scans is calculated as the abundance of the corresponding peptide (Supplemental Figure 7)).^1,18 The term “LC-MS data set” refers to the set of all of the peptide identification and quantitation data that are obtained from the AMT tag processing of a single LC-MS analysis. One LC-MS data set usually contains data from hundreds of peptides.

Data Preprocessing and Peptide Filtering

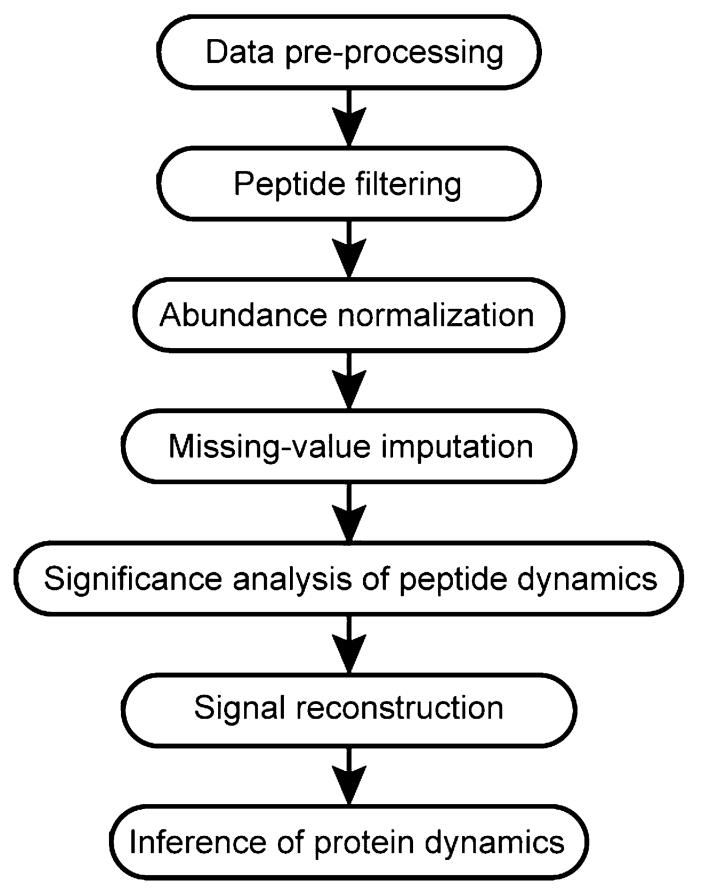
After obtaining the peptide abundance data, a procedure designed to extract significant temporal patterns is performed (outlined in Figure 1). Data preprocessing and filtering steps are designed to identify missing values and to remove peptides that have questionable assignments. Each LC-MS analysis results in the identification and quantification of a set of peptides; however, these sets of observed peptides are generally unique, even among technical replicates. Preprocessing the data results in a universal peptide set for all of the LC-MS analyses, and peptides that are not observed in a particular LC-MS analysis are treated as missing.

Figure 1.

Flowchart of the data analysis procedure.

A time series of observation counts (i.e., the number of times a peptide is observed among the technical replicates) is obtained for each peptide, and peptides that are difficult to identify are filtered out based on the time series of observation counts. This filtering step is necessary because of random events that occur during LC-MS and subsequent data processing (e.g., deisotoping and peptide identification).¹ For a peptide to be retained, it is required to have been observed a certain number of times among all of the technical replicates and a certain number of times across the entire time series. Additionally, the time series of observation counts for all of the peptides can be used to identify one or more time window(s) within which peptides show interesting dynamic behavior.

Data from peptides potentially derived from multiple proteins (i.e., degenerate peptides) are also removed. Otherwise, two negative consequences could result from including these degenerate peptides in the analysis. First, the correct peptide dynamic pattern could be confounded by the dynamics of multiple proteins and hence would be very hard or even impossible to deconvolute. The deconvolution parameters at various time points would generally be very difficult to determine since the relative abundances of specific peptides could be very different. Second, protein dynamic patterns inferred from degenerate peptides would be less confident since the ambiguity in the behavior of the degenerate peptide would propagate to the inferred protein dynamics and thus lead to a misinterpretation of the data. However, if the ambiguity is resolved, this filtering step can be skipped.

After this filtering process, all of the peptides that pass the filters are considered for further data analyses, and those peptides that do not are discarded.

Abundance Normalization

The abundance values of the filter-passing peptides are normalized using the following linear regression technique. Let y_ij represent the measured peptide abundance value for peptide i in LC-MS data set j where j = 1, 2, ..., J with J denoting the total number of LC-MS data sets. Then y_ij can be written as

$$y_{ij}=k_j{x}_{ij}+{∊}_{ij}$$ (1)

where x_ij denotes the true abundance value for peptide i in LC-MS data set j, k_j denotes the multiplicative factor due to the systematic variation in the experimental process for data set j, and ∊_ij denotes the random error. When a pair of LC-MS data sets is considered and one of the data sets is taken as a reference, the abundance values of most of the peptides in one data set can also be related to the corresponding abundance values in the reference data set in the same format as in eq 1. This is because an LC-MS analysis is usually proteome-wide and the abundance values of a majority of the peptides usually do not change much from one LC-MS analysis to another. The objective of abundance normalization is to remove the systematic shift k_j (i.e., k_j = 1 after the normalization) that exists between an LC-MS data set and a reference LC-MS data set. k_j is estimated using a linear regression between the reference LC-MS data set and the LC-MS data set that is to be normalized. Specifically, the abundance values of those peptides that are observed in both LC-MS analyses are plotted on a scatter plot with the reference data set represented by the x-axis and the data set to be normalized represented by the y-axis. k_j will be the slope of the linear regression line.

1. Normalization Procedure

In a time-course study, the dynamic patterns of the peptide and protein abundance values are central to the study. To extract the patterns, the abundance values at different time points have to be normalized using the same reference so that the relative change in abundance values among different time points can be compared. Therefore, the LC-MS data sets corresponding to different time points have to be normalized against the same LC-MS reference data set. Additionally, systematic shifts between the technical replicate data sets at each time point should be removed so that average/median peptide abundance values can be calculated for the purpose of imputing missing peptide abundance values.

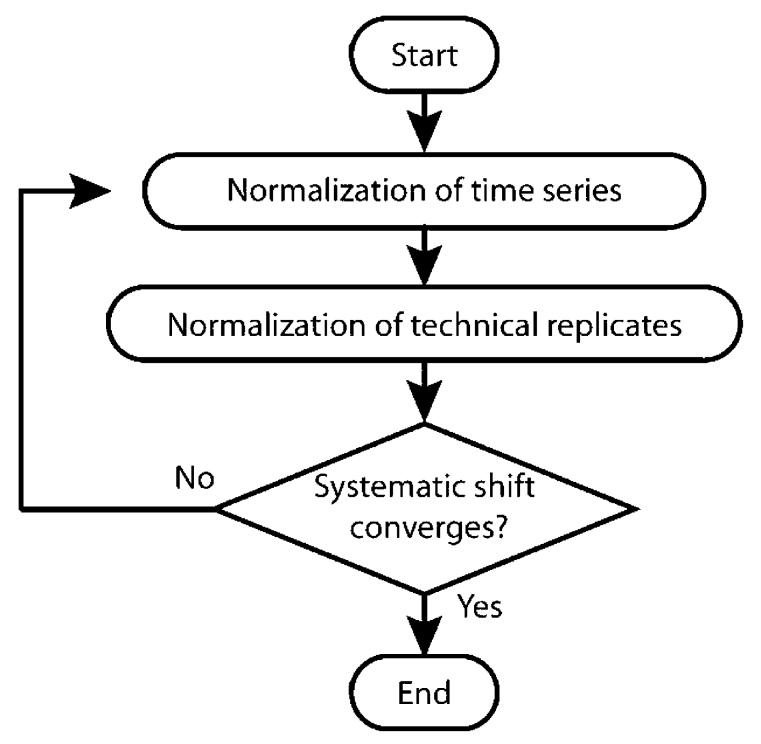
In an experimental design wherein blocking is used, data sets within the same time block can be normalized separately from data sets within a different time block since instrument variation is expected to be small during the same block. Normalization of data sets within the same block against a reference data set within the same block carries a smaller risk of bringing artifacts to the data than normalization of data sets in all blocks against the same reference data set. As a result, two stages of normalization are performed sequentially: normalization of the time series data followed by normalization of the technical replicate data.

Since normalization of the technical replicate data could produce a systematic shift in the time series data and vice versa, the normalization process is iterative wherein multiple rounds of normalization of the time series and technical replicate data are performed (outlined in Figure 2). This iteration continues until the difference in the systematic shifts between two adjacent iterations converges to a very small, preset value.

Figure 2.

Iterative process of abundance normalization.

During each iteration, the first stage of normalization is performed on the set of time series data within each block and is achieved via a regression analysis between the abundances of common peptides in the reference data set and in the data set to be normalized. On the basis of the model described in eq 1, a linear regression is used to approximate the systematic shift between replicates and their reference baseline, and a simple affine transformation is applied to the data to normalize the abundances so that the regression line between the two replicates after the normalization approaches 45°. All of the data sets within a time block are normalized against a single reference data set that is in the same time block. Each time block is normalized separately and all of the reference data sets correspond to the same time point (Supplemental Figure 2A).

The second stage of normalization within each iteration is performed on each technical replicate data set group at each time point. At this stage, each LC-MS data set representing one technical replicate is normalized with respect to a reference technical replicate that corresponds to the same time point; that is, the technical replicate data sets are grouped in terms of time points and the normalization of different groups is performed separately. Implementation of this normalization is the same as that for the time series. All of the references that correspond to different time points should be within the same block (Supplemental Figure 2B).

The nonuniform distribution of the peptide abundance values necessitates upper and lower abundance thresholds to prevent the small percentage of peptides with very large abundances and the much larger percentage of peptides with very small abundances from asserting unequal leverage on the regression line. To determine the regression line, an iterative process is needed wherein the calculated regression line converges through the removal of outliers. During each iteration of regression, the perpendicular distances between the identified regression line and the peptide abundance values (i.e., the residuals) are calculated. The distribution of all of the distances is then used to identify abundance values that are at least two standard deviations away from the regression line. These abundance values are considered outliers, and after they are removed, the regression line is recalculated. This process continues until the regression line converges. If the abundance data cannot be modeled as in eq 1 (e.g., an intensity-dependent trend exists between two LC-MS data sets), then other nonlinear regression methods should be used. Appropriate normalization techniques include the LOWESS, smoothing spline, and piece-wise linear trend algorithms.

The criterion for the convergence of the abundance normalization iterative process is that the total sum D of the slope differences between adjacent iterations approaches zero. D is defined as

$$D=\sum _{t=1}^T\sum _{r=1}^R\mid k_{tr}^{\left(j\right)}-k_{tr}^{(j-1)}\mid$$ (2)

where $k_{tr}^{\left(j\right)}$ denotes the slope of the regression line for technical replicate r at time point t. The superscript (j) denotes iteration number. R represents the total number of technical replicates and T is the total number of time points. D is calculated separately for the normalization of data from technical replicates and time series, and convergence is reached when both are less than a preset threshold. This convergence is important in that it indicates that the iterative normalization gradually reduces the systematic shifts in the data until there is no detectable systematic shift anymore in both the time series and technical replicate data. If the iterative process does not converge, another noniterative normalization approach can be employed; that is, all the data sets are normalized against the same reference data set for a single time. This approach carries a larger risk of bringing artifacts to the data than the iterative approach, especially in the situation wherein the time is far apart when different blocks of data sets are analyzed by LC-MS.

2. Identification of Optimal References

The determination of which time point and which LC-MS block should be selected to be the reference data sets for normalization must be resolved. The optimal reference from the technical replicates is found through an exhaustive search that considers each technical replicate as the reference and then choosing the block (each block contains one technical replicate for each time point) that results in the largest total correlation after normalization. Here, the total correlation is defined as the sum of the correlation values between all of the technical replicates and their corresponding references, that is,

$$\rho =\sum _{t=1}^T\sum _{r=1}^R{\rho }_{tr}$$ (3)

where ρ_tr denotes the Pearson Product Moment Correlation between the rth technical replicate data set and its reference data set at time point t.

The optimal reference for normalizing the time series data is found in the same manner, that is, by identifying the time point which results in the largest total correlation for all the LC-MS blocks.

Missing-Value Imputation

Missing abundance values can be caused by a number of reasons and the easiest way to impute them is to fit a curve to the incomplete time-course data and impute the missing abundance values with the curve’s fitted values. However, there is a drawback to this approach in that the time series will be forced to abide by the temporal structure of the fitted curves, and thus, it is very likely that artifacts will be brought into the data. Another approach is to impute each missing abundance value based on the abundance values that correspond to the nearby time points. Implicitly, it is assumed that the abundance values at the nearby time points do not change dramatically.

In using nearby time points for missing value imputation, let A = ⌈a_i,j⌉; i = 1, 2, ..., R; j = 1, 2, ..., T represent all of the abundance values of a peptide where i represents the index of the technical replicate and j represents the time point. Thus, in matrix A, each row corresponds to the time series ordered in ascending time, and there are a total of R time series for the peptide. The imputation starts with those rows that have at least ⌈2T/3⌉ available measurements (⌈2T/3⌉ represents the minimum integer that is ≥2T/3) and the imputation is based on the available abundances in the same row of A as the missing value(s). The reason for starting with these time series is that these data are usually sufficient to establish a reliable temporal trend in the series that can then be utilized to impute the missing values with confidence. The 2T/3 was chosen empirically. Different scenarios can be encountered, and each scenario requires a different imputation approach to determine the missing values (denoted as nan):

1. A single missing value is sandwiched between two measurements, a_i,1 a_i,2 ··· a_{i, j-1} nan a_i,j+1 ··· a_i,T. In this case, the average of the two available values is used to fill in the missing value, that is,

   $$a_{i,j}=(a_{i,j-1}+a_{i,j+1})∕2$$ (4)
2. Two or more missing values occur consecutively and are sandwiched between two measurements a_i,1 a_i,2 ··· a_i,j-1 nan nan a_i,j+2 ··· a_i,T. Interpolation is performed as in Scenario 1, and all of the missing values are replaced with the same interpolated value. For example, if two consecutive values are missing, then their interpolated values are

   $$a_{i,j}=a_{i,j+1}=(a_{i,j-1}+a_{i,j+2})∕2$$ (5)

   Note that when the total number of time points is large, a proportional number of consecutively missing values can occur as well. When the absolute time interval between the two available measurements a_i,j-1 and a_i,j+2 is large, a simple average would be inappropriate to substitute for the missing values.

3. A single missing value occurs at the first time point or a few missing values occur consecutively starting from the first time point, nan nan ··· a_i,j-1 a_i,j a_i,j+1 ··· a_i,T. The available abundance data at the earliest time point is used to fill in the missing values, that is,

   $$a_{i,1}=a_{i,2}=a_{i,j-1}$$ (6)

   This is statistically well-justified when the time interval between the first time point and time j-1 is relatively small.

4. A single missing value occurs at the last time point or a few consecutive missing values end at the last time point, a_i,1 a_i,2 ··· a_i,j-1 ··· a_i,T-2 nan nan. In this case, an approach similar to that used in Scenario 3 is used.

   $$a_{i,T-1}=a_{i,T}=a_{i,T-2}$$ (7)

After the imputation is performed for the time series data with at least ⌈2T/3⌉ observations for each peptide, the time series data for this peptide with less than ⌈2T/3⌉ observations are considered. Since the available measurements for this time series cannot reveal the temporal trend, missing values are imputed based on the available abundance values in the same column of A as the missing value. The basic idea is to identify the existence of a statistical structure in the available measurements. If the available measurements do not appear to be random and do form a cluster, then the statistical median of the available measurements is used to fill in the missing values after any outliers are removed.

Inference of Dynamic Protein Abundance Patterns

Identifying proteins that have significant temporal expression patterns (and thus are of potential biological importance) are essential for analyzing the dynamics of the corresponding biological processes. The temporal pattern of a protein is inferred from the temporal patterns of at least two peptides belonging to this protein. The inference is pattern-centric and is based on the pattern of change in relative abundance rather than in absolute abundances. This process is termed here as “pattern rollup”.

In pattern rollup, the first step is to scale the normalized abundance values so that all the abundance values that correspond to the same peptide are within the same maximum and minimum limits. The scaling is carried out separately for each peptide and is applied on all the abundance values for a peptide. This scaling is necessary because different peptides have different detection efficiency (that can be caused by such factors as different ionization efficiency) in the LC-MS analysis process, and thus, the measured abundance values of two different peptides might be different even when the same amount of peptides has been injected into the LC-MS analysis system. The scaling preserves the temporal peptide patterns and avoids the issue that the absolute abundance values of different peptides might not be comparable. Specifically, the scaling is performed as follows:

$$A_{\text{scaled}}=K\times A+B$$ (8)

where A is the same as that defined in Missing-Value Imputation and K and B are the scaling parameters that are computed as:

$$K=\frac{{\mathrm{Abun}}_{\max }-{\mathrm{Abun}}_{\min }}{A_{\max }-A_{\min }}$$ (9)

$$B={\mathrm{Abun}}_{\max }-K\times A_{\max }$$ (10)

where Abun_max and Abun_min are the preset maximum and minimum abundance limits, and A_max and A_min are the maximum and minimum values of matrix A, respectively.

The second step is to extract significant temporal patterns of peptides from all the observed peptide patterns. “Significant” here means that the temporal pattern/signal is very different from a flat line of abundance values across time. The identification of significant peptide patterns can be achieved using software tools such as EDGE.^24,25 EDGE performs a hypothesis test to determine whether the temporal pattern of each peptide is flat and computes a p-value and a q-value to quantify how significantly the peptide abundance values change across time. The list of peptides that have significant temporal structures can be obtained by filtering on the p-value or q-value.

The third step is to reconstruct the continuous dynamic peptide patterns. Peptide abundance values are measured at discrete time points, and from these discrete measurements, the continuous trend is reconstructed for the purpose of recovering and visualizing raw dynamic abundance patterns. This reconstruction becomes even more important when an in-depth analysis of the robustness and stability of a biological system is needed in a systems biology study. Since the continuous and discrete abundance values across time form temporal signals, Shannon’s sampling theorem^26,27 can be applied to reconstruct the raw signal. On the basis of this theorem, if the sampling frequency is at least twice the highest frequency component in the continuous signal, then the discrete signal will be a true representation of the continuous one and the continuous peptide abundance signal can be reconstructed as follows:

$$y_c\left(t\right)=\sum _{n=-\infty }^{n=\infty }{y}_d\left(n\right)\sin c(t-n)$$ (11)

where y_c denotes the continuous signal to be reconstructed, y_d denotes the discrete signal that is measured, and sin c(t) is the sinc function.

The last step in the pattern rollup process is to infer the temporal protein abundance patterns from the temporal peptide abundance patterns. Specifically, a hierarchical clustering algorithm is used to cluster the measured peptide abundances based on their patterns. The distance metric can be based on the Euclidean distance and average linkage can be used as the linkage method in the clustering analysis. The centroid of the largest cluster is used to represent the protein pattern.

Ultimately, an EDGE analysis can be performed a second time on the protein dynamic patterns to quantify the significance of the patterns and to compute the p- and q-values that correspond to each protein pattern. However, this second EDGE analysis can typically be omitted because of the strict criteria employed in the pattern rollup process; that is, it can be reasonably assumed that all of the obtained protein patterns are statistically significant.

Results and Discussion

Data Preprocessing and Peptide Filtering

After data pre-processing, a total of 17 952 peptides were observed in the time-course study. Figure 3 (left) shows the observation count for each of these peptides versus time. Note that peptides appearing in the upper part of Figure 3 (left) were most likely detected by chance as they appear only sporadically. Peptides observed consistently among the five technical replicates and across the 10 time points (i.e., the lower portion of Figure 3 (left) are expanded in Figure 3 (right). All peptides were filtered using observation counts and each peptide was required to have been observed at least three times among the five technical replicates and at least seven times across the 10 time points. This criterion guaranteed that peptides that passed the filter were observed consistently among the five technical replicates and that the available temporal measurements were numerous enough to establish a temporal trend. After filtering, 7479 peptides (Figure 3 (right)) were retained for further data analysis. These retained peptides accounted for 42% of the total number of peptides in the unfiltered data.

Figure 3.

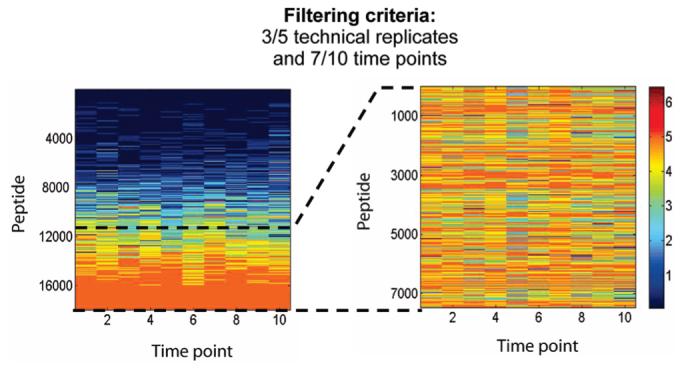
Filtering using peptide observation counts. (Left) Peptide observation counts for the five technical replicates. The peptide observation counts are indicated by the color bar. (Right) Filtering based on observation counts among the five technical replicates and across all 10 of the time-points.

Abundance Normalization and Missing Value Imputation

Prior to normalization, the median of the abundance values in many of the LC-MS data sets deviated from each other, which highlighted the need for abundance normalization (Supplemental Figure 3A shows boxplots of the 50 LC-MS data sets prior to normalization). Prominent data sets requiring normalization included one data set at time point 1, one data set at time point 5, and two data sets at time point 8.

Table 1 lists the Pearson correlation coefficients between the data set at each time point and the data set at the reference time point 4 within the same block. The correlation coefficients in each row correspond to a particular block. Since the Pearson correlation coefficient represents the strength of a linear relationship between two random variables and a majority of the coefficients in Table 1 are quite large (>0.90), a linear regression line was able to capture most of the relationships between each pair of LC-MS data sets within a block. As a result, there was no need to use loess or smoothing spline regression.

Table 1.

Person Correlation Coefficients between Data Sets at Different Time Points and the Data Set at Time Point 4 within the Same Block

	t1	t2	t3	t4	t5	t6	t7	t8	t9	t10
b1	0.7687	0.9258	0.9018	1.0000	0.9712	0.9704	0.9006	0.9445	0.9193	0.9564
b2	0.9805	0.9758	0.8574	1.0000	0.8290	0.9477	0.9858	0.9889	0.9891	0.9807
b3	0.9804	0.9777	0.9921	1.0000	0.9403	0.9875	0.9892	0.9631	0.9673	0.9740
b4	0.9742	0.9197	0.9865	1.0000	0.9818	0.9792	0.9655	0.8568	0.9828	0.8110
b5	0.7851	0.9470	0.9709	1.0000	0.8003	0.9156	0.9649	0.9523	0.7473	0.9483

Iterative normalization of the data from the time series followed by normalization of the data from the technical replicates was performed on the entire data set. Time point 4 was determined to be the optimal reference for the time series data normalization, and similarly, LC-MS block 3 was determined to be the optimal reference for the technical replicate data normalization. After the normalization, the systematic shifts among LC-MS data sets are removed (Supplemental Figures 3, 4, and 5).

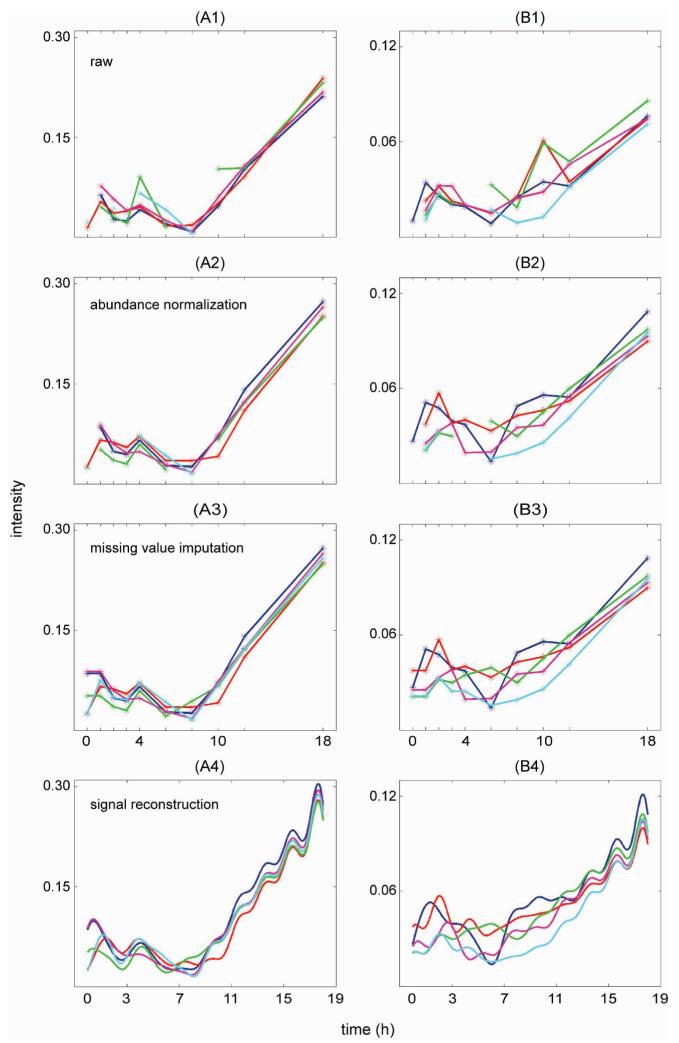
Figure 4 summarizes the results of abundance normalization, missing-value imputation, and signal reconstruction for a single peptide. In Figure 4A, which shows the peptide abundance values versus time before normalization, the abundance values shown in red at the zeroth hour (i.e., time point 1) and 10th hour (i.e., time point 8), and the abundance values shown in green at the fourth hour (i.e., time point 5) and 10th hour (i.e., time point 8) appear very different from the other technical replicate abundance values. On the basis of the boxplot shown in Supplemental Figure 3A and the heat map shown in the top row of Supplemental Figure 5, these “outliers” appear to have resulted from a systematic shift in the measurement process, and as such, normalized abundance values (Figure 4B) clustered with the other technical replicate abundance values. In contrast, the obvious deviation of the measured abundance value shown in cyan at the sixth hour (i.e., time point 6) within block 5 was not due to a systematic shift in the experimental process and, therefore, was not corrected by normalization. The general temporal trend in abundance values became discernible only after the normalization, which demonstrates the necessity of normalization for identifying temporal patterns.

Figure 4.

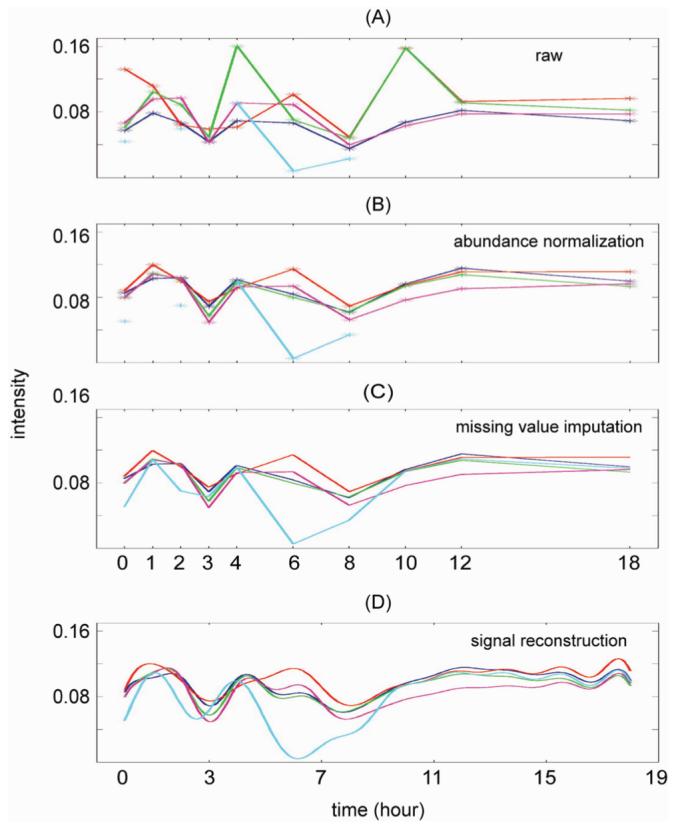
Results of abundance normalization, missing value imputation, and signal reconstruction for one representative peptide. Different colors denote different blocks with blocks 1, 2, 3, 4, and 5 shown in blue, red, green, magenta, and cyan, respectively. (A) Peptide abundance values versus time before normalization. (B) Peptide abundance values versus time after normalization. (C) Peptide abundance values after imputation. (D) Reconstructed, continuous peptide abundance signal based on Shannon’s sampling theorem.

Missing values also existed in the time series data for technical replicate 5, which are shown in cyan in Figure 4A and B. Since there were only five observations for this time series, imputation was based on abundance values from other technical replicates for each time point rather than on the temporal trend identified from the available measured abundance values. Regardless of the imputation method used, a general requirement for imputing the missing values in temporal data was that the imputed values abide by the existing trends and not introduce artifacts to the time series data.

Signal Reconstruction and Identification of Dynamic Abundance Patterns of Proteins

After missing-values were imputed, the resultant peptide abundance values underwent EDGE significance analysis. A list of significant peptide patterns was obtained after filtering on the p-values. A cutoff p-value was set at 0.001, and any peptide pattern whose p-value was less than the cutoff p-value was considered significant.

On the basis of the observed abundance values of the significant peptides at the discrete time points, the original continuous abundance values were reconstructed using eq 11. Figure 4D shows the reconstructed continuous signal based on the discrete abundance values. Since the sampled abundance values were collected at 0, 1, 2, 3, 4, 6, 8, 10, 12, and 18 h and the sampling was not uniform, an interpolation was performed so that an abundance value was available at each hour and a uniform sampling was obtained. On the basis of the equally spaced sampled abundance values, the reconstructed signal displayed a smooth trend. The uniform sampling interval was 1 h, which assumed that the maximum frequency component in the original continuous signal was less than one cycle per 2 h. If this assumption did not hold, then an under-sampling issue would have existed in the experimental design and there would have been no way to reconstruct the continuous signal correctly.

The protein-level dynamic patterns were derived from the continuous, significant, peptide-level patterns. For each protein, the significant peptide-level patterns were clustered and the largest cluster was determined. At least two peptides were required in the largest cluster, and at least half of the total peptides were required to be members of the largest cluster to perform the pattern rollup. The protein pattern was computed as the median of the largest cluster. Figure 5A-C shows the rollup of peptide patterns to protein patterns for three technical replicates. Since the other two technical replicates did not pass the pattern rollup requirement, protein patterns were derived from only three sets of technical replicate peptide patterns. For each technical replicate, two significant peptide patterns formed the most prevalent cluster, and the median of the cluster (shown in black) was the derived protein pattern. The peptide pattern shown in red was for a peptide that belonged to this protein, but appeared different from the pattern in the prevalent cluster. This pattern was reproducible among the three technical replicates and may indicate that the peptide was modified, such as by phosphorylation. In this sense, pattern analysis has the potential to shed light on possible peptide modifications that may have occurred.

Figure 5.

Inference of protein-level dynamic patterns from peptide-level dynamic patterns. (A-C) Each graph corresponds to one technical replicate. The dashed lines denote the peptides that were used for the inference. The black, thick lines denote the inferred protein temporal patterns. The dotted lines denote peptides that were not in the largest cluster and thus were not used in the inference. (D) Inference of final dynamic protein patterns from its technical replicate patterns. A cluster analysis was performed on all the technical replicate patterns, and the median of the largest cluster was computed as the final dynamic protein pattern shown in blue.

Figure 5D shows the final protein pattern computed from the three technical replicate protein patterns shown in Figure 5A-C. This pattern was derived from the technical replicate protein patterns by performing a cluster analysis of the technical replicate protein patterns, and the median of the most prevalent cluster was computed as the protein pattern.

Value of the Computational Strategy for Biology

The shift from aerobic metabolism to photosynthetic metabolism in R. sphaeroides is accompanied by a period of no growth, which was monitored by the ten time points described above. Previous proteomic comparisons between the two metabolic states have shown a dramatic relative abundance increase in much of the photosynthetic machinery.⁵ However, little if any metabolic activity occurs during this lag period and the few biological processes that are occurring are likely directly related to initiating the development of the photosynthetic cell state. Thus, we only expected a “handful” of proteins exhibiting temporal patterns. The roughly 18 000 peptides originally identified, the number of missing values, and systematic variability posed a challenge in trying to identify the small subset of peptides having significant temporal trends above the large degree of random noise that so often accompanies label-free quantitative approaches.

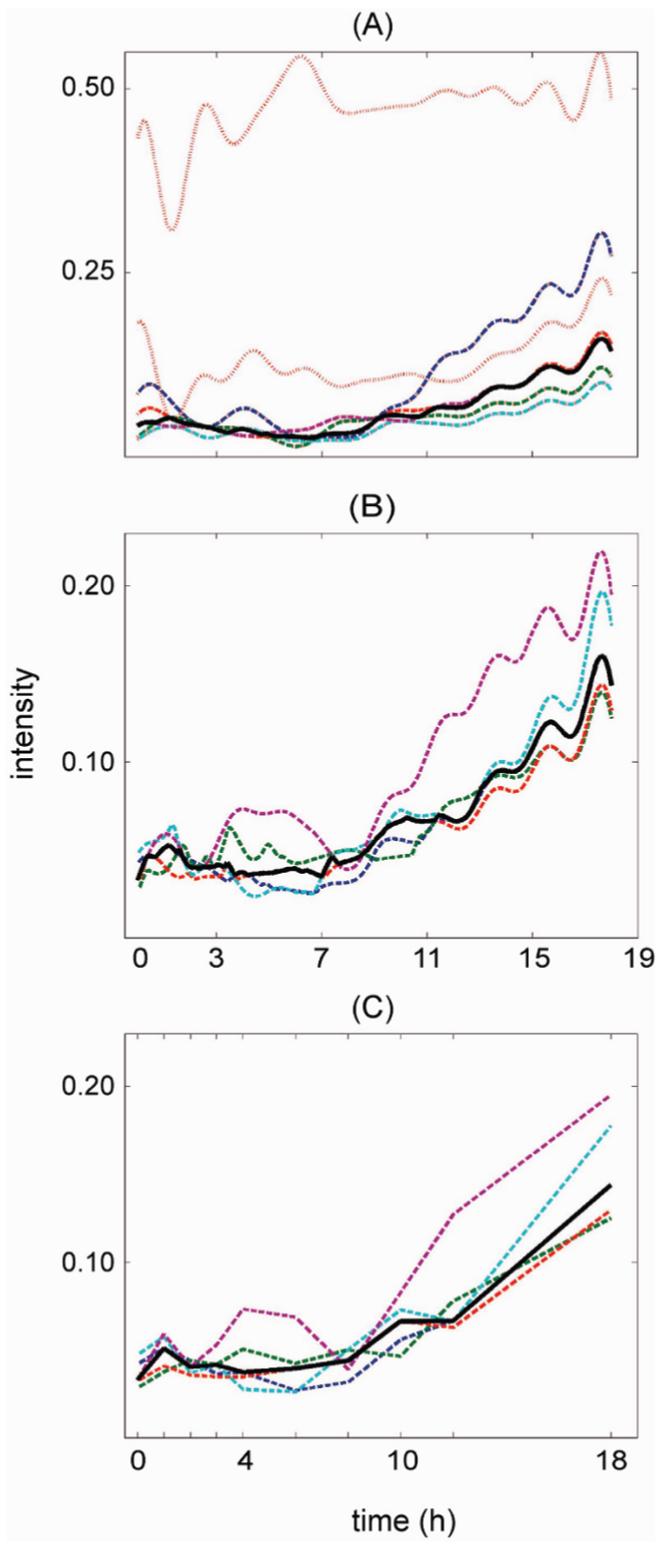
The computational strategy presented allowed us to identify approximately 50 proteins with significant temporal trends during this lag phase. For example, the final temporal trends of peptides for the protein spheroidene monooxygenase (CrtA) are shown in Figure 6 along with the improvements made to this trend with each step of the computational strategy and Figure 7 shows the temporal pattern for this protein. Spheroidene monooxygenase catalyzes the conversion of spheroidene to spheroidenone, the end product of the carotenoid production pathway.²⁸ This biomolecule is important to stabilizing the B800-850 light harvesting complex and preventing oxidative damage as a result of singlet oxygen formation in the presence of light.²⁹ The abundance increase in CrtA suggests that this protein is an important precursor to development of the photosynthetic apparatus. Further biological analysis of this protein’s temporal trend in relation to the temporal trends of other identified proteins and the photosynthetic apparatus is now warranted because of the successful application of this computational strategy.

Figure 6.

Value of the data analysis strategy to extract temporal patterns. The temporal patterns are shown for two peptides that belong to protein spheroidene monooxygenase (CrtA) in the left and the right column, respectively.

Figure 7.

Pattern rollup for protein spheroidene monooxygenase. (A) Pattern rollup for one of the five technical replicates. A total of seven significant peptides were identified for this protein and the most prevalent cluster contains five peptides (dashed lines). The remaining two peptides (dotted lines) that are not in the prevalent cluster are in red. The solid black curve represents the protein pattern. (B) The final protein pattern shown in black that is obtained from the five technical replicate protein patterns. (C) The discrete version of (B).

Conclusions

To extract useful biology from temporal proteomics studies through data mining and modeling, the temporal abundance change of a network of significant proteins can be modeled and analyzed using theories such as the rich systems theory.^30-32 This type of analysis requires abundance measurements at many time points such that there is no obvious under-sampling issue in the observed data. Ultimately, the extracted biological information should provide a better understanding of the mechanism of a biological system. However, fulfillment of this aim demands a quantitative measurement of the abundance change of proteins over time.

The strategy described in this paper uses abundance normalization, missing-value imputation, and inference of peptide- and protein-level dynamic patterns to form a data analysis framework for analyzing temporal bottom-up proteomics data. The specifics of each step can be modified based on the data to be analyzed. Demonstration of this strategy using data from a R. sphaeroides time-course study of the temporal transition between two metabolic states (aerobic respiration and photosynthesis) illustrates the value of this approach for extracting significant temporal protein patterns. The data analysis algorithms have been implemented in a software package that is publicly available at http://ober-proteomics.pnl.gov/software/Du_TimeCourseAnalysis_01072008.zip.