An Epistatic Genetic Basis for Physical Activity Traits in Mice

Abstract

We recently identified several (4–8) quantitative trait loci (QTL) for 3 physical activity traits (daily distance, duration, and speed voluntarily run) in an F₂ population of mice derived from an original intercross of 2 strains that exhibited large differences in activity. These QTL cumulatively explained from 11% to 34% of the variation in these traits, but this was considerably less than their total genetic variability estimated from differences among inbred strains. We therefore decided to test whether epistatic interactions might account for additional genetic variation in these traits in this same population of mice. We conducted a full genome epistasis scan for all possible interactions of QTL between each pair of 20 chromosomes. The results of this scan revealed an abundance of epistasis, with QTL throughout the genome being involved in significant interactions. Overall, epistatic effects contributed an average of 26% of the total variation among the 3 activity traits. These results suggest that epistatic interactions of genes may play as important a role in the genetic architecture of physical activity traits as single-locus effects and need to be considered in future candidate gene identification studies.

It is known that physical activity is an important contributor to human health, and in recent years, it has been increasingly appreciated that inactivity can lead to a number of health problems (Blair et al. 2004; Chakravarthy and Booth 2004; Manson et al. 2004). Given this, it is somewhat surprising that little is known about the genetic architecture of various measures of physical activity. Some previous studies have estimated the broad-sense heritability of activity traits such as wheel-running behavior in mice to be as high as 50% or greater (Houle-Leroy et al. 2000; Lerman et al. 2002; Lightfoot et al. 2004), but this tells us little about the identity or action of the genes involved.

Recently, Lightfoot et al. (2008) performed an interval mapping experiment to search for quantitative trait loci (QTL) controlling the distance, duration, and speed voluntarily run by mice. They used an F₂ population of mice bred from 2 inbred strains (C57/J and C3H/HeJ) that previously had been shown to exhibit large differences in these 3 physical activity traits (Lightfoot et al. 2004). A number of QTL were discovered for each of these traits, including 2 (on chromosome 9 at 7 cM and chromosome 13 at 11 cM) that reached experimentwise significance and several others (chromosome 2, 5, 8, and 12) that reached the chromosomewise (suggestive) level of significance. Further, some of these QTL exhibited prominent dominance genotypic effects (Lightfoot et al. 2008). Cumulatively, QTL variation explained only from 11% to 34% of the variation in these traits, considerably less than their total genetic variability estimated from differences among inbred strains (Lightfoot et al. 2004). The authors suggested that beyond single-locus effects of the QTL on these traits, epistatic effects of QTL might contribute additional genetic variability (Lightfoot et al. 2008).

We therefore tested for the importance of epistasis on these 3 physical activity traits in the same population of mice. We performed a full genome epistasis scan to search for QTL on each pair of chromosomes that might significantly interact to affect the distance, duration, or speed run by mice in this population. Our scan in fact revealed an abundance of epistasis affecting the activity traits, and in this paper, we document the evidence for this epistasis and its impact on the 3 physical activity traits.

Materials and Methods

The Population and Traits

To generate the F₂ population of mice used for the QTL analyses, we first crossed 10 mice from each of 2 inbred strains, C57L/J and C3H/HeJ, previously identified as exhibiting the greatest divergence in measures of physical activity (Lightfoot et al. 2004). These mice were reciprocally crossed (using males and females from each strain) and produced 63 F₁ mice that were weaned at 21–28 days. Five male and 5 female mice from each of the 2 F₁ reciprocal classes then were randomly chosen for reciprocal crossing and eventually produced a total of 310 F₂ offspring (all first litters except for 4 matings that produced 2 successive litters). All mice were housed in the same room maintained at 18–21 °C and 20–40% humidity with 12-h light/dark cycles; food (Harland Teklad 8604 Rodent Diet, Madison, WI), and water were provided ad libitum. Each mouse was weighed to the nearest tenth of a gram weekly.

All F₂ mice were weaned at 21–28 days and individually measured for 3 physical activity traits during a 21-day interval starting at age 63 days (9 weeks). The 3 traits included total daily distance (kilometers) and total daily exercise time (minutes) that were recorded every 24 h and average daily running speed (meters/minute) obtained by dividing distance by duration. Within 7 days after the phenotyping was completed, the mice were anesthetized and the kidneys harvested for subsequent DNA extraction. Genotyping was accomplished for 129 single-nucleotide polymorphisms that were polymorphic between the progenitor strains. These covered the entire mouse genome (including the X chromosome) with an average intermarker interval of 13.7 cM. Details regarding the measurement and genotyping process are given in Lightfoot et al. (2008). All mouse procedures were approved by the UNC Charlotte Institutional Animal Care and Use Committee. In addition, we followed the guidelines for ethical use of animals from the American Physiological Society and the American College of Sports Medicine.

Epistasis Analysis

Before conducting the epistasis analyses, we adjusted each of the physical activity traits for any differences due to reciprocal effects, sex, litter size, rearing block, or body weight found to be significant in an analysis of covariance. These adjustments helped to decrease nongenetic trait variation and promote normality in the trait distributions (see Lightfoot et al. 2008). We then conducted separate 2-way genome scans to test for epistasis for each of the 3 (adjusted) physical activity traits in all mice from the F₂ population.

To accomplish these scans, we first assigned additive genotypic index values of −1, 0, and +1 and dominance genotypic index values of −0.5, +0.5, and −0.5 for C3H/HeJ homozygotes, heterozygotes, and C57L/J homozygotes, respectively, at the site of each single-nucleotide polymorphism (SNP) marker. We also imputed genotypic index values for all locations 2 cM apart between flanking SNP markers on each chromosome from the probabilities that each individual was homozygous (for either parent allele) or heterozygous. These probabilities were calculated from the recombination percentages given in the Mouse Genome Database (Eppig et al. 2005), and the equations in Haley and Knott (1992). Canonical correlation analyses were conducted for all pairs of locations on each of the 190 possible pairs of 20 chromosomes. Each analysis used an activity measure as the variable in one group and all 4 interactions of the additive and dominance genotypes scores from the 2 chromosomes as the variables in the other group, while partialing the main effects associated with these scores.

Every canonical correlation analysis conducted for each pair of locations generated a probability associated with the F-approximation to the multivariate Wilks’ Lambda statistic. We plotted all probabilities of 10% or less generated for each chromosomal pair and assumed those pairs of positions exhibiting the lowest probability (0.05 or less) within the probability valleys were potential QTL combinations exhibiting epistasis. Our plots often yielded several such valleys for individual chromosomal pairs, and when clearly separated by ridges (areas with probabilities greater than 10%), each valley was accepted as a separate instance of epistasis (Leamy et al. 2005).

We next conducted multiple regression analyses of each physical activity trait on the additive and dominance genotypic index values (and all 4 of their pairwise products) at each of the combinations of sites previously identified as significant. The regression coefficients generated for each of these 4 interactions were used to estimate additive-by-additive (aa), additive-by-dominance (ad), dominance-by-additive (da), and dominance-by-dominance (dd) genotypic epistatic terms. Additive-by-additive epistasis for 2 loci (say A and B) occurs when the single-locus additive genotypic value (difference between the 2 homozygotes) at one locus (A) differs depending on what genotype (B/B, B/b, or b/b) is at another locus (B) and vice versa. Additive by dominance epistasis occurs when the single-locus additive genotypic value for a locus A differs depending on the genotype at another locus B, whereas the single-locus dominance genotypic value (difference between the heterozygous and mid-homozygote values) at B differs depending on the locus A genotype (and vice versa for dominance-by-additive epistasis). Dominance by dominance epistasis occurs when the single-locus dominance genotypic value at locus A differs depending on the genotype at locus B and vice versa (Cheverud 2000). Tests for the individual significance of each of these 4 genotypic epistasis terms were done via individual t-tests.

Probability Considerations

Although we recorded all epistatic combinations reaching significance at the conventional 5% level in the genome scans for each of the physical activity traits, clearly many of these would be expected to be significant by chance alone. To address the multiple comparisons problem inherent in these analyses, we used an approach outlined by Cheverud (2000, 2001). This approach involved first calculating the effective number of independent tests for each chromosome as M_e = M(1 − V_λ(M − 1)/M²), where M is the number of markers scored on each chromosome and V_λ is the variance of the eigenvalues of the correlation matrix of markers. We then were able to calculate the total number of independent epistasis tests by the sum of the cross products of the effective number of markers for all 190 pairs of chromosomes. This calculation yielded a sum of 4296, suggesting that we might expect about 215 tests to be significant at the 5% level, 43 at the 1% level, and 4 at the 0.1% level because of chance alone. Significant epistasis therefore was indicated if the observed number of F values reaching significance for epistasis significantly exceeded its expected number (as tested by a chi-square statistic associated with 1 degree of freedom).

Once overall significance for epistasis was determined at these various probability levels, it was possible to assess the probability of false-positive instances of epistasis. This is the false-discovery rate (FDR; Storey and Tibshirani 2003) and was simply estimated by the number of epistatic tests expected to be significant by chance alone divided by the total number actually found to be significant. Calculation of these FDR values was helpful in quantifying the level of evidence for epistasis.

Beyond testing for significant overall epistasis for each of the 3 traits, it also was possible to test individual instances of epistasis. This was accomplished by calculating the 0.05 Bonferroni threshold level of significance as 0.05/4296 = 1.16 × 10⁻⁵. Thus, the probability associated with the F-statistic for any individual epistatic combination was considered “significant” if it reached or exceeded this probability value (Leamy et al. 2002; Peripato et al. 2002). This is a rather stringent individual threshold level, however, so we also calculated a more liberal cutoff level by making use of the number of chromosome pairs, as suggested by Holland (1998). This approach yields a smaller threshold probability of 0.05/190 = 2.63 × 10⁻⁴. We will refer to any epistatic combinations reaching this probability level (but not the 1.16 × 10⁻⁵ level) as being “suggestive” of epistasis.

Results

The epistasis genome scans produced 238, 239, and 226 pairwise QTL combinations for distance, duration, and speed, respectively, that reached significance at the 5% level. The number expected at this level by chance alone was 215, and chi-square tests showed that none of these values were significantly different from 215 (P > 0.05 in all cases). On the other hand, the sum of these values for all 3 traits, 703, was significantly different (P < 0.05) from the total of 644 expected by chance alone. In general, at this 5% significance level, however, there is little evidence for epistasis affecting the individual traits.

At the 1% significance level, the results were quite different (see Table 1). The number of significant epistatic combinations exceeded the number expected by chance (43) for all 3 traits (P < 0.01). FDRs obtained by dividing 43 by the number of significant epistatic combinations vary from 0.52 to 0.55. Significant epistatic effects for each of the traits were found for QTL on all 20 chromosomes, with chromosomes 2, 11, and 12 being particularly involved. The distribution of significant aa, ad/da, and dd epistatic genotypic values follows the expected 1:2:1 for all 3 traits (P > 0.05 in chi-square tests). Over all pooled traits, however, this distribution significantly differs (P < 0.01) from expectations, with an excess of dd epistatic effects. The means of the significant epistatic values range from 0.33 to 0.84 standard deviations (SDs), with the dd values being consistently highest. Across all 3 traits, the dominance-by-dominance epistatic genotypic values average 80% of the SD of these traits.

Table 1.

Numbers of epistatic combinations significant at the 1% level for distance, duration, and speed

	Number significant	FDR	aa	ad	da	dd	Chromosomes most involved
Distance	78	0.55	0.33 (26)	0.55 (41)	0.56 (27)	0.79 (40)	2, 9, 11, 12
Duration	83	0.52	0.33 (31)	0.51 (35)	0.50 (35)	0.77 (40)	2, 5, 10, 11
Speed	78	0.55	0.36 (21)	0.58 (36)	0.50 (31)	0.84 (28)	2, 7, 12

All are significantly greater (P < 0.01 from chi-square tests) than the theoretical number (43) of epistatic interactions expected to be significant at this level. Means of the absolute standardized values of the 4 epistatic components (and the number significant) as well as the chromosomes most involved in epistasis also are given.

Ten pairwise combinations of QTL showed epistasis for distance that reached significance at the 0.1% level (Table 2), this being greater (P < 0.05) than the 4.3 (0.001 × 4296) combinations expected by chance alone (FDR = 4.3/10 = 0.43). The probabilities associated with the F-tests for epistasis range from 0.000124 to 0.000705. Thus, none reach the significant threshold level of 1.16 × 10⁻⁵ although 2 combinations (QTL on chromosomes 3/10 and 6/15) reach the suggestive probability level of 2.63 × 10⁻⁴. A total of 22 epistatic components also reach significance (at the conventional 5% level), with all except 1 of the 10 pairwise QTL combinations exhibiting 2 or 3 different epistatic forms. Their magnitude varies from 0.28 to 1.26 SDs, with the highest values being seen for the dd type.

Table 2.

Locations in centimorgan (cM) from the centromere for QTL on each pair of chromosomes (CH1 and CH2) exhibiting significant (P < 0.001) epistasis for distance

CH1	cM	CH2	cM	F	Probability F	aa	ad	da	dd
1	99	7	32	5.48	0.000291	0.35	−0.39	−0.50
1	109	8	76	5.13	0.000527	−0.41	−0.59
2	61	3	46	5.11	0.000549			−0.42	−0.93
3	74	9	69	4.96	0.000705				−1.26
3	62	10	34	5.98	0.000124*		−0.37	0.81
4	54	X	94	4.76	0.000996			−0.39	−1.00
6	80	15	4	5.80	0.000169*			−0.70	0.83
9	25	19	37	4.81	0.000916		−0.53		−0.81
11	26	12	55	5.48	0.000292	−0.28	−0.71		0.75
13	17	18	56	5.12	0.000537	−0.31	−0.70		0.62

Shown are the F-statistics that test overall epistasis with their associated probabilities (*P < 0.05 at the suggestive Bonferroni threshold level). For each pairwise QTL combination, the individual standardized epistatic components that reached statistical significance also are given.

As an example of epistatic effects on distance, the combination of da and dd epistatic effects generated by the QTL on chromosomes 6 and 15 is illustrated in Figure 1A. Note that the QTL on chromosome 15 shows underdominance (heterozygote less than either homozygote) for the chromosome 6 QTL LL (C57L/C57L) and HL genotypes but overdominance (heterozygote greater than either homozygote) for the chromosome 6 QTL HH (C3H/C3H) homozygote. Further, the chromosome 6 QTL homozygotes are similar in magnitude for distance for the chromosome 15 QTL HH homozygotes but differ considerably for chromosome 15 QTL HL and LL genotypes.

Figure 1.

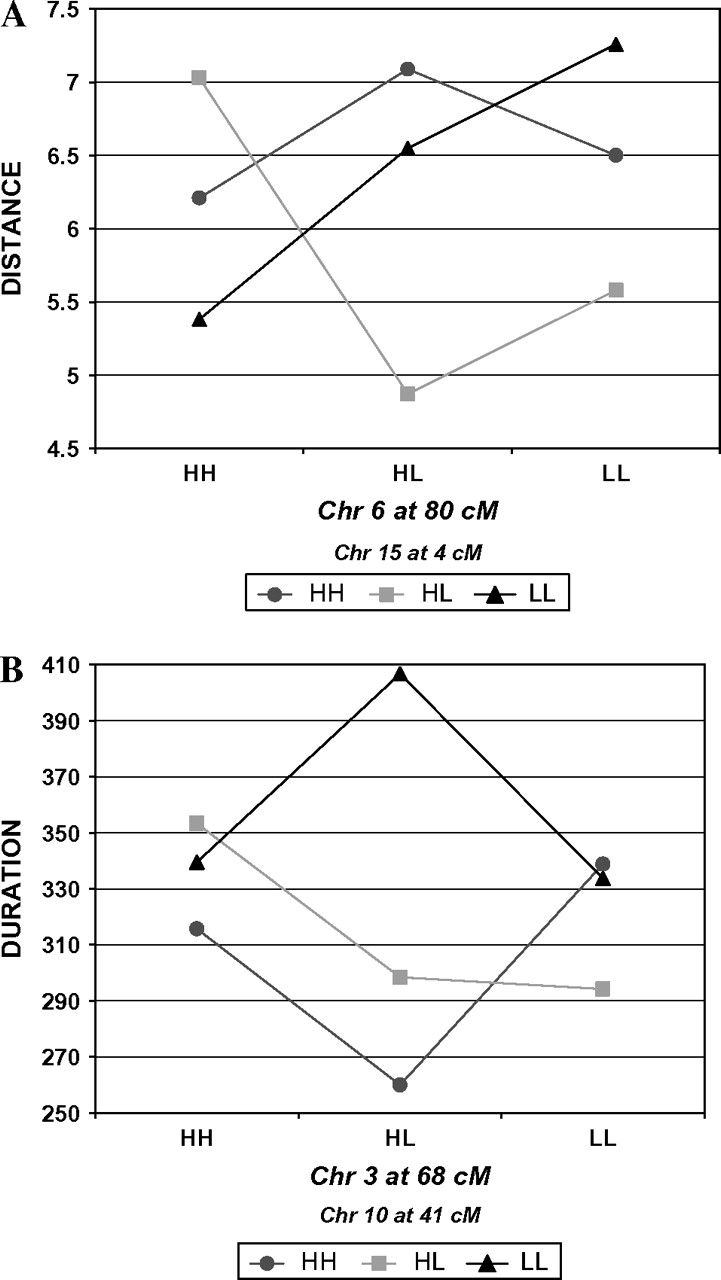
Epistatic interactions between QTL on chromosomes 6 and 15 affecting distance (A) and between QTLs on chromosomes 3 and 10 affecting duration (B). HH, C3H/C3H homozygotes; HL, C3H/C57L heterozygotes; and LL, C57L/C57L homozygotes.

To assess the total impact of epistasis on the variability of distance, we ran a multiple regression of distance on the (22) significant epistatic components associated with the 10 QTL pairs. Whereas the regression of distance on the additive and dominance index values for the 6 QTL originally found to be significant showed that they contributed 18% (adjusted R²) of the total variation (Lightfoot et al. 2008), addition of the 22 significant epistatic components to this model increased the adjusted R² value to 42%. This increase is statistically significant (P < 0.01) and suggests that epistatic effects of just these 10 QTL combinations are sufficient to account for 24% of the total variability of distance.

For duration, 12 QTL combinations showed significant epistasis at the 0.1% level (Table 3), and again this is more than expected by chance alone (P < 0.01 in a chi-square test) and generates an FDR value of 0.36. Four combinations of QTL (on chromosomes 1/8, 3/10, 6/15, and 11/12) are on the same chromosomes at approximately the same locations at those for 4 combinations significant for distance (Table 2), whereas the remaining 8 combinations are unique to duration. The lowest probability is 0.000074 for QTL on chromosomes 3 and 10 but does not reach the 5% stringent Bonferroni level of significance. This combination and 3 others (total of 4), however, do reach the suggestive level of significance.

Table 3.

Locations in centimorgan (cM) from the centromere for QTL on each pair of chromosomes (CH1 and CH2) exhibiting significant (P < 0.001) epistasis for duration

CH1	cM	CH2	cM	F	Probability F	aa	ad	da	dd
1	25	4	64	5.00	0.000670				−0.87
1	107	8	74	5.68	0.000207*	−0.35	−0.69
2	109	5	85	5.38	0.000346		−0.65
3	68	10	41	6.29	0.000074*		−0.33	0.68
4	110	14	32	5.62	0.000228*		0.64		−0.69
5	19	11	54	5.59	0.000242*		0.35		0.90
5	35	19	55	5.33	0.000377			−0.40	0.77
6	74	11	94	4.84	0.000865		−0.69	−0.43
6	84	15	6	5.44	0.000312			−0.58	0.77
10	0	17	53	4.88	0.000810	0.58
11	28	12	53	5.25	0.000432	−0.32	−0.64		0.61
12	17	14	15	5.64	0.000227*	0.33		0.71

Shown are the F-statistics that test overall epistasis with their associated probabilities (*P < 0.05 at the suggestive Bonferroni threshold level). For each pairwise QTL combination, the individual standardized epistatic components that reached statistical significance also are given.

The 12 pairwise combinations of QTL are associated with 22 significant epistatic components that vary in magnitude from 0.33 to 0.90 SDs. As was the case with distance, the highest such values occur for the dd epistatic components. In multiple regression analyses, the contribution of the additive and dominance effects for the 4 QTL originally found to be significant for duration was 11% (Lightfoot et al. 2008). The addition of the 22 significant epistatic components (Table 3) to this model increased the adjusted R² value to 47% (P < 0.01), suggesting that epistatic effects account for a greater proportion (36%) of the variability in duration than do single-locus effects.

Figure 1B illustrates the primarily ad and da epistatic effects that QTL on chromosomes 3 and 10 have on duration. As may be seen, the additive effects (half the difference of the 2 homozygotes) for the chromosome 3 QTL are opposite in sign depending on whether it is associated with the HH (C3H/C3H) versus the HL genotypes of the QTL on chromosome 10. The same is true for the chromosome 10 QTL: the direction and magnitude of its additive effect varies depending on the genotype of the chromosome 3 QTL.

For speed, only 8 pairwise QTL combinations reached significance at the 0.1% level in epistasis tests (FDR = 0.54), and this was not significantly different (P > 0.05) from the 4 expected by chance alone. For completeness, however, these combinations are listed in Table 4. Again, no combinations reach the significant, but 2 reach the suggestive, level of individual significance. One combination includes QTL on chromosomes 13 and 18 that are at locations similar to those for one combination statistically significant for distance (see Table 2); the other 7 combinations once again are unique. The pattern of the individual epistatic components (total of 13) also showed that the dd values tend to be the highest in magnitude. Multiple regression analyses suggest that these significant epistatic components increase the percentage of the total variation explained from 30% by single-locus effects (Lightfoot et al. 2008) to 48%, this increase of 18% being significant (P < 0.01).

Table 4.

Locations in centimorgan (cM) from the centromere for QTL on each pair of chromosomes (CH1 and CH2) exhibiting significant (P < 0.001) epistasis for speed

CH1	cM	CH2	cM	F	Probability F	aa	ad	da	dd
2	71	7	38	4.91	0.000767	−0.23			−0.83
4	92	11	18	5.07	0.000593	−0.47
8	88	X	32	5.40	0.000334				−1.38
10	80	11	56	6.57	0.000046*		0.71
10	48	19	15	5.03	0.000626				−1.00
12	25	15	8	5.97	0.000126*	0.39	0.70
13	15	18	58	5.50	0.000281		−0.78	−0.43
15	10	19	55	4.86	0.000835	−0.40	0.45	−0.46

Shown are the F-statistics that test overall epistasis with their associated probabilities (*P < 0.05 at the suggestive Bonferroni threshold level). For each pairwise QTL combination, the individual standardized epistatic components that reached statistical significance also are given.

Discussion

Impact of Epistasis

This study is the first to consider the relative importance of epistasis in the genetic regulation of any exercise behavior. Although previous studies have found suggestive and significant single-QTL effects on daily activity traits in both human and animal models, their generally low-to-moderate overall contribution (Simonen et al. 2003; Lightfoot et al. 2008) has suggested a limited genetic basis for these sorts of traits (Simonen et al. 2002). Our study documents a number of epistatic interactions of QTL throughout the genome that make substantial additional contributions to the genetic variation in all 3 activity traits.

The evidence for epistatic effects on the physical activity traits in this population of mice was based primarily on the finding of an excess of significant epistatic interactions beyond the number expected by chance at the 1% and 0.1% probability levels. Even at this most stringent probability level (0.1%), however, 4 interactions were expected to be significant by chance alone, and this resulted in FDRs for the individual traits that were quite high, varying from 0.36 to 0.54. But Peripato et al. (2002) used a randomization test to show that the method devised by Cheverud (2001) that we used to estimate the number of independent epistatic is quite conservative. If in fact the true number of independent epistatic combinations for our mouse population is actually 2664 (the equivalent reduction found by Peripato et al. 2002), then FDR rates at the 0.1% probability level would drop to 0.22–0.33. Whatever the true number of false instances of epistasis is, it is also nonetheless true that many of these QTL–QTL combinations reaching significance presumably represent real instances of epistasis.

It was not particularly surprising that none of the individual epistatic combinations reached significance at the 1.16 × 10⁻⁵ Bonferroni threshold level. With the large number of epistasis tests, this is a very conservative threshold and it prompted our use of the additional, more liberal 2.63 × 10⁻⁴ threshold level. As will be recalled, 9 pairwise QTL interactions affecting the physical traits reached significance at this level. Using an F₂ population of mice produced from an original intercross of the large and small inbred strains, Peripato et al. (2004) found several individual epistatic interactions affecting litter size whose probabilities reached a 10% Bonferroni threshold of 3.7 × 10⁻⁵. Leamy et al. (2005) also discovered several individual epistatic interactions affecting molar fluctuating asymmetry in this same population of mice that reached significance at a threshold probability of 5.41 × 10⁻⁵. Both investigators used a nonorthogonal model of epistasis, however, and thus their results are not strictly comparable to ours generated from an orthogonal model.

Theoretical considerations aside, the impact of epistasis on the physical activity traits was impressive. The mean of the absolute significant epistatic components (Tables 2–4) was 0.61 SDs, a value considerably higher than that of 0.35 for the mean of the additive genotypic values of the QTL affecting distance, duration, and speed (Lightfoot et al. 2008). This was somewhat surprising because most past studies have found that the magnitude of epistatic effects are near or only slightly above that for single-locus effects. For example, Cheverud et al. (2001) discovered a number of QTL for adiposity, tail length, necropsy weight, and 10-week weight in a population of 510 F₂ mice whose (absolute) standardized additive single-locus effects varied from 0 to 0.47 and averaged 0.25 but whose QTL–QTL epistatic effects varied from 0.19 to 0.57 and averaged 0.31. The high magnitude of epistatic effects we found for the physical activity traits therefore should be viewed with caution, especially given that none reached the stringent experimentwise level of significance. These values most likely are a consequence of the level of sampling variation generated by the relatively modest number of mice (310) we used as well as the inherent variability in the physical activity traits (see Lightfoot et al. 2008).

Beyond the absolute magnitude of the epistatic effects, their percentage contribution to the total variability in the physical activity traits also was considerable (average over all 3 traits = 26%), especially for duration (36%), where it well exceeded that for the single-locus QTL effects (11%). It is possible that these estimates are inflated, however, because they were calculated using the individual significant epistatic effects produced from all QTL combinations reaching significance at the 0.1% level when 4 of these 10 combinations are expected by chance to be false positives. On the other hand, any potential inflation in these estimates may be offset to some extent because we did not use any epistatic components associated with QTL pairs reaching significance at the 1% level, a number of which should be true instances of epistasis.

Genetic Architecture of Physical Activity

The results of the epistasis analysis suggest that the overall contribution of epistasis to the physical activity traits (mean = 0.26) is comparable to that from single-locus (additive and dominance) effects (mean = 0.20) estimated by Lightfoot et al. (2008). This estimate of the impact of epistasis also is nearly the same as the narrow-sense heritability of 0.28 calculated for wheel running in a previous selection experiment (Swallow et al. 1998). If we therefore assume that single- and multilocus genetic effects each contribute 0.20–0.30 of the total phenotypic variance in these traits, we should expect their total genetic variance to be about 0.5–0.6. In fact, estimates of broad-sense heritabilities of wheel-running activities typically have been precisely in this range (Lerman et al. 2002; Lightfoot et al. 2004).

This genetic profile for distance, duration, and speed suggests that these sorts of physical activity traits are intermediate with respect to their importance to the overall fitness of the mice. Major fitness traits tend to have very low narrow-sense heritabilities (few additive QTL) but substantial nonadditive (dominance and epistatic) genetic variance that contributes to their total phenotypic variance (Malmberg and Mauricio 2005). For example, Peripato et al. (2002, 2004) showed that litter size and maternal performance in an LG/J by SM/J F₂ intercross population of mice were significantly affected by only 2 individual QTL but by a number of epistatic combinations of QTL that contributed considerable nonadditive genetic variance. On the other hand, minor fitness traits such as body size and skeletal size and shape generally are controlled by many single-locus QTL (Cheverud et al. 1997; Leamy et al. 1999; Klingenberg et al. 2001; Workman et al. 2002) that contribute more to the total genetic variance than do epistatic effects (Wolf et al. 2005, 2006).

Dominance was an important feature of some of the QTL affecting distance, duration, and speed in the original study (Lightfoot et al. 2008), and it was interesting that we found dominance-by-dominance (dd) epistatic effects on these traits to be prominent as well. This type of epistasis occurs when differences in the phenotypic values for homozygotes versus those for heterozygotes at a given locus are affected by the genotypes at another locus. Both underdominance (heterozygotes less than homozygotes) or overdominance (homozygotes less than heterozygotes) are possible depending on the sign of the epistatic values. In those QTL combinations reaching significance at the 0.1% level of significance (Tables 2–4), however, epistatic effects on the activity traits were complex, mostly being combinations of 2 or more epistatic types.

Some of the QTL discovered for the physical activity traits had pleiotropic effects on more than one of these traits (Lightfoot et al. 2008), and it therefore was not surprising to see this pattern reflected to some extent in the epistatic combinations as well. Distance and duration are very highly correlated traits (r = 0.92), and as previously described in the results, 4 epistatic combinations appear to be common to both of these traits (Tables 2 and 3). Epistatic pleiotropy, however, will only contribute to the covariance between 2 traits if they share identical patterns of effects (see Wolf et al. 2005). Inspection of these 4 combinations in fact shows that they share identical epistatic effects with both traits; for example, the combination of genes on chromosomes 1 and 8 both generate significant aa and ad epistatic components. Further, all the signs of these components also are identical, suggesting that these 4 instances of epistasis all will act to increase the covariation of distance and duration. Other undetected epistatic interactions that commonly affect these 2 traits also may act to increase their correlation. However, the other epistatic combinations shown previously at the 0.1% significance level are different for these 2 traits and suggest some independence in the interactions of genes affecting distance versus duration.

It was interesting to note that none of the epistatic interactions significant at the 0.1% level in our genome scan (Tables 2–4) involved any pair of the QTLs for distance (total of 6), duration (4), or speed (8) discovered in the initial study (Lightfoot et al. 2008). In fact, epistasis tests among each pair of QTL for all 3 traits revealed only a single significant (P < 0.05) interaction between QTL on chromosomes 5 and 9 that affected distance (Lightfoot et al. 2008). However, 4 of these QTL may be participating in the epistatic interactions listed in Tables 2–4 because they share very similar locations. These include 1 QTL on chromosome 5 (95 cM) affecting duration, 1 on chromosome 8 (88 cM) affecting both distance and speed, 1 on chromosome 12 (27 cM) affecting speed, and 1 on chromosome 13 affecting distance (11 cM) and speed (9 cM). It is interesting in this regard that the epistatic interactions of these QTL with other unknown genes would not have been discovered without this full genome epistasis scan. This suggests caution in inferring the extent of epistasis from tests done only on pairs of QTL found in single-locus QTL scans.

Conclusion

We have provided evidence for epistatic genetic interactions that contribute significantly to the variation in daily physical activity in a cohort of mice developed from high and low active progenitors. In conjunction with single-locus genetic effects that we previously reported (Lightfoot et al. 2008), these epistatic effects account for the total genetic variance in physical activity as estimated from broad-sense heritabilities. Our results suggest an important role for epistasis in the genetic architecture of physical activity traits and provide an additional direction for future gene/mutation identification studies.

Funding

National Institutes of Health (NIDDK DK61635 to J.T.L., NIAMS AR050085 to J.T.L and L.J.L., and NIDDK DK076050 to D.P.).