Abstract
Purpose:
To clinically assess a previously described method (Rieke et.al. Magn Reson Med 2004) to produce more motion-robust MRI-based temperature images using data acquired during MRI-guided focused ultrasound surgery (MRgFUS) of uterine fibroids.
Methods:
The method (“referenceless thermometry”) uses surface fitting in non-heated regions of individual phase images to extrapolate and then remove background phase variations that are unrelated to temperature changes. We tested this method using images from 100 sonications selected from 33 patient MRgFUS treatments. Temperature measurements and thermal dose contours estimated with the referenceless method were compared to those produced with the standard phase-difference technique. Fitting accuracy and noise level were also measured.
Results:
In 92/100 sonications, the difference between the two measurements was less than 3°C. The average difference in the measurements was 1.5±1.4°C. Small motion artifacts were observed in the phase-difference imaging when the difference was greater than 3°C. The method failed in two cases. The mean absolute error in the surface fit in baseline images corresponded to a temperature error of 0.8±1.4°C. The noise level was approximately 40% lower than the phase-difference method. Thermal dose contours calculated from the two methods agreed well on average.
Conclusions:
Based on the small error when compared to the standard technique, this method appears to be adequate for temperature monitoring of MRgFUS in uterine fibroids and may prove useful for monitoring temperature changes in moving organs.
Keywords: MRI thermometry, Focused Ultrasound Surgery, Thermal Ablation
INTRODUCTION
A growing consensus has indicated that the temperature sensitivity of the water proton resonant frequency (PRF) (1) is the most well-suited parameter to exploit to create temperature maps for MRI guidance of thermal therapies. Typically, changes in water PRF are estimated using phase-difference images of a gradient echo sequence (2). Difference images are necessary to remove variations caused by inhomogeneities in the magnetic field. The method is sensitive to changes in the local magnetic field between scans which appear as temperature variations. These changes can result from several sources, including drift in the static field (3), patient motion outside of the imaging plane, and local or global changes in magnetic susceptibility, which can be altered by heating (4,5). The most problematic source of error in this MRI-based thermometry method appears to be its sensitivity to motion which causes a misregistration between the images used in the phase subtractions, resulting in artifacts in the resulting temperature estimation. The magnitude of these artifacts depend on the local magnetic field gradients, and will thus likely be largest at regions with a large magnetic susceptibility mismatch, such as adjacent to bowel or lung. While promising correction methods using respiratory gating (6,7), navigator echoes (6,8), and multiple baselines to sample periodic motion (6,9,10) have been tested, a method that eliminates the need for image subtraction would clearly be highly desirable.
Recently, a method for PRF-based thermometry was described that uses a single phase map instead of phase difference images to estimate temperature changes (11,12). In this method, unheated areas in the phase maps that surround the heated zone are fit to a surface and used to estimate the phase distribution in the heated area via extrapolation. The resulting temperature maps are thus inherently insensitive to changes unrelated to temperature in the background magnetic field that occur after the acquisition of the baseline image, as well as misregistration errors. In previous tests of this method, it was shown feasible and temperature maps were generated during animal experiments (11,13). However, the robustness of the method over a large number of ablations in multiple subjects has not been evaluated, and its use in human clinical treatments has not been tested. The purpose of this work was to test the accuracy of this method, termed referenceless thermometry, during MRI-guided focused ultrasound surgery (MRgFUS) of uterine fibroids, a noninvasive thermal ablation method (14-16).
METHODS
MRI-based temperature images were acquired during MRgFUS of uterine fibroids at our institution. The treatments were performed using the ExAblate 2000® device (InSightec, Haifa, Israel), which incorporates a phased array transducer, RF amplifier, computer-controlled positioning device, and user interface with a standard 1.5 T MRI unit (GE Healthcare, Milwaukee, WI). Technical and clinical details concerning these treatments, including patient selection criteria, are described elsewhere (14-16). Briefly, multiple overlapping sonications were delivered sequentially to thermally ablate a portion of the fibroid in order to provide symptom relief. For each sonication, a cylindrically shaped volume is thermally ablated with dimensions up to approximately one cm wide by 3 cm long, depending on the ultrasound exposure parameters. During each 16-20s sonication, a time series of of 7-9 MRI-based temperature maps are acquired in a single plane chosen by the operator. The treatments were performed with patients in the prone position with intra-venous conscious sedation. While this sedation did not prevent patient motion, previous analysis of the treatments (xxx) indicates that any small fibroid motion that occurred did not induce artifacts in the thermometry. Our institutional review board approved the treatments and retrospective analysis of the data, and all patients gave written informed consent for both. The trials in which these patients were treated were HIPAA compliant.
Fast spoiled gradient echo (FSPGR) images were used to estimate changes in the water PRF (TR/TE: 40/20 ms, flip angle: 30°, field of view: 28cm, matrix: 256×128, bandwidth: ±3.6 kHz, slice thickness: 3mm). The low value for the bandwidth was selected to increase the SNR and because of limitations on the MR scanner software. The scanner was programmed to reconstruct the real and imaginary data in addition to the standard magnitude reconstruction. PRF changes were estimated by dividing the phase changes by 2π times TE, the time which the phase developed. A temperature sensitivity for the water PRF of −0.01 ppm/°C was used to create the temperature maps (1).
Images from 100 sonications in 33 patients were randomly chosen from a pool of patients that were reported in an earlier study evaluating the temperature mapping during MRgFUS (xxx). So residual heating was not present in the area that was assumed to be unheated, sonications were chosen that were more than 3cm away from a previous sonication or were delivered 5 min after previous sonications. In addition, sonications were chosen where the peak temperature rise reached at least 23°C (i.e., absolute peak temperature at least 60°C assuming a body temperature of 37°C), so that for each sonication, a wide range of temperatures could be compared as the tissue heated up and then cooled. Fifty-seven of the sonications were imaged in the sagittal plane (parallel to beam direction); the other 43 were imaged in the coronal plane (perpendicular to the ultrasound beam direction in the focal plane).
For referenceless thermometry, an 11 voxel wide unheated strip was chosen that surrounded an ROI containing the heated area (Figure 1). The (unwrapped) phase in this strip was fit to a surface defined by a two dimensional polynomial and then extrapolated into the central ROI containing the heated area. This extrapolated phase was subsequently subtracted off, leaving behind only the phase changes produced by the heating. The polynomial orders for the the fit were determined by testing different values in a baseline (unheated) image and choosing those that minimized the root mean square error in central ROI. Orders from zero to seven were tested. The heated ROI's had dimensions of 21×21 voxels (coronal) or 21×61 voxels (sagittal). These sizes were chosen so that the outer strips were outside of the heated zone, including heating along the beam path. Voxels inside these ROI's that were outside the fibroid or that contained large blood vessels (as evidenced by phase artifacts in the imaging) were excluded by manual segmentation. The percentage of the excluded regions ranged from 0-51% (median: 6%) for coronal imaging and 2-64% (median: 32%) for sagittal imaging. In every sagittal sonication a portion of the ROI was outside of the fibroid and excluded, with subcutaneous fat being the most common and largest region excluded.
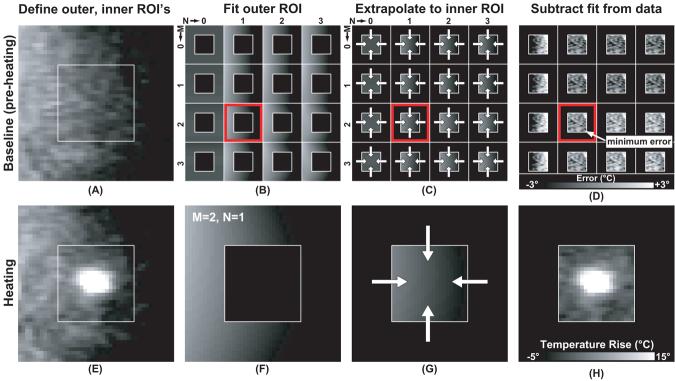
Figure 1.
Referenceless thermometry method. For each sonication, two ROI's were defined in the phase maps (A, E): one containing the heated zone and a second one surrounding it. In a baseline image, the phase distribution in the outer ROI was fit to different surfaces defined by polynomials of orders (M,N) ranging from zero to seven (only 0-3 shown in B-D). The equations defining these polynomials were used to extrapolate the data into the central ROI (C). This extrapolated data was then subtracted from the real phase data, and the orders of the polynomial fit were identified that produce the smallest error (D). These values (M=2, N=1 in the example in the figure) were then used to fit the data in the outer ROI in phase maps acquired during heating (F). After extrapolating the fit data into the central ROI (G), a temperature map free of background phase variation was produced (H). This example used coronal imaging (perpendicular to the direction of the ultrasound beam in the focal plane).
Previous analysis of the patients from which these sonications were selected found little error in the temperature maps in non-heated regions within the fibroid for most of the sonications (xxx). This small error and analysis of the magnitude reconstructions of the imaging used for the thermometry indicate that the fibroids were relatively stationary during the treatments, so thermometry made using phase-difference images were treated as a gold-standard. For phase subtraction, a complex phase subtraction scheme (17) and pair-wise image subtraction were used to avoid phase wrap. The temperature change estimated by the referenceless and phase-difference methods were compared voxel by voxel in a 9×9 (coronal) or 9×31 (sagittal) voxel ROI centered on the hottest voxel.
The mean absolute error per sonication (±S.D.) was calculated in the baseline (unheated) referenceless images. For this measurement, the absolute value of the central ROI in the baseline image (i.e., the baseline phase minus the fit surface) was calculated for each sonication. Any net non-zero value was assumed to be indicative of error of the baseline polynomial fit and in extrapolating into the central ROI. The mean standard deviation of these measurements was assumed to give a measure of the noise level in the referenceless temperature images. This measure of noise was compared to the mean standard deviation measured in ROI's in the phase-difference images selected in unheated areas.
The mean error (±S.D.) in the temperature measurements during heating was then calculated for the referenceless thermometry measurements using the phase-difference images as a comparison. The slope, y-intercept, and correlation coefficient were also calculated via linear regression for this comparison using the referenceless thermometry measurements as the dependent variable. Differences between coronal and sagittal imaging were compared using an unpaired student's t-test.
The thermal dose (18) was also calculated using thermometry generated by the two methods. Voxels were identified that reached a thermal dose of at least 240 equivalent minutes at 43°C (TEM43°C), a conservative threshold for thermal necrosis found in animal work (19) that is often used to guide thermal ablation. The number of voxels and the dimensions of the thermal dose contours at this threshold were compared.
All data and statistical analysis was performed using software written in Matlab (version 7.0, The Mathworks, Natick, MA, USA). For the polynomial fitting, the phase data was weighted by the square of the magnitude signal (11). Unwrapping was performed using software written in-house. For this procedure, the data in each column of the ROI was first unwrapped by using a simple algorithm that changed phase jumps greater than π to their 2π complement. Next, each row was examined, and any phase jump greater than π with its neighbor were found and corrected so that a smooth phase distribution resulted.
RESULTS
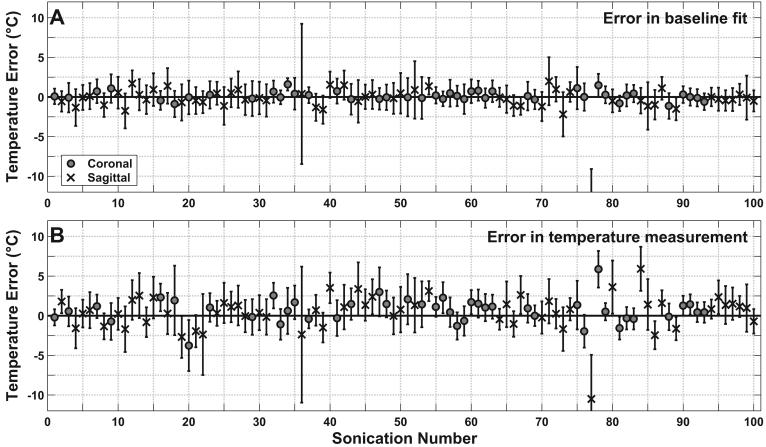
Overall, the two thermometry methods agreed for most sonications. The mean absolute error in the baseline images corresponded to a temperature change less than 1°C (Table 1). In only two sonications were large errors observed in the baseline fit (Figure 2A). In one case (with the large standard deviation), no clear cause was observed. In the other (with the large error), the patient had a surgical clip in her uterus from a previous surgery that caused a large susceptibility artifact (Figure 3). Overall, a small but significant (P<0.05) difference between sagittal and coronal imaging was observed in the error present in the baseline fits, with sagittal imaging performing slightly worse (mean error of 1.0±1.8°C vs. 0.4±0.4°C). The average standard deviation in the baseline images (1.8±0.9°C) was lower than the average standard deviation observed in non-heated areas in the phase-difference method (2.9±.0°C). In most (69%) of the sonications, the optimal order for the polynomial fit was found to be between two and four (Table 2).
Table 1.
Summary of analysis of the baseline fitting and referenceless temperature measurements. All values are expressed either as means ± standard deviation over the 100 sonications tested or the range of values encountered. Absolute errors are shown.
| Coronal | Sagittal | Combined | Range | ||
|---|---|---|---|---|---|
| Baseline | Error (°C) | 0.4 ± 0.4 | 1.0 ± 1.8 | 0.8 ± 1.4 | (0.0 - 13.6) |
| S.D. (°C) | 1.5 ± 0.5 | 2.0 ± 1.1 | 1.8 ± 0.9 | (0.8 - 8.9) | |
| Temperature measurement |
Error (°C) | 1.3 ± 1.1 | 1.7 ± 1.6 | 1.5 ± 1.4 | (0.0 - 10.5) |
| S.D. (°C) | 1.9 ± 0.7 | 2.4 ± 1.2 | 2.2 ± 1.0 | (1.0 - 8.6) | |
| Slope | 1.0 ± 0.1 | 0.9 ± 0.1 | 1.0 ± 0.1 | (0.5 - 1.1) | |
| y-intercept | 0.8 ± 1.6 | 1.1 ± 2.0 | 1.0 ± 1.8 | (−8.4 - 6.2) | |
| R | 0.96 ± 0.04 | 0.93 ± 0.06 | 0.94 ± 0.05 | (0.68 - 0.99) | |
Figure 2.
(A) Error in the baseline fit for 100 sonications. (B) Error in the temperature maps created by the referenceless method for 100 sonications using the phase-difference method as a gold standard.
Figure 3.
(A) Magnitude reconstruction of the FSPGR image of a fibroid being heated. Right: corresponding temperature maps produced by the referenceless and phase-difference methods. (B) Large errors were produced in the temperature maps during several of the sonications in this patient, who had surgical clips nearby that created susceptibility artifacts. These errors were evident in both thermometry methods. Regions that were excluded from the procedure by manual segmentation are indicated.
Table 2.
Number of sonications with different polynomial orders in the fit of the baseline phase maps.
| Order of polynomal fit: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | total |
|---|---|---|---|---|---|---|---|---|---|
| Coronal, LR direction: | 0 | 6 | 8 | 12 | 7 | 5 | 5 | 0 | 43 |
| Coronal, SI direction: | 0 | 3 | 10 | 8 | 10 | 6 | 4 | 2 | 43 |
| Sagittal, AP direction: | 0 | 1 | 10 | 15 | 14 | 13 | 1 | 3 | 57 |
| Sagittal, SI direction: | 0 | 12 | 18 | 18 | 8 | 1 | 0 | 0 | 57 |
LR=left/right, SI=superior/inferior, AP=anterior/posterior
On average, temperature measurements for referenceless and phase-difference methods agreed well (Figure 2B). The overall mean absolute difference was less than 2°C, and linear regression of the individual voxels for the two measurements yielded a slope close to 1.0, an intercept close to 0.0, and a correlation coefficient close to 1.0 (Table 1). The two sonications where the baseline fit was poor also showed poor agreement when the temperature measurements were compared. Otherwise, the difference in measurements was less than 3°C for 92 of the remaining 98 sonications. In the six that were greater than 3°C, examination of the phase-difference images indicated that small motion artifacts were present, such as that shown in the example in Figure 4. The small difference in error for the coronal and sagittal imaging was not significant (P>0.05).
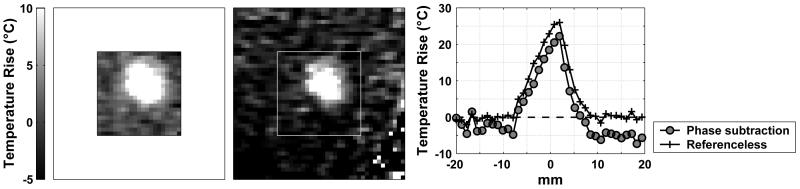
Figure 4.
(A) Temperature map created by the referenceless method. (B) corresponding temperature map created with the phase-difference method. Small motion artifacts seen in the phase-difference image appeared to be corrected by the referenceless method. (C) Spatial profile drawn across the focal heating.
The appearance of the heating and thermal dose contours created with both methods agreed well qualitatively (Figure 5), with those created using referenceless thermometry having less apparent noise. In four sagittal sonications, the dose contours disagreed sharply between the two methods. These were the two described above where the fitting in referenceless method broke down, and two others where the contours extended substantially to adjacent areas in the phase-difference method, presumably because of small motion between scans. Excluding those four, the mean ratio (referenceless/phase-difference) in the numbers of voxels that reached 240 TEM43°C was 1.1±0.2, and the numbers were strongly correlated (R=0.94). Differences were largely limited to voxels near this threshold at the edge of the heated zone. For example, 94% of the dimensions of the dose contours in the superior/inferior and left/right directions (i.e. directions perpendicular to the ultrasound beam propagation) differed by two voxels or less, indicative of a difference limited to a one voxel wide strip at the edge of heated region. The dimensions along the direction of the ultrasound beam where the thermal gradients were less sharp differed by two voxels or less in 67% of the sonications. In two sagittal sonications, including that shown at top right in Figure 5, noise in the phase-difference method resulted in the contours differing in several voxels within the heated zone.
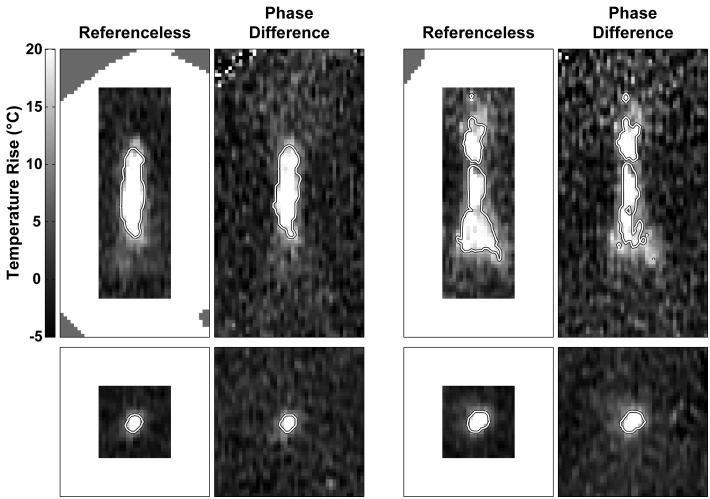
Figure 5.
Temperature maps generated by the referenceless method (left) and by the phase-difference method (right) for four sonications. Thermal dose contours at 240 equivalent min at 43°C are superimposed on the images. The contours produced from referenceless temperature maps appeared to have less noise. Top: two cases with imaging acquired parallel to the direction of the ultrasound beam (sagittal). Bottom: two cases with imaging acquired perpendicular to the ultrasound beam in the focal plane (coronal). Regions that were excluded in sagittal imaging from the procedure by manual segmentation are indicated.
DISCUSSION
The referenceless method appears to be adequate for temperature monitoring of MRgFUS in fibroids. These results are encouraging, because targets where this method will likely be most useful, moving organs such as the liver or kidney, will be at a similar depth in tissue and will also neighbor gas-filled bowel loops that produce large susceptibility variations. Such areas produce a local inhomogeneity in magnetic field and make the phase-difference method particularly motion sensitive in neighboring tissues. Here, relatively stationary tissues were imaged with minor motion present during some sonications. This is expected to simulate the situation with liver or kidney treatments that will use sonications performed during breath holds or controlled apnea. Our study did not investigate or encounter any sonications during large tissue motion and it is not clear if the method would work in such situations. A formal study of motion in such cases, as would occur in liver or kidney, will be the subject of future work.
Future work should also evaluate the method for different applications. One needs to ensure that the heating is completely contained within the central region of interest and that the outside strip used in the fit is at a constant temperature. These criteria were easily attained here, since the heat source was small compared to the available non-heated regions in the surrounding tissues. With different targets and heating sources, these criteria may not be achievable, or longer periods than desired between different ablations may be necessary to allow the surrounding tissue temperature to stabilize. Furthermore, the error may increase for larger heated regions, as the distance required to extrapolate into will increase. In addition, in order to track the cumulative thermal dose in a moving organ, registration techniques to align data acquired at different time points will be needed.
There are some limitations of the method as employed here. Manual removal of areas outside the target organ and those containing large blood vessels was time-consuming, and could limit the usefulness of the method unless robust automatic methods can be developed. In addition, when the heated area reaches the edge of the organ, it may be difficult to apply this method, and the method also does not correct for phase artifacts induced due to intra-scan motion. Finally, this method requires phase unwrapping, which was straightforward with the data in this study, but might be non-trivial in general. It may be possible to fit the real and imaginary data separately, perhaps removing the need for phase unwrapping (12).
The method might have been improved by including the subcutaneous fat in the polynomial fits. It was excluded because the chemical shift between the hydrogen proton resonant frequencies of water and lipids caused a jump in the phase image and confounded the fitting. Methods to include the lipid signal have been proposed (13,20) and would be useful in many applications, particularly since the lipid PRF is not temperature-sensitive (21). Optimization of the choice of the regions to perform the polynomial fit might also improve the method (12).
The noise level, as expressed as the standard deviation in non-heated regions, was lower with the referenceless method. This finding was expected, as the referenceless method subtracts simulated data without noise to generate thermal maps. Barring other sources of noise, the noise level in the phase-difference images should be larger by a factor of √2, close to our measured factor of 1.6 (±2.9°C vs. ±1.8°C). Having more noise also resulted in a slight enlargement in the thermal dose contours for the phase-difference method. This result was also expected, as the exponential term used in the thermal dose equation (18) will skew noisier temperature measurements to higher thermal dose values.
An unexpected finding was that the baseline fitting error was significantly smaller for coronal imaging. This difference might be explained by our needing to remove more voxels in sagittal imaging because of subcutaneous fat. Another explanation could be differences in eddy currents or the through-plane magnetic gradients for the different imaging orientations, resulting in shorter T2* values and lower SNR for sagittal imaging. Indeed, the noise level in the sagittal images was higher for sagittal imaging (±2.0°C vs. ±1.5°C). Alternatively, it could be simply that larger regions were extrapolated into for sagittal imaging. There were no obvious differences between imaging orientations in the orders of the polynomial fits found to be optimal.
In conclusion, this data indicates that the referenceless thermometry method was accurate during MRgFUS thermal ablation of uterine fibroids. In most sonications, the method agreed well with the standard phase-difference method, failing in only two of 100 sonications analyzed. It appeared to correct small motion-related artifacts evident in the phase-difference method in several cases.
ACKNOWLEDGMENTS
This work was funded by NIH grants P01CA067165 & U41RR019703. The clinical study was funded by InSightec.
REFERENCES
- 1.Hindman JC. Proton resonance shift of water in the gas and liquid states. J Chem Phys. 1966;44:4582–4592. [Google Scholar]
- 2.Ishihara Y, Calderon A, Watanabe H, Okamoto K, Suzuki Y, Kuroda K. A precise and fast temperature mapping using water proton chemical shift. Magn Reson Med. 1995;34:814–823. doi: 10.1002/mrm.1910340606. [DOI] [PubMed] [Google Scholar]
- 3.De Poorter J, De Wagter C, De Deene Y, Thomsen C, Stahlberg F, Achten E. The proton-resonance-frequency-shift method compared with molecular diffusion for quantitative measurement of two-dimensional time-dependent temperature distribution in a phantom. J Magn Reson B. 1994;103:234–241. [Google Scholar]
- 4.Stollberger R, Ascher PW, Huber D, Renhart W, Radner H, Ebner F. Temperature monitoring of interstitial thermal tissue coagulation using MR phase images. J Magn Reson Imaging. 1998;8:188–196. doi: 10.1002/jmri.1880080132. [DOI] [PubMed] [Google Scholar]
- 5.Peters RD, Hinks RS, Henkelman RM. Heat-source orientation and geometry dependence in proton-resonance frequency shift magnetic resonance thermometry. Magn Reson Med. 1999;41:909–918. doi: 10.1002/(sici)1522-2594(199905)41:5<909::aid-mrm9>3.0.co;2-n. [DOI] [PubMed] [Google Scholar]
- 6.Vigen KK, Daniel BL, Pauly JM, Butts K. Triggered, navigated, multi-baseline method for proton resonance frequency temperature mapping with respiratory motion. Magn Reson Med. 2003;50:1003–1010. doi: 10.1002/mrm.10608. [DOI] [PubMed] [Google Scholar]
- 7.Lepetit-Coiffe M, Quesson B, Seror O, et al. Real-time monitoring of radiofrequency ablation of rabbit liver by respiratory-gated quantitative temperature MRI. J Magn Reson Imaging. 2006;24:152–159. doi: 10.1002/jmri.20605. [DOI] [PubMed] [Google Scholar]
- 8.de Zwart JA, Vimeux FC, Palussiere J, et al. On-line correction and visualization of motion during MRI-controlled hyperthermia. Magn Reson Med. 2001;45:128–137. doi: 10.1002/1522-2594(200101)45:1<128::aid-mrm1017>3.0.co;2-m. [DOI] [PubMed] [Google Scholar]
- 9.Shmatukha AV, Bakker CJ. Correction of proton resonance frequency shift temperature maps for magnetic field disturbances caused by breathing. Phys Med Biol. 2006;51:4689–4705. doi: 10.1088/0031-9155/51/18/015. [DOI] [PubMed] [Google Scholar]
- 10.de Senneville BD, Mougenot C, Moonen CT. Real-time adaptive methods for treatment of mobile organs by MRI-controlled high-intensity focused ultrasound. Magn Reson Med. 2007;57:319–330. doi: 10.1002/mrm.21124. [DOI] [PubMed] [Google Scholar]
- 11.Rieke V, Vigen KK, Sommer G, Daniel BL, Pauly JM, Butts K. Referenceless PRF shift thermometry. Magn Reson Med. 2004;51:1223–1231. doi: 10.1002/mrm.20090. [DOI] [PubMed] [Google Scholar]
- 12.Kuroda K, Kokuryo D, Kumamoto E, Suzuki K, Matsuoka Y, Keserci B. Optimization of self-reference thermometry using complex field estimation. Magn Reson Med. 2006;56:835–843. doi: 10.1002/mrm.21016. [DOI] [PubMed] [Google Scholar]
- 13.Rieke V, Kinsey AM, Ross AB, et al. Referenceless MR thermometry for monitoring thermal ablation in the prostate. IEEE Trans Med Imaging. 2007;26:813–821. doi: 10.1109/TMI.2007.892647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Tempany CM, Stewart EA, McDannold N, Quade BJ, Jolesz FA, Hynynen K. MR Imaging-guided focused ultrasound surgery of uterine leiomyomas: a feasibility study. Radiology. 2003;226:897–905. doi: 10.1148/radiol.2271020395. [DOI] [PubMed] [Google Scholar]
- 15.Hindley J, Gedroyc WM, Regan L, et al. MRI guidance of focused ultrasound therapy of uterine fibroids: early results. AJR Am J Roentgenol. 2004;183:1713–1719. doi: 10.2214/ajr.183.6.01831713. [DOI] [PubMed] [Google Scholar]
- 16.McDannold N, Tempany CM, Fennessy FM, et al. Uterine leiomyomas: MR imaging-based thermometry and thermal dosimetry during focused ultrasound thermal ablation. Radiology. 2006;240:263–272. doi: 10.1148/radiol.2401050717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chung AH, Hynynen K, Colucci V, Oshio K, Cline HE, Jolesz FA. Optimization of spoiled gradient-echo phase imaging for in vivo localization of a focused ultrasound beam. Magn Reson Med. 1996;36:745–752. doi: 10.1002/mrm.1910360513. [DOI] [PubMed] [Google Scholar]
- 18.Sapareto SA, Dewey WC. Thermal dose determination in cancer therapy. Int J Radiat Oncol Biol Phys. 1984;10:787–800. doi: 10.1016/0360-3016(84)90379-1. [DOI] [PubMed] [Google Scholar]
- 19.Meshorer A, Prionas SD, Fajardo LF, Meyer JL, Hahn GM, Martinez AA. The effects of hyperthermia on normal mesenchymal tissues. Application of a histologic grading system. Arch Pathol Lab Med. 1983;107:328–334. [PubMed] [Google Scholar]
- 20.Rieke V, Ross AB, Nau WH, Diederich CJ, Sommer G, Butts K. Referenceless thermometry in the presence of phase discontinuities between water and fat; Proceedings of the Thirteenth Meeting of the International Society for Magnetic Resonance in Medicine; Miami Beach, FL. 2005. p. 147. [Google Scholar]
- 21.De Poorter J. Noninvasive MRI thermometry with the proton resonance frequency method: study of susceptibility effects. Magn Reson Med. 1995;34:359–367. doi: 10.1002/mrm.1910340313. [DOI] [PubMed] [Google Scholar]