Abstract
A mechanism-based model was developed to describe the time course of arthritis progression in the rat. Arthritis was induced in male Lewis rats with type II porcine collagen into the base of the tail. Disease progression was monitored by paw swelling, bone mineral density (BMD), body weights, plasma corticosterone (CST) concentrations, and TNF-α, IL-1β, IL-6, and glucocorticoid receptor (GR) mRNA expression in paw tissue. Bone mineral density was determined by PIXImus II dual energy x-ray densitometry. Plasma CST was assayed by HPLC. Cytokine and GR mRNA were determined by quantitative real-time polymerase chain reaction. Disease progression models were constructed from transduction and indirect response models and applied using S-ADAPT software. A delay in the onset of increased paw TNF-α and IL-6 mRNA concentrations was successfully characterized by simple transduction. This rise was closely followed by an up-regulation of GR mRNA and CST concentrations. Paw swelling and body weight responses peaked approximately 21 days post induction while bone mineral density changes were greatest at 23 days post induction. After peak response the time course in IL-1β, IL-6 mRNA, and paw edema slowly declined towards a disease steady-state. Model parameters indicate TNF-α and IL-1β mRNA most significantly induce paw edema while IL-6 mRNA exerted the most influence on BMD. The model for bone mineral density captures rates of turnover of cancellous and cortical bone and the fraction of each in the different regions analyzed. This small systems model integrates and quantitates multiple factors contributing to arthritis in rats.
INTRODUCTION
Models describing the time course of disease progression are becoming increasingly important in drug development as they provide a mathematical structure by which to evaluate drug efficacy, make clinical predictions, and better discern how drugs may be used to target specific markers alone or in combination while avoiding toxicities (Lalonde et al., 2007; Lesko, 2007). Development of these mathematical systems for drug effect analysis is relatively recent. Chan and Holford reviewed drug treatment effects on disease progression in multiple disease scenarios, placing emphasis on understanding the natural disease progression in the absence of drug (Chan and Holford, 2001). Post and Danhof presented a variety of equations for describing disease progression using pharmacodynamic indirect response models, a mechanistic paradigm for describing turnover of response and drug effect (Dayneka et al., 1993; Post et al., 2005). Other diseases have been described including bacterial cell-growth and irreversible loss following drug therapy, fasting plasma glucose in diabetes, and pain and bone mineral density progression in osteoarthritis (Jusko, 1971; Ravn et al., 1996; Meunier et al., 1999; Frey et al., 2003; Pillai et al., 2004; de Winter et al., 2006). Mechanism-based disease progression models are continually being derived as their insight into how various pathologies contribute to progression and how drugs exert their effects on specific processes is essential to optimizing therapy (Holford and Peace, 1992b; Holford and Peace, 1992a; Nemeroff, 1994; Hoogendoorn et al., 2005; Holford et al., 2006; Meier et al., 2007; Woo et al., 2007). To date there are limited mechanism-based models relevant to osteoarthritis and none specific to anti-inflammatory drug effects in rheumatoid arthritis (RA). Furthermore low dose corticosteroid therapy has been suggested recently to halt joint erosion in RA (Svensson et al., 2005; Wassenberg et al., 2005; Da Silva et al., 2006). However before corticosteroid mechanisms can be appreciated in RA, the natural disease baseline must be aptly described by the relevant molecular factors regulating the disease.
This investigation aims at 1) developing a mechanistic model to describe the natural time course of the molecular factors that drive chronic inflammatory arthritis in the rat and are relevant to corticosteroid effect (Part I), and 2) integrating drug binding assumptions into the disease progression model to explain pharmacodynamic effects of corticosteroids (CS) and further resolve disease progression parameters (Part II). The molecular factors assayed to describe disease progression include pro-inflammatory cytokine mRNA for tumor necrosis factor–α (TNF-α), interleukin-1β (IL-1β), and interleukin-6 (IL-6) and factors relevant to endogenous corticosteroid dynamics including glucocorticoid receptor (GR) mRNA and plasma corticosterone (CST). It is well established that TNF-α, IL-1β, and IL-6 increase immune cell-trafficking and proliferation and cause up-regulation of GR and plasma CST (Turnbull and Rivier, 1999; Choy and Panayi, 2001; Neeck et al., 2002). In turn, GR and CST are thought to suppress cytokine expression by inhibiting the action of transcription factors nuclear factor - κB and activator protein 1 (Turnbull and Rivier, 1999; Choy and Panayi, 2001; Neeck et al., 2002). These inter-regulation processes between cytokines and endogenous corticosteroid account for limiting inflammation during progression and provide common factors for which dexamethasone (DEX) drug effect may be observed and used to explain treatment effects on disease endpoints. Overall disease progression is monitored by edema in the paw, and by femur and lumbar bone mineral density (BMD). The production of edema is directly correlated with immune cell infiltration and pro-inflammatory cytokine concentrations. Bone production and loss has also been related to the presence of TNF-α, IL-1β, and IL-6 (Rifas, 1999; Gravallese, 2002; Lerner, 2004; Summey and Yosipovitch, 2006; McCormick, 2007). These cytokines not only reduce osteoblast activity, but are also thought to increase receptor activator of nuclear factor-κB (RANKL) expression and subsequent activation of osteoclasts.
Part I presents one of the first mechanistic models of auto-immune arthritis progression in the rat as described by pro-inflammatory cytokine mRNA, GR mRNA, CST, paw edema and BMD. Equations were constructed with the fifth-generation model of corticosteroid dynamics and extended beyond with transduction and indirect response models describing disease initiation and the turnover of primary disease mediators (Ramakrishnan et al., 2002). Model equations were fitted to data and simulations performed to identify the contributions of each cytokine to paw edema and BMD. These pathways provide insight into the extent that both corticosteroids and other therapies targeting cytokines may impact reduction in edema and protect BMD during progression of RA.
METHODS
Animals
Male Lewis rats, age six to nine weeks, were purchased from Harlan Sprague Dawley, Inc. weight matched to approximately 150 grams. Animals were housed individually in the University Laboratory Animal Facility and acclimatized for one week under constant temperature (22° C), humidity (72%), 12 h light/12 h dark. Rats had free access to rat chow and water. All protocols followed Principles of Laboratory Animal Care (National Institute of Health publication 85–23, revised 1985) and were approved by the University at Buffalo Institutional Animal Care and Use Committee.
Induction of Collagen-Induced Arthritis in Lewis Rats
The induction of collagen-induced arthritis (CIA) in Lewis Rats followed protocols and reagent supplied by Chondrex, Inc (Redmond, WA). Porcine collagen type II (2 mg/mL) in 0.05 M acetic acid was emulsified with incomplete Freund’s adjuvant (IFA, Sigma Aldrich, St. Louis, MO) using an electric homogenizer (Virtis) equipped with a small blade of 10 mm in diameter. Equal amounts of collagen (2 mg/mL) and IFA were mixed in an ice water bath, adding the collagen drop-wise to the IFA at the lowest speed setting. The Virtis speed was increased to 30,000 rpm for 2.5 minutes, then 0 rpm for 2.5 minutes, and a final mix at 30,000 rpm for 2.5 minutes. The emulsion was ready when it appeared to be a stiff white substance that congealed instead of dissipating when dropped in water. Ensuring proper time for the solution to cool in the ice bath is critical to prevent collagen degradation (2.5 min was used in between homogenizations). Rats were anesthetized with ketamine/xylazine (75/10 mg/kg) and received 0.2 mL of collagen emulsion by intra-dermal injection at the base of the tail. Booster injections were administered on the seventh day of the study with 0.1 mL emulsion to the same injection site.
Experimental Design
On study day zero 48 rats were injected with collagen emulsion. Animals received booster injections on day 7. Animal body weights and paw edema were monitored on study days 0, 7, 9–26, 28, and 30. Three to four rats with arthritis (depending on the availability of rats that had developed arthritis symmetrically in both paws) were killed on study days 9, 12, 15, 17, 19, 21, 23, 25, and 30. Healthy control animals were housed alongside arthritic animals throughout the duration of the study. One healthy rat was sacrificed on study days 9, 15, 19, 23, and 30. Animals were sacrificed by aortal exsanguinations and blood was collected in syringes containing sufficient ethylenediaminetetraacetic acid (EDTA) to yield 1.5 mg/mL (4 mM) final concentration (Samtani and Jusko, 2005). Samples were centrifuged at 1800 × g for 10 min at 4° C. Plasma was collected and stored at −80° C. Skin was removed from hind paws and the paws were cut off above the ankle and flash frozen in liquid nitrogen prior to storage at −80° C.
An additional 20 rats were induced with arthritis for assessment of bone mineral density in the femur, paw, and lumbar regions. Fourteen of the animals that developed the edema in both paws were scanned with the PIXImus II instrument (GE Healthcare, WI) to assess changes in bone mineral density. Ten of these rats were scanned for the femur region only on days 8, 10, 13, 15, 19, 22, 27, 35. Four additional rats were scanned for the femur, lumbar, and paw regions on days 2, 9, 12, 15, 19, 23, and 27. Four healthy controls were also scanned for the femur, lumbar, and paw regions on days 1, 8, 16, 19, 23, 27, and 35.
Paw and body weight data and tissues from preliminary pilot studies in our laboratory and from part II were also included in the model development. A total of 162 healthy and arthritic rats were used for all paw mRNA measurements. From this 220, 214, and 212 data points were used for TNF-α IL-1β and IL-6 mRNA (1–2 paws were used per rat). Plasma corticosterone was assayed from 177 rats (177 data points) and paw edema was determined from 314 rats (4340 data points, 13 points per rat). Bone mineral density was assayed from 46 animals and a total of 1464 data points from 5 different scanned regions were modeled. Only the paw mRNA measures and plasma CST were collected by sparse sampling means. The non-invasive measures, paw edema and bone mineral density, were collected serially.
Measurement of Edema and Body Weight
Edema was indicated by swelling of the rat’s hind paws. Two cross-sectional areas were determined with digital calipers (VWR Scientific, Rochester, NY), one on the forefoot (paw) and the other at the ankle. Two measurements were made on each section, perpendicular to each other, to define the length and height of the ellipse from which the area was determined. Measurements were made side-to-side and top-to-bottom across the paw at the base of the last foot pad. Measurements on the ankle were made side-to-side and front-to-back at a 45 degree angle across the ankle. The area contained in the ellipse is:
| (1) |
where a is the length of the side-to-side measurement and b is the length of either the front-to-back or top-to-bottom measurements by the calipers. Edema was indicated by the sum of the paw and ankle area measures for each hind foot.
Extraction of Total RNA from Rat Hind Paws
Frozen whole paws (excluding skin) cut off above the ankle were ground with mortar and pestle under liquid nitrogen. Right and left hind paws were analyzed individually. Total RNA was extracted from the pulverized tissue using column purification with RNeasy mini-kits (Qiagen Inc, Valencia, CA). Manufacturer’s instructions were followed with inclusion of an on-column Proteinase-K digestion (Ambion, Austin, TX). Tissue samples were homogenized in an ice-water bath for two 15 sec durations with a 20 sec period in between to cool. Homogenizations were done with a Kinematica Polytron homogenizer model PT10–35 (Kinematica Inc, Newark, NJ) on speed setting 3.5. After column purification, DNAase digestions were performed with RQ-1 DNAase from Promega (Madison, WI). Sample tubes with enzyme were incubated at 37° C for 30 min. Samples were repurified with the RNeasy columns. The purity and the integrity of the RNA was confirmed by the ratio of optical densities at 260 and 280 nm and by agarose formaldehyde gel electrophoresis. Total RNA concentrations were determined with 2 μL samples in triplicate using a NanoDrop spectrophotometer, model ND-1000 (Thermo Fisher Scientific, Wilmington, DE). RNA samples were diluted in nuclease free water to 25 ng/μL and stored at −80° C prior to quantitative real-time PCR analysis.
Construction of cRNA Standards for TNF-α, IL-1β, and IL-6
Regions consisting of 708 bp for rat TNF-α (Accession #NM_012675), 807 bp for rat IL-1β (Accession #NM_031512), and 996 bp for rat IL-6 (Accession #NM_012589) were cloned into pCR® II-TOPO (Invitrogen, Carlsbad, CA). Primers for TNF-α, IL-1β, and IL-6 were custom synthesized by Integrated DNA Technologies (Coralville, IA). Primers for TNF-α cloning were: forward 5′(ATGAGCACGGAAAGCATGA)3′ and reverse 5′(TCACAGAGCAATGACTCCAAA)3′. Primers for IL-1β cloning were: forward 5′(AAAGAATTCTGAAGCAGCTATGGCAACTG)3′ and reverse 5′(GGCAAGCTTGGGTTCCATGGTGAAGTCAA)3′. Primers for IL-6 cloning were: forward 5′(CTGTCTCGAGCCCACCAG)3′, and reverse 5′(TGCAAGAAACCATCTGGCTA)3′. The cRNA standards specific to TNF-α, IL-1β, and IL-6 were synthesized from the cloned constructs by in vitro transcription. The pCR® II-TOPO plasmid-clone constructs were linerized using Bam H1 followed by in vitro transcription using the MEGASCRIPT T7 polymerase kit (Ambion, Austin, TX). Purity of cRNA was checked by the ratio of 260 and 280 nm optical densities and electrophoresis on 5% acrylamide/8M urea gels. Concentrations of transcribed cRNA clones were determined by absorbance at 260 nm. The GR cRNA standards were cloned previously (Sun et al., 1998).
Quantitative Real-Time PCR
Quantitative real-time PCR (QRTPCR) was carried out employing the Stratagene MX3005P fluorescence based thermal cycler (Stratagene, La Jolla, CA). TAQMAN primers and probes specific to TNF-α, IL-1β, and IL-6 were designed with Primer Express software (Applied Biosystems, Foster City, CA) and custom synthesized by Biosearch Technologies (Novato, CA). Table 1 indicates primer and probe sequences, fluorescent reporter dyes on the 5′ end of the probe, and relevant assay concentrations for probes, primers, and MgCl2. The assay was run with the Brilliant 1-step Quantitative RT-PCR Core Reagent Kit (Stratagene, La Jolla, CA). PCR was conducted with the following cycle parameters: 45° C for 30 min, 95° C for 10 min, and 40 cycles of 95° C for 15 sec and 60° C for 1 min. Standard curves were generated for each cytokine mRNA assay with cloned cRNA standards, which were assayed in duplicate for each experiment and samples were assayed in triplicate. A single additional control tube was run for each sample excluding the reverse transcriptase to test for genomic DNA contamination. No significant amplification was observed for all control tubes. Inter- and intra-day assay variation was less than 15% coefficient of variation for all QRTPCR assays.
Table 1.
Primer and Probe Sequences
| Gene | Oligonucleotide | Conc., nM | Sequence 5′-3′ | MgCl2, mM |
|---|---|---|---|---|
| TNF-α | Forward Primer | 200 | CTGTACCTTATCTACTCCCAGGTTCTC | 2.5 |
| Reverse Primer | 200 | TCTCCTGGTATGAAATGGCAAA | ||
| FAM-labeled Probe | 100 | TGCTCCTCACCCACACCGTCAGC | ||
| IL-1β | Forward Primer | 200 | CTCGACAAGAGCTTCAG | 3.5 |
| Reverse Primer | 250 | CACGGGCAAGACATAG | ||
| FAM-labeled Probe | 100 | AAGGCAGTGTCACTCATTGTGGC | ||
| IL-6 | Forward Primer | 250 | TCAACTCCATCTGCCCTTCAG | 2.5 |
| Reverse Primer | 350 | TGTCAACAACATCAGTCCCAAGA | ||
| CY5-labeled Probe | 100 | TCTCTCCGCAAGAGACTTCCAGCCAGTT | ||
| GR | Forward Primer | 300 | AACATGTTAGGTGGGCGTCAA | 5 |
| Reverse Primer | 300 | GGTGTAAGTTTCTCAAGCCTAGTATCG | ||
| FAM-labeled Probe | 100 | TGATTGCAGCAGTGAAATGGGCAAAG |
Corticosterone Extraction and HPLC Analysis
Rat plasma was thawed and 0.1–1.0 mL aliquots were extracted with methylene chloride (MeCl2) in 7 ml glass Pyrex tubes (Corning Glass Works, Corning, NY). Tubes were shaken for 45 min before washing the MeCl2 phase with 0.5 mL of 0.1 N sodium hydroxide. The NaOH phase was removed following centrifugation and the MeCl2 phase was washed twice with 0.5 mL water, discarding the water after each wash. MeCl2 was evaporated off with purified air, leaving a residue that was reconstituted in 110 μL of mobile phase. Chromatography conditions involved a mobile phase of 600 mL MeCl2, 350 mL heptane, 10 mL glacial acetic acid and 54 mL ethanol, a Zorbax normal phase column, Waters model 1515 isocratic pump and Waters model 2487 dual wavelength absorbance detector (Haughey and Jusko, 1988). The lower limit of quantification was 5 ng/mL with an intra-day coefficient of variation of less than 10%.
Measurement of Bone Mineral Density
Bone mineral density (BMD) measurements were performed using the PIXImus II dual energy x-ray absorptiometer (GE Healthcare, WI). Rats were anesthetized with 4% isoflurane and maintained at 1.5% isoflurane for the duration of the scan. Animals awakened within 30 sec to 1 min following removal from isoflurane. Before the investigation started an instrument calibration was run. Quality controls were examined daily using the supplied phantom (BMD = 0.0664 g/cm2, percent fat = 10.4 %). Anesthetized rats were positioned on the PIXImus trays and their tail or hind paw was taped to secure the rat in three positions for determination of BMD in the femur, lumbar, and paw regions of interest.
The 90 degree position was used for the femur scans as proposed by Binkley et al and applied by Soon et al (Binkley et al., 2003; Soon et al., 2006). The position for the lumbar region of interest was also adapted from these two references. The paw scans were done with the rat lying on its side, back away from the machine, and the upper leg taped back so the bottom leg could rest freely with the paw on its side. Scans of the whole paw and lower leg from the side were obtained. Paw scans were included to determine if the localized edema in the paw affected BMD more than in the femur or lumbar regions. BMD was quantified by the Lunar PIXImus II software version 2.00, with a threshold value of 1345. Four regions of interest (ROI) in the femur were analyzed and are shown in Figure 1 with the corresponding pixel dimensions of each ROI.
Figure 1.
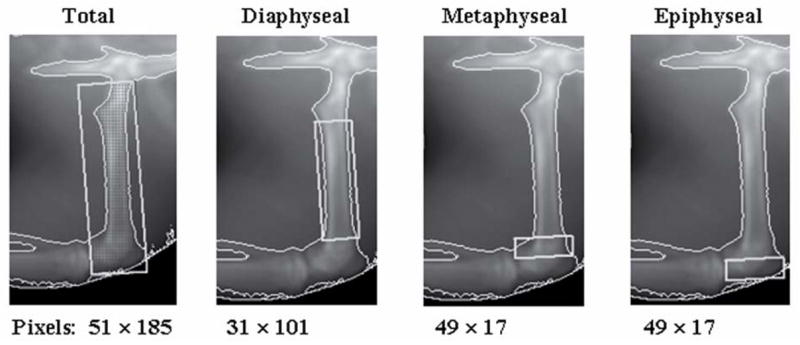
Rat femur regions of interest and software pixel dimensions for each area.
Mechanism-Based Disease Progression Model
Figure 2 shows a general schematic for the entire arthritis progression model. All compartments in this model are described by differential equations that maintain homeostasis when unperturbed. Disease progression is initiated by the transit compartments preceding each cytokine mRNA.
Figure 2.
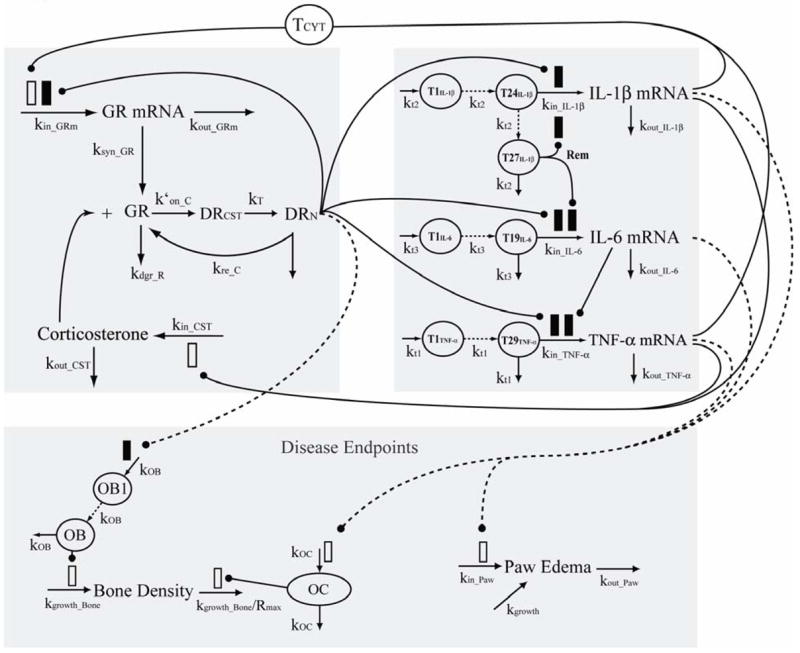
Model schematic for corticosteroid and cytokine inter-regulation during arthritis progression. Parameters and symbols are explained in the text and tables. Lines with arrows indicate conversion to or turnover of the indicated responses. Lines ending in closed circles indicate an effect is being exerted by the connected factors. Open and solid boxes differentiate between stimulatory and inhibitory effects. Dashed lines depict pathways of molecular biomarker influence on disease endpoints. The upper left panel depicts factors related to corticosteroid dynamics. The upper right panel depicts factors related to cytokine mRNA turnover. The lower panel indicates factors and processes relevant to the disease endpoints bone mineral density and paw edema.
Corticosterone and GR dynamics
The fifth-generation model for corticosteroid dynamics proposed by Ramakrishnan et al and modified by Hazra et al was adapted and applied to the effects of endogenous corticosterone via the glucocorticoid receptor on cytokine mRNA production, GR mRNA production, paw edema, and bone mineral density (Ramakrishnan et al., 2002; Hazra et al., 2007a; Hazra et al., 2007b; Hazra et al., 2007c). The equation describing GR mRNA turnover is
| (2) |
where kin_GRm is the first-order production rate of GR mRNA. Drug bound to receptor is indicated by DR. After the DR complex translocates to the nucleus it is defined as DRN. The first-order translocation constant (kT=58.2 hr−1) between DR and DRN was derived previously (Ramakrishnan et al., 2002; Hazra et al., 2007a; Hazra et al., 2007b; Hazra et al., 2007c) and is fixed for all CS in this model. IC50_GRm/DRN is the concentration of DRN required to inhibit GR mRNA production by 50%, and γDR is the Hill coefficient for inhibition by DRN. The rate constant kout_GRm describes the first-order loss for GR mRNA and is defined through the steady-state baseline condition:
| (3) |
The variable Tcyt is representative of an overall cytokine protein expression and accounts for the slow onset of GR mRNA relative to the rapid rise in cytokine response. The differential equation for Tcyt is denoted by
| (4) |
where Acyt is the contribution of pro-inflammatory cytokine mRNA on the production of Tcyt:
| (5) |
The α1 and α2 are the intrinsic activities of each cytokine mRNA for producing cytokine protein, Tcyt. Correlation with IL-6 cytokine mRNA in previous model generations indicated that IL-6 contribution to GR mRNA was negligible (i.e. α3 for IL-6 < 10−8). This was fixed to zero for simplicity in this model.
Depletion of the free glucocorticoid receptor (GR) due to translocation to the nucleus, degradation, limited synthesis rate, and redistribution play major roles in governing the shape of time course of effects from corticosterone and synthetic glucorticoids. The equations describing concentrations of free GR are
| (6) |
where ksyn_GR is the first-order synthesis rate from GR mRNA and kdgr_GR is the first-order loss rate constant. DRN_C is the amount of CST-GR complex in the nucleus and DRN equals DRN_C for the disease progression model without drug effect. The parameter kRE_C describes the rate of which corticosterone bound to receptor returns from the nucleus and RF is the fraction that returns intact and active. The values for kdgr_GR and RF were fixed from the literature (Ramakrishnan et al., 2002; Hazra et al., 2007a; Hazra et al., 2007b; Hazra et al., 2007c). The second-order binding rate constant for CST was defined as where 279.45 g is the molecular weight of CST and 18.64 nM is the literature reported KD for CST (Buchwald, 2007). The parameter ffGC·kon_C accounts for the fraction of drug in plasma that is capable of binding in tissue. The model assumes that CST equilibrium between tissue and vasculature is instantaneous. Bound CST-receptor complex in the cytosol is defined as
| (7) |
where kT is the first-order rate constant for translocation of bound CST-GR complex to the nucleus as reported previously. Concentrations of bound CST-GR complex in the nucleus are described by
| (8) |
This notation is important for pharmacodynamic models when other corticosteroids are present. In this case, when no drug is present: DRN = DRN_C. The parameters GR0, DR0, and DRN0 are the amounts of the glucocorticoid receptor, corticosteroid bound to receptor, and corticosteroid bound to receptor in the nucleus at time zero under baseline conditions at steady-state and when kdis values are set to 1. These baseline values at time zero are defined as:
| (9) |
| (10) |
| (11) |
Plasma CST concentrations are described by
| (12) |
where kin_CST is the first-order rate constant for the production of CST and BCYT is the influence of pro-inflammatory cytokines on CST up-regulation defined as
| (13) |
where β1 and β2 are the intrinsic activities of each individual cytokine on CST up-regulation. Correlation with IL-6 cytokine mRNA in previous model generations indicated that IL-6 contribution to plasma corticosterone was also exceedingly small (i.e. β3 for IL-6 < 10−8) given the linear model structure and β3 for IL-6 was fixed to zero for simplicity in this model.
Pro-inflammatory Cytokine Dynamics
For animals that are induced with the disease, the production rate (kt·R0) for cytokine mRNA is increased to a new disease steady-state value (kt·R0_mRNA·kdis_mRNA) at time of induction, time = 0 hr. For the natural healthy state, the pro-inflammatory cytokines are never turned on and kdis_mRNA maintains a value of 1.0. The equations and initial conditions describing the first event compartment for cytokine mRNA regulation for time ≥0 hr are
| (14) |
| (15) |
| (16) |
where T1 indicates the first transit compartment relevant for the series of events that takes place prior to when disease onset is observed. The values of kt indicate the turnover rate constant for each compartment in this series. Baseline values for the cytokine mRNAs are indicated for when time < 0 hr and kdis_mRNA is equal to one. The final transit compartments in each series are defined by
| (17) |
| (18) |
| (19) |
where subscripts denote the relevant mRNA. Transduction models with different numbers of compartments were tested for each cytokine mRNA independently of each other or other model components to capture the number of compartments required to account for both a large delay and rapid rise to a new disease steady-state using data from animals without DEX treatment. The meaning of each compartment is arbitrary other than being a component of a series of events that take place during the onset of arthritis in the rats. This interpretation is more true to the underlying physiology than a delay or onset time which is also more numerically difficult to compute. Onset times additionally do not provide the smooth rise observed early in the onset of cytokine mRNA expression
Cytokine mRNA is governed by many different factors and thus equations describing the production and loss of each cytokine are different. The turnover of TNF-α mRNA is described by
| (20) |
where kin_TNF describes the first-order production rate dependent upon transit compartment T29TNFα. DRN is endogenous corticosterone bound with receptor in the nucleus, IC50_TNFα/DRN is the concentration of DRN required to inhibit TNF-α production 50%, and γ1 is the Hill coefficient for the inhibition by DRN. The first subscript for each IC50 parameter following the underscore denotes the factor being altered. The subscript for each IC50 parameter following the backslash indicates the factor that is causing the inhibition. The term IL6mRNA describes the amount of IL-6 mRNA and IC50_TNFα/IL6 denotes the amount of IL-6 mRNA necessary to inhibit TNF-α production 50% of maximal capacity (0.3). The rate constant kout_TNFα describes the first-order loss for TNF-α mRNA and is defined through the steady-state baseline condition as
| (21) |
where DRN0 and IL60 describe the baseline values of DRN and IL-6 mRNA.
The turnover of IL-1β mRNA is described by
| (22) |
where kin_IL1β describes the first-order production rate dependent upon transit compartment T19IL1β. The IC50_IL1β is the concentration of DRN required to inhibit IL-1β mRNA production 50%. The term Rem describes an increase in other factors that control the decline in inflammation and is defined by Rem = T27IL1β − R0_IL1β. The parameter Rem was important to account for an apparent remission in IL-6 and IL-1β mRNA that CST alone could not explain. Changes in IL-6 and IL-1β mRNA resulting from high CST concentrations were not as evident as those from DEX. The apparent lack of sensitivity of these factors to CST was important in determining how much effect CST had on the biomarkers after DEX was administered and CST concentrations plummeted. If CST entirely explained the degree of remission for both cytokines then in part II after DEX was administered predicted IL-6 and IL-1β mRNA concentrations would spike well above the observed baseline when DEX concentrations fell and CST concentrations remained low. The parameter IC50_IL1β/Rem denotes the amount of Rem necessary to inhibit IL-1β mRNA production to 50% of maximal capacity (0.7). The rate constant kout_IL1β describes the first-order loss rate-constant for IL-1β mRNA and is defined through the steady-state baseline condition:
| (23) |
The turnover of IL-6 mRNA is defined by
| (24) |
where kin_TNFα describes the first-order production rate dependent upon transit compartment T24IL6. The parameter IC50_IL6/DRN is the concentration of DRN required to inhibit IL-6 mRNA production by 50%, and γ3 is the Hill coefficient for inhibition by DRN. The rate constant kout_IL6 describes the first-order loss for IL-6 mRNA and is defined through the steady-state baseline condition:
| (25) |
Dynamics of Paw Edema
Paw edema was modeled as production from natural growth (kgrowth), production from cytokines (kin_Paw), and loss of the edema (kin_Paw/R0_Paw) that was produced by cytokines (i.e. when edema is not present only kgrowth affects paw size) as follows:
| (26) |
| (27) |
Pcyt describes the total contribution of cytokine mRNA to the overall edema. The values of π for each cytokine reflect intrinsic activities of each cytokine on the production of paw edema.
Dynamics of Bone Mineral Density
Bone mineral density was modeled from five different regions of interest (4 femur, 1 lumbar). The major assumptions governing this model are 1) there are two types of bone, cancellous (Canc) and cortical (Cort), that contribute to BMD in each scan and 2) each region analyzed is composed of different fractions of cancellous and cortical bone. The parameters from the equations for the two types of bone turnover are the same for all regions; the only difference is the fraction of cancellous bone that is modeled for each specific region. Equations for cancellous and cortical bone mineral density are
| (28) |
| (29) |
and are based on the logistic function with modifications. The parameters kgrowth and BMDmax indicate the first-order growth constant and maximum value of bone density for each type. Two hypothetical compartments were created to account for effects of cytokines and corticosteroids on BMD. Pro-inflammatory cytokines are thought to exert their effects on bone loss primarily through the up-regulation of receptor activator of nuclear factor-κB (RANKL) and activation of osteoclasts. Hypothetical osteoclast (OC) activity was described by the following compartment with a baseline of 1 for simplicity.
| (30) |
where Rcyt is defined as
| (31) |
and each ρ value indicates the individual contribution of that cytokine to the production of OC which stimulates bone loss in Equations 27 and 28.
A hypothetical compartment for osteoblasts (OB) was assumed which are thought to be reduced in number and activity by corticosteroids. The effect of DRN on BMD was delayed by nine transit compartments before inhibiting osteoblast production. The baseline was fixed to 1.0 for simplicity. Model equations are
| (32) |
| (33) |
| (34) |
where kOB describes the turnover rate of the hypothetical osteoblast compartment. The value of IC50_GC is the concentration of DRN required for 50% inhibition of ‘osteoblast’ production.
While the above equations were used to model the turnover of cortical and cancellous bone, BMD in each region was modeled as a function of cancellous and cortical bone densities and the fraction of bone in each region that is cancellous (FTF, FDF, FMF, FEF, FLR,) and the fraction of bone that is cortical (1−Fi). Equations for each specific region are:
| (35) |
| (36) |
| (37) |
| (38) |
| (39) |
Subscripts are indicative of each specific region (TF = total femur, DF = diaphyseal femur, MF = metaphyseal femur, EF = epiphyseal femur, and LR = lumbar region) or bone type (cancellous or cortical).
Model Fitting and Nonlinear Regression Analysis
Owing to the model complexity and amount of paw edema and BMD data compared to cytokine data, the model was constructed in two phases: 1) fitting of molecular biomarkers and 2) fitting disease endpoints. Additionally, all dexamethasone drug effect data presented in part II were incorporated and fitted in the disease progression analysis simultaneously. The first segment of the model to be fitted were disease and drug effects on cytokine mRNA, GR mRNA, and plasma corticosterone. The relevant parameters were obtained and then fixed for the model fitting of paw edema and BMD data. Arthritis disease progression related data, parameters, and model fitted curves are presented here.
Model fittings were performed using the maximum likelihood algorithm in S-ADAPT (BMSR, University of Southern California, San Diego, CA) with the OPTIMIZE module. The pooled-fit command was used to permit a NONMEM type dataset to be used with the lsoda algorithm for solving differential equations. The Nelder-Mead simplex search algorithm was implemented for the model relevant to the molecular biomarkers and paw edema as this was an exploratory analysis and initial estimates are difficult given the lack of available literature data for these biomarkers and complexity of the model. The Broyden-Fletcher-Goldfarb-Shanno variable metric method was used for the BMD model as convergence is achieved faster than the nelder-mead simplex and initial estimates were more robustly obtained from features of the BMD data and from available literature values (Bilezikian et al., 2002). Both algorithms converged successfully. Simulations and model code from S-ADAPT were cross-checked using Berkeley Madonna Software (University of California, Berkeley, CA) and all simulation data for figures were done with Berkeley Madonna implementing the Rosenbrock (stiff) method for solving differential equations. All data was pooled and initial attempts at a population analysis employing the complete model for all measured biomarker responses were not successful due to sparse and variable mRNA data and computational limitations owing to the size and complexity of the model.
RESULTS
Disease Progression of TNF-α, IL-1β, and IL-6 mRNA
The disease progression for pro-inflammatory cytokine mRNA for TNF-α, IL-1β, and IL-6 is shown over 960 hours (34 days) following induction of CIA in Lewis rats in Figure 3, Panel A. Marked delays of 240, 288, and 360 hours were observed prior to rapid rises in IL-6, TNF-α, and IL-1β mRNA profiles. Expression of TNF-α and IL-1β mRNA expression rose to plateaus of 110 and 97 ng mRNA/mg total RNA and remained elevated for the remainder of the monitored time course. On the other hand, IL-6 mRNA rose to an abrupt peak at 6225 ng mRNA/mg total RNA on day 19 (456 hr) before declining to an apparent steady-state disease amount of approximately 1300 ng mRNA/mg total RNA. Interestingly the expression of IL-6 mRNA was induced to a much larger extent than either TNF-α or IL-1β mRNA peaking at 6225 ng mRNA/mg total RNA at 456 hours post induction. The inter-animal percent coefficients of variation were between 35% and 60% for each time point in the arthritic groups with 5 to 9 samples per time point. Figure 3, Panel B shows the baseline mRNA expression in healthy rats. Baseline values for cytokine mRNAs were determined as the average of the observed values for all time points from healthy rats and are presented in Table 2. The number of available healthy samples at each time point was fewer at n= 2–4. No time dependency in expression of cytokine mRNA from healthy rats was observed.
Figure 3.
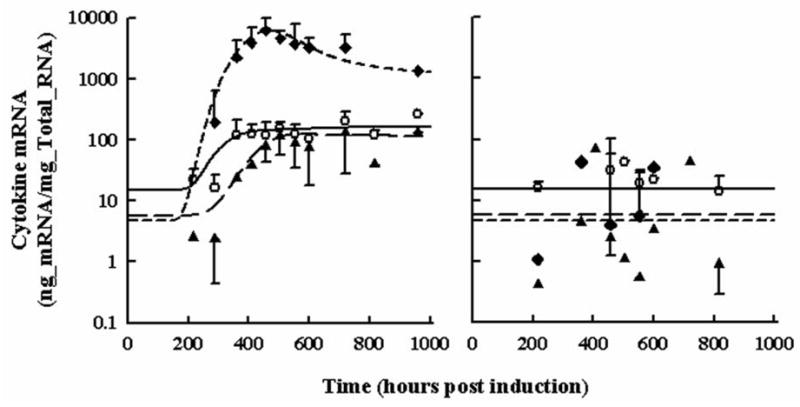
Time courses for pro-inflammatory cytokine paw mRNA expression in arthritic (Panel A) and healthy rats (Panel B). Open circles depict TNF-α mRNA. Black triangles depict IL-1β mRNA. Black diamonds depict IL-6 mRNA. All observations are reported as mean ± one standard deviation. Model fittings are shown as a solid line for TNF-α, long-dashed line for IL-1β, and short-dashed line for IL-6.
Table 2.
Pro-inflammatory Cytokine mRNA Disease Progression Parameters
| Parameter (units) | Description | Estimatea |
|---|---|---|
| TNF0(ng/mg_RNA) | TNF-α mRNA baseline | 14.97b |
| kt1 (hr−1) | TNF-α transduction rate constant | 0.08889b |
| kin_TNFα(hr−1) | TNF-α mRNA synthesis rate constant | 186.5 |
| kdis_TNFα(ng/mg_RNA) | TNF-α mRNA disease steady-state | 13.11 |
| IC50_TNFαDRN(nMol) | IC50 for CST effects on TNF-α mRNA via GR | 550.0 |
| γ1 | Hill coefficient of CST effects on TNF-α mRNA | 2.000b |
| IL1β0(ng/mg_RNA) | IL-1β mRNA baseline | 5.730b |
| kt2 (hr−1) | IL-1β mRNA transduction rate constant | 0.0345b |
| kin_IL1β(hr−1) | IL-1β mRNA synthesis rate constant | 24.82 |
| kdis_IL1β(ng/mg_RNA) | IL-1β mRNA disease steady-steady without remission | 70.11 |
| IC50_IL1β/DRN | IC50 for CST effects on IL-1β mRNA via GR | 32.55 |
| IL60(ng/mg_RNA) | IL-6 mRNA baseline | 4.698b |
| kt3 (hr−1) | IL-6 mRNA transduction rate constant | 0.0550b |
| kin_IL6 (hr−1) | IL-6 mRNA synthesis rate constant | 75.21 |
| kdis_IL6 (ng/mg_RNA) | IL-6 mRNA disease steady-state without remission | 3398 |
| IC50_IL6/DRN(nMol) | IC50 for CST effects on IL-6 mRNA via GR | 4.503 |
| γ3 | Hill coefficient of CST effects on IL-6 mRNA | 2.000b |
| IC50_TNF/IL6(ng/mg_RNA) | IC50 for IL-6 inhibition of TNF-α mRNA | 1080 |
| IC50_Rem | Remission Constant for effects on cytokine expression | 15.00b |
S-ADAPT Software was unable to generate CV%
Parameter value was fixed
Model fittings in Figure 3 appear to fit the data well. The number of transit compartments necessary to account for the disease progression varied between cytokine type. TNF-α mRNA required 29 compartments to account for the delay with a faster transit time to account for the abrupt rise. The rise in IL-1β mRNA expression was slower and delayed further than TNF-α or IL-6; 24 compartments were necessary to describe the onset of IL-1β mRNA with a longer transit time. The onset of IL-6 mRNA was the earliest with the fastest rise of all the measured cytokine markers and 19 transit compartments were needed. Parameter estimates for cytokine disease progression are shown in Table 2. Baseline values for each cytokine were fixed to the average of all measured responses from each time point in healthy rats. The IC50 values indicated the sensitivity of the cytokine to CST-GR complex in the nucleus. Interleukin-6 mRNA appeared to be the most sensitive to DRN (IC50_IL6= 4.50 nM). The IC50 for IL-1β was 7-fold higher at 32.5 nM and even higher for TNF-α at 550 nM. The kdis values indicate the maximum mRNA expression in the disease state without the presence of endogenous CST and DRN inhibiting the production of these cytokines.
GR mRNA and Plasma CST Concentrations
Figure 4 shows the disease progression time course for GR mRNA (Panel A) in paw tissue and plasma corticosterone concentrations (Panel B). In both cases a delay of 240 hours was observed before the onset of response to CIA. The GR mRNA rose slowly and did not reach a plateau during the monitored time course of disease progression. The highest observed response was the second-to-last measured time point with a mean value of 620 ng mRNA/mg total RNA. CST rose rapidly at the same time with a similar trend to TNF-α mRNA. Mean CST concentrations did not exceed 350 ng/mL. Model parameters for the fifth-generation model of corticosteroid dynamics and for the turnover of GR mRNA and CST are presented in Table 3. Baseline values were fixed to the average of the data from healthy animals. Intrinsic activity parameters for effect of cytokine mRNA on GR mRNA or plasma CST showed that TNF-α had the greatest effect on these two responses during disease progression. The value of α3 and β3 for IL-6 was set to zero as there was a decline in response of IL-6 mRNA as the disease progressed and this decline was not observed for GR mRNA or CST concentrations. This is likely why estimates of α3 and β3 tended toward zero (estimates resulting in values less than 10−8) during early model fittings. While it is known that high CST concentrations suppress GR mRNA, this was not readily observed in the data as a continual rise in GR occured, despite a continual rise in plasma CST. That GR concentrations increase while cytokine concentrations reach a plateau, suggests that GR mRNA increases in part because of genomic regulation and not simply due to immune cell infiltration into paw tissue. Also, the IC50 for CST effects on GR mRNA was estimated at 550 nM similar to the value for TNF-α mRNA inhibition. Model fittings are shown as lines in Figure 4 and appeared to capture the disease trend well.
Figure 4.
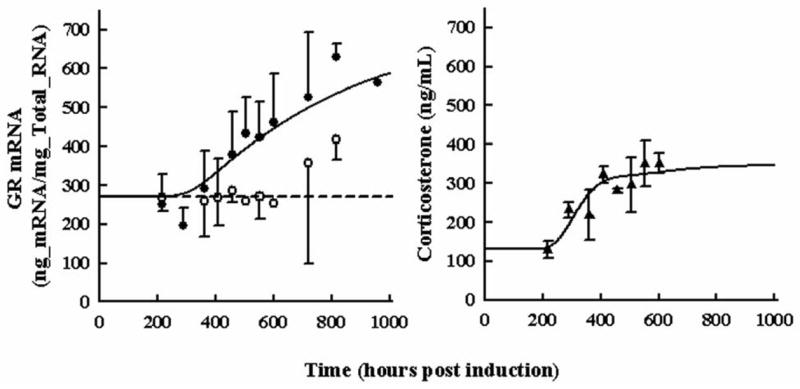
Time courses for glucocorticoid receptor mRNA in paw (Panel A) and plasma corticosterone concentrations (Panel B) during rat CIA progression. Open circles depict GR mRNA expression in healthy rats. Black circles show GR mRNA expression in rats with CIA. Black triangles show plasma corticosterone in rats with CIA. All observations are reported as mean ± one standard deviation. Model fittings are shown as a solid lines for data from diseased rats and short-dashed lines for data from healthy rats.
Table 3.
Model Parameters for Glucocorticoid Receptor and Corticosterone Regulation.
| Parameter (units) | Description | Estimatea |
|---|---|---|
| α1 (ng_GR/ng_TNF) | Intrinsic activity of TNF-α mRNA on GR synthesis | 0.01010 |
| α2 (ng_GR/ng_IL-1β) | Intrinsic activity of IL-1β mRNA on GR synthesis | 0.0002894 |
| kin_GRm (hr−1) | Synthesis rate constant for GR mRNA | 102.5 |
| GRm0(ng/mg_RNA) | Glucocorticoid receptor mRNA baseline | 268.1b |
| IC50_GRm/DRN (nMol) | IC50 for CST effects on GR mRNA via GR | 545.7 |
| γDR | Hill coefficient of CST effects on GR mRNA | 10.00b |
| β1 (ng_CST·mL−1·ng_TNF−1) | Intrinsic activity of TNF-α mRNA on CST synthesis | 0.01118 |
| β2 (ng_CST·mL−1·ng_IL1β −1) | Intrinsic activity of IL-1β mRNA on CST synthesis | 0.00001159 |
| kin_CST (hr−1) | Synthesis rate constant for plasma CST | 1575 |
| CST0 (ng/mL) | Plasma CST baseline | 129.4b |
| ksyn_GR (nM hr−1 ng_GRmRNA−1) | Synthesis rate constant for glucocorticoid receptor | 0.1053 |
| ffGC·kon_C (hr−1) | Binding rate for steroid in plasma to receptor in tissue | 0.2530 |
| kRE_C (hr−1) | Release constant for CST & GR complex from nucleus | 85.04 |
| kt5 (hr−1) | Transduction constant for cytokine effects on GR mRNA | 0.002374 |
| kdgr_GR (hr−1) | Degradation rate constant for free glucocorticoid receptor | 0.054b |
| kT (hr−1) | Rate constant for DR complex translocation to the nucleus | 58.2b |
| RF | Fraction of DRN returned to free glucocorticoid receptor | 0.93b |
S-ADAPT Software was unable to generate CV%
Parameter value was fixed
Paw Edema Progression
The disease progression of CIA as indicated by paw edema is shown in Figure 5. Similar to cytokine mRNA expression there is a delay in onset of 288 hours, a peak of 140 mm2, and slight remission to a response of 120 mm2 during CIA progression. The increase in mean observed paw size from natural animal growth was modest increasing from 77 to 86 mm2. The model was described by a first-order production and first-order loss of edema dependent upon the presence of pro-inflammatory cytokines and the extent of edema and successfully described the data. Model parameters are shown in Table 4. Values of π1, π2, and π3 indicate the extent to which TNF-α, IL-1β, and IL-6 mRNA contribute to the edema. Larger π values for TNF-α and IL-1β mean less mRNA is required to contribute to the edema than for IL-6 where more expression is required for the same response, similar to a measure of potency. Being dependent on cytokine mRNA production, the remission observed in paw swelling is then explained by the remission observed in IL-6 mRNA expression. The CV% for paw parameters were low, but dependent upon the validity of the fixed cytokine mRNA model.
Figure 5.
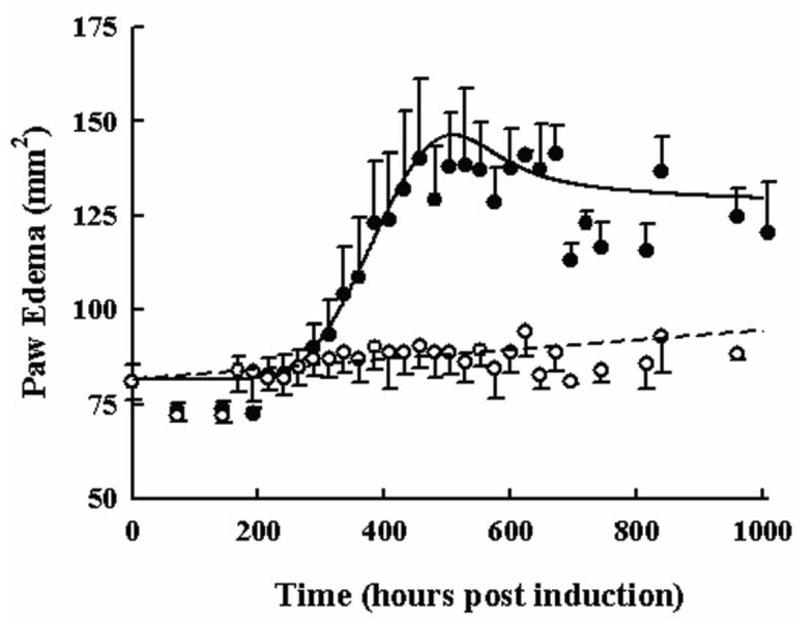
Time course of paw edema in arthritic and healthy rats. Black circles and the solid line depict the measured responses and model fitting for rats with CIA. Open circles and the dashed line show the measured responses and model fitting for rats with no disease. All data are plotted as mean ± one standard deviation.
Table 4.
Model Parameters for Paw Edema.
| Parameter (units) | Description | Estimate | CV% |
|---|---|---|---|
| π1 (mm2·ng_TNF−1) | Intrinsic activity of TNF-α mRNA on Paw edema | 0.0021662 | 4.19 |
| π2 (mm2·ng_TNF−1) | Intrinsic activity of IL-1β mRNA on Paw edema | 0.001750 | 8.58 |
| π3 (mm2·ng_TNF−1) | Intrinsic activity of IL-6 mRNA on Paw edema | 0.00005530 | 4.88 |
| kin_PAW (hr−1) | Synthesis rate constant for paw edema | 6.787 | 7.35 |
| PAW0 (mm2) | Initial value of paw size in Lewis rats 8 weeks old | 81.68 | 0.362 |
| kgrowth (mm2 hr−1) | Zero-order synthesis rate constant for natural paw growth | 0.01297 | 8.55 |
Simulations of the paw edema model were done with and without inhibition of different cytokine effects on edema to indicate how each cytokine mRNA contributes to the overall edema, relevant to newer RA therapies that target blocking of cytokine effects. Figure 6 shows these simulations. Panels A-C show paw edema response following continual inhibition of TNF-α, IL-1β, or IL-6 mRNA by 0%, 50%, and 100%. Panels C-D depict the paw edema progression when mRNA of two cytokines are inhibited jointly by 0%, 50%, and 100%. The 100% joint inhibition of two cytokines yields a profile of paw edema that is indicative of the contribution the uninhibited cytokine has on edema production. These 100% dual inhibition profiles in Panels C-D appear to have the same trend in progression as the unihibited cytokine due to the linear relationship between mRNA and production of edema.
Figure 6.
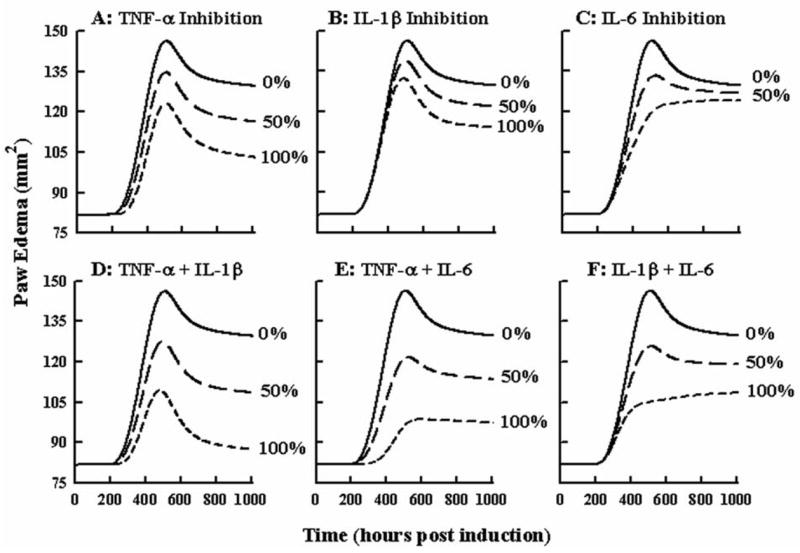
Model sensitivity analysis for cytokine effects on paw edema. Panels A–C show simulated time courses of paw swelling for 0, 50, or 100 % inhibition of TNF-α, IL-1β, or IL-6 cytokine mRNA expression. Panels D–F show simulated time courses for 0, 50, or 100 % inhibition of TNF-α and IL-1β, TNF-α and IL-6, or IL-1β and IL-6 cytokine mRNA jointly.
Bone Mineral Density Progression
Figures 7 shows femoral and lumbar BMD in healthy controls and during CIA in Lewis rats. Scans of ankle and paw BMD yielded no change and high variation, most likely due to multiple overlapping bones when scanned from the side. However, changes in BMD were quite apparent in the femur. Skeletal growth was observed throughout the time course of healthy rats. In arthritic animals reduced BMD occurred beginning at 420 hours post induction, later than the onset of cytokine mRNA. Changes in BMD were less apparent in the lumbar region between the two groups.
Figure 7.
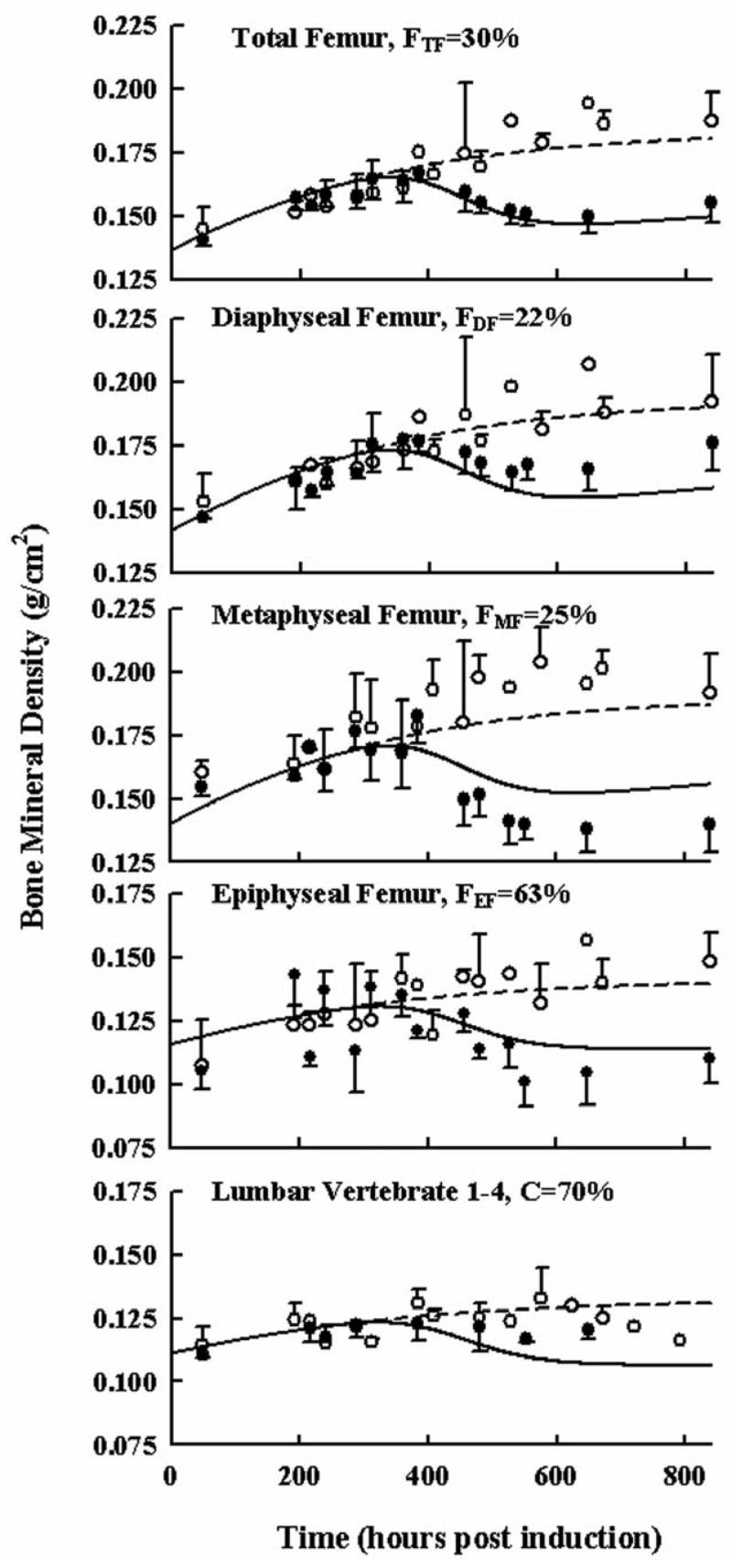
Time courses of bone mineral density in different regions of the rat femur and lumbar vertebrate in healthy (○) and arthritic rats (●). All observations are reported as mean ± one standard deviation. Model fittings are shown as a solid lines for diseased rats and short-dashed lines for data from healthy rats. The F value indicates the model-fitted percentage of cancellous bone in the specified region of interest.
In general the model fitted the data well, considering that there were two fairly restrictive assumptions 1) only cancellous and cortical bone contributes to BMD, and 2) differences in each region of interest are solely due to different fractions of cancellous and cortical bone. Parameter estimates for bone turnover are presented in Table 5. Initial values at time zero and maximal bone densities for each bone type were as expected, being lower for cancellous bone and higher for cortical bone. The parameter estimates for fractions of cancellous bone are reported in Table 6. These were surprisingly close to literature reported values (Bilezikian et al., 2002) for sections of long bone with 20 and 30% of bone being cancellous and values for the distal end of the femur in the knee joint (epiphyseal femur) and the lumbar region were higher at 63% and 70%.
Table 5.
Model Parameters for Cancellous and Corticol Bone Mineral Density.
| Parameter (units) | Description | Estimate | CV% |
|---|---|---|---|
| Canc0(g/cm2) | Value of cancellous bone density on study day 0 | 0.08720 | 27.9 |
| kgrowth_Cancellous (hr−1) | Synthesis rate constant for cancellous bone | 0.0002252 | 1370 |
| BMDmax_Cancellous (g/cm2) | Maximum density of cancellous bone | 0.1001 | 16.4 |
| Cort0(g/cm2) | Value of cortical bone density on study day 0 | 0.1586 | 141 |
| kgrowth_Cortical (hr−1) | Synthesis rate constant for cortical bone | 0.003855 | 41.3 |
| BMDmax_Corticol (g/cm2) | Maximum density of corticol bone | 0.2242 | 18.6 |
| ftcort | Fractional effect of ‘Osteoclast’ CMT on cortical bone | 0.09133 | 1460 |
| focort | Fractional effect of ‘Osteoblast’ CMT on cortical bone | 0.7720 | 874 |
| kOC (hr−1) | Synthesis rate constant for ‘OC’ CMT | 0.5985 | 770 |
| ρ1 (ng_TNF−1) | Intrinsic activity of TNF-α mRNA on ‘OC’ CMT | 4.931 × 10−6 | 1690 |
| ρ2 (ng_IL-1β−1) | Intrinsic activity of IL-1β mRNA on ‘OC’ CMT | 5.662 × 10−3 | 1430 |
| ρ3 (ng_IL-6−1) | Intrinsic activity of IL-6 mRNA on ‘OC’ CMT | 6.578 × 10−4 | 1480 |
| kosteoblast (hr−1) | Transit rate constant for glucocorticoid effect | 0.09105 | 43.0 |
| IC50_GC (nM) | Concentration for 50% inhibition of glucocorticoid effect | 984.8 | 137 |
Table 6.
Model Parameters for Regional Bone Mineral Density.
| Parameter | Description | Estimate | CV% |
|---|---|---|---|
| FTF | Fraction of cancellous bone in total femur | 0.3053 | 709 |
| FDF | Fraction of cancellous bone in diaphyseal femur | 0.2309 | 104 |
| FMF | Fraction of cancellous bone in metaphyseal femur | 0.2534 | 918 |
| FEF | Fraction of cancellous bone in epiphyseal femur | 0.6127 | 199 |
| FLR | Fraction of cancellous bone in lumbar vertebrate 1–4 | 0.6807 | 150 |
DISCUSSION
Development of a mechanistic model for rheumatoid arthritis is complex owing to the many molecular factors that affect disease progression. The model was derived based on biomarkers that are well-known as major mediators of inflammation and bone erosion. It is well established that there is an endocrine link between pro-inflammatory cytokine production and glucocorticoid receptor and corticosterone regulation. This partly explains disease remission with increased expression of GR mRNA and CST following CIA onset and permits a mechanistic framework to examine the effects of other corticosteroids.
The structure of the disease progression model integrates endogenous glucocorticoid effects with cytokine mRNA expression in an effort to model the effects of DEX in an animal model of arthritis (Part II). DEX is a synthetic glucocorticoid that perturbs many inflammatory pathways and all measured biomarkers acting through the same mechanisms as CST. The turnover of these markers within the disease progression and their effects on disease endpoints can be obtained from the PD data following DEX administration. The disease progression data alone cannot resolve all parameters. Rationalization of these remaining equations and parameters require information from DEX PD and is presented here to a limited extent and in more detail in part II.
The model describing disease progression in paw cytokine mRNA starts as a simple transduction model with a rate constant to account for the delay, baseline steady-state initial condition for the healthy response, and the kdis rate constant to increase the cytokine mRNA to a new disease steady-state at time of induction. This is a new application of transduction compartments to describe four aspects of disease progression: time of induction, delay in disease onset, rate of progression, and new disease-steady state response. Equations for individual cytokine mRNAs were complicated by inhibition of mRNA production by CST-GR complex in the nucleus, possible disease remission, and cross-talk between IL-6 and TNF-α mRNA. Since DEX and CST are assumed to act similarly, many of these modeling complexities were resolved from the DEX PD data (Part II).
Initially the decline in IL-6 paw mRNA was explained by CST binding to GR and DRN inhibiting IL-6 mRNA production as DRN rose above the IC50 for IL-6 (4.5 nM) mRNA inhibition during disease progression. However, early simulations indicated that CST alone could not account for the entire remission of IL-6. If DRN rose rapidly as in the case of CS administration CST would be suppressed rapidly and for a prolonged time (see Part II), such that when DRN returned to normal and CST remained suppressed, the IL-6 mRNA production would overshoot the measured response.
Abrupt DEX PD changes in cytokine mRNA indicated that rate constants relevant to the loss of mRNA were much faster than the transduction rate constants describing disease progression. This observation forced the production and loss constants for cytokine mRNA to be modeled separately from the transduction rate constants. Literature indicates rapid production and loss of cytokines within hours whereas disease effects may be drawn out over days. Using transduction equations to describe disease progression provides a conceptual link between slower rate-limiting disease steps and measured responses with faster turnover.
The localized nature of the disease in paw/joint tissue made measurements of TNF-α, IL-1β, or IL-6 protein in paw tissue impractical. The authors tried measuring these cytokine proteins in homogenized paw tissue diluted with phosphate buffered saline and plasma. Background/matrix effects were a problem and the TNF-α, IL-1β, and IL-6 ELISA assay kits (Promega Corp. Madison, WI) were not valid for tissue analysis. The cytokine ELISA kits for protein measurements were not sensitive enough for plasma cytokine concentrations in arthritic rats. Given these experimental limitations the model uses the available methods to relate physiogically relevant events. Owing to the rapid turnover of both cytokine protein and mRNA in tissue and that these proteins are constitutively expressed in response to an antigenic stimulus, time courses of cytokine mRNA may be reflective of synthesized cytokine. Thus correlations between cytokine mRNA and effects on disease progression may be useful if the turnover rates of disease endpoints are slower than those of cytokine protein.
The DEX PD data helped resolve Hill coefficients for DRN effect from different doses. For TNF-α and IL-6 mRNA these values were fixed to 2.0 as this agreed with both the initial model estimations and the physiological homo-dimerization of CST-GR complex in the nucleus.
Paw edema was monitored in every animal which developed the disease. There were 4943 paw edema data points used in the disease progression, healthy animal profiles, and pharmacodynamic analysis compared to 439 points for mRNA of each cytokine. Due to variation in paw edema progression among animals, describing paw swelling during simultaneous fitting of all data initially biased the model fitting as it placed most emphasis on the how the paw edema was modeled and little on the cytokine mRNA driving the edema. Without capturing the mRNA responses first, the development of the structural model describing cytokine mRNA and paw edema was difficult and unclear. The numerous feedback loops by DRN on most inflammatory factors and these factors on GR and CST meant that if one variable was altered, model descriptions for all other biomarkers were altered also. Thus the model describing cytokine mRNA, GR mRNA, and plasma CST was developed first and fixed for evaluating the structural model for paw edema dependent on the cytokine mRNA expression. This permitted shorter model fitting times and better model revisions for the complex feedback model between cytokine and CST-GR regulation.
The final model for paw edema was relatively simple and driven by contributions from all three cytokines. Paw edema increased early as affected by TNF-α and IL-6, and the decline in IL-6 mRNA after day 21 helped explain the similar decline to a steady-state in paw edema. These individual contributions of cytokines on edema were further resolved by administration of DEX which inhibited each cytokine mRNA profile at different rates and extents while correlating these mRNA amounts to paw edema.
There is increasing interest for treating rheumatoid arthritis with biologics aimed at inhibiting the effects of TNF-α and IL-1β. Model simulations continually inhibiting the effects of each cytokine by 50 or 100% were performed to predict extent of edema reduction. Because TNF-α, IL-1β, IL-6 and other pro-inflammatory cytokines have overlapping functions in producing edema, completely suppressing the inflammatory response by targeting only one or two of these pathways results in incomplete reduction of edema. The myriad pathways contributing to inflammation emphasizes the role of corticosteroids in treatment of RA for their inherent ability to suppress many different inflammatory processes simultaneously. Understanding the extent to which dexamethasone, prednisolone, or other CS reduce each inflammatory signaling pathway in light of how other therapies affect these common disease factors may contribute to determining optimal treatment regimens for agents given alone or in combination.
Bone mineral density was modeled in each region by the sum of the cancellous bone plus the cortical bone. As these amounts were not known, the fraction of cancellous bone was modeled in each region. Physiological understanding that bone turnover is more rapid in cancellous bone is in agreement with model estimates for initial and maximum BMD in both bone types. However, the turnover rate constant for cancellous bone was slightly lower than that for cortical bone. This is caused in part by the parameter ftc that reduces the effect of the ‘OC’ on cortical bone turnover.
The model does not consider proximity to inflamed joints as a factor and as such the lumbar region is treated as if equal to the knee joint in terms of inflammatory effects. While disease effects may not be readily apparent in the lumbar region of the rat, differences are observed in human RA in the spine. The time course of response may need to be carried out longer to observe these inflammatory effects on BMD in the rat lumbar region.
High CV% for bone parameters were rather surprising as these parameters appeared to stabilize quickly and shifted very little during model convergence. It is likely that the high CV% came from inter-animal variation in onset of disease progression and rate of bone loss. Precision measurements for Total BMD have been reported (Binkley et al., 2003; Soon et al., 2006). In all cases the CV% was less than 10%. It is possible this CV% also comes from not having measured cancellous or cortical bone directly. However, the value of the parameter estimates appeared reasonable.
Trends in both disease progression and pharmacodynamic responses to dexamethasone (Part II) were necessary to discern model behavior of pro-inflammatory cytokine mRNA and their effect on driving disease progression in paw edema as well as endogenous CST and GR mRNA that in turn regulate the production of TNF-α, IL-1β, and IL-6 mRNA. Other components such as immune cell presence in tissue, amounts of transcription factors in the nucleus, and additional inflammatory regulators (e.g. prostaglandins, nitric oxide, TH-2 cytokines) are valuable components to understanding inflammation. Despite the absence of these other factors in the model, edema and BMD appear to be well described by the major cytokines that drive the production of inflammation. This is the first detailed mechanistic model for CIA progression in the rat and model qualification may come with future studies. Defining and developing translational assumptions between disease progression in the rat and clinical disease observations may not be possible for all biomarkers. However, it is likely that for BMD the extent of disease or drug effect will correlate well, even if the rates of turnover are different because these are chronic conditions with chronic therapies and disease progression and drug responses tend toward steady-state values over time. Owing to the endogenous link between CST and cytokine mRNA, treatments with DEX and other corticosteroids in the clinic along with pre-determined knowledge of drug receptor binding may aid in relevant clinical predictions. Future experiments aim to validate the model by predicting the response to methylprednisolone dosing to arthritic rats. Experiments with other therapeutics may prove informative if the drug effects are limited individual pathways in the model. Anti-cytokine antibodies are a good example of therapeutic agents that may block specific signaling components in order to identifiy the relative contributions of certain cytokines on disease endpoints.
Acknowledgments
Supported by NIH Grant GM24211 and by a Fellowship from Amgen Inc. for J. C. Earp
Nonstandard abbreviations
- BMD
Bone Mineral Density
- CIA
Collagen Induced Arthritis
- CS
Corticosteroid
- CST
Corticosterone
- DEX
Dexamethasone
- IL-1β
Interleukin-1β
- IL-6
Interleukin-6
- OB
Osteoblast
- OC
Osteoclast
- PD
Pharmacodynamic
- TNF-α
Tumor Necrosis Factor-α
Footnotes
Recommended Section Assignment: Inflammation, Immunopharmacology, and Asthma
References
- Bilezikian JP, Raisz LG, Rodan GA. Principles of bone biology. Academic Press; San Diego: 2002. [Google Scholar]
- Binkley N, Dahl DB, Engelke J, Kawahara-Baccus T, Krueger D, Colman RJ. Bone loss detection in rats using a mouse densitometer. J Bone Miner Res. 2003;18:370–375. doi: 10.1359/jbmr.2003.18.2.370. [DOI] [PubMed] [Google Scholar]
- Buchwald P. Glucocorticoid receptor binding: A biphasic dependence on molecular size as revealed by the bilinear LinBiExp model. Steroids. 2007 doi: 10.1016/j.steroids.2007.10.001. [DOI] [PubMed] [Google Scholar]
- Chan PL, Holford NH. Drug treatment effects on disease progression. Annu Rev Pharmacol Toxicol. 2001;41:625–659. doi: 10.1146/annurev.pharmtox.41.1.625. [DOI] [PubMed] [Google Scholar]
- Choy EH, Panayi GS. Cytokine pathways and joint inflammation in rheumatoid arthritis. N Engl J Med. 2001;344:907–916. doi: 10.1056/NEJM200103223441207. [DOI] [PubMed] [Google Scholar]
- Da Silva JA, Jacobs JW, Kirwan JR, Boers M, Saag KG, Ines LB, de Koning EJ, Buttgereit F, Cutolo M, Capell H, Rau R, Bijlsma JW. Safety of low dose glucocorticoid treatment in rheumatoid arthritis: published evidence and prospective trial data. Ann Rheum Dis. 2006;65:285–293. doi: 10.1136/ard.2005.038638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dayneka NL, Garg V, Jusko WJ. Comparison of four basic models of indirect pharmacodynamic responses. J Pharmacokinet Biopharm. 1993;21:457–478. doi: 10.1007/BF01061691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Winter W, DeJongh J, Post T, Ploeger B, Urquhart R, Moules I, Eckland D, Danhof M. A mechanism-based disease progression model for comparison of long-term effects of pioglitazone, metformin and gliclazide on disease processes underlying Type 2 Diabetes Mellitus. J Pharmacokinet Pharmacodyn. 2006;33:313–343. doi: 10.1007/s10928-006-9008-2. [DOI] [PubMed] [Google Scholar]
- Frey N, Laveille C, Paraire M, Francillard M, Holford NH, Jochemsen R. Population PKPD modelling of the long-term hypoglycaemic effect of gliclazide given as a once-a-day modified release (MR) formulation. Br J Clin Pharmacol. 2003;55:147–157. doi: 10.1046/j.1365-2125.2003.01751.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gravallese EM. Bone destruction in arthritis. Ann Rheum Dis. 2002;61(Suppl 2):ii84–86. doi: 10.1136/ard.61.suppl_2.ii84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haughey DB, Jusko WJ. Analysis of methylprednisolone, methylprednisone and corticosterone for assessment of methylprednisolone disposition in the rat. J Chromatogr. 1988;430:241–248. doi: 10.1016/s0378-4347(00)83159-x. [DOI] [PubMed] [Google Scholar]
- Hazra A, DuBois DC, Almon RR, Jusko WJ. Assessing the dynamics of nuclear glucocorticoid-receptor complex: adding flexibility to gene expression modeling. J Pharmacokinet Pharmacodyn. 2007a;34:333–354. doi: 10.1007/s10928-007-9049-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hazra A, Pyszczynski N, DuBois DC, Almon RR, Jusko WJ. Modeling receptor/gene-mediated effects of corticosteroids on hepatic tyrosine aminotransferase dynamics in rats: dual regulation by endogenous and exogenous corticosteroids. J Pharmacokinet Pharmacodyn. 2007b;34:643–667. doi: 10.1007/s10928-007-9063-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hazra A, Pyszczynski NA, Dubois DC, Almon RR, Jusko WJ. Modeling of Corticosteroid Effects on Hepatic Low-Density Lipoprotein Receptors and Plasma Lipid Dynamics in Rats. Pharm Res. 2007c doi: 10.1007/s11095-007-9371-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holford NH, Chan PL, Nutt JG, Kieburtz K, Shoulson I. Disease progression and pharmacodynamics in Parkinson disease - evidence for functional protection with levodopa and other treatments. J Pharmacokinet Pharmacodyn. 2006;33:281–311. doi: 10.1007/s10928-006-9012-6. [DOI] [PubMed] [Google Scholar]
- Holford NH, Peace KE. Methodologic aspects of a population pharmacodynamic model for cognitive effects in Alzheimer patients treated with tacrine. Proc Natl Acad Sci U S A. 1992a;89:11466–11470. doi: 10.1073/pnas.89.23.11466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holford NH, Peace KE. Results and validation of a population pharmacodynamic model for cognitive effects in Alzheimer patients treated with tacrine. Proc Natl Acad Sci U S A. 1992b;89:11471–11475. doi: 10.1073/pnas.89.23.11471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoogendoorn M, Rutten-van Molken MP, Hoogenveen RT, van Genugten ML, Buist AS, Wouters EF, Feenstra TL. A dynamic population model of disease progression in COPD. Eur Respir J. 2005;26:223–233. doi: 10.1183/09031936.05.00122004. [DOI] [PubMed] [Google Scholar]
- Jusko WJ. Pharmacodynamics of chemotherapeutic effects: dose-time-response relationships for phase-nonspecific agents. J Pharm Sci. 1971;60:892–895. doi: 10.1002/jps.2600600618. [DOI] [PubMed] [Google Scholar]
- Lalonde RL, Kowalski KG, Hutmacher MM, Ewy W, Nichols DJ, Milligan PA, Corrigan BW, Lockwood PA, Marshall SA, Benincosa LJ, Tensfeldt TG, Parivar K, Amantea M, Glue P, Koide H, Miller R. Model-based drug development. Clin Pharmacol Ther. 2007;82:21–32. doi: 10.1038/sj.clpt.6100235. [DOI] [PubMed] [Google Scholar]
- Lerner UH. New Molecules in the Tumor Necrosis Factor Ligand and Receptor Superfamilies with Importance for Physiological and Pathological Bone Resorption. Crit Rev Oral Biol Med. 2004;15:64–81. doi: 10.1177/154411130401500202. [DOI] [PubMed] [Google Scholar]
- Lesko LJ. Paving the critical path: how can clinical pharmacology help achieve the vision? Clin Pharmacol Ther. 2007;81:170–177. doi: 10.1038/sj.clpt.6100045. [DOI] [PubMed] [Google Scholar]
- McCormick RK. Osteoporosis: integrating biomarkers and other diagnostic correlates into the management of bone fragility. Altern Med Rev. 2007;12:113–145. [PubMed] [Google Scholar]
- Meier DS, Weiner HL, Guttmann CR. Time-series modeling of multiple sclerosis disease activity: a promising window on disease progression and repair potential? Neurotherapeutics. 2007;4:485–498. doi: 10.1016/j.nurt.2007.05.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meunier PJ, Vignot E, Garnero P, Confavreux E, Paris E, Liu-Leage S, Sarkar S, Liu T, Wong M, Draper MW. Treatment of postmenopausal women with osteoporosis or low bone density with raloxifene. Raloxifene Study Group. Osteoporos Int. 1999;10:330–336. doi: 10.1007/s001980050236. [DOI] [PubMed] [Google Scholar]
- Neeck G, Renkawitz R, Eggert M. Molecular aspects of glucocorticoid hormone action in rheumatoid arthritis. Cytokines Cell Mol Ther. 2002;7:61–69. doi: 10.1080/13684730412331302081. [DOI] [PubMed] [Google Scholar]
- Nemeroff CB. The clinical pharmacology and use of paroxetine, a new selective serotonin reuptake inhibitor. Pharmacotherapy. 1994;14:127–138. [PubMed] [Google Scholar]
- Pillai G, Gieschke R, Goggin T, Jacqmin P, Schimmer RC, Steimer JL. A semimechanistic and mechanistic population PK-PD model for biomarker response to ibandronate, a new bisphosphonate for the treatment of osteoporosis. Br J Clin Pharmacol. 2004;58:618–631. doi: 10.1111/j.1365-2125.2004.02224.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Post TM, Freijer JI, DeJongh J, Danhof M. Disease system analysis: basic disease progression models in degenerative disease. Pharm Res. 2005;22:1038–1049. doi: 10.1007/s11095-005-5641-5. [DOI] [PubMed] [Google Scholar]
- Ramakrishnan R, DuBois DC, Almon RR, Pyszczynski NA, Jusko WJ. Fifth-generation model for corticosteroid pharmacodynamics: application to steady-state receptor down-regulation and enzyme induction patterns during seven-day continuous infusion of methylprednisolone in rats. J Pharmacokinet Pharmacodyn. 2002;29:1–24. doi: 10.1023/a:1015765201129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ravn P, Clemmesen B, Riis BJ, Christiansen C. The effect on bone mass and bone markers of different doses of ibandronate: a new bisphosphonate for prevention and treatment of postmenopausal osteoporosis: a 1-year, randomized, double-blind, placebo-controlled dose-finding study. Bone. 1996;19:527–533. doi: 10.1016/s8756-3282(96)00229-3. [DOI] [PubMed] [Google Scholar]
- Rifas L. Bone and cytokines: beyond IL-1, IL-6 and TNF-alpha. Calcif Tissue Int. 1999;64:1–7. doi: 10.1007/s002239900570. [DOI] [PubMed] [Google Scholar]
- Samtani MN, Jusko WJ. Stability of dexamethasone sodium phosphate in rat plasma. Int J Pharm. 2005;301:262–266. doi: 10.1016/j.ijpharm.2005.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soon G, Quintin A, Scalfo F, Antille N, Williamson G, Offord E, Ginty F. PIXImus bone densitometer and associated technical measurement issues of skeletal growth in the young rat. Calcif Tissue Int. 2006;78:186–192. doi: 10.1007/s00223-005-0191-8. [DOI] [PubMed] [Google Scholar]
- Summey BT, Yosipovitch G. Glucocorticoid-induced bone loss in dermatologic patients: an update. Arch Dermatol. 2006;142:82–90. doi: 10.1001/archderm.142.1.82. [DOI] [PubMed] [Google Scholar]
- Sun YN, DuBois DC, Almon RR, Jusko WJ. Fourth-generation model for corticosteroid pharmacodynamics: a model for methylprednisolone effects on receptor/gene-mediated glucocorticoid receptor down-regulation and tyrosine aminotransferase induction in rat liver. J Pharmacokinet Biopharm. 1998;26:289–317. doi: 10.1023/a:1023233409550. [DOI] [PubMed] [Google Scholar]
- Svensson B, Boonen A, Albertsson K, van der Heijde D, Keller C, Hafstrom I. Low-dose prednisolone in addition to the initial disease-modifying antirheumatic drug in patients with early active rheumatoid arthritis reduces joint destruction and increases the remission rate: a two-year randomized trial. Arthritis Rheum. 2005;52:3360–3370. doi: 10.1002/art.21298. [DOI] [PubMed] [Google Scholar]
- Turnbull AV, Rivier CL. Regulation of the hypothalamic-pituitary-adrenal axis by cytokines: actions and mechanisms of action. Physiol Rev. 1999;79:1–71. doi: 10.1152/physrev.1999.79.1.1. [DOI] [PubMed] [Google Scholar]
- Wassenberg S, Rau R, Steinfeld P, Zeidler H. Very low-dose prednisolone in early rheumatoid arthritis retards radiographic progression over two years: a multicenter, double-blind, placebo-controlled trial. Arthritis Rheum. 2005;52:3371–3380. doi: 10.1002/art.21421. [DOI] [PubMed] [Google Scholar]
- Woo S, Krzyzanski W, Jusko WJ. Pharmacodynamic model for chemotherapy-induced anemia in rats. Cancer Chemother Pharmacol. 2007 doi: 10.1007/s00280-007-0582-9. [DOI] [PMC free article] [PubMed] [Google Scholar]


