SUMMARY
The power of statistical tests to measure effect sizes in the presence of population stratification is an important issue for the design and analysis of population-based association studies. Comparisons of statistical tests have shown that the power of different statistical approaches varies in different genetic scenarios. However, the impact of stratified population parameters on statistical power is not yet understood in a general statistical framework, particularly the impact of correlated population parameters. To investigate such impact in detail, we implemented a genetic model for population-based association studies with stratified samples and evaluated the impact on power with different genetic scenarios. The investigation shows that correlation between disease prevalence and risk allele frequency among subpopulations impacts statistical power. In a model with five subpopulations and moderate population divergence (Fst=0.01), the correlation accounts for more than 85% of power difference. Our results also show that the estimation of genetic effect for candidate loci is biased by population divergence. Beneficial alleles could be wrongly characterized as risk alleles when prevalence differences and divergences of risk loci are large among subpopulations.
Keywords: Population stratification, statistical power, relative risk, genomic control, association study
INTRODUCTION
The population-based case-control study is an essential tool for identification of disease loci underlying complex traits (Clark, 2003; Risch & Merikangas, 1996). Because the genetic contribution of disease loci is often weak, hundreds even thousands of individuals are required for a well-designed study to achieve enough statistical power for screening candidate loci (Dahlman et al. 2002; Hirschhorn & Daly, 2005). Problems arise with using large sample sizes for loci with weak genetic contributions because the population stratification often leads to spurious associations. The number of such spurious associations could be much larger than the number of real positive results in a large-scale association study with many genetic markers (Campbell et al. 2005; Freedman et al. 2004; Helgason et al. 2005; Lander & Schork, 1994; Marchini et al. 2004).
In the traditional case-control approach, many investigators base their analysis on the assumption that samples are collected from unrelated individuals with similar genetic backgrounds. However, this assumption could be problematic for a large-scale project because the genetic background of human populations is not as uniform as assumed (Freedman et al. 2004). Previous studies have revealed much information on the genetic structure of modern human populations (Bowcock et al. 1991; Campbell et al. 2005; Cavalli-Sforza & Feldman 2003; Garrigan & Hammer 2006; Helgason et al. 2005; Rosenberg et al. 2002; Shi et al. 2004). Many genetic variants with extreme differences of allele frequencies have been observed among different human populations, not only on mitochondrial DNA and the Y chromosome but also on other parts of the human genome (Collins-Schramm et al. 2002; Collins-Schramm et al. 2004; Rosser et al. 2000; Seielstad et al. 1998). A slight genetic background difference between cases and controls is enough to affect the results of a large-scale association study. Although genetic differentiation (measured by Fst) is only about 0.01 among European populations, the divergence is large enough to inflate type I error rate (Bacanu et al. 2000; Morton, 1992; Nicholson et al. 2002; Price et al. 2006). Furthermore, disease prevalence differences among different geographic areas also contribute to the heterogeneity of the genetic background (Bersaglieri et al. 2004; Sabeti et al. 2002). Therefore, a careful study of the impact of population stratification on the design of association studies is warranted.
Several different methods have been proposed to detect population stratification and to control the false positive rate for case-control association studies with stratified samples. In 1999, Pritchard and Rosenberg detected population stratification by using a multilocus chi-square test (Pritchard & Rosenberg, 1999). Subsequently, the use of Bayesian clustering with a likelihood statistical test was proposed with a similar aim, and it was important that the new approach could be used to estimate unknown population parameters (Pritchard et al. 2000a). Based on the estimated parameters, a statistical method called ‘structured association’ (SA) was presented, which could test case-control differences while keeping the false positive rate at a reasonable level (Pritchard et al. 2000b). Genomic control (GC) is an alternative approach in which the traditional chi-square statistic is replaced by a new statistic that divides the traditional chi-square statistic by an inflation factor. Through careful calculation and simulation, it has been shown that the GC method could control the rate of false positive results very well (Devlin & Roeder, 1999; Reich & Goldstein, 2001). Many researchers have modified and improved the two existing approaches, GC and SA, in the past few years (Gorroochurn et al. 2006; Rosenberg & Nordborg, 2006; Satten et al. 2001; Yu et al. 2006). More recently, Price et al. combined principal component analysis (PCA) with the Armitage trend test to control the false positive rate when hundreds or more loci were available (Price et al. 2006). All the approaches mentioned above have shown success in controlling the type I error rate in case-control designs with stratified populations.
Power issues are important in genetic studies of complex traits, especially in the era of genome-wide association study (Lin, 2006; Storey & Tibshirani, 2003; Wang et al. 2005). Previous reports proposed methods for controlling spurious associations and compared the power of the different statistical approaches (Bacanu et al. 2000, Gorroochurn et al. 2006, Price et al. 2006). However, only a limited number of population parameters were thoroughly evaluated with respect to the power issue (Marchini et al. 2004, Devlin et al. 2001). In addition, one report showed that population stratification led to loss of statistical power in a population-based association study without control for spurious associations (Shi et al. 2004); however, details of the power loss were still not well investigated. Some researchers have realized that prevalence differences among subpopulations lead to sampling bias and make type I error control and the calculation of odds ratios difficult (Satten et al. 2001). Nevertheless, no careful exploration of the impact of prevalence differences on statistical power has been carried out. For a more complete characterization, the relationships between power difference and parameters of population stratification need to be investigated under different genetic scenarios.
GC theory was introduced with an elegant genetic model by Devlin et al. (2001). Their method and conclusion, based on a discrete-population model, can be generalized to scenarios with admixture among the population groups or continuous variation across geographic space (Gorroochurn et al. 2006; Rosenberg & Nordborg, 2006). The genetic model with multiple discrete population groups supplies us an opportunity to view power differences in a clear and explicit manner. Here, using a similar model, we show that correlation of population parameters introduces serious power differences to statistical tests in association studies with population stratification. The investigation also shows that the effects of candidate alleles will be difficult to estimate accurately in stratified samples.
MODEL
We assume that the population in a local area is composed of several subpopulations with different genetic backgrounds. Each subpopulation is in Hardy-Weinberg equilibrium (HWE) and indicated with ci (i = 1, 2, 3…). We also suppose that our case and control samples were randomly collected in this area without regard for the population structure.
Case-control effect size
Case-control effect size is a measure of difference between case and control groups. Statistical tests on case-control effect size are the basis of population-based association studies. In the Devlin et al. paper, case-control effect size is defined as frequency difference of allele A between case and control groups, (Devlin et al. 2001) where is the frequency of allele A in the case group and is the allele frequency in the control group. For a biallelic locus with alleles A and a, the frequency of allele A in the case or control group can be calculated as
| (1) |
where and are the frequencies of individuals who come from subpopulation c and carry genotype AA or Aa in the case group, respectively; and are the frequencies of individuals who come from subpopulation c and carry genotype AA or Aa in the control group, respectively.
Expectation of the effect size
Based on the definition of effect size and equation 1, expectation of effect size can be calculated as
| (2) |
We use , and as notations for penetrances of each genotype of the biallelic disease locus in subpopulation c, , and . Suppose individuals of subpopulation c appeared in the local population with frequency pc and . Hence, given disease prevalence pD , the frequencies of individuals who come from subpopulation c and carry different genotypes in case group or control group can be calculated as
| (3) |
or
| (4) |
respectively, where , and are genotype frequencies in the subpopulation c. We assume that all parameters on the right-hand side of equations 3 and 4 are well known. By replacing expectations of genotype frequencies in equation 2 with the frequencies from equations 3 and 4, we can calculate the expected case-control effect size.
Variance of the effect size
Let the vector PD denote the frequencies of individuals who come from different subpopulations and carry different genotypes in the case group,
where . The superscript T denotes the transposition operator on a vector. Suppose N individuals were involved in the case group. Given that the sampling distribution of elements of NPD follows a multinomial distribution when the sample size is large, the variance and covariance of elements of PD can be obtained:
| (5) |
| (6) |
Both pi and pj are elements of vector P.
Using equations 5 and 6, the variance of the frequency of allele A in the case group, , can be calculated:
| (7) |
Similarly, the vector of the frequencies of individuals who come from different subpopulations and carry different genotypes in the control group is
For simplicity, the same sample size (N) is assumed for the control group. Therefore, the variance of the frequency of allele A in the control group, , can be calculated:
| (8) |
Each term of the right-hand side can be obtained from equations 5 and 6 by replacing pi and pj with the elements of frequency vector of control group.
All the elements of vectors PD and Pd were given previously in equations 3 and 4.
Statistical test and power calculation
When frequencies of allele A in each of the case and control groups, and , are independent random variables and are approximated with normal distribution because sample size is large, the asymptotic distribution of effect size follows normal distribution (Lehmann, 1999). We can compose a statistic,
| (9) |
The distribution of this statistic follows a chi-square distribution with one degree of freedom and with a noncentral parameter,
| (10) |
Under the hypothesis that there is no population stratification and no genetic contribution from candidate loci, the distribution of χ2 will follow a central chi-square distribution with one degree of freedom (Abramowitz & Stegun, 1972). We can conduct a statistical test for the null hypothesis by using equation 9.
The statistical test still works even if population stratification exists. Conditioning on the population divergence, the statistic conforms to a noncentral chi-square distribution with a noncentral parameter λ0 under the null hypothesis, where the relative risk (We use RR in text and R in equations to denote relative risk below) of alleles of candidate locus is 1 (Abramowitz & Stegun, 1972; Hoel, 1962). The λ0 can be obtained from equation 10 with aforementioned model and population parameters. Under the alternative hypothesis considering both population divergence and case-control effect size, the statistic conforms to a non-central chi-square distribution with a noncentral parameter λT, The λT is calculated in equation 10 according to the RR and other population parameters (See previous sections and appendix for detail).
We calculated statistical power in two different ways: with or without adjustment for type I error. For the estimate of power without adjustment for type I error, the distribution of the statistic follows a noncentral chi-square distribution with a non-central parameter λT under the alternative hypothesis, whereas the distribution of the statistic follows a central chi-square distribution under the null hypothesis. For the estimate of power with adjustment for type I error, the distribution of the statistic also follows a noncentral chi-square distribution with a non-central parameter λT, under the alternative hypothesis, whereas the distribution of the statistic follows a noncentral chi-square distribution with a noncentral parameter λ0 under the null hypothesis. The degree of freedom of the statistical distributions is the same in the two different ways.
Parameters of the model
All the population parameters on the right-hand side of equations 3 and 4 are necessary for the power study. However, we give frequency and penetrance of each genotype in subpopulations in an indirect way for good comparability with the results in other reports.
Because all the subpopulations are in HWE, we can calculate genotype frequencies from allele frequencies in the subpopulations. To focus on the key aspects of the power issue in an explicit manner, we assume that there are only two subpopulations with the same size in a local area. Given divergence of candidate loci (measured by Fst) and frequency of allele A in the local population, the frequency of allele A in each of the two subpopulations could be calculated as
| (11) |
where pA is the frequency of allele A in the local population. is the allele frequency in subpopulation A, and is the allele frequency in subpopulation B. In equation 11, we specify that the allele frequency in subpopulation A is always higher than that in subpopulation B.
Knowledge of the penetrance of each genotype of disease locus is necessary to calculate frequency of each genotype in the case or control group (Equations 3 and 4). Since RR of a risk allele has appeared more frequently in reports of association studies for complex traits, we follow this common choice in our study also. Given RR of risk allele, penetrance of each genotype of the biallelic locus is calculated under different disease models when disease prevalence and genotype frequencies are known (See appendix for detail). To simplify the model, we assume that RR of risk allele is the same in different subpopulations, RR=RRc1=RRc2. This assumption is similar to that in a fixed effect model for genetic meta-analysis and has been widely used for other purposes.
Disease prevalence differences among different subpopulations introduce sampling bias in sample collection. Individuals who come from subpopulations with higher prevalence will have more chance to be involved in the case group than those who come from ubpopulations with lower prevalence. For simplicity, the term ‘correlation’ is used below to describe the relationship between disease prevalence and allele frequency among subpopulations. In the two-subpopulation model, there is a positive correlation between prevalence and allele frequency when the prevalence of subpopulation A is higher than that of subpopulation B, since the frequency of risk allele A is always higher in subpopulation A than in subpopulation B. Conversely, there is a negative correlation when the prevalence in subpopulation A is lower than that in subpopulation B.
ANALYTIC INVESTIGATION AND SIMULATION
Model with two subpopulations
Given the parameters mentioned above (Fst, allele frequency of local population, RR, model of disease, and disease prevalence), the aforementioned two-subpopulation model offers an opportunity to analytically investigate power difference in different genetic scenarios. Statistical power, type I error rate, and other important variables of the statistical test for case-control effect can be obtained from equations 9 and 10. We use a sample set with 1000 individuals in the case group and the same size in the control group to investigate patterns of power difference in different scenarios. A statistical test with P≤0.05 is considered significant. Results of the analytical investigation are presented in Table 1 and Figures 1, 3, and 4. Calculations were performed in R (The R Project for Statistical Computing, release 2.4.1, www.r-project.org).
Table 1.
Statistical power with different prevalence ratios in a two-subpopulation model without adjustment for type I error
| Allele frequencya | Genetic divergenceb | Power with different ratio of prevalencec | ||||
|---|---|---|---|---|---|---|
| 0.02/0.06 | 0.03/0.05 | 0.04/0.04 | 0.05/0.03 | 0.06/0.02 | ||
| 0.1 | 0 | 0.263 | 0.263 | 0.263 | 0.263 | 0.263 |
| 0.01 | 0.05 | 0.103 | 0.258 | 0.486 | 0.714 | |
| 0.05 | 0.438 | 0.055 | 0.239 | 0.742 | 0.973 | |
| 0.5 | 0 | 0.564 | 0.564 | 0.564 | 0.564 | 0.564 |
| 0.01 | 0.156 | 0.331 | 0.556 | 0.765 | 0.904 | |
| 0.05 | 0.088 | 0.111 | 0.523 | 0.913 | 0.996 | |
| 0.9 | 0 | 0.232 | 0.232 | 0.232 | 0.232 | 0.232 |
| 0.01 | 0.053 | 0.105 | 0.229 | 0.422 | 0.643 | |
| 0.05 | 0.191 | 0.05 | 0.216 | 0.676 | 0.964 | |
RR of the allele is 1.2 in each of the two subpopulations.
Three different divergence levels were given in Fst.
The ratios of prevalence of subpopulations A and B are shown at the head of each data column.
Figure 1.
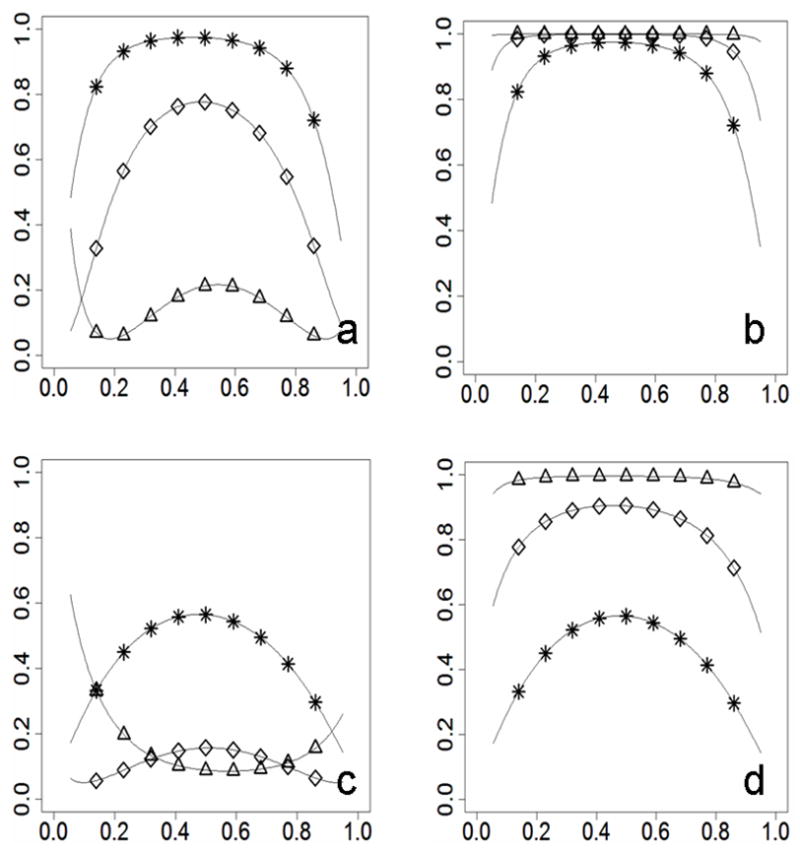
Power differences in two-subpopulation scenarios without adjustment for type I error (statistical power on the y-axis; risk allele frequency on the x-axis). For Figures 1a and 1b, RR=1.4. For Figures 1c and 1d, RR=1.2. Figures 1a and 1c show patterns when the prevalence and the risk allele frequency are correlated negatively between subpopulations (prevalence_A=0.02, prevalence_B=0.06, frequency_A≥frequency_B). Figures 1b and 1d show patterns when the prevalence and the risk allele frequency are correlated positively between subpopulations (prevalence_A=0.06, prevalence_B=0.02, frequency_A≥frequency_B). Curves are marked for different divergence levels (* for Fst=0, ⋄ for Fst=0.01, Δ for Fst=0.05).
Figure 3.

Bias of observed RR on the y-axis; risk allele frequency on the x-axis). For Figures 3a and 3b, RR=1.4. For the Figures 3c and 3d, RR=1.2. Figures 3a and 3c show patterns when the prevalence and the risk allele frequency are correlated negatively between populations (prevalence_A=0.02, prevalence_B=0.06, frequency_A ≥ frequency_B). Figures 3b and 3d show patterns when the prevalence and the risk allele frequency are correlated positively between populations (prevalence_A=0.06, prevalence_B=0.02, frequency_A ≥ frequency_B). Curves are marked for different divergence levels (* for Fst=0, ⋄ for Fst=0.01, Δ for Fst=0.05).
Figure 4.
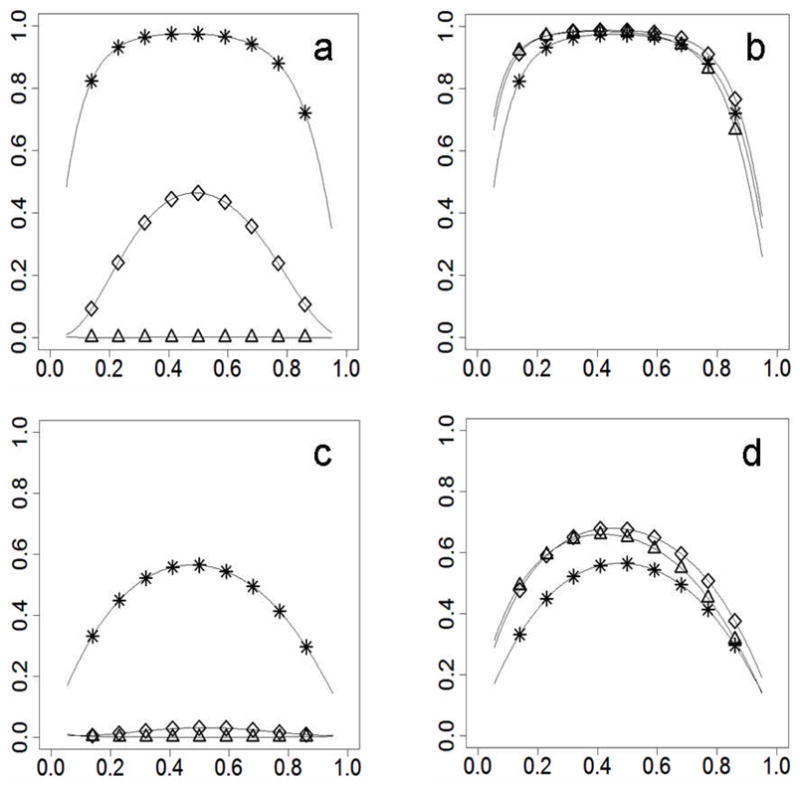
Power differences with adjustment for type I error. Figures 4a and 4c show results when the prevalence and the risk allele frequency are correlated negatively between populations (prevalence_A=0.02, prevalence_B=0.06, frequency_A≥frequency_B). Figures 4b and 4d show results when the prevalence and the risk allele frequency are correlated positively between populations (prevalence_A=0.06, prevalence_B=0.02, frequency_A≥frequency_B). For Figures 4a and 4b, RR=1.4. For Figures 4c and 4d, RR=1.2. Statistical power on the y-axis; risk allele frequency on the x-axis. Curves were marked for different divergence levels (* for Fst=0, ⋄ for Fst=0.01, Δ for Fst=0.05).
Model with multiple subpopulations
Although, only scenarios with two subpopulations were discussed above, our general model still holds when more than two subpopulations exist. We ran a simulation to generalize our findings to scenarios with more than two subpopulations. To achieve parameters for the model with multiple subpopulations, we assume there are five subpopulations of the same size in the local area. We also assume that divergence of the risk allele among the subpopulations is Fst=0.01 and frequencies of the risk allele follow a beta distribution with mean pA and variance pA (1 − pA)Fst . While pA was given, the risk allele frequencies of the five subpopulations were randomly generated in R with the above assumptions. Namely, the generated frequencies kept all the assumptions to be true. Disease prevalence of the five subpopulations was randomly assigned with uniform distribution in range from 0.03 to 0.05. Hence, given RR of the risk allele to be 1.2 for each of the five subpopulations, statistical power was calculated with the same method and sample size as before. A total of 1000 simulations were performed as described above. Statistical power from the simulations is shown in Figure 2 with Pearson’s coefficient of correlation between risk allele frequencies of subpopulations and subpopulations’ disease prevalence.
Figure 2.
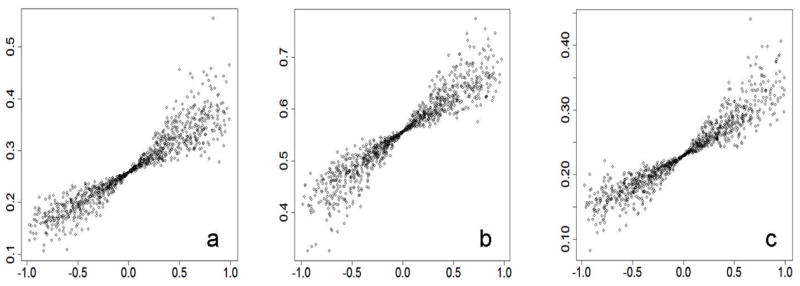
Correlation between prevalence and risk allele frequency contributes to statistical power. The correlation is shown on the x-axis as Pearson’s coefficient, and statistical power is shown on the y-axis without adjustment for type I error. Suppose five subpopulations are of the same size in a local area and the RR of a risk allele is 1.2 in the local population. The Figure 2a shows results for a risk allele with frequency of 0.1 in the local population; the Figure 2b shows results for a risk allele with frequency of 0.5 in local population; the Figure 2c shows results for a risk allele with frequency of 0.9 in the local population.
RESULTS
Property of the model under strong assumptions
Before discussing the pattern of power changes in our model in detail, we explore its basic property in a special scenario with multiple subpopulations. Based on the definition of case-control effect size and the genetic model, we rewrite the effect size in Bayes’ theorem as
| (12) |
We assume subpopulations are with allelic correlation defined by Fst (Wright, 1969) and that allele frequency in subpopulations is an independent and identically distributed random variable, with mean pA and variance pA (1 − pA)Fst . When the sample size is large enough, hence assuming
is a constant, the variance of the effect size can be approximated as
| (13) |
In this equation, the larger genetic divergence leads to the larger variance of expected case-control effect size. Based on equation 9, the value of our statistic will be smaller with the increase of variance when effect size is a constant. Consequently, the statistical test is less powerful when population divergence is larger.
Power differences in scenarios without adjustment for type I error
In many published association studies, no effort was made to control extra spurious associations in statistical tests. In other words, the association studies were conducted in the ‘traditional’ manner without considering population divergence. Here, we show that the correlation between disease prevalence and risk allele frequency among subpopulations plays a critical role in the power differences of the statistical test in the case-control study. In the discussion, “allele frequency” or “frequency of the risk allele” is the frequency of risk allele in a local population if there is no other specific indication.
I. Power differences in scenarios with two subpopulations
Statistical power differed significantly in the aforementioned model with two subpopulations (Figure 1). Similar patterns of power difference were observed in different scenarios with RR=1.2 or RR=1.4, with disease prevalence of 0.02 in subpopulation A and 0.06 in subpopulation B. In those scenarios, statistical power was generally reduced with an increase in genetic divergence (Figure 1a, 1c). The reduction is more than 20% in scenarios with structured populations with moderate genetic divergence (Fst=0.01). Furthermore, population divergence impacts power more for risk alleles with lower RR and lower minor allele frequency (MAF). Due to the striking power loss, there is little probability of discovering a disease locus with weak genetic contribution when genetic divergence is severe. By contrast, while prevalence of disease is 0.06 in subpopulation A and 0.02 in subpopulation B, there is an increase of statistical power with increase of genetic divergence (Fig. 1b, 1d).
It has been shown that the power of a statistical test is reduced with a decrease in MAF of risk loci when no population stratification existed and RR was a constant (Wang et al. 2005). However, the power changes presented a different pattern in our model while the genetic divergence was large (Fst=0.05). The weakest power did not appear with the lowest or the highest risk allele frequency when disease prevalence was 0.02 in subpopulation A and 0.06 in subpopulation B (Figure 1a, 1c). Rather, the weakest power was found where the allele frequency was slightly lower than 0.2 or higher than 0.8 in the scenario with RR=1.4 (Figure 1a). In the scenario with RR=1.2, the weakest power appeared where the risk allele frequency was about 0.6 (Figure 1c). By contrast, when the prevalence was 0.06 in subpopulation A and 0.02 in subpopulation B (Figure 1b, 1d), the pattern of the power decrease with MAF change was similar with that of the previous report (Wang et al. 2005). However, the statistical test is more powerful for samples with large population divergence than those with less divergence in the scenarios (Figure 1b, 1d).
Although the scenarios which were explored in Figure 1 are very limited, the exploration has shown us a crucial result that correlation of disease prevalence and allele frequency among subpopulations is very important for changes in statistical power. To look more into the importance of the correlation, we present results from more scenarios in Table 1. As expected, statistical power generally increases with increasing prevalence ratios of subpopulations A and B in all three risk allele frequencies (0.1, 0.5, and 0.9) and two of three divergence levels (0.01 and 0.05). For ratio smaller than 0.04/0.04, power generally decreases with increases in divergence, and power generally increases with increases of divergence for ratios larger than 0.04/0.04. The correlation between allele frequencies and prevalence of subpopulations changed from ‘negative’ to ‘positive’ as the ratio increases because the allele frequency of subpopulation A is always higher than the frequency of subpopulation B in our model. This observation consolidates our point that the correlation is important for statistical power in divergent populations.
When prevalence is the same in two different subpopulations (Table 1, 0.04/0.04), there is a minor power reduction with increase of population divergence. Based on our model, the expectation of effect size was no difference in these scenarios even though population divergence changed. So the power decrease must be due solely to population divergence. We have given a mechanism for this observation in a previous section with a simplified approach (Equation 13). The current observation shows that our previous conclusion (from Figure 1) can be generalized to more common scenarios. The observation also shows that population divergence is not solely responsible for the power differences in different scenarios, since the power difference is larger when we have both population divergence and prevalence difference at the same time.
II. Power differences in scenarios with multiple subpopulations
To validate our discovery and extend our conclusion to scenarios with more than two subpopulations, we performed a simulation and generated plots to show the relationship of statistical power and Pearson’s coefficient of correlation between disease prevalence and risk allele frequency among subpopulations (Figure 2). Details of the simulation have been described above (model with multiple subpopulations). All three plots for three different risk allele frequencies indicate that there is a tight relationship between statistical power and Pearson’s coefficient. Positive coefficients generally lead to power increases and negative coefficients generally lead to power decreases. Conditioning on our setting for the simulation, the coefficient of determination demonstrates that Pearson’s coefficient (on the x-axis) explains most of the variance of the power change (r2=0.904 for Figure 2a, r2=0.898 for Figure 2b, r2=0.868 for Figure 2c). Another interesting observation from Figure 2 is that the variance of the power changes is smaller when Pearson’s coefficient is closer to zero. The observations emphasize that Pearson’s coefficient is important but is not enough to explain all of the power differences. Value of exact allele frequency and disease prevalence of each subpopulation were necessary for a full explanation.
Biased estimation of relative risk
The aforementioned power increase with increasing genetic divergence (Figures 1b and 1d) must be due to the increase of case-control effect size in stratified samples, since we have shown that the variance of case-control effect size increases with increase of genetic divergence, leading to a reduction in power when case-control effect size is a constant (Equation 13 and Table 1). Penetrance of genotypes is an important component of case-control effect size (Equations 2, 3, and 4). Based on the relationship of population parameters in genetic models (see appendix for details), the case-control effect size changes with change of genetic divergence in our model while other population parameters are fixed. Subsequently, the estimation of the RR from the case-control effect size would be biased if the population stratification were ignored. We estimated the RR of a risk allele, without considering the population divergence, from observed effect sizes in the aforementioned scenarios with two subpopulations (used for Figure 1). The estimated RR varies, especially with larger genetic divergence and allele frequency extremes (Figure 3). Moreover, the results show that a risk allele could be mistaken for a protective one if population substructure were not considered in association analysis (Figures 3a, 3c). Thus, population stratification could be an important cause of ‘flip-flop’ associations, in which, for example, an allele identified as a risk allele in recent report had been identified as a beneficial allele in previous reports. Increasing numbers of ‘flipflop’ associations were reported when recent publications replicated previously reported disease-marker associations (Lin et al. 2007). Even if the “flip-flop” did not happen, the biased RR would weaken the power of meta-analysis for disease loci. Meta-analysis is more important than ever as investigators use meta-analysis to guard against the lack of power in whole-genome association studies.
Power changes with adjustment for type I error
Population stratification increases statistical bias and makes the distribution of a statistic more dispersed, which leads to an increase in type I error (Devlin et al. 2001). Using a fully parameterized model, we can calculate the noncentral parameter of the statistical distribution for our statistic under the null hypothesis that the genetic variant does not contribute to a phenotype trait, even if population stratification exists. A new rejection criterion from the noncentral chi-square distribution can keep type I error rate at p≤0.05 accuracy for the statistical test based on case-control effect size. In other words, commonly used criteria, which come from a central chi-square distribution, were replaced with stricter criteria in our approach. At the same time, the chi-square statistic, which was used before, was kept. Power changes for this approach are shown in Figure 4. To make the results comparable with the previous results, which were without adjustment for type I error (Figure 1), all population parameters are the same as those used in the previous sections.
In the current approach, statistical power is reduced with increased genetic divergence when disease prevalence and allele frequency are negatively correlated (Figures 4a, 4c). The reduction shows a similar pattern but is more serious than that shown in Figures 1a and 1c. The lowest power appears with the lowest or highest allele frequency in the current approach. This pattern is the same as that observed in the scenarios without population stratification, but different from that shown in Figure 1a and 1c.
When the correlation between the allele frequencies of subpopulations and the subpopulations’ prevalence is positive and the RR is high (RR=1.4), the power increase is negligible, even with large genetic divergence (Figure 4b). Although, in the previous approach, the population stratification causes a clear power increase (Figures 1b, 1d). There still is slight power improvement in samples with moderate or large genetic divergence when the RR is low (Figure 4d). But overall statistical power decreases in stratified samples when there is the same probability of a negative or positive correlation, because the power difference is larger when disease prevalence and allele frequencies are negatively correlated.
DISCUSSION
One of the most important motivations for studying the effect of population stratification in association studies is to prompt investigators to pay more attention to population structure and try their best to eliminate potential impacts of population stratification through optimized research designs and sampling strategies. With the same goal, we built our model on structured populations without admixture and presented the power differences in an explicit manner. Those ideas in this study can be generalized to a complex model upon structured population with admixture. However, a complicated model with more population parameters is less helpful to introduce our ideas and will not lead to more important conclusions than that of our study.
The possible difference in statistical power in different genetic models of disease is one of the essential concerns in this study. We calculated the statistical power in dominant, multiplicative, and recessive models separately. Only results based on the multiplicative model were presented in this report, because no obvious difference was observed among the different genetic models when other population parameters were held constant (data not shown). In other words, the pattern of the power differences is model-independent when the sample size is large.
Our study is valuable because it relates to several issues considered important by many investigators. First, genetic contribution from single disease locus is often weak for common disease (Lohmueller et al. 2003). Our investigation identified that population stratification affects statistical power more when a risk allele has lower RR. Second, the prevalence of many complex diseases, such as melanoma and prostate cancer, is evidently different in different populations (Ries et al. 2007). We pointed out that this difference could increase the impact of population stratification. Third, the number of main components in structured populations is often limited, especially for populations in a limited area (Rosenberg et al. 2002). As we showed above (using the two-subpopulation model), the power differences are large for association studies if a population is composed of two genetic components and divergence (measured by Fst) of candidate loci are large (Figures 1a, 1c, 4a, 4c).
Risk allele frequency is one of the essential factors that contribute to prevalence of diseases. A reasonable assumption is that populations with higher disease prevalence have a greater probability of carrying a risk allele with higher frequency. If the assumption is realistic, population stratification would benefit association studies of common disease in some special cases. For example, there is clearly a power increase if disease prevalence and risk allele frequency are positively correlated, even if type I error is controlled well (Figure 4d).
It is assumed in GC theory that allele frequencies are not correlated with the prevalence of complex diseases among ancestral populations (Devlin et al. 2001). However, this assumption may not be realistic. Populations with tighter genetic relations are more likely to share similar living habits and other environmental factors. Given our results above, differences in statistical power will be large for stratified samples when there is a substantial correlation between risk allele frequencies and disease prevalence among subpopulations. Therefore, more attention should be paid to sample divergence in association studies, not only for reducing false positive results but also for acquiring more powerful research designs.
Acknowledgments
Support for work on this paper was provided by NIDA grants DA11170 and DA020830. We gratefully acknowledge Lisa Jack and Denise Nishita for their assistance with manuscript preparation. We also thank two anonymous reviewers for their helpful comments.
Appendix
Suppose all subpopulations are in HWE. We calculate penetrances of genotypes by means of the two equations
| (A.1) |
| (A.2) |
where Rc is RR of risk allele in subpopulation c and fc is prevalence of disease in subpopulation c . pA is the frequency of risk allele A in the subpopulation.
I. Multiplicative model
In multiplicative model, we defined
| (A.1.1) |
Based on the definition of RR, we have
Because
we replace r with Rc and rewrite the equation as
Replacing the values of the r and in equation A.1.1, we get penetrances of all the three genotypes, , and .
II. Dominant model
In the dominant model, we have two different penetrance levels:
RR could be written as
With the equation
penetrances will be
III. Recessive model
Penetrances in the recessive model are
We rewrite RR as
With the equation
we have
References
- Abramowitz M, Stegun IA, editors. Handbook of mathematical functions: with formulas, graphs, and mathematical tables (NBS Applied Mathematics Series 55) Washington, DC: National Bureau of Standards; 1972. [Google Scholar]
- Bacanu SA, Devlin B, Roeder K. The power of genomic control. Am J Hum Genet. 2000;66:1933–1944. doi: 10.1086/302929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bersaglieri T, Sabeti PC, Patterson N, Vanderploeg T, Schaffner SF, et al. Genetic signatures of strong recent positive selection at the lactase gene. Am J Hum Genet. 2004;74:1111–1120. doi: 10.1086/421051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowcock AM, Kidd JR, Mountain JL, Hebert JM, Carotenuto L, et al. Drift, admixture, and selection in human evolution, a study with DNA polymorphisms. Proc Natl Acad Sci USA. 1991;88:839–843. doi: 10.1073/pnas.88.3.839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campbell CD, Ogburn EL, Lunetta KL, Lyon HN, Freedman ML, et al. Demonstrating stratification in a European American population. Nat Genet. 2005;37:868–872. doi: 10.1038/ng1607. [DOI] [PubMed] [Google Scholar]
- Cavalli-Sforza LL, Feldman MW. The application of molecular genetic approaches to the study of human evolution. Nat Genet. 2003;33(Suppl):266–275. doi: 10.1038/ng1113. [DOI] [PubMed] [Google Scholar]
- Clark AG. Finding genes underlying risk of complex disease by linkage disequilibrium mapping. Curr Opin Genet Dev. 2003;13:296–302. doi: 10.1016/s0959-437x(03)00056-x. [DOI] [PubMed] [Google Scholar]
- Collins-Schramm HE, Chima B, Morii T, Wah K, Figueroa Y, et al. Mexican American ancestry-informative markers, examination of population structure and marker characteristics in European Americans, Mexican Americans, Amerindians and Asians. Hum Genet. 2004;114:263–271. doi: 10.1007/s00439-003-1058-6. [DOI] [PubMed] [Google Scholar]
- Collins-Schramm HE, Phillips CM, Operario DJ, Lee JS, Weber JL, et al. Ethnic-difference markers for use in mapping by admixture linkage disequilibrium. Am J Hum Genet. 2002;70:737–750. doi: 10.1086/339368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dahlman I, Eaves IA, Kosoy R, Morrison VA, Heward J, et al. Parameters for reliable results in genetic association studies in common disease. Nat Genet. 2002;30:149–150. doi: 10.1038/ng825. [DOI] [PubMed] [Google Scholar]
- Devlin B, Roeder K. Genomic control for association studies. Biometrics. 1999;55:997–1004. doi: 10.1111/j.0006-341x.1999.00997.x. [DOI] [PubMed] [Google Scholar]
- Devlin B, Roeder K, Wasserman L. Genomic control, a new approach to genetic-based association studies. Theor Popul Biol. 2001;60:155–166. doi: 10.1006/tpbi.2001.1542. [DOI] [PubMed] [Google Scholar]
- Freedman ML, Reich D, Penney KL, McDonald GJ, Mignault AA, et al. Assessing the impact of population stratification on genetic association studies. Nat Genet. 2004;36:388–393. doi: 10.1038/ng1333. [DOI] [PubMed] [Google Scholar]
- Garrigan D, Hammer MF. Reconstructing human origins in the genomic era. Nat Rev Genet. 2006;7:669–680. doi: 10.1038/nrg1941. [DOI] [PubMed] [Google Scholar]
- Gorroochurn P, Heiman GA, Hodge SE, Greenberg DA. Centralizing the non-central chi-square: A new method to correct for population stratification in genetic case-control association studies. Genet Epidemiol. 2006;30:277–289. doi: 10.1002/gepi.20143. [DOI] [PubMed] [Google Scholar]
- Helgason A, Yngvadottir B, Hrafnkelsson B, Gulcher J, Stefansson K. An Icelandic example of the impact of population structure on association studies. Nat Genet. 2005;37:90–95. doi: 10.1038/ng1492. [DOI] [PubMed] [Google Scholar]
- Hirschhorn JN, Daly MJ. Genome-wide association studies for common diseases and complex traits. Nat Rev Genet. 2005;6:95–108. doi: 10.1038/nrg1521. [DOI] [PubMed] [Google Scholar]
- Hoel PG. Introduction to mathematical statistics. New York: John Wiley & Sons, Inc; 1962. [Google Scholar]
- Lander ES, Schork NJ. Genetic dissection of complex traits. Science. 1994;265:2037–2048. doi: 10.1126/science.8091226. [DOI] [PubMed] [Google Scholar]
- Lehmann EL. Elements of large-sample theory. New York: Springer-Verlag Inc; 1999. [Google Scholar]
- Lin DY. Evaluating statistical significance in two-stage genomewide association studies. Am J Hum Genet. 2006;78:505–509. doi: 10.1086/500812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin PI, Vance JM, Pericak-Vance MA, Martin ER. No gene is an island: the flip-flop phenomenon. Am J Hum Genet. 2007;80:531–538. doi: 10.1086/512133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lohmueller KE, Pearce CL, Pike M, Lander ES, Hirschhorn JN. Meta-analysis of genetic association studies supports a contribution of common variants to susceptibility to common disease. Nat Genet. 2003;33:177–182. doi: 10.1038/ng1071. [DOI] [PubMed] [Google Scholar]
- Marchini J, Cardon LR, Phillips MS, Donnelly P. The effects of human population structure on large genetic association studies. Nat Genet. 2004;36:512–517. doi: 10.1038/ng1337. [DOI] [PubMed] [Google Scholar]
- Morton NE. Genetic structure of forensic populations. Proc Natl Acad Sci USA. 1992;89:2556–2560. doi: 10.1073/pnas.89.7.2556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicholson G, Smith AV, Jónsson F, Gústafsson Ó, Stefánsson K, et al. Assessing population differentiation and isolation from single-nucleotide polymorphism data. J R Statist Soc (B) 2002;64:695–715. [Google Scholar]
- Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, et al. Principal components analysis corrects for stratification in genome-wide association studies. Nat Genet. 2006;38:904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
- Pritchard JK, Rosenberg NA. Use of unlinked genetic markers to detect population stratification in association studies. Am J Hum Genet. 1999;65:220–228. doi: 10.1086/302449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard JK, Stephens M, Donnelly P. Inference of population structure using multilocus genotype data. Genetics. 2000a;155:945–959. doi: 10.1093/genetics/155.2.945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard JK, Stephens M, Rosenberg NA, Donnelly P. Association mapping in structured populations. Am J Hum Genet. 2000b;67:170–181. doi: 10.1086/302959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reich DE, Goldstein DB. Detecting association in a case–control study while correcting for population stratification. Genet Epidemiol. 2001;20:4–16. doi: 10.1002/1098-2272(200101)20:1<4::AID-GEPI2>3.0.CO;2-T. [DOI] [PubMed] [Google Scholar]
- Ries LAG, Melbert D, Krapcho M, Mariotto A, Miller BA, et al. SEER cancer statistics review, 1975–2004. Bethesda, MD: National Cancer Institute; 2007. http://seer.cancer.gov/csr/1975_2004/ based on November 2006 SEER data submission, posted to the SEER web site, 2007. [Google Scholar]
- Risch N, Merikangas K. The future of genetic studies of complex human diseases. Science. 1996;273:1516–1517. doi: 10.1126/science.273.5281.1516. [DOI] [PubMed] [Google Scholar]
- Rosenberg NA, Nordborg M. A general population-genetic model for the production by population structure of spurious genotype-phenotype associations in discrete, admixed or spatially distributed populations. Genetics. 2006;173:1665–1678. doi: 10.1534/genetics.105.055335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenberg NA, Pritchard JK, Weber JL, Cann HM, Kidd KK, et al. Genetic structure of human populations. Science. 2002;298:2381–2385. doi: 10.1126/science.1078311. [DOI] [PubMed] [Google Scholar]
- Rosser ZH, Zerjal T, Hurles ME, Adojaan M, Alavantic D, et al. Y-chromosomal diversity in Europe is clinal and influenced primarily by geography, rather than by language. Am J Hum Genet. 2000;67:1526–1543. doi: 10.1086/316890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sabeti PC, Reich DE, Higgins JM, Levine HZ, Richter DJ, et al. Detecting recent positive selection in the human genome from haplotype structure. Nature. 2002;419:832–837. doi: 10.1038/nature01140. [DOI] [PubMed] [Google Scholar]
- Satten GA, Flanders WD, Yang Q. Accounting for unmeasured population substructure in case-control studies of genetic association using a novel latent-class model. Am J Hum Genet. 2001;68:466–477. doi: 10.1086/318195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seielstad MT, Minch E, Cavalli-Sforza LL. Genetic evidence for a higher female migration rate in humans. Nat Genet. 1998;20:278–280. doi: 10.1038/3088. [DOI] [PubMed] [Google Scholar]
- Shi Y, Zhao X, Yu L, Tao R, Tang J, et al. Genetic structure adds power to detect schizophrenia susceptibility at SLIT3 in the Chinese Han population. Genome Res. 2004;14:1345–1349. doi: 10.1101/gr.1758204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storey JD, Tibshirani R. Statistical significance for genomewide studies. Proc Natl Acad Sci USA. 2003;100:9440–9445. doi: 10.1073/pnas.1530509100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang WY, Barratt BJ, Clayton DG, Todd JA. Genome-wide association studies: theoretical and practical concerns. Nat Rev Genet. 2005;6:109–118. doi: 10.1038/nrg1522. [DOI] [PubMed] [Google Scholar]
- Wright S. Evolution and the Genetics of Populations. Chicago: University of Chicago Press; 1969. [Google Scholar]
- Yu J, Pressoir G, Briggs WH, Vroh Bi I, Yamasaki M, et al. A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nat Genet. 2006;38:203–208. doi: 10.1038/ng1702. [DOI] [PubMed] [Google Scholar]


