Exact Trait-Model-Free Tests for Linkage Detection in Pedigrees

Abstract

A number of trait-model-free tests have been proposed for linkage detection between a genomic region and a trait. These tests involve testing the dependence in segregation between a trait and marker alleles by assigning a score to every possible identity-by-descent configuration of the pedigree members without modeling the trait, and then averaging the scores over all such configurations compatible with the observed marker genotypes and genealogical relationship of the pedigree members. In this paper we propose a permutation test as an alternative to the existing exact trait-model-free tests for linkage detection. The proposed test is computationally efficient and is applicable on complex multigeneration pedigree structures. In this paper, we have compared the performance of the permutation test with two other exact trait-model-free tests for linkage detection on simulated datasets. We have demonstrated that the proposed permutation test is fully robust against mispecification of marker allele frequencies and has very good power for linkage detection. The permutation test is implemented in the program lm_ibdtests within the framework of MORGAN 2.8 (http://www.stat.washington.edu/thompson/Genepi/MORGAN/Morgan.shtml).

1 Introduction

Genetic mapping of a trait by linkage analysis involves locating regions of the genome that have influence on the trait. The method includes establishing the dependence in the segregation of alleles at a region and the trait from founders to non-founders in a pedigree. Under no linkage between a trait and the genomic region, there is Mendelian segregation of alleles from founders to non-founders and the amount of sharing of founder alleles among non-founders is a function of their family relationship and has nothing to do with trait values. In presence of linkage, due to the trait-dependent segregation of alleles, non-founders with concordant phenotypes have excess sharing of some founder alleles than expected under no linkage. On the other hand, non-founders with discordant phenotypes have lack of sharing of those founder alleles than expected under no linkage (Feingold, 2001). The sharing of copies of same founder allele mentioned above is referred as identity by descent (ibd) sharing. Linkage analysis approaches establish linkage between a trait and a genomic region by studying the observed ibd sharing among members in a pedigree and compare it with what is expected under the null hypothesis H₀ of no linkage (Shih and Whittemore, 2001).

Several researchers have proposed testing the null hypothesis H₀ of no linkage using statistics based on the ibd sharing among pedigree members affected with the trait (Day and Simons, 1976; Fishman et al., 1978; Suarez and Hodge, 1979; Weeks and Lange, 1988; Whittemore and Halpern, 1994; Kruglyak et al., 1996). These statistics do not require knowledge of the mode of disease inheritance. The general approach is to construct an score to quantify the excess ibd sharing among affected relatives at a genomic region, and then averaging the scores over all such configurations compatible with the observed marker genotypes and genealogical relationship of the pedigree members (Whittemore and Halpern, 1994). A number of tests have been suggested to test for linkage using these ibd-scoring statistics. Kruglyak et al. (1996) suggested a test based on the normality assumption of the test statistic under H₀. Davis et al. (1996) suggested an exact test by resimulating marker data on affected individuals conditional on the marker data of unaffected individuals. Kong and Cox (1997) suggested a likelihood-ratio test. Thompson and Basu (2003) and Thompson and Geyer (2007) have proposed tests which condition on the observed marker genotypes for assessing the significance of an ibd-scoring statistic.

All these approaches do not make any assumption about the genetic model of the trait, such as trait allele frequencies, mode of inheritance. In this paper, they are referred as trait-model-free approaches of linkage analysis. They are robust against trait model misspecification, but all these approaches require to use a marker model such as marker allele frequencies and the genetic map between the markers in order to impute the possible ibd configurations given the observed marker data on the family members. Higher the uncertainty in the marker data about these latent ibd configurations, more is the impact of marker model misspecification on these trait-model-free approaches. The extent of use of the marker model differ among these approaches, hence they suffer up to different extent from marker model mis-specification. It is important to know the extent to which the power and robustness of all these trait-model-free approaches are affected under marker model misspecification.

In this paper we have proposed a new permutation test that conditions on the exchangeable permutation of the observed marker data and hence does not get terribly affected by misspecification of marker allele frequencies. We have also studied the effect of misspecification of marker allele frequencies on the three exact trait-model-free tests for linkage detection including the permutation test. The permutation test has been developed following the method of Churchill and Doerge (1994). Using simulated data, we have compared the performance of our permutation test with two other exact trait-model-free tests. One is based on resimulation (more generalized version of the test proposed by Davis et al. (1996)) and the other based on the fuzzy-p approach of Thompson and Geyer (2007). According to our simulation study, The permutation test was fully robust against misspecification of marker allele frequencies unlike the resimulation based approach and the fuzzy-p approach. The power of our permutation test was much higher than the fuzzy-p approach and was comparable to the resimulation-based approach under the correct marker model.

2 Methods

Consider a location x which is linked to the collected set of markers. We wish to test for linkage between x and a trait using a trait-model-free approach. Since no trait model is specified, trait-model-free tests for linkage detection must condition on the trait data Φ. Suppose ν is an inheritance vector (Lander and Green, 1987) specifying the segregation of alleles at x from founders to the non-founders of a pedigree. Trait-model-free methods are designed to test the null hypothesis H₀ of no linkage between x and the trait Φ. Under H₀, we observe Mendelian segregation at x, that is

$${\mathrm{P}}_0\left[\nu |\mathrm{\Phi }\right]={\left(\frac{1}{2}\right)}^N,$$ (1)

where N is the total number of meioses in a pedigree. Here, the subscript 0 denotes a probability or expectation under the null hypothesis H₀. Hence it is equally likely to observe any one of the inheritance vectors under the null hypothesis H₀.

There is generally missing ibd information on some of the individuals in a pedigree, and the marker data Y do not completely determine ν at x. All three exact tests mentioned above use an ibd measure s(ν,Φ) to score the ibd sharing among individuals for a specific ν. Two of these tests use a test statistic of the form T(Y,Φ) = E₀(s(ν,Φ)|Y), while the fuzzy-p approach uses the conditional distribution of s(ν,Φ) given Y directly. The tests differ in the degree to which they condition on the marker data Y. The resimulation-based test does not condition on Y. The fuzzy-p approach conditions fully on Y. Our proposed permutation test is intermediate, it partially conditions on Y.

For the resimulation-based test, the distribution of T(Y,Φ) under the null hypothesis is found by resimulating marker data on the pedigree, independent of Φ. New marker datasets Y^* are simulated by first assigning founder genotypes under the assumption of Hardy-Weinberg equilibrium at each marker locus and linkage equilibrium between marker loci using the given marker allele frequencies and the marker map. Second, marker genotypes on non-founders are realized by gene-dropping down the pedigree, realizing the recombination events in each meiosis in accordance with the genetic map of the markers. Third, marker genotypes that are unobserved in the actual data Y are discarded. For each simulated Y^*, the statistic

$$\mathrm{T}(Y^{*},\mathrm{\Phi })=E_0(s(\nu ,\mathrm{\Phi })|Y^{*})={\displaystyle \sum _{\nu }s(\nu ,\mathrm{\Phi })\mathrm{P}[\nu |Y^{*}]}$$

is computed or estimated, which provides an estimate of the null distribution of the test statistic T(Y,Φ). The p-value of the observed test statistic T(Y,Φ) is computed as the proportion of T(Y^*,Φ) ≥ T(Y,Φ).

The fuzzy-p approach conditions on both trait data Φ and marker data Y, using s(ν,Φ) as a latent test statistic. If ν were observable, the p-value would be p(ν) = P₀(s(ν^*,Φ) ≥ s(ν,Φ)|Y), where ν^* is an inheritance vector realized under Mendelian segregation. The fuzzy-p distribution is then the conditional distribution of p(ν) given Y. To obtain a test with type-1 error α, we reject H₀ with probability P(p(ν) ≤ α|Y). This test is computationally efficient since it does not require any resimulation of datasets Y^* to estimate the null distribution of the test statistic.

The permutation test proposed here is also a conditional exact test, which conditions on the trait data Φ and partially conditions on the marker data Y. In fact, the permutation test conditions on configurations of the marker data Y on a pedigree that are exchangeable under H₀. The test permutes the marker data of the individuals within each sibship of a pedigree keeping their trait data fixed. In our permutation scheme, we do not permute data of any individual with descendants. This is due to the reason that permutation of marker data of such an individual may produce inconsistent marker data for the decesdants. This permutation scheme can also be viewed as permuting the trait data of individuals without descendants within a sibship keeping their marker data fixed. One can permute the trait data of the individuals following the above scheme and produce a collection of Φ^*s. One can then calculate the ibd measures s(ν,Φ^*)|Y) for all Φ^*s simultaneously for a ν realized from the distribution P[ν|Y]. The resampled Φ^* can then be used to calculate the statistics T(Y,Φ^*) = E₀(s(ν,Φ^*)|Y), which provide an estimate of the null distribution of the test statistic T(Y,Φ) = E₀(s(ν,Φ)|Y). This permutation scheme provides an exact permutation distribution of T(Y,Φ) under the null hypothesis and the p-value is a p-value of an exact permutation test (see Appendix).

The permutation test is implemented in the MORGAN program lm_ibdtests released in MORGAN version 2.8. The current version of the permutation test in MORGAN can only handle binary trait, but it can easily be modified to incorporate continuous trait. The program samples valid permutations of trait data Φ^* by permutating the observed trait data Φ on individuals. For each realized ν from the distribution Pr[ν|Y], the program computes a IBD measure s(ν,Φ^*) along with s(ν,Φ). The observed statistic and the statistics based on permuted dataset are estimated by averaging the ibd measures over the realized ν-values. The program allows choice of several different ibd measures (Basu, 2005). For every marker location, it finally returns a p-value for the observed data, computed under the permutation distribution. This fuzzy-p approach is implemented in the MORGAN program lm_pval released in MORGAN 2.7. The resimulation-based approach mentioned earlier is implemented in the MORGAN program lm_ibdtests, released in MORGAN version 2.8.

3 Results

We studied the performance of all three trait-model-free tests for a binary trait. We assumed that the individuals in each pedigree can have three trait phenotypes: affected, unaffected or unknown. We compared the performance of these three exact tests in terms of power and robustness against marker model misspecification, and computational efficiency. We considered moderate-sized pedigrees for the comparison. We ensured that for each comparison study, the observed test statistic T(Y,Φ) was the same for all three tests. Each test was different in it’s way of estimating the null distribution of the test statistic.

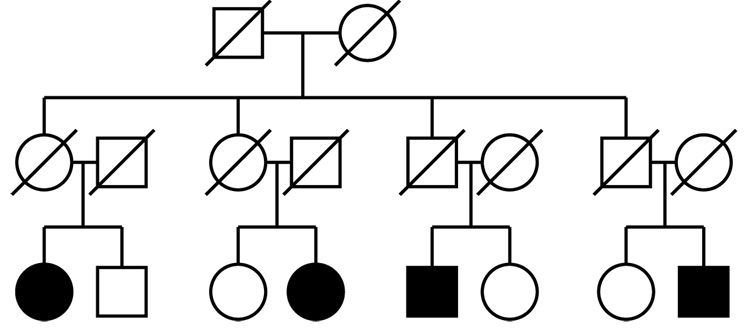
We studied the performance of these three exact tests for linkage detection on 10 pedigrees (Figure 1) each with 18 individuals. There were 6 founders and 12 non-founders in each pedigree with 4 affected and 4 unaffected individuals. This dataset structure permits many permutations. There are 2⁴ = 16 on each pedigree, and hence a potential 16¹⁰ on each dataset. For the trait model, we used trait allele frequencies (.05,.95) and penetrances (.95,.80,.05). We used the ibd measure s_pairs (Whittemore and Halpern, 1994) for our performance study. We assumed marker data (Y) on the grand children only. The marker was assumed to have four alleles with frequencies .4, .3, .2, and .1.

Figure 1.

A pedigree with 18 individuals: each data set of our simulation study consists of 10 such pedigrees. Trait and marker data are available only on the grand-children. The shaded individuals are the affected individuals in the pedigree. Other individuals among the grandchildren are unaffected.

The comparison of type-I error and power among tests was performed by simulating 5000 marker datasets each consisting of 10 pedigrees. Each simulation was done by first simulating an inheritance vector (ν_T) at a trait locus T conditional on the trait data: that is, from P[ν_T|Φ]. Then marker data are simulated conditional on ν_T and the marker allele frequencies given above. The marker data were simulated at a locus x at a recombination fraction 0, .05, .1, .2, and .5 from the trait locus. The program markerdrop in MORGAN (http://www.stat.washington.edu/thompson/Genepi/pangaea.shtml) was used for this conditional simulation of marker data. For clarity, we refer to these data as the real data. For the tests proposed and compared in this paper, we used the MCMC sampler of the MORGAN software (http://www.stat.washington.edu/thompson/Genepi/MORGAN/Morgan.shtml). This sample pairs two block-Gibbs samplers, the locus (l) sampler of Heath (1997) and a meiosis (m) sampler to form the lm-sampler (Thompson, 2000). Note that, since we have only a single marker, we can obtain independent realizations from the conditional distribution of ν given Y. The MCMC lm-sampler of the MORGAN programs reduces, in this case, to independent sampling using the l-sampler of Heath (1997).

The MORGAN programs genedrop and lm_ibdtests were used to perform the resimulation-based test. We used genedrop to simulate 5000 marker data sets Y^* under the null hypothesis using the same allele frequencies that were used to simulate Y. For each resimulated marker data Y^*, we estimated our test statistic T(Y^*,Φ) = E₀[s(ν,Φ)|Y^*] using lm_ibdtests. The p-value of the test statistic was calculated by comparing the proportion of T(Y^*,Φ) ≥ T(Y,Φ). For each real dataset Y, the null hypothesis of no linkage was rejected if the p-value is less than 0.05.

The MORGAN program lm_pval was used to study the performance of the fuzzy-p approach of Thompson and Geyer (2007). For each real dataset Y, we computed the distribution function of the fuzzy-p random variable, using the latent test statistic s_pairs. For each real dataset Y, the null hypothesis of no linkage was rejected with the probability that the fuzzy-p-value was less than 0.05.

The program lm_ibdtests was used to perform the permutation test. For each Y, we sampled 10000 set of affectation statuses Φ^* under our permutation scheme. We decided to sample 10000 Φ^*s under the permutation scheme as opposed to 5000 Y^*s under the resimulation-based approach, since computationally it did not make much difference to sample 10000 Φ^*s compared to 5000 Φ^*s. For each Φ^*, we computed the ibd measure s(ν,Φ^*) using ibd measure s_pairs. The statistic T(Y,Φ^*) = E₀[s(ν,Φ^*)|Y] for each Φ^* was estimated by averaging over the sampled νs. For each real dataset Y, the p-value of the statistic T(Y,Φ) was estimated by $p=\frac{1}{10000}\left[\{j:\mathrm{T}(Y,{\mathrm{\Phi }}^{*j})\ge \mathrm{T}(Y,\mathrm{\Phi }),j=1,\mathrm{\dots },10000\}\right]$. The null hypothesis was rejected if the p-value was less than 0.05.

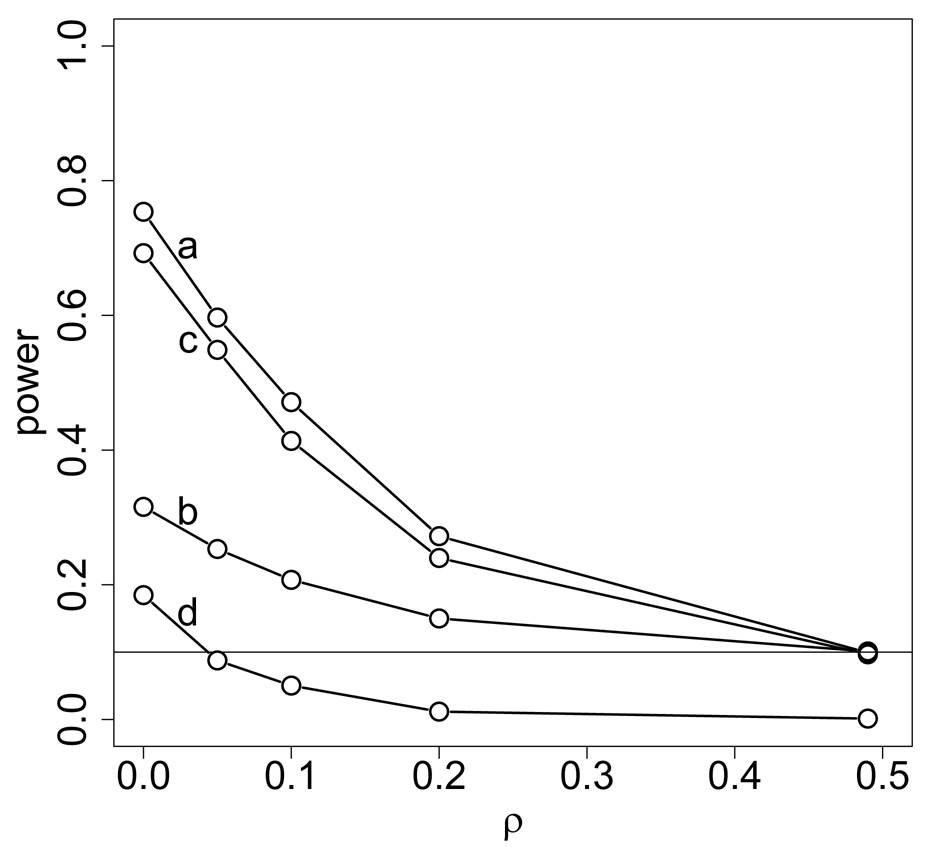
In order to compare the power of these tests, we calculated the proportion of times over the 5000 datasets that the null hypothesis was rejected. This was done for each test at each of the recombination fractions 0, .05, .1, .2, .5 between the marker locus and the trait locus. These power curves are shown in Figure 2. For demonstration purpose, we have also included the power curve under the normality-based test (Kruglyak et al., 1996) using the same datasets, the same test statistic T(Y,Φ) = E₀[s(ν,Φ)|Y] and the same ibd measure s_pairs. As pointed out by many researchers (Kong and Cox, 1997; Kruglyak et al., 1996), the normality-based test was conservative (Figure 2) for using the upper-bound variance σ₀(s(ν,Φ)) in order to standardize the test statistic.

Figure 2.

Power comparison of four linkage detection tests: (a) resimulation-based test, (b) fuzzy p-value test (c) permutation test, and (d) conservative Kruglyak-Lander test.

The resimulation-based approach had maximum power at each of these different recombination fractions under the correct marker model. The fuzzy-p based test had the lowest power among three approaches. This is due, at least in part, to the high uncertainty in the marker-locus ibd in these datasets. On the other hand, the permutation test performed very well on these data and had power close to that of the resimulation-based test under the correct marker model.

All these tests are trait-model-free in the sense that the type-1 error is not dependent on specification of any trait model. The same is not true, however, for the marker model, and marker models may also often have significant uncertainty in either map or allele frequencies. Since we have here only one marker, we studied the robustness of the three exact tests to misspecification of the marker allele frequencies. We repeated the analyses described above twice more for each of the 5000 datasets Y generated at each true recombination fraction 0, .05, .1, .2 and .5. For the first reanalysis we used marker allele frequencies (.25, .25, .25, .25), and for the second we used (.1, .2, .3, .4). Recall the allele frequencies used to generate these datasets are (.4, .3, .2, .1). Thus the first misspecification is a moderate misspecification such as might be encountered in practice. The second is more extreme.

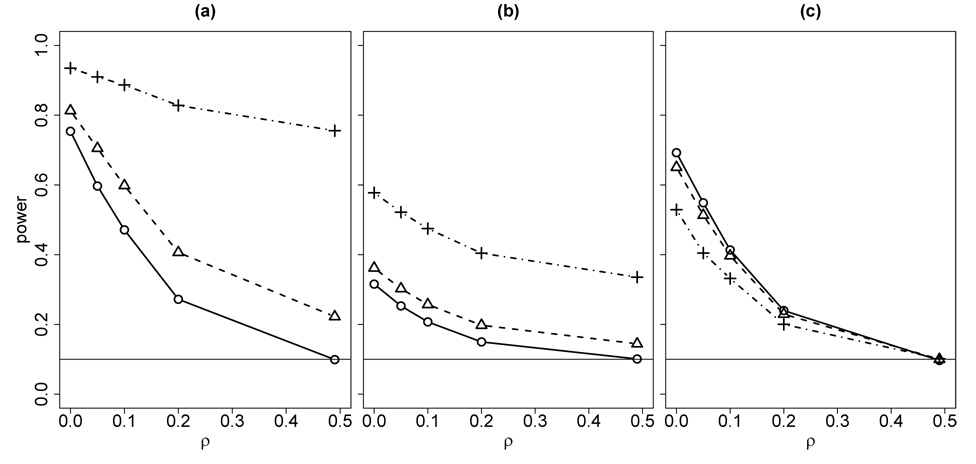
Figure 3 shows the effect on power and type-1 error for all these tests when the marker model is specified incorrectly. The resimulation-based test, which uses the misspecified allele frequencies in the resimulation of data sets Y^*, is very non-robust, and leads to a highly inflated type-1 error, with consequent false-positive conclusions of linkage. The partially conditional resimulation approach of Davis et al. (1996) was designed to give a more robust approach, but this conditional resimulation is not easily implemented on general pedigrees, and the resimulation itself can be computationally intensive. Since it does not use resimulated Y^* the fuzzy-p based test is more robust, but marker alleles frequencies still affect the conditional distribution of the ibd measure given the marker data Y. By contrast, the permutation test is fully robust in terms of type-1 error, and suffers only a small decrease in power due to allele frequency misspecification.

Figure 3.

Power to detect linkage under marker model misspecification for the resimulation-based test (a), fuzzy p-value approach (b) and permutation test (c). The solid line in each graph shows the power to detect linkage at recombination fractions 0,.05, .1,.2,.5 between the marker locus and the trait locus under the correct marker allele frequencies (.4, .3, .2, .1). The dashed line in each graph shows the power at different recombination fractions when the marker allele frequencies were misspecified as (.25,.25,.25,.25). The dotted line shows the power at different recombination fractions when the marker allele frequencies were misspecified as (.1, .2, .3, .4).

4 Discussion

The permutation test is developed to implement trait-model-free methods for linkage detection using small number of pedigrees. In many real studies, trait and marker data are collected on a small number of complex extended pedigrees. The permutation test will have correct type-1 error for linkage detection in such a situation. According to our simulation study, the permutation test was fully robust against marker model misspecification and had very good power for linkage detection under the correct marker model.

Implementation of the resimulation-based approach can be very computationally intensive on extended pedigrees with multiple markers, since each resimulated marker dataset may require to be analyzed using MCMC. Both the fuzzy-p approach and the permutation test require only one run of MCMC using the actual marker data in order to estimate the null distribution of the test statistic. Specifically, we can compare times for a single analysis of a dataset consisting of 10 copies of the 18-member test pedigree (Figure 1), and, as in our simulation study, a single marker. The computations were run on a PC with Dual AMD Opteron 1.8GHz processors running Linux with 4G memory and each analysis used 10,000 realizations of the inheritance vector ν at the marker location given the marker data Y. For the permutation test, 10,000 permutations of affectation status Φ^* were evaluated, while for the resimulation-based test 10,000 marker datasets Y^* were resimulated. Using the fuzzy-p approach the analysis was completed in 22 seconds, whereas the permutation test took 39 seconds. These two tests do the same amount of Monte Carlo realization of inheritance vectors given marker data, but the permutation test takes longer since it must evaluate each of the 10,000 permutations of affectation status for each realization. On the other hand, the resimulation-based test took 210021 (21 × 10000 + 21) seconds to perform the analysis, since the Monte Carlo to realize the ν given Y^* must be done for each of the 10,000 Y^*. Clearly, the fuzzy-p and permutation approaches are far more computationally efficient than the resimulation approach.

Both the resimulation-based approach and fuzzy-p based test are more sensitive to marker model misspecification as compared to the permutation test. The resimulation-based approach requires marker model to resimulate the marker data Y^* to estimate the null distribution of the test statistic. Hence marker model misspecification greatly impacts the type-1 error and the power for the resimulation-based approach. Since it does not require to resimulate Y^* the fuzzy-p based test is more robust, but misspecified marker alleles frequencies still affect the conditional distribution of the latent ibd measure given the marker data Y. By contrast, the permutation test is fully robust to marker model misspecification, since it conditions on the exchangeable configurations of the marker data. As a consequence, the power of the permutation test remains unaffected by the mis-specified marker allele frequencies, whereas both resimulation-based test and the fuzzy-p approach suffer great reduction in power.

The permutation test showed very good power to detect linkage in our simulation studies. Under the correct marker map and allele frequencies, the resimulation based test had the maximum power since it is an unconditional test for linkage. The power for permutation test closely followed the resimulation-based approach under the correct marker model. Since the permutation test partially conditions on the marker data, it has lower power than the resimulation-based approach under the correct marker model. The fuzzy-p approach had substantially lower power than the other tests. This approach conditions fully on the observed marker data and hence suffers greatly from lack of power.

The current version of the permutation test permutes the affectation status of the siblings in a sibship keeping their marker data fixed. In each permutation. it samples a number of individuals from a sibship, which is same as the observed number of affected in the sibship and assign them as affected. Hence the power of the permutation test depends on the lack of ibd sharing between the observed set of affected individuals and the resampled group of individuals within a sibship. A sibship with only affected individuals is thus not informative for this permutation test, since there is no distinct permutation of affectation status in such a sibship. In fact, inclusion of such sibships in the test reduces the difference between the test statistics based on permuted data and the observed test statistic, and hence reduces it’s power to detect linkage. For example, this permutation test cannot be used for a study using affected sib pairs. The main application of this test is where exact tests are preferable such as studies using a limited number of extended pedigrees. In extended pedigrees, generally one collects marker data on both affected and unaffected idividuals. The current version of the permutation test in lm_ibdtests excludes the sibships only with affected individuals and provides a list of pedigrees that are thus ignored by the permutation test. One can implement some other test, preferably an exact test, on those pedigrees. Then the p-value obtained from the permutation test and the p-value obtained from the other test implemented on the set of pedigrees ignored by the permutation test can be combined using Fisher’s combined probability approach (Fisher, 1935).

Appendix

Theorem

Suppose ν_x is an inheritance vector at a marker locus x. Suppose Φ is the observed trait data and Φ^* is a new trait data generated by a permutation π under our permutation scheme. If we denote by C′ the set of all permutations that can be generated under our permutation scheme, then for any Φ^* in C′,

$${\mathrm{P}}_0[(Y,{\mathrm{\Phi }}^{*})]={\mathrm{P}}_0[(Y,\mathrm{\Phi })]$$ (2)

Proof

We assume that marker data Y is observed at a locus x unlinked to the trait. We denote by ν_x and F_x an inheritance vector and a simulated founder marker genotypic configuration at locus x respectively. Let ${\mathrm{G}}_{lj}^{(o)}({\nu }_{\mathrm{x}},{\mathrm{F}}_{\mathrm{x}})\text{and}{\mathrm{G}}_l^{(P)}({\nu }_{\mathrm{x}},{\mathrm{F}}_{\mathrm{x}})$ denote the genotypes of the j-th offspring (j=1,…,k_l) and the genotypes of the parents in the l-th sibship of a pedigree respectively (l = 1, …, p) for a specific ν_x and F_x. Note that, a parent can be a founder too. In that case ${\mathrm{G}}_l^{(P)}({\nu }_{\mathrm{x}},{\mathrm{F}}_{\mathrm{x}})$ is simply the genotype of that founder corresponding to the realized F_x. Also, the marker data Y may not be consistent with all realized F_x and ν_x. Let us assume that we are only considering the (F_x, ν_x) that are consistent with the observed Y. In other words, for every pair of (F_x, ν_x)

$$\mathrm{P}\left[Y|{\mathrm{F}}_{\mathrm{x}},{\nu }_{\mathrm{x}}\right]=1.$$

Let the permutation π^* switches the genotypes ${\mathrm{G}}_{lj}^{(o)}({\nu }_{\mathrm{x}},{\mathrm{F}}_{\mathrm{x}})\mathrm{s}(j=1,\mathrm{\dots },k_l)$ at loci x between individuals in l-th sibship (l = 1, …, p) whose trait data are permuted by a permutation π. In our permutation scheme, we only permute the trait data of individuals within a sibship of a pedigree. Note that given the marker model, for the j-th offspring in the l-th sibship in a pedigree.

$$\begin{array}{ccc}\mathrm{P}[{\mathrm{G}}_{lj}^{(o)}({\nu }_{\mathrm{x}},{\mathrm{F}}_{\mathrm{x}}),{\mathrm{\Phi }}_{lj}^{*}|{\mathrm{G}}_l^{(P)}({\nu }_{\mathrm{x}},{\mathrm{F}}_{\mathrm{x}}),{\mathrm{\Phi }}_l^{*(P)}]\hfill & =\hfill & \mathrm{P}[{\pi }^{*}({\mathrm{G}}_{lj}^{(o)}({\nu }_{\mathrm{x}},{\mathrm{F}}_{\mathrm{x}})),{\mathrm{\Phi }}_{lj}|{\mathrm{G}}_l^{(P)}({\nu }_{\mathrm{x}},{\mathrm{F}}_{\mathrm{x}}),{\mathrm{\Phi }}_l^{*(P)}]\hfill \\ \hfill & =\hfill & \mathrm{P}[{\pi }^{*}({\mathrm{G}}_{lj}^{(o)}({\nu }_{\mathrm{x}},{\mathrm{F}}_{\mathrm{x}})),{\mathrm{\Phi }}_{lj}|{\mathrm{G}}_l^{(P)}({\nu }_{\mathrm{x}},{\mathrm{F}}_{\mathrm{x}}),{\mathrm{\Phi }}_l^{(P)}],\hfill \end{array}$$ (3)

because essentially the dataset $({\mathrm{G}}_{lj}^{(o)}({\nu }_{\mathrm{x}},{\mathrm{F}}_{\mathrm{x}}),{\mathrm{\Phi }}_{lj}^{*})\text{and}({\pi }^{*}({\mathrm{G}}_{lj}^{(o)}({\nu }_{\mathrm{x}},{\mathrm{F}}_{\mathrm{x}})),{\mathrm{\Phi }}_{lj})$ are the same on j th individual in l th sibship. Also, in our permutation scheme, we do not permute the trait data of the individuals with descendants. Hence ${\mathrm{\Phi }}_l^{(P)}\text{and}{\mathrm{\Phi }}_l^{*(P)}$ is the same trait data. Moreover,

$${\mathrm{P}}_0[{\pi }^{*}({\mathrm{G}}_{lj}^{(o)}({\nu }_{\mathrm{x}},{\mathrm{F}}_{\mathrm{x}})),{\mathrm{\Phi }}_{lj}|{\mathrm{G}}_l^{(P)}({\nu }_{\mathrm{x}},{\mathrm{F}}_{\mathrm{x}}),{\mathrm{\Phi }}_l^{(P)}]={\mathrm{P}}_0[{\mathrm{G}}_{lj}^{(o)}({\nu }_{\mathrm{x}},{\mathrm{F}}_{\mathrm{x}})),{\mathrm{\Phi }}_{lj}|{\mathrm{G}}_l^{(P)}({\nu }_{\mathrm{x}},{\mathrm{F}}_{\mathrm{x}}),{\mathrm{\Phi }}_l^{(P)}],$$ (4)

under the null hypothesis of no linkage between trait and location x.

Therefore, for any Φ^* in the set C′

$$\begin{array}{ccc}{\mathrm{P}}_0[Y,{\mathrm{\Phi }}^{*}]\hfill & =\hfill & {\displaystyle \sum _{{\mathrm{F}}_{\mathrm{x}},{\nu }_{\mathrm{x}}}\left[{\mathrm{P}}_0[{\mathrm{F}}_{\mathrm{x}},{\nu }_{\mathrm{x}},Y,{\mathrm{\Phi }}^{*}]\right]}\hfill \\ \hfill & =\hfill & {\displaystyle \sum _{{\mathrm{F}}_{\mathrm{x}},{\nu }_{\mathrm{x}}}\left[{\displaystyle \prod _{l=1}^p{\mathrm{P}}_0[{\mathrm{G}}_l^{(P)}({\nu }_{\mathrm{x}},{\mathrm{F}}_{\mathrm{x}}),{\mathrm{\Phi }}_l^{*(P)}]\left({\displaystyle \prod _{j=1}^{k_l}{\mathrm{P}}_0[{\mathrm{G}}_{lj}^{(o)}({\nu }_{\mathrm{x}},{\mathrm{F}}_{\mathrm{x}}),{\mathrm{\Phi }}_{lj}^{*}|{\mathrm{G}}_l^{(P)}({\nu }_{\mathrm{x}},{\mathrm{F}}_{\mathrm{x}}),{\mathrm{\Phi }}_l^{*(P)}]}\right)}\right]}\hfill \\ \hfill & =\hfill & {\displaystyle \sum _{{\mathrm{F}}_{\mathrm{x}},{\nu }_{\mathrm{x}}}\left[{\displaystyle \prod _{l=1}^p{\mathrm{P}}_0[{\mathrm{G}}_l^{(P)}({\nu }_{\mathrm{x}},{\mathrm{F}}_{\mathrm{x}}),{\mathrm{\Phi }}_l^{*(P)}]\left({\displaystyle \prod _{j=1}^{k_l}{\mathrm{P}}_0[{\pi }^{*}({\mathrm{G}}_{lj}^{(o)}({\nu }_{\mathrm{x}},{\mathrm{F}}_{\mathrm{x}})),{\mathrm{\Phi }}_{lj}|{\mathrm{G}}_l^{(P)}({\nu }_{\mathrm{x}},{\mathrm{F}}_{\mathrm{x}}),{\mathrm{\Phi }}_l^{*(P)}]}\right)}\right]}\hfill \\ \hfill & \hfill & \hfill (\text{from equation}3)\hfill \\ \hfill & =\hfill & {\displaystyle \sum _{{\mathrm{F}}_{\mathrm{x}},{\nu }_{\mathrm{x}}}\left[{\displaystyle \prod _{l=1}^p{\mathrm{P}}_0[{\mathrm{G}}_l^{(P)}({\nu }_{\mathrm{x}},{\mathrm{F}}_{\mathrm{x}}),{\mathrm{\Phi }}_l^{(P)}]\left({\displaystyle \prod _{j=1}^{k_l}{\mathrm{P}}_0[{\pi }^{*}({\mathrm{G}}_{lj}^{(o)}({\nu }_{\mathrm{x}},{\mathrm{F}}_{\mathrm{x}})),{\mathrm{\Phi }}_{lj}|{\mathrm{G}}_l^{(P)}({\nu }_{\mathrm{x}},{\mathrm{F}}_{\mathrm{x}}),{\mathrm{\Phi }}_l^{(P)}]}\right)}\right]}\hfill \\ \hfill & \hfill & \hfill (\text{from equation}3)\hfill \\ \hfill & =\hfill & {\displaystyle \sum _{{\mathrm{F}}_{\mathrm{x}},{\nu }_{\mathrm{x}}}\left[{\displaystyle \prod _{l=1}^p{\mathrm{P}}_0[{\mathrm{G}}_l^{(P)}({\nu }_{\mathrm{x}},{\mathrm{F}}_{\mathrm{x}}),{\mathrm{\Phi }}_l^{(P)}]\left({\displaystyle \prod _{j=1}^{k_l}{\mathrm{P}}_0[{\mathrm{G}}_{lj}^{(o)}({\nu }_{\mathrm{x}},{\mathrm{F}}_{\mathrm{x}}),{\mathrm{\Phi }}_{lj}|{\mathrm{G}}_l^{(P)}({\nu }_{\mathrm{x}},{\mathrm{F}}_{\mathrm{x}}),{\mathrm{\Phi }}_l^{(P)}]}\right)}\right]}\hfill \\ \hfill & \hfill & \hfill (\text{from equation}4)\hfill \\ \hfill & =\hfill & {\mathrm{P}}_0[Y,\mathrm{\Phi }].\hfill \end{array}$$

which completes the proof of the theorem.