Abstract
We report substantial improvements to the previously introduced automated NOE assignment and structure determination protocol known as PASD. The improved protocol includes extensive analysis of input spectral data to create a low-resolution contact map of residues expected to be close in space. This map is used to obtain reasonable initial guesses of NOE assignment likelihoods which are refined during subsequent structure calculations. Information in the contact map about which residues are predicted to not be close in space is applied via conservative repulsive distance restraints which are used in early phases of the structure calculations. In comparison with the previous protocol, the new protocol requires significantly less computation time. We show results of running the new PASD protocol on six proteins and demonstrate that useful assignment and structural information is extracted on proteins of more than 220 residues. We show that useful assignment information can be obtained even in the case in which a unique structure cannot be determined.
Keywords: automated structure determination, automated NOE assignment, Xplor-NIH
1 Introduction
The most labor intensive non-experimental aspect of NMR structure determination has traditionally been the NOE assignment process, where peaks in multidimensional NOE spectra are matched to assigned protons so that useful distance restraint information can be extracted. Automated methods for assigning NOE spectra data have recently become widely available and are now in common use (Güntert, 2003). The approaches available (Nilges et al., 1997; Herrmann et al., 2002a; Kuszewski et al., 2004; Huang et al., 2006) have widely varying convergence properties and tolerances for bad data.
In previous work (Kuszewski et al., 2004), we introduced a powerful NOE assignment protocol known as PASD (for Probabilistic Assignment Algorithm for Structure Determination) in which likelihoods are determined for each potential assignment of each NOE peak in a probabilistic fashion. Key features of the original structure calculation protocol included allowing multiple assignments to be active for each NOE peak and using a soft energy term linear in assignment violation during early stages of refinement. We found the resultant protocol to be highly tolerant of bad NOE data.
This current paper presents significant improvements over our previous work in that more information is extracted from NOE spectra. These data are now subjected to an initial processing phase based on the network of all possible assignments of the observed peaks to assign initial assignment likelihoods before structure calculations commence in an approach similar to that of other work (Herrmann et al., 2002a; Huang et al., 2006). In this work this network analysis is used in such a way that most bad assignments are assigned low initial likelihood. The new preprocessing procedure allows us to reduce the number of structure calculation passes from 3 in the previous protocol to 2, with a concomitant reduction in computation time.
Glossary of Terms and Symbols.
active assignment An NOE assignment which contributes to the linear (Pass 1) or quadratic (Pass 2) restraint terms. Whether an assignment is active or inactive is determined from its assignment likelihoods via the procedure described in Section 2.2.5.
active peak An NOE peak with one or more active assignments.
assignment likelihood λ(i, j) The probability of the correctness of assignment j of peak i. λp is the previous likelihood of an assignment based on previously obtained information; in Pass 1 λp is denoted and is based on the network contact map, while in Pass 2 previous likelihoods are based on distance violations of the structures calculated in Pass 1. The violation likelihood λv is the probability of correctness of an assignment based on distance violations in the current structure. The overall peak assignment likelihood λo is a weighted average of previous and violation likelihoods. The assignment likelihood λa is used to determine which single assignment to use for a given peak during Pass 2.
broad tolerance ΔB The size of chemical shift bins used in the initial assignment procedure. [Section 2.1.2]
calibration peak NOE peaks corresponding to intraresidue or backbone sequential connectivities, used for stripe correction and network analysis. [Section 2.1.2]
characteristic violation distance Δ rc Distance used in determining assignment likelihood λv. Smaller values reduce the likelihood of assignments with large violations. [Eq. 13]
linear NOE potential Elin Energy term used in Pass 1 which is linear in NOE violation. [Eq. 6]
network score R(a,b) The residue pair score between residues a and b, based on connectivities deduced from the initial collection of possible NOE assignments. R’(a,b) is the normalized score used for assigning initial likelihoods; associated assignments are specified as active for R’ > Rc. Larger R’ corresponds to a larger number of connections. [Eqs. 1 and 2]
peak assignment A specific NOE peak assignment relating a single peak to a pair of assigned chemical shifts.
previous likelihood weight wp Weight determining the contribution of λp and λv to λo. [Eq. 14]
quadratic NOE potential Equad Energy term used in Pass 2 which is quadratic in NOE violation. [Eq. 10]
repulsive distance potential Erepul Energy term used in Pass 1 which repels atoms associated with shift assignments which are inactive. [Eq. 11]
stripe coverage C The fraction of calibration peaks consistent with a particular chemical shift assignment. [Section 2.1.2]
symmetry partners Two NOE peaks with from- and to- assignments reversed.
tight tolerance ΔT The size of chemical shift bins used during peak assignment after the stripe correction procedure. [Section 2.1.2]
The first pass of the current protocol also now employs conservative repulsive distance restraints encapsulating more information gleaned from the network analysis. Several groups (de Vlieg et al., 1986; Summers et al., 1990; Brüschweiler et al., 1991; Wilcox et al., 1993; Grishaev and Llinás, 2002) have previously demonstrated structure calculations in which the absence of an apparent NOE cross peak between two protons is translated into a structural restraint, forcing the two protons to maintain a certain minimum distance. In most of these cases the number of such restraints is quite large, typically 2-5 times the number of ordinary NOE distance restraints. Due to the fact that a large fraction of the expected NOE cross peaks are generally not observed for one reason or another, there is the danger that the inferred large number of spurious repulsive interactions will result in significantly distorted structures. For this reason, in our protocol the repulsive restraints are enabled only during the first structure calculation pass and entirely disabled during the second pass. As in our previous work (Kuszewski et al., 2004) only assignment information is passed from the first to the second pass of structure calculation: structural information is not passed.
With the advent of successful and useful structure determination methods based on combining chemical shift data with molecular modelling (CSMM) (Cavalli et al., 2007; Shen et al., 2008), one might wonder whether approaches to solving the NOE assignment problem or even NOE experiments themselves are outmoded and no longer necessary. First, it should be noted that CSMM methods are limited to proteins of about 130 residues or less so that other approaches are required for larger proteins. Furthermore, CSMM approaches depend critically on the chemical shift database of known motifs and on the ability of the torsion angle molecular modelling to handle a particular system. In structure determination this database and model replace the direct experimental 3D structural information present in NOEs. While often successful, CSMM methods are known to fail for some proteins, and there is no a priori reason to think that the failure will be detectable. So, while we encourage the use of CSMM methods, we believe that NOE-based determination or at least validation of protein structures will continue to be necessary for the foreseeable future.
In the next section we completely describe the current PASD protocol, including the initial matching of NOE peaks to possible atomic targets, the generation of a residue contact map based on the initial NOE assignments, and the two passes of structure determination. We then go on to show the successful use of this protocol on six proteins and describe how useful assignment information can be generated using this protocol even if a unique structure cannot be determined. Finally, we introduce a maximum likelihood algorithm to identify multiple well-determined subregions of structures which do not have high overall similarity.
2 Methodology
Our present work uses three fundamental concepts: shift assignments, peaks, and peak assignments. A shift assignment corresponds to an entry (or entries) in the chemical shift tables associated with the shift assignments for the relevant proton(s) and, depending upon the experiment type, the directly-bonded heavy atom. A shift assignment’s protons typically include a group of magnetically equivalent protons (e.g. a methyl group’s protons, or a pair of aromatic protons in fast exchange), but can be expanded automatically to cover all atoms in a stereopair. In order to facilitate analysis of symmetry and NOE completeness, a shift assignment is associated with only one of the two proton axes in an NOE spectrum: either the from- or to- axis. If a given atom can appear on both axes in a particular NOE spectrum, a second shift assignment is used, and the two shift assignments are called to-from symmetry partners. A peak corresponds to an entry in an NOE peak location table. Associated with the peak are its position (in ppm) along each spectral dimension, its intensity, and the approximate distance bounds generated from that intensity. A peak assignment represents a possible pairing of a peak with two shift assignments (one from-, and one to- assignment). Associated with each peak assignment is a value of the likelihood that it is the correct assignment. This likelihood is generated either by analysis of preliminarily-assigned spectral and primary sequence information, or by analysis of calculated three dimensional structures. An overview of the complete PASD algorithm is given in Figure 1.
Fig. 1.

Schematic overview of the current PASD protocol.
If more than one NOE spectrum is available (e.g. 3D 13C and 3D 15N separated NOE spectra), entirely separate sets of shift assignments, peaks and related peak assignments are created. Some processing steps are applied to each spectrum independently, but most steps are performed with the data from all the available spectra simultaneously, as discussed below.
2.1 Spectral data processing
A structure calculation with PASD begins by running scripts that import chemical shift and peak location data. A table of assigned chemical shifts is read and used to create a set of shift assignments appropriate to the NOE experiment at hand. A table of peak locations and intensities from that NOE experiment is read and used to create a set of peaks. Once the data are imported, the spectrum’s peaks and shift assignments are matched to each other with a very broad tolerance, to allow for relatively large differences in chemical shift between the assigned values in the chemical shift table and the peak positions in the spectrum. The chemical shift values in the shift assignments are then corrected to match the actual peak positions in each NOE spectrum. The existing peak assignments are removed, and the peaks are re-matched to these corrected shift assignments, using a tighter tolerance. If there are multiple NOE spectra available for a system, this process is repeated for each spectrum independently. The resulting sets of peak assignments are then subjected to an NOE connectivity network analysis. Peak assignments which are inconsistent with this analysis are given values of zero for their previous likelihood, but are not removed from later consideration. Information from the network analysis is also used during the first structure calculation pass to define repulsive atomic interactions.
2.1.1 Matching Shift Assignments to Peaks
At the beginning of a structure calculation, shift assignments are created by reading a chemical shift table, and peaks are created by reading a peak location table. Shift assignments can be created from chemical shift tables in PIPP (Garrett et al., 1991), nmrPipe (Delaglio et al., 1995), and NMR-STAR (BMRB, 2004) formats. Peaks can be created from peak location tables in PIPP, nmrPipe, and XEASY (Bartels et al., 1995) formats. All stereoassignments in the shift table are, by default, expanded to cover both members of a stereopair. Where appropriate, specific stereoassignments can be respecified later during a subsequent refinement calculation. Peaks and shift assignments are then correlated with each other, and corresponding peak assignments are created, in the following way. A peak is said to match from- and to- shift assignments if both chemical shift positions along both spectral axes (un-aliased, if necessary) match the chemical shift values of the shift assignments within a given tolerance, and if the peak’s observed sign matches that expected (Clore and Gronenborn, 1991a) along each dimension. If the peak’s position and sign match those of the shift assignments, a new peak assignment is created, linking that peak to the pair of shift assignments. The unaliased chemical shift position of the peak along each spectral dimension is used in the shift assignment stripe correction method described below.
Distance bounds are estimated from peak intensity using a simple protocol (Clore and Gronenborn, 1989; Clore and Gronenborn, 1991a; Clore and Gronenborn, 1991b) in which the peaks are binned into four classes based on their intensity: 0-20% (very weak), 20-50% (weak), 50-80% (medium) and 80-100% (strong), with associated distance ranges of 1.8-6.0 Å, 1.8-5.0 Å, 1.8-3.3 Å, and 1.8-2.7 Å, respectively. 0.5 Å is added to the upper bound of distances involving methyl groups in order to correct for the larger than expected intensity of methyl crosspeaks (Clore et al., 1987). These distance bounds are used throughout the calculation.
2.1.2 Shift assignment stripe correction
Sample conditions used during NOE data collection are often slightly different from those during collection of through-bond correlation spectra used for making chemical shift assignments such that the chemical shift values can vary (after systematic changes are accounted for) and some sort of correction to chemical shift values is desirable. Our correction consists of consistently replacing chemical shift values with those corresponding to NOE peaks. Since different sample conditions are also often seen between different NOE spectra (either due to different solvent conditions, or simply because of sample aging), we apply this correction to each spectrum independently.
In our present work the identity of the correct chemical shift value is determined by employing preliminary calibration peak assignments corresponding to intraresidue and backbone-sequential connectivities. Peaks corresponding to intraresidue connectivities are typically used to provide an internal chemical shift reference in manual NOE assignment (Garrett et al., 1991), largely because intraresidue connectivities correspond to short, often invariable, distances, so they are almost always observed. Likewise, peaks corresponding to backbone-sequential connectivities (i.e., crosspeaks between HN, Hα or Hβ atoms of residue i and the HN, Hα or Hβ atoms of residues i ± 1) are observed nearly as often as intraresidue crosspeaks (Billeter et al., 1982), and thus also offer useful chemical shift references (Huang et al., 2006).
Initially, the peaks of a given spectrum are matched to shift assignments using a very broad tolerance ΔB (0.075 ppm for 1H dimensions and 0.75 ppm for heavy atom dimensions), so that a relatively large chemical shift mismatch can be accommodated. All of these calibration peak assignments for each shift assignment are gathered up and considered candidate chemical shift targets. Because of the broad shift tolerances used, the candidate chemical shift targets can overlap with multiple calibration peaks, and most of the candidate shift targets are internally inconsistent. We therefore seek to extract from the list of candidate chemical shift targets a subset that is self-consistent and which covers the largest number of calibration NOE peaks.
A tight tolerance ΔT (0.02 ppm for proton dimensions, and 0.2 ppm for heavy atom dimensions) is used in determination of the shift assignment consistency. A set of candidate chemical shift targets is determined to be self-consistent if the following criteria are met: (1) the chemical shift values of the calibration peaks assigned to shift assignments in the to- and from- dimensions must agree to within ΔT in both proton dimensions; (2) the chemical shift targets of to-from-symmetry partners (if observed) must match within ΔT; (3) the heavy atom shift values of geminal partners (those which select the same heavy atom but different protons) must match within ΔT; and (4) the proton chemical shift targets of stereo partners must disagree by more than ΔT. If no consistent candidate assignment can be made for a chemical shift assignment, the corresponding chemical shift value is not corrected, but rather used as-is in the tight-tolerance matching of NOE peaks described below.
After filtering out inconsistent chemical shift targets, the remaining shift assignments are assigned chemical shift targets based on C, the stripe coverage of each assignment, which is calculated as the fraction of calibration peaks consistent with the shift assignment. The stripe coverage is corrected such that a single count is given to multiple peaks whose assignment involves the same pair of shift assignments. The following Monte Carlo procedure is used: (1) all shift assignments are randomly assigned chemical shift targets from the available candidates and CT, the sum of all stripe coverages for the spectrum is computed; (2) each shift assignment is revisited and a new candidate is chosen if a random number between zero and one is less than exp[-(C/0.1)2], where C is the stripe coverage of that new candidate; (3) the new set of candidates is accepted if a random number between zero and one is less than exp[-(ΔCT/0.005)2], where ΔCT is the difference between the current and previous stripe coverage sums; and (4) steps 2 and 3 are repeated 5 times.
After correcting each shift assignment’s chemical shift value(s) to the NOE calibration peaks, all peaks and shift assignments are re-matched using the tight tolerance value ΔT. Previous peak assignments made via the broad-tolerance matching are thereafter ignored. The procedure allows a maximum drift of ΔB in chemical shift value between the assignment and NOE spectra, while the correction procedure typically reduces the number of peak assignments per peak by about 70%, relative to the initial broad-tolerance matching, without significantly reducing the amount of good long-range NOE data.
2.1.3 Initial Likelihoods: Network Analysis Contact Map
The set of peak assignments generated by the tight-tolerance match still contain a preponderance of bad data: typically between 75-95% of the long range peak assignments are inconsistent with the true structure. In our previous work (Kuszewski et al., 2004), we began structure calculations using this very large set with initial peak assignment likelihoods all set to one. In order to improve robustness and decrease computational effort we have implemented network connectivity analysis to obtain a better estimate of initial peak assignment likelihoods. The approach is based on the observation that a good peak assignment (i.e. one which is not violated in the true structure) is generally well-supported by other peak assignments connecting other protons in the same pair of residues. In contrast, bad peak assignments (i.e. ones which are violated in the true structure) generally have few supporting peak assignments. Therefore, if there are a relatively large number of peak assignments connecting a particular pair of residues, then that pair of residues is judged to be in contact in the true structure, and peak assignments between them are flagged as likely to be correct. If there are a small number of peak assignments connecting a particular pair of residues, then that pair of residues is judged to not be in contact in the true structure, and peak assignments between them are flagged as unlikely to be correct. Previous automated NMR structure determination approaches (Herrmann et al., 2002a; Herrmann et al., 2002b; Huang et al., 2006) have used this sort of network connectivity analysis to cull peak assignments. Like previous approaches, our network analysis algorithm results in a low-resolution, residue-by-residue contact map of the structure. However, we do not use the contact map to permanently remove peak assignments from consideration, but rather to assign initial likelihoods to each assignment. Peaks which are assigned a zero likelihood based on network analysis can and are reactivated during the structure calculation passes. Additionally, the network-derived contact map is utilized in a novel fashion during the first pass of structure calculations to define repulsive interactions between protons in residues which are not in contact.
The contact map is based on a network residue pair score R(a,b) which counts the weighted connections between residues a and b arising from initial peak assignments for each spectrum:
| (1) |
where m and n range over all from- and to- shift assignments in residues a and b for spectrum s; NR(a,b) is the total number of possible to-from and from-to shift assignment pairs for this pair of residues in all spectra; and σ(m,n;s) is the weight given to the connection associated with the shift assignment pair m,n in spectrum s as defined in Eqs. 5 and 4.
Due to differences in the NOE completeness, R(a,a) varies considerably from residue to residue (supplemental Figure 1). Thus, more uniform results are obtained if this raw score value is normalized by its intraresidue values:
| (2) |
where
| (3) |
The cutoff value Rmin = 0.2 prevents residues with very low intraresidue scores from contributing disproportionally to R’(a,b).
The shift assignment connection weights σ(m,n;s) are initialized based on N(m,n), the number of peak assignments of the peak associated with the pair m,n:
| (4) |
where N*(m,n) is the number of peak assignments which are calibration peak assignments (Section 2.1.2). This choice reflects the ordinary assumption (Garrett et al., 1991) that calibration peak assignments are nearly always the correct assignment for a peak and if there is no calibration peak assignment, initial shift assignment pair weights are evenly distributed over all initial peak assignments.
R’(a,b) is then computed and the values of the connection weights are updated via:
| (5) |
where here a and b are the residues connected by the shift assignments m and n and the sum is over all residue pairs c,d which have peak assignments for the peak associated with shift assignment pair m,n. If the pair m,n is associated with more than one peak, then the largest value of σ(m,n;s) is used. σ(m,n;s) is set to zero if there is no peak corresponding to shift assignment m,n. The values of R’(a,b) are then re-evaluated using the updated values of σ(m,n;s), and the process repeated until the values converge. We found that five iterations is sufficient to achieve convergence.
After network residue pairs scores have been calculated, residues a and b are determined to be in contact if R’(a,b) > Rc, where Rc = 0.2 in this work. If the residues are in contact, all peak assignments which connect them are assigned initial likelihoods . All other peak assignments are assigned .
2.2 Structure Calculations
Initial estimates of NOE peak assignment likelihoods based on network analysis are refined to likelihoods consistent with molecular structures via two passes of structure calculations. Each of these calculations employs torsion angle molecular dynamics simulation protocols with potential energy functions tailored to the NOE assignment problem. During each pass, peak likelihoods are calculated as a weighted average of previous likelihoods generated before the calculation and likelihoods based on the current structures. For the first pass the previous likelihoods are based on the network contact map, but the second pass previous likelihoods are calculated from the first pass structures.
2.2.1 NOE Potential Energy functions
As in our previous work (Kuszewski et al., 2004), early stages of our algorithm use a linear potential energy function so that the magnitude of atomic forces is identical for all violated active peak assignments of a given peak. The form of this energy function was slightly modified for this work so that its first derivative is continuous. The new linear energy term is
| (6) |
with
| (7) |
where klin is an overall scale factor, the index j sums over all ηi active peak assignments of peak i, rsw is the degree of violation at which the function takes its asymptotic linear form (1 Å in this work), and the distance violation Δ rij is given by the piecewise linear function
| (8) |
with
| (9) |
where and are, respectively, lower and upper distance bounds for assignment j of peak i, and rij is the structure-calculated distance associated with this peak assignment. If the shift assignments corresponding to assignment j of peak i contain more than one atom each (e.g. for a methyl group), the distance is calculated using the usual (Σr-6)-1/6 summation (Nilges, 1993).
As in our previous work, the final pass of the new PASD algorithm utilizes a quadratic potential term in which each active NOE peak (the determination of which is described in Section 2.2.5) has only a single active peak assignment contributing an energy:
| (10) |
where kquad is an overall scale factor and j denotes the single active peak assignment of peak i.
2.2.2 Repulsive Distance Restraints
Just as the presence of an NOE peak suggests that protons lie close in space, the absence of a peak may suggest that the protons are not close. This information is encapsulated in the network contact map introduced in section 2.1.3 and it is used to create additional structural restraints during the first pass of the PASD algorithm. These restraints incorporate information about pairs of residues that are not in contact and are thus implemented as a repulsive potential preventing atoms in shift assignments of these residues from approaching too closely during the first pass of structure calculations. The restraints are implemented using the energy
| (11) |
where the sum extends over all shift assignment pairs which experience the repulsive force and krepul is a scale factor for this term. The associated violation Δρi is
| (12) |
where ρi is the distance between shift assignment pair i, ρ- = 4 Å and ρ+ = ∞.
The repulsive interaction is included between all shift assignment pairs connecting residues a and b for which R’(a,b) < 0.2 (Eq. 2), but it is disabled for four classes of shift assignment pairs. Shift assignment pairs corresponding to any active peak assignment do not repel each other. The algorithm used to generate the network contact map consistently misses contacts between shift assignments that are close in primary sequence (see Figure 2), mostly due to there being relatively few connections between sidechain protons in these residues. Therefore, we include no repulsive restraints between shift assignments in residues separated by fewer than five residues. As we use torsion angle restraints derived from chemical shift values to provide information on secondary structure, such restraints are largely unnecessary anyway. NOE peaks whose folded position lies within 0.01 ppm of the diagonal or 0.05 ppm of any automatically-detected solvent line are unlikely to be seen, so repulsion of shift assignment pairs associated which such peaks is omitted. Finally, shift assignments corresponding to stereopairs do not repel: we want to allow the assignment to flip and be treated in a manner consistent with that discussed in Section 2.1.1 for initial matching.
Fig. 2.
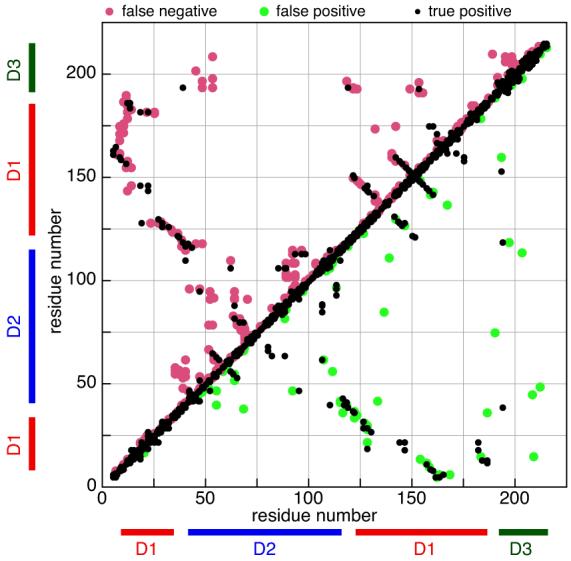
Network contact map for ThTP generated from its NOE datasets versus a contact map derived from the reference structure (PDB ID 2JMU, Song et al., 2008). Black dots denote residue pairs for which network analysis and the reference structure agree that a contact is made. Red dots in the upper triangle mark residue pairs that network analysis did not predict to be in contact but which are in contact in the reference structure. Green dots in the lower triangle denote residue pairs predicted by network analysis to be in contact, but which are not in contact in the reference structure. Blank space (in white) corresponds to correctly identified regions which are not in contact. Predicted contacts are those residue pairs a,b for which R’(a,b) > 0.2 as described in Section 2.1.3. The reference structure derived contact map was constructed by considering a pair of residues to be in contact if any of their constituent protons were within 2.7 Å of each other. Bars along the axes denote residues’ domain identity. It can be seen that the reference structure has very few long-range contacts between the domains, and that network analysis misses most of those.
The repulsive distance restraint potential is motivated by the fact that the network contact map overwhelmingly agrees with the actual contact map for those residues which do not make contacts (see Figure 2). However, mistakes resulting in repulsions between atoms that are truly close in space can distort structures, so we use these repulsive restraints quite conservatively. In this regard, these restraints are only enabled during the first pass of structure calculation. It should also be noted that the repulsive distance of 4 Å used here is generally short enough to avoid severe distortion (de Vlieg et al., 1986).
It should be noted that the vast majority of protons can interact via this repulsive interaction and that the number of these interactions increases as the square of the size of the system. Thus, great computational savings was obtained by periodically computing a shift assignment pair list in analogy to the pair list normally used in nonbonded atom interactions (Verlet, 1967).
2.2.3 Specification of the Two Structure Calculation Passes
Initial peak assignments are generated using the results of the two-step matching procedure discussed in Section 2.1.1. After this point in the PASD protocol NOE peak assignments are never permanently removed: they can be activated and deactivated at many subsequent points in the protocol. Initial likelihoods are generated from the network contact map as discussed in Section 2.1.3 and used as previous likelihoods during the first pass of the structure calculations. Starting from a structure with no violated bonds, bond angles, or improper dihedral angles, 500 starting structures are calculated differing in their random initial torsion angles and velocities. The energies of the structures are then minimized in torsion-angle space using energy terms corresponding to bonds, bond angles, improper dihedral angles, repulsive interactions to avoid atomic overlap and ϕ/ψ torsion angle restraints (Clore et al., 1986) derived1 from TALOS (Cornilescu et al., 1999) analysis of chemical shift values for backbone 1H, 13C and 15N nuclei. Molecular dynamics calculations are then performed in torsion angle space using the IVM facility (Schwieters and Clore, 2001) of Xplor-NIH (Schwieters et al., 2003; Schwieters et al., 2006) during which atomic masses are set uniformly to 100 amu. During the first pass of structure calculation, the linear PASD NOE energy and the repulsive restraint terms (Eqs. 6 and 11, respectively) are used in combination with the terms used during initial minimization. During the first pass, probabilistic activation/deactivation of peak assignments is carried out 10 times at regular intervals using the likelihoods from Eq. 14 with the previous likelihood weight wp = 1, i.e. using solely the prior likelihoods obtained from the network contact map. The next phase of calculations is performed in both passes: a high temperature (4000K) dynamics run with wp = 1 and active peak assignment determination at 10 regular intervals. As this point simulated annealing is performed by performing torsion-angle molecular dynamics while gradually decreasing the temperature from 4000K to 100K. During these annealing portions of the two phases wp is linearly reduced from 1/2 to zero, while the characteristic violation distance Δ rc (defined in the next section) is also reduced linearly (see Table 1). During the simulated annealing cooling phase, active peak assignment determination is performed 64 times at random intervals and energy scaling terms and other parameters are scaled geometrically as specified in Table 1. As in our previous work (Kuszewski et al., 2004), only assignment information is passed from the first to the second structure calculation pass: for both passes starting structures are randomly generated.
Table 1.
Summary of Simulated Annealing Protocols in the PASD Algorithma
| first pass | second pass | |
|---|---|---|
| High Temperature Phase I | ||
| duration (ps) | 20 | 50 |
| klin (kcal/mol/Å) | 1 | 0 |
| kquad (kcal/mol/Å2) | 0 | 3 |
| krepul (kcal/mol/Å) | 5 | 0 |
| Δrc (Å) | ∞ | ∞ |
| wp | 1 | 1 |
| number of NOE re-evaluations | 10 | 10 |
| knb (kcal/mol/Å4) | 0 | 1 |
| snb | 1.2 | |
| nonbonded interactions | none | Cα-Cα only |
| kdihed (kcal/mol/radians2) | 200 | 10 |
| kRAMA (kcal/mol) | 0.2 | 0.002 |
| High Temperature Phase II | ||
| duration (ps) | 60 | |
| klin (kcal/mol/Å) | 1 | |
| kquad (kcal/mol/Å2) | 0 | |
| krepul (kcal/mol/Å) | 5 | |
| Δrc (Å) | 10 | |
| wp | 0.5 | |
| number of NOE re-evaluations | 10 | |
| knb (kcal/mol/Å4) | 0 | |
| snb | ||
| nonbonded interactions | none | |
| kdihed (kcal/mol/radians2) | 200 | |
| kRAMA (kcal/mol) | 0.1 | |
| Cooling Phase | ||
| duration (ps) | 250 | 250 |
| klin (kcal/mol/Å) | 1→30 | 0 |
| kquad (kcal/mol/Å2) | 0 | 3→30 |
| krepul (kcal/mol/Å) | 5 | 0 |
| Δrc (Å) | 10→2 | 2→0.7 |
| wp | 0.5→0 | 0.5→0 |
| number of NOE re-evaluations | 64 | 64 |
| knb (kcal/mol/Å4) | 0.04→4 | 0.04→4 |
| snb | 0.9→0.8 | 0.9→0.8 |
| nonbonded interactions | all atoms | all atoms |
| kdihed (kcal/mol/radians2) | 200 | 200 |
| kRAMA (kcal/mol) | 0.1→10 | 0.002→1 |
klin, kquad and krepul are scale factors for energy terms in Eqs. 6, 10 and 11, respectively. Δrc is the characteristic distance violation used in Eq. 13. wp is the previous likelihood weight used in Eqs. 14 - 16. knb, kdihed, and kRAMA are scale factors for the repulsive quartic nonbonded potential (Nilges et al., 1988), the piecewise quadratic torsion angle potential (Clore et al., 1986) with target values generated by TALOS (Cornilescu et al., 1999) and the torsion angle database potential of mean force (Kuszewski et al., 1996; Clore and Kuszewski, 2002), respectively. snb is the radius scale factor used in the nonbonded potential (Nilges et al., 1988).
2.2.4 Calculating Likelihoods Using Converged Structures
After each structure pass of the PASD calculation, the best structures are used to calculate peak assignment likelihoods. Likelihoods calculated from first pass structures are used as previous likelihoods during the second pass of calculation and likelihoods calculated from second-pass structures are used to determine final NOE peak assignments. For each structure the number of NOE peaks violated by less than 0.5 Å is evaluated, and the 10% of the structures with the fewest violated peaks are selected for calculating peak assignment likelihoods. Likelihoods for each peak assignment are then calculated as the fraction of structures for which the peak assignment is not violated.
2.2.5 Determination of Active Peak Assignments
A very large combination of active peak assignments is sampled at numerous points during simulated annealing in the two PASD calculation phases. The current set of active peak assignments are determined using a Monte Carlo optimization procedure which considers the prior likelihoods of peak assignments specified at the beginning of a calculation pass (denoted λp and described below) and likelihoods based on NOE violations of the current molecular structure (denoted λv).
During the first pass of structure calculation prior likelihoods are based on the network contact map as specified in Section 2.1.3, while during the second pass, prior likelihoods are based on analysis of structures calculated at the end of the first pass (specified in the previous section). The violation likelihood of assignment j of peak i is
| (13) |
where Δ rij is defined in Eq. 8 and Δ rc is a characteristic violation distance which is reduced during the course of a calculation pass making larger violations increasingly unlikely.
Both prior and violation likelihoods are included in determining a peak assignment’s overall likelihood λo(i, j):
| (14) |
where wp is the weight factor which determines the contribution of the prior likelihood. wp is reduced from 1 to 0 during the course of a pass of structure calculations, such that the peak assignment likelihood is initially solely based on previous likelihood, and at the end it is solely based on structural information.
During the first pass, a random number between zero and one is generated for each peak assignment and that peak assignment is activated if the number is less than λo(i, j), making it possible that more than one peak assignment is active for a given peak. If no peak assignment is active for a peak, that peak is said to be inactive. During the second pass, a maximum of one peak assignment is active for each peak, the identity of which is determined using this normalized assignment likelihood:
| (15) |
with normalized likelihoods and . Each assignment j of peak i is allocated a bin of size λa(i, j) and a random number between zero and one is chosen. The assignment is then chosen from the bin corresponding to that random number. To determine whether the peak is active, the selected peak assignment’s overall likelihood λo(i, j) is compared to another random number between 0 and 1 as during the first pass.
In both structure calculation passes, the set of active peak assignments is optimized via a Monte Carlo procedure in which five successive complete sets of active peak assignments are generated by the same procedure as the first. A complete set is evaluated in comparison with the previous set and accepted or rejected based on a probability P associated with the two sets:
| (16) |
where is the difference in average PASD violation energy between the current and previous assignment sets of active assignments, is a characteristic average energy whose value varies during the calculation, is the average difference in previous likelihoods between the current and previous sets of active assignments, and is a characteristic average previous likelihood whose value is taken to be 0.1 (determined by trial and error) throughout the calculation. In Eq. 16 the overbar denotes the average over all active assignments. The violation energy Ev is calculated using the energy associated with the particular pass, so that Eq. 6 is used (with klin = 1 kcal/mol/Å) for calculating P during pass 1 and Eq. 10 is used (with kquad = 1 kcal/mol/Å2) during pass 2.
2.3 Using the PASD protocol
The PASD protocol is available as the PASD module of the Xplor-NIH biomolecular structure determination package (Schwieters et al., 2003; Schwieters et al., 2006). The complete protocol and an annotated example case are included in the standard Xplor-NIH download from http://nmr.cit.nih.gov/xplor-nih/.
The PASD protocol has been designed as a black box, with little in the way of parameters for users to adjust. In addition to the structure sequence, one only needs to provide the chemical shift assignment and NOE peak information in one of the formats listed in Section 2.1.1. [If one works with an unsupported format, please contact the authors so that support can be added quickly.] The user must enter information about NOE spectrum folding (spectral widths and peak signs), and which protons and heavy atoms are involved in a particular experiment (e.g. for 3D 15N-separated NOE experiments, proton HN and directly bonded heavy atom N on two axes, and any proton on the third axis). One can also specify any known disulfide bonds. Distance restraints obtained from other sources, such as previously determined NOE assignments, can be included in the structures passes by the use of the traditional NOE potential term (Schwieters et al., 2003; Schwieters et al., 2006).
In any sort of automated NOE assignment procedure, it is essential to ascertain the reliability of the result. One cannot simply take the final average structure and output list of NOE assignments without examining quality metrics. The two most important quality metrics in PASD are final structure precision and the NOE coverage, or the number of high-likelihood (> 90%) long-range (shift assignments separated by more than 5 residues in primary sequence) peak assignments per residue. It is important to consult both of these values after a PASD calculation to gain confidence it its convergence. It is also possible that a calculation results in poor structure precision, but still yields valuable assignment information as we show below with the ThTP calculation.
While the computational requirements of the PASD protocol have been significantly reduced relative to the original protocol described in Kuszewski et al. (2004), a cluster of computers is still required. Using 60 fairly modern CPU cores, we find that computational times vary from less than 8 hours for mth1743 (70 residues) to slightly more than 2 days for ThTP (224 residues).
3 Results
We illustrate the use of the PASD protocol using six proteins: cyanovirin-N (CVN) (Bewley et al., 1998), human interleukin-4 (IL4) (Powers et al., 1993; Wlodawer, 1992), Yersinia pestis modulating protein YmoA (YmoA) (McFeeters et al., 2007), Methanobacterium thermoautotrophicum hypothetical protein mth1743 (mth1743) (Yee et al., 2002), the small subunit of E. coli nitrite reductase (NiRD) (Ramelot et al., 2008), and mouse thiamine triphosphatase (ThTP) (Song et al., 2008). In addition to the NOE data summarized in Table 2, we employed the following number of chemical shift-derived backbone ϕ, ψ torsion angle restraints inferred from chemical shift tables as described in Section 2.2.3: 132 (CVN), 188 (IL4), 102 (YmoA), 106 (mth1743), 146 (NiRD) and 318 (ThTP).
Table 2.
Initial NOE statisticsa
| Spectrum | Npeak | picking method | ||
|---|---|---|---|---|
| CVN | ||||
| 3dC | 2619 | CAPP | 382 | 383 |
| 3dN | 2304 | CAPP | 124 | 505 |
| IL-4 | ||||
| 3dC | 2419 | CAPP | 550 | 558 |
| 3dN | 671 | CAPP | 132 | 604 |
| 4dCC | 5388 | CAPP | 550 | 550 |
| YmoAb | ||||
| 3dC | 5236 | Xeasy | 305 | 377 |
| 3dN | 428 | Xeasy | 66 | 353 |
| 4dCC | 4238 | Xeasy | 305 | 305 |
| 4dCN | 705 | Xeasy | 303 | 66 |
| mth1743 | ||||
| 3dC | 1987 | unknown | 293 | 385 |
| 3dN | 754 | unknown | 69 | 385 |
| NiRD | ||||
| 3dC aliphatic | 3070 | unknown | 444 | 618 |
| 3dC aromatic | 191 | unknown | 32 | 618 |
| 3dN | 1427 | unknown | 128 | 617 |
| 4dCC | 2281 | unknown | 484 | 455 |
| ThTP | ||||
| 3dC aliphatic | 5839 | hand | 801 | 1118 |
| 3dC aromatic | 273 | hand | 39 | 1118 |
| 3dN | 2886 | hand | 238 | 1118 |
For each system, the available spectra are listed, together with the numbers of NOE peaks, the method by which the peaks were picked, and the numbers from- and to- shift assignments associated with the particular experiment. The following shorthand is used for the various NOE spectra types: 3dC for 3D 13C-separated NOE, 3dN for 3D 15N-separated NOE, 4dCC for 4D 13C-separated/13C-separated NOE, and 4dCN for 4D 13C-separated/15N-separated NOE. Peak lists and chemical shift tables for CVN, IL-4, and YmoA were obtained directly from the authors. Peak lists and chemical shift tables for mth1743, NiRD, and ThTP were obtained from the BioMagResBank (accession codes 5106, 15139, and 15063, respectively). In each case, diagonal and solvent peaks were removed before initial matching, and they are not included in the total number of peaks listed here. The number of shift assignments created for each spectrum depends upon the number of entries in the chemical shift table, the particular atoms that can appear along each dimension of the spectrum, and the spectral widths along the proton dimensions of each spectrum.
The numbers for the YmoA 3dC and 4dCC spectra represent half of the total number actually picked. Because those spectra were picked at an extremely low level, the weakest 50% of peaks in those spectra were omitted after removing diagonal and solvent peaks.
Table 2 provides information about spectral data input to the PASD protocol, including the number of NOE peaks picked, the method used for peak-picking, and the number of from- and to- shift assignments after the two-step matching phase. For these systems, not all expected combination of nuclei were actually given chemical shift assignments. The percentage of nuclei with assigned expected chemical shifts is: CVN: 94%, IL-4: 90%, YmoA: 83%, mth1743: 97%, NiRD: 97%, and ThTP: 87%.
3.1 Efficacy of the two-step matching algorithm
The improvement over a simple tight-tolerance matching protocol achieves in most instances an increase in good long-range peak assignments of about 10%, but we have encountered cases where the improvement is much larger (e.g. for IL-4, the number of good long-range peak assignments is increased by a factor of two). However, the fraction of bad long-range NOE data present after matching ranged from 73-91% for the structures analyzed here. The structure calculation passes of the original PASD protocol (Kuszewski et al., 2004) were shown to be capable of handling up to 80% bad long-range data, so that the additional network analysis preprocessing stage is necessary to mark as unlikely a large percentage of the bad data. Further analysis of the stripe correction performance for the datasets studied here can be found in the Supplementary Information.
3.2 Network contact map
An example contact map is shown for ThTP in Figure 2. While the number of incorrectly predicted contacts and missed contacts seem large, it is seen that there is good general agreement between network-predicted contacts and those determined from the reference structure, with most regions of true contact being represented by the network contact map, and most mispredicted contacts being close in sequence to true contacts. Most importantly, the vast majority of the plot is empty, corresponding to correct predictions of regions of non-contact. This information is represented by the repulsive NOE potential which prevents the protons corresponding to shift assignments representing these regions of the protein from approaching too closely during the first pass of structure calculations. Based on the network contact map, initial likelihoods are calculated as specified in Section 2.1.3. For the systems studied here, the fraction of bad long-range NOE data (corresponding to peaks with an active assignment whose violation is greater than 0.5 Å) with nonzero likelihood ranges from 9-24%, an amount which can readily be handled by the structure calculation passes.
3.3 PASD Results
The results for CVN and IL-4 in Table 3 can be compared with those generated by the original PASD protocol described in Kuszewski et al. (2004). Assignment statistics and structural accuracy to the respective reference structures improved, with the CVN and IL-4 NOE coverage values increasing from 3.3 and 2.0, respectively, in the original protocol to 4.7 and 2.5 in the current work. At the same time, the backbone accuracy improved from 1.1 Å to 0.9 Å for CVN and from 1.52 Å to 1.4 Å for IL-4. It is interesting to note that the 101 residue CVN protein is an example of a structure for which the current implementation of the CSMM technique CS-Rosetta (Shen et al., 2008) is unable to correctly determine. Of the ten lowest energy CS-Rosetta structures, that closest to the reference CVN structure differs by more than 7.5 Å(unpublished data).
Table 3.
Statistics for PASD-generated Structuresa
| System | CVN | IL-4b | YmoA | mth1743c | NiRD | ThTP overall | ThTP dom. 1 | ThTP dom. 2 | ThTP dom. 3 | EIN |
|---|---|---|---|---|---|---|---|---|---|---|
| Reference Structure | 2EZM | 1ITI | 2JVP | 1RYJ | 2JO6 | 2JMU | 2JMU | 2JMU | 2JMU | 2EZA |
| method | NOE+RDC | NOE | NOE+RDC | NOE | NOE | NOE | NOE | NOE | NOE | NOE+T1/T2 |
| defined residues | 1-101 | 8-129 | 2-67 | 7-69 | 3-108 | 5-215 | 10-34,122-188 | 38-117 | 194-215 | 1-259 |
| backbone precision (Å) | 0.2±0.02 | 0.4±0.03 | 0.4±0.1 | 0.7±0.1 | 0.8±0.1 | 1.1±0.2 | 1.0±0.2 | 0.8±0.2 | 0.7±0.1 | 0.8±0.2 |
| heavy atom precision (Å) | 0.5±0.03 | 0.8±0.03 | 0.5±0.1 | 1.3±0.1 | 1.4±0.1 | 1.6±0.2 | 1.6±0.2 | 1.3±0.2 | 1.2±0.2 | 1.1±0.2 |
| PASD Structure Results | ||||||||||
| backbone accuracy (Å) | 0.9 | 1.3 | 1.9 | 1.6 | 1.2 | 13.3 | 2.5 | 2.7 | 1.6 | 16.4 |
| heavy atom accuracy (Å) | 1.4 | 2.1 | 3.0 | 2.2 | 2.0 | 13.3 | 3.2 | 3.2 | 2.1 | 16.9 |
| backbone precision (Å) | 0.7±0.2 | 0.7±0.1 | 0.8±0.2 | 1.2±0.5 | 1.1±0.3 | 5.9±3.3 | 2.9±1.0 | 2.7±0.9 | 1.3±0.7 | 13.4±1.8 |
| heavy atom precision (Å) | 1.2±0.2 | 1.3±0.1 | 1.4±0.2 | 1.7±0.5 | 1.6±0.4 | 6.4±3.3 | 3.6±1.1 | 3.3±0.9 | 2.0±0.8 | 14.0±1.8 |
| PASD NOE Assignment Statistics | ||||||||||
| coverage | 4.7 | 2.5 | 4.6 | 2.2 | 8.7 | 3.8 | 5.5 | 7.7 | 0.9 | 0.06 |
| discrimination (%) | 86.2 | 81.8 | 91.1 | 76.3 | 88.3 | 64.8 | 69.5 | 69.0 | 77.2 | 67.8 |
For each dataset, the reference structure PDB ID, the published structurally-defined region, and the published coordinate precision are listed, together with the coordinate precision and accuracy of the converged structures from the PASD calculation. The coordinate accuracy is defined as the r.m.s. difference between the regularized mean coordinates of the 50 converged structures and the reference structure’s coordinates, calculated over the published set of structurally-defined residues. The coordinate precision is defined as the mean r.m.s. difference between the 50 converged structures and their regularized mean coordinates. In addition, three measures of NOE assignment quality are reported: NOE coverage, that is the per-residue number of high-likelihood (> 90%) peak assignments with long-range (> 5 residues apart in primary sequence) shift assignments; and NOE discrimination, that is the percentage of peak assignments with likelihood > 90% or < 10%. Residual dipolar coupling restraints were included in the reference structure calculation for CVN and YmoA, but not for IL-4, mth1743, NirD, or ThTP.
Comparison with the IL4 X-ray structure (PDB ID 1RCB) solved at 2.25 Å resolution yields very similar results: 1.3 Å and 2.3 Å backbone and heavy atom accuracy, respectively.
Because the published structure of mth1743 was calculated without torsion angle restraints of any kind, we refined it, starting from the published coordinates 1RYJ, using the published assigned NOE restraints (PDB ID 1RYJ.mr) and TALOS restraints determined from its published chemical shift table (BMRB accession code 5106, Yee et al., 2002), using a standard simulated annealing refinement protocol in Xplor-NIH (Schwieters et al., 2006) which included the same non-PASD energy terms as used in the PASD structure calculations.
To further test the new PASD protocol, we examined YmoA, mth1743 and NiRD, small to intermediate-sized proteins with α-, α/β- and β-structures, respectively, as seen in Figure 3. Steroeviews of best-fit superpositions of the 50 best structures calculated in the second pass of structure calculations are shown in the Supplementary Information. Convergence of the PASD algorithm was indicated with the resulting coverage range of 2.2-8.7 and structural precision values of 0.8-1.2 Å. Convergence in coordinate and assignment space is verified in that the resulting mean structures all give an accuracy of better than 2 Å when they are compared with their respective reference structure, as shown in Table 3.
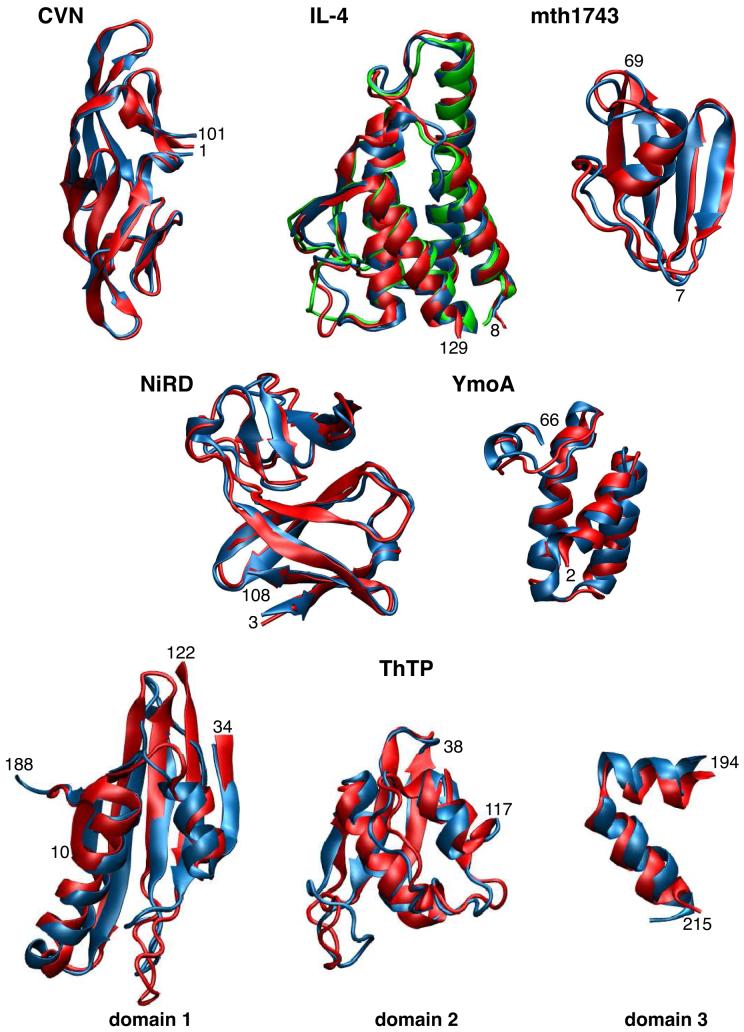
Fig. 3.
Results of the PASD algorithm for six proteins. Reference NMR structures are drawn in red. The reference X-ray structure of IL-4 is drawn in green. The regularized mean coordinates of the converged second-pass PASD structures are drawn in blue. ThTP consists of three domains whose relative orientations were not determined, but the individual domains were solved, as shown. Termini of the defined regions (see Table 3) are labeled.
Of these first five systems whose PASD calculations successfully converged, YmoA had the YmoA had the worst accuracy relative to its reference system. YmoA was peak-picked at an extremely low level, such that there were an enormous number of peaks contributing bad information after the two-step matching procedure described in Sections 2.1.1 and 2.1.2. The numbers reported in Table 3 represent results obtained by dropping the weakest 50% of the 3dC and 4dCC NOE peaks so that the amount of data would be commensurate with the small size (66 residues) of this protein. This use of a reduced dataset appears justified in that YmoA’s structural precision and NOE coverage value indicate good convergence in the PASD calculation. The PASD algorithm was subsequently run on the full set of NOE peaks to see if the results would be degraded. Although the > 9000 discarded peaks contained overwhelmingly bad data, the PASD calculation converged well, giving identical structural precision values to those reported in table 3 but with the NOE coverage value increasing to 6.8, indicating that approximately 50% more long-range peaks were assigned from the previously discarded data. Interestingly, the accuracy of the average structure to the reference structure decreased from the value 1.9 Å using half of the 3dC and 4dCC peaks to 2.4 Å, when all of the NOE data were included. This result coupled with the increased NOE coverage suggests that the PASD-generated structures are more consistent with the NOE data than the reference structure.
In contrast to these first five cases in which the PASD algorithm successfully assigned NOE spectra and calculated fairly accurate structures, the N-terminal domain of enzyme I of the Escherichia coli phosphoenolpyruvate:sugar phosphotransferase system (EIN) (Garrett et al., 1997; Tjandra et al., 1997) as described by incomplete 10 year old data represents a system that the PASD algorithm cannot currently handle. The protocol clearly failed for this 259 residue protein as evidenced by the 14.1 Å structural precision of the calculated structures, and the NOE coverage value of 0.1. This coverage value represents only 26 high-likelihood long-range NOE peaks. However, all of these high-likelihood peaks are good. Moreover, 99% of the 2209 short range NOE assignments which PASD determined to be high-likelihood are correct. It should be noted that the structure of EIN was not originally determined de novo from these spectra: an NMR structure was deduced from long-range NOE data manually peak-picked and manually assigned based on a previously determined crystal structure. In fact, given EIN’s reference structure, a sufficient number of good long-range peaks can be identified by PASD in the 3D 13C-separated NOE spectrum. However, a large fraction of calibration peaks (intraresidue and backbone-sequential) can not be resolved by hand- or auto-picking such that the shift assignment stripe correction and network contact analysis do not produce useful results, and PASD’s structure calculation passes are therefore overwhelmed with bad data. With higher field spectrometers (800 and 900 MHz), cryoprobes, and improved pulse sequences providing higher signal-to-noise 3D and 4D NOE spectra with higher resolution, it is likely that the PASD protocol would be successful for this protein. The bottom line is that the PASD algorithm provides useful NOE assignment information even in the case that it fails to find enough assignments to calculate a converged structure.
With this understanding of success and failure modes of the PASD protocol we examine the results for the 224 residue ThTP in table 3. The backbone precision of the calculation is 5.9 Å, with a large deviation indicating that a single structure could not be determined from the assigned NOEs. The accuracy of 13.3 Å of the calculated mean structure further indicates that the PASD protocol failed. However, the NOE coverage value of 3.8 puts the results squarely in the successful category by that metric, so further analysis was warranted.
The calculated ThTP structures were post-processed by an iterative fitting procedure which identified independent subregions of the 50 calculated PASD structures which were more precisely determined. This fitting procedure employs a maximum likelihood (ML) algorithm based on the work of Theobald and Wuttke (2006a) which does not require human intervention to identify regular protein regions (see Appendix). After removing the first fit region, the procedure is repeated, omitting the previously determined region(s), such that it could be determined which parts, if any, of the ThTP structure were correctly determined. This ML domain decomposition facility is implemented within the Xplor-NIH package and is further described in the Appendix A.
The ML domain decomposition procedure identified three regions of well-determined structure within the ensemble of PASD-calculated structures, referred to as domains 1-3 in Table 3 and in Figure 3. While the computed precisions and accuracies of these domains are generally lower than the other successfully computed structures, Table 3 and Figure 3 shows that the overall folds of these domains were computed correctly. Thus, while the PASD algorithm was unable to fully assign the NOE spectra of ThTP, 181 of 224 residues of the structure were located in identifiable, correctly determined regions.
An understanding of the difficulty in determining the relative positions of the three domains can be obtained by examining ThTP’s contact map in Figure 2, in which regions of the three domains are indicated along each axis. In this contact map it can be seen that there are essentially no contacts between domains 1 and 2 in the reference structure. Domain 3 does have a few contacts with domains 1 and 2 in the reference structure, but little of this information is captured by the network contact map, and it is mostly lost in the course of the PASD calculation. The final set of long-range high-likelihood assignments contains no restraints between domains 1 and 2 or between domains 2 and 3, while domains 1 and 3 are connected by just two long-range high-likelihood assignments. It should be noted that the X-ray structure of the human version of ThTP (PDB ID 3BHD, Busam et al., 2008) has been determined and it is folded over into a much more compact configuration involving large displacement of domains 2 and 3 relative to domain 1 in comparison with the structure of mouse ThTP. Thus, it may be that the three domains which we determined populate multiple configurations in solution.
Figure 4 provides some insight into the workings of individual stages of the PASD calculation for all 6 systems studied here. The stages are as follows: (B) peak assignments obtained by the initial broad tolerance matching, (T) peak assignments after stripe correction and tight tolerance matching, (N) the effect of including likelihoods from the network analysis, and the effect of including likelihoods generated from the first (1) and second (2) passes of structure calculation. For stages B and T all peak assignments were given a likelihood of one for the purposes of this figure. For panels A and B NOE assignments for all peaks were calculated based solely on likelihoods at each stage using the pass 2 assignment algorithm described in Section 2.2.5, such that each peak has at most one assignment. As such, the results in these panels represent initial likelihoods for an additional hypothetical pass 2 structure calculation initiated at each stage. It is seen that the fraction of good long range peaks increases monotonically through stage N, with the bulk of the increase due to the network analysis. The fraction of good long range assignments does not change dramatically during the structure calculation stages. However, panel B shows that the number of good long range assignments increases monotonically throughout the structure calculation stages. Note that the number of good long range assignments frequently decreases at the network analysis stage due to the incomplete nature of the network contact map resulting in lowering many long-range peak assignment likelihoods. However, because these peak assignments are not dropped from consideration, they are recovered during the structure calculation passes.
Fig. 4.
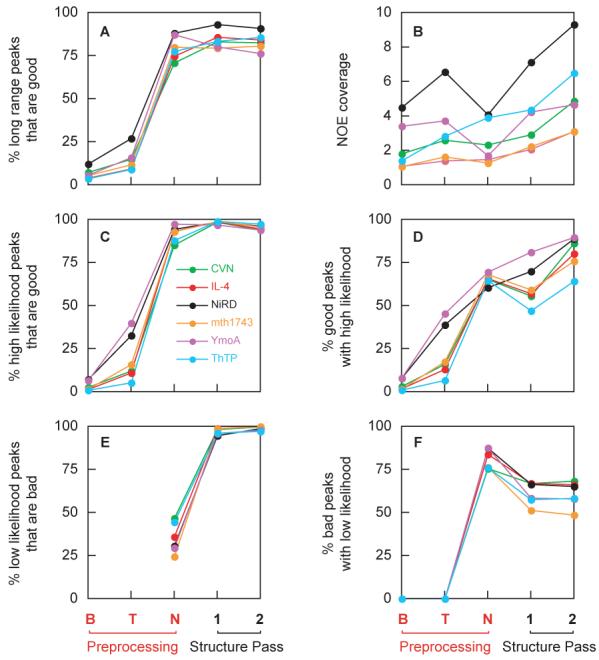
NOE statistics at various points during the progress of the PASD protocol. The x-axis represents different stages of the structure determination, with B and T corresponding to initial broad-tolerance matching and tight tolerance matching, respectively. For the first two stages, all matched peak assignments are assumed 100% likely. N corresponds to results after the network analysis stage where likelihoods are assigned via the network contact map. 1 and 2 correspond to results after the first and second structure passes, respectively. Plotted are (A) the percent long range peaks (no assignments within 5 residues in primary sequence) that are good (have violations of < 0.5 Å) as measured by the appropriate reference structure; (B) is the NOE coverage, or number of high-likelihood (> 90% likely), long-range peak assignments per residue; (C) the percent of high likelihood peaks that are good according to the reference structure; (D) the percent good peaks which have high likelihood; (E) the percent low likelihood peaks that are bad (for stages B and T all peaks are assumed to be high-likelihood such that this measure is not defined); and (F) the percentage of bad peaks with low likelihood. A peak is considered to be bad if it has an active peak assignment with an associated violation of > 0.5 Å when measured on the appropriate reference structure coordinates.
Panels C and D of Figure 4 display results for those peaks assignments with likelihoods > 90%. In Panel C the fraction of high-likelihood peak assignments that are good at each stage mirror the corresponding values in panel A, but the final values are much higher because peak assignments with likelihoods < 90% are omitted and because short-range peaks are also included. This is the subset of peak assignments which we report as assignments at the end of the calculation, and this panel shows that they are overwhelmingly (> 95%) good. Panel D shows that for the fully converged calculations the PASD calculation picks up about 75% of all possible peaks which are consistent with the reference structure. For the special case of ThTP the number drops to about 60% of the peaks, corresponding to loss of certain structural features as discussed above. Conversely, panels E and F consider peaks assignments with likelihoods < 10%, and it is seen that peaks which are flagged as low-likelihood are overwhelmingly bad for all cases studied. On the other hand, the fraction of bad peaks that have low likelihood takes intermediate values, which are not improved during the structure calculation. These results reinforce our decision to specify final peak assignments using the > 90% criterion. These assignments are overwhelmingly good, and peaks with low likelihood are overwhelmingly bad. The fraction of peaks whose assignments have either high or low likelihood is given by the NOE discrimination, reported in Table 3. Of course, higher values of discrimination are preferable but peak assignments with intermediate likelihoods represent possible additional distance restraint information which might be recovered in further analysis when using the PASD facility in an iterative mode.
4 Conclusions
In this paper we have described major enhancements of our PASD algorithm which improve its robustness and efficiency primarily by including more data from NOE spectra. Information from preliminarily assigned spectra and primary sequence information results in a network contact map allowing assignment of initial likelihoods, such that one fewer pass of structure calculations is necessary, thereby reducing the computation cost by one third. The contact map is further utilized by including conservative repulsive restraints between residues not in contact during the initial structure calculations.
The resulting updated PASD algorithm includes two builtin quality metrics to assess success of a calculation: structural precision and NOE coverage. We have shown that one can have high confidence in structures and assignments if the precision value is small and the NOE coverage is large. If the calculated structures are not precise, a large NOE coverage indicates that much assignment information has been recovered, and it is likely that some subregions of the structure have been determined. We have described an automatic procedure for identifying these subregions.
Certain selective labeling schemes, such the use of Leu/Val/Ile methyl protonated, otherwise fully deuterated, 13C-labeled (Goto et al., 1999) or U-[15N/13C/2H]/[1H-(methyl/methine)-Leu/Val] samples (Tang et al., 2005) might require small adjustments to the PASD protocol, in particular to the network analysis likelihood assignment step since many intramolecular crosspeaks would be absent for such samples. The most likely modification would be a simple downward adjustment of the network cutoff value Rc from its nominal value of 0.2.
In any event, further refinement and validation of structures determined using any automated method is essential. One might first run a second, additional PASD pass 2 structure calculation to try to extract more data from the spectrum. In further stages of refinement one would add distance restraints reflecting deduced hydrogen bonding and enable appropriate stereo assignments disabled in the PASD calculation. Finally, additional sources of structural information can be useful in validation and refinement. Residual dipolar coupling experiments are quite useful in providing orientational information (Bax et al., 2001), while solution scattering data (SAXS and SANS) (Grishaev et al., 2005; Schwieters and Clore, 2007) can be useful to help define overall molecular shape.
Supplementary Material
Acknowledgements
This work was supported by the CIT (to CDS) and NIDDK (to GMC) Intramural Research Programs of the NIH.
Appendix: Domain Determination Using A Maximum Likelihood Fitting Procedure
In order to fit subregions of structures which do not have high overall similarity, we have implemented a version of the maximum likelihood (ML) algorithm developed by Theobald and Wuttke (2006a) with a minor simplifying alteration which yields slightly improved results. In short, we have implemented the algorithm outlined in the supplementary material of Theobald and Wuttke (2006b) in which the following quantity is maximized:
| (17) |
where |U| denotes determinant of matrix U and ||A||B = Tr ATBA. Xi is a K × 3 matrix of coordinates of the input structures, 1K is a K-dimensional vector with all elements set to one, Ri and ti are, respectively, the rotation matrix and translation vector determined in the fitting process, while M corresponds to the average coordinates
| (18) |
Σ is the K × K coordinate covariance matrix whose inverse weights the fit of the coordinates such that coordinates with larger variances do not contribute as much to the fit. If Σ is set to the identity matrix Eq. 17 reduces to standard least squares coordinate fitting. Coordinate precision can be expressed in terms of Σ in a form analogous to the standard least squares RMSD:
| (19) |
Maximizing Eq. 17 balances two objectives: making structures as similar as possible to the mean, while minimizing the structure spread. The maximum likelihood estimate for the covariance matrix is
| (20) |
where the sum is over all structures to fit. Expressions for the ML estimates of Ri and the associated coordinate translation ti can be found in Theobald and Wuttke (2006b). ML coordinate fitting is an iterative process since each structure’s translation and rotation depend on Σ, which in turn depends on the translation and rotation. However, convergence typically occurs fairly rapidly (in fewer than 30 iterations).
Now, strictly speaking, Σ cannot be inverted because it always has zero eigenvalues due in part to invariance of overall translation and rotation. In Theobald and Wuttke (2006b) trial values of Σ are perturbed such that the eigenvalues obey an inverse gamma distribution. However, as the off-diagonal covariances are fairly meaningless (and hence not considered in their default algorithm), they resort to approximating the eigenvalues as the diagonal atomic variances. We find the whole procedure cumbersome and unwarranted, since the diagonal elements are poor estimates of the true eigenvalues. Instead we simply perturb Σ with a small value:
| (21) |
where is a K × K unit matrix and ε is a small value (typically 10-4). For multiple systems we find that this procedure works slightly better (converges in fewer iterations) and gives nearly identical fits to the method of Theobald and Wuttke (2006b).
In our iterative domain determination method we take the 50 structures of the second PASD structure calculation, fit them using this modified fitting procedure, and collect those atoms with a fit positional RMSD threshold less than ρthresh. We consider residues to be contiguous if their primary sequence difference is less than Dmin, the number of residues in the smallest domain considered. If RMSDML < 1.5 Å we consider the selected atoms to be in a single domain. Otherwise, we repeat the procedure, considering only this subset of atoms, and we decrement ρthresh by Δρthresh. This process is repeated until the first domain is determined. Successive domains are determined by repeating the procedure, excluding the atoms in the previously determined domains. We use the parameters ρthresh = 3.5 Å, Δρthresh = 0.5 Å (decremented every other iteration), and Dmin = 20 residues. For the ThTP domain determination it should be noted that the domain identification was found to be fairly insensitive to the RMSD threshold value. A script implementing this domain determination algorithm is now distributed with the Xplor-NIH package.
Footnotes
Target values and widths (θt and θw, respectively) for this dihedral potential are calculated as and , where θmin and θmax are, respectively, the maximum and minimum values of torsion angle among TALOS’s database matches for a given residue.
References
- Bartels C, Xia TH, Billeter M, Güntert P, Wüthrich K. The program XEASY for computer-supported NMR spectral analysis of biological macromolecules. J. Biomol. NMR. 1995;6:1–10. doi: 10.1007/BF00417486. [DOI] [PubMed] [Google Scholar]
- Bax A, Kontaxis G, Tjandra N. Dipolar couplings in macromolecular structure determination. Meth. Enzymol. 2001;339:127–174. doi: 10.1016/s0076-6879(01)39313-8. [DOI] [PubMed] [Google Scholar]
- Busam RD, Lehtio L, Arrowsmith CH, Collins R, Dahlgren LG, Edwards AM, Flodin S, Flores A, Graslund S, Hammarstrom M, Hallberg BM, Herman MD, Johansson A, Johansson I, Kallas A, Karlberg T, Kotenyova T, Moche M, Nilsson ME, Nordlund P, Nyman T, Persson C, Sagemark J, Sundstrom M, Svensson L, Thorsell AG, Tresaugues L, Van den Berg S, Weigelt J, Welin M, Berglund H. Crystal Structure of Human Thiamine Triphosphatase. To be Published. [Google Scholar]
- Bewley CA, Gustafson KR, Boyd MR, Covell DG, Bax A, Clore GM, Gronenborn AM. Solution structure of cyanovirin-N, a potent HIV-inactivating protein. Nat. Struct. Biol. 1998;5:571–578. doi: 10.1038/828. [DOI] [PubMed] [Google Scholar]
- Billeter M, Braun W, Wüthrich K. Sequential resonance assignments in protein 1H nuclear magnetic resonance spectra: computation of sterically allowed proton-proton distances and statistical analysis of proton-proton distances in single crystal protein conformations. J. Mol. Biol. 1982;155:321–346. doi: 10.1016/0022-2836(82)90008-0. [DOI] [PubMed] [Google Scholar]
- BMRB NMR-STAR data dictionary. 2004 http://www.bmrb.wisc.edu/-dictionary/htmldocs/nmr_star/dictionary.html.
- Brüschweiler R, Blackledge M, Ernst RR. Multi-conformational peptide dynamics derived from NMR data: a new search algorithm and its application to antamanide. J. Biomol. NMR. 1991;1:13–11. doi: 10.1007/BF01874565. [DOI] [PubMed] [Google Scholar]
- Cavalli A, Salvatella X, Dobson CM, Vendruscolo M. Protein structure determination from NMR chemical shifts. Proc Natl Acad Sci USA. 2007;104:9615–9620. doi: 10.1073/pnas.0610313104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clore GM, Gronenborn AM, Nilges M, Ryan CA. he three-dimensional structure of potato carboxypeptidase inhibitor in solution: a study using nuclear magnetic resonance, distance geometry and restrained molecular dynamics. Biochemistry. 1987;26:8012–8023. doi: 10.1021/bi00398a069. [DOI] [PubMed] [Google Scholar]
- Clore GM, Nilges M, Sukuraman DK, Brünger AT, Karplus M, Gronenborn AM. The three-dimensional structure of α1-purothionin in solution: combined use of nuclear magnetic resonance, distance geometry and restrained molecular dynamics. EMBO J. 1986;5:2729–2735. doi: 10.1002/j.1460-2075.1986.tb04557.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cornilescu G, Delaglio F, Bax A. Protein backbone angle restraints from searching a database for chemical shift and sequence homology. J. Biomol. NMR. 1999;13:289–302. doi: 10.1023/a:1008392405740. [DOI] [PubMed] [Google Scholar]
- Clore GM, Gronenborn AM. Determination of three-dimensional structures of proteins and nucleic acids in solution by nuclear magnetic resonance spectroscopy. Crit. Rev. Biochem. Mol. Biol. 1989;24:479–564. doi: 10.3109/10409238909086962. [DOI] [PubMed] [Google Scholar]
- Clore GM, Gronenborn AM. Applications of three- and four-dimensional heteronuclear NMR spectroscopy to protein structure determination. Progr. Nucl. Magn. Reson. Spectroscopy. 1991;23:43–92. [Google Scholar]
- Clore GM, Gronenborn AM. Two, three and four dimensional NMR methods for obtaining larger and more precise three-dimensional structures of proteins in solution. Ann. Rev. Biophys. Biophys. Chem. 1991;20:29–63. doi: 10.1146/annurev.bb.20.060191.000333. [DOI] [PubMed] [Google Scholar]
- Clore GM, Kuszewski J. χ1 Rotamer Populations and Angles of Mobile Surface Side Chains Are Accurately Predicted by a Torsion Angle Database Potential of Mean Force. J. Am. Chem. Soc. 2002;124:2866–2867. doi: 10.1021/ja017712p. [DOI] [PubMed] [Google Scholar]
- Delaglio F, Grzesiek S, Vuister GW, Zhu G, Pfeifer J, Bax A. NMRPipe: a multidimensional spectral processing system based on UNIX pipes. J. Biomol. NMR. 1995;6:277–293. doi: 10.1007/BF00197809. [DOI] [PubMed] [Google Scholar]
- de Vlieg J, Boelens R, Scheek RM, Kaptein R, van Gunsteren WF. Restrained molecular dynamics procedure for protein tertiary structure determination from NMR data: a lac repressor headpiece structure based on information on J-coupling and from presence and absence of NOEs. Isr. J. Chem. 1986;27:181–188. [Google Scholar]
- Garrett DS, Powers R, Gronenborn AM, Clore GM. A common sense approach to peak picking two-, three- and four-dimensional spectra using automatic computer analysis of contour diagrams. J. Magn. Reson. 1991;95:214–220. doi: 10.1016/j.jmr.2011.09.007. [DOI] [PubMed] [Google Scholar]
- Garrett DS, Seok Y-J, Liao DT, Peterkofsky A, Gronenborn AM, Clore GM. Solution structure of the 30 kDa N-terminal domain of enzyme I of the Escherichia coli phosphoenolpyruvate:sugar phosphotransferase system by multidimensional NMR. Biochemistry. 1997;36:2517–2530. doi: 10.1021/bi962924y. [DOI] [PubMed] [Google Scholar]
- Goto NK, Gardner KH, Mueller GA, Willis RC, Kay LE. J. Biomol. NMR. 1999;13:369–374. doi: 10.1023/a:1008393201236. [DOI] [PubMed] [Google Scholar]
- Grishaev A, Llinás M. CLOUDS, a protocol for deriving a molecular proton density via NMR. Proc. Natl. Acad. Sci. USA. 2002;99:6707–6712. doi: 10.1073/pnas.082114199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grishaev A, Wu J, Trewheela J, Bax A. Refinement of multidomain structures by combination of solution small-angle X-ray scattering and NMR data. J. Am. Chem. Soc. 127:166212005. doi: 10.1021/ja054342m. 16628. [DOI] [PubMed] [Google Scholar]
- Güntert P. Automated NMR protein structure calculation. Prog. Nucl. Magn. Reson. Spectrosc. 2003;43:105–125. [Google Scholar]
- Herrmann T, Güntert P, Wüthrich K. Protein NMR Structure Determination with Automated NOE Assignment Using the New Software CANDID and the Torsion Angle Dynamics Algorithm DYANA. J. Mol. Biol. 2002a;319:209–227. doi: 10.1016/s0022-2836(02)00241-3. [DOI] [PubMed] [Google Scholar]
- Herrmann T, Güntert P, Wüthrich K. Protein NMR structure determination with automated NOE-identification in the NOESY spectra using the new software ATNOS. J. Biomol. NMR. 2002b;24:171–189. doi: 10.1023/a:1021614115432. [DOI] [PubMed] [Google Scholar]
- Huang YJ, Tejero R, Powers R, Montelione GT. A Topology-Constrained Distance Network Algorithm for Protein Structure Determination From NOESY Data. Prot. Struct. Funct. Bioinf. 2006;62:587–603. doi: 10.1002/prot.20820. [DOI] [PubMed] [Google Scholar]
- Kuszewski J, Gronenborn AM, Clore GM. Improving the quality of NMR and crystallographic protein structures by means of a conformational database potential derived from structure databases. Protein Sci. 1996;5:1067–1080. doi: 10.1002/pro.5560050609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuszewski J, Schwieters CD, Garrett DS, Byrd RA, Tjandra N, Clore GM. Completely Automated, Highly Error-Tolerant Macromolecular Structure Determination from Multidimensional Nuclear Overhauser Enhancement Spectra and Chemical Shift Assignments. J. Am. Chem. Soc. 2004;26:6258–6273. doi: 10.1021/ja049786h. [DOI] [PubMed] [Google Scholar]
- McCammon JA, Harvey SC. Dynamics of Proteins and Nucleic Acids. Cambridge University Press; Cambridge: 1987. [Google Scholar]
- McFeeters RL, Altieri AS, Cherry S, Tropea JE, Waugh DS, Byrd RA. The high-precision solution structure of Yersinia modulating protein YmoA provides insight into interaction with H-NS. Biochemistry. 2007;46:13975–13982. doi: 10.1021/bi701210j. [DOI] [PubMed] [Google Scholar]
- Nilges M, Gronenborn AM, Brunger AT, Clore GM. Determination of three-dimensional structures of proteins by simulated annealing with interproton distance restraints: Application to crambin, potato carboxypeptidase inhibitor and barley serine proteinase inhibitor 2. Protein Eng. 1988;2:27–38. doi: 10.1093/protein/2.1.27. [DOI] [PubMed] [Google Scholar]
- Nilges M. A calculation strategy for the solution structure determination of symmetric dimers by 1H-NMR. Proteins. 1993;17:297–309. doi: 10.1002/prot.340170307. [DOI] [PubMed] [Google Scholar]
- Nilges M, Macias MJ, O’Donoghue SI, Oschkinat H. Automated NOESY interpretation with ambiguous distance restraints: the refined NMR solution structure of the Pleckstrin homology domain from β-Spectrin. J. Mol. Biol. 1997;269:408–422. doi: 10.1006/jmbi.1997.1044. [DOI] [PubMed] [Google Scholar]
- Powers R, Garrett DS, March CJ, Frieden EA, Gronenborn AM, Clore GM. The High-Resolution, Three-Dimensional Solution Structure of Human Interleukin-4 Determined by Multidimensional Heteronuclear Magnetic Resonance Spectroscopy. Biochemistry. 1993;32:6744–6762. doi: 10.1021/bi00077a030. [DOI] [PubMed] [Google Scholar]
- Ramelot TA, Cort JR, Yee AA, Guido V, Lukin JA, Arrowsmith CH, Kennedy MA. to be published. [Google Scholar]
- Rieping W, Habeck M, Bardiaux, Bernard A, Malliavin TE, Nilges M. ARIA2: automated NOE assignment and data integration in NMR structure calculation. Bioinformatics. 2007;23:381–382. doi: 10.1093/bioinformatics/btl589. [DOI] [PubMed] [Google Scholar]
- Schwieters CD, Clore GM. Internal coordinates for molecular dynamics and minimization in structure determination and refinement. J. Magn. Reson. 2001;152:288–302. doi: 10.1006/jmre.2001.2413. [DOI] [PubMed] [Google Scholar]
- Schwieters CD, Kuszewski JJ, Tjandra N, Clore GM. The Xplor-NIH NMR molecular structure determination package. J. Magn. Reson. 2003;160:66–74. doi: 10.1016/s1090-7807(02)00014-9. [DOI] [PubMed] [Google Scholar]
- Schwieters CD, Kuszewski JJ, Clore GM. Using Xplor-NIH for NMR molecular structure determination. Progr. NMR Spectroscopy. 2006;48:47–62. [Google Scholar]
- Schwieters CD, Clore GM. A physical picture of atomic motions within the Dickerson DNA dodecamer in solution derived from joint ensemble refinement against NMR and large angle X-ray scattering data. Biochemistry. 2007;46:1152–1166. doi: 10.1021/bi061943x. [DOI] [PubMed] [Google Scholar]
- Shen Y, Lange O, Delaglio F, Rossi P, Aramini JM, Liu G, Eletsky A, Wu Y, Singarapu KK, Lemak A, Ignatchenko A, Arrowsmith CH, Szyperski T, Montelione GT, Baker D, Bax A. Consistent blind protein structure generation from NMR chemical shift data. Proc. Natl. Acad. Sci USA. 2008;105:4685–90. doi: 10.1073/pnas.0800256105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song J, Bettendorff L, Tonelli M, Markley JL. Structural basis for the catalytic mechanism of mammalian 25 kDa thiamine triphosphatase. J. Biol. Chem. 2008;283:10939–10948. doi: 10.1074/jbc.M709675200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Summers MF, South TL, Kim B, Hare DR. High-resolution structure of an HIV zinc fingerlike domain via a new NMR-based distance geometry approach. Biochemistry. 1990;29:329–340. doi: 10.1021/bi00454a005. [DOI] [PubMed] [Google Scholar]
- Tang C, Iwahara J, Clore GM. Accurate determination of leucine and valine side-chain conformations using U-[15N/13C/2H]/[1H-(methyl/methine)-Leu/Val] isotope labeling, NOE pattern recognition and methine CγHγ/CβHβ residual dipolar couplings: application to the 34 kDa enzyme IIAChitobiose. J. Biomol. NMR. 2005;33:105–121. doi: 10.1007/s10858-005-1206-5. [DOI] [PubMed] [Google Scholar]
- Theobald DL, Wuttke DS. Empirical Bayes hierarchical models for regularizing maximum likelihood estimation in the matrix Gaussian Procrustes problem. Proceedings of the National Academy of Sciences. 2006a;103:18521–18527. doi: 10.1073/pnas.0508445103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Theobald DL, Wuttke DS. THESEUS: Maximum likelihood superpositioning and analysis of macromolecular structures. Bioinformatics. 2006b;22:2171–2172. doi: 10.1093/bioinformatics/btl332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tjandra N, Garrett DS, Gronenborn AM, Bax A, Clore GM. Defining long range order in NMR structure determination from the dependence of heteronuclear relaxation times on rotational diffusion anisotropy. Nature Struct. Biol. 1997;4:443–449. doi: 10.1038/nsb0697-443. [DOI] [PubMed] [Google Scholar]
- Verlet L. Computer “Experiments” on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules. Phys. Rev. 1967;159:98–103. [Google Scholar]
- Wilcox GR, Fogh RH, Norton RS. Refined structure in solution of the sea anemone neurotoxin ShI. J. Biol. Chem. 1993;268:24707–24719. [PubMed] [Google Scholar]
- Wlodawer A, Pavlovsky A, Gustchina A. Crystal structure of human recombinant interleukin-4 at 2.25Å resolution. FEBS Lett. 1992;309:59–64. doi: 10.1016/0014-5793(92)80739-4. [DOI] [PubMed] [Google Scholar]
- Yee A, Chang X, Pineda-Lucena A, Wu B, Semesi A, Le B, Ramelot T, Lee GM, Bhattacharyya S, Gutierrez P, Denisov A, Lee CH, Cort JR, Kozlov G, Liao J, Finak G, Chen L, Wishart D, Lee W, McIntosh LP, Gehring K, Kennedy MA, Edwards AM, Arrowsmith CH. An NMR approach to structural proteomics. Proc. Natl. Acad. Sci. USA. 2002;99:1825–30. doi: 10.1073/pnas.042684599. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.