“Smooth” Semiparametric Regression Analysis for Arbitrarily Censored Time-to-Event Data

Abstract

Summary

A general framework for regression analysis of time-to-event data subject to arbitrary patterns of censoring is proposed. The approach is relevant when the analyst is willing to assume that distributions governing model components that are ordinarily left unspecified in popular semiparametric regression models, such as the baseline hazard function in the proportional hazards model, have densities satisfying mild “smoothness” conditions. Densities are approximated by a truncated series expansion that, for fixed degree of truncation, results in a “parametric” representation, which makes likelihood-based inference coupled with adaptive choice of the degree of truncation, and hence flexibility of the model, computationally and conceptually straightforward with data subject to any pattern of censoring. The formulation allows popular models, such as the proportional hazards, proportional odds, and accelerated failure time models, to be placed in a common framework; provides a principled basis for choosing among them; and renders useful extensions of the models straightforward. The utility and performance of the methods are demonstrated via simulations and by application to data from time-to-event studies.

1. Introduction

Regression analysis of censored time-to-event data is of central interest in health sciences research, and the most widely used approaches are based on semiparametric models. While representing some feature of the relationship between time-to-event and covariates by a parametric form, these models leave other aspects of their distribution unspecified.

Among such models, Cox's proportional hazards model (PH) (Cox, 1972) is unquestionably the most popular and is used almost by default in practice when data are right-censored, owing to straightforward, widely-available implementation. The hazard given covariates is represented as a parametric form modifying multiplicatively an unspecified baseline hazard function. This proportional hazards assumption is often not checked; however, effects of prognostic covariates often do not exhibit proportional hazards (e.g., Gray, 2000). Accordingly, there is considerable interest in alternative semiparametric regression models.

The accelerated failure time model (AFT) (Kalbfleisch and Prentice, 2002, sec. 2.2.3), in contrast to the PH model, where survival time and covariate effects are modeled indirectly through the hazard, represents the logarithm of event time directly by a parametric function of covariates plus a deviation with unspecified distribution, lending it practical appeal. However, this and similar models are used infrequently, likely due to computational challenges that undoubtedly dictate lack of commercially-available software. Although the iterative fitting method of Buckley and James (1979) (see also, e.g., Lin and Wei, 1992) for right-censored data is simple to program, it can exhibit problematic behavior, such as oscillation between two “solutions” (Jin, Lin, and Ying, 2006). Competing approaches based on rank tests (e.g., Tsiatis, 1990; Wei, Ying, and Lin, 1990; Jin et al., 2003) may also admit multiple solutions (or have no solutions at all), can be computationally intensive (Lin and Geyer, 1992), and/or can involve rather complicated estimation of sampling variance.

The proportional odds (PO) model (Murphy, Rossini, and van der Vaart, 1997; Yang and Prentice, 1999) instead represents the logarithm of the ratio of the odds of survival given covariates to the baseline odds as a parametric function of covariates, where the associated baseline survival function is left unspecified. Despite its pleasing interpretation, the PO model is rarely used, again likely due to difficulty of implementation.

Hence, although the regression parameters in all of these models have intuitive interpretations, and although one model may be more suitable for representing the data than another, only the PH model is widely used. The PH and PO models are special cases of the linear transformation model (Cheng, Wei, and Ying, 1995; Chen, Jin, and Ying, 2002); Cheng, Wei, and Ying (1997) and Scharfstein, Gilbert, and Tsiatis (1998) also discuss a general class of models that includes both. The AFT and PH models are cases of the “extended” hazards model of Chen and Jewell (2001), including the “accelerated hazards” model of Chen and Wang (2000). However, there is no accessible framework that includes all three models and, indeed, further competitors, in which selection among them may be conveniently placed.

Moreover, the majority of developments for semiparametric time-to-event regression have been for right-censored (independently given covariates) event times. Fitting the PH model is straightforward under these conditions, but with interval censoring, specialized methods are required (Finkelstein, 1986; Satten, Datta, and Williamson, 1998; Goetghebeur and Ryan, 2000; Pan, 2000; Betensky et al., 2002), as they are for alternative models (e.g., Betensky, Rabinowitz, and Tsiatis, 2001; Sun, 2006). This require the analyst to seek out specialized, distinct techniques for different censoring patterns, even for the familiar PH model.

In this paper, we propose a general framework for semiparametric regression analysis of censored time-to-event data that (i) provides a foundation for selection among competing models; (ii) unifies handling of different patterns of censoring, obviating the need for specialized techniques; and (iii) is computationally tractable regardless of model or censoring pattern. To achieve simultaneously (i)–(iii), we sacrifice a bit of generality relative to traditional semiparametric methods by making the unrestrictive assumption that the distribution associated with unspecified model components has a density satisfying mild “smoothness” assumptions. Indeed, large sample theory for traditional methods requires similar assumptions (e.g., Ritov, 1990; Tsiatis, 1990; Jin et al., 2006). We assume that densities lie in a broad class whose elements may be approximated by the “SemiNonParametric” (SNP) density estimator of Gallant and Nychka (1987), tailored to provide an excellent approximation to virtually any plausible survival density. Many authors have used smoothing techniques in time-to-event regression (e.g., Kooperberg and Clarkson, 1997; Joly, Commenges, and Letenneur, 1998; Cai and Betensky, 2003; Komárek, Lesaffre, and Hilton, 2005). Our SNP approach endows likelihood-based inference for any of these models with “parametric-like” features and a virtually closed-form objective function under arbitrary censoring patterns that admits tractable implementation with standard optimization software. Competing models may be placed in a unified likelihood-based framework, providing a convenient, defensible basis for choosing among them via standard model selection techniques.

In Section 2, we review the SNP representation and describe its use in approximating any plausible survival density. We discuss SNP-based semiparametric time-to-event regression analysis with arbitrary censoring in Section 3. Simulation studies in Section 4 demonstrate performance. In Section 5, we apply the methods to two well-known data sets.

2. SNP Representation of a Survival Density

Gallant and Nychka (1987) gave a mathematical description of a class $\mathcal{H}$ of k-dimensional “smooth” densities that are sufficiently differentiable to rule out “unusual” features such as jumps or oscillations but that may be skewed, multi-modal, or fat- or thin-tailed. When k = 1, $\mathcal{H}$ includes almost any density that is a realistic model for a (possibly transformed), continuous time-to-event random variable and excludes implausible candidates. For k = 1, densities h ε $\mathcal{H}$ may be expressed as an infinite Hermite series $h\left(z\right)=P_{\infty }^2\left(z\right)\psi \left(z\right)$ plus a lower bound on the tails, where P_∞(z) = a₀ + a₁z + a₂z² + · · · is an infinite-dimensional polynomial; ψ(z) is the “standardized” form of a known density with a moment generating function, the “base density;” and h(z) has the same support as ψ(z). The base density is almost always taken as $\mathcal{N}$(0, 1), but need not be (see below). For practical use, the lower bound is ignored and the polynomial is truncated, yielding the so-called SNP representation

$$h_K\left(z\right)=P_K^2\left(z\right)\psi \left(z\right),P_K\left(z\right)=a_0+a_{1}z+z_2{z}^2+\cdots +a_K{z}^K,\mathit{a}={(a_0,a_1,\dots ,a_K)}^T,$$ (1)

With a such that ∫ h_K(z) dz = 1 and K suitably chosen, h_K(z) provides a basis for estimation of h(z). The SNP representation has been widely used, particularly in econometric applications. Web Appendix A gives more detail on the SNP and its properties.

Zhang and Davidian (2001) noted that requiring $\int h_K\left(z\right)dz=\int P_K^2\left(z\right)\psi \left(z\right)dz=1$ is equivalent to requiring $E\left\{P_K^2\left(U\right)\right\}={\mathit{a}}^T\mathit{Aa}=1$, where U has density ψ, and A is a known positive definite matrix easily calculated for given ψ. Thus, a^TAa = c^Tc = 1, suggesting the spherical transformation c₁ = sin(ϕ₁), c₂ = cos(ϕ₁) sin(ϕ₂), . . . , c_K = cos(ϕ₁) cos(ϕ₂) · · · cos(ϕ_K−1) sin(ϕ_K), c_K+1 = cos(ϕ₁) cos(ϕ₂) · · · cos(ϕ_K−1) cos(ϕ_K) for −π/2 < ϕ_j ≤ π/2, j = 1, . . . , K. Web Appendix B presents examples of this formulation. Thus, for fixed K, (1) is “parameterized” in terms of ϕ (K × 1) and we write $h_K(z;\varphi )=P_K^2(z;\varphi )\psi \left(z\right)$; estimation of the finite-dimensional “parameter” ϕ leads to an estimator for h(z).

With K = 0 in (1), $P_K^2\left(z\right)\equiv 1$, and h_K(z) reduces to the base density; i.e., h_K(z) = ψ(z). Values K > 1 control the extent of departure from ψ and hence flexibility for approximating the true h(z) (K is not the number of components in a mixture). Several authors (e.g., Fenton and Gallant, 1996; Zhang and Davidian, 2001) have shown that h_K(z; ϕ) with K ≤ 4 can well-approximate a diverse range of true densities.

We now describe how we use (1) to approximate the assumed “smooth” density f₀(t) of a continuous, positive, time-to-event random variable T₀ with survival function S₀(t) = P(T₀ > t), t > 0. As T₀ is positive, we assume that we may write

$$\log \left(T_0\right)=\mu +\sigma Z,\sigma >0,$$ (2)

where Z takes values in (−∞, ∞). We consider two formulations that together are sufficiently rich to support an excellent approximation to virtually any f₀(t). In (2), it is natural to assume that Z has density h ε $\mathcal{H}$ that may be approximated by (1) with $\mathcal{N}$(0, 1) base density ψ(z) = φ(z) for suitably chosen K, so that T₀ is lognormally distributed when K = 0. Although this can approximate very skewed or close-to-exponential f₀ with large enough K, an alternative formulation better suited to this case is to assume that Z* = e^Z has density h ε $\mathcal{H}$ that may be approximated by (1) with standard exponential base density ψ(z) = ε(z) = e^−z, so that Z has an extreme value distribution (Kalbfleisch and Prentice, 2002, sec. 2.2.1) when K = 0. As discussed in Section 3, we propose choosing the representation (normal or exponential) and associated K best supported by the data.

In both cases, approximations for f₀(t) and S₀(t) follow straightforwardly. Under the normal base density representation, for fixed K and θ = ( μ, σ, ϕ^T )^T , we have for t > 0

$$\begin{array}{c}\hfill f_{0,K}(t;\theta )={\left(t\sigma \right)}^{-1}{P}_K^2\{(\log t-\mu )∕\sigma ;\varphi \}\phi ((\log t-\mu )∕\sigma \},\hfill \\ \hfill S_{0,K}(t;\theta )={\int }_{(\log t-\mu )∕\sigma }^{\infty }{P}_K^2(z;\varphi )\phi \left(z\right)dz.\hfill \end{array}$$ (3)

Because $P_K^2$(z; ϕ) may be written as ${\sum }_{k=0}^{2K}{d}_k{z}^k$ , where the d_k are functions of the elements of ϕ, S_0,K(t;θ) in (3) may be written as a linear combination of integrals of the form $I(k,c)={\int }_c^{\infty }{z}^k\phi \left(z\right)dz$ that satisfy I(k, c) = c^k−1φ(c) + (k − 1)I(k − 2, c) for k ≥ 2, where I(0, c) = 1 − Φ(c), I(1, c) = φ(c), and Φ(·) is the $\mathcal{N}$(0, 1) cumulative distribution function (cdf). For the exponential base density representation, we have approximations

$$\begin{array}{c}\hfill f_{0,K}(t;\theta )={\left(\sigma e^{\mu ∕\sigma }\right)}^{-1}{t}^{(1∕\sigma -1)}{P}_K^2\{{(t∕e^{\mu })}^{1∕\sigma };\varphi \}\epsilon \left\{{(t∕e^{\mu })}^{1∕\sigma }\right\}\hfill \\ \hfill S_{0,K}(t;\theta )={\int }_{{(t∕e^{\mu })}^{1∕\sigma }}^{\infty }{P}_K^2(z;\varphi )\epsilon \left(z\right)dz,\hfill \end{array}$$ (4)

where, similar to the normal base case, the integral in (4) may be calculated using the recursion I(k, c) = c^kε(c) + kI(k − 1, c), k > 0, with I(0, c) = e^−c. Note, then, that for fixed K, except for the need for a routine to calculate the normal cdf, the approximations of f₀(t) and S₀(t) using either base density representation are in a closed form depending on the “parameter” θ, whose finite dimension depends on K. This offers computational advantages and makes handling of arbitrary censoring patterns straightforward, as we demonstrate next.

3. Censored Data Regression Analysis Based on SNP

3.1 Popular Regression Models

Let X_i be a vector of time-independent covariates and T_i be the event time, with (T_i, X_i) independent and identically distributed (iid) for i = 1, . . . , n. The usual PH model is

$$\lambda (t\mid \mathit{X};\beta )={\lim }_{\delta \to 0^{+}}{\delta }^{-1}P(t\le T<t+\delta \mid T\ge t,\mathit{X})={\lambda }_0\left(t\right)\exp \left({\mathit{X}}^T\beta \right),t>0,$$ (5)

where λ₀(t) is the baseline hazard function corresponding to X = 0. Letting S(t|X;β) = P (T > t|X) be the conditional survival function for T given X, it is straightforward (Kalbfleisch and Prentice, 2002, sec. 4.1) to show that S(t|X;β) = S₀(t)^exp(XTβ), where $S_0\left(t\right)=\exp \{-{\int }_0^t{\lambda }_0\left(u\right)du\}$ is the baseline survival function associated with λ₀(t). Usually, λ₀(t) is left completely unspecified, whereupon (5) is a semiparametric model, and β characterizing the hazard relationship is estimated via partial likelihood (PL; Kalbfleisch and Prentice, 2002, sec. 4.2). We instead impose the mild restriction that S₀(t) is the survival function of a random variable T₀ satisfying (2) with density f₀(t), and that f₀(t) and S₀(t) may be approximated by either (3) or (4). Letting the conditional density of T|X be f(t | X;β), we obtain approximations to S(t | X;β) and f(t | X;β) for fixed K given by

$$S_K(t\mid \mathit{X};\beta ,\theta )=S_{0,K}{(t;\theta )}^{\exp \left({\mathbf{X}}^T\beta \right)},f_K(t\mid \mathit{X};\beta ,\theta )=e^{{\mathbf{X}}^T\beta }{\lambda }_{0,K}(t;\theta )S_K(t\mid \mathit{X};\beta ,\theta ),$$ (6)

where λ_0,K(t;θ) = f_0,K(t;θ)/S_0,K(t;θ). As we demonstrate shortly, the approximations in (6) may be substituted into a likelihood function appropriate for the censoring pattern of interest, upon which estimation of (β,θ) and choice of K and the base density may be based. We propose a similar formulation for the usual AFT model

$$\log \left(T_i\right)={\mathit{X}}_i^T\beta +e_i\mathrm{iid}.$$ (7)

Rather than taking the distribution of the “errors” e_i to be completely unspecified, we assume that e_i = log(T_0i), where T₀ has survival function S₀(t) and “smooth” density f₀(t) that may be approximated by (3) or (4). For fixed K, this leads to approximations to the conditional survival and density functions of T|X, S(t | X;β) and f(t|X;β), given by

$$S_K(t\mid \mathit{X};\beta ,\theta )=S_{0,K}(t{e}^{-{\mathbf{X}}^T\beta };\theta ),f_K(t\mid \mathit{X};\beta ,\theta )=e^{-{\mathbf{X}}^T\beta }{f}_{0,K}(t{e}^{-{\mathbf{X}}^T\beta };\theta ).$$ (8)

The same principle may be applied to the PO model, which in its usual form assumes

$$\frac{S(t\mid \mathit{X};\beta )}{1-S(t\mid \mathit{X};\beta )}=\left\{\frac{S_0\left(t\right)}{1-S_0\left(t\right)}\right\}\exp (-{\mathit{X}}^T\beta ),$$ (9)

where S₀(t) is the baseline survival function, assumed to have density f₀(t), and S(t | X;β) is the conditional survival function given X with density f(t|X;β). Model (9) implies S(t | X;β) = S₀(t)/{e^{XT β} + S₀(t)(1 − e^{XT β})}; thus, assuming S₀(t) and f₀(t) may be approximated by (3) or (4), S(t | X;β) and f(t|X;β) may be approximated by

$$S_K(t\mid \mathit{X};\beta ,\theta )=S_{0,K}(t;\theta )a_{0,K}^{-1}(t,\mathit{X};\beta ,\theta ),f_K(t\mid \mathit{X};\beta ,\theta )=f_{0,K}(t;\theta )e^{{\mathbf{X}}^T\beta }{a}_{0,K}^{-2}(t,\mathit{X};\beta ,\theta )$$ (10)

for fixed K, where a_0,K(t, X;β,θ) = e^XTβ + S_0,K(t;θ)(1 − e^XTβ).

We may now exploit these developments. Assuming as usual that the censoring mechanism is independent of T given X, we demonstrate when T may be (i) interval-censored, known only to lie in an interval [L, R]; (ii) right-censored at L (set R = ∞); or (iii) observed (set T = L = R). For (i) and (ii), Δ = 0; else, Δ = 1 (iii). With iid data (L_i, R_i, Δ_i, X_i), i = 1, . . . , n, assuming that f(t|X) and S(t|X) may be represented as in (6), (8), or (10), for fixed K, the loglikelihood for (β,θ), conditional on the X_i, is ${\ell }_K(\beta ,\theta )={\sum }_{i=1}^n\left[{\Delta }_i\log \left\{f_K(L_i\mid {\mathit{X}}_i;\beta ,\theta )\right\}+(1-{\Delta }_i)\log \{S_K(L_i\mid {\mathit{X}}_i;\beta ,\theta )-S_K(R_i\mid {\mathit{X}}_i;\beta ,\theta )\}\right]$.

For fixed K, base density, and model, ${\ell }_K(\beta ,\theta )$ may be maximized in (β,θ) using standard optimization routines; we use the SAS IML optimizer nlpqn (SAS Institute, 2006). Choice of starting values is critical for ensuring that the global maximum is reached. In Web Appendix C, we recommend an approach where ${\ell }_K(\beta ,\theta )$ is maximized for each of several starting values found by fixing ϕ over a grid and using “automatic” rules to obtain corresponding starting values for (α, σ,β). Although elements of ϕ are restricted to certain ranges, unconstrained optimization virtually always yields a valid transformation so that ∫ h_K(z; ϕ)dz = 1. The declared estimates correspond to the solution(s) yielding the largest ${\ell }_K(\beta ,\theta )$.

Following other authors (e.g., Gallant and Tauchen, 1990; Zhang and Davidian, 2001), for a given model (PH, AFT, PO), we propose selecting adaptively the K-base density combination by inspection of an information criterion over all combinations of base density (normal, exponential) and K = 0, 1, . . . , K_max. Our extensive studies show K_max = 2 is generally su cient to achieve an excellent fit. With q = dim(β,θ), criteria of the form $-{\ell }_K(\beta ,\theta )+qc$ have been advocated, with small values preferred. Ordinarily, the Akaike Information Criterion (AIC), Bayesian Information Criterion (BIC), and Hannan-Quinn (HQ) criteria take c = 1, log(n)/2, and log{log(n)}, respectively; AIC tends to select “larger” models and BIC “smaller” models, with HQ intermediate. As noted by Kooperberg and Clarkson (1997, Section 3), with censored data, dependence of c on n may be suspect; for right-censored data, replacing n by d = number of failures has been proposed (e.g., Volinsky and Raftery, 2000), although a similar adjustment under interval censoring is not obvious. It is nonetheless common practice to base c on n. We have found in the current context that replacing n by d has little effect on the K-base density choice. We use HQ with c = log{log(n)} in the sequel.

The SNP approach is an alternative to traditional semiparametric methods such as PL when one is willing to adopt the assumption of a “smooth” density f₀(t). The formulation also supports selection among competing models (e.g., PH, AFT, PO): that for which the chosen K-base density combination yields the most favorable value of the information criterion may be viewed as “best supported” by the data. This may be used objectively or in conjunction with other evidence, e.g., the outcome of a formal test of the proportional hazards assumption (e.g., Gray, 2000; Lin, Zhang, and Davidian, 2006), in adopting a final model.

To obtain standard errors and confidence intervals for the estimator for β, the parameter ordinarily of central interest, as well as for any other functional of the conditional distribution of T|X based on a final selected representation, we follow other authors and treat the chosen K, base density, and model as predetermined. That is, we approximate the sampling variance of the resulting estimator $\widehat{\beta }$ or of any functional d($\widehat{\beta },\widehat{\theta }$) via the inverse “information matrix” acting as if the chosen ${\ell }_K(\beta ,\theta )$ were the loglikelihood under a predetermined parametric model. This matrix is readily obtained from optimization software. For $\widehat{\beta }$, the square root of the relevant diagonal element of this matrix yields immediately our proposed standard error; for general functionals, we use the delta method. Assuming that these quantities have approximately normal sampling distributions, 100(1 − α)% Wald confidence intervals may be constructed as the estimate ± the normal critical value × the estimated standard error. Although the choice of K and base density is made adaptively, which would seem to invalidate this practice, results cited in Web Appendix A support it, and simulations in Section 4 demonstrate that this approach yields reliable inferences in realistic sample sizes.

Several useful byproducts follow from the SNP approach. Selection of a model with K = 0 suggests evidence favoring the parametric model implied by the chosen base density; e.g., the AFT model with K = 0 and normal base density corresponds to assuming T given X is lognormally distributed. Because “smooth” estimates of baseline densities and survival functions are immediate, predictors of survival probabilities and calculation of associated confidence intervals as in Cheng et al. (1997) are easily handled.

3.2 Model Extensions

A “parametric” representation makes otherwise difficult-to-implement extensions of standard time-to-event regression models straightforward. In Web Appendices D and E, we exhibit two possibilities: extension of the AFT model to incorporate so-called “heteroscedastic errors” and extension of this model to accommodate time-dependent covariates.

4. Simulation Studies

We report on simulations to evaluate performance of the SNP approach. For all SNP fits, we considered K_max = 2 and both the normal and exponential base densities.

In the first set of scenarios, data were generated under the PH model (5) with continuous covariate X uniformly distributed on (0, 1) and 25% independent uniform right censoring, with true baseline hazard λ₀(t) corresponding to a lognormal with mean 2.9 and scale 0.66; a Weibull with shape 0.9 and scale 25.0; a gamma with shape and scale 2.0; and a log-mixture of normals found by exponentiating draws from the bimodal normal mixture $0.3\mathcal{N}(0.2,,0.36)+0.7\mathcal{N}(1.8,0.36)$. In all cases, the true value of β = 2.0, n = 200, and 1000 Monte Carlo (MC) data sets were generated. For each, the PH model was fitted by PL via SAS proc phreg and by the SNP approach, with comparable results, as shown in Table 1(a). The SNP-based AFT and PO models (7) and (9) were also fitted to each data set, and Table 1(a) summarizes how often HQ selected each model. Percentages do not necessarily add to 100% across the three models; because fits with K = 0 and exponential base density lead to the same value of HQ for the AFT and PH models, HQ supports more than one model when this configuration is selected, so the percentages reflect the proportions of times this occurred. Under the Weibull, selection of the AFT or PH model corresponds to choosing a PH model (Kalbfleisch and Prentice, 2002, p. 44). “Correct” indicates the percentage of data sets for which HQ supported selection of the (true) PH model under these conditions and indicates that inspection of HQ across SNP fits of competing models can be useful for deducing the appropriate model, a capability that grows with sample size. The true PH model was identified over 90% of the time for all distributions when n = 500.

Table 1.

Simulation results based on 1000 Monte Carlo data sets when the true model is the PH or PO model with baseline density f₀(t). Mean is Monte Carlo mean of the 1000 estimates of β when the true model is fitted, SD is their Monte Carlo standard deviation, SE is the average of the 1000 estimated delta method standard errors, and CP is Monte Carlo coverage probability, expressed as a percent, of 95% Wald confidence intervals. For right-censored data, SNP and PL indicate fitting using the SNP approach with K and the base density chosen via HQ and partial likelihood, respectively. All of the AFT, PH, and PO models were fitted to each data set under right-censoring; the columns AFT, PH, and PO indicate the percentage of 1000 data sets for which that model was chosen based on HQ, and Correct indicates the percentage of data sets supporting the PH model; see the text. For interval-censored data, only SNP was used. (a) PH model: true value of β = 2.0 in all cases. (b) PO model: true value of β = 2.0 (lognormal, Weibull) or β = −2.0 (log-mixture).

f0(t)	n	Cens. rate	Method	Mean	SD	SE	CP	AFT	PH	PO	Correct
(a) True PH model
Right-censored data
lognormal	200	25%	SNP	2.02	0.32	0.31	95.4	9.4	86.5	5.2	86.5
			PL	2.00	0.32	0.32	96.3
Weibull	200	25%	SNP	2.02	0.31	0.31	95.5	86.7	88.0	2.8	97.2
			PL	2.01	0.32	0.32	96.3
gamma	200	25%	SNP	2.06	0.32	0.31	94.3	66.8	81.6	6.3	81.6
			PL	2.02	0.32	0.32	95.2
log-mixture	200	25%	SNP	2.04	0.34	0.33	94.9	2.4	73.6	24.0	73.6
			PL	2.02	0.33	0.33	95.5
Interval-censored data
gamma	200	18% right, 82% interval	SNP	2.04	0.30	0.29	93.9
log-mixture	200	20% right, 80% interval	SNP	2.04	0.30	0.30	94.8
(b) True PO model
Right-censored data
lognormal	200	25%	SNP	2.01	0.18	0.18	94.6	0.7	2.2	97.1	97.1
Weibull	200	25%	SNP	2.00	0.46	0.45	94.6	29.4	19.7	65.1	65.1
log-mixture	200	25%	SNP	−1.99	0.46	0.45	95.3	1.4	15.4	83.2	83.2
Interval-censored data
log-mixture	200	20% right, 80% interval	SNP	−2.01	0.48	0.47	95.7

Informally, the information on λ₀(t) and β is roughly “orthogonal,” so it is not unexpected that imposing smoothness assumptions on λ₀(t) and fitting the SNP-based PH model does not yield increased precision for estimating β relative to PL. For the PH model, the real advantage of the SNP approach is the ease with which it handles interval- and other arbitrarily-censored data. Under the gamma and log-mixture-normal scenarios, we generated interval-censored data for each subject by drawing five random examination times, where the times between each were independently lognormally distributed, and then generated independently an event time from the PH model. This led to the percentages of right- and interval-censored data in Table 1(a). Results of fitting the PH model by SNP for 1000 MC data sets with n = 200 show that the approach leads to reliable inferences.

The second set of scenarios involved a true PO model (9) with X and either independent 25% uniform right censoring or interval censoring as above, β = 2.0 or −2.0, n = 200, and 1000 data sets generated with f₀(t) lognormal with mean and scale 13.8 and 0.53, log-mixture-normal from $0.3\mathcal{N}(1.2,0.36)+0.7\mathcal{N}(-1.8,0.36)$, and Weibull with shape and scale 1.0 and 5.0. From Table 1(b), when the true PO model is fitted via SNP, reliable inferences on β obtain, and HQ is able to identify the true PO model well except for the Weibull; for this case, performance improves with increasing sample size.

In the third set of scenarios, data were generated from the AFT model (7) with X as above; β = 2.0; and f₀(t) lognormal with mean 0.5 and scale 1.31, Weibull with shape 2.0 and scale 16.0, gamma with shape and scale 2.0, and the log-mixture of normals $0.3\mathcal{N}(0.2,,0.36)+0.7\mathcal{N}(-1.8,0.36)$ (bimodal). For each of 1000 data sets with independent uniform right censoring, the AFT model was fitted via SNP; the Buckley-James method; and the rank-based method of Jin et al. (2003), with both logrank and Gehan-type weight functions, using the R function aft.fun (Zhou, 2006). Table 2 shows that the SNP method yields reliable inferences and compares favorably to competing semiparametric methods, achieving marked relative gains in efficiency in some cases. With n = 200 and 50% censoring, the SNP procedure continues to perform well. Undercoverage of SNP Wald confidence intervals in the log-mixture-normal case is resolved for n = 500. The PH and PO models were also fitted. In all but the gamma scenario, HQ strongly supports the AFT model; increasing to n = 500 in the gamma case vastly improves identification of the correct model. The similarity of the gamma distribution to a Weibull may be responsible for the difficulty the criterion has distinguishing the AFT and PH models for the smaller sample size.

Table 2.

Simulation results based on 1000 Monte Carlo data sets when the true model is the AFT model with baseline density f₀(t). For right-censored data, SNP, BJ, Gehan, and LR indicate fitting using the SNP approach with K and the base density chosen via HQ, the Buckley-James method, and the rank-based method of Jin et al. (2003) using Gehan-type and log-rank weight functions, respectively. All other entries are as in Table 1. For interval-censored data, only SNP was used. True value of β = 2.0 in all cases.

f0(t)	n	Cens. rate	Method	Mean	SD	SE	CP	AFT	PH	PO	Correct
Right-censored data
lognormal	200	25%	SNP	2.02	0.27	0.26	94.4	80.2	8.0	12.3	80.2
			BJ	2.02	0.27	0.26	94.2
			Gehan	2.02	0.27	0.28	95.3
			logrank	2.01	0.29	0.29	94.7
	200	50%	SNP	2.02	0.30	0.30	93.3
Weibull	200	25%	SNP	2.00	0.14	0.15	95.9	71.0	88.7	1.1	98.9
			BJ	2.00	0.18	0.19	96.3
			Gehan	2.00	0.17	0.17	95.7
			logrank	2.00	0.14	0.15	96.1
	200	50%	SNP	2.01	0.20	0.20	94.8
gamma	200	25%	SNP	2.00	0.20	0.19	94.0	65.0	66.4	11.4	65.0
			BJ	2.00	0.22	0.23	96.0
			Gehan	2.00	0.21	0.22	95.4
			logrank	2.00	0.20	0.21	95.4
	200	50%	SNP	2.00	0.26	0.24	92.9
	500	25%	SNP	2.00	0.06	0.06	94.0	98.8	1.2	0.0	98.8
log-mixture	200	25%	SNP	1.99	0.19	0.18	91.9	100.0	0.0	0.0	100.0
			BJ	1.99	0.42	0.28	80.5
			Gehan	1.99	0.29	0.29	95.6
			logrank	2.00	0.41	0.43	96.5
	200	50%	SNP	1.98	0.23	0.22	91.5
	500	25%	SNP	2.00	0.05	0.05	94.8
	500	50%	SNP	2.00	0.06	0.06	93.5
Interval-censored data
gamma	200	20% right, 80% interval	SNP	2.01	0.22	0.21	92.2
gamma	500	16% right, 84% interval	SNP	2.00	0.06	0.06	94.7
log-mixture	200	17% right, 83% interval	SNP	2.05	0.27	0.23	90.3
log-mixture	500	17% right, 83% interval	SNP	2.00	0.07	0.06	94.0

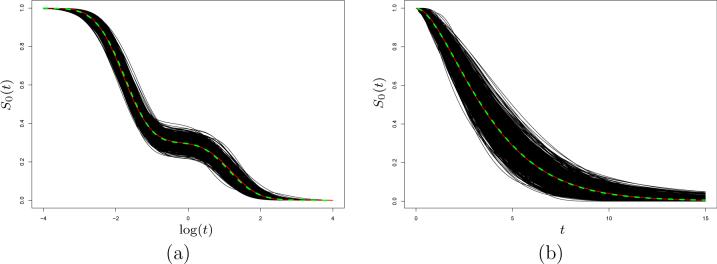
Byproducts of the SNP approach for any model are estimates of the corresponding density f₀(t) and survival function S₀(t). Figure 1 shows the 1000 estimates of S₀(t) under two of the AFT scenarios, demonstrating that its true form can be recovered with impressive accuracy.

Figure 1.

SNP estimates of S₀(t) for the AFT model based on 1000 Monte Carlo data sets, with the true S₀(t) (white solid line) and average of 1000 estimates (dashed line) superimposed. (a) log-normal mixture scenario with n = 500, 50% right censoring. (b) gamma scenario with n = 200, 25% right censoring.

We also carried out simulations for the true AFT model for gamma and log-mixture-normal scenarios under interval censoring, each with 1000 data sets generated as for the PH model to yield the censoring patterns in Table 2. The AFT model was fitted to each using the SNP approach; as for PH, the results demonstrate the reliable performance of the method, with undercoverage of confidence intervals for n = 200 under the log-mixture-normal.

For all three model scenarios, Table 3 presents for selected configurations the number of times each K-base density combination was chosen by HQ when fitting the true model. Not surprisingly, the normal base density is chosen most often when f₀(t) is lognormal and log-mixture normal, and the exponential base density is preferred for the Weibull and gamma.

Table 3.

Numbers of times each K-base density combination was chosen by the HQ criterion when fitting the true model (PH, AFT, PO) for selected configurations in Tables 1 and 2.

Base Density			Standard Normal			Standard Exponential
			K			K
f0(t)	n	Cens. rate	0	1	2	0	1	2
			True PH Model
lognormal	200	25%	873	43	19	11	33	21
Weibull	200	25%	9	0	35	854	74	28
gamma	200	25%	140	12	33	644	143	28
log-mixture	200	25%	239	26	721	0	0	14
gamma	200	18% right, 82% interval	302	28	8	645	12	5
log-mixture	200	20% right, 80% interval	505	62	241	9	6	177
			True AFT Model
lognormal	200	25%	873	49	18	10	30	20
Weibull	200	25%	3	0	24	890	54	29
gamma	200	25%	65	16	49	624	212	34
log-mixture	200	25%	0	153	847	0	0	0
gamma	200	20% right, 80% interval	223	32	17	640	68	20
log-mixture	200	18% right, 82% interval	0	567	432	0	0	1
			True PO Model
lognormal	200	25%	878	81	19	0	6	16
Weibull	200	25%	31	3	40	830	82	14
log-mixture	200	25%	0	225	774	0	0	1
log-mixture	200	18% right, 82% interval	0	620	350	0	6	24

Undercoverage of Wald intervals in some instances with n = 200 in Table 2 suggests that the delta method approximation may be less reliable for the AFT model than for PH and PO. We thus investigated replacing delta method standard errors by those from a nonparametric bootstrap, where the K-base density for the AFT model is chosen by HQ for each bootstrap data set. E.g., for the interval censored log-mixture scenario, for the first 300 of the 1000 MC data sets, the MC mean, standard deviation, average of delta method standard errors, and associated coverage are 2.05, 0.26, 0.23, and 90.3, respectively. The MC average of bootstrap standard errors using 50 bootstrap samples and coverage of the associated interval are 0.28 and 94.3, suggesting that this approach can correct underestimation of sampling variation.

The foregoing results involved simple models with a single covariate in order to allow reporting for a number of scenarios with straightforward interpretation. Given failure to achieve nominal coverage for some settings for the AFT model, further evaluation of the SNP-based approach in this case is warranted. Moreover, demonstration of computational stability and feasibility of the proposed methods for all three models under more complex conditions is required. Accordingly, we carried out additional simulations. We report on representative scenarios, each involving 1000 MC data sets with n = 200 or 500 and 25% independent uniform right censoring and generated from the AFT model (7), where X = (X₁, X₂, X₃)^T with X₁ distributed as uniform on (0,2), X₂ Bernoulli with P(X₂ = 1) = 0.5, and $X_3\sim \mathcal{N}(0.5,1)$ and the true value of β = (2.5, 0.5, −0.8)^T . Table 4 shows results for fitting the AFT model when the true f₀(t) was lognormal with mean 54.6 and scale 7.3, gamma with with shape 2.0 and scale 6.0, and log-mixture of normals $0.3\mathcal{N}(1.2,,0.36)+0.7\mathcal{N}(-1.8,0.36)$ (bimodal). In all scenarios, no computational issues were encountered for any data sets, and performance is similar to that for the simpler models above, with analogous undercoverage of Wald intervals for components of β in some cases. HQ chose K-base density combinations in proportions similar to those in Table 3 in all cases. For the gamma and log-mixture scenarios with n = 200, we used a nonparametric bootstrap with 50 bootstrap replicates as described above to obtain alternative standard errors for the first 300 MC data sets; results are indicated by an asterisk in Table 4 and suggest that, as above, use of bootstrap standard errors to form Wald intervals yields reasonable performance.

Table 4.

Simulation results for the SNP approach based on 1000 Monte Carlo data sets when the true model is the AFT model with baseline density f₀(t) and multiple covariates under right censoring. Entries are as in Table 1. The True β column gives the true values of the elements of β. Entries with an asterisk (*) at the sample size indicate results for the first 300 Monte Carlo data sets, for which both delta method and nonparametric bootstrap standard errors were used, where SE_boot and CP_boot denote the average of bootstrap standard error and Monte Carlo coverage probability expressed as a percent, of 95% Wald confidence intervals using the bootstrap standard errors, respectively. For each scenario, N_K and E_K, K = 0, 1, 2, indicate the number of times the configuration of normal (N) or exponential (E) base density with the indicated K was chosen by HQ.

f0(t)	n	Cens. rate	True β	Mean	SD	SE	CP	SEboot	CPboot
lognormal	200	25%	2.5	2.51	0.27	0.26	94.8
			0.5	0.49	0.15	0.15	93.5
			−0.8	−0.81	0.30	0.29	94.6
	(N0 = 853, N1 = 64, N2 = 19, E0 = 8, E1 = 38, E2 = 18)
gamma	200	25%	2.5	2.50	0.16	0.11	93.3
			0.5	0.50	0.06	0.06	92.3
			−0.8	−0.80	0.12	0.11	92.1
	(N0 = 50, N1 = 16, N2 = 60, E0 = 594, E1 = 237, E2 = 43)
	200*	25%	2.5	2.50	0.11	0.11	93.3	0.13	96.0
			0.5	0.51	0.07	0.06	92.7	0.07	95.0
			−0.8	−0.79	0.12	0.11	91.3	0.13	96.3
	500	25%	2.5	2.50	0.07	0.07	93.7
			0.5	0.50	0.04	0.04	93.1
			−0.8	−0.80	0.07	0.07	93.8
	(N0 = 0, N1 = 3, N2 = 68, E0 = 418, E1 = 464, E2 = 47)
log-mixture	200	25%	2.5	2.49	0.10	0.09	94.1
			0.5	0.50	0.06	0.05	92.8
			−0.8	−0.80	0.11	0.10	91.8
	(N0 = 0, N1 = 197, N2 = 803, E0 = 0, E1 = 0, E2 = 0)
	200*	25%	2.5	2.49	0.09	0.09	95.3	0.10	96.7
			0.5	0.50	0.06	0.05	93.0	0.06	94.0
			−0.8	−0.80	0.11	0.10	91.7	0.11	93.0
	500	25%	2.5	2.49	0.06	0.06	94.7
			0.5	0.50	0.03	0.03	94.7
			−0.8	−0.80	0.07	0.06	94.5
	(N0 = 0, N1 = 16, N2 = 984, E0 = 0, E1 = 0, E2 = 0)

We also carried out analogous simulations under the PH and PO models, representative results of which are in Web Appendix F. Again, computation was stable and straightforward in every situation we tried, and, as in the single covariate case reported above, coverage of delta method intervals achieved the nominal level for both models.

Overall, the simulations demonstrate that the SNP approach is computationally straightforward and yields reliable performance under the “smoothness” assumption and provides a tool for practical model selection. Simulations showing performance of the SNP approach for the model extensions described in Section 3.2 are given in Web Appendices D and E.

5. Applications

5.1 Cancer and Leukemia Group B Protocol 8541

Lin et al. (2006) discuss Cancer and Leukemia Group B (CALGB) protocol 8541, a randomized clinical trial comparing survival for high, moderate, and low dose regimens of cyclophosphamide, adriamycin, and 5-flourouacil (CAF) in women with early stage, node-positive breast cancer. Following the primary analysis, interest focused on the prognostic value of baseline characteristics. We consider estrogen receptor (ER) status; ER-positive tumors are more likely to respond to anti-estrogen therapies than those that are ER-negative. ER status is available for 1437 of the 1479 subjects, of whom 64% were ER-positive, with 64% right-censored survival times. Figure 1 of Lin et al. (2006) suggests that the relationship of survival to ER status does not exhibit proportional hazards, a finding corroborated by their spline-based test for departures from proportional hazards (p-value=< 0.001).

We fit the AFT, PH, and PO models with binary covariate X_i (=1 if ER-positive) using SNP; here and in Section 5.2 we considered the normal and exponential base densities and K_max = 2. The HQ criterion was 10177, 10197, and 10192 for the preferred K-base density combinations for AFT, PH, and PO, respectively. Both the PL and SNP fits of the PH model yielded an estimated hazard ratio of 0.77. The AFT model is best supported by the data, consistent with the evidence discrediting the PH model. The preferred AFT fit takes K = 1 with normal base density, with an estimate of β of 0.45 (SE 0.08). Here, the effect of a covariate is multiplicative on time itself rather than on the hazard, leading to the interpretation that failure times for ER-positive women are “decelerated” relative to those for ER-negative women: the probability that an ER-positive woman survives to time t is the same as the probability that an ER-negative woman survives to time 0.64t, so that, roughly, being ER-negative curtails survival times by 64% relative to being ER-positive. A possible explanation is that ER-positive women may have received anti-estrogen therapy during follow-up, enhancing their survival.

Further analyses of the CALBG 8541 data are in Web Appendix F.

5.2 Breast Cosmesis Study

The famous breast cosmesis data (Finkelstein and Wolfe, 1985) involve time to cosmetic deterioration of the breast in early breast cancer patients who received radiation alone (X = 0, 46 patients) or radiation+adjuvant chemotherapy (X = 1, 48 patients). Deterioration times were right-censored for 38 women. Times for the 56 women experiencing deterioration were interval-censored due to its evaluation only at intermittent clinic visits. Numerous authors have used these data to demonstrate methods for interval censored data.

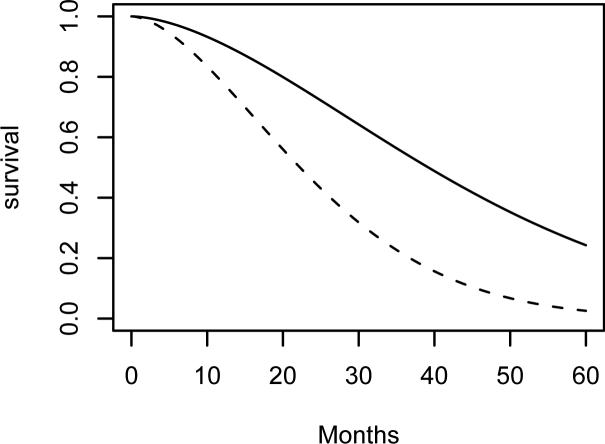
We fitted the AFT, PH, and PO models using the SNP approach, obtaining HQ values of 309, 309, 317, respectively, for the chosen K-base density combination, supporting AFT and PH. The preferred fit for each uses K = 0 and the exponential base density; this configuration is equivalent to a Weibull regression model, for which the PH and AT models are the same. This is consistent with the adoption of the PH (e.g., Goetghebeur and Ryan, 2000; Betensky et al., 2002) or AFT (e.g., Tian and Cai, 2006) models by many authors. The SNP estimate of β = 0.95 (SE 0.280) in (5) is consistent with the results from several methods for fitting the PH model with interval censored data reported by Goetghebeur and Ryan (2000) and Betensky et al. (2002). The corresponding Wald statistic for testing β = 0 is 3.35, in line with the score statistic of Finkelstein (1986) of 2.86 and Wald statistics implied in Table 2 of Goetghebeur and Ryan (2000). Figure 2 shows the SNP estimates of S(t | X = 0) and S(t | X = 1) based on the PH fit; compare to Figure 1 of Goetghebeur and Ryan (2000).

Figure 2.

Estimated survival functions for time to cosmetic deterioration for the radiation only group (solid line) and radiation+chemotherapy group (dashed line) based on the SNP fit of the PH (AFT) model to the breast cosmesis study data.

6. Discussion

We have proposed a general framework for regression analysis of arbitrarily censored time-to-event data under the mild assumption of a “smooth” density for model components ordinarily left unspecified under a semiparametric perspective. The methods are straightforward to implement using standard optimization software, and computation is stable across a range of conditions. A SAS macro is available from the first author. Although we focused on the PH, AFT, and PO models, the approach allows any competing models, such as generalizations of (7), models with nonlinear covariate effects, and linear transformation models to be placed in a common framework, providing a basis for model selection. Standard errors and Wald confidence intervals may be obtained using standard parametric asymptotic theory in most cases; however, this approximation is less reliable for the AFT model, so we recommend using a nonparametric bootstrap with small samples/numbers of failures in this case. A rigorous proof of consistency and asymptotic normality of the estimators for β and functionals of f₀(t) in the general censored-data regression formulation here is an open problem.

It should be possible to adapt the approach to problems involving both censoring and truncation (Joly et al., 1998; Pan and Chappell, 2002). Because with the SNP representation f(t|X;β) and S(t|X;β) are in “parametric” form, the likelihood function is straightforward under the usual assumption that censoring and truncation are independent of event time.

A further advantage, not illustrated here, is that an efficient rejection sampling algorithm for simulation from a fitted SNP density is available (Gallant and Tauchen, 1990). This may be used to simulate draws from the fit of f₀(t) under the preferred model and hence draws of T_i from f(t|X) for any X, allowing any functional of this distribution to be approximated.

Supplementary Material

supplementary

Supplementary Materials

Web Appendices A–F, referenced in Sections 2, 3.1, 3.2, 4, and 5.1, are available under the Paper Information link at the Biometrics website http://www.biometrics.tibs.org.