Effects of Reinforcer Delay and Variability in a Successive-Encounters Procedure

Abstract

Pigeons responded in a successive-encounters procedure that consisted of a search period, a choice period, and a handling period. The search period was either a fixed-interval or mixed-interval schedule presented on the center key of a three-key chamber. Upon completion of the search period, the center key was turned off and the two side keys were lit. A pigeon could either accept a delay followed by food (by pecking the right key) or reject this option and return to the search period (by pecking the left key). During the choice period, a red right key represented the long alternative (a long handling delay followed by food), and a green right key represented the short alternative (a short handling delay followed by food). The experiment consisted of a series of comparisons for which optimal diet theory predicted no changes in preference for the long alternative (because the overall rates of reinforcement were unchanged), whereas the hyperbolic-decay model predicted changes in preference (because the delays to the next possible reinforcer were varied). In all comparisons, the results supported the predictions of the hyperbolic-decay model, which states that the value of a reinforcer is inversely related to the delay between a choice response and reinforcer delivery.

The successive-encounters procedure was developed by Lea (1979) to serve as a laboratory analog to a foraging situation in which an animal searches for, pursues, and consumes different types of prey. The procedure typically consists of a search period, a choice period, and a handling period. In the search period, the animal must wait for a prey item to appear. In the choice period, the animal can either accept the prey item or reject it and return to the search period. If a prey item is accepted, the animal enters the handling period—a reinforcement schedule that is meant to be analogous to the time needed to capture and consume the prey. For example, in one condition of Lea's experiment with pigeons, each trial began with a fixed-interval (FI) 5-s schedule on a white center key (the search period). When a pigeon completed the FI schedule, the choice period began. The center key remained white, and a side key was lit either green or red (with equal probability), and these two key colors represented two different types of “prey” that were associated with two different handling times. The green key represented a prey item with a short handling time (an FI 5-s schedule leading to food), and the red key represented a prey item with a long handling time (an FI 20-s schedule leading to food). With either alternative, the pigeon could accept the prey (by pecking the green or red key) or reject it (by pecking the white key three times, which would return the pigeon to the search period and the beginning of a new FI 5-s schedule). The pigeons almost always accepted the short alternative (the green key), which is not surprising because rejecting it and returning to the search period would always increase the delay to the next food delivery. Of greater theoretical interest were the pigeons' choices when the long alternative (the red key) was presented.

To predict whether the pigeons would accept or reject the long alternative, Lea (1979) relied on a version of optimal foraging theory now known as optimal diet theory (Cook & Cockrell, 1978; Sih & Christensen, 2001). Stated simply, optimal diet theory predicts that the animal should only accept the long alternative if, on average, it provides a greater amount of food per unit time than could be obtained by returning to the search period (cf. Goss-Custard, 1977; Krebs, Erichsen, Webber, & Charnov, 1977; Snyderman, 1983). For this specific example, optimal diet theory states that the pigeon should always reject the long alternative, because a strategy of continually returning to the search period until the short alternative (the green key) is presented would result in an average of one food delivery every 15 s (since it would take an average of two presentations of the 5-s search period to reach the 5-s handling period for the short alternative), which is shorter than the 20-s handling time for the long alternative.

Suppose, however, that the search period is FI 7.5 s rather than FI 5 s. Now optimal diet theory predicts indifference between acceptance and rejection of the long alternative, because the average time to food is 20 s whether the animal accepts the long alternative or returns to the search period. (In this case, if the long alternative were always rejected, it would take an average of two presentations of the 7.5-s search period to reach the 5-s handling period for the short alternative, which is a total of 20 s.) Furthermore, if the search period is longer than 7.5 s, optimal diet theory predicts that the animal should always accept the long alternative, because rejecting it would, on average, result in an average time to food of more than 20 s. In summary, for this example the theory predicts that the long alternative should always be rejected if the duration of the search period is less than 7.5 s, and it should always be accepted in the duration of the search period is more than 7.5 s.

The results from Lea's (1979) study provided only mixed support for optimal diet theory. As predicted by the theory, the pigeons were more likely to accept the long alternative when the search period was longer. However, acceptance percentages for the long alternative increased gradually as the duration of the search period increased, whereas optimal diet theory predicted that preference should be all-or-none. Furthermore, whereas optimal diet theory predicted that the switch from rejection to acceptance of the long alternative should occur when the search period was 7.5 s, the pigeons continued to reject the long alternative on a majority of the trials when the search period was much longer than 7.5 s. Using a similar procedure, Abarca and Fantino (1982) found better support for the predictions of optimal diet theory when they used variable-interval (VI) schedules rather than FI schedules in the handling periods. Abarca and Fantino also showed that delay-reduction theory (e.g., Fantino, 1969: Squires & Fantino, 1971) makes the same predictions as optimal diet theory for this situation (rejection of the long alternative when the search period is less than 7.5 s and acceptance when the search period is longer than 7.5 s). Later studies examined other variations of the successive-encounters procedure, and in most cases the findings were consistent with the predictions of both optimal diet theory and delay-reduction theory (e.g., Abarca, Fantino, & Ito, 1985; Fantino & Preston, 1988; Hanson & Green, 1989).

One prediction of optimal diet theory that has not been supported by experimental results is that the type of schedule (e.g., fixed or variable) used in the search and handling periods should make no difference as long as the mean rates of food presentations are the same. Mazur (2007) used a successive-encounters procedure similar to Lea's (1989), but the search periods consisted of FI schedules in some conditions and mixed-interval (MI) schedules in other conditions (in which the duration of the interval on any given trial could either be short or long, with equal probability). In addition, the handling periods consisted of fixed-time (FT) schedules in some conditions and mixed-time (MT) schedules in other conditions. The main finding was that the types of schedules had a large effect on acceptance of the long alternative. The pigeons were more likely to accept the long alternative when the search periods were FI schedules than when they were MI schedules, and they were more likely to reject the long alternative when the handling periods were FT schedules than when they were MT schedules.

Mazur (2007) showed that although these schedule-based differences were not consistent with optimal diet theory (or with delay-reduction theory), they were consistent with the predictions of the hyperbolic-decay model (Mazur, 1987, 2001). This model states that the value or strength of a reinforcer is inversely related the delay between a choice response and the delivery of a reinforcer. The hyperbolic-decay model can be expressed as follows:

$$V=\sum _{i=1}^n{P}_i\left(\frac{A}{1+K{D}_i}\right),$$ 1

where V is the value of a reinforcer that could be delivered after any one of n possible delays. P_i is the probability that the reinforcer will be delivered after a delay of D_i seconds, A represents the size of the reinforcer, and K is a parameter that determines how rapidly V decreases with increases in D_i. This equation states that when the time to reinforcement can be one of several different delays, the value of that alternative is an average of the values of the different possible delays, each weighted by its probability of occurrence. The model assumes that in a choice situation, an animal will choose whichever alternative has the larger V. This equation has been successfully applied to a variety of different choice situations, including self-control choice (Mazur, 1987), choice between fixed and variable reinforcer delays (Mazur, 1984), and choice between certain and uncertain reinforcers (Mazur, 1989; Mazur & Romano, 1992). Many studies have also applied the principle of hyperbolic discounting to economic choices made by humans (e.g., Hantula & Bryant, 2005; Madden, Begotka, Raiff, & Kastern, 2003; Overton & MacFadyen, 1998).

For analyzing choice in the successive-encounters procedure, the most important implication of the hyperbolic-decay model is that variable delays should be preferred over fixed delays with the same average time to reinforcement. To see why the model makes this prediction, suppose an animal must choose between a FT 20-s schedule and an MT 4-s 36-s schedule (in which the delay to reinforcement could be 4 s or 36 s, with equal probability). We can arbitrarily set A = 100 and K = 1 in Equation 1. With these values, Equation 1 predicts that V = 4.76 for the FT 20-s schedule. For the MT 4-s 36-s schedule, V = 11.35, because this is the average of the values of reinforcers delivered after a 4-s delay (V = 20) and after a 36-s delay (V = 2.70). The model therefore predicts that, because of its higher value, the MT schedule will be preferred in a choice situation. The prediction that MT schedules will be preferred over FT schedules is not dependent on these particular parameter values: The prediction holds for any values of A and K greater than zero.

For a successive-encounters procedure, the hyperbolic-decay model predicts that each time an animal encounters the long alternative, the decision to accept or reject is based on which of these options has greater value, as calculated by Equation 1. Consider the finding of Mazur (2007) that the long alternative was accepted more often when it was MT 4 s 36 s than when it was FT 20 s. The model predicted this result because, as just shown, the value of a MT 4-s 36-s schedule is greater than the value of an FT 20-s schedule. Mazur also found that the long alternative was accepted more often when the search period was an FI schedule (e.g., FI 5 s) rather than an MI schedule of the same mean duration (e.g., MI 0.5 s 9.5 s). The model predicted this result because if the animal rejected the long alternative and returned to an MI search schedule, there was a 50% chance that the next search period would be of short duration, whereas there was no such possibility with an FI search schedule. The value of returning to the search period was therefore higher with the MI schedule. In summary, the different acceptance rates with fixed and mixed schedules were consistent with the predictions of the hyperbolic-decay model, whereas according to optimal diet theory the type of schedule should have made no difference.

The present experiment used the same pigeons and the same general procedure as in Mazur's (2007) experiment. The purpose of this experiment was to extend the findings of the previous study by testing several additional cases for which optimal diet theory and the hyperbolic-decay model make distinctly different predictions. In each comparison, optimal diet theory predicted that the manipulation should have no effect because the average rates of reinforcement for the accepting and rejecting the long alternative were unchanged. In contrast, the hyperbolic-decay model predicted that the manipulation should affect the acceptance rate for the long alternative, because the distribution of delays between a choice response and food delivery was altered.

The first phase of this experiment compared conditions in which the search period was either an FI or a MI schedule, and the handling periods for both alternatives were MT schedules (MT 2.5 s 7.5 s for the short alternative, and MT 10 s 30 s for the long alternative). The hyperbolic-decay model predicted that the pigeons should be more likely to reject the long alternative when the search period was an MI schedule, because there was a 50% chance that the next search period could be a short one, and the next prey item might be the short alternative. Similar schedules were used in Mazur's (2007) experiment, but because of the particular schedule values used, the hyperbolic-decay model predicted only a small difference between the FI and MI conditions, and only a small difference was found. However, with the less extreme components in the two handling schedules used in the present experiment, the hyperbolic-decay model predicted a larger difference: the pigeons should be more likely to reject the long alternative when the search period was an MI schedule. This phase of the experiment also included a set of conditions in which the handling period for the long alternative was changed from MT 10 s 30 s to FT 20 s, but the handling period for the short alternative was not changed. The hyperbolic-decay model predicted that the pigeons should be more likely to reject the long alternative when it is FT 20 s, because according to Equation 1, the value of FT 20 s is lower than the value of MT 10 s 30 s.

The next phase of the experiment compared two conditions with an MI 1-s 19-s search period, and the handling periods were MT schedules for both the long and the short alternatives. In one condition, every 1-s search period was followed by the short alternative, and every 19-s search period was followed by the long alternative. (Because a short search period led to a short handling schedule and a long search period led to a long handling schedule, this will be called the SS/LL condition.) In the other condition (the SL/LS condition), this situation was reversed: every 1-s search period was followed by the long alternative, and every 19-s search period was followed by the short alternative. The hyperbolic-decay model predicted that the pigeons would be more likely to reject the long alternative in the SS/LL condition, because returning to the search period could lead to a shorter delay to food than in the SL/LS condition. Optimal diet theory predicted no difference between these two conditions, because the long and short alternatives were the same in both conditions, and the mean time to food after a return to the search period was also the same in both conditions.

The final phase of the experiment included two conditions in which the long alternative was an MT 10 s 30 s schedule that delivered food on only 50% of the trials. In one condition, food was delivered whenever the handling period was 10 s, but not when the handling period was 30 s. These conditions were reversed in the second condition: food was presented after all 30-s handling periods but not after 10-s handling periods. The hyperbolic-decay model predicted that the pigeons would be more likely to accept the long alternative in the former condition because there was a 50% chance that food would be delivered after a delay of only 10 s, whereas this could not occur in the latter condition. Optimal diet theory predicted no difference between the two conditions, because in both conditions the average rate of food presentations during the long handling periods was one reinforcer every 40 s.

In summary, this experiment included a series of tests using a successive-encounters procedure for which optimal diet theory predicted there should be no change in acceptance of the long alternative because the mean reinforcement rates for acceptance and rejection were held constant. In each case, the hyperbolic-decay model predicted a change in acceptance of the long alternative because the schedules were changed in ways that altered the values of acceptance and rejection, as calculated with Equation 1.

Method

Subjects

The subjects were four male White Carneau pigeons (Palmetto Pigeon Plant, Sumter, South Carolina) maintained at approximately 80% of their free-feeding weights. They had previously participated in Mazur's (2007) experiment that used the same type of successive-encounters procedure.

Apparatus

The experimental chamber was 30 cm long, 30 cm wide, and 31 cm high. The chamber had three response keys, each 2 cm in diameter, mounted in the front wall of the chamber, 24 cm above the floor and 8 cm apart, center to center. A force of approximately 0.15 N was required to operate each key. Behind each key was a 12-stimulus projector (Med Associates, St. Albans, VT) that could project different colors or shapes onto the key. A hopper below the center key provided controlled access to grain, and when grain was available, the hopper was illuminated with a 2-W white light. The chamber was enclosed in a sound-attenuating box containing a ventilation fan. All stimuli were controlled and responses recorded by a personal computer using MED-PC software.

Procedure

Experimental sessions were usually conducted six days a week. The experiment consisted of 16 conditions, each continuing until a pigeon satisfied certain stability criteria, as described below. Each session included of a series of trials that consisted of a search period, a choice period (in which a reinforcer was either accepted or rejected), and, if the reinforcer was accepted, a handling period (a delay followed by food). The 16 conditions, and the order in which they were presented to each pigeon, are shown in Table 1.

Table 1.

For each condition, the search key stimulus, search interval, long handling time, and order of conditions for each pigeon are shown. The short handling schedule was MT 2.5 s 7.5 s in all conditions. All durations are in seconds.

Type of Condition	Search Key Stimulus	Search Interval	Long Handling Time	Condition Order
				P1	P2	P3	P4
FI-MT	horizontal line	2.5	10 or 30	1	2	5	6
FI-MT	white	10	10 or 30	3	4	7	8
FI-MT	triangle	15	10 or 30	2	1	6	5
FI-MT	square	20	10 or 30	4	3	8	7
MI-MT	horizontal line	0.25 or 4.75	10 or 30	5	6	1	2
MI-MT	white	1 or 19	10 or 30	7	8	3	4
MI-MT	triangle	1.5 or 28.5	10 or 30	6	5	2	1
MI-MT	square	2 or 38	10 or 30	8	7	4	3
MI-MT/FT	horizontal line	0.25 or 4.75	20	9	10	9	10
MI-MT/FT	white	1 or 19	20	11	12	11	12
MI-MT/FT	triangle	1.5 or 28.5	20	10	9	10	9
MI-MT/FT	square	2 or 38	20	12	11	12	11
SS/LL	white	1 or 19a	10 or 30	14	14	13	13
SL/LS	white	1 or 19b	10 or 30	13	13	14	14
S+/L−	white	10	10(food) or 30(no food)	16	16	15	15
S−/L+	white	10	10(no food) or 30(food)	15	15	16	16

^aIn the SS/LL condition, the short alternative always followed a 1-s search, and the long alternative always followed a 19-s search.

^bIn the SL/LS condition, the long alternative always followed a 1-s search, and the short alternative always followed a 19-s search.

FI-MT conditions

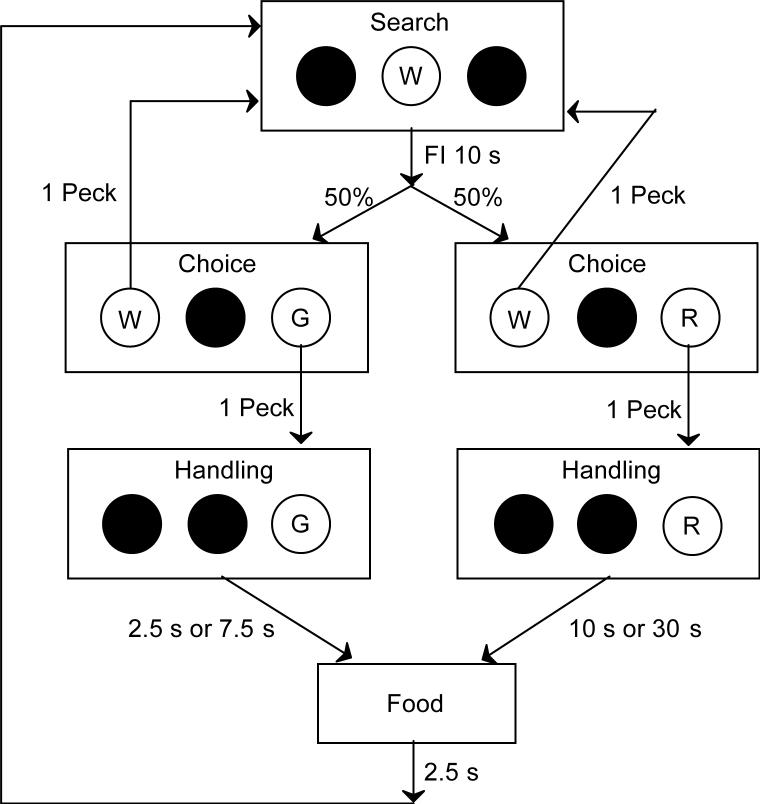
In these four conditions, the search period was an FI schedule, and the handling schedules were MT 2.5 s 7.5 s for the short alternative and MT 10 s 30 s for the long alternative. Figure 1 diagrams the procedure for one of these conditions, in which the search schedule was FI 10 s. Each trial began with the search period, in which the center key was white and an FI 10-s schedule in effect. Once the pigeon completed the FI requirement, the center key became dark, and the choice period began, with the left key white and the right key either green or red (with key color chosen randomly with the constraint that in every 20 trials, each color occurred 10 times). If the right key was green, this indicated that the short alternative (MT 2.5 s 7.5 s) was available. The pigeon could either accept the short alternative by pecking the green key or return to the search period by pecking the white key. If the green key was pecked, the left key became dark and the right key remained green for the handling period (which was either 2.5 s or 7.5 s), followed by a 2.5-s food presentation. Only the white light above the food hopper was lit during all food presentations. After each food presentation, the white center key was turned on and the search period of the next trial began.

Figure 1.

A diagram of the procedure in one of the FI-MT conditions, with an FI 10-s search period.

If the right key was red during the choice period, this indicated that the long alternative (MT 10 s 30 s) was available, and the pigeon could accept this alternative by pecking the red key or return to the search period by pecking the white key. If the red key was pecked, the left key became dark and the right key remained red for the handling period (which was either 10 s or 30 s), followed by a 2.5-s food presentation and then the start of the next trial.

During both the search period and the choice period, every effective peck on an illuminated key produced a feedback click. Pecks on the right key during the handling periods did not produce feedback clicks, nor did pecks on dark keys. Sessions ended after 60 food presentations or 60 min, whichever came first.

In the other three FI-MT conditions, the procedure was the same except that different FI schedules were used during the search period, and each FI schedule was associated with a different stimulus on the center and left keys, as shown in Table 1. For example, in the condition with an FI 20-s search period, a white square was projected on the center key during the search period, and on the left key during the choice period.

MI-MT conditions

In these four conditions, the handling schedules were the same as in the FI-MT conditions, but the search periods were two-component MI schedules instead of FI schedules. Each condition used a different MI schedule, and in each MI schedule the larger interval was 19 times as long as the smaller interval (see Table 1). For example, in one condition, the search period was MI 2 s 38 s. Each time the search period was entered, the interval requirement was either 2 s or 38 s, selected at random with the constraint that each interval occurred 5 times in every 10 entries into the search period. The mean durations of the four MI schedules were matched to the durations of the four FI schedules used in the FI-MT conditions (e.g., the mean duration of the MI 2-s 38-s search period was 20 s, thereby matching it to the condition with a FI 20-s search period). As shown in Table 1, the stimuli that appeared on the center key during the search period and on the left key during the choice period were the same as in the FI-MT condition to which each MI-MT condition was matched. Therefore, except for the change from FI to MI search periods, the procedure was exactly the same as in the FI-MT conditions.

MI-MT/FT conditions

These four conditions included the same schedules as the MI-MT conditions, except that the handling schedule for the long alternative was FT 20 s instead of MT 10 s 30 s. The handling schedule for the short alternative continued to be MT 2.5 s 7 5 s. Because the hyperbolic-decay model predicts preference for variable over fixed delays, it predicted that the pigeons would be more likely to accept the long alternative when it was MT 10 s 30 s than when it was FT 20 s. Optimal diet theory predicted no difference, because the mean delay to food was 20 s in both cases.

SS/LL and SL/LS conditions

In these two conditions, the search schedule was MI 1 s 19 s, the short handling schedule was MT 2.5 s 7.5 s, and the long handling schedule was MT 10 s 30 s. However, unlike previous conditions (in which either the long or short alternative was equally likely to follow either a short or long search period), which alternative occurred depended on whether the search period was 1 s or 19 s. In the SS/LL condition, if the search period was short (1 s), the short alternative (MT 2.5 s 7.5 s) always followed. If the search period was long (19 s), the long alternative (MT 10 s 30 s) always followed. Therefore, whenever a pigeon returned to the search period, the total time to the next possible reinforcer (MI duration plus the MT duration) could be any one of the following: 3.5 s, 8.5 s, 26.5 s, or 49.5 s.

In the SL/LS condition, the schedules that followed the short and long components of the MI schedule were reversed. If the search period was short (1 s), the long alternative (MT 10 s 30 s) always followed. If the search period was long (19 s), the short alternative (MT 2.5 s 7.5 s) always followed. Therefore, whenever a pigeon returned to the search period, the total time to the next possible reinforcer could be any one of the following: 11 s, 31 s, 21.5 s, or 26.5 s. Notice that in both the SS/LL and SL/LS conditions, the average time from the beginning of the search period to the next possible reinforcer was 22.5 s, so optimal diet theory predicted that there should be no difference in the rate of long alternative rejections. However, the hyperbolic-decay model predicted a higher likelihood of rejecting the long alternative in the SS/LL condition, because if the pigeon returned to the search period, there was a 50% chance that the time to the next reinforcer would be either 3.5 s or 8.5 s. In the SL/LS condition, if the pigeon returned to the search period, the two shortest possible delays to food were 11 s and 21.5 s. For any values of A and K greater than zero, Equation 1 predicts that returning to the search period should have a higher value in the SS/LL condition, so the animals should be more likely to reject the long alternative and return to the search period in this condition.

S+/L− and S−/L+ conditions

In these two conditions, the search schedule was FI 10 s and the short handling schedule was MT 2.5 s 7.5 s. The long handling schedule was a modified MT 10-s 30-s schedule in which food was delivered on only half of the trials. In the S+/L− condition, food was delivered at the end of every 10-s handling period of the long alternative, but no food was delivered after a 30-s handling period (in which case the red right key was simply turned off and a new search period began). In the S−/L+ condition, food was never delivered after a 10-s handling period but it was always delivered after a 30-s handling period. The hyperbolic-decay model predicted that the pigeons would be more likely to accept the long alternative in the S+/L− condition because of the possibility of a short (10-s) delay to food.

Stability Criteria

Conditions were terminated for individual pigeons as follows. To assess stability, the percentage of long alternatives accepted was calculated for each session. A condition was terminated immediately if the long acceptance percentage was either 0% or 100% for six consecutive sessions. Otherwise, each condition lasted for a minimum of 12 sessions, and was terminated for each subject individually when the following criteria were met: (a) neither the highest nor the lowest single-session percentage could occur in the last six sessions of a condition, and (b) the mean percentage across the last six sessions could not be the highest or the lowest six-session mean of the condition. An exception to these criteria was made for one subject (Pigeon P1) in the SS/LL condition. In its initial exposure to this condition, this pigeon accepted the long alternative on 100% of the trials, so it never experienced the consequences of rejecting the long alternative and returning to the search period. To encourage rejection of the long alternative, five sessions were conducted in which the long alternative was changed to FT 30 s, and during these sessions the pigeon began to reject the long alternative on more than half the trials. Then the long alternative was switched back to MT 10 s 30 s and the condition continued until the usual stability criteria were met.

Results

The number of sessions per condition needed to satisfy the stability criteria ranged from 6 to 33 (median = 13.5 sessions). For each pigeon and each condition, the results from the six sessions that satisfied the stability criteria were used in all data analyses. Almost any theory of choice would predict that the pigeons should accept the short alternative every time it was presented, and their actual performance came close to this ideal. In 66 out of 72 cases (4 pigeons in 16 conditions), the short alternative was accepted more than 99% of the time. In only one case was the short alternative accepted less than 85% of the time (74% by Pigeon P1 in Condition 10). Overall, the short alternative was accepted 98.5% of the time.

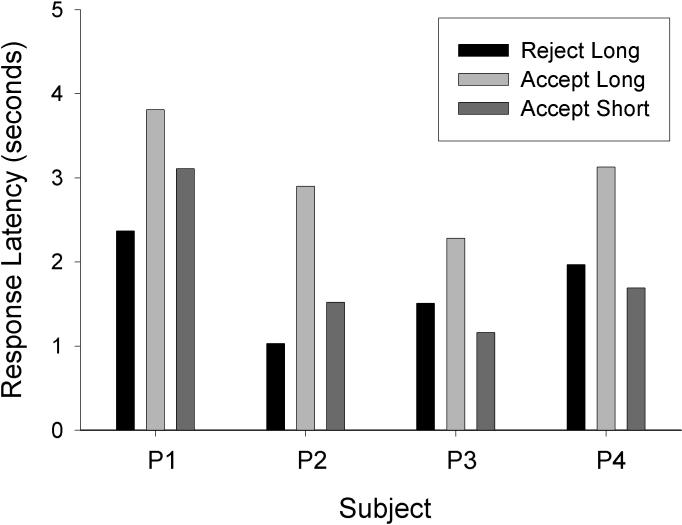
During the choice period, the pigeons typically responded quickly on one of the two side keys. For each pigeon, Figure 2 shows the mean response latencies for rejecting the long alternative, accepting the long alternative, and accepting the short alternative. Latencies for rejecting the short alternative are not shown because there were very few such cases. The latencies shown are means from the last six sessions from all 16 conditions. For all four pigeons, response latencies were longer when accepting the long alternative than when rejecting the long alternative or accepting the short alternative. A repeated-measures analysis of variance (ANOVA) found a significant effect of response type, F(2, 6) = 19.65, p < .01. A Tukey HSD test showed that latencies for accepting the long alternative were significantly longer than for either rejecting the long alternative or accepting the short alternative (ps < .01).

Figure 2.

For each pigeon, mean response latencies for rejecting the long alternative, accepting the long alternative, and accepting the short alternative are shown. The data are averaged across the last six sessions of all 16 conditions.

Many theories (including optimal diet theory, delay-reduction theory, and the hyperbolic-decay model) predict that in a successive-encounters procedure, acceptance of the long alternative should be all-or-none: Either the animal should accept the long alternative every time or reject it every time. However, previous studies using this procedure generally have not found all-or-none selection of the less desirable alternative (e.g., Lea, 1979; Mazur, 2007; Snyderman, 1983). Instead, the animals accepted the less desirable alternative on some trials and rejected it on others. Such gradations in acceptance percentages for the long alternative were also common in the present experiment. Figure 3 shows the long acceptance percentages for each pigeon in the first 12 conditions of the experiment. Although there were some cases in which the long acceptance percentages were at or close to 0% or 100%, all four pigeons had many conditions in which they were not. Possible reasons for these gradations of preference will be discussed later. For now, we can compare the theories on a more qualitative level, examining their predictions about which factors should and should not affect a pigeon's acceptance or rejection of the long alternative.

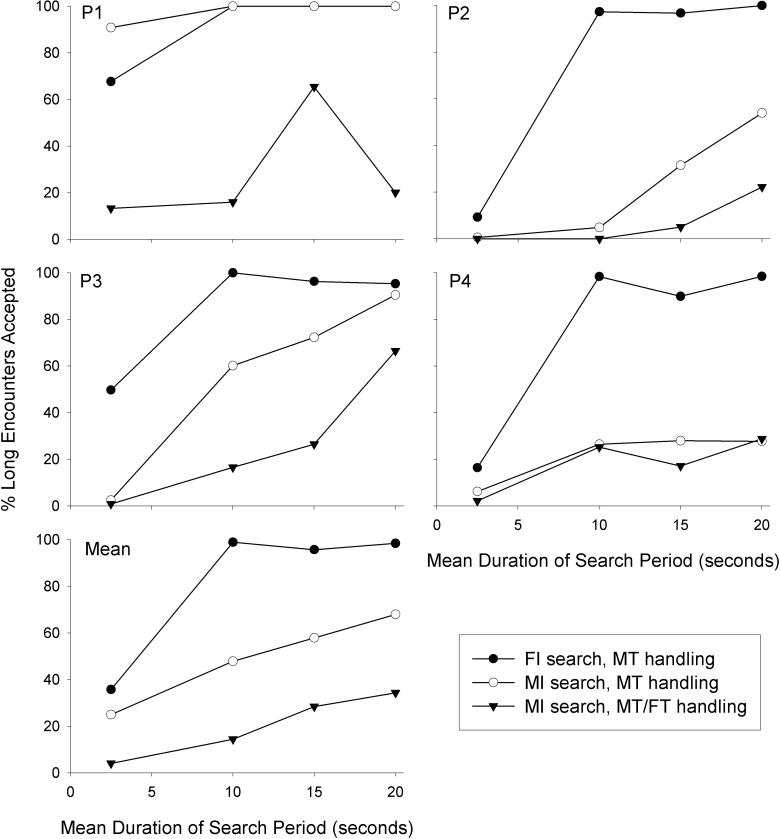
Figure 3.

For each pigeon and the group mean, the percentage of long encounters accepted is shown as a function of the mean duration of the search period for each of the FI-MT, MI-MT, and MI-MT/FT conditions.

Both optimal diet theory and the hyperbolic-decay model predict that animals should be more likely to accept the long alternative as the duration of the search period increases. Figure 3, which presents the results from conditions in which the search period ranged from 2.5 s to 20 s, shows that the long acceptance percentages increased with longer search periods. A two-way repeated-measures ANOVA found a significant effect of search schedule duration, F(3,9) = 16.69, p < .001. However, the two models differ in their predictions about the effects of the different schedule types that were used in this experiment. Optimal diet theory predicted that for any given search duration, there should be no differences in the FI-MT, MI-MT, and MI-MT/FT conditions, because the mean durations of the search and handling schedules were the same in these three types of conditions. As explained in the Introduction, the hyperbolic-decay model predicted that the long acceptance percentages should be highest in FI-MT conditions, intermediate in the MI-MT conditions, and lowest in the MI-MT/FT conditions. The results from individual subjects were consistent with these predictions, except that Pigeon P1 had acceptance percentages at or near 100% in most of the FI-MT and MI-MT conditions. The ANOVA found a significant effect of schedule type, F(2,6) = 14.22, p < .01. There was a significant linear contrast for schedule type, F(1,3) = 512.85, p < .001, with the highest long acceptance percentages in the FI-MT conditions and the lowest in the MI-MT/FT conditions. The interaction was between search schedule duration and schedule type was not significant, F(6,18) = 2.30.

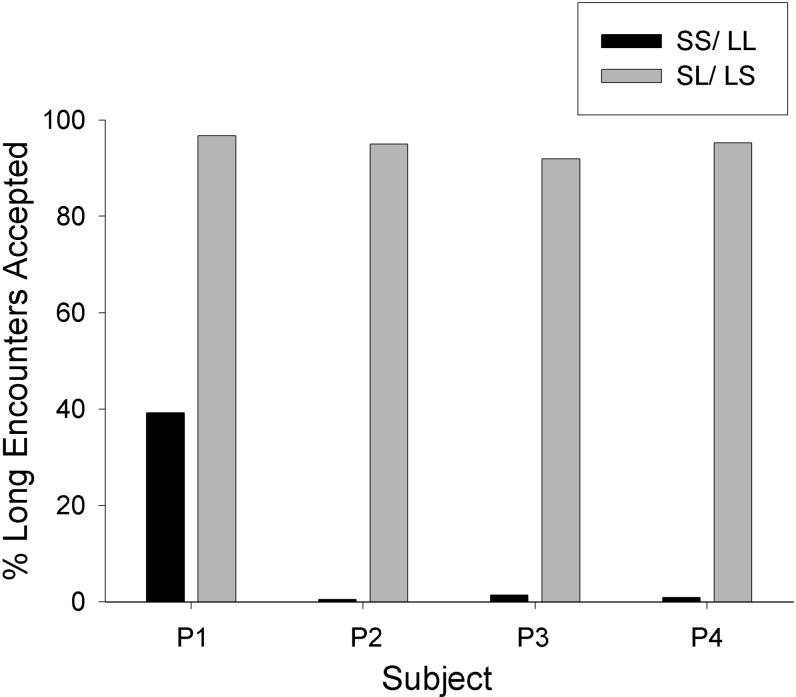
As explained in the Introduction, the hyperbolic-decay model predicted that the pigeons would be less likely to accept the long alternative in the SS/LL condition than in the SL/LS condition, because in the SS/LL condition there was a chance that rejecting the long alternative would be followed by a short search period and then the short alternative. Optimal diet theory predicted no difference between the two conditions because the mean search and handling times were the same in both. Figure 4 shows that the long acceptance percentages for all four pigeons were much lower in the SS/LL condition (M = 10.5%) than in SL/LS condition (M = 94.5%). The difference between the two conditions was significant, t(3) = 9.42, p < .01.

Figure 4.

For each pigeon, the percentage of long encounters accepted is shown for the SS/LL and SL/LS conditions.

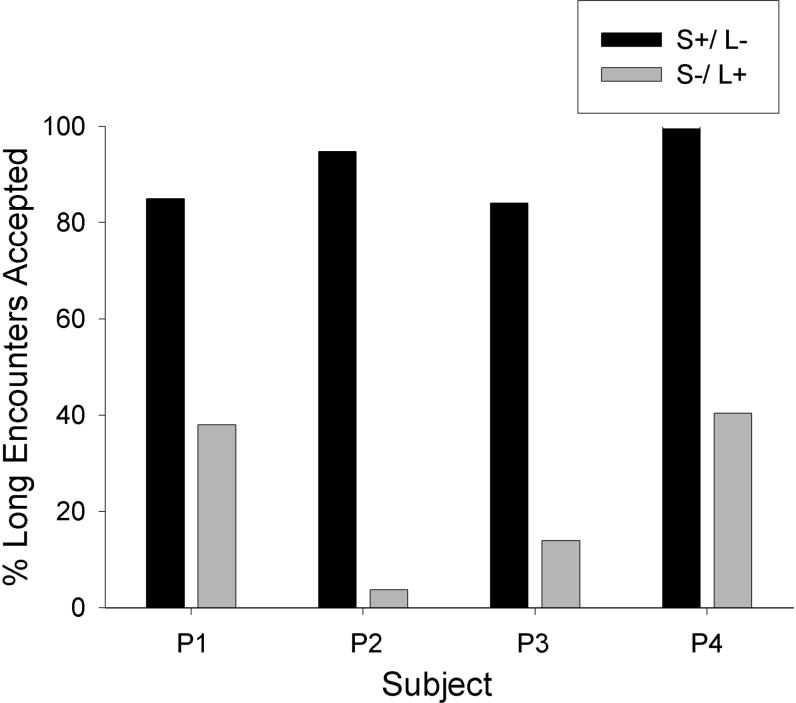
In the S+/L− condition, the long alternative delivered food after 10 s on half the trials, whereas in the S−/L+ condition the long alternative delivered food after 30 s on half the trials. Because of the possibility of a short delay to food, the hyperbolic-decay model predicted that the pigeons would be more likely to accept the long alternative in the S+/L− condition than in the S−/L+ condition. Once again, optimal diet theory predicted no difference between the two conditions because the mean search and handling times were the same in both conditions. Figure 5 shows that the long acceptance percentages for all four pigeons were much higher in the S+/L− condition (M = 90.9%) than in S−/L+ condition (M = 24.0%). The difference between the two conditions was significant, t(3) = 7.20, p < .01.

Figure 5.

For each pigeon, the percentage of long encounters accepted is shown for the S+/L− and L+/S− conditions.

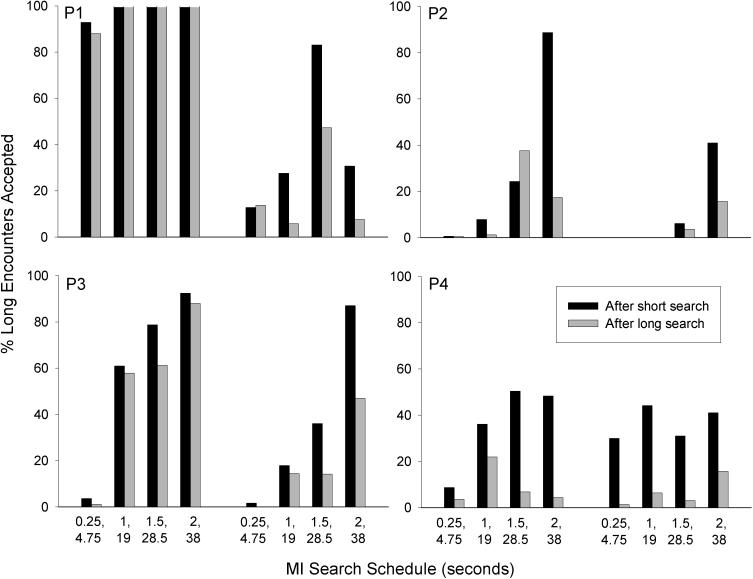
Mazur (2007) found that in conditions with MI search periods, the long acceptance percentages were often higher following the shorter component of the MI search schedule than after the longer component. This same pattern was found in the present experiment. For instance, when the search schedule was MI 1 s 19 s, the pigeons were more likely to accept the long alternative after a 1-s search period than after a 19-s search period. For the four MI-MT schedules and the four MI-MT/FT schedules, Figure 6 shows the long acceptance percentages after the shorter component of the MI schedule (black bars) and after the longer component (grey bars). These eight conditions from the four pigeons provide a total of 32 comparisons. In 5 of these cases, the percentages were either 0% or 100% after both the short and long MI components, but in 24 of the remaining 27 cases, the long acceptance percentage was higher after the shorter component. In some cases (e.g., the MI 2-s 38-s schedules for Pigeons P2 and P4), the differences in percentages were very large. Averaged across these eight conditions, the long acceptance percentages were 39.3% after a short MI component and 27.8% after a long MI component.

Figure 6.

For eight conditions with MI search schedules, the percentage of long encounters accepted after a short search period and after a long search period are shown. The left half of each panel shows the percentages from the four MI-MT conditions, and the right half shows the percentages from the four MI-MT/FT conditions.

Discussion

Optimal diet theory and the hyperbolic-decay model represent two different ways of conceptualizing an animal's decision-making as it chooses to accept or reject food opportunities in a successive-encounters procedure. Optimal diet theory represents a molar or global perspective, because it assumes that an animal's choices will be guided by the long-term rates of reinforcement: The animal will accept a less favorable prey item when, in the long run, it offers a higher rate of reinforcement than could be obtained by rejecting it and returning to the search period. The hyperbolic-decay model represents a more molecular or local perspective, because it is built on the assumption of delay discounting—that a reinforcer's value decreases with increasing delay, and an animal will choose whichever alternative has the higher value at the moment a choice is made.

Sometimes these two different approaches make the same prediction. For instance, in the successive-encounters procedure, both theories predict that animals should accept the more favorable alternative whenever it is encountered (and in the present experiment and previous ones, nearly complete acceptance of the more favorable alternative has been found; Abarca & Fantino, 1982; Lea, 1979; Mazur, 2007). However, in many cases these two approaches make distinctly different predictions about an animal's choices in a successive-encounters procedure. The present experiment included several cases in which the hyperbolic-decay model predicted a change in the pigeons' acceptance of the long alternative, whereas optimal diet theory predicted no change. In each case, the results supported the predictions of the hyperbolic-decay model. The long alternative was accepted less in the MI-MT conditions than in the FI-MT conditions, and still less in the MI-MT/FT conditions (Figure 3). Acceptance of the long alternative was much higher in the SL/LS conditions than in the SS/LL conditions (Figure 4), and much higher in the S+/L− conditions than in the S−/L+ conditions (Figure 5). For each of these comparisons, optimal diet theory predicted no differences in acceptance of the long alternative because the mean rates of reinforcement for accepting or rejecting the long alternative were identical across conditions. However, the values of accepting or rejecting the long alternative, as determined by the hyperbolic-decay model, did vary across conditions in each of these comparisons. The results therefore support the idea that choice in a successive-encounters procedure is not determined by the long-term reinforcement rates, but rather by the delay-discounted values of accepting or rejecting the long alternative.

Although the results of this experiment supported the hyperbolic-decay model at a qualitative level, the pigeons did not show the all-or-none acceptance of the long alternative that the model predicts. Because the values of accepting and rejecting the long alternative are the same on every trial of a session, an animal should presumably accept the long alternative every time or reject it every time (depending on whether its value is greater than or less than the value of returning to the search period). For similar reasons, both optimal diet theory and delay-reduction theory also predict that preference should be all-or-none in this procedure. In this experiment, the long acceptance percentages were close to 0% or 100% for some subjects in some conditions, but in many conditions they were not. Previous studies with the successive-encounters procedure have also found such intermediate acceptance percentages (e.g., Abarca & Fantino, 1982; Abarca et al., 1985; Fantino & Preston, 1988; Lea, 1979; Mazur, 2007). There are several possible explanations of this finding. One possibility is that with more exposure to a given condition, acceptance percentages would eventually reach 0% or 100%. This possibility seems unlikely. Although conditions changed every few sessions in Lea's (1979) original experiment, later studies used from 12 to 20 sessions per condition (Abarca & Fantino, 1982; Fantino & Preston, 1988; Mazur, 2007). In the present experiment, the stability criteria were included to try to ensure that choice percentages had stabilized, and it seems doubtful that longer exposure to each condition would have led to exclusive acceptance or rejection of the long alternative.

As another possibility, Mazur (2007) suggested that the values of accepting or rejecting the long alternative might vary over trials as a result of random sequences of events (such as several trials in a row in which the long alternative was encountered). Figure 6 shows that in the conditions with MI search schedules, the pigeons were more likely to accept the long alternative after a short search than after a long search. The reason for this behavior is unclear, but one explanation is that the pigeons detected and responded to slight variations in the probabilities of long and short search intervals. Because every 10 search periods included 5 short intervals and 5 long intervals, there was a slightly higher probability that a short search period would be followed by a long one (and vice versa) than that two short or two long search periods would occur in succession. Whether or not this procedural detail was the cause of the different acceptance percentages, they show that the pigeons' choices were not stable throughout a session, but rather that they varied as a function of short-term events.

A third possibility is that non-exclusive acceptance or rejection could be due to “errors” that the animals make because of failures of discrimination, association, or memory (cf., Davison & Jenkins, 1985; Jones & Davison, 1998). Another approach to this problem is to postulate a mechanism that leads to a gradual shift in preference rather than a step function. For example, in Grace's (1994) contextual-choice model, the probability of prey acceptance is described by a power function with an exponent that incorporates the ratio of handling time to search time, and this model predicts a gradual increase in acceptance of the long alternative as search time increases. Finally, Lea (1979) proposed that animals might have a tendency to vary their choices, sometimes accepting an alternative and sometimes rejecting it, because this strategy could help them detect any change in the reinforcement contingencies that might occur over time. Any of these possibilities might account for the non-exclusive preference observed in studies with the successive-encounters procedure, and the available data do not clearly favor one explanation over another.

In this article, optimal diet theory has been presented and tested in its most basic form, which makes specific quantitative predictions for the successive-encounters procedure (as explained in the Introduction). The main assumption of this theory is unambiguous—that animals will make choices that maximize the overall rate of reinforcement. However, over the years, many other foraging theories have been proposed that include additional assumptions and features to account for such factors as the stochastic nature of foraging environments (Oaten, 1977; Stephens & Charnov, 1982), variability in prey densities between and within patches (Chesson, 1978), a predator's tolerance for risk (Caraco, 1981), and so on. It is certainly possible that some of these theories, with their additional assumptions, may make predictions that are more similar to those of the hyperbolic-decay model and more consistent with the results of this experiment than the basic optimal diet model. If the main premise of this article is correct, the most successful foraging theories will be those that give more weight to immediate consequences than to delayed consequences.

In summary, optimal diet theory and the hyperbolic-decay model have been presented as two distinctly different approaches to animal choice, one that is based on the principle of delay discounting and one that is not. It should be pointed out, however, that the hyperbolic-decay model permits different rates of discounting, depending on the value of K, which may vary for different species, different individuals, and different situations (e.g., Green, Fry, & Myerson, 1994; Johnson, Bickel, & Baker, 2007). If K is set to zero, this represents the extreme case in which there is no delay discounting, and at this point the predictions of the hyperbolic-decay model become the same as those of optimal diet theory for the successive-encounters procedure. That is, if the values of all reinforcers are equal regardless of their delays, the hyperbolic-decay model also predicts that the choice between prey rejection and acceptance will be depend on which strategy will deliver more reinforcers in the long run. However, setting K equal to zero may not be a realistic option in practice. Numerous studies, conducted with many different species, have shown the major effects that delay has on reinforcer value, and they suggest that cases where there is no delay discounting are rare, and perhaps nonexistent.