Abstract
A central tenet of evolutionary social science holds that behaviors, such as those associated with social dominance, produce fitness effects that are subject to cultural selection. However, evidence for such selection is inconclusive because it is based on short-term statistical associations between behavior and fertility. Here, we show that the evolutionary effects of dominance at the population level can be detected using noncoding regions of DNA. Highly variable polymorphisms on the nonrecombining portion of the Y chromosome can be used to trace lines of descent from a common male ancestor. Thus, it is possible to test for the persistence of differential fertility among patrilines. We examine haplotype distributions defined by 12 short tandem repeats in a sample of 1269 men from 41 Indonesian communities and test for departures from neutral mutation-drift equilibrium based on the Ewens sampling formula. Our tests reject the neutral model in only 5 communities. Analysis and simulations show that we have sufficient power to detect such departures under varying demographic conditions, including founder effects, bottlenecks, and migration, and at varying levels of social dominance. We conclude that patrilines seldom are dominant for more than a few generations, and thus traits or behaviors that are strictly paternally inherited are unlikely to be under strong cultural selection.
Keywords: cultural evolution, Indonesia, neutral theory, selection, Red Queen
Evolutionary social scientists analyze the fitness consequences of behavior, where the currency of fitness is reproductive success. Many studies have argued that reproductive skew biased toward dominant or high-ranking men is very common in human communities: “In more than one hundred well studied societies, clear formal reproductive rewards for men are associated with status: high-ranking men have the right to more wives” (1). Demographic statistics collected over short time scales support these claims (2). Although variation in male fitness is known to occur, an important unanswered question is whether such differences are heritable and persist long enough to have evolutionary consequences at the population level. In this report we show that it is possible to use genetic markers to test for the signature of heritable reproductive skew within population groups.
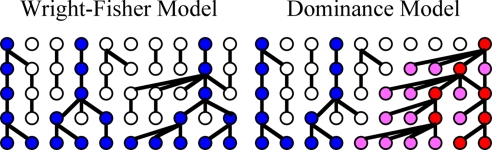
Several authors have modeled the effects of reproductive skew in different contexts (3, 4). Fig. 1 contrasts two models: the standard Wright-Fisher model in which all individuals produce offspring with equal probability (i.e., no reproductive skew) and a model of male dominance in which individuals whose parents had many offspring are more likely to have more children themselves. Investigations of genetic variation on the nonrecombining portion of the Y chromosome provide an opportunity to ask which of these models better characterizes a given population. Here, we genotype 12 short tandem repeats (Y-STRs) and a battery of SNPs on the Y chromosomes of 1269 men from 41 Indonesian communities. We then construct Y-chromosome haplotypes for each sample [supporting information (SI) Table S1]. Unlike human genetic studies that sample unrelated individuals from a broad geographical watershed and thus fail to capture community-level processes, we sample male residents of several indigenous and relatively isolated communities. These populations include neolocal Borneo hunter-gatherers and Central Javanese rice farmers, matrilocal horticulturalists on Flores, patrilocal Balinese wet-rice farmers, and patrilocal horticultural clans on Sumba, Nias, and Flores.
Fig. 1.
Population models. Colored dots represent individuals who have descendants in the final generation. Red dots represent dominant individuals who are more likely to reproduce. Pink dots represent nondominant individuals having a dominant ancestor. Blue dots represent nondominant individuals having no dominant ancestor. Dominant individuals in 1 generation are chosen at random from the offspring of dominant individuals in the previous generation. (See SI Text Population Models for more details.)
To detect evidence of heritable reproductive skew, we use statistical procedures that are based on the Ewens sampling formula (5). In particular, we apply Slatkin's exact test of neutrality, which is based on the haplotype frequency distribution (6, 7). Communities experiencing reproductive skew among patrilines will tend to have haplotype frequency distributions that, over time, become unlikely under the neutral model, skewed toward an excess of common haplotypes (patrilines). Such skewed distributions would provide evidence for cultural selection, defined as the heritable nongenetic transmission of any kind of behavior that affects reproductive success (see ref. 8).
Results
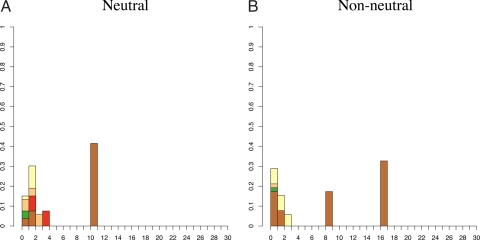
Strikingly, we find that only 5 of 41 communities (12%) have haplotype frequency distributions that are unlikely under the neutral model (i.e., rejected the null hypothesis of neutrality). Fig. 2 shows the haplotype frequency distributions of 1 of these 5 communities (Fig. 2B), and a neutral deme (Fig. 2A). All 5 cases that rejected neutrality show a similar pattern: 1 or more common haplotype(s) (i.e., a high-frequency patriline) paired with a large number of low-frequency haplotypes (Fig. S1). This contrasts with patterns produced under the neutral model with different population sizes. Observed haplotype frequency distributions typical of large communities (i.e., in which the genetic diversity of the sampled population is high) are characterized by many unique haplotypes and a few high-frequency lineages. Smaller communities with reduced neutral diversity tend to have fewer low-frequency haplotypes and fewer common patrilines.
Fig. 2.
Example haplotype distributions. The height of column i is the number of individuals whose haplotype is represented i times in the sample (normalized by sample size). (A) An example of a community haplotype distribution that does not show evidence of departure from neutrality based on the exact test: Sumba/Mamboro. (B) An example of a community showing departure from neutrality based on the exact test: Sumba/Wanokaka. Although nonneutral cases often appear to have mass shifted to the right, it generally is not possible to determine the outcome of the exact test by inspection. Colors indicate Y chromosome haplogroup membership (C, F, K, M, O, or S). All 41 distributions and the color key are given in Fig. S1. Additional haplogroup information is in Table S5.
Dominance Model and Power of the Exact Test.
Given these findings, we wanted to know how often the Ewens exact test fails to reject neutrality when male dominance is in fact occurring. The Ewens test is nonparametric and is not based on any specific model. It is independent of both village effective population size and Y-STR mutation rate. We constructed an analytical model to determine the ability of this test to detect departures from neutral equilibrium as a result of heritable reproductive skew caused by social dominance. In this model, dominant males comprise a fraction δ of the total population and have a selective advantage σ over the nondominant males. Offspring in the next generation are chosen according to a haploid Wright-Fisher model with competition between the 2 classes, dominant and nondominant. To maintain the fraction of dominant males at δ for each subsequent generation, a proportion of sons of the dominant males is chosen at random to be dominant for the next iteration of the model. Thus, for this 2-parameter model, either δ = 0 or σ = 0 yields neutral populations (see SI Text Population Models for additional details).
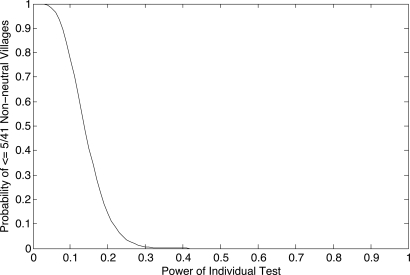
To calculate the power of the Ewens exact test under this model, we simulate nonneutral populations, sample them, and apply the exact test to observe departures from the expectation under neutrality. To condition the simulations on our Indonesian data, we simulate populations taking (i) samples of size 20 from smaller villages having effective population size 100 using 10 Y-STRs, and (ii) samples of size 35 from larger villages having effective population size 300 using 12 Y-STRs. Tables S2 and S3 show the results of these analyses for all parameters. For example, for a village of size 300 with only 4% of the men producing twice as many offspring (σ = 1), the power of our test is 0.39. Assuming this level of dominance, the probability that 5 (or fewer) of 41 villages rejects neutrality is ≈0.02%. Thus, even weak dominance would be detectable in a sample of 41 villages. Fig. 3 gives this probability for the power calculated from any model of selection.
Fig. 3.
Probability of seeing 5 or fewer (of 41) nonneutral villages for a given power of the individual tests to detect departure from neutrality. If the power of the individual tests is 0.2, the probability of observing ≤5 is ≈0.2. If the power of the individual tests is > 0.3, then this probability is vanishingly small.
Demographic Effects.
Departures from neutrality can arise from both selective and demographic causes (e.g., changes in population size and structure). Consequently, inferring whether observed cases result from reproductive skew or from other factors is not straightforward. There are 2 possibilities. First, demographic processes might mask the effects of male dominance and make villages appear neutral when in fact they are experiencing heritable reproductive skew, leading to false negatives. Alternatively demographic processes might cause neutral populations to appear nonneutral (i.e., leading to false positives). In this section we discuss the effects of 2 classes of demographic process on the Ewens test: reductions in population size (including founder effects and bottlenecks) and migration.
In general, bottlenecks (or founder events) reduce genetic variation (Fig. S2) by leading to the rapid loss of rare lineages. Eventually, if the bottleneck remains strong, more common lineages will be lost also. In the phase of population recovery after a bottleneck, new mutations tend to occur on different Y chromosomes. Thus, during the bottleneck phase we expect to find a reduction in the frequency of rare haplotypes, whereas in the recovery phase we expect to see an excess of rare haplotypes compared with the expectation for a population in neutral equilibrium. For false positives, the most extreme case is a neutral population undergoing a bottleneck in which all individuals possess the same haplotype. This is conceivable, for example, in the case of a founding event by a small kin group. Thus, neutral populations may test as nonneutral in the period immediately following a strong bottleneck (Fig. S3A) (see Materials and Methods).
In a population experiencing reproductive skew as a result of male dominance, a bottleneck will reduce genetic variation further. Because a reduction in haplotype diversity reduces the power of the exact test, dominance will be more difficult to detect during the recovery phase. Simulations indicate that populations return to the nonneutral condition in ∼20 generations as long as dominance remains constant (Fig. S3B). This raises the question of whether we are underestimating the importance of male dominance as a result of low power to reject neutrality after a bottleneck. We believe this to be unlikely for several reasons. First, the mean village size, at 280 male household heads, is sufficiently large to indicate that frequent bottlenecks occurring in the past few generations are very unlikely (Table S4). Second, haplogroup diversity (i.e., the number and relative abundance of Y-chromosome lineages as defined by SNPs) is relatively high (Table S5). Finally, reductions in effective population size that one expects to accompany a bottleneck are not seen. The bottlenecks simulated here are quite extreme, with reductions in population size of 90% for 10 generations. Moreover, if bottlenecks do occur, they also independently will reduce the demographic effects of male dominance. For example, if a population is reduced from size 300 to 35 for 10 generations, then the chance that any individual has a descendant in a recovering population is < 2% (this becomes < 1% if the bottleneck lasts for 20 generations) (Fig. S2). Thus, it is unlikely that Y-chromosome lineages of dominant males would survive a severe population bottleneck.
Migration is another factor that affects patterns of diversity within populations. Increasing the number of new alleles entering the population each generation by migration is functionally equivalent to increasing the mutation rate, μ, in a Wright-Fisher model. Consequently, migration will not cause false positives because the exact test is not dependent on the mutation rate under this model. However, for villages experiencing reproductive skew, high migration reduces the power of the Ewens exact test. In our sample, the highest migration rates are expected in Balinese villages because they often are adjoining and speak the same language. We simulated an Isolation with Migration model to estimate migration rates (see SI Text Estimation of Balinese Migration Rates). To determine whether this could impact the power of our tests significantly, we simulated moderate and high migration (m = 0.01, 0.03/gen) as part of our power analyses (Tables S2 and S3). Even when sample sizes are small and dominance is weak, the reduction in power with these levels of migration is minimal, amounting to only a few percent. For example, with 4% dominant males producing 3 times as many children as nondominant males, high migration reduces the power from 32% to 26% in small village simulations (Table S2).
Nonheritable Reproductive Skew.
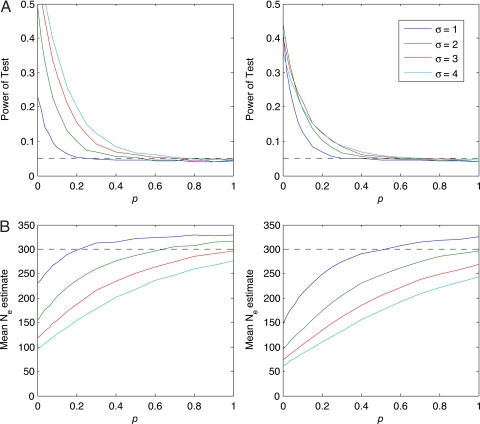
We also consider another model of reproductive skew in which the composition of the dominant group varies. The distinction between the heritable and nonheritable cases is important: any basis for cultural selection must involve some heritable behavior or trait that confers a reproductive advantage. In the context of social dominance, this distinguishes between situations in which, over multiple generations, males persistently pass dominance to their sons versus situations in which the membership of reproductively dominant groups is transient. To consider this case, we add a parameter p to the model of dominance. This parameter gives the fraction of the dominant class that enters from the nondominant class in a given generation. Consequently, for example, if p = 0.05, then a dominant lineage will span, on average, 20 = 1/0.05 generations. If p = 1, then reproductive skew is uncorrelated between generations. In that limiting case, dominant individuals produce significantly more offspring than nondominants, but this tendency is attained randomly in each generation. Values of p significantly >0 could result in a “Red Queen” effect, in which even acute competition between patrilines does not translate into lasting dominance (8). The power analysis for this model shows a small reduction in power for the case p = 0.05. For p = 0.15, dominant lines persist on average only 6 or 7 generations, and, not surprisingly, we find a clear reduction in power for this case. The power of selection to structure the genetic composition of the community also is reduced as p increases and the composition of the dominant group becomes more fluid (Fig. 4A). Concomitant with this result, we also find in our simulations a clear reduction in the village effective population size, Ne, for small values of p and some reduction for all values (Fig. 4B). To look for reductions in Ne, we estimated the effective population sizes of sampled communities based on the number of haplotypes and compared these values with best-estimate demographic data made available by village records or the local Indonesian government. For the communities in which the neutrality test was not rejected, effective size estimates (compensating for migration) are similar to census demographic values (Table S4). In contrast, the nonneutral communities have Ne estimates that are much smaller than the number of male heads of households, in some cases dramatically smaller. Because we do not see a marked reduction in Ne for the villages that test neutral, and these villages maintain high levels of haplogroup diversity (Table S5), it appears that values of p ≫ 0 are uncommon for the communities in our sample. This argues against significant reproductive skew, which would reduce both Ne and diversity quickly in small communities.
Fig. 4.
Effects of adding nonheritable reproductive skew to a simulated population of size n = 300. The first column shows simulation results for δ = 0.02, the second column for δ = 0.06. (A) Reduction of power. As p increases, the power to detect skew is reduced. However, the length of time lineages are dominant also decreases, nullifying any long-term evolutionary advantage of dominance. (B) Ne reduction. Effective population size remains depressed for all values of p, providing an additional way to assess the strength of both heritable and nonheritable skew. Estimates eventually exceed the actual population size because the estimator is biased upwards.
Cases That Depart from Neutral Expectations.
Finally, we investigate possible explanations for departures from neutrality for each of the 5 nonneutral communities. Three communities come from Sumba, a remote island in which residence is patrilocal, descent is traced through the patriline, marriage is polygamous, and competition for status and resources among clans is endemic (9). Given these circumstances, it perhaps is remarkable that the remaining 5 Sumbanese communities we sampled failed to show statistically significant evidence of heritable reproductive skew. In Bali, where residence is patrilocal and there is competition among patrilineal descent groups, the only nonneutral community is South Batur. This village was part of the larger village of Batur, which fragmented in 1948 after a period of rivalry between factions that often were associated with descent groups. A very recent process of village fissioning led to resettlement of some households based on lineage affiliation (10). The remaining nonneutral community is a patrilineal and patrilocal community in central Flores. It once was the site of a minor princedom that became an administrative center during the Dutch colonial era and now serves as a district capital (“kecamatan”). Our sample includes a large proportion of civil servants born elsewhere, probably accounting for its diverse haplotype distribution.
In sum, most of the sampled populations do not show evidence of a departure from neutral stochastic equilibrium with respect to male lineages. If reproductive skew inherited between generations were a pervasive and ongoing process, we would expect to observe frequent rejections of the Ewens exact test of neutrality. We do not observe such rejection in 88% of our Indonesian communities. Even our nonneutral Indonesian communities may not necessarily reflect the action of male reproductive skew but rather the signature of a very recent or nonneutral founding group. For the reasons discussed earlier, recent bottlenecks are unlikely to be masking significant skew. We conclude that male reproductive skew is at best weak in most of our sampled population groups, despite their varied subsistence strategies and kinship practices.
Discussion
The implications of our results extend beyond the Indonesian cases described here to the broader question of the relationship between reproductive skew and the genetic structure of human communities. The genetic or cultural-evolutionary effects of dominance become apparent only by extending analyses from the inclusive fitness of individuals to population-level consequences over the course of multiple generations. Here, we take a population-genetic approach to infer selection by detecting departures from neutral drift-mutation equilibrium at the population level rather than from variation in the reproductive success of individuals (11–13). Our results indicate that dominance effects generally do not persist over multiple generations. The lack of evidence of reproductive skew in these communities means that heritable traits or behaviors that are passed paternally, be they genetic or cultural, are unlikely to be under strong selection.
The discovery that neutral processes can explain most haplotype frequency distributions in these communities parallels earlier results from the development of neutral theory in genetics and ecology. As Kimura (14) observed in his original article, the prevalent opinion in the 1960s held that almost all mutations are under selection. This opinion was slow to change. More recently, ecologists similarly have suggested that a neutral model, in which species in the same trophic level are functionally equivalent or neutral with respect to each other, might adequately explain species-abundance distributions in ecological communities (15–17). In anthropology, the recent availability of appropriately sampled community-level polymorphism data now enables us to distinguish both genetic and cultural selection from neutral demographic processes with surprising precision. In these Indonesian communities, male dominance seldom translates into increased fertility among descendents over evolutionary timescales.
Materials and Methods
Ewens Sampling Formula.
Our statistical methods are based on the appropriateness of the Ewens sampling formula (5) as a null model for the process under study. This sampling formula applies to closed populations in situations that meet the following criteria for samples, genetic data, infinite alleles, and equilibrium:
Samples: The sample size n is small compared with the constant haploid population size, N.
Genetic Data: Each mutation is selectively neutral, taking place from 1 generation to the next with probability μ.
Infinite Alleles: Each mutation gives rise to a novel haplotype.
The population is in equilibrium.
The sampling formula gives the distribution of a sample taken from the assumed equilibrium frequency distribution or configuration of the population. A configuration is denoted by b = (b1,b2,…) where bi is the number of haplotypes represented i times in a sample of n individuals. Thus, possible sampling configurations satisfy Σiibi = n. The Ewens sampling formula states that this configuration has probability
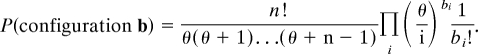 |
The choice of θ generally is approximately equal to 2Neμ where Ne is the effective population size.
We now examine the assumptions individually. Then we show how the Ewens sampling formula forms the basis for a test of neutrality and an estimator of θ based on the number of haplotypes. We apply the test and the estimator to the sample sites. Finally, we introduce a 2-parameter model to assess the impact of these departures from neutrality and the power of the test and compare our method with another approach.
1. Samples.
In total, 1269 Y chromosomes were collected from 41 communities on 6 islands (Bali, Borneo, Flores, Java, Nias, Sumba) in Indonesia (Fig. S4). Sample sizes range from 16 to 54 individuals. All samples were collected from volunteer donors with written informed consent and appropriate permits from the Indonesian Government via the Eijkman Institute for Molecular Biology. The University of Arizona Human Subject Committee approved sampling protocols. In all cases, care was taken to exclude individuals related within the last 3 generations, as determined by detailed personal genealogies. This aspect of the sampling procedure effectively eliminates the effects of recent demographic events.
Samples were designed to be a small proportion of the village. The number of samples n in each community is given in Table S1. The assumption of constant population is a part of our null hypotheses. Departures from the constant population assumption will be considered in our power analysis.
2. Genetic data.
The polymorphic sites from the nonrecombining part of human Y chromosome included a set of 74 previously published binary markers (18) and 4 additional polymorphisms: M208, M210, M346, and M356 (19–22). Binary markers were analyzed with a hierarchical strategy (23, 24) when additional sample genotyping was restricted to the appropriate downstream mutations along the haplogroup tree.
For the microsatellite analysis, 10 STRs (DYS19, DYS388, DYS389I, DYS389II, DYS390, DYS391, DYS392, DYS393, DYS426, and DYS439) were typed as described by Redd et al. (25). Some sites also were scored for DYS438 and DYS457 loci. Table S1 indicates the total number of STRs typed for each sampling location.
A haplotype is defined by its sequence of repeat numbers. Consequently, a haplotype mutates if at least 1 STR mutates. If we let M denote the number of STRs, and let νi denote the mutation rate for the ith Y-STR, then we can calculate the mutation rate for Y-STR haplotypes as
 |
Consequently, μ depends only on the average mutation rate, not its variability. Using the average STR mutation rate of 0.0021 per generation (26, 27) for the average above, we calculate:
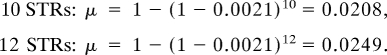 |
3. Infinite alleles.
Y-STRs mutate by either increasing or decreasing their repeat number. The measure of the failure of the infinite alleles assumption is the mean frequency of STR mutations that do not result in a novel haplotype. This possibility of 2 individuals being identical in state but not identical by descent is called “homoplasy.”
A variety of STR mutation models have been studied (28–30). Mutation models that permit multiple repeat changes are less likely to mutate to an existing haplotype than mutation models that permit only a mutation changing the repeat number by1. In addition, as we shall see, homoplasy affects tests for neutrality and estimates for θ only if it reduces the number of haplotypes in the sample. Irrespective of the model, the impact of homoplasy is to reduce the number of haplotypes and to increase the fraction of individuals that belong to common haplotypes.
4. The population is in equilibrium.
Neutral models for the evolution of the configuration of individuals are Markov chains. For Markov chains that model this evolution, the distribution of the configuration of haplotypes converges to its equilibrium. The questions arise: What is the time needed for this convergence, and what is the nature of the convergence? Analytical results and simulations (data not shown here) confirm that these Markov chains possess a cutoff phenomenon. The cutoff occurs at approximately Ne (logθ)/θ generations. Here, we take a generation to be 31 years (31).
The analysis also shows that a neutrally evolving population has reached equilibrium if each individual in the population has experienced at least 1 mutation along the line of descent connecting that individual to a founding member of the population. If a community is neutrally evolving but the genetic data have not yet reached equilibrium, then the current population will have some signature of the founding population. Fig. S3A shows this phenomenon for a single neutral population that began with all individuals sharing the same haplotype.
Statistical Procedures.
The Ewens sampling formula is a 1-parameter probability distribution function. It can be expressed as the product of two terms
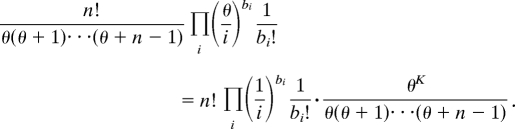 |
For a fixed value of K, the first term gives the likelihood for a given configuration b. The second shows that the number of haplotypes K = 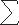 i bi is a sufficient statistic for the parameter θ. Note that the form of this product shows that, given the number of haplotypes, the distribution of haplotypes does not depend on the parameter θ and consequently does not depend on either the population size or the mutation rate.
i bi is a sufficient statistic for the parameter θ. Note that the form of this product shows that, given the number of haplotypes, the distribution of haplotypes does not depend on the parameter θ and consequently does not depend on either the population size or the mutation rate.
Test for Neutrality.
Based on the first term in the product of the Ewens sampling formula, Slatkin (6, 7) developed an exact test for significant departures from the neutral hypothesis. The exact test calculates the probability of all configurations with fixed sample size, n, and fixed haplotype number, K, and sums the probabilities of the configurations that are less likely than the observed configuration. That value, PE, is reported in Table S1. The test is 2-tailed: values of PE < 0.025 indicate a departure from neutrality in the direction of a distribution that is “too even,” often taken to indicate the presence of balancing selection. Values of PE > 0.975 indicate departure in the direction of an “overly uneven” distribution, which can indicate either the presence of positive selection or demographic history. Table S1 shows the values of PE for all of the sampled villages. Highlighted departures from neutrality have PE > 0.975.
Power Analysis.
To determine the power of the test to detect neutrality under the dominance model, populations were simulated under a range of parameters values for σ and δ under 2 choices for village population size and 2 levels of migration (Tables S2 and S3). For each set of parameters, 10,000 samples were simulated, the exact test was applied, and the number testing as nonneutral was counted. The estimated power of the test is the fraction testing as nonneutral. See SI Text for further details of the analysis
Estimate of θ.
The maximum likelihood estimator of θ is found by solving (32):
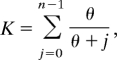 |
where n is the sample size. Using value of μ given earlier, we are able to estimate effective population size, Ne, using K. The values for K and the estimated values for θ for each community are given in Table S1. We compare these estimates with the number of male household heads known from census data in Table S4. Estimates for θ are biased upwards.
Supplementary Material
Acknowledgments.
We thank these individuals for their analysis of the genetic data at the Hammer Laboratory of the University of Arizona: Meryanne Tumonggor, Yuliana Ling, Daniel Teberg, Megan Dragony, Emily Landeen, Fernando Mendez, and Rachel Stewart. We also thank John Schoenfelder, who provided the sampling locations map, Jennifer Dunne, John Pepper, and two anonymous reviewers for comments, and the 1269 Indonesian men who made this study possible. Genetic samples were obtained by JSL and HS and by Golfiani Malik, Wuryantari Setiadi, Loa Helena Suryadi, and Meryanne Tumonggor of the Eijkman Institute, with the assistance of Indonesian Public Health clinic staff, following protocols for the protection of human subjects established by both the Eijkman Institute and the University of Arizona Institutional Review Boards. This work was supported by the National Science Foundation, the James McDonnell Foundation Robustness program at the Santa Fe Institute, and the Eijkman Institute for Molecular Biology, Jakarta, Indonesia. Permission to conduct research in Indonesia was granted by the Indonesian Institute of Sciences.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/cgi/content/full/0710158105/DCSupplemental.
References
- 1.Clarke AL, Low BS. Testing evolutionary hypotheses with demographic data. Popul Dev Rev. 2001;27:633–660. [Google Scholar]
- 2.Winterhalder B, Smith E. Analyzing adaptive strategies: Human behavioral ecology at twenty-five. Evol Anthropol. 2000;9:51–72. [Google Scholar]
- 3.Cannings C. The latent roots of certain Markov chains arising in genetics: A new approach, I. Haploid models. Adv Appl Probab. 1974;6:260–290. [Google Scholar]
- 4.Sibert A, Austerlitz F, Heyer E. Wright-Fisher revisited: The case of fertility correlation. Theor Popul Biol. 2002;62:181–197. doi: 10.1006/tpbi.2002.1609. [DOI] [PubMed] [Google Scholar]
- 5.Ewens WJ. The sampling theory of selectively neutral alleles. Theor Popul Biol. 1972;3:87–112. doi: 10.1016/0040-5809(72)90035-4. [DOI] [PubMed] [Google Scholar]
- 6.Slatkin M. A correction to the exact test based on the Ewens sampling distribution. Genet Res. 1996;68:259–260. doi: 10.1017/s0016672300034236. [DOI] [PubMed] [Google Scholar]
- 7.Heyer E, Sibert A, Austerlitz F. Cultural transmission of fitness: Genes take the fast lane. Trends Genet. 2005;21(4):234–239. doi: 10.1016/j.tig.2005.02.007. [DOI] [PubMed] [Google Scholar]
- 8.Van Valen L. A new evolutionary law. Evol Theor. 1973;1:1–30. [Google Scholar]
- 9.Lansing JS, et al. Coevolution of languages and genes on the island of Sumba, eastern Indonesia. Proc Natl Acad Sci USA. 2007;104:16022–16026. doi: 10.1073/pnas.0704451104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lansing JS. Perfect Order: Recognizing Complexity in Bali. Princeton, New Jersey: Princeton Univ Press; 2006. [Google Scholar]
- 11.Fisher RA. The Genetical Theory of Natural Selection. Oxford, UK: Clarendon Press; 1930. [Google Scholar]
- 12.Hofbauer J, Sigmund K. The Theory of Evolution and Dynamical Systems. Cambridge, UK: Cambridge Univ Press; 1991. [Google Scholar]
- 13.Nowak M. A. Evolutionary Dynamics: Exploring the Equations of Life. Cambridge, Massachusetts: Harvard Univ Press; 2006. [Google Scholar]
- 14.Kimura M. Evolutionary rate at the molecular level. Nature. 1968;217:624–626. doi: 10.1038/217624a0. [DOI] [PubMed] [Google Scholar]
- 15.Hubbell SP. The Unified Neutral Theory of Biodiversity and Biogeography. Princeton, New Jersey: Princeton Univ Press; 2001. [Google Scholar]
- 16.Hu X-S, He F, Hubbell SP. Neutral theory in macroecology and population genetics. Oikos. 2006;113:548–556. [Google Scholar]
- 17.Alonso D, Etienne R, McKane A. The merits of neutral theory. Trends Ecol Evol. 2006;21:451–457. doi: 10.1016/j.tree.2006.03.019. [DOI] [PubMed] [Google Scholar]
- 18.Karafet TM, et al. Balinese Y-chromosome perspective on the peopling of Indonesia: Genetic contributions from pre-Neolithic hunter-gatherers, Austronesian farmers, and Indian traders. Hum Biol. 2005;77:93–114. doi: 10.1353/hub.2005.0030. [DOI] [PubMed] [Google Scholar]
- 19.Kayser M, et al. Reduced Y-chromosome, but not mitochondrial DNA, diversity in human populations from West New Guinea. Am J Hum Genet. 2003;72:281–302. doi: 10.1086/346065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kayser M, et al. Melanesian and Asian origins of Polynesians: MtDNA and Y-chromosome gradients across the Pacific. Mol Biol Evol. 2006;23:2234–2244. doi: 10.1093/molbev/msl093. [DOI] [PubMed] [Google Scholar]
- 21.Hudjashov G, et al. Revealing the prehistoric settlement of Australia by Y chromosome and mtDNA analysis. Proc Natl Acad Sci USA. 2007;104:8726–8730. doi: 10.1073/pnas.0702928104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Sengupta S, et al. Polarity and temporality of high-resolution Y-chromosome distributions in India identify both indigenous and exogenous expansions and reveal minor genetic influence of Central Asian Pastoralists. Am J Hum Genet. 2005;78:202–221. doi: 10.1086/499411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Underhill PA, et al. Y chromosome sequence variation and the history of human populations. Nat Genet. 2000;26:358–361. doi: 10.1038/81685. [DOI] [PubMed] [Google Scholar]
- 24.Hammer MF, et al. Hierarchical patterns of global human Y-chromosome diversity. Mol Biol Evol. 2001;18:1189–1203. doi: 10.1093/oxfordjournals.molbev.a003906. [DOI] [PubMed] [Google Scholar]
- 25.Redd AJ, et al. Forensic value of 14 novel STRs on the human Y chromosome. Forensic Sci Int. 2002;130:97–111. doi: 10.1016/s0379-0738(02)00347-x. [DOI] [PubMed] [Google Scholar]
- 26.Dupuy BM, Stenersen M, Egeland T, Olaisen B. Y-chromosomal microsatellite mutation rates: Differences in mutation rate between and within loci. Hum Mutat. 2004;23:117–124. doi: 10.1002/humu.10294. [DOI] [PubMed] [Google Scholar]
- 27.Gusmão L, et al. Mutation rates at Y chromosome specific microsatellites. Hum Mutat. 2005;26:520–528. doi: 10.1002/humu.20254. [DOI] [PubMed] [Google Scholar]
- 28.Di Rienzo A, et al. Mutational processes of simple-sequence repeat loci in human populations. Proc Natl Acad Sci USA. 1994;91:3166–3170. doi: 10.1073/pnas.91.8.3166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sainudiin R, Durrett RT, Aquadro CF, Nielsen R. Microsatellite mutation models: Insights from a comparison of humans and chimpanzees. Genetics. 2004;168:383–395. doi: 10.1534/genetics.103.022665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Watkins JC. Microsatellite evolution: Markov transition functions for a suite of models. Theor Popul Biol. 2007;71:147–159. doi: 10.1016/j.tpb.2006.10.001. [DOI] [PubMed] [Google Scholar]
- 31.Fenner JN. Cross-cultural estimation of the human generation interval for use in genetics-based population divergence studies. Am J Phys Anthropol. 2005;128:415–423. doi: 10.1002/ajpa.20188. [DOI] [PubMed] [Google Scholar]
- 32.Tavaré S., Zeitouni O. Lectures on Probability Theory and Statistics. Ecole d'Etés de Probabilité de Saint-Flour XXXI. New York: Springer-Verlag; 2004. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.