The nonequilibrium mechanism for ultrasensitivity in a biological switch: Sensing by Maxwell's demons

Abstract

The Escherichia coli flagellar motor senses the intracellular concentration of the response regulator CheY-P and responds by varying the bias between its counterclockwise (CCW) and clockwise (CW) rotational states. The response is ultrasensitive with a large Hill coefficient (≈10). Recently, the detailed distribution functions of the CW and the CCW dwell times have been measured for different CW biases. Based on a general result on the properties of the dwell-time statistics for all equilibrium models, we show that the observed dwell-time statistics imply that the flagellar motor switch operates out of equilibrium, with energy dissipation. We propose a dissipative allosteric model that generates dwell-time statistics consistent with the experimental results. Our model reveals a general nonequilibrium mechanism for ultrasensitivity wherein the switch operates with a small energy expenditure to create high sensitivity. In contrast to the conventional equilibrium models, this mechanism does not require one to assume that CheY-P binds to the CCW and CW states with different affinities. The estimated energy consumption by the flagellar motor switch suggests that the transmembrane proton motive force, which drives the motor's rotation, may also power its switching. The existence of net transitional fluxes between microscopic states of the switch is predicted, measurement of these fluxes can test the nonequilibrium model directly. Both the results on the general properties of the dwell-time statistics and the mechanism for ultrasensitivity should be useful for understanding a diverse class of physical and biological systems.

High sensitivity has been observed in many signaling systems in biology ranging from calcium signaling in skeletal muscle (1) to chemotaxis response in Escherichia coli (2, 3). One of the most studied systems is the flagellar motor switch, where the key component of the switching complex is a ring of around 34 identical FliM proteins (4). The motor switches stochastically between the CCW and the CW states, with a bias affected by the binding of CheY-P to FliM. The conventional picture described the switch by an equilibrium two-state model where the free energies of the two states depend on the CheY-P concentration, and the transition is driven by thermal fluctuation (5, 6). The large Hill coefficient in the motor CheY-P response curve (7) is then explained in terms of cooperative interactions between the FliM molecules. Models falling within this equilibrium framework include the classical Monod–Wyman–Changeux (MWC) allosteric model (8–10) and the Ising-type model (11) with nearest-neighbor interactions. Indeed, cooperative protein interaction has been proposed as a general mechanism for understanding ultrasensitivity in signaling (12). However, most biological complexes, such as the FliM ring, are embedded in and could strongly interact with other components in the system. A fundamental question therefore arises on how good an approximation these equilibrium models are in describing the underlying biological processes. Are there any relevant nonequilibrium effects? If so, how can they be detected and characterized? In this article, we try to address these general questions while also focusing on understanding the mechanism for E. coli flagellar motor's ultrasensitive response to CheY-P. Our choice of this particular system is motivated by the recent experimental measurements of detailed single motor switching statistics (13).

Results

Nonexponential Dwell-Time Statistics and the Breakdown of Detailed Balance.

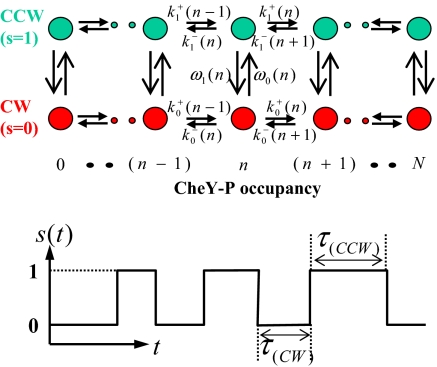
The observable state of the flagellar motor is represented by a binary variable s: s = 0, 1 corresponds to the CW and CCW rotational states of the motor. The internal state of the switch is described by an integer variable n: n = 0, 1, 2, …, N corresponds to the CheY-P occupancy among the N(= 34) FliM monomers. The stochastic switching kinetics is determined by the transition probability rates between these 2 × (n + 1) states as illustrated in Fig. 1. The CheY-P binding and unbinding rates for a given state (s, n) are k_s⁻(n) and k_s⁺(n), which depends on the CheY-P concentration [Y]. The switching rate from the s state to the (1 − s) state for a given FliM occupancy n is ω_s(n). Given these transition rates, the steady state probability p_s⁽⁰⁾(n) in state (s, n), the CW (CCW) bias B_CW (B_CCW), and the distribution function P_s(τ) for dwell time τ in the s state can be determined either by numerical simulation or by solving the master equations (see Materials and Methods for details).

Fig. 1.

Illustration of the general kinetic model for flagellar motor switching in the state space spanned by two state variables s and n, which represent the rotational state and the CheY-P occupancy of the switch, respectively. A stochastic switching time series is shown for the observable state variable s(t).

For equilibrium systems, detailed balance is satisfied between pairs of states, e.g., ω₀(n)p₀⁽⁰⁾(n) = ω₁(n)p₁⁽⁰⁾(n), and, equivalently, the transition rates obey thermodynamic relations, e.g., k₀⁺(n)ω₀(n + 1)k₁⁻(n + 1)ω₁(n) = k₀⁻(n + 1)ω₁(n + 1)k₁⁺(n)ω₀(n). By using these relations in analyzing the master equations for P_s(τ), we discover that the dwell-time distribution function can be expressed as a sum of exponential decay functions with positive definite coefficients [see supporting information (SI) Text for details of the proof]:

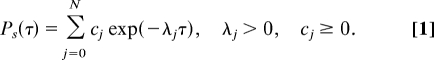We emphasize that this result is valid for any equilibrium model with detailed balance, including the Ising-type model (see SI Text and Fig. S1 for details). From Eq. 1, P_s(τ) satisfies a set of constraints:

in particular, it should be monotonically decreasing (m = 1) and convex (m = 2). For nonequilibrium systems, some of the coefficients c_j can become negative and consequently some of the constraints for P_s(τ) can be violated.

This general property of the dwell-time statistics provides a powerful tool in identifying possible nonequilibrium effects. Violation of any constraints in Eq. 2 is sufficient (but not necessary) to imply breakdown of detailed balance in the underlying kinetics. For the E. coli flagellar motor, detailed statistics of the single motor switching kinetics were measured recently by the Cluzel laboratory (13), for a series of given CW biases and at a higher resolution than previous experiments (14). The distribution functions of the CW and CCW dwell times are found to have a distinctive peak at a finite value. The accuracy of the measured P_s(τ) for small τ can be affected by experimental resolution as well as ambiguity in defining the CCW and CW states when the system is in the transitional states. However, the switching between CCW and CW states is extremely fast, occurring on the millisecond time scale (15); therefore, the observed peaks in P_s(τ) at times of up to 0.4 sec (13) are experimentally very well resolved. According to our general theory on dwell-time statistics, the presence of such peaks in P_s(τ) clearly indicates that the flagellar motor switch operates out of equilibrium. Thus, we suggest that the conventional models of flagellar motor switching need to be modified in a fundamental way to reflect the breakdown of thermodynamic relations and the violation of detailed balance.

Dissipative Allosteric Model and the Nonequilibrium Mechanism for High Sensitivity.

To capture the nonequilibrium nature of the switching kinetics, we modify the equilibrium transition rates ω_s^(e)(n) by a factor γ_s(n): ω_s(n) = γ_s(n)ω_s^(e)(n) with γ₀(n) ≠ γ₁(n). k_BT ln(γ₀(n)) and k_BT ln(γ₁(n)) can be interpreted as the decreases of the energy barrier from the CW and CCW sides of the double-well potential respectively (k_B is the Boltzmann constant, T is the absolute temperature). The equilibrium model corresponds to the special case when γ₀(n) = γ₁(n) for all n.

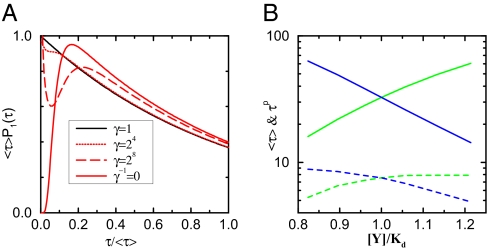
For this article, ω_s^(e)(n) are taken to be the same as in the equilibrium MWC allosteric model (8) with two dissociation constants K_d,0 and K_d,1 for CheY-P binding to FliM in the CW and CCW states, respectively. The general behavior of the dissipative allosteric model is studied with the simple choice of constant γ_0,1(n) in separate regions of n: γ₁(n ≥ n_U) = γ, γ₁(n < n_U) = 1; γ₀(n ≤ n_L) = γ, γ₀(n > n_L) = 1 with n_U ≥ n_L. Other choices of γ_0,1(n), such as exponential dependence γ₀(n) = γ₁(N − n) = b^N/2−n with b > 1, do not change the qualitative behaviors of the model (see Fig. S2 for results for other choices of γ_0,1(n) studied). The dwell-time statistics and the sensitivity of the switch are determined by solving the master equations for different model parameters. In Fig. 2A, we show the changes of the CCW dwell-time distribution functions P₁(τ) as γ increases. For γ = 1 (the equilibrium model), P₁(τ) follows an exponential-like distribution. As γ increases, nonequilibrium characteristics, such as concavity and nonmonotonicity, develop progressively in P₁(τ) as predicted from our theory. As shown in Fig. 2B, the average dwell time〈τ〉 and the dwell time τ^p at the peak of the dwell-time distribution function for the CCW (CW) state decrease (increase) with the CheY-P concentration, in qualitative agreement with the experimental observation (13).

Fig. 2.

The behaviors of the dwell-time distribution and its dependence on γ and [Y]. (A) System starting from being exponential for the equilibrium model (black line) with γ = 1, P₁(τ) shows progressively stronger nonequilibrium signatures as γ increases: concavity for γ = 16 (dotted red line), nonmonotonicity for γ = 256,∞ (dashed and solid red lines). The solid red line is for the limit γ arrow ∞ and ω̄ arrow 0 with ω̄ γ = 12.8, which corresponds to the unidirectional case where at least one of the transitional rates ω₀(n) or ω₁(n) is zero for any given n: ω₀(n)ω₁(n) = 0. Only in this unidirectional case, P₁(τ) vanishes at τ = 0. All of the curves correspond to [Y]/K_d = 1 (or B_CW = 0.5), other parameters used here are n_L = 12, n_U = 22, C = 1, ω̄ = 0.05 (except for the solid red line). (B) The average dwell time 〈τ〉 (solid lines) and the peak time τ^p dotted lines) versus CheY-P concentration [Y] from our model with γ = 256 and other parameters the same as in A, the CCW state (blue lines) and the CW state (green lines) show opposite dependence on [Y].

The most important function of the flagellar motor switch is its ultrasensitive response to CheY-P. For the equilibrium model (γ = 1), the response to CheY-P is driven by the difference in CheY-P-binding affinities to the CCW and the CW states, i.e., C ≡ K_d,0/K_d,1 < 1. Quantitatively, a Hill coefficient of 10 in the equilibrium models requires a more than 4-fold difference in CheY-P binding (C ≤ 0.25). Despite much effort, this has not been observed (16). In contrast, for the nonequilibrium model even when CheY-P binds equally to FliM in CCW and CW states (C = 1), highly sensitive response to CheY-P develops for large values of γ as shown in Fig. 3A. The sensing of CheY-P in the nonequilibrium model depends on the two amplification factors γ₀(n) and γ₁(n). Intuitively, these two nonequilibrium factors can be understood as resulting from the actions of two Maxwell demons (17, 18). In the context of our model, the two demons operate to irreversibly enhance the CW → CCW or CCW → CW transition rates beyond their equilibrium values in different regions of the switch's CheY-P occupancy state space (n ≤ n_L or n ≥ n_U, respectively). Their opposing actions with different dependence on CheY-P level give rise to the dependence of the switch's CW bias on CheY-P concentration. Effectively, the two demons act as the switch's sensors for the CheY-P concentration. A highly sensitive switch can be made, provided γ is large, and the operation regions for the two opposing demons are well separated (large Δn ≡ n_U − n_L).

Fig. 3.

The response curves and the energy dissipation. (A) The response curves for different values of γ = 1,2²,2⁴,2⁶,2⁸,2¹⁰, with C = 1 and other parameters ω̄ = 0.01, n_U = 22, n_L = 12. The black line (γ = 1) corresponds to the equilibrium case with a constant response (zero sensitivity) for C = 1. (B) The effective Hill coefficient H_eff (red line) of the response curves in A and the energy dissipation ΔW/k_BT (black line) are plotted for different γ values on a semilog plot.

The second law of thermodynamics prescribes that the Maxwell demons consume energy to carry out their work, i.e., to sense and respond to CheY-P. The rate of energy consumption Ẇ can be calculated from our model (19, 20):

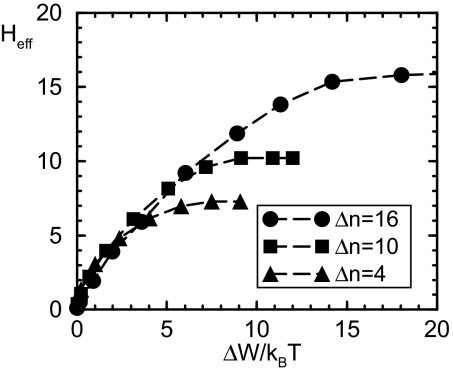
where the sum is over all pairs of states 〈AB〉, J_AB is the probability flux from state A to state B. The net flux from A to B: ΔJ_AB ≡ J_AB − J_BA is nonzero only in nonequilibrium systems because of the breakdown of detailed balance. In fact, measurements of this net flux can be used to directly test the validity of the nonequilibrium models (see SI Text for a detailed calculation of these fluxes). The average energy dissipated per switch cycle (CCW to CW to CCW) is ΔW = (τ₁ + τ₀)Ẇ, where τ₀ and τ₁ are the average dwell time for CW and CCW states, respectively. In Fig. 3B, the energy dissipation ΔW/k_BT and the Hill coefficient of the corresponding response curve H_eff ≡ 2 × d(lnB_CW)/d(ln[Y])|_BCW = 0.5 for given values of γ are plotted together. Our result clearly shows that in our nonequilibrium model, sensitivity is powered by energy dissipation, and more energy is needed to generate higher sensitivity (H_eff). Eventually, H_eff is limited by the size of the operation range Δn, as shown in Fig. 4, where H_eff is plotted versus the energy dissipation ΔW/k_BT for different values of Δn.

Fig. 4.

The dependence of the Hill coefficient H_eff on the energy dissipation for three different sizes of the operation gap Δn = n_U − n_L: n_L = 15, n_U = 19 (triangle); n_L = 12,n_U = 22 (square); n_L = 9,n_U = 25 (circle). Other parameters are the same as in Fig. 3.

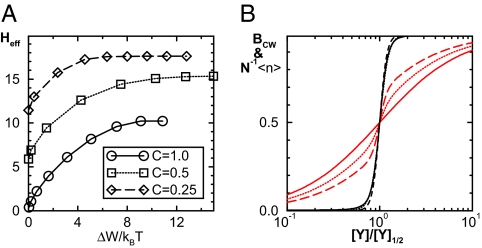
Despite the different origins of the equilibrium (γ = 1, C < 1) and the nonequilibrium (γ > 1) mechanisms for high sensitivity, they can coexist as shown in Fig. 5A, where H_eff is shown for different values of C and ΔW (by varying γ). For a given C, H_eff increases from its equilibrium value at ΔW = 0 (γ = 1) as the energy dissipation ΔW increases. However, although both mechanisms can generate high sensitivity (black lines in Fig. 5B), their predicted dependence of average FliM occupancy 〈n〉 on CheY-P concentration differs significantly. The CheY-P occupancy curve for the equilibrium model (C = 0.25, γ = 1) has a steep region in the operating range of the CheY-P concentration, whereas the FliM occupancy for the nonequilibrium model (C = 1, γ = 256) follows a gradual binding function $\frac{[\text{Y}]}{[\text{Y}]+{[\text{Y}]}_{1/2}}$ for all CheY-P concentrations, as shown in Fig. 5B (red lines). Therefore, careful measurement of FliM occupancy is critical to distinguish between these two mechanisms. The other significant difference between the two mechanisms is their opposite dependence between the switching frequency and sensitivity. We find that increasing γ (>1) in the nonequilibrium model not only increases the sensitivity (H_eff), it also increase the switching frequencies τ_0,1⁻¹. On the contrary, for the equilibrium models, higher sensitivity (with smaller C) leads to slower switching rates (11) akin to the well known phenomenon of critical slowing down for equilibrium systems.

Fig. 5.

Comparison of the equilibrium and nonequilibrium models. (A) The effective Hill coefficient H_eff versus the energy dissipation ΔW/K_BT for different values of binding affinity ratio: C = 1.0 (black line), C = 0.5 (red line), and C = 0.25 (blue line), other parameters being the same as in Fig. 3. The equilibrium cases correspond to ΔW = 0. (B) Almost indistinguishable response curves (black lines) with high sensitivity H_teff = 10 can be achieved for different values of C with different levels of energy dissipation (or γ), but the behaviors of the average fractional FliM occupancy N⁻¹〈n〉 (red lines) are very different. Three cases with parameters (C,γ) = (1, 256),(0.5,16),(0.25,1) are plotted as the solid, the dotted, and the dashed lines, respectively.

Discussion

The general theory on the properties of the dwell-time distribution obtained in this article holds true for all equilibrium systems with detailed balance. This theory provides a powerful tool in detecting relevant nonequilibrium effects in all systems and should be particularly useful in biology, where most interesting systems operate out of equilibrium. The nonequilibrium characteristics in the dwell-time distribution function, such as nonmonotonicity (peak), concavity, and other higher-order behaviors, generally appear at time scales much smaller than the average dwell time. Therefore, high-resolution experiments are required to unravel these subtle but highly informative features. Depending on the strength of the nonequilibrium effects, extra care may also be needed to control the signal to prevent weakening of these features by averaging over different signal strengths. For example in the case of the E. coli flagellar motor switch, peaks in P_s(τ) became visible only when P_s(τ) were determined for fixed CW biases (13). There is a recent report of a similar peak in dwell-time distribution in the kinesin motor for its waiting-time (between steps) distribution at low ATP concentration (21); it would be interesting to study the implication of these observations in light of our work. The strong connection between the dwell-time statistic and the underlying kinetics established here will hopefully stimulate more such careful measurements of P_s(τ), particularly for small dwell times, for motors as well as other biological systems.

For the E. coli flagellar motor, the nonequilibrium effects are not only necessary in explaining the observed dwell-time statistics; more importantly, they provide a mechanism by which the system dissipates a small amount of energy to produce a highly sensitive, fast response to the signal (CheY-P). To generate the observed high sensitivity for a single flagellar motor, the amount of energy per switch cycle (CCW–CW–CCW) dissipated is in the range of 7–12 k_BT for a variety of detailed models (see Fig. 4 and Fig. S3). Interestingly, this small switching energy is roughly equal to the work done by one to two protons moving through a membrane potential of −170 mV at room temperature, so the energy source for the switch could be the same proton gradient that drives the flagellar motor rotation. Therefore, in addition to the spontaneous switching (controlled solely by CheY-P level), we propose a proton-assisted switching mechanism. The energy released by each proton passage through the membrane, instead of always being converted to mechanical motion, may also (with a small probability) be used in carrying out switching as illustrated in Fig. 6. The probability of this proton-assisted switching can depend on the internal state of the switch, i.e., its rotational sense (CW or CCW) and the CheY-P occupancy of the FliM, this dependence being described by γ_0,1(n) in our model. The existence of this proton-assisted switching is supported by the important observation by Fahrner, Ryu, and Berg (22) that the average switching frequency depends on the rotational speed of the motor or, equivalently, the proton flux. Molecularly, the FliM ring can tap into the proton energy source through its coupling to the FliG ring (23, 24), which interacts directly with the stator (MotA/MotB) complex, where protons pass through the membrane. Detailed information on these interactions (FliM/FliG/MotAB/proton, etc.) is needed to elucidate the molecular (energy-consuming) switching kinetics. Quantitative switching statistics, such as those measured in ref. 13 but with different loads and proton motive forces, will help determine the quantitative forms of γ_0,1(n) in our model, their dependence on the proton flux, and the molecular origin of these Maxwell demons. However, independently of the molecular details, our study here clearly demonstrate that the flagellar switch does not operate as an equilibrium apparatus isolated from the rest of the motor as previously conceived. The general nonequilibrium model framework proposed here provides a crucial step toward understanding the switch as a part of the integrated motor system.

Fig. 6.

Illustration of the proposed dual roles of the proton flux. In addition to drive the motion of the motor (time frames 1 and 2 for CCW; time frames 4–6 for CW), each passage of proton (red circle) through the cell membrane may also, with a small probability, drive the switching between CCW and CW states of the motor (time frame 3, the gray box).

One important general feature of the nonequilibrium mechanism for high sensitivity is that it does not require different binding affinities of the signaling molecule to the two different states of the switch, in contrast to the classical equilibrium allosteric mechanism. The measurement of the ligand-binding curve for a single motor in CCW and CW state can therefore be used to distinguish between these two mechanisms. Our nonequilibrium model also predicts the existence of nonzero net transitional fluxes between any pair of microscopic states of the switch; in vivo CheY-P/FliM-binding measurements together with the motor switching measurements for the same single motor can be used to measure the net transitional fluxes and test microscopically whether detailed balance is violated in the switching kinetics. Besides the flagellar motor, we speculate that this more robust [details of γ_0,1(n) do not matter] nonequilibrium mechanism for creating highly sensitive switches with a small energy expenditure may be preferred by a large class of cellular processes to an equilibrium mechanism that requires fine tuning of the binding affinity ratio and the allosteric interaction strength (11). Many signaling systems, especially those with allosteric interactions, such as Ca signaling for cardiac filament activation (25) and signal transduction by MCP chemoreceptor clusters (3, 26–28), should be reexamined in light of the nonequilibrium model developed here.

Materials and Methods

Master Equations for Determining the Dwell-Time Distribution Functions.

The master equation for the probability p_s(n,t) of being in state (s, n) at time t is

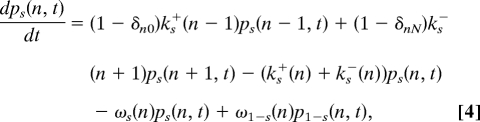where s = 0, 1 and n = 0, 1, 2, …, N. The steady-state distribution p_s⁽⁰⁾(n) is obtained by setting the right hand side of Eq. 4 to 0. The CW bias B_CW is derived from _s⁽⁰⁾((n):

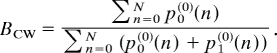To obtain the dwell-time distribution functions for CW and CCW, assume that the motor switches from the (1 − s) state to the s state at time t = 0, and define Q_s(n, τ) as the subsequent “survival” probability that the motor is still in the s state with n occupied FliM at time t = τ > 0. The master equation for Q_s(n,τ) is

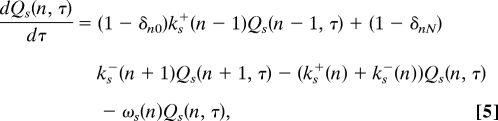s = 0,1. The survival probability Q_s(n, τ) can be solved from the above equation with the initial condition determined by the steady-state distribution of the (1 − s) state: Q_s(n, τ = 0) = A_sω_1−s(n)p_1−s⁽⁰⁾(n), where A_s is normalization factor A_s = (Σ_n=0^Nω_1−s(n)p_1−s⁽⁰⁾(n))⁻¹.

Eqs. 4 and 5 are solved by using standard linear algebra and eigenvalue/eigenvector analysis for any given choices of model parameters. Finally, from Q_s(n, τ), the distribution function for dwell time τ can be obtained:

Details of the Kinetic MWC Model.

The equilibrium part of the dissipative allosteric model studied here is the same as the Monod–Wyman–Changeux (MWC) model (8). Following the energetic representation of the MWC model (29), the free energy (in units of k_BT) for state (s, n) is given by

where E is the energy difference between the CCW and CW states when n = 0. We set E = N/2ln C, known to be optimum in generating high sensitivity (11, 29). The free energy G_m(n) for the intermediate state is chosen in this article to have the same simple dependence on n and [Y]:

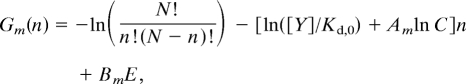where A_m, B_m are constants, chosen to be A_m = ½, B_m = ½ in this article. The equilibrium switching rate ω_s^(e)(n) = ω̄ exp(−ΔG_s) depends on the free-energy difference: ΔG_s(n) ≡ −G_s(n) + G_m(n), where mac]ω is the (geometrical) average of all these equilibrium rates given the way we choose the intermediate-state free energy. For independent CheY-P/FliM binding (30), we have: k_s⁺(n) = (N − n)k_s^on, k_s⁻(n) = nk_soff, where k_0,1^off are the on and off rates for individual CheY-P to FliM binding in the CW and CCW states. These rates are related to the dissociation constants K_d,s and the CheY-P concentration [Y]: k_s^on/k_s^off = [Y];K_d,s We let the off rates be k_s^off = 1 (for both CCW and CW) to set the (fast) time scale for our model. We also let the dissociation constant for CW be K_d,0 = 1 to set the scale for CheY-P concentration [Y]. The variable parameters for the equilibrium part of the model studied in this article are ω̄ ≪ 1 and C ≤ 1.

Net Transition Fluxes and Energy Dissipation in the Dissipative MWC Model.

One distinctive feature of a nonequilibrium system is the existence of a nonzero net transition flux ΔJ_AB ≠ 0 from state A to state B in the system because of breakdown of detailed balance. Quantitatively, the net flux from state (s, n) to state (s, n + 1) is:

The net CCW to CW switching flux (Fig. S4) from state (1, n) to state (0, n) is:

the net flux from CW to CCW is just the opposite: ΔJ₀^(v)(n) = −ΔJ₁^(v)(n). The total energy dissipated in the system can be decomposed into terms for each link in the transitional network. For the links between states (s, n) and (s, n + 1), the energy dissipation rate is

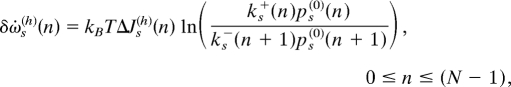whereas for links between states (1, n) and (0, n), the energy dissipation rate is

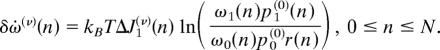Summing over all of the links in the system, we obtain the energy dissipation rate for the whole system: Ẇ = Σ_s,nδ̇ w_s^(h)(n) + Σ_nδ̇ w^(v)(n).