Bayesian motion estimation accounts for a surprising bias in 3D vision

Abstract

Determining the approach of a moving object is a vital survival skill that depends on the brain combining information about lateral translation and motion-in-depth. Given the importance of sensing motion for obstacle avoidance, it is surprising that humans make errors, reporting an object will miss them when it is on a collision course with their head. Here we provide evidence that biases observed when participants estimate movement in depth result from the brain's use of a “prior” favoring slow velocity. We formulate a Bayesian model for computing 3D motion using independently estimated parameters for the shape of the visual system's slow velocity prior. We demonstrate the success of this model in accounting for human behavior in separate experiments that assess both sensitivity and bias in 3D motion estimation. Our results show that a surprising perceptual error in 3D motion perception reflects the importance of prior probabilities when estimating environmental properties.

Humans use visual information to respond to dangers and opportunities from a distance. This allows time to prepare motor responses before critical events occur. Expert sportsmen, for instance, make fine judgments about the flight of small, fast-moving balls before they impact with their bodies (1–3). More mundanely, adults rarely allow themselves to be hit unintentionally on the head by objects moving in 3D space. How does the brain ensure this successful behavior?

To understand the mechanisms supporting motion estimation, we exploit a surprising bias: when viewing 3D motion, observers overestimate angular trajectories to report that an object will miss them when it is actually on a collision course with their head (4). This bias has been reported independently under different experimental settings involving both computer presentation (5–10) and real-world object motion (5, 11). However, given the importance of 3D motion estimation, this bias remains controversial as the general expectation is that experience-driven calibration should remove systematic errors.

Much less controversial are reports that perceived motion in the fronto-parallel plane is biased under some circumstances. Specifically, low-contrast stimuli are reported to move slower than higher-contrast stimuli when speeds are equivalent (12, 13). This has been accounted for by Bayesian estimation, whereby sensory evidence is combined with prior knowledge of the probability of encountering motion in the environment. In particular, it has been proposed that the visual system expects near zero net motion of the environment, and the influence of this prior expectation depends on the reliability of the available sensory evidence (14, 15): low-contrast stimuli provide less reliable information, so the brain relies more heavily on its expectation that motion will not be encountered. Here we develop a Bayesian model for the more complicated case of 3D motion estimation using independently estimated parameters of the “velocity prior” used by the brain (15). Our starting point is a consideration of the geometry of binocular vision that provides good reasons to expect differences in the reliability with which the brain can estimate sideways (lateral) movement as opposed to approaching motion (motion-in-depth). This differential reliability tempers the influence of the slow velocity prior, with the result that motion-in-depth is estimated to be slower than equivalent lateral motion, explaining biased estimates of trajectory when these signals are contrasted. Using a series of experiments, we show that this model accounts for both observers' sensitivity and bias when estimating movement. Further, we verify an expectation of the model that degrading an observer's ability to see lateral motion leads to an increased influence of the prior and thus less biased behavior.

Our results explain a seemingly counterintuitive bias when making judgments about the dynamic environment. Motion signals about motion-in-depth and lateral motion are differentially reliable, and thus influenced to greater and lesser extents by internalized knowledge about the probability of encountering motion. Our results also point to the importance of signal reliability in modifying the influence of the prior. Previous work has shown the differential influence of the prior through large changes in luminance contrast (14, 15). However, we find that the brain's differential reliance on sensory data corresponds to underlying differences in the reliability of computations performed on the same highly visible input. This suggests that the computation of signal reliability pertains directly to the signals themselves rather than relying on ancillary markers.

Results

We first consider the geometry of binocular vision, and its consequences for the reliability with which lateral motion and motion-in-depth can be estimated. We then formulate a Bayesian model for motion estimation that takes into account the higher reliability for lateral motion. Finally, we show that this model accounts for bias in 3D motion estimation, and moreover that bias is predictably reduced when external noise decreases the reliability of lateral motion estimation.

Geometrical Considerations.

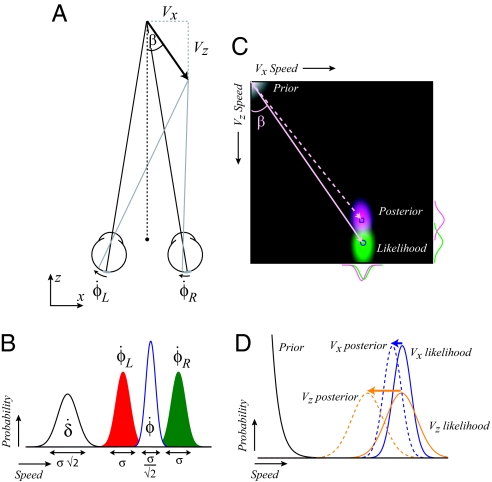
An approaching motion can be described by two orthogonal components: one lateral (V_x) and one in depth (V_z; Fig. 1A) whose ratio relates to the angle of approach (β). Using the motion vectors at each eye (Fig. 1A: φ̇_L, φ̇_R), two basic properties can be computed: the rate of change of azimuth (φ̇) and the rate of change of disparity (δ̇):

Importantly, the reliability of these signals differs: independent measurement noise in the two eyes would mean that the SD (σ) of the δ̇ signal is twice that of the φ̇ signal (Fig. 1B). This affects the reliability with which the visual system can estimate lateral motion and motion-in-depth. Specifically, V_x is related to both φ̇ and δ̇, whereas V_z relates only to the higher-variance δ̇ signal:

where i is the spacing between the observer's eyes and d the viewing distance. (Note, as is commonly done [16], these equations relate to motions originating in the median plane of the head for their mathematical simplicity.) These equations have the consequence that estimates of lateral motion are, by definition, more reliable than those of motion-in-depth. Empirically, it is well established that observers are better at detecting lateral motion than motion-in-depth (17–19).

Fig. 1.

Illustration of binocular viewing geometry and the Bayesian model. (A) A movement at angle β can be described by a lateral component, V_x, and a motion-in-depth component, V_z. The movement produces excursions at the two eyes: φ̇_L, φ̇_R. For illustration, the vectors are shown as retinal motions; however, eye rotation signals in combination with retinal motion are likely used by the brain. (B) Hypothetical probability distributions for the retinal motion vectors φ̇_L, φ̇_R. The distributions have equal, but independent, noise (σ). The SD of the difference signal is twice that of the mean signal. These differential reliabilities influence the reliability with which V_x and V_z are estimated. (C) A depiction of the Bayesian model shows the prior (depicted in white/gray in the top left-hand corner), the likelihood distribution (green), and the posterior distribution (purple). The variability of the likelihood is greater in the Vz than Vx direction, meaning that the prior has a differential influence. The angle estimated on the basis of the maximum of the posterior distribution (dotted mauve line) is more eccentric than that specified by the likelihood (solid mauve line). The square and circular markers represent the peak of the posterior and likelihood distributions respectively. (D) An illustration of the Bayesian model. The likelihood distribution is more variable in the V_z dimension than the V_x dimension, meaning that the posterior is more influenced by the prior in the V_z dimension. The differential biasing effect of the prior results in biased estimates of trajectory (β) when V_x and V_z are contrasted.

Bayesian Model.

We formulated a model in which estimated velocity (V) corresponds to the maximum of the posterior distribution formed by the product of the sensory likelihood distribution and the prior probability of experiencing motion (Fig. 1C):

where α is a normalizing constant. The prior distribution p(V) was formulated using Stocker and Simoncelli's (15) measures. Similarly, likelihood distributions for φ̇_L and φ̇_R were described by log-normal distributions whose width is constant over a range of speeds (15). The model calculates the likelihood of V_x and V_z using Eqs. 3 and 4, where the interocular spacing is assumed to be known, and viewing distance is derived from eye vergence (vertical disparities would provide limited information under our setup). Simple trigonometry shows that estimated angle can be calculated using the estimates (denoted by a circumflex ^) of V_x and V_z:

As illustrated in Fig. 1D, the important behavior of the model comprises the following: (i) variability in the posterior distribution for V_x is considerably lower than V_z; and (ii) for equal physical speeds, estimated speed is lower for V_z than V_x, with the consequence that (iii) motion-in-depth trajectories are considerably overestimated (Fig. 1C). We conducted three experiments to test this model's account of 3D motion perception.

Differential Reliability when Estimating Lateral Motion and Motion-in-Depth.

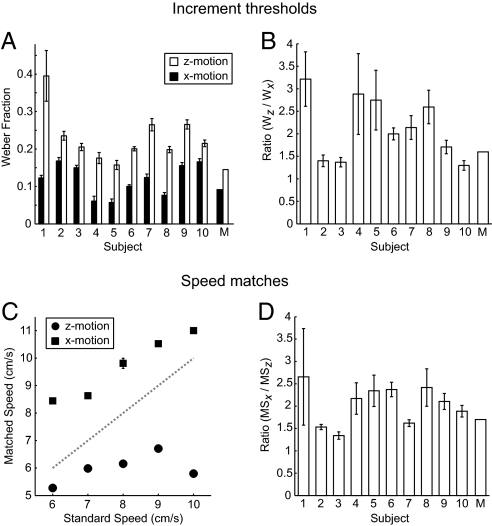
First (experiment 1), we assessed how well observers judged differences in movement when a target moved laterally or in depth. We measured increment thresholds, presenting observers with two sequential movements of a small target point (either both lateral or both in depth) and asking them to decide which moved further. Weber fractions (Fig. 2A) confirmed previous reports (17, 18) that observers are more sensitive to lateral motion than motion-in-depth (t₉ = 5.65, P < 0.01). The ratio of the Weber fractions (Fig. 2B) suggests that observers can judge differences in target movement between 1.5 and 3 times better for pure lateral motion than for motion directly toward them. This is in line with the ratio of thresholds obtained from simulations of the model (1.58).

Fig. 2.

Perceptual assays of lateral motion and motion-in-depth. (A) Increment thresholds, expressed as a Weber fraction, for motion in the plane of the computer screen (V_x motion) and motion in the mid-sagittal plane (V_z motion). Results from 10 observers and model simulations (M) are shown. Error bars show SE of the increment threshold estimate. (B) Ratio of Weber fractions (Wz/Wx) for each observer and the Bayesian model. Error bars show SE estimates of the ratio. (C) Speed match data from one observer. Square markers depict data obtained when the observer adjusted motion-in-depth (V_z) to match lateral motion (V_x). Circular markers show data obtained when observers adjusted V_x to V_z. The dotted diagonal line represents perceived speed of V_x equals perceived speed of V_z. Error bars (not all visible) depict the SE of the speed match. For each observer, the mean speed match ratio (MSx/MSz) was calculated across the presented standard speeds. (D) Ratio of speed matches for all 10 observers and the Bayesian model (M). Error bars represent SEM.

Bias when Estimating Motion Extent and Trajectory Angle.

Next we asked observers to compare the speed of a small target point when movement was lateral or toward the observer. Observers viewed two movements (one lateral, one in depth) and decided whether the first or second was faster (experiment 2). Using a staircase algorithm to control one of the speeds, we obtained estimates of perceived speed of lateral motion in terms of motion-in-depth, and vice versa, for a range of speeds. Observers reduced the lateral speed of a target to match the perceived speed of a target moving toward them (Fig. 2C, circular markers) and increased the speed of a motion-in-depth target to match the perceived speed of a laterally moving target (Fig. 2C, square markers). Consistent with a previous report (20), lateral motion was reported as 1.3–2.7 times faster than motion-in-depth (Fig. 2D), with model simulations yielding a ratio of 1.7.

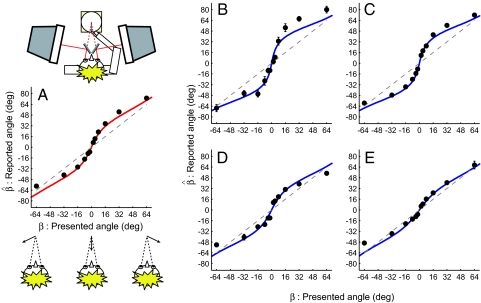
In a third experiment (experiment 3) we measured observers' reports of the approach angle of a small point. A range of motions left and right of the head were presented, and observers used a pointing device like a clock face with one hand (cf. refs. 4–6) to indicate the perceived approach trajectory (this method is discussed further later). Consistent with previous reports, observers showed bias (i.e., deviation from x = y, χ² = 142.87, df = 11, P < 0.01), reporting that motion trajectories near the visual midline were more eccentric than presented (Fig. 3A).

Fig. 3.

Reports of approach angle. (A) Between-subject mean reported angle as a function of presented angle (n = 10). A sketch of the apparatus (observer, pointing device, and CRT stereoscope) is presented above the graph. Error bars (±SEM) lie within the plotting symbols. The dashed diagonal line depicts reported angle equal to presented angle. The sigmoidal curve shows the performance of the Bayesian model. (B–E) Plots of reported trajectories from the two subjects who had the highest (B and C) and lowest (D and E) ratios of differences in sensitivity/speed matches for V_x and V_z targets. Note the differential extent of bias. Error bars depict SEM. The sigmoidal curve shows the Bayesian model; unlike A, the model is fit to these data by adjusting the ratio between the variability of the likelihood distribution along the V_x and V_z dimensions.

Observers' bias in reports of 3D motion trajectories was described very well by the bias produced by the Bayesian model (Fig. 3A, solid red line) with parameters formulated based on Stocker and Simoncelli's (15) data. This suggests that their estimates of both the shape of the prior and the amount of variability in the likelihood distribution provide a good account of the mean performance of our subjects. However, it is expected that the likelihood distribution depends on both the viewing situation (e.g., ref. 21) and the individual observer. Our initial experiments (experiments 1 and 2) provided evidence for between-subject differences in the ratio of increment thresholds and speed matches (Figs. 2 B and D). Examining reports of angular trajectory (experiment 3) provided evidence for a correspondence between an individual's threshold or speed match ratios and the extent of bias in trajectory estimates (Fig. 3 B–E). Specifically, observers with a large difference between their sensitivity to lateral motion and motion-in-depth displayed more bias (e.g., Fig. 3 B and C) than did observers for whom the sensitivities were more similar (e.g., Fig. 3 D and E).

To quantify this observation we fit each subject's data using the Bayesian model in which a single free parameter (the ratio of variability of the likelihood distribution in the V_x and V_z dimensions) controlled the extent of bias. Using regression analyses we contrasted the ratio of the best-fitting likelihood widths with the ratio with increment thresholds or speed matches for individual subjects. There was evidence of an association between the extent of bias in trajectory estimates and threshold (R² = 0.403, F_1,8 = 5.407, P < 0.05) and speed match (R² = 0.69, F_1,8 = 17.818, P < 0.005) ratios. This provides further support for the notion that biased estimates of angular approach are a consequence of the differential influence of a prior favoring slow velocities, in which the prior's influence depends on differences in lateral motion and motion-in-depth estimation.

Changing Bias by Manipulating Sensitivity.

To test further the notion that the influence of the prior depends on the reliability of the sensory input, we tested the prediction that degrading an observer's ability to see lateral motion would result in less biased behavior. Specifically, we reasoned that if biased trajectory estimates result from lateral motion estimates being less influenced by the prior, degrading an observer's ability to see lateral motion but not motion-in-depth should cause both estimates to be similarly influenced by the prior, resulting in less bias when the signals are contrasted. We therefore designed a noise-masking paradigm to disrupt lateral motion discrimination while leaving motion-in-depth performance relatively unaffected.

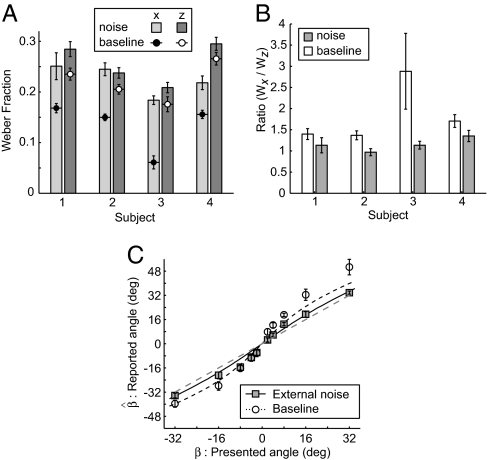
As in previous experiments, observers viewed a small point moving along trajectories defined by combinations of lateral motion and motion-in-depth. The difference was the presence of a large disk of randomly positioned dots that moved in the plane of the screen providing relative motion signals between the target dot and the surrounding mask dots. Measurements of increment thresholds (experiment 4) under these conditions confirmed that the presence of the mask affected observers' abilities to judge differences in movements (Fig. 4A; F_1,3 = 92.87, P < 0.01). Although increment thresholds were elevated for both lateral motion and motion-in-depth conditions, there was an interaction (F_1,3 = 16.13, P < 0.05) as lateral motion discrimination was affected more than motion-in-depth performance. This had the consequence that the ratio of thresholds was closer to unity in the presence of the noise mask (Fig. 4B; mean ratio without noise = 1.84, mean ratio with noise = 1.15). As predicted, reports of angular trajectory (experiment 5) were less biased in the presence of the noise mask (deviation from x = y model, χ² = 25.68, df = 9, P < 0.01) than they were when the target dot was presented alone (Fig. 4C; χ² = 111.31, df = 9, P < 0.01). This met our expectation that degrading lateral motion estimation increases the influence of the prior favoring slow velocities, biasing the lateral motion estimate by a comparable degree to the motion-in-depth estimate. This has the consequence that the ratio of lateral motion and motion-in-depth estimates is closer to the presented motion signal, resulting in less biased behavior.

Fig. 4.

Results of the noise-masking experiment. (A) Increment thresholds for motion-in-depth (V_z) and lateral motion (V_x) in the absence (baseline) and presence of a noise mask. Error bars show SE of the increment threshold estimate. (B) Ratio of distance increment thresholds in the absence (white bars) and presence (gray bars) of the noise mask. Error bars show SE estimates of the ratio. (C) Between-subject mean reported angle as a function of presented angle (n = 4). Open symbols show data obtained without the noise mask present. Filled symbols data obtained in the presence of the noise mask. Error bars represent SEM. The sigmoidal curves show model predictions in which the ratio of increment thresholds from A is used to model the ratio of the variability of the likelihood distribution along the V_x and V_z dimensions.

Controls for Report Bias.

To examine the perception of 3D motion, we have used a method reliant on observers providing a description of their perception. The use of such a measure can be problematic as we have no way of determining whether an observer's perception is biased, or whether their reports of their perception are biased. Previous studies have looked for a correlation among a number of different measures to provide evidence for a genuine perceptual bias (4, 5) whereas others have used discrimination measures (10). Here, we reasoned that if bias in trajectory estimates results from differential sensitivity to lateral motion and motion-in-depth, bias should not be observed under conditions in which an observer's sensitivity to the two components of motion that make up a trajectory is the same. From a consideration of the brain's processing of information about elevation (y-position), there is no principled reason why motion sensitivity should differ from sensitivity to lateral motion; the brain can average the retinal signals from the two eyes in both cases. Measures of sensitivity to lateral and vertical motion (increment thresholds) confirmed very similar performance in the two cases (experiment 6). We therefore examined reports of angular trajectories when movement was in the x–y plane rather than the x–z plane (experiment 7). Observers viewed angular trajectories composed of lateral and vertical motion and indicated their perception by using the pointing device positioned in the x-y plane (rather than the x-z plane as in previous experiment).

As expected, and in contrast to our previous results, very little bias was observed under these conditions [supporting information (SI) Fig. S1A; deviation from x = y model χ² = 10.52, df = 9, P = 0.31]. This manipulation also allowed us to conduct a useful control experiment. Our interpretation of judgments in the presence of the noise mask (experiment 5) is that the noise mask reduced the reliability of the V_x signal with the result that the prior influenced V_x and V_z similarly to reduce bias. However, as we could not be sure how the noise mask affects judgments per se, we measured estimates of x-y trajectories in the presence of the noise mask. We found that observers' estimates were very similar to those obtained without the noise mask (Fig. S1B; F_1,2 = 13.59, P = 0.07). This result is expected, as the noise mask should interfere equally with the processing of lateral and vertical motion, but it bolsters our interpretation of judgments in the x-z plane made in the presence of noise.

Interestingly, Poljac and colleagues (8) observed that bias for movements in the y-z plane is lower than in the x-z plane. This might suggest that the reliability of vertical motion signals is more similar to that of motion-in-depth than lateral motion, as both would be influenced by the prior to a similar degree, thereby accounting for lower bias. However, we noted no such asymmetry in measures of thresholds for lateral and vertical motion, nor in bias for judgments in the x-y plane. The setup of Poljac et al. (8) was somewhat different from our own (notably, a much smaller range of angles was used), and subjects were required to make repeated pointing movements to a small number of target impact locations, potentially leading to error-driven correction (7).

Discussion

Our study provides evidence that biased reports of 3D motion are caused by the brain's use of prior probabilities that favor the interpretation of retinal signals in terms of slow real-world velocity. Specifically, our results suggest that this prior has a differential influence on estimates of lateral motion and motion-in-depth as a result of the underlying differences in the reliability with which the brain can estimate these quantities. This results in bias when these signals are contrasted to estimate approach angles. Independently estimated parameters of the velocity prior provide a very good account of our empirical data. Further, experimentally reducing the reliability of the lateral motion signal leads to less biased behavior, compatible with an increase in the width of the likelihood distribution for lateral motion to a level similar to that for motion-in-depth.

These results are consistent with work examining 2D motion estimation (14, 15). However, the brain's use of a velocity prior is not universally accepted, and a recent study challenged the Bayesian interpretation of speed perception. Specifically, Hammett et al. (22) reported that the perceived speed of a sinusoidal grating is faster when presented at low luminance than high luminance (contrasting with the established result obtained for manipulations of stimulus contrast). On the assumption that the reliability of sensory encoding is reduced with luminance, this challenges a Bayesian account of motion perception, as the influence of the prior should be greater for low-luminance stimuli, leading to a decrease in perceived speed. Hammett and colleagues (22) suggested that Stocker and Simoncelli's (15) measures of the velocity prior provided a re-description of the empirical data with little predictive power. In contrast, our results suggest that the prior formulated by Stocker and Simoncelli (15) provides a very good account of motion estimation under radically different conditions and thereby extends beyond inferring the prior by data fitting (9). Further, our data suggest that the influence of the prior depends on the reliability of the sensory data per se, rather than some ancillary marker of signal reliability (23). Specifically, our results suggest that the prior has a differential influence on lateral motion and motion-in-depth estimators when these signals depend on the same underlying retinal input. Thus, the computation of stimulus reliability, rather than gross changes in stimulus properties (e.g., an order of magnitude change in luminance), appear to be responsible for tempering the influence of the prior.

What are the implications of the Bayesian estimation model for everyday behaviors involving objects moving in 3D space? It could be argued that biased 3D motion estimation is confined to experimental settings, rather than reflecting real-world behavior. However, there are empirical and theoretical reasons to believe that our results are not a mere laboratory curiosity. First, to isolate individual sources of information, we have used computer presentation and considered a restricted range of trajectories originating in the median plane of the head. As a consequence, information from retinal blur and accommodative signals was absent, potentially reducing the reliability of the depth estimates (24). In addition, observers' previous experience with computer displays might have established a prior for planar depth in this viewing situation. Even so, we (5) and others (11) have found biased estimates of trajectories when real objects move in the environment. Second, there are sound theoretical reasons to believe that the reliability of signals relating to approach motions will be lower than that of information about lateral motion under most circumstances. Lateral motion generally results in larger retinal excursions than motion-in-depth, and for binocular observers there is an inherent noise reduction advantage when registering changes in visual direction that is not available for changes in binocular disparity. As such, we expect that motion-in-depth signals will be routinely influenced by prior probabilities to a greater extent than signals regarding lateral motion.

Biased motion-in-depth estimates relative to less biased lateral motion estimates will have implications for decisions that rely on contrasting lateral motion and motion-in-depth. It is possible therefore that everyday motor responses rely on separate calibration functions depending on whether objects are approaching or translating. Such differential mappings would bypass any perceptual bias to allow unbiased motor output. However, to be effective, such a scheme would depend on knowing the relative influence of the prior on the two motion components. As we have demonstrated here, this depends on the underlying reliability of the sensory data. Such a moment-by-moment dependence on knowing the influence of the prior would seem to defeat the purpose of different calibration functions for different types of motion. Alternatively, the visual system may use control strategies based on changes in individual signals over time, as monitoring the change in a biased estimator does not necessitate that this change signal is itself biased. An example of such a monitoring strategy has been known by mariners for a long time: intercepting another ship can be achieved by taking a collision bearing wherein the direction of the target ship is kept constant while distance decreases.

The use of this simple heuristic of monitoring lateral position as distance decreases has been suggested for visual navigation on foot and by car (25, 26). Measurements of interceptive behavior of observers viewing rapidly moving tennis balls (11) are consistent with the use of a strategy based on monitoring lateral movement rather than reconstructions of 3D movement trajectories. Certainly, judgments of approach from changing disparity or size cues are likely to be very unreliable for distances greater than a few meters, so many everyday decisions are likely to be driven largely by information about lateral translation (3). A recent study (6) advanced a similar argument, providing evidence that observers do not use motion-in-depth when judging 3D motion and suggesting that changing visual direction is used instead. Specifically, Harris and Drga (6) found that observers' estimates of approach trajectory did not vary when a range of approach angles were presented in which lateral motion was held constant and the motion-in-depth displacement was varied. Conversely, observers' judgments changed when angular trajectories were presented in which the magnitude of the lateral motion component was varied but motion-in-depth remained fixed, implying that observers' behavior depended only on lateral motion signals.

To gain further insight into these findings, we conducted an experiment (experiment 8) using Harris and Drga's logic (6). Consistent with our previous findings, judged angle varied in conditions of both fixed lateral motion and fixed motion-in-depth (Fig. S1 C and D), implying that behavior depended on both components. Interestingly, one observer provided results that replicated Harris and Drga's findings (6) (Fig. S1 E and F). She had the worst performance when discriminating depth displacements (Fig. 2A, subject 1), suggesting low reliability in estimating motion-in-depth. We suggest that the reliability of observers' motion-in-depth estimates was low in Harris and Drga's study (6), so observers were heavily influenced by the slow velocity prior, thus providing results that form a special case of the hypothesis advanced here. This reduced motion-in-depth reliability could have arisen as a result of the large disparities used in their study. Also, the viewing distance was shorter in our study, and the weight given to disparity information is reduced as viewing distance increases (27). The suggestion that the bias in estimates of approach angles varies according to the reliability of the motion-in-depth signals available in Harris and Drga's study (6) complements our evidence for the converse finding that observers rely more on the motion-in-depth component when the reliability of lateral motion is degraded by the presence of a noise mask (experiment 5).

In summary, perceptual biases offer the potential to gain insight into the mechanisms that mediate behavior in everyday life. Here, we examine a bias when viewing 3D motion trajectories and provide evidence that this bias reflects the contribution of a prior for slow velocity. Inaccurate estimation of a rapidly approaching object involves a high cost function, likely to make observers circumspect and eager to initiate an avoidance response even when the possibility of being hit is remote.

Materials and Methods

Stimulus and Apparatus.

The stimulus consisted of a small square target (6.9′) surrounded by a peripheral reference plane of squares (side length = 20′). To isolate disparity (cf., refs. 4–6), the target's retinal size was constant (no looming cue available). [A control experiment confirmed that bias persists when changing size information is included in Fig. S2.] A fixation cross (55′ × 69′) with nonius lines was presented between each trial. Stimuli were presented on a two cathode ray tube haploscope (viewing distance 50 cm; for details see ref. 5). Trajectory estimates were measured using a pointing device (see ref. 5) containing a calibrated circular potentiometer. Experiments were conducted in the dark.

Procedures.

Experiment 1.

Increment thresholds for lateral motion and motion-in-depth were measured using a two-interval, forced-choice protocol. Target displacement was 5 cm plus an increment value (method of constant stimuli). Lateral motion and motion-in-depth trials were randomly interleaved.

Experiment 2.

Observers matched speed by deciding whether the first or second of two motion samples was faster. One interval contained a standard stimulus and the other contained a comparison whose speed was controlled using a one-up/one-down staircase algorithm (maximum, 12 reversals). The speed match was the mean of the last eight reversals. Runs contained two types of trial: (i) standard lateral motion, comparison motion-in-depth and (ii) standard motion-in-depth, comparison lateral motion. The duration of each motion exposure was randomly varied (μ = 500 ms, σ = 70 ms). Different trial types (lateral, in depth) and speeds (6, 7, 8, 9, or 10 cm/s) were randomly interleaved.

Experiment 3 (pointer task).

The target moved out of the plane of the screen toward the observer on one of six trajectories (2°, 4°, 8°, 16°, 32°, 64°). Target displacement (μ = 8 cm, σ = 1 cm) and speed (μ = 8 cm/s, σ = 2 cm/s) were randomized on each trial, so trials were of variable duration (500–2500 ms). After viewing a trajectory, observers used their right hand to move the pointer to match the approach angle, and the rotation was recorded by the computer. (An additional experiment in which observers used their left hand suggested that a slight left/right asymmetry in reports [e.g., Fig. 3] resulted from the physical constraints of rotating the pointer [Fig. S3].) The experimenter then illuminated a desk lamp to reset the pointer, allowing observers to view their hand and reducing dark adaptation. An experimental run consisted of 48 trials. Observers were free to move their eyes. Observers partook in testing sessions of 1–2 h and completed at least three sessions to provide the data for experiments 1, 2, and 3 (blocks from each experiment pseudorandomly interleaved).

Experiment 5 (noise masking).

The noise mask consisted of 400 dots (identical to the target) randomly positioned within a circular aperture (r = 10 cm). The mask was moved around the display by generating a random displacement (x, y) from the start position and translating to this position over 120 ms. After 120 ms a new displacement was generated and the mask moved from its previous position. Displacements were generated from uniform distributions (range: x = ±0.36 cm, y = ±0.18 cm).

Experiments 6, 7 (y-motion).

For trajectories in the x-y plane, the pointing device was fronto-parallel with the pointer horizontal. Observers rotated the pointer upward or downward to indicate their perception of the viewed trajectory.

Experiment 8 (fixed motion component).

Trajectories were created by holding constant either the lateral or motion-in-depth component across a range of angles (5°, 10°, 15°, 20°). For fixed motion-in-depth, V_z = 5 cm, and V_x was {0.4, 0.9, 1.4, 1.8} cm. For fixed lateral motion, V_x = 0.9 cm, and V_z was {10.1, 5, 3.3, 2.4} cm. Target speed was randomized (μ = 8 cm/s, σ = 2 cm/s).

Observers.

Ten right-handed observers (three men) were paid for their participation. They were naïve and gave informed consent. Subjects had normal/corrected visual acuity and effective stereopsis (RandDot test). Age ranged from 22 to 26 years (mean, 23.5 y).

Implementation of the Bayesian Model.

Speed was represented using a modified logarithm that accounts for deviation from the Weber-Fechner law at low speeds, ν̃ = ln(1 + ν/ν₀), where v₀ = 0.3°/s. The standard deviation of the log-normal likelihood function for retinal motion was fixed at 0.22 log units [figure 4 in Stocker and Simoncelli (15)]. The prior was defined to be spatially isotropic such that:

where the gradient and intercept parameters were obtained from Stocker and Simoncelli [figure 4, left panel fit using Matlab polyfit function (15)]. The Bayesian model was implemented in Matlab using Eqs. 1 to 6 and data simulations (100,000 samples per estimate). First, retinal motion at the two eyes was calculated using:

Distributions of φ̇ and δ̇ were simulated based on the assumption that they are Gaussian in the log domain with σ_φ̇ and σ_δ̇. A set of simulated measures of disparity and azimuth changes were produce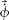d ( and ), and these were used to provide a set of measures of V_x and V_z based on Eqs. 5 and 6. Specifically, V⃗_x and V⃗_z were calculated by assuming that interpupillary spacing (i) is a known and viewing distance (d⃗) is derived from eye vergence, where eye position estimates are normally distributed (μ = 50 cm, σ = 0.22). To ensure smooth likelihood functions for V⃗_x and V⃗_z, we used a Gaussian in the log domain to provide a (good) descriptor of the simulated data [Matlab normfit function; V_x ∼ N (μ_x, σ_x²), V_z ∼ N(μ_z, σ_z²)]. The likelihood distribution was defined in V_x − V_z velocity space (Fig. 1C) as:

The likelihood was combined with the prior (Eq. 7) to obtain the posterior distribution of velocity in V_x−V_z space. The maximum value of the posterior provided estimators of velocity (V̂_x, and V̂_z). The assumption that real-world motion maps to a Gaussian likelihood distribution that is then estimated by the mode of the posterior distribution is an obvious simplification; issues of encoding and reading out motion signals from neural populations is a current area of active investigation (28).

To estimate increment thresholds, the posterior distributions produced by lateral motion or motion-in-depth were compared with a range of standards, and the resultant psychometric functions were fit [psignifit toolbox (29)] to estimate the 68% threshold. Speed matches were obtained by contrasting V̂_x, and V̂_z over the range of speeds. Finally, estimates of angle (Eq. 6) were calculated using the estimators V̂_x, and V̂_z. All calculations based on real-world geometry were carried out in the linear domain.

Modeling relied on the data published by Stocker and Simoncelli (15) except for fits to individual subject's data. Here, the best fitting ratio of the likelihood widths (σ_x/σ_z) was estimated using a user intervention–minimization procedure in which the minimum squared deviation between the model and the data was obtained by searching across a range of values (three iterations, range was progressively reduced). This was necessary as the use of simulations meant that, although the error function was globally smooth, local variations caused error-minimization algorithms to fail.