A prototype instrument for single pinhole small animal adaptive SPECT imaging

Abstract

The authors have designed and constructed a small-animal adaptive SPECT imaging system as a prototype for quantifying the potential benefit of adaptive SPECT imaging over the traditional fixed geometry approach. The optical design of the system is based on filling the detector with the region of interest for each viewing angle, maximizing the sensitivity, and optimizing the resolution in the projection images. Additional feedback rules for determining the optimal geometry of the system can be easily added to the existing control software. Preliminary data have been taken of a phantom with a small, hot, offset lesion in a flat background in both adaptive and fixed geometry modes. Comparison of the predicted system behavior with the actual system behavior is presented, along with recommendations for system improvements.

INTRODUCTION

Traditional SPECT imaging systems have fixed geometries meant to accommodate objects of various dimensions and characteristics as well as a variety of different imaging tasks. This means that the system is generally not optimized for any given patient and task that needs to be performed. This can mean decreased sensitivity and resolution, which translate into higher required doses for the subject as well as images that result in decreased observer performance (i.e., less accurate diagnoses). Optimization of the system parameters in real time has the potential to reduce dose while simultaneously improving image quality.

Adaptive SPECT imaging puts the geometry of the system under continuously variable real-time computer control. With this capability, the system can optimize itself for every given subject and task (i.e., tumor volume estimation) to be performed. The basic approach to determining the optimal system geometry is to take an initial set of coarsely sampled data from which properties of the object can be calculated. This information is used in conjunction with a set of feedback rules to compute the optimal system geometry. The final data are then taken on a more finely sampled grid in the optimal configuration. Various feedback rules can be applied, and ideally they would depend on the task being performed. Barrett et al.¹ have detailed a mathematical framework for evaluating SPECT systems in the context of an objective task-based approach and have also proposed a set of potential feedback rules. On the experimental side, Hestermanet al.² have built a flexible small-animal SPECT system that allows for off-line adjustment of system magnification and pinhole schemes to validate task-based optimization schemes.

In this work, we have developed a single pinhole, small animal prototype imager as a test bed for adaptive SPECT imaging, where the geometry of the system is under real-time computer control. In order to make the prototype design tractable, we have started with a set of assumptions about the system design. The first is that the system will be a one-detector system with object viewing angles sampled by rotating a vertically oriented object. In addition, the system will have one on-axis pinhole with discrete diameter control. In this framework, the adjustable parameters of the system are the object-to-pinhole distance, the pinhole-to-detector distance, and the pinhole diameter. Complications such as multiple pinhole functionality are left to a future design. Future iterations of this prototype design could be used as one module in a multidetector, horizontally oriented system by taking advantage of the type of gantry system developed for the FastSPECT II instrument.³

Since the prototype is meant to be used for a variety of imaging tasks, the initial design was based on optimizing the field of view, resolution, and sensitivity in the projection images. However, the flexibility of the control software means that various feedback rules that include additional information, such as the task, can be easily implemented and tested with the system.

Section 2 describes the detector module and data processing used in order to produce projection images. Equations that describe the system performance and govern the current adaptive feedback rules are derived in Sec. 3. A description of the mechanical layout of the system is given in Sec. 4, the software interface and control are detailed in Sec. 5, and the results of a phantom study are given in Sec. 6. Preliminary reconstructions are presented in Sec. 7. Finally, Sec. 8 provides a discussion of the system performance and recommendations for future modifications.

DETECTOR

Our prototype instrument has drawn on much of the existing technology developed in the Center for Gamma-Ray Imaging at the University of Arizona, particularly in terms of the gamma-ray detection process. The detector module and control electronics are virtually identical to those used in the existing FastSPECT II system. A detailed description of that system can be found in Refs. ^{3, 4} and will be briefly summarized here. Additional analysis in terms of position estimation accuracy is also presented.

The modular gamma-ray detector system consists of three main components: the detector itself, the control electronics, and the control software. The detector is made up of a solid 114.3 mm×114.3 mm×5 mm NaI(Tl) scintillation crystal attached to a 10 mm thick quartz light guide and a 3×3 array of 1.5-in. diameter end-on Hamamatsu photomultiplier tubes (PMTs). A single gamma-ray hit on the detector face produces an output current pulse from each of the nine PMTs. These current pulses are then sent to the control electronics for processing.

The control electronics consist of a front-end board that processes the current pulses and a backend board that interfaces to the computer. The control software, written in LABVIEW™ and C, communicates with the backend board to save the processed PMT outputs for each qualified gamma-ray event. Data acquired using this system are saved in list-mode format. That is, each qualified gamma-ray event that hits the detector face produces nine values that represent the number of secondary photons hitting each PMT. These nine values are saved as one line in an output list. To recover a traditional binned-mode image (number of gamma-ray hits as a function of position on the detector face), the nine PMT values for each qualified gamma-ray event are converted into a position estimate via a maximum likelihood algorithm onto a 79×79 pixel image grid.⁴

Using that procedure, we can also calculate an error in our ability to determine the correct position by looking at our position estimates for a series of gamma rays with known incident locations. To do this, we simply collect about 6000 events hitting the detector at a known location and perform the position estimation procedure. An error in the estimated position is then determined as simply the average difference between the known and estimated positions.

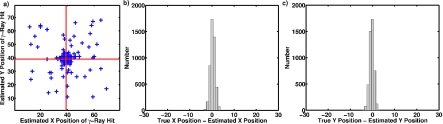
Figure 1 shows the results of these calculations for a location in the center of the detector face. Figure 1a is a spatial map of the detector face, where the estimated positions of approximately 6000 photons are shown as crosses. The two reference lines mark the true position of all of these photons. Since positions are discretized (only allowed to fall on one of the 6241 positions on the 79×79 grid), the number of photons that were assigned a specific position are not indicated in this graph. Therefore, if 2000 gamma rays were assigned to a position, it would look the same as if only one gamma ray was assigned to that position. In order to get a better idea of the overall distribution, Fig. 1b plots a histogram of the true minus estimated X positions for all of the photons in Fig. 1a and Fig. 1c shows the analogous histogram for the Y direction. The mean radial position error is about 2.3 mm.

Figure 1.

(a) Spatial map of the detector face in units of pixels where one pixel is 1.5 mm. Small crosses show the estimated positions of 6000 gamma-ray events, while the large cross shows the true position of those gamma rays. Number is not indicated on this plot, and positions are discretized. This means that if 2000 gamma rays were assigned to a given position on the detector face, it would look the same as if only one gamma ray was assigned to that position; (b) histogram of true minus estimated X position in pixels (1 pixel =1.5 mm) for each of the qualified gamma rays in (a); and (c) histogram of true minus estimated Y position in pixels (1 pixel =1.5 mm) for each of the qualified gamma rays in (a).

These graphs show the position error for the center of the detector face; however, the error does vary depending on the detector position. To get an idea of the spatial variation in resolution over the detector face, this calculation was repeated for every possible position of the 79×79 pixel grid sampled in the mean detector response function (MDRF) measurement. This analysis shows that the position error is relatively low in the central portion of the detector, but rises to values as high as 18 mm at the very edges of the scintillator crystal. This level and distribution of position errors correspond to typical position errors in indirect detectors with solid NaI scintillation crystals.

OPTICAL DESIGN

Our basic system assumptions (described in Sec. 1) as well as the existing detector design already give us a good general idea of how the system will look and behave. In this section, the details of the optical design are presented to determine the exact behavior of the system for a given object. This means that, given a particular object, our optical design will determine what system geometry (object-pinhole distance, pinhole-detector distance, and pinhole diameter) will give the optimal system performance, as well as calculate the predicted performance of the system.

In order to do this, we must first define what we mean by optimal performance. Ideally, the optimal performance of the system is that which maximizes the observer’s performance for a specific task.^{5, 6, 7} For example, if the task is tumor volume estimation, then the optimal performance is that which allows the observer to perform the most accurate tumor volume estimation. This would imply that the optimal performance of the system is dependent not only on the object but also on the task being performed. In this case, a new optical design is needed for each task that one would like to perform with the instrument. Since this prototype instrument is being designed for use with many possible tasks, we have chosen to focus on a more general optimization to define the possible geometry ranges of the system. The initial system control software will use this optical design to control the system geometry. However, in the future, more complex, task-dependent geometry control codes can be written for use with the same instrument.

The system performance parameters that we have chosen to consider in the design are the field of view (FOV), sensitivity, and resolution of the system. Therefore, in the context of this prototype system, the geometry is considered optimal when the image approximately fills the detector face, the sensitivity of the system is as high as possible, and the resolution in object space of a projection image is as high as possible. The remainder of this section will be devoted to calculating how the FOV, sensitivity, and resolution depend on the system geometry as well as determining how to control the system geometry to obtain the desired values for these parameters.

Calculating system performance as a function of system geometry

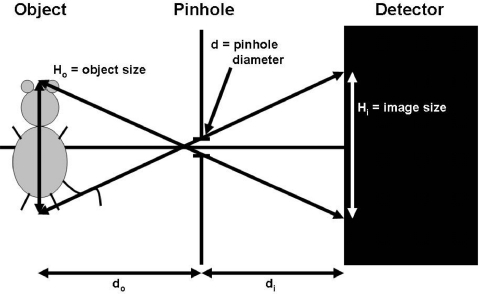
Definitions of the relevant system parameters are listed in Table 1 and illustrated in Fig. 2. The next few sections calculate how the image size, sensitivity, and resolution depend on these system parameters.

Table 1.

Definition of system variables.

Variable	Description
d	Diameter of pinhole
do	Positive distance from object plane to pinhole
di	Positive distance from pinhole to image plane
Ho	Height of object

Figure 2.

Diagram showing some defined variables.

Image size

The image size can be calculated by looking at how the most extreme rays of the object travel through the system. This takes into account the finite diameter of the pinhole. After going through the calculation, the image size can be written as

$$H_i=d+\frac{d_i}{d_o}\left(d+H_o\right).$$ (1)

Sensitivity

The sensitivity of the system is simply the number of counts per second detected by the system divided by the total number of photons emitted by the object per second. This value can be determined by looking at how the solid angle subtended by the pinhole compares to 4πsr, because the object is emitting in all directions, but only light that passes through the pinhole can reach the detector. Using the exact formula for the solid angle and assuming that the image is entirely contained within the detector face, we arrive at the following expression for the system sensitivity:

$$\text{Sensitivity}=3.7\times {10}^7\left(\frac{1}{2}-\frac{d_o}{\sqrt{4d_o^2+d^2}}\right),$$ (2)

where the leading factor gives a sensitivity in counts∕s/mCi.

Resolution

The resolution of the system has at least three major contributions: blur due to the finite pinhole diameter $\left(h_o^{\text{pin}}\right)$, blur due to the position estimation process $\left(h_o^{\text{est}}\right)$, and blur due to the thickness of the scintillation crystal $\left(h_o^{\text{sci}}\right)$. The overall resolution of the system can be calculated by adding all of its components in quadrature

$$h_o^{\text{total}}=\sqrt{{\left(h_o^{\text{pin}}\right)}^2+{\left(h_o^{\text{est}}\right)}^2+{\left(h_o^{\text{sci}}\right)}^2}.$$ (3)

This equation assumes that the components are all independent and Gaussian, which may be a poor assumption in some cases. We will now go through a calculation of each of these three components. Since we are interested in how small of a thing we can resolve in the object, we will calculate the blur in image space and then project it back into object space. This gives a resolution that represents the smallest thing we can resolve in the object in a single projection image.

The blur due to the pinhole diameter can be calculated by looking at how a single point in object space maps to image space. Since we have a finite pinhole diameter, this will map to a disk in image space, the size of which we can calculate by drawing rays from one point in object space through the top and bottom of the pinhole for a point in object space offset in the z direction. When we do this, and use the magnification equation to project back to object space, we find that the blur in object space is given by

$$h_o^{\text{pin}}=d\left(\frac{d_o}{d_i}+1\right).$$ (4)

When a gamma ray hits the detector, there is some uncertainty in determining the exact position where that gamma ray hit the detector face. The process by which the position of a gamma ray is determined, as well as the uncertainties involved in that process, was discussed in Sec. 2. In that section, it was demonstrated that the uncertainty was spatially dependent over the detector face with a value in the center of approximately 2.3 mm. Here we simply take a value of 2.5 mm and project that back into object space to obtain the blur due to the position estimation process

$$h_o^{\text{est}}=2.5\text{mm}\left(\frac{d_o}{d_i}\right).$$ (5)

Since the scintillation crystal has a finite thickness, photons that enter the crystal at an angle will have a blur in their position due to the fact that the interaction depth of the photon in the crystal corresponds to slightly different detected positions in image space. Assuming that the photons have an equal probability of interacting at any depth, we can quantify this blur by calculating the range of possible locations that a photon can be absorbed in the crystal thickness along its trajectory and project those locations on to the detector plane. This blur increases as the angle of incidence increases and can be calculated via simple right triangles as

$$h_o^{\text{sci}}=\frac{t_c}{2d_i}\left(d+H_o\right),$$ (6)

where t_c is the thickness of the scintillation crystal and $h_o^{\text{sci}}$ is the blur already transferred to the object plane. However, because photons are more likely to interact at shallow depths of the crystal, the true resolution is not quite this severe. Assuming an exponential absorption profile and defining the blur as corresponding to the spread induced when 75% of the incoming photons are absorbed, we find that the resolution in object space due to this effect is given by

$$h_o^{\text{sci}}=\frac{\text{ln}4}{\mu d_i}\frac{2d_o\left(d+H_o\right)}{{\left(4d_o^2+{\left(d+H_o\right)}^2\right)}^{1∕2}},$$ (7)

where μ is the linear attenuation coefficient of NaI at 140 keV.^{8, 9}

Note that, depending on the crystal thickness and the angle of the gamma ray hitting the crystal, it may take the entire thickness of the crystal to absorb 75% of the incoming photons. In this case, we revert back to the approximate equation [Eq. 6] in order to not overestimate the blur.

Controlling geometry to improve system performance

From equations derived in the previous section, we can easily calculate the system FOV, sensitivity, and resolution for a specific system geometry. The next step is to understand how to vary the system geometry in order improve values for FOV, sensitivity, and resolution. In the following subsections we describe the approach we use to choose the system parameters in an effort to achieve improved system performance. There are, presumably, many different approaches to dealing with this problem. The approach that we have taken here is not an optimization, so much as one possible adaptation choice.

Choosing the object-to-pinhole distance

We have started off by examining the equation for sensitivity and noticing that, for a given source strength and pinhole diameter, the sensitivity is completely determined by the object-to-pinhole distance as long as the entire image is confined to the detector and there is no vignetting. This means that, if we minimize the object-to-pinhole distance, we maximize the sensitivity. As a result, we begin by making the object-to-pinhole distance as small as possible given a series of constraints. The constraints that we consider are mechanical, object size, obliquity, and vignetting constraints. Each of these is discussed in detail below.

Mechanical constraint

There exists a minimum possible object-to-pinhole distance that the system can achieve solely due to mechanical constraints. These restrictions are things such as how close we can get a linear stage (and therefore the pinhole) to the object, how thick the pinhole plate is, what needs to be surrounding the object for veterinary monitoring purposes, etc. In our system, this distance is approximately 1∕2 in. (12.7 mm).

Object size constraint

The object size constraint is simply a minimum possible object-to-pinhole distance determined by the object geometry. If we assume that we are interested in imaging the entire object, and that the object-to-pinhole distance is defined from the center of the object, then the minimum possible object-to-pinhole distance is simply the radius of the object itself. However, the situation becomes more complicated when we are interested, not in the entire object, but only a small region of interest (ROI) inside of the object (e.g., a small interior lesion). In this case, the minimum object-to-pinhole distance due to the object size constraint varies not only with the specific object geometry, but also the viewing angle of the object itself.

For these calculations, we have assumed a cylindrical object where the ROI is the entire object. Note that we will always assume that the diameter of the object is 0.31 of the length of the object. This value is based on typical mouse and rat dimensions. In this case, the object-to-pinhole distance is restricted to

$$d_o\ge \frac{0.31H_o}{2}.$$ (8)

Obliquity constraint

Since the scintillation crystal has a finite thickness, photons that enter the crystal at an angle will have a blur in their position due to the fact that the interaction depth of the photon in the crystal corresponds to slightly different positions in image space. In Sec. 3A3, we derived the resolution in object space as a function of the system geometry [Eqs. 6, 7]. We can now examine these equations to determine a lower limit on d_o to keep the resolution in object space less than the blur due to the position estimation process. For the approximate equations (ignoring the exponential absorption profile of the crystal), we find

$$d_o\ge \frac{t_{c}F\left(d+H_o\right)}{2r_{\text{est}}},$$ (9)

where F is how much smaller we want the blur due to scintillator thickness to be versus blur due to the position estimation process (a larger number is more strict) and r_est is the blur size due to the position estimation process.

The same analysis performed on the equations that take into account the exponential absorption profile of the crystal give

$$d_o\ge \frac{(d+H_o)∕2{\left(1-{\mu r_{\text{est}}∕(F\text{ln}4)}^2\right)}^{1∕2}}{\mu r_{\text{est}}∕(F\text{ln}4)}.$$ (10)

Vignetting constraint

As a result of the pinhole not being ideal (i.e., having a thickness), gamma rays from the object can be vignetted. The term vignetting is used to denote when a gamma ray that would pass through an ideal (i.e., infinitely thin) pinhole plate gets blocked by the geometry of the pinhole that is necessary in a pinhole plate of finite width. Here we calculate the smallest d_o in order to eliminate vignetting. This assumes that no gamma rays can pass through any part of the pinhole plate. In this case, the maximum angle of light that can pass through the pinhole is

$$\beta =2{\text{tan}}^{-1}\left(\frac{d}{t_i}\right),$$ (11)

where d is the pinhole diameter and t_i is the thickness of the keel edge of the pinhole. The geometry of the pinhole is taken to be a thick plate with an opening angle machined into either side of the plate and a hole drilled through the center such that there is a small flat area (the keel edge) near the center of the plate. Calculating the minimum possible d_o that allows all gamma rays from the object to pass through the pinhole gives

$$d_o\ge \frac{H_o}{2\text{tan}(\beta ∕2)},$$ (12)

and plugging in for β gives

$$d_o\ge \frac{t_i{H}_o}{2d}.$$ (13)

For the adaptive system, the pinholes were machined with an opening angle of 82° and a keel edge defined to produce a 75° opening angle, assuming that the keel edges are completely opaque to gamma rays. Note that, if gamma rays could pass through the edges of the pinhole, that would imply that there was less vignetting and, therefore, the requirement on d_o due to vignetting would be less strict. As a result, these calculations are a worst-case scenario.

Choosing the pinhole-to-detector distance

Once the object-to-pinhole distance is fixed, the pinhole-to-detector distance can be used to control the magnification of the object on the detector. The objective is to keep the size of the image equal to a fraction, f, of the detector face, where f is chosen to nearly fill the detector and the image is taken to be the image of the ROI. The ROI could include the entire animal or a smaller, localized region of the animal. The main limitation on the pinhole-to-detector distance is that there is a maximum overall length of the system, D_max, where D_max is the distance from the center of the object to the front of the detector face. This restriction is simply to enforce a reasonable system size. For this system, D_max was chosen to be 283 mm (or 11.14 in.), a value based partially on the commercially available linear motorized stages.

In this scenario, the pinhole-to-detector distance can be calculated by setting Eq. 1 equal to 114.3×f and solving for the pinhole to detector size, where 114.3 represents the size of one side of the square detector face in millimeters. This gives

$$d_i=\left(114.3\times f-d\right)\frac{d_o}{d+H_o}.$$ (14)

If this equation gives a d_i that results in a total system length, D, greater than D_max, then the total system length is fixed to D_max, and d_o is changed to enforce filling the fraction f of the detector. In this case, d_o is no longer determined by the constraints previously mentioned. When D and f are fixed in this manner, d_o can be solved for as

$$d_o=\frac{D\left(d+H_o\right)}{114.3\times f+H_o},$$ (15)

and then d_i is simply given as

$$d_i=D_{\text{max}}-d_o.$$ (16)

Choosing pinhole diameter

Once the system parameters are defined by the above equations, the pinhole diameter can be varied using a resolution-throughput tradeoff. To do this, the resolution blur due to the pinhole diameter is compared with the other resolution contributions. If the resolution contribution from the pinhole diameter is smaller than the other contributions, and increasing the pinhole diameter to the next available size would not make the pinhole contribution larger than the other contributions, then the pinhole diameter is increased to the next available diameter. In this case, the sensitivity of the system can be increased without significantly affecting the resolution of the system. If, however, the pinhole contribution is larger than the other contributions and enough photons are hitting the detector, then the pinhole diameter is decreased in order to improve the resolution. The counts∕s/mCi threshold used in this case is, somewhat arbitrarily, set to 200 counts∕s/mCi for our system.

System performance versus object size

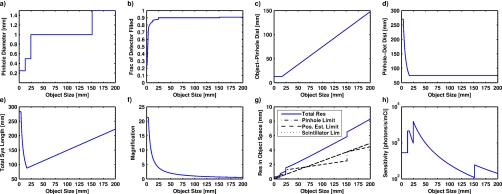
From the equations derived in Secs. 3A, 3B, we can calculate the system behavior and performance as a function of object size. The considered system is described in Secs. 1, 3A, 3B and consists of a single pinhole, small animal SPECT system with four pinhole choices (0.25, 0.5, 1.0, and 1.5 mm) and a maximum system length of 283 mm. Figures 3a, 3b, 3c, 3d, 3e, 3f, 3g, 3h show results of these calculations. For reference, a typical length for a rat is about 186 mm, while a mouse is typically 83 mm long. The width of a mouse is generally about 25 mm. While the system is designed to have the capability to image an entire animal, imaging a smaller ROI inside of the animal (i.e., ROIs on the order of ∼25 mm or smaller) is the main focus of this study.

Figure 3.

These figures show the following parameters, determined via the algorithm in Sec. 3B, as a function of object size: (a) pinhole diameter, (b) fraction of detector filled, (c) object-to-pinhole distance, (d) pinhole-to-detector distance, (e) total system length, (f) magnification, (g) resolution in object space of a projection image (overall system resolution is shown as well as the three individual components), and (h) sensitivity (counts∕s/mCi). These results are for the imaging system diagrammed in Fig. 2, where the single pinhole has four diameter choices (0.25, 0.5, 1.0, 1.25 mm) and the system has a maximum length of 283 mm.

In Fig. 3a, we see that the pinhole diameter increases as the object size increases. This is due to the fact that, as the object size gets bigger, the pinhole plate gets pushed further from the object, and the contribution to the overall resolution from the pinhole diameter gets smaller. When this happens, the pinhole diameter can be increased without making the overall resolution significantly worse. The graph is discontinuous because there are only four available pinhole diameters (0.25, 0.5, 1.0, and 1.5 mm).

The fraction of the detector filled as a function of object size is shown in Fig. 3b. We have specified that we would ideally like this value to be 0.9 times the size of the detector face. For larger object sizes, this is relatively easy for the system to achieve. However, for very small objects, the system has difficulty because there is an imposed maximum system length and, therefore, a maximum magnification. As a result, it is impossible for the system to sufficiently magnify very small objects.

Figure 3c shows the object-to-pinhole distance as a function of object size. At small object sizes, this parameter is dominated by the mechanical constraints, which have a flat profile. At larger object sizes, the object size, vignetting, and obliquity constraints come into play, with the obliquity constraint being the dominating factor. This constraint has a linear behavior that forces the pinhole plate out as the object gets larger to avoid the outermost rays becoming too steep.

In Fig. 3d, the pinhole-to-detector distance is plotted as a function of object size. At small object sizes, this distance is very large because the system is attempting to magnify the object as much as possible. The plateau at the smallest object sizes occurs because the system hits its maximum system length. This distance then decreases until it hits a constant value. The constant behavior at large object sizes is simply a consequence of how the equations cancel in that regime.

Figure 3e shows the total system length as a function of object size. This is the distance from the center of the object to the front of the detector face. For small objects, this value is large because the system is trying to magnify the objects as much as possible. The total system length then gets larger for large objects as the plates move out together away from the object.

Figure 3f shows the magnification of the system as a function of object size. Smaller objects are magnified as much as possible until the system hits its maximum possible magnification at about 21. For very large objects, the system actually demagnifies them in order to fit the entire object onto the detector face.

The system resolution in object space of a single projection image as a function of object size is given in Fig. 3g. The overall system resolution is shown as a solid line, whereas the three individual components as discussed in Sec. 3A3 are shown in broken lines. The contribution from the scintillator thickness is overlapping the contribution from the position estimation process. This happens simply because we chose that to be the case when we set our constraints on the object-to-pinhole distance (see Sec. 3B1). Since the scintillator thickness is the dominating factor in those constraints for most of the object sizes, these two lines match most of the time. The contribution due to the pinhole diameter is discontinuous because there are only four discrete pinhole diameters to choose from. If the system only had a single 1-mm pinhole, that line would remain flat, following its slope near the middle of the object size range. In this case, the resolution at very small object sizes would be significantly worse; however, the system is able to adjust itself to obtain the best resolution possible from the available geometries. The achievable overall resolution for a size about equal to the width of a mouse is approximately 1 mm, which is good for a research small-animal system. For smaller object sizes, the resolution improves significantly. For example, the predicted resolution for a 5-mm object is only 0.31 mm.

Figure 3h shows the sensitivity of the system as a function of object size. For comparison, one camera of the FastSPECT II system in its standard geometry would look like a flat line with a value of about 600 counts∕s/mCi.¹⁰ For small object sizes, we generally do better than this value. In order to improve the sensitivity further, we can simply modify the comparison value used to perform the resolution∕throughput tradeoff when determining the pinhole diameter. Sensitivities at larger object sizes are less than the equivalent FastSPECT II value, but only because the object is being demagnified so that it can fit onto the detector face.

An example object: Small lesion within larger object

In order to demonstrate the type of performance that this system can achieve, here we examine more carefully the type of situation that might occur in a real imaging scenario. The specific example that we consider is of a mouse-sized object (a cylinder with a diameter of 25.4 mm and a height of 83 mm) with an interior spherical tumor. The tumor has a diameter of 5 mm and is offset 5 mm from the center of axis of rotation of the object. It is assumed that all of the activity in the object is localized in the spherical tumor. A typical task that might be performed in this situation is tumor volume or activity estimation for determining the efficacy of a particular treatment.

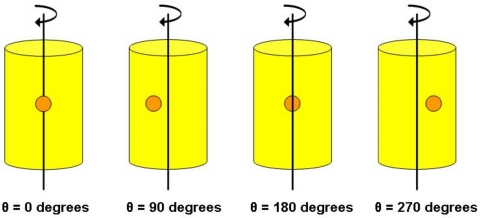
In the previous calculations, we assumed that the object of interest had a fixed extent, independent of viewing angle. Here, the extent of the object of interest, namely the tumor, changes with the viewing angle of the object (see Fig. 4). Although the tumor has a fixed size, its offset from the center of the overall object means that its apparent distance from the center of the overall object changes with the viewing angle. Since the detector of the system is not steerable, this implies that the field of view must be adjusted for each angle in order to ensure that the tumor is utilizing the maximum amount of detector space at all times. As a result, the chosen system geometry will change for each viewing angle.

Figure 4.

Orientation of example object for Figs. 5a, 5b, 5c, 5d, 5e, 5f, 5g, 5h. The reader is viewing the images as if they were the detector (i.e., the tumor is closest to the detector atθ=0°). The example object consists of a cylinder (diameter =25.4 mm, height =83 mm) meant to estimate the size of a mouse, plus an offset sphere (diameter =5 mm, distance from central axis of rotation of cylinder =5 mm) to simulate a lesion.

In the beginning of this section, we calculated the predicted system behavior as a function of object size. Here, we do the same calculations, but this time as a function of object viewing angle for this specific example case. Figure 4 shows the angle orientation as if the reader is the detector and Figs. 5a, 5b, 5c, 5d, 5e, 5f, 5g, 5h show the results of these calculations. In Figs. 5a, 5b, 5c, 5d, 5e, 5f, we see how the geometry of the system changes over the imaging sequence, and Figs. 5g, 5h show the range of resolution and sensitivity values that would be acquired for an adaptive data set. As the example object rotates, the distance from the lesion to the pinhole changes from its minimum at 0° to its maximum at 180°. In addition, the FOV necessary to capture the entire lesion is a minimum at 0° and 180° and a maximum at 90° and 270°. In this geometry, we would expect that the imaging parameters would be identical at 90° and 270° since the lesion is at the exact same distance from the pinhole and requires the same FOV to be fully imaged. We also expect that the imaging parameters would be symmetric about 0° and 180°, but not exactly the same at these two rotation angles due to the difference in the lesion to pinhole distance. Inspection of Figs. 5a, 5b, 5c, 5d, 5e, 5f, 5g, 5h show the expected trends with the exception of Figs. 5a, 5c, where the imaging values are identical at 0° and 180° due to the system hitting mechanical limitations. In the case of Fig. 5a, the same pinhole diameter is chosen at both 0° and 180° because the system has a limited number of pinhole diameters to choose from, whereas in the case of Fig. 5c, the system is pushing the pinhole right up against the outside of the object itself and cannot move any further.

Figure 5.

These figures show the following parameters as a function of example object viewing angle for the object shown in Fig. 4: (a) pinhole diameter, (b) fraction of detector filled, (c) object-to-pinhole distance, (d) pinhole-to-detector distance, (e) total system length, (f) magnification, (g) overall resolution, and (h) sensitivity.

For this particular task, the expected resolution values for a projection image are all submillimeter, ranging between 0.3 and 0.8 mm. The sensitivity values range from 700 to 12 000 counts∕s/mCi, all higher than the equivalent FastSPECT II system. These simulation results clearly show that adaptive imaging has the potential to significantly improve image quality over standard, fixed geometry systems.

MECHANICAL DESIGN

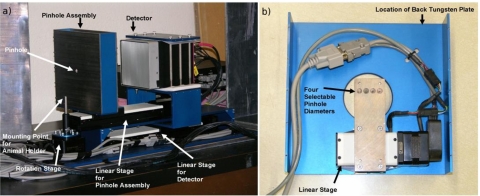
The basic design of the adaptive system has a vertically oriented animal, one on-axis pinhole and one detector. Viewing angles are achieved by rotating the object. To allow real-time adaptability of the system geometry, the camera position, pinhole position, pinhole diameter, and object viewing angle are all mounted on a series of four motorized stages manufactured by Newmark Systems, Inc. All four stages are controlled via a single Galil Motion Control, Inc. controller so that one command produces simultaneous motion of all four stages. The user interface for the motors is integrated into the overall system control LABVIEW™ software described in Sec. 5. Figure 6a shows a picture of the assembled system.

Figure 6.

(a) Close-up of the adaptive imaging system. The object stand can be seen sitting on top of the rotation stage, to the right of that is the pinhole assembly, and slightly further to the right the detector is shown. (b) Picture showing detail of the pinhole assembly. The top tungsten plate has been removed.

The entire system sits on a single aluminum plate that can be bolted to a breadboard via a series of 1∕4–20 holes for stability. The animal is mounted on a rotation stage that sits at one end of the board. A linear stage with an 8-in. travel range bolts to the base plate. Above this is a small aluminum stand on which bolts another linear stage with a 6-in. travel range. An extension piece bolts to the slide of the 8-in. linear stage and wraps around the upper stage. The camera is attached to this extension piece via a set of six 1∕4–20 bolts that clamp an aluminum plate on the top of the camera. Nylon sheets are used between the camera and the aluminum clamp to eliminate electrical contact.

The pinhole assembly [see Fig. 6b] bolts to the slide on the linear stage with a 6-in. travel range. The assembly consists of two tungsten plates with oversized holes for the gamma-ray beam to pass without vignetting. Behind the first tungsten plate is a smaller tungsten sandwich that has four small pinholes with diameters of approximately 0.25, 0.5, 1.0, and 1.5 mm, where the two larger diameters are drilled directly into the tungsten and the two smaller diameters are drilled through a small piece of gold foil placed between the two tungsten plates. All of the pinholes are machined so that they are located in the center of the thickness of the tungsten sandwich. They each have an opening angle of approximately 75° restricted by a keel edge from an outer opening angle of 82°.

This entire tungsten sandwich is bolted to a small linear stage with a 1-in. travel range that then bolts on the large back tungsten plate. This allows the small pinhole plate to slide against the large front tungsten plate to pick off the desired pinhole diameter.

The majority of the shielding for the system is provided by the tungsten in the large and small pinhole plates. The large pinhole plates are 1∕8 in. thick, while the small pinhole plate has an overall thickness of 1∕4 in. Additional shielding for the system is provided via a large 1∕8-in.-thick lead-lined box that fits snugly over the entire assembly. The entire system also sits on an additional sheet of 1∕8-in. lead, and small sheets of loose lead have also been placed near the bottom of the object rotation stage.

CONTROL SOFTWARE

The adaptive system has a total of six different mechanical components that must be electronically controlled. These include the camera, its power supply, and the four motorized stages. Computer interface software for the camera, written in LABVIEW™ and C, has already been developed for several similar detectors in the CGRI group and is used with little modification here. Additional LABVIEW™ and C code has been written to handle control of the camera power supply, the four motorized stages, and the adaptive algorithms. The camera power supply is a National Instruments device and therefore can be controlled easily via LABVIEW™ with pre-existing software provided by the manufacturer. The four motorized stages are controlled via an RS-232 interface with a single controller. The manufacturer has a series of programs written in C and LABVIEW™ that can be interfaced through LABVIEW™ for relatively straightforward user control.

The user interface for the adaptive system brings all of these components together into a single, simple control panel. Upon startup, the software automatically initializes the system and allows the user to reorient the object to any desired starting rotation angle. The user must then take a set of fixed-geometry images before any adaptive images can be acquired. To do this, the user simply specifies the total exposure time, the number of imaging angles, and the geometry of the system (pinhole diameter, object-to-pinhole distance, and pinhole-to-detector distance). The software proceeds to take and save the data and motor positions to a series of output files. The motor positions are saved for every image so that the exact geometry is known and can be used in subsequent reconstructions. The total exposure time is distributed evenly over each of the viewing angles. After acquiring the data, the software automatically performs an estimation of the object size for each imaging angle and saves this information for later use. The details of the object size estimation algorithm are described in the following subsection. Once an initial set of fixed-geometry images have been acquired, the user can choose to take either fixed or adaptive images in any combination they desire. The system will automatically recalculate and update estimates of the object size for each imaging iteration.

In order to take adaptive images, the user enters the total exposure time and number of imaging angles. Information about the object size determined in the last set of images is used here to calculate the desired geometry of the system according to the previously described algorithm. If more angles are desired for the current imaging sequence than the previous imaging sequence, object sizes are linearly interpolated onto the finer angle grid. For the adaptive images, the total exposure time is divided among the different viewing angles in order to keep the number of counts in each projection image constant. This calculation relies on the comparisons between the throughput for the chosen geometry of each viewing angle and ignores leakage.

Note that the current software is implemented using the estimated object size to determine the desired system geometry based on the optical design in Sec. 3. However, the software has been written such that alternative feedback rules could be easily added to the current software.

Object size estimation

The estimation of the size of the ROI is perhaps one of the most difficult tasks of the adaptive system and can have a significant effect on performance of the system. The ideal algorithm would be able to determine the size of the ROI with little or no user input. However, this is difficult to achieve since the ROI is object and task dependent. As a result, some user interaction may be required for effective implementation in real imaging systems. One might envision an algorithm that requires the user to pick from a predetermined set of tasks, independently calculates the size of the ROI, then requests user verification.

The current algorithm uses the fact that the size of the lesion is known and simply calculates the position of the lesion in order to determine its distance off-axis. It works by performing a 7×7 binning on the image to get a smaller, binned image and picks the maximum of the binned image as the position of the lesion. This procedure is repeated 49 times, each time shifting the binning template by 1 pixel in either the x or y directions to get a new binned image. The largest maximum value is taken from all of the binned images to obtain the actual estimated position of the lesion. This shifting process allows the position of the lesion to be determined on a grid finer than the 7×7 binning scale. Once the position of the lesion is known, the size of the FOV is calculated by combining that position with the known 8.1-mm size of the lesion and the known magnification of the system to obtain the full estimated “object size.” This sort of algorithm would be applicable for any sort of background activity distribution as long as the maximum activity per volume of the background was never greater than the maximum activity per volume of the tumor. In the case of our phantom, the background is uniform and always has a lower activity per volume than the tumor. There are two main drawbacks to this specific approach. First, the known size of the lesion must be used in the calculation and, second, the magnification of the lesion is not exactly known. The magnification of the lesion is different if it is located in front of or behind the center of object space. Since the position of the lesion is not known during the scout image acquisition, the magnification of the center of the object space is used. This results in the system underestimating the FOV when the lesion is closer to the detector and overestimating the FOV when the lesion is further from the detector. One might consider using a similar approach for more general objects as long as an estimated lesion size is known. One example might be tumor volume estimation of tumors implanted on mouse limbs, where the tumors can be reasonably visualized. An overestimation of the lesion size would still allow functionality of the adaptive system, albeit at somewhat reduced performance.

Although the algorithm does have drawbacks, it does a reasonable job of calculating the estimated object size in this scenario (see Sec. 6). As a result, it can be used to take adaptive phantom data that give an indication of the utility of the adaptive nature of the system. However, future work is required to develop an object size determination algorithm more applicable to real-life situations.

PHANTOM STUDY

We have collected phantom data with the adaptive system in fixed geometry and adaptive modes in order to verify that the system performs as it was designed. In the following sections, the phantom is described, projection images are presented, analysis of leakage fraction is discussed, and a comparison of the predicted and actual adaptive behavior is performed.

The phantom

We have developed a phantom to simulate a spherical, offset lesion in a flat background (see Fig. 7). The background reservoir is an acrylic tube with an inner diameter of 28.65 mm and an inner height of 66.91 mm. A cap, that has two offset holes drilled into it, fits over the top of this background reservoir. The first hole has a diameter of just over 12 mm and is 0.3125 in. from the center of the cap. This is the position from which the phantom lesion is suspended. The second hole is also offset from the center, which simply serves as a fill access to the background reservoir when the phantom is fully assembled. The spherical lesion consists of an 8.1-mm inner diameter hollow polypropylene ball with a small puncture that allows the ball to be filled with a radioactive source. This spherical ball is secured into a 12-mm outer diameter plastic test tube, which has several punctures in the sides to allow fluid flow. The top of this test tube is attached to the large offset hole in the cap of the background reservoir with a small amount of putty. After the phantom is fully assembled, a syringe is used to fill the lesion with a radioactive source. This is then sealed with super glue and allowed to dry. The background reservoir is then filled with a cooler radioactive source to produce the flat background.

Figure 7.

Phantom used for the imaging study. The large cylinder holds the background source while the small sphere holds the tumor source. The small sphere is a plastic, hollow ball.

The data

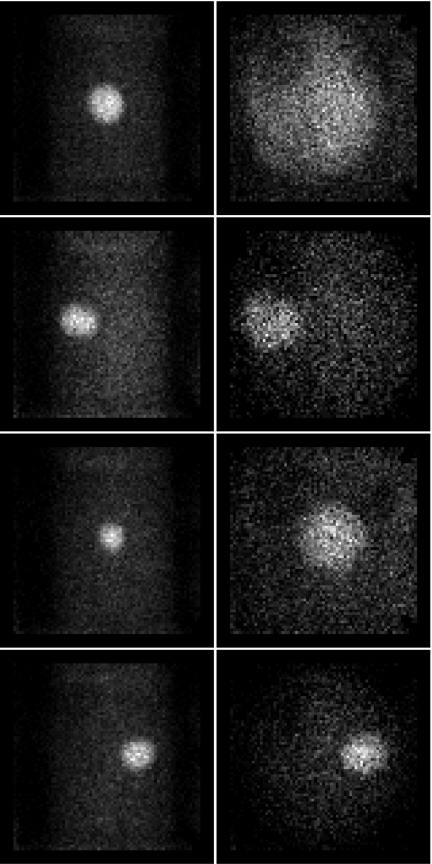
Tomographic data were acquired of the phantom in both adaptive and fixed-geometry modes with the same instrument. The adaptive data consist of one set of scout images with 12 angles and a final set of adaptive images with 50 angles. The fixed-geometry data consist of a single set of images with 50 angles, where the exposure time was set to be equal to that of the scout plus adaptive imaging sequence when radioactive decay was taken into account. To make the imaging sequences comparable, both the scout data and the fixed-geometry data were taken with FastSPECT II standard geometry (pinhole diameter of 1.0 mm, object-to-pinhole distance of 48.26 mm, and pinhole-to-detector distance of 116.84 mm). Figure 8 shows a sequence of four projection images at different angles in the fixed and adaptive geometry configurations.

Figure 8.

(Left) Projection images from fixed-geometry data set. (Right) Analogous projection images from adaptive data set.

Leakage fraction

In order to estimate the fraction of detected leaked events, data with the pinhole covered and uncovered were taken for the adaptive system in the FastSPECT II configuration. An analysis of these data gives a leakage fraction of approximately 39% for the list-mode data (i.e., before MDRF processing with the likelihood of windowing), 27% after MDRF processing, and 15% after MDRF processing and with the outer five rows and columns of pixels set to zero. While these data give an indication of what the leakage fraction is for this particular geometry, the flexibility of the adaptive system means that the leakage fraction will vary for any given geometry. Therefore, a more complete leakage analysis should be done to fully understand the leakage behavior. This level of leakage is high for a SPECT imaging system and could introduce artifacts in the reconstructed images of the system. The mobility of the system makes shielding difficult, and future modifications of the system should attempt to reduce this effect to provide better system performance.

Actual versus predicted system behavior

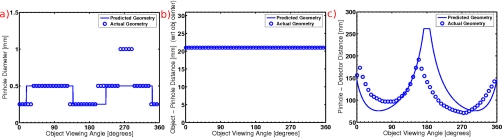
Since the positions of each motorized stage are recorded for every image, the actual behavior of the system can be compared with its predicted behavior. Figures 9a, 9b, 9c show the actual system behavior versus predicted system behavior.

Figure 9.

These figures show the following parameters as a function of imaging angle: (a) predicted and actual pinhole diameters, (b) predicted and actual object-to-pinhole distance, and (c) predicted and actual pinhole-to-detector distance.

Figure 9a shows the predicted and actual pinhole diameters used as a function of viewing angle. The actual pinhole diameter seems to follow the general trend of the predicted pinhole diameter with some mild deviations. The source of these deviations could arise from differences between the modeled and actual phantom, object size estimation errors, errors in machining of the pinhole plates, photon noise, and leakage in the system. In order to determine the pinhole diameter, the algorithm performs a calculation of the expected throughput for the next possible pinhole diameter based on solid angle calculations. These calculations are based on the pinholes being perfectly machined to their specified diameters and having no leakage through the surrounding pinhole plate. Even in the event of a perfectly machined pinhole plate, there is certainly leakage through the keel edge and opening angle of the pinhole. We have also seen that leakage in the system is significant, which would cause the throughput of the system to not scale as expected. The issue of leakage could be taken into account by incorporating measured leakage values into the algorithm after the amount of leakage has been minimized as much as possible with shielding. Object size estimation errors could also contribute to deviations in the pinhole diameter, but their effect is more obvious in Fig. 9c and so will be discussed there. Note that another effect of large leakage in the system is an incorrect distribution of the exposure time for the different viewing angles.

Figure 9b plots the predicted and actual object-to-pinhole distance as a function of viewing angle. In this case, the system behaves exactly as expected simply because the pinhole plate is running into a limit the entire time. This limit is not due to mechanical abilities of the system, but rather to the extent of the overall object. The distance of 21 mm is the closest that the pinhole plate can get to the phantom edge without hitting it. The system has the capability to provide smaller object-to-pinhole distances for objects with smaller overall diameters.

Finally, Fig. 9c shows the predicted and actual pinhole-to-detector distances. Again, the system behavior follows the predicted trend but does have some systematic deviations. In this case, the deviations are caused mainly by errors in the object size estimation and zero-angle positioning errors in conjunction with sparse angular sampling of the scout images. In this case, errors in the object size strongly affect the actual pinhole-to-detector distance used because this distance is what controls the magnification of the system. The strong dependency of the pinhole-to-detector distance on object size can clearly be seen by examining Fig. 3d. For this study, the object size is relatively small, around 8.1 mm, so that the pinhole-to-detector values are chosen from the area of the curve that is steepest on this plot. Between object sizes of 5 and 15 mm, the pinhole-to-detector distance ranges from 270 to 75 mm. That means that an error in estimating the object size by only 1 mm will cause an error in the pinhole-to-detector distance of approximately 20 mm.

The other main contributing factor to the error in the chosen pinhole-to-detector distance is the sparse angle sampling of the scout images. For these data, the scout images consist of measurements taken over 12 angles. In order to determine the object sizes for all 50 angles of the final adaptive data, estimated object sizes from the scout images are linearly interpolated. This means that, if the extreme angles are not seen in the scout images, they will not be properly accounted for in the adaptive images. The reason that 12 angles were chosen for the scout images was to eliminate this effect, since this results in data being taken for angles of 0°, 90°, 180°, and 270° in addition to others. This means that provided the object of interest is at an extreme value for angle 0°, all of the extreme values of the object orientation will be properly sampled. However, if the zero-angle orientation of the object is not properly aligned, errors will be incurred during the angle interpolation. In these data, the zero-angle orientation was offset by approximately 8°, causing the above-mentioned interpolation problems. This can be seen in Fig. 9c by the fact that the maximum pinhole-to-detector distances are not separated by 180°. With the current software setup, it is difficult to align the zero angle properly because it requires visual inspection of the actual object by the user. Fortunately, this error could be easily remedied by including a real-time projection image viewer that displays an acquired image of the object to the user after each angle update of the object orientation.

RECONSTRUCTIONS

Simulations were conducted to compare the adaptive and fixed-geometry imaging approaches. The three-dimensional (3D) phantom used for this study consisted of six hot cylinders of diameter 0.625 mm, with edge-to-edge separations of 0.625 mm, sitting in a colder phantom of diameter 27.5 mm. The activity ratio of the cylinders to the background was 10:1. Reconstructions were performed with an ML-EM algorithm on a 0.25-mm grid and all results are shown after 20 iterations. Figure 10a shows the central slice of the 3D phantom and Figs. 10b, 10c give the reconstructions of noise-free data for the fixed-geometry and adaptive systems (where only the final adaptive data has been used in the adaptive image reconstruction). Poisson noise was then added to the projection data with 10 000 000 mean total projection counts for the fixed-geometry data and, assuming equal imaging time, 4 001 000 mean total projection counts for the adaptive system. Reconstructions are given in Fig. 10d for the fixed-geometry system and in Fig. 10e for the adaptive system. While the fixed-geometry reconstructions demonstrate fewer artifacts in both the noise-free and noise-present cases, it is clear that identification and quantification of individual hot cylinders is far improved with the adaptive reconstructions.

Figure 10.

A comparison of reconstructions with fixed-geometry and adaptive systems. (a) Central slice of a simulated 3D phantom with six hot cylinders (diameter of 0.625 mm and edge-to-edge separations of 0.625 mm) embedded in a colder phantom (diameter 27.5 mm). The activity ratio is 10:1. (b) Reconstruction of noiseless phantom data for a fixed-geometry system. (c) Reconstruction of noiseless phantom data for the adaptive system. (d) Reconstruction of noise-present phantom data (10 000 000 mean total projection counts) for a fixed-geometry system. (e) Reconstruction of noise-present phantom data (4 001 000 mean total projection counts) for the adaptive system. While the adaptive system displays more artifacts in its reconstructions, identification of the six hot cylinders is much improved over the fixed-geometry system.

The streak artifacts in the reconstructions of the adaptive data set arise from the truncated projections. Areas very close to the ROI have minimal artifacts since there is complete data for every viewing angle. However, in areas far from the ROI, data are unavailable for some of the viewing angles, resulting in the increased artifacts. This means that, by design, the areas of most interest (i.e., the ROI) will have minimal artifacts, while the areas of least interest will be subject to more pronounced artifacts. The result is that information is preferentially transferred to the areas of most interest at the expense of areas that are of least diagnostic value. Some improvement of the artifacts may be possible by performing reconstructions that utilize the scout images in addition to the final adaptive data set. This approach would allow the incorporation of additional data in regions outside of the ROI without requiring further data acquisition. While further development of the details of the reconstruction algorithm are outside of the scope of this work, our group is currently investigating the utility of these sorts of methods.

DISCUSSION

We have successfully designed and constructed an adaptive small-animal SPECT imaging system as a proof-of-concept instrument. The current system is a one-detector module with a vertically oriented animal that serves as a testbed for a future, large-scale, SPECT imaging system with a horizontally oriented animal. We have demonstrated that construction of the adaptive system is not only feasible, but that it performs as designed. The system has a complete software package that handles user input, controls all of the mechanical adaptive components and saves their encoder-based position information, computes geometry feedback rules, and communicates with the detector to take and save all relevant data for future data processing. A phantom has been designed for system testing that has a hot offset lesion in a flat background. Data have been successfully acquired with this phantom in both adaptive and fixed-geometry configurations. For these data, feedback rules that force the lesion to fill the detector were employed, although the system software can be easily modified to handle additional feedback rules. In the context of the current implementation, the objective is to improve image quality in a single ROI that may or may not include multiple lesions. Reconstructions for fixed-geometry and adaptive systems of a simulated 3D resolution phantom were performed and showed that, while the adaptive system produces more artifacts in the reconstructed data, it allows for improved identification and quantification of the individual resolution elements.

During the construction and testing of the adaptive SPECT system, many valuable lessons were learned that should contribute to the improvement of its performance in future modifications. In terms of hardware, the main and most difficult issue that needs to be addressed is the large leakage fraction of the system, as well as the fact that it varies with the system geometry. Although variation of the leakage fraction with system geometry is probably inevitable, its effect can be lessened by reducing the overall leakage fraction. Currently, the shielding only reduces the leakage fraction to 39% for FastSPECT II geometry, which is poor by SPECT imaging standards. In terms of software, improved zero-angle animal orientation adjustment as well as a more accurate object size estimation algorithm could both lead to better performance of the adaptive system by allowing more accurate determination of the object properties from the scout imaging sequence data. Future development of the object size determination algorithm will probably need to be task dependent and may need to employ user interaction to verify that the object size estimation was satisfactory. In addition, adjusting the throughput∕resolution tradeoff employed for adjusting the pinhole diameter used a fixed count rate cutoff. Conversion of this fixed cutoff value to a value dependent on the source strength could result in a significant improvement in the performance of the adaptive system. In the reconstructed data, some of the streak artifacts evident in the adaptive data may be alleviated by the implementation of a reconstruction algorithm that takes into account both the scout data and the final adaptive data.

The feedback rules employed for this study were based on filling the detector with the ROI for every viewing angle, maximizing the sensitivity, and minimizing the resolution. While these are useful rules to apply for initial testing purposes, they do not take task-based measures of image quality into account. Appropriate task-based feedback rules have been discussed¹ and should be relatively straightforward to implement with the system given the flexible software interface. Addition of these types of feedback rules has the potential to produce significantly improved image quality in comparison to traditional, fixed-geometry systems. Quantification of the dependence of the image quality on specific object and system properties must be evaluated using a task-based approach (as developed in Barrett et al.¹) and is outside of the scope of this study. To address this question, our group is currently performing a task-based study, using this same prototype instrument and feedback rule, for future publication.