Crystal structure of the pressure-induced metallic phase of SiH₄ from ab initio theory

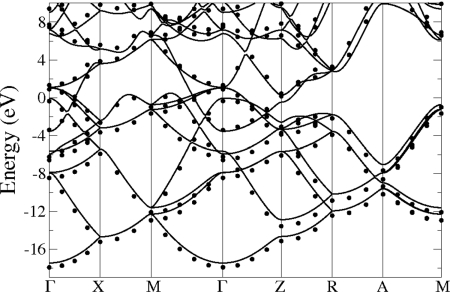
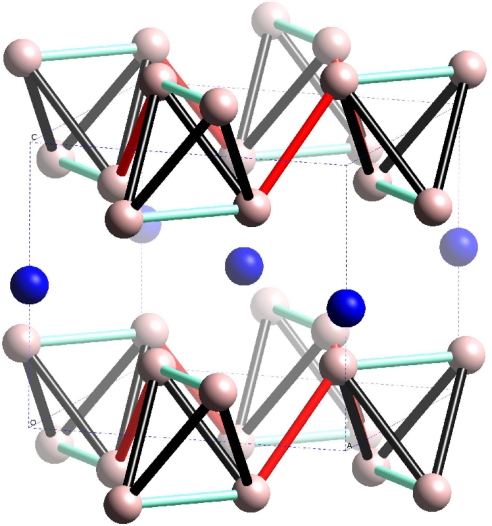
Abstract

Metallization of pure solid hydrogen is of great interest, not least because it could lead to high-temperature superconductivity, but it continues to be an elusive goal because of great experimental challenges. Hydrogen-rich materials, in particular, CH₄, SiH₄, and GeH₄, provide an opportunity to study related phenomena at experimentally achievable pressures, and they too are expected to be high-temperature superconductors. Recently, the emergence of a metallic phase has been observed in silane for pressures just above 60 GPa. However, some uncertainty exists about the crystal structure of the discovered metallic phase. Here, we show by way of elimination, that a single structure that possesses all of the required characteristics of the experimentally observed metallic phase of silane from a pool of plausible candidates can be identified. Our density functional theory and GW calculations show that a structure with space group P4/nbm is metallic at pressures >60 GPa. Based on phonon calculations, we furthermore demonstrate that the P4/nbm structure is dynamically stable at >43 GPa and becomes the ground state at 97 GPa when zero-point energy contributions are considered. These findings could lead the way for further theoretical analysis of metallic phases of hydrogen-rich materials and stimulate experimental studies.

High-pressure experiments on hydrogen-rich materials such as CH₄, SiH₄, and GeH₄ represent a model for study of metallic hydrogen (1) because enormous technical difficulties still prevent the achievement of metallization in pure solid hydrogen (2, 3). In these hydrogen-rich materials, chemical pressure leads to a collapse of the hydrogen network, which is predicted to induce metallization and even superconductivity (1).

Recently, it has been observed from infrared-reflectivity measurements in silane (SiH₄) at room temperature that the reflectivity increases at 60 GPa, pointing toward the existence of a Drude-like metallic phase (4). In the subsequent experiments (5), the transition from insulating molecular solid to metallic state was confirmed for even lower pressures of 50 GPa. Furthermore, the critical temperature for superconductivity was determined at 96 GPa and 120 GPa as T_c = 17 K. Based on X-ray diffraction measurements, the hexagonal P6₃ space group was suggested for this phase. Precise positions could only be deduced with certainty for silicon atoms, because the assignment of hydrogen sites is almost not possible from the X-ray data.

Before these experimental findings, several theoretical studies were carried out on the subject of metallic silane. Feng et al. (6) suggested the existence of a semimetallic phase with the Pmna structure at 91 GPa, which becomes superconducting at higher pressure. However, it is important to note that the authors stated that a correction for the band gap would shift the transition toward higher pressure. Another theoretical article (7) focused on a comparison of the enthalpies of random atomic configurations and determined several phases that possess lower enthalpies than that of the Pmna structure. In particular, the insulating phase having the I4₁/a structure was found to have the lowest enthalpy among the tested structures in the pressure range of 50–200 GPa, which has become the accepted ground state of silane in this pressure regime assured by many researchers. Interestingly, in the work above (7), it was also predicted that at >260 GPa, a metallic phase having C2/c symmetry becomes stabilized; we refer to this structure in the following as C2/c (1). A different structure also belonging to the C2/c space group was introduced as a potential metallic phase for pressures <150 GPa (12); for distinction, this structure is referred to as C2/c (2) in the following. Even though the C2/c (2) structure could not be stabilized against the I4₁/a structure when solely comparing enthalpies, the calculated zero-point energy correction leads to a reduction of the energy difference by 0.068 eV/f.u. at 150 GPa (12).

Despite two successive experimental findings of metallic silane at <100 GPa (4, 5), theoretical predictions have focused mainly on pressure regimes >150 GPa. Because hydrogen contributes considerable zero-point energy to the system, it is essential to include zero-point corrections in any enthalpy comparison of different phases (8). Even if we assume that the I4₁/a structure is indeed the ground state <100 GPa, there remains the possibility for a dynamically stabilized phase to appear as a metastable one, which is a common phenomenon observed in materials under high pressure (9–12).

Here, we present a systematic theoretical approach to determine the structure of a metallic phase of silane for pressure <100 GPa. For a large pool of suggested space groups, we performed a series of tests to eliminate candidates that do not meet criteria that the correct metallic phase of silane should fulfill. Because of the well-known shortcoming of standard density functional theory (DFT) for underestimating the band gap, we can safely discard any phase that is found to be nonmetallic from DFT. Phonon calculations can provide a critical assessment of the dynamical stability in a given system, whereas zero-point energy corrections to the enthalpy can be decisive when it comes to small differences in enthalpy. Finally, the GW correction yields a reliable band structure of any candidate structure to ensure that it is indeed metallic.

In the present study, we have used DFT (further details are presented in Methods) to solve the electronic Schrödinger equation. It has recently been noted (13) that the high-pressure phases of solid hydrogen can be treated by using DFT (8). Specifically for silane, recent computational investigations have successfully used the DFT method (6, 7, 12). In one particularly noteworthy article (14), experimental and theoretical results were directly compared and it was found that the DFT calculations are in good agreement with the measurements. As for theory–experiment comparisons of our results in the present article, we were able to match vibrational frequencies in silane obtained with DFT to experimental Raman data (Figs. 1 and 2). All such findings can be regarded as evidence supporting the idea that DFT is suitable for the investigation of hydrogen-rich high-pressure phases, in general, and for silane specifically.

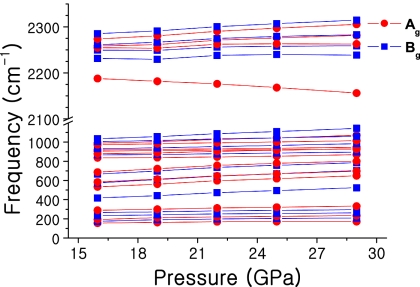
Fig. 1.

Vibrational Raman frequencies as a function of pressure calculated for the P2₁/c structure of silane. The solid lines are guides to the eye.

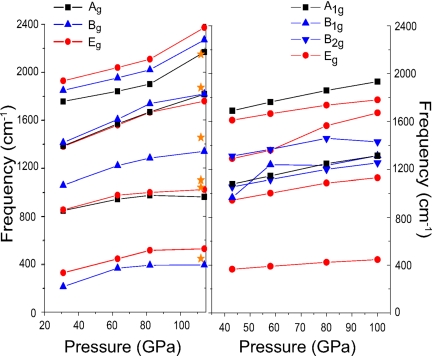
Fig. 2.

Raman frequencies for the I4₁/a (Left) and the P4/nbm (Right) structures as a function of pressure. The orange stars correspond to experimental Raman data from ref. 5. at 112 GPa.

The P2₁/c and the I4₁/a structures are considered as the ground state in the low-pressure (0–29 GPa) and high-pressure (50–200 GPa) regimes, respectively. Thus, we will use them in our study as reference phases with which to compare any potential candidate phases.

Results and Discussion

Before coming to the elimination process to determine a suitable structure of metallic nature, we present in Fig. 1 results from our Raman calculations of the P2₁/c structure in the lower-pressure regime (i.e., <30 GPa). We would like to remark here that, based on our theoretical analysis, the Raman data for phase V presented in ref. 4 do not match with the I4₁/a structure, but are found to be in good agreement with the results for the P2₁/c structure. As it shown in ref. 14, at about a pressure of 21 GPa, the P2₁/c structure does indeed become the ground-state phase of silane. The good agreement between the experimental measurements in phase V (4) and our theoretical Raman results for the structure with space group P2₁/c lends support to the accuracy of our ab initio calculations. In particular, we emphasize that the general behavior of each Raman mode is in good agreement with experiment (4). The P2₁/c structures possess 30 Raman active modes, Γ_vib = 15A_g + 15B_g. The softening of one A_g mode at ≈2,200 cm⁻¹ corresponds to the bond stretching of discrete SiH₄ groups, a result measured reproducibly by two different groups (4, 5).

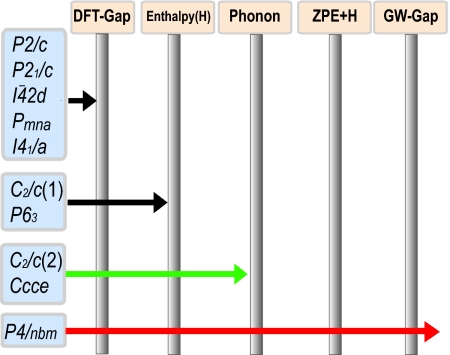
We now come to the elimination processes that we applied to determine from ab initio the correct structure that exhibits metallization <100 GPa in ref. 4. Testing possible candidate space groups suggested in the literature against a series of conditions, all of which only the correct structure can simultaneously fulfill, we successively rule out every space group but one. Fig. 3 represents a schematic of this elimination process and serves as an overview of our findings. As it is shown, we considered the following space groups in our study: P6₃ from ref. 5, Pmna from ref. 6, P2/c, I42̄d, I4₁/a, C2/c(1), and P4/nbm from ref. 7, P2₁/c from ref. 14, and C2/c(2) and Ccce from ref. 12. For C2/c, two different structures exist, both of which we considered; hence, it is listed twice in Fig. 3.

Fig. 3.

A schematic illustration of the elimination scheme applied in this study. The end points of the arrows indicate for which criteria a certain space group failed to pass the test.

The first criterion that any accurate structure of silane must fulfill is to be of metallic nature. Thus, we probed the existence of band gap for all candidate space groups from the electronic dispersion relations calculated within standard DFT (GGA). The result of this first test is that half of the candidate structures are eliminated, namely, those having P2/c, P2₁/c, I42̄d, Pmna, and I4₁/a symmetry, which all possess a finite band gap, rendering them insulating or semiconducting. The remaining five structures are found to be of metallic nature, possessing no band gap.

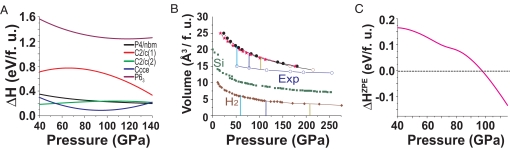
Next, we considered the enthalpies of the various structures (Fig. 4A). Here, we find that in the high-pressure regime, the I4₁/a structure is energetically most stable. Second lowest in enthalpy are the Ccce and C2/c(2) structures (12), followed by the P4/nbm structure. Because the energy differences between these three structures and the I4₁/a structure are very small (Fig. 4A), it is important to consider zero-point energy, which can provide a significant contribution in hydrogen-rich materials such as silane. We will come to the discussion of the specific effects from zero-point energy in the over-next stage of our elimination process. Before that, we note that, based on enthalpy considerations, the P6₃ and C2/c(1) structures are therefore ruled out, because their enthalpy differences to the four structures (I4₁/a, P4/nbm, C2/c(2), and Ccce) are too large to be possibly overcome by zero-point energy contributions, which are typically found to be ≈0.2 eV/f.u. in silane for structures existing in this pressure regime. However, we see that the C2/c(1) structure becomes stabilized with respect to enthalpy >170 GPa; a similar behavior for this structure at 260 GPa was also reported in ref. 7. Regarding the P6₃ structure, we note that phonon calculations that we carried out resulted in a dynamically unstable state for this structure at pressure values in at ≈60 GPa. Furthermore, an assessment of the mechanical stability of this structure revealed that the slightest displacement of Si atoms from their equilibrium positions causes the delicate balance of forces in the system to no longer cancel out and the whole unit cell changes its structure, implying mechanical instability. We thus find that the provided structure of the P6₃ symmetry (5) does not appear to be a stabilized structure based on our theoretical investigations. Fig. 4B shows the calculated pressure–volume relation for the P6₃, P4/nbm, and I4₁/a structures of silane. As it appears, all three structures of silane display a virtually identical change of volume with increasing pressure. The experimental data from ref. 5 are seen, however, to be in stark contrast to any of the silane structures, with a significantly reduced volume in the analyzed pressure range. It seems that the experimental data may be more likely to describe a phase with a stoichiometry of SiH₂ rather than SiH₄, because the difference in volume between the phase having P6₃ symmetry and experiment matches with the volume of molecular H₂ when the effective pressure in the system due to additional chemical pressure is taken into account. Furthermore, we find that the proposed P6₃ structure is mechanically highly unstable. However, our calculations indicate that a reduction in stoichiometric hydrogen content can lead to a stabilized structure with the Si atoms at the positions determined from X-ray diffraction (5). More specifically, we find that the removal of only two hydrogen atoms in the unit cell and subsequent optimization can lead to a structure with significantly reduced forces in which the two Si atoms occupy the (1/3, 2/3, 0) and (2/3, 1/3, 1/2) sites in agreement with X-ray diffraction data, whereas the six remaining H atoms are located at (0.033, 0.193, 0.269), (0.984, 0.991, 0.625), (0.301, 0.825, 0.329), (0.022, 0.012, 0.913), (0.742, 0.603, 0.199), and (0.688, 0.328, 0.838). Although this structure appears reasonably stabilized and is consistent with the X-ray diffraction data (as far as the Si positions are concerned), we emphasize that other possible structures having P6₃ symmetry may exist that could explain the experimental data as well.

Fig. 4.

Variation of enthalpy differences and volume with pressure. (A) Enthalpy difference as a function of pressure for the metallic candidate structures relative to the I4₁/a structure. (B) Comparison of the pressure-volume relation for various structures of silane with those for silicon (15) and molecular hydrogen (16). Experimental data points are from ref. 5. Further details are discussed in the text. (C) Enthalpy difference as a function of pressure for the P4/nbm structure relative to the I4₁/a structure with zero-point energy corrections considered. Above 97 GPa, the P4/nbm structure becomes energetically favored over the structure having I4₁/a symmetry. The spacing of pressure data points was 20 GPa or denser and there are at least two data points for each structure in the ΔH^ZPE < 0 regime. The curve is a cubic-spline fit to the calculated data points.

We are thus left with only three space groups, namely, Ccce, C2/c(2), and P4/nbm. Even though structures of the former two possess smaller enthalpy differences from the I4₁/a structure than the P4/nbm structure, we observe from phonon calculations that they are actually dynamically unstable at <100 GPa The Ccce structure is found to be unstable in both our calculations and ref. 12. For the C2/c(2) structure, the authors of ref. 12 used ultrasoft pseudopotentials (USPPs) with an energy cutoff of 40 Ry and reported a stabilized phonon density of states at 65 GPa and 150 GPa. Our own calculations with the projector-augmented wave (PAW) method found that the C2/c(2) structure should be unstable at 35, 62, and 100 GPa, respectively. It is worth noting that the recommended energy cutoff for hydrogen is 700 eV by default for high-pressure studies with PAW, requiring a lower-energy cutoff than USPP in general. Only the P4/nbm structure turns out to be dynamically stable. Fig. 5 shows that the phonon density of states displays stability for pressures >43 GPa. Below a threshold pressure that lies in the interval 32–43 GPa, an instability appears along the Γ(0 0 0)–M(½ ½ 0) symmetry line, including at about the Γ point. We studied the dynamical stability for a pressure up to 113 GPa in the P4/nbm structure and found no precursor that would imply a softening of modes, which confirms that the P4/nbm structure is indeed dynamically stabilized from 43 GPa until >113 GPa. At a lower pressure (31 GPa), the I41/a structure possesses three distinct frequency regimes (Fig. 5): the lowest regime is assigned to Si vibrations (<15 THz), H–Si–H bending motions lie in the middle (20–45 THz), and hydrogen stretching motions of the SiH₄ unit are found in the highest regime (>50 THz). As the pressure is rising, the gaps between the frequency regimes become narrower (this can also be seen in Fig. 2 Left, which we discuss further below). Between 82 GPa and 114 GPa, the frequencies of the highest regime increase rapidly, indicating that the isolated SiH₄ vibrations become enhanced.

Fig. 5.

Phonon frequencies for the P4/nbm structure (Upper) and the I4₁/a structure (Lower). The phonon density of states for the P4/nbm structure exhibits imaginary frequencies at 32 GPa, pointed out by the arrow.

When the pressure reaches 97 GPa, we find that consideration of zero-point energy (ZPE) can even lead to the energetic stabilization of the P4/nbm structure compared with the I4₁/a structure. The difference in enthalpy, defined as ΔH^ZPE = H_P4/nbm^ZPE − H_I41/a^ZPE, is ≈0.15 eV/f.u. at 50 GPa and decreases monotonically with pressure (Fig. 4C). The accuracy of our ZPE calculations was tested by varying the density of the k-point meshes. As a representative example, when comparing the ZPE result of the I4₁/a structure at a pressure of 101 GPa obtained for a 4 × 4 × 4 k-points mesh with that obtained for a 6 × 6 × 6 mesh, the energy is found to change by 0.114 meV; subsequent comparison between a 6 × 6 × 6 and an 8 × 8 × 8 mesh yields a change of only 0.017 meV. The 8 × 8 × 8 mesh was used by us throughout for all ZPE calculations.

From Fig. 4A, we can see that the enthalpy difference between the I4₁/a structure and the P4/nbm structure is monotonically decreasing with increasing pressure. At 40 GPa, the energy difference is found to be ≈0.35 eV/f.u., whereas for 140 GPa, the difference has decreased to ≈0.20 eV/f.u. For the ZPE calculations, it can be expected that a metallic phase possesses a lower ZPE than an insulating phase. In the specific case of the phases of silane having P4/nbm and I4₁/a symmetry, we found this difference to lie between 0.20 and 0.25 eV. Thus, even without the accurate comparison presented in Fig. 4C, one could already guess that the ZPE correction can tip the balance to make the P4/nbm structure the ground-state configuration. The key point is that P4/nbm is the only dynamically stabilized structure of metallic nature identified in our investigation and, for that reason, P4/nbm can become the ground state structure of silane at >100 GPa.

To confirm the metallic nature of the P4/nbm structure, we calculated the corresponding band structure by using the GW approximation (17, 18). Contrary to standard density functional theory, the excited state properties are properly described by this theory and the validity of the GW approximation has been confirmed by many calculations and shown to be a reliable tool to reproduce the value of the band gap for a variety of materials. Because the experimental results indicate that metallic behavior sets in at 60 GPa (4), we performed a GW calculation at this pressure for the P4/nbm structure and found indeed that this structure possesses a finite density of states at the Fermi level, as shown by the corresponding band structure displayed in Fig. 6. The large number of bands crossing the Fermi level are typical of a good metal and the dispersion of the bands is found to be quite large. Having passed this final step in our elimination process, we can conclude that the P4/nbm space group is indeed the most promising candidate structure for the metallic phase of silane reported in ref. 4.

Fig. 6.

Band structure along high-symmetry lines for SiH₄ in the P4/nbm structure at 60 GPa. The full line represents results from DFT-GGA calculations, and the dots correspond to the GW correction.

We now take a closer look at the structural properties of silane in the P4/nbm structure. As seen from Fig. 7, at 72 GPa, a layered structure prevails with H located at fractional coordinates (0.3511, 0.1489, 0.2090) and Si at (0.5, 0.5, 0.5). Si atoms form a single layer perpendicular to the z axis and are sandwiched between two double layers of hydrogen atoms. In these layers, four hydrogen atoms form a distorted tetrahedron, through which the double layer of hydrogen is linked in the x-y plane. To study the structural change of the hydrogen layers with pressure, we define three distinct lengths (see Fig. 7), d₁, d₂, and d₃. At 32 GPa, the ratio d₁/d₂ is 0.889 and d₃/d₂ is 1.036, meaning that a hydrogen molecule is weakly formed in the layer and conduction between H₂ units could be driven along d₂. The d₃/d₂ ratio is monotonically decreasing with rising pressure and at 100 GPa d₃ eventually becomes comparable to d₂ (d₃/d₂ = 1.005). This implies that more channels become available for conduction through the double layer of hydrogen atoms.

Fig. 7.

Crystal structure of SiH₄ at 72 GPa having P4/nbm symmetry. Si atoms (blue solid spheres) are surrounded by H atoms (pink solid spheres). H atoms outside of the unit cell (dashed lines) are included for clarity to show complete tetrahedra. We define d₁ (cyan bond) as the intradistance of a tetrahedron in the lower and upper hydrogen layer, d₂ (red bond) as the interdistance of two nearest tetrahedra, and d₃ (black bond) as the intradistance of a tetrahedron between two layers.

Degtyareva et al. (14) reported that both the P2/c and the Pmna structures are favored over the P2₁/c structure for pressures >7 GPa. The P2/c structure was described as a configuration with zigzag chains of H-bonded Si atoms along the c axis and the Pmna structure possesses sheets of Si atoms sandwiched between double sheets of H layers, which are preferred over the P2₁/c structure. Note that the P4/nbm structure is similar to the Pmna structure in the sense that Si layers are sandwiched by double-sheet H layers and the transformation from the P2/c to the P4/nbm space group has been shown previously (7). Furthermore, it was reported in ref. 5 that the experimentally observed metallic phase may coexist with the insulating tetragonal phase having I41/a symmetry for pressures >110 GPa. Such a coexistence would appear to be more likely if the metallic phase were of tetragonal shape as well, as is the case for the P4/nbm space group, but one should note that this is not a necessary requirement for coexistence.

Finally, we also present theoretical predictions of the Raman spectrum of the metallic and insulating phases. Fig. 2 shows the evolution of Raman shifts with pressure for the structures having I4₁/a and P4/nbm symmetry, respectively. The I4₁/a structure possesses 11 Raman-active modes, Γ_vib = 3A_g + 4B_g + 4E_g, most of which monotonically increase, whereas the three lowest modes A_g, B_g, and E_g are saturated at 961 cm⁻¹, 528 cm⁻¹, and 394 cm⁻¹, respectively, and are mostly associated with Si motions. The Raman shifts for the I4₁/a structure are in good agreement with previous Raman measurements (shown as orange stars in Fig. 2). The highest A_g mode, which is the breathing mode of the SiH₄ unit, matches exactly with experiment. The highest A_g mode is also in good agreement with experiment, whereas the other modes calculated are slightly underestimated by 50–120 cm⁻¹. This deviation can be explained by the common overestimation of the bond length, as it is typical for DFT calculations employing the generalized gradient approximation. The P4/nbm structure possesses 9 Raman-active modes, Γ_vib = 2A_1g + 1B_1g+ 2B_2g + 4E_g. Contrary to the other modes, the B_1g rapidly increases in the pressure interval 43–55 GPa and only thereafter follows the overall trend. The highest mode in the P4/nbm structure, A_1g, is much lower than that of the I4₁/a structure because of delocalized electrons in the metallic phase, which lead to a weakening of the Si–H bonds, causing the observed shift in the Raman frequencies.

Conclusions

In summary, we have carried out a systematic test of selected structures in different space groups with the purpose of identifying the stable phase of metallic nature for silane <100 GPa. Based on the band-gap estimation and enthalpy calculations obtained from density functional theory, we confirm that the I4₁/a structure is the ground state >50 GPa. However, the structures having C2/c and P4/nbm symmetry, with a single sheet of Si layer between double sheets of H, possess a enthalpy comparable to the ground state in the high-pressure regime. The P4/nbm structure becomes the ground state at 97 GPa when zero-point energy contributions are considered. GW calculations of the band structure also predict that the P4/nbm structure is of a metallic nature for pressures <60 GPa. Phonon calculations for pressure of 30–100 GPa demonstrate that the P4/nbm structure is dynamically stable at >43 GPa. Taking all results into account, we conclude that the structure having P4/nbm symmetry is likely to be the correct candidate for the metallic phase of silane reported in ref. 4. It is hoped that this work will open paths not only to further theoretical studies of related metallic materials, but also for experimental measurements to test our predictions for metallic silane at <100 GPa.

Methods

Geometry optimizations were performed within the framework of the generalized gradient approximation (GGA) (21) with the Perdew–Burke–Ernzerhof parameterization (22) for the exchange-correlation functional to DFT (23, 24) by using the projector-augmented wave (PAW) method (25), as implemented in the Vienna ab initio simulation package (VASP) (26). The PAW potential with the valence states 3s²3p² for Si has been used with plane waves up to a cutoff energy of 1,000 eV. The density of states has been calculated with an 11 × 11 × 11 k-points mesh.

To calculate the phonon density of states, the PHONON 4.28 code (27) with the ab initio force–constant method (28) was used, as implemented by Parlinski (27). The phonon dispersion calculations for metallic phases tend to be more challenging than those for insulating phases, because the larger variation in the phonon dispersion requires a denser mesh for the k-points sampling. For example, in the P4/nbm structure, the 2 × 2 × 2 supercell containing 80 atoms was sampled by using a 6 × 6 × 6 k-points mesh generated by the Monkhorst–Pack scheme. This corresponds to a grid of 48 × 48 × 48 for the ten-atom primitive cell. A cutoff energy of 1,000 eV was used consistently throughout all calculations. We furthermore expanded the size of the supercell to 3 × 3 × 3 (for phonon calculations), when an unstable phonon density of states was obtained, to confirm the force constants convergence with respect to the interatomic distances. The results obtained with the 2 × 2 × 2 supercell and the 3 × 3 × 3 supercell were found to be equivalent; thus, judging from this test and the converged force constants plot, we conclude that the 2 × 2 × 2 supercell can be considered sufficient for the phonon calculations.

Regarding the calculation of zero-point energy, we adopted the following procedure. Once a stabilized phonon density of states g_i,μ(ω) has been obtained, we calculated the internal energy E of the primitive cell within the quasi-harmonic approximation by summing the internal energies of all atoms (index μ) over all degrees of freedom (index i).

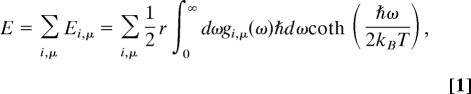where r is the number of degrees of freedom in the primitive unit cell, g(ω) is the density of states with respect to the phonon frequency ω, and T is the temperature in kelvins.

In the low-temperature limit (which yields the zero-point energy by definition), this becomes:

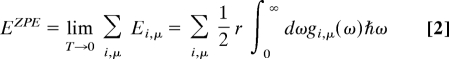The partial densities of states g_i,μ(ω) are then sampled by using Monte Carlo techniques as implemented in the PHONON code. The accuracy of the zero-point energy calculation depends on the richness of this sampling. We have tested the corresponding convergence successfully; for the sampling setting used by us, the zero-point energy did not change when the sampling density was increased further. In other words, once the phonon dispersion has been obtained, there is no additional uncertainty introduced from numerical errors in the sampling process.

The GW calculations were performed by using the implementation described in refs. 19 and 20. In particular, the self-energy was calculated by using the plasmon-pole approximation.