Abstract
Purpose
To present a single-step deterministic procedure for unwrapping MRI phase maps.
Materials and Methods
Using an algorithm previously developed for optical applications, Laplacian operators were applied in the Fourier space of the MRI phase map. The original Fourier-based phase unwrapping algorithm was modified so that demodulation accomplished the required signal symmetrization in Fourier space. To evaluate the method's performance in the presence of thermal noise, a set of wrapped phase maps were simulated at different levels of noise in k-space, and the response of the algorithm at different levels of signal-to-noise ratio (SNR) was evaluated for stability. To demonstrate its utility in MRI, the algorithm was applied to the wrapped phase maps of susceptibility-weighted imaging (SWI) studies, which were then used to generate venograms.
Results
In simulated phase wrapping, the algorithm correctly reproduced the original phase for a wide range of phase gradients and noise. The procedure was fast and produced useful maps of venous structures in SWI images.
Conclusion
A fast and stable single-step deterministic method for unwrapping MRI phase maps is available for such applications as SWI and mapping of static magnetic field inhomogeneity.
Keywords: MRI phase map, susceptibility-weighted imaging, SWI, venography, phase unwrapping
DETERMINING THE TRUE PHASE from its principal value in a wrapped phase map is an important task in many fields of applied physics and medicine, such as holography, ultrasound, and MRI (1,2). Many unwrapping techniques are computationally demanding and can suffer in the presence of noise (3). A single-step deterministic algorithm that is fast, reliable, and robust has been published in the optics literature (4,5). It is the purpose of this Technical Note to demonstrate that a modification of this procedure can serve as a useful tool for processing MRI phase maps. An application in MRI venography (1,2) serves as an illustration of its utility.
Given a map of wrapped phase (i.e., the true phase modulo 2π), it has been shown (5) that the Laplacian operator can be used to form an estimate, within a constant, of the true value of the phase. In this method, an operation in Fourier space performs the function of the Laplacian. In phase unwrapping, the problem at hand is an estimate of the number of integer multiples of 2π to be added to the wrapped map in order to render a map of the true phase. Applying the Fourier technique to calculate the forward and inverse Laplacian operators imposes a boundary condition on the estimate of the integer multiple of 2π (4,5). To address this requirement, the discrete cosine transform (DCT) can be employed. If DCT is not available, image symmetrization, followed by iterative procedure (4,5) employing the discrete Fourier transform (DFT) will accomplish phase unwrapping. However, although symmetrization addresses the boundary condition problem, it demands more computation time and memory and also may not completely unwrap the phase, since the boundary conditions are only approximated. We have found that, for conditions typical of MRI, demodulating and mirroring the signal in Fourier space can replace image symmetrization for the boundary condition problem.
MATERIALS AND METHODS
Theory
All phase unwrapping techniques address the problem that the recovered phase is mathematically limited to the interval (–π,π] corresponding to the principal value of the arctangent function. Generally, the true phase ranges over an interval greater than 2π, in which case the recovered phase contains discontinuities. Unwrapping these discontinuities is a matter of adding an appropriate integer multiple of 2π to each pixel element of the wrapped phase map. In practice, however, the presence of noise and residues complicates effective phase unwrapping, hence the ongoing interest in developing algorithms to overcome these difficulties (6).
Following Schofield and Zhu (4), we assume that the true (unwrapped) phase and the wrapped phase are related by the following relationship: ϕ(r) = ϕw(r) + 2πn(r) where ϕ(r) is the true phase, ϕw(r) is the wrapped phase, and n(r) is the integer multiple of 2π needed to produce the true phase for position r. The factor n(r) can be estimated by rounding (to the nearest integer) the solution to the following equation:
| (1) |
where and are the forward and inverse two-dimensional Laplacian operators, respectively. As Schofield and Zhu (4) and Volkov and Zhu (5) explain, the (discrete) Laplacian operators can be calculated by the application of forward and inverse fast Fourier transforms (FFTs):
| (2) |
| (3) |
where (x,y) and (p,q) are real-space and Fourier-space pixel coordinates, respectively, FFT denotes the fast Fourier transform operation, and N is the input image size in pixels.
Since ϕw(r) is measured, an estimate of n(r) is available if an estimate of the discrete Laplacian of ϕ(r) can be calculated. This relationship is established in Schofield and Zhu (4):
| (4) |
Applying Fourier techniques to calculate the forward and inverse Laplacian imposes periodic boundary conditions on the solution obtained for n(r). This is generally not realistic. Since the n(r) are integers, it is more realistic that the gradient of n(r) normal to the boundary vanishes. This boundary condition is easily implemented by use of the DCT (which in our experiment would be calculated via a fast cosine transform) rather than the full FFT. Since the fast cosine transform is not always available, symmetrization of the input wrapped phase has been suggested, thus changing the dimension of the input image from N×N to 2N×2N (4,5). However, while symmetrization allows the use of full FFTs, it has a cost in increased computation and memory demands, and also increases the number of iterations for convergence.
In MRI the objects to be imaged are usually centrally located in the field of view (FOV), and the borders of most brain amplitude and phase MR do not contain much important information. The phase map data is N×N-dimensional real. If the data is modulated with a carrier signal of N/2, its power is shifted in the conjugate Fourier space so that it is centered in the conjugate space. The frequency shift modulation key (FSMK) method can be used to modulate the signal. Shifting and symmetrization of the phase map can be achieved by an N/2 modulation, with the modulation exponent varying from −N/2 to +N/2. The negative part of the modulator [−N/2, 0] mirrors the signal and the positive part [0, N/2] acts like a shift operator in Fourier space. Therefore, if an even periodic signal with unit magnitude is assumed as a modulator, modulation of the complex images with real and imaginary parts can be achieved.
Simulation
To evaluate the algorithm, a phase map simulation was constructed, with all physical and technical steps from signal acquisition to image reconstruction.
An analytical phase map with arbitrary amplitude was simulated for a 2D circle with radius of R0. Amplitude and phase maps were generated using the following functions:
| (5) |
| (6) |
where f(r) and G(φ) denote amplitude and phase functions, respectively. Equation [6] guarantees a nonlinear phase map (G(φ)) with values in range [π,–π]. The real and imaginary maps in K-space can be obtained by taking an inverse FFT of the real and imaginary maps in the time domain: U(r,φ) = IFFT [Re(reiφ)] and V(r,φ) = IFFT [Im(reiφ)]. Complex Gaussian noise was added to the to U and V time-domain images, and the images were then reconstructed by standard FFT methods. To wrap the phase map, the reconstructed components in the frequency domain were passed through the arctangent function (7). Figure 1, left-hand column, shows simulated wrapped images with two different levels of signal-to-noise ratio (SNR) (100:1 and 25:1) in the phase map.
Figure 1.
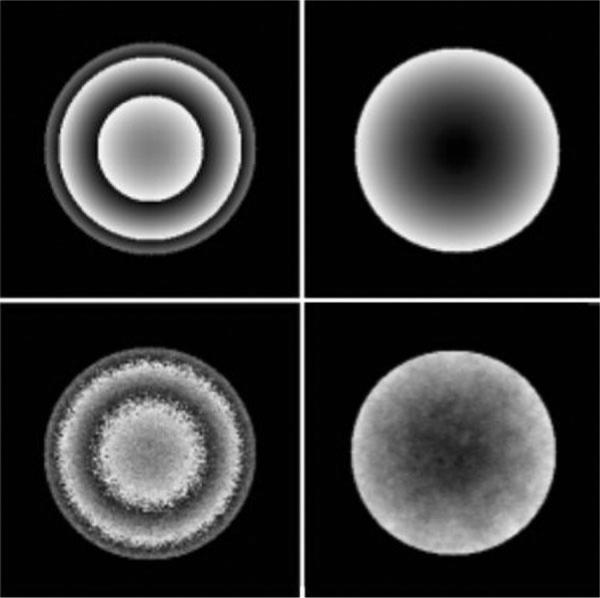
Simulated wrapped (left) and unwrapped (right) images at different levels of phase map SNR. Top row: SNR = 100:1. Bottom row: SNR = 25:1.
Experiment
To evaluate the algorithm with real data, A 7T (25 cm clear bore) Bruker small-animal magnet with gradients of 250 mT/m interfaced to an Avance console running Paravision V2.1.1 was used to acquire a 3D (matrix = 256 × 256 × 64, TE/TR = 10 msec/30 msec, FOV = 32 × 32 × 16 mm) brain susceptibility-weighted imaging (SWI) data set in a male Fisher rat with a rat (9L) gliosarcoma cell line (9L) tumor 14 days postimplantation.
To test the algorithm for a clinical dataset, an SWI image for a human brain was acquired by a gradient-echo-3T MRI system. In human images with a larger matrix, a 3D spoiled gradient-echo sequence (matrix = 512 × 512 × 128 TE/TR = 20 msec/33 msec, FOV = 240 × 240 × 240 mm) with tridirectional flow compensation was run in a patient with glioblastoma multiforme.
For both animal and human data sets, the algorithm was implemented to produce unwrapped phase maps, after which the magnitude and unwrapped phase maps were used as input to the standard MR-venography procedure (1,8–10). in these practices for producing venographic maps, long-range variations were nulled by dividing the unwrapped phase map by its low-pass filtered version (unitary filter = 5 × 5 and 7 × 7 for the rat images and human images, respectively). A linear map was constructed from the resulting high-spatial frequency phase maps and used to multiply the magnitude images of the MRI (1,10). Finally, a minimum intensity projection (MIP) allowed the visualization of venous structures across 11 slices for the animal and nine slices for the human.
RESULTS
Figure 1 presents the wrapped and unwrapped images for two simulated phase maps at different levels of signal to noise ratio (100:1 and 25:1) using the technique described above.
Figure 2 illustrates wrapped, unwrapped, and SWI venography maps in the brain of a Fisher rat implanted with a 9L cerebral tumor.
Figure 2.
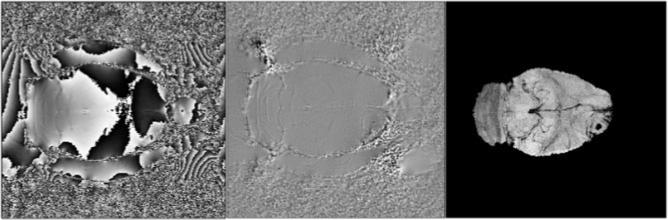
Rat brain implanted with a 9L tumor: wrapped phase map (left), unwrapped phase map (middle), and susceptibility-weighted image in this animal (right).
Figure 3 presents the algorithm applied to the human data set (subcortical glioblastoma multiforme). The first row of Fig. 3 presents the amplitude image and the wrapped and unwrapped phase maps. In the second row of Fig. 3, a venography map produced using the unwrapped phase maps is shown, along with profiles of the wrapped and unwrapped phase maps along the line shown in Figs. 3b and c, respectively. The venography shown in Figs. 2 and 3 demonstrates that the algorithm provides good contrast for venous structures.
Figure 3.
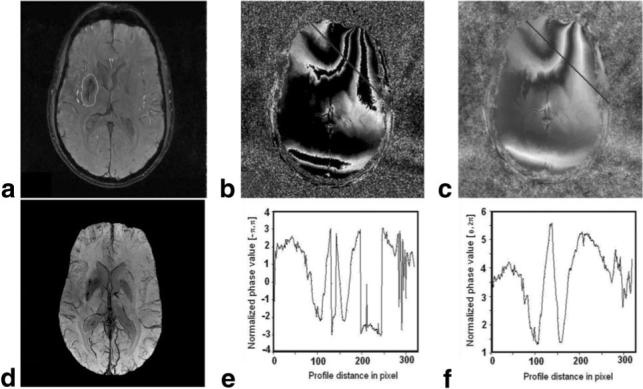
MRI in the brain of a patient with a subcortical glioblastoma. a: Amplitude; contour presents the tumor area. b: Wrapped phase map. c: Unwrapped phase map. d: SWI in this patient, showing the increased vascularity in the tumor region. e: Phase profile of the unwrapped phase along the line in image b. f: Phase profile in the unwrapped phase map along line in image c.
DISCUSSION
A phase unwrapping algorithm was introduced and modified by use of demodulated FFT signals instead of DCT, thus emulating the DCT properties. The method works with the original dimension (N) of phase image instead of its doubled (2N) dimension, which decreases the number of operations, and thus the time of computation, by a factor of . The effects of complex thermal noise on the phase map were evaluated using an analytical simulation, and the performance of the algorithm was assessed at different levels of thermal noise. High-quality maps of venography were generated using SWI images and the unwrapping algorithm. The performance of the proposed algorithm was tested against simulation and real data acquired for rat and human brains, and found to generate usable unwrapped maps in an efficient manner.
In considering the efficiency of the algorithm, we note that a recent (2007) work by Karasev et al (11) available online (see: http://radar2007.org/PINsummaries/1450.pdf) allows a comparison of the relative computational speeds of the single-step algorithm presented herein vs. a commonly used iterative procedure, the weighted least-squares (WLS) method.
Consider the innermost loop of an unwrapping procedure, which essentially dictates its computational time. The innermost loop of the algorithm presented herein requires eight FFTs, and requires 16N2log2N number of floating-point operations to achieve the result, where N is the dimension of one side of the (typically square) image. For the WLS method, 11,712 iterations have been reported for a particularly diffi-cult 512 × 512 image (11). At a minimum, since a point-by-point gradient calculation is required, 4N2 operations are needed for each trial in the WLS method. If 100 iterations were needed instead of the reported 11,712, about 400N2 floating-point operations would be required for a 512 × 512 image. This is still three times more than the number of operations (144N2) needed by the method presented herein. Thus, we conclude that computational time in the single-step algorithm will be at least of the order of iterative methods.
As we have noted, applying Fourier techniques to calculate the forward and inverse Laplacian imposes periodic boundary conditions on the solution obtained for n(r). This is generally not realistic and, since the n(r) are integers, it is more realistic that the gradient of n(r) normal to the boundary vanishes. However, since the algorithm works in a single step, it reduces the possibility of imposing periodic boundary conditions on the solution obtained for n(r). Therefore, when highly wrapped objects are located on the image boundary, the algorithm might rarely demonstrate some instability and necessitate an iterative approach to the generation of the phase map. Generally speaking, examples of such a failure are rare in MRI, since good imaging technique generally suppresses out-of-frame signal by appropriate slice selection and/or some variety of outer-volume suppression. Thus, since most image boundaries are free of highly wrapped signals (low n(r) gradient), this effect is rarely seen.
In summary, the single-step algorithm is an efficient method for unwrapping phase maps in MRI. In the rare event of failure due to a nonzero gradient of phase at the image border, an iterative approach can be implemented. In its application, the algorithm can increase image contrast and reveal venous anatomic structures not visible on the wrapped images. Additionally, other applications, such as correcting the effect of a static magnetic field inhomogeneity, are possible.
ACKNOWLEDGMENT
We acknowledge Mark Haacke's encouragement and helpful discussion regarding the implementation of SWI venography maps.
Contract grant sponsor: National Institutes of Health (NIH); Contract grant numbers: 1RO1 HL70023, PO1-23393.
REFERENCES
- 1.Reichenbach J, Barth M, Haacke E, Klarhofer M, Kaiser W, Moser E. High-resolution MR venography at 3.0 Tesla. J Comput Assist Tomogr. 2000;24:949–957. doi: 10.1097/00004728-200011000-00023. [DOI] [PubMed] [Google Scholar]
- 2.Haacke EM, Cheng NY, House MJ, et al. Imaging iron stores in the brain using magnetic resonance imaging. Magn Reson Imaging. 2005;23:1–25. doi: 10.1016/j.mri.2004.10.001. [DOI] [PubMed] [Google Scholar]
- 3.Xu W, Cumming I. A region growing algorithm for InSAR phase unwrapping. IEEE Trans Geosci Remote Sens. 1999;1:124–134. [Google Scholar]
- 4.Schofield M, Zhu Y. Fast phase unwrapping algorithm for interferometric applications. Opt Lett. 2003;1:1194–1197. doi: 10.1364/ol.28.001194. [DOI] [PubMed] [Google Scholar]
- 5.Volkov V, Zhu Y. Deterministic phase unwrapping in the presence of noise. Opt Lett. 2003;1:2156–2158. doi: 10.1364/ol.28.002156. [DOI] [PubMed] [Google Scholar]
- 6.Kadono H, Takei H, Toyoka S. A noise-immune method of phase unwrapping in speckle interferometry. Opt Lasers Eng. 1997;1:151–162. [Google Scholar]
- 7.Kattoush A. A new recurrent approach for phase unwrapping. Int J Appl Sci Eng. 2005;3:135–143. [Google Scholar]
- 8.Rauscher A, Sedlacik J, Barth M, Mentzel H, Reichenbach J. Magnetic susceptibility-weighted MR phase imaging of the human brain. Am J Neuroradiol. 2005;1:736–742. [PMC free article] [PubMed] [Google Scholar]
- 9.Haacke EM, Herigault G, Yu Y-J, et al. Observing tumor vascularity noninvasively using magnetic resonance imaging. Image Anal Stereol. 2002;1:107–113. [Google Scholar]
- 10.Haacke E, Xu Y, Cheng Y, Reichenbach J. Susceptibility weighted imaging (SWI). Magn Reson Med. 2004;1:612–618. doi: 10.1002/mrm.20198. [DOI] [PubMed] [Google Scholar]
- 11.Karasev PA, Campbell DP, Richards MA. Proceedings of the IEEE Radar Conference. IEEE; Boston, MA: Apr 17−20, 2007. Obtaining a 35× speedup in 2D phase unwrapping using commodity graphics processors. pp. 574–578. 2007. [Google Scholar]


