Relative Information Content and Top-down Proteomics by Mass Spectrometry: The Utility of Ion/Ion Proton-transfer Reactions in Electrospray-based Approaches

Abstract

Computer simulations of electrospray ionization (ESI) and collision-induced dissociation (CID) experiments were employed to examine the informing power associated with “top-down” proteomics implemented with some commonly used mass analyzers, i.e. the quadrupole ion trap (QIT), the Fourier transform-ion cyclotron resonance mass spectrometer (FT-ICRMS) and the time-of-flight (TOF) mass spectrometer. Using a ratio of the separated (or resolved) peaks to the total number of predicted peaks as a measure of informing power, the ESI/MS simulation of a mixture of proteins showed that the FT-ICRMS exhibited the highest informing power among the three instruments being studied, with the QIT giving the lowest informing power, which was expected from the analysis of the “component capacity” of the three approaches. Also as expected on the basis of resolving elements per component, a dramatic increase in the informing power of the approach was obtained when ion/ion proton-transfer reactions were used to reduce the number of peaks and to minimize overlap between ions of different mass and charge but similar mass-to-charge ratio. With the assumptions made in this study, the informing power of the TOF+ion/ion approach rivaled or even exceeded that of the FT-ICRMS approach, despite significantly lower mass resolution. This result stemmed both from a reduction in the number of peaks and their dispersion over a much wider range of mass-to-charge ratios. Similar results were obtained from the CID simulation, where the informing power of different approaches was evaluated on the basis of the ratio of the number of ions for which a mass could be determined unambiguously to the total number of ions in the spectra.

Introduction

With the introduction of soft ionization methods, mass spectrometry has become a dominant technology in protein identification and characterization. Particularly in the case of ESI,^1–3 the formation of a distribution of multiply charged ions from a single protein is typical. The multiple charging phenomenon associated with ESI provides several advantages in protein mass measurement; i) it enables the mass measurement of a high mass species using a mass analyzer with a modest upper limit of mass-to-charge ratio and ii) the production of a distribution of charge states allows for multiple mass-to-charge ratio measurements for a single protein species.² Multiple charging has also been noted to facilitate the derivation of protein primary structure information via dissociation experiments.^4–7 The multiple charges on a highly charged protein, particularly at relatively high charge states, reduce its kinetic stability and make higher collision energies obtainable at a given acceleration potential. Furthermore, the availability of different charge states for subsequent ion activation can be an advantage due to the complementary information that is often forthcoming from different precursor ion charge states.^3,7–15 However, the multiple charging phenomenon can also complicate mass measurement when mixtures of ions of different mass and charge are present. Such a scenario prevails, for example, in the ESI of protein mixtures and in the dissociation of a multiply-charged precursor ion. In the case of the ESI of a complex protein mixture, a large number of peaks tend to be concentrated within a relatively narrow range of mass-to-charge values, resulting in a mass spectrum with potentially severe peak overlap. In this case, the multiplicity of peaks associated with each mixture component actually complicates the extraction of mass information from the mass spectrum. A similar situation is often created in the dissociation of a multiply-charged precursor ion, although the number of different charge states per product ion is usually much smaller than the number of charge states per protein in an ESI mass spectrum.

The fact that an ion charge state is not known a priori in an ESI experiment places a premium on the ability to assign charge states in order to assign masses. When at least two ions with known differences in charge and mass are present, it is straightforward to determine the charges of the ions from the measurement of their mass-to-charge ratios.^16–18 Mass spectrometers with even modest resolving powers are capable of making such measurements in relatively simple spectra. The requirement of the presence of two charge states of a known charge and mass relationship is circumvented if the mass-to-charge spacings of adjacent isotopes within a charge state envelope can be measured,¹⁹ which for whole protein ions is best provided via FT-ICRMS or Orbitrap^20,21 mass analysis. Algorithms have been developed to simplify complex spectra by converting an ESI spectrum to a “zero-charge” spectrum,^22–26 based on the measurement of peak spacings between charge states, but they are most reliable for very simple mixtures. Alternatively, charge state manipulation via either ion/molecule²⁷ or ion/ion^28–30 reactions can facilitate charge state determination. Regardless of the approach to charge state and mass determination, however, at some level of mixture complexity, peak overlap can become a limiting factor in providing the information of interest.

For any analytical method, the extent of peak overlap is determined by both the mixture complexity and the peak capacity, or informing power, of the approach. The informing power of an approach determines the maximum number of peaks resolvable in a spectrum and, in the case of mass spectrometry, depends largely on the resolving power (RP) and accessible mass-to-charge (m/z) ratio range (i.e. the m/z region actually occupied by the ions) of the mass analyzer employed. Therefore, strategies to minimize peak overlap associated with mixtures of multiply charged ions involve an increase of the RP of the mass analyzer, manipulation of the accessible mass-to-charge ratio range, reduction in the number of peaks/component, or a combination of two or more of these approaches. For example, it is well-known that FT-ICRMS can allow more information to be extracted from ESI mass spectra of protein mixtures than can quadruple mass filter mass analysis due to its 10²–10³ higher RP.^31,32

In the case of the ESI of protein mixtures, it is also possible to consider increasing the accessible m/z range by reducing protein ion charge states and thereby decompressing the protein ion signals that ESI normally concentrates into a relatively narrow range of m/z values. Such an approach, of course, requires that the ions remain within the range of m/z values that the mass spectrometer can analyze. A number of approaches are available for charge reduction of a multiply charged positive ion. Gas phase charge reduction of multiply protonated ions with strong bases has been effected through ion/molecule reactions in the interface area^33,34 or inside the high vacuum region of the mass spectrometer.^35–37 Although ion/molecule reactions can be readily implemented, the limited extent to which charge states can be reduced and the degree that cluster ion formation competes with proton-transfer have limited the use of this strategy for protein mixture analysis via ESI. The use of ion/ion proton-transfer reactions has proved to be a more robust approach for charge manipulation of multiply charged ions, either prior to ion sampling into the mass spectrometer^38,39 or within an electrodynamic ion trap.⁴⁰ The latter approach allows ion/ion reactions to be used between stages of a multi-stage mass spectrometry experiment. The underlying factors that make ion/ion proton-transfer reactions superior to ion/molecule proton-transfer reactions for charge state manipulation of high mass ions have been discussed in detail elsewhere.^41,42

The extremely high mixture complexities often associated with proteomics measurements has brought particular attention to approaches with high informing power/peak capacities. Among them are various mass spectrometry-based approaches, often coupled with on-line or off-line separations. The simulation of peak capacities of FT-ICRMS and TOF MS, in conjunction with liquid chromatography, was recently described⁴³ that is directly relevant to “bottom-up” proteomics, in which the mixture is comprised of proteolytic peptides. In this case, multiple charging is less of an issue than with whole proteins and the FT-ICRMS was shown to provide the highest peak capacities due to its high resolving power. In this work, we have examined the relative information content associated with several ESI/MS-based approaches applied to whole protein ions, where multiple charging is a more complicating factor than it is with tryptic peptides. In this study, we have employed computer simulations of the ESI/MS of protein mixtures of varying complexity and the analysis of product ion mixtures derived from the dissociation of multiply-charged precursor ions. The informing powers of three commonly used mass analyzers, i.e. the FT-ICRMS, QIT and TOF mass analyzer, were examined, as well as informing power of the latter two analyzers when coupled with ion/ion proton-transfer reactions.

While the overall performance of any top-down proteomics approach based on mass spectrometry is determined by a range of factors, such as the range of available activation methods, mass measurement accuracy, detection efficiency, etc., this work is focused on the key characteristic of informing power or peak capacity. The performance of different MS platforms in the simulation depends upon assumptions regarding the performance characteristics of the mass analyzers, which were chosen to be typical values, rather than the highest ever recorded. Comparisons between mass analyzers, therefore, are more dependent upon the assumptions than comparisons for a given platform with and without the use of ion/ion reactions.

Methods

A program written in C++ was used to compare the information capacity of FT-ICRMS, TOF and QIT alone or in combination with ion/ion chemistry in the ESI and CID simulations.

ESI Simulations

Masses of proteins in a mixture were randomly generated with uniform probability over the mass range of 5,000 – 50,000 Da by use of the C++ built-in random function generator. The charge state distribution for each protein from ESI was generated based on constraints derived from the body of empirical observations of ESI of proteins: i.e., the highest charge number was estimated by dividing the protein mass value by 700 and rounding-down to the next integer value and the lowest charge number was estimated by dividing the protein mass value by 2000 and rounding-down to the next integer value. It was assumed that the protein yielded signals for all intermediate charge states. Subsequently, the m/z values from all proteins were calculated, sorted from low to high and stored in an array, which resembled an ESI mass spectrum. The separated peaks in this simulated spectrum can be found by calculating the m/z difference between the adjacent peaks. Two adjacent peaks separated at half of the peak height were assumed to be separated from each other and a peak separated from both its leftmost and rightmost neighbors was regarded as a separated peak. The number of separated peaks with m/z values within the instrument mass-to-charge range was counted. The ratios of the separated (or resolved) peaks to the total number of predicted peaks (SP/TP) from the simulated ESI spectra were employed as the criterion to evaluate the informing power of a mass spectrometry based approach in the context of ESI experiments.

Masses randomly selected from the Swiss-Prot Yeast sequence database were also subjected to the simulation. All yeast protein sequences from the Swiss-Prot database were retrieved through the sequence retrieval system (SRS) from the ExPASy server. The total entries obtained were 12014. The molecular weight (MW) information was extracted from each entry through a home-written C++ program. Proteins with MW from 5000 to 50,000 Da were pooled by the C++ program and a protein from this pool of 6806 proteins was randomly selected as one component of the protein mixture by the simulation program. All other steps in the simulation from this point were identical to those used for the protein mixtures generated randomly.

Ion/Ion Reaction Simulations

In the examination of the change in informing power by coupling ion/ion proton-transfer reactions with QIT, TOF, or FT-ICRMS the pre-ion/ion abundances, viz. the abundances after ESI, of the protein charge states were all assumed to be 1 and the charge states with abundances less than 0.01 were assumed to be unobservable in the post-ion/ion spectra. The singly-charged anions used to reduce protein ion charge states were assumed to be present in excess, which is a readily obtainable condition in electrodynamic ion traps, such that the time evolution of the protein charge states can be modeled as a set of consecutive, irreversible, pseudo-first-order reactions.²⁸ In this work, a constant anion density of 6.5×10⁷ anions/cm³ and a rate constant for the +1/−1 reaction of 8.2×10⁻⁸ cm³·ion⁻¹·s⁻¹ were assumed, which gives a +1/−1 reaction rate of approximately 5.3 s⁻¹. The reaction rates for cations of higher charge states were taken as the rate for the +1/−1 reaction multiplied by the square of the cation charge.²⁸

CID Simulations

A precursor ion with m/z = 700 Th and a charge state equal to +57 was considered in the CID simulation. By the use of the Box-Muller transform algorithm,⁴⁴ the m/z values of CID product ions were generated randomly with a Gaussian distribution having a mean of 700 Th and an arbitrarily defined standard deviation (σ). Each CID product ion was composed of several isotopes and it was assumed that the number of isotopes (n) can be calculated from the monoisotopic mass (m) of the ion as shown below⁴³:

$$n=0.001m+2.0492$$ (3)

A charge number randomly generated with uniform probabilities over +1 ~ +57 was assigned to a product ion on the condition that the resulting neutral mass of this fragment ion was less than that of the precursor ion. When ion/ion reactions were combined with a QIT, TOF, or FT-ICRMS approach, each product ion was assumed to be present in both the +1 and +2 charge states. The ions in the pre-ion/ion CID spectrum with resolvable isotopes and no overlap with the isotope distribution of a neighboring peak contain both charge state and m/z information and are defined in this exercise as “informative ions”. For an ion/ion reaction coupled approach, the number of informative ions was determined as the number of non-overlapping peaks in the post-ion/ion spectrum. The ratio of the number of informative ions over the total number of ions in a spectrum was an indicator of the informing power of an approach and was used as a criterion to compare the informing power of the five mass spectrometry based approaches in the context of an MS/MS CID experiment.

Results and Discussion

Resolving Elements (or Peak Capacity) in the ESI/MS of >5 kDa Polypeptides Mixtures

The term ‘peak capacity’ is ordinarily used within the context of a separation technique, such as liquid chromatography, and is intended to convey the maximum number of peaks that can be separated on a given column.⁴⁵ It is a value that applies to an ideal case because it assumes the optimal distribution of retention times so as to minimize peak overlap. It is well-known that the actual number of components that can be resolved in real samples, in which the retention times are randomly distributed, is only a small fraction of the peak capacity.^46,47 In the case of mass spectrometry, for example, the issue of peak capacity within the context of tryptic peptide mixture analysis, has been discussed.⁴³ In the case of unmodified singly-charged tryptic peptides, the peak capacity is constrained by the fact that regions of mass-to-charge are precluded from being occupied. This situation does not prevail, however, in the case of polypeptides greater than about 5 kDa and when multiple charging is involved. Assuming no constraints on the possible mass-to-charge ratio values of ions in a protein mixture, the number of resolving elements for a mass analyzer is given by:

$$\mathit{\text{RE}}={\displaystyle \underset{{(m/z)}_1}{\overset{{(m/z)}_2}{\int }}\frac{\mathit{\text{RP}}}{(m/z)}·d(m/z)}$$ (1)

Where RP is the resolving power, here using the (m/z)/Δ(m/z)_FWHM definition, and (m/z)₂ and (m/z)₁ are, respectively, the highest and lowest m/z values associated with the mixture. The assumption is made here that the m/z range accessible to the analyzer can be made to accommodate the m/z range of the mixture components. Under this condition, the m/z range relevant to the determination of the number of resolving elements is established by the mixture and not by the range of m/z values examined by the mass analyzer.

The number of resolving elements, which is equivalent to the “peak capacity”, depends both upon the RP, the functional dependence of RP on ion m/z ratio, and the m/z range over which the peaks are dispersed. The RP dependence upon m/z has important implications for the use of charge state reduction strategies for mixture analysis. For analyzers with a RP independent of m/z, relationship (1) becomes

$$\mathit{\text{RE}}=\mathit{\text{RP}}\text{ln}\frac{{(m/z)}_2}{{(m/z)}_1}$$ (2)

whereas for analyzers with RP inversely related to m/z, such as the the FT-ICR mass spectrometer, the relationship becomes

$$\mathit{\text{RE}}=C_{\mathit{\text{ICR}}}\left(\frac{1}{{(m/z)}_1}-\frac{1}{{(m/z)}_2}\right)$$ (3)

where C_ICR is a constant. Note that the relationship for a mass analyzer with a (m/z)^−½ functional dependence for RP, as might be expected for an Orbitrap mass analyzer,^20,21 is

$$\mathit{\text{RE}}=C_{\mathit{\text{OT}}}\left(\left(\frac{1}{\sqrt{{(m/z)}_1}})-(\frac{1}{\sqrt{{(m/z)}_2}}\right)\right)$$ (4)

where C_OT is a constant.

In this work, we have made the simplifying assumption that RP of the ion trap and TOF analyzers are independent of m/z, and are 1000 and 10,000, respectively. Our experience with such analyzers over m/z ranges extending up to tens of thousands of m/z units has indicated that RP is not strongly dependent upon m/z ratio for these analyzers.^48,49 The RP in FT-ICRMS, however, is inversely related to the m/z ratio of the ion and directly related to magnetic field strength and transient measurement time.⁵⁰ The RP of FT-ICRMS used in this study was calculated using an equation described by Marshall et al.⁵⁰ in which C_ICR is given as 1.274×10⁷·B·T, where B, the magnetic field strength, is taken as 7 Tesla and T, the transient time, is 1 s. The RP assumptions used here are intended to reflect performance levels readily accessible with modern instrumentation.

Peak capacity in chromatography is usually considered with the assumption that each mixture component gives rise to a single peak. The electrospray process, with its tendency for multiple charging of proteins, generally yields multiple peak envelopes (which comprise the isotopic distribution) per component and tends to concentrate the ions into a relatively narrow m/z range. The formation of a distribution of charge states for a given mixture component gives rise to the “component capacity” of the technique being significantly smaller than the “peak capacity” in proportion to the number of peaks per component. The fact that there are multiple peaks per component and that the peaks are concentrated into a narrow range of m/z values has important implications for protein mixture analysis when electrospray ionization is employed. In fact, the multiple charging phenomenon is a major reason why only single proteins, or very simple mixture of proteins, are generally subjected to electrospray ionization.

The generation of multiple peaks per component and concentration of peaks within a relatively narrow mass-to-charge range motivated the generation of charge state reduction techniques for protein mixture analysis. The utility of the approach is dependent upon the capability of the analyzer to accommodate the mass-to-charge range of the charge reduced species. Both TOF and ion trap approaches have been employed, the latter of which requires the use of resonance ejection at relatively low q_z values.⁵¹ The benefit of a charge reduction approach, however, is also dependent upon the relationship between RP and m/z. Table 1 summarizes an illustrative comparison of the number of resolving elements (RE) and the number of resolving elements normalized on the basis of the number of peaks per component (RE/component) for two scenarios for the analysis of a mixture of proteins in the mass range of 5,000–50,000 Da. Relationships (2)–(4) were used to determine the number of resolving elements over the m/z range 500–2,000 (RE_(500–2000)) and over the m/z range of 5,000–50,000 (RE_{(5000–50000)}). The former case represents the range in which the bulk of the protein signals might be expected from a conventional electrospray ionization experiment. The latter range applies to a condition in which most of the ions have been reduced in charge to +1. An average number of peaks per component of 10 was used to determine RE_(500–2000)/component, whereas two peaks per component were used to determine RE_{(5000–50000)}/component. For proteins that range in mass from 5,000 to 50,000 Da an average of 10 charge states per component is low for most electrospray conditions but the key overall trends are reflected in the table. The comparisons of Table 1 make clear that the use of a charge reduction technique is most beneficial for analyzers in which RP is independent of m/z. For example, while the number of resolving elements differs modestly for the two m/z ranges, the RE/component values are roughly an order of magnitude larger after the deprotonation reactions reduce the number of peaks/component. At the opposite extreme, in which RP is inversely related to m/z, the number of resolving elements drops dramatically in the higher m/z region. Thus, in the case of the FT-ICR, the larger number of peaks per component in the normal electrospray mass spectrum is likely to be roughly compensated for by the significantly larger peak capacities at lower m/z. Given the loss in detection response for ions of lower charge, and other compromises that might arise from analysis of high m/z ions, a charge state reduction strategy is much less attractive in FT-ICR than it is when a TOF or QIT mass analyzer is used.⁵² Of course, the ways in which the relevant m/z ranges are filled differ in the pre- and post-charge state reduction scenarios. Hence, there may be cases even in FT-ICR in which at least a partial charge state reduction could be beneficial in separating protein signals. The intermediate case, in which RP is related to (m/z)^−½, is interesting because the loss in number of RE at the higher m/z range is less dramatic than in the FT-ICR case such that RE/component may very well be higher after charge state reduction.

Table 1.

Number of resolving elements (RE) and number of resolving elements per component for the cases of constant RP (e.g., time-of-flight), RP inversely related to (m/z)^½ (e.g., Orbitrap), and RP inversely related to m/z (e.g., FT-ICRMS).

	RE(500–2000)	RE(500–2000) per componentd	RE(5000–50000)	RE(5000–50000) per componente
aConstant RP	13,863	1,386	23,026	11,513
bRP∝(m/z)−½	44,721	4,472	19,340	9,670
cRP∝ (m/z)−1	133,770	13,377	16,052	8,026

^aRP = 10,000

^bC_OT = 2×10⁶

^cC_ICR = 8.918×10⁷

^d10 peaks per component

^e2 peaks per component

Simulation of ESI of Protein Mixtures

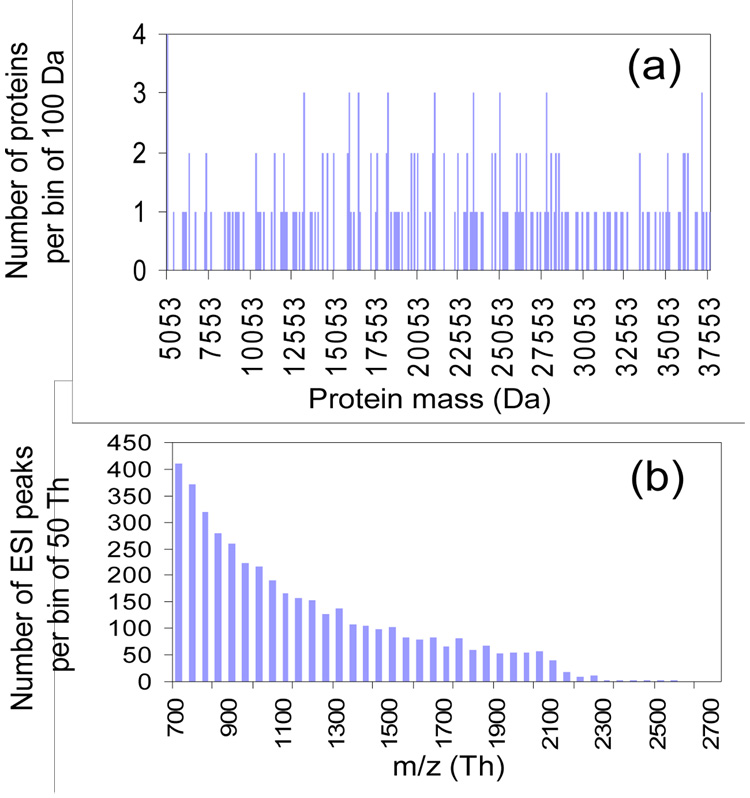
The preceding discussion provides information regarding the number of resolving elements and the number of resolving elements per component that apply to the scenarios discussed above. However, the number of resolved components for any given mixture is determined by how the available m/z range is filled. A measure of the success of resolving components derived from a protein mixture is the ratio of separated (or resolved) peaks to the total number of peaks, SP/TP. We have run a number of simulations to determine how the SP/TP ratio changes as the number of proteins in the mixture varies under several top-down mixture analysis scenarios. We have made the simplifying assumption throughout that the mass distribution of these proteins is statistically random with uniform probability over a wide mass range. The distribution of protein masses in such protein mixtures can be conveniently simulated by computer using the C++ built-in random number generator over a specific mass range (i.e., 5,000–50,000 Da in this study). Figure 1(a), for example, shows a mass distribution of a mixture containing 200 protein components generated by this approach, which reflects an almost evenly distributed set of mass values over the specified mass range. Assuming all proteins to be ionized, a charge state distribution is generated for each component. A characteristic feature of many protein ESI mass spectra is that the width of charge state distribution is about half of the highest charge state and that the average charge state is approximately proportional to the protein mass.³ For the purposes of this simulation, the highest charge state was estimated by dividing the protein mass by 700 and lowest charge state by dividing the protein mass by 2000. With these approximations, the charge states from all proteins in a mixture can be largely observed within a mass-to-charge ratio window of 700–2000 Th. Figure 1(b), for example, shows the m/z distribution of the charge states, viz. ESI peaks, from a mixture of 200 protein components whose mass distribution is shown in Figure 1(a). The gradual decrease in the number of ESI peaks per bin with the increase of m/z, as shown in Figure 1(b), arises from the fact that the lower the charge state, the larger the m/z difference between two neighboring charge states of a protein. Note also that the assumption is made here that each charge state is equally probable, whereas a distribution of abundances is characteristic of a typical ESI charge state distribution. However, for the purpose of this study, which is focused on the issue of peak separation, the relative differences between the different approaches, i.e., pre-charge reduction versus post-charge reduction, should be adequately reflected with the assumption of equal abundances. Also, for simplicity, monoisotopic species were assumed in these simulations. For this reason, the SP/TP ratios determined from the simulations are higher than would be expected from the inclusion of isotope peaks, which broaden peak profiles and lead to greater overlap, for all of the approaches examined. However, the inclusion of isotope peaks is not expected to significantly impact conclusions regarding the relative abilities of the various approaches for resolving components.

Figure 1.

(a) The mass distribution of 200 proteins (bin size = 100 Da) randomly generated over 5,000 – 50,000 Da with uniform probability and (b) the m/z distribution (bin size = 50 Th) of the ESI peaks produced by these 200 proteins.

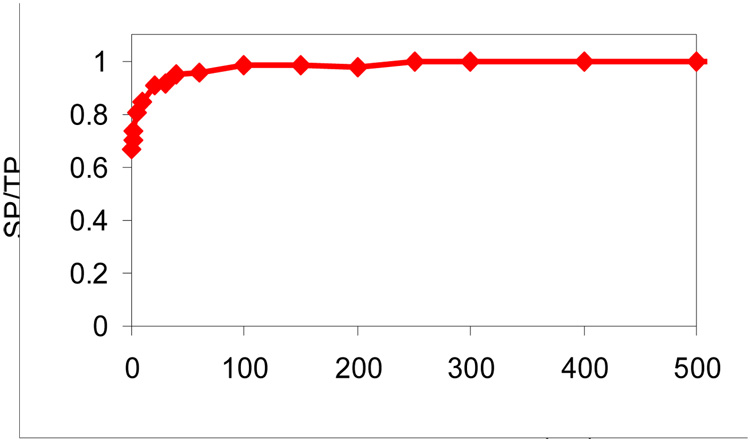
The extent of peak overlap in the simulated spectra can be summarized by the SP/TP ratio whereby low ratios indicate extensive peak overlap and ratios approaching unity indicate a high fraction of resolved peaks. High SP/TP ratios correlate with high “peak capacities”. For methods that employ charge state reduction either by ion/ion or ion/molecule reactions, reaction time is an experimental variable that can impact the SP/TP ratio, via the role of reaction time on the number of peaks/component and the fact that there are significantly larger m/z spacings between adjacent charge states as the charge decreases. Simulations for the use of ion/ion reactions in conjunction with TOF mass analysis were conducted as a function of reaction time using the conditions mentioned above to determine the reaction time to use in subsequent simulations. The results are summarized in Figure 2, which shows a plot of SP/TP versus reaction time for a mixture of 100 protein components with randomly generated masses.

Figure 2.

SP/TP (ratio of separated peaks to total predicted peaks) from TOF mass spectra as a function of ion/ion reaction time for a mixture of 100 proteins.

The data indicate that much of the benefit associated with charge reduction via the ion/ion proton-transfer reactions is gained within the first 100 ms of reaction time. Within this period, the most abundant charge state per component becomes the +1 ion. However, signals due to the +2 ions do not fall below the relative abundance threshold of 0.01 until nearly 500 ms of reaction time. A reaction time of 500 ms was selected for subsequent simulations because it provides an indication of the maximum possible improvement in SP/TP that can be obtained by reducing the number of peaks per component. However, it is also clear that substantially shorter reaction times can be used without compromising significantly the improvement that charge reduction can provide.

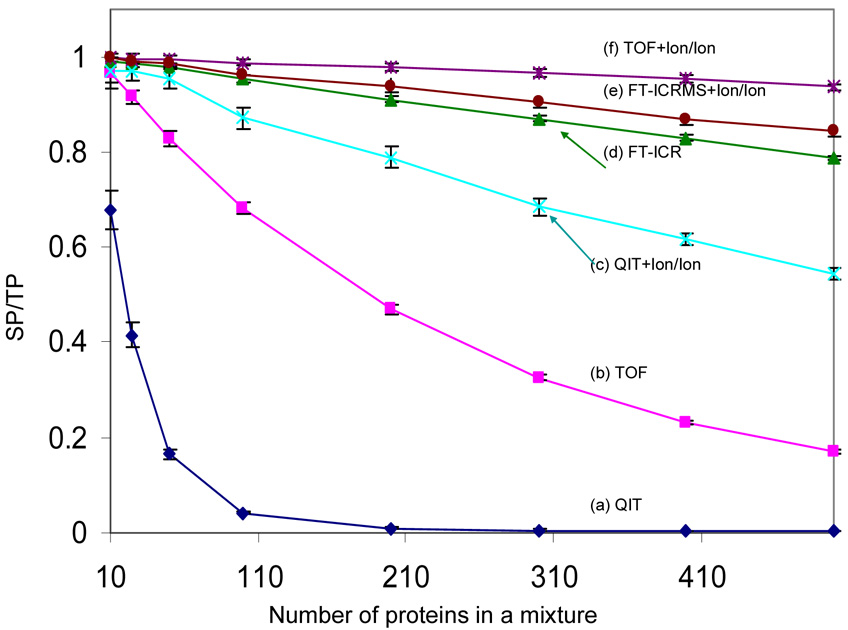
Figure 3 shows the SP/TP ratios as a function of the number of protein components for several whole protein mixture analysis approaches.

Figure 3.

Comparison of the SP/TP (ratio of resolved peaks to the total number of predicted peaks) from six mass spectrometry based approaches: (a) QIT, (b) TOF, (c) QIT coupled with ion/ion reaction, (d) FT-ICRMS, (e) FT-ICRMS coupled with ion/ion reaction and (f) TOF coupled with ion/ion reaction (ion/ion reaction time: 500 ms), in the context of the ESI simulation. Each data point is the average of 20 simulations and the error bars reflect the standard deviation.

The discussion related to Table 1 indicated that significant improvements in the number of resolving elements/per component are expected to result from reduction in the number of peaks per component via charge state reduction, particularly for mass analyzers that provide roughly constant resolving power with m/z. The simulation of the application of ion/ion proton-transfer reactions to the protein mixtures followed by QIT mass analysis (Figure 3, trace (c)) and TOF mass analysis (Figure 3, trace (f)) provides information regarding the performance implications of the increases in RE/component. By comparison of curves (a) and (b) with curves (c) and (f) in Figure 3, respectively, it is clear that dramatic increases in SP/TP ratios are noted, with the relative change increasing with number of protein components. For example, when a mixture of 500 proteins was used, the SP/TP value increased from 0.169 for the stand-alone TOF approach to 0.936 for the ion/ion reaction coupled TOF approach (TOF+Ion/Ion). The SP/TP ratio of the TOF+Ion/Ion approach decreased slowly with increasing number of proteins in the mixture in a manner similar to that of FT-ICRMS approach (curve (d)). While the slope of the SP/TP vs. protein number curve of the TOF+Ion/Ion approach was somewhat less negative than that of the FT-ICRMS approach for this particular simulation, general comparisons between the two approaches should not be drawn from Figure 3 because the curves are sensitive to the input assumptions (e.g., resolving power and reaction time). Nevertheless, the simulation does indicate that the roughly comparable RE/component values of the TOF+Ion/Ion approach and the 7 Tesla FT-ICRMS approach without charge state reduction (see Table 1) lead to comparable abilities to resolve mixture components. (The somewhat higher SP/TP ratios found in the simulation for the TOF+Ion/Ion approach relative to the FT-ICRMS approach, while the relevant RE/component values in Table 1 show the FT-ICRMS approach to be higher, is likely due to the assumption of 10 peaks/component, used to derive the values in Table 1, which is an underestimate for the average peaks per component in the simulation.) The simulation clearly shows the potential benefit to be gained by implementing charge reduction for ESI protein mixture analysis with QIT and TOF instruments. The largest relative gains are noted for the analyzer with lower resolving power, i.e., the QIT. For example, almost no separated peaks resulted (SP/TP = 0.009) when a mixture of 200 proteins was subjected to simulation using the stand alone QIT approach, but nearly 80% of the peaks became separated (SP/TP = 0.789) when the QIT+Ion/Ion approach was employed. The use of ion/ion reactions in conjunction with FT-ICRMS mass analysis (curve (e)) showed very modest improvement over FT-ICRMS alone. The values given in Table 1 suggest that the use of ion/ion reactions with the FT-ICRMS would give poorer performance but the assumption of ten charges per protein used for the values given in the figure underestimates the average charge of the proteins used in the simulation. In any case, the simulation bears out the expectation that charge state reduction in the FT-ICRMS of protein mixtures provides little improvement in component capacity.

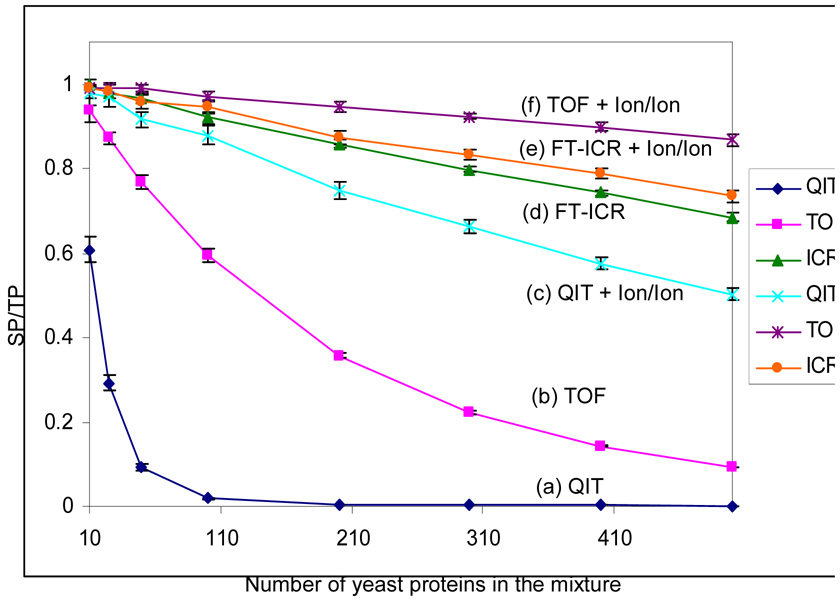
In order to evaluate the use of random protein masses to approximate what might be encountered with any particular proteome, a series of simulations were performed on mixtures derived from the Swiss-Prot Yeast database. In this scenario, the values of the possible protein masses are constrained by the biological system. Masses of proteins within the range of 5–50 kDa were randomly selected from the data-base and subjected to simulation. The results are summarized in Figure 4. The SP/TP ratios for all approaches decrease slightly more rapidly for the mixtures for which masses were selected from the Swiss-Prot database than for those in which no constraints were placed on the mass values that could be included in the simulation. This reflects the fact that masses are not randomly distributed with equal probability in the protein database. Overall, however, the observed behavior is very similar to that found for the simulations summarized in Figure 3 suggesting that the assumption of random protein masses is likely to reflect reasonably well the behavior to be expected from a specific proteome.

Figure 4.

Comparison of the SP/TP (ratio of separated peaks to the total number of predicted peaks) from six mass spectrometry based approaches: (a) QIT, (b) TOF, (c) QIT coupled with ion/ion reaction, (d) FT-ICRMS and (e) FT-ICRMS coupled with ion/ion reaction and (f) TOF coupled with ion/ion reaction (ion/ion reaction time: 500 ms), in the context of the ESI simulation. Each data point is the average of 20 simulations and the error bars reflect the standard deviation.

Simulation of Collision-Induced Dissociation Product Ion Spectra

The product ion spectrum derived from the collision induced dissociation of a multiply charged whole protein ion is analogous to the mass spectrum of a mixture of whole proteins in that it represents a mixture of ions of different mass and charge. However, the two scenarios are distinct in significant ways such that a separate set of simulations is warranted to examine the utility of charge reduction techniques from the standpoint of informing power. For example, while there can often be several charge states per fragment, there are usually far fewer peaks per component in a CID spectrum than in the mass spectrum of a protein mixture. From the standpoint of reducing the number of peaks per component, there is less motivation for charge reduction of CID spectra than for mass spectra of mixtures. However, there is a tendency for product ions derived from highly charged precursor ions to be concentrated in the mass-to-charge region that surrounds the precursor ion. This phenomenon can be rationalized by considering the protein ion to be a collection of equally spaced charges on a string. A cleavage at any site along the string will yield ions of different mass and charge but very similar mass-to-charge ratios. While this is certainly an overly simplified model, protein CID product ion spectra of highly charged ions tend to show behavior that approximates this picture. That is, they tend to show a distribution of product ion m/z ratios centered about that of the precursor ion. Hence, rather than being randomly distributed within the relevant range of mass-to-charge ratios, the product ions tend to be clustered in a relatively narrow m/z region.

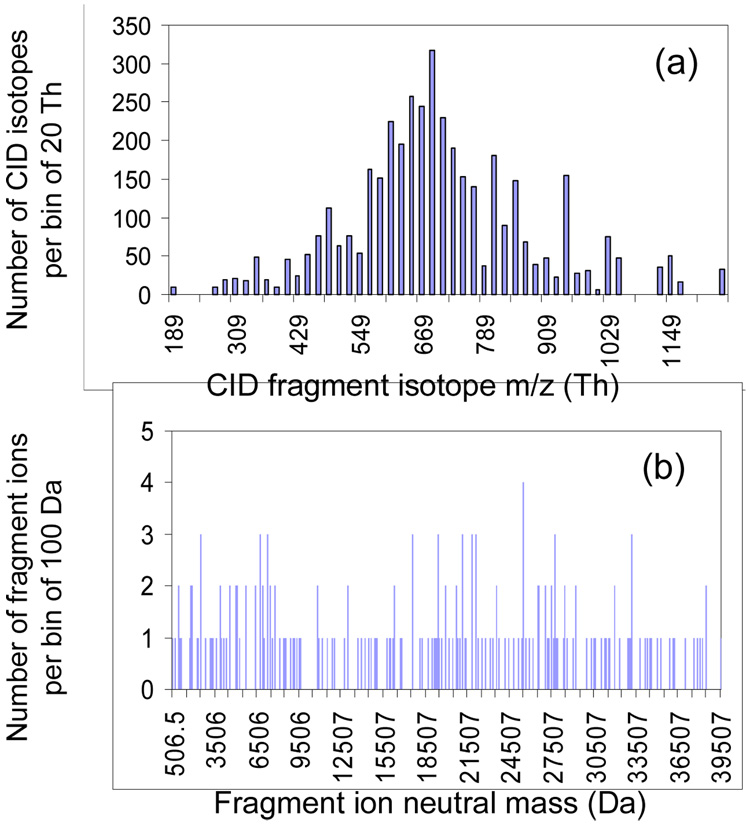
A key objective of a protein ion MS/MS experiment is to generate fragment mass information to use for searching against a protein data-base. In this context, we can define a figure of merit as the fraction of informative product ions relative to the total number of product ions (II/TI), where an informative ion is defined as any product ion for which both the charge and mass-to-charge ratio can be established without ambiguity. This differs from the criterion used above for protein mixtures because a separated peak may not be informative in the CID spectrum if the charge state of the ion giving rise to the signal cannot be established. Using this ratio as a criterion, experiments were simulated for the six approaches discussed above for protein mixture mass analysis and applied in this case to product ion analysis. In the CID simulation, a Gaussian distribution of CID product peaks and their corresponding charge states were generated randomly by the approach described in the methods section. In this case, product ion isotopes were included because the ability to resolve isotope peaks can allow for the establishment of an informative ion. Figure 5(a) shows an example of the m/z distribution of 4036 isotopes of 200 product ions generated by the computer using a Gaussian distribution with a mean of 700 Th and a standard deviation of 200 Th. When the charge carried by the product ion is assumed to be randomly distributed uniformly from +1 to that of precursor ion, viz. +57 in this study, the neutral mass of the product ion has a distribution shown in Figure 5(b).

Figure 5.

Bar graphs of (a) the isotope m/z distribution and (b) the neutral mass distribution of 200 product ions derived from CID simulation on a +57 precursor ion with m/z 700 Th. The fragment ion m/z was generated randomly with a probability of Gaussian distribution having a mean of 700 Th and a standard deviation of 200 Th, and the charge on the ion is randomly generated with uniform probability from +1 to +57.

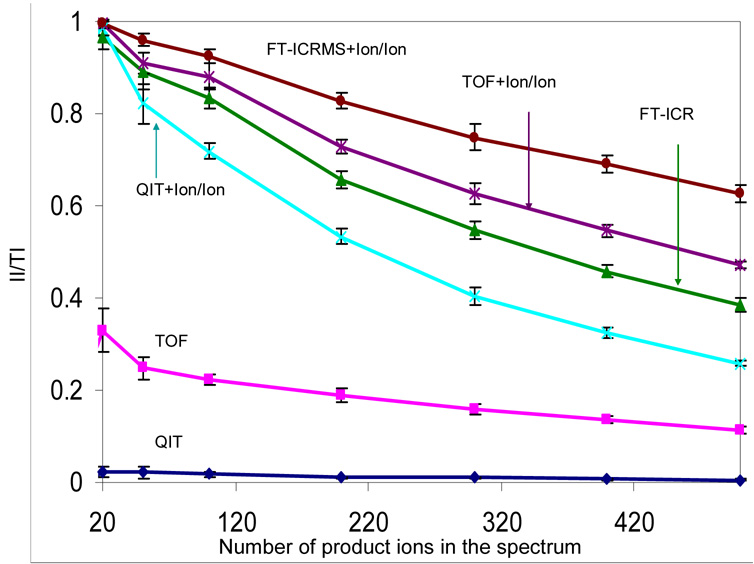
The II/TI ratios derived from multiple simulations of product ion spectra measured via the six methods discussed above are plotted in Figure 6 as a function of the number of fragments for a precursor ion of charge +57 and m/z ratio = 700 Th. As expected, the II/TI ratio decreased with increasing product ion number for all approaches. The number of informative ions in a spectrum collected by stand alone QIT, TOF or FT-ICRMS instrument, is strongly dependent on the resolving power of the mass analyzer. For example, with a set of 200 simulated product ions, there were 132, 40 and 2 informative ions present in the spectra collected by the FT-ICRMS, TOF, and QIT approaches, respectively. For these approaches, the ability of the FT-ICRMS to resolve isotope peaks, which enables charge state determination, underlies much of its advantage in deriving information from the product ions. For many of the products ions measured by TOF or QIT mass analysis, the peaks may be separated but the charge state is not readily defined because the isotope spacings are not resolved. Clear improvements in the II/TI ratios were noted when charge reduction was used in concert with all forms of mass analysis. A key factor in this improvement derives from the fact that all ions can be converted largely to the +1 charge state, thereby allowing for the confident assignment of product ion charge. In all the simulations summarized by Figure 6, the II/TI ratios followed the order of FT-ICRMS+Ion/Ion > TOF+Ion/Ion > FT-ICRMS > QIT+Ion/Ion > TOF >> QIT. Even with relatively low numbers of product ions, the QIT mass analysis alone was unable to provide many informative ions. In this case, the implementation of charge state reduction led to a dramatic increase in the II/TI ratio. This is not a surprising result given the relatively large number of protein product ion spectra derived from ion trap collisional activation that have been rendered interpretable only after the product ion charge states have been manipulated via ion/ion reactions.^11–15 The identification of a priori unknown proteins has similarly been enabled by application of the QIT+Ion/Ion approach to product ions derived from ion trap collisional activation.^53–54 The use of ion/ion reactions shows more relative improvement with FT-ICRMS for the CID case than the protein mixture case (see Figure 3 and Figure 4) due to differences in how the m/z space is filled for the two analysis scenarios. The assumption of a Gaussian distribution of mass-to-charge ratio values in the case of the product ion spectra results in a greater degree of overlap. Hence, chare state reduction in this case results in a greater separation of the peaks, relative to the protein mixture case, such that even FT-ICR can benefit somewhat from the use of ion/ion reactions, despite the loss in resolving power at higher m/z ratios.

Figure 6.

Comparison of the informing power of six mass spectrometry based approaches, QIT, TOF, FT-ICRMS, QIT coupled with ion/ion reaction, TOF coupled with ion/ion reaction and FT-ICRMS coupled with ion/ion reaction in the context of the CID simulation. All sets of product ions have a Gaussian distribution with a mean of 700 Th and standard deviation of 200 Th. Data are averaged from 20 simulations and the error bars show the standard deviation.

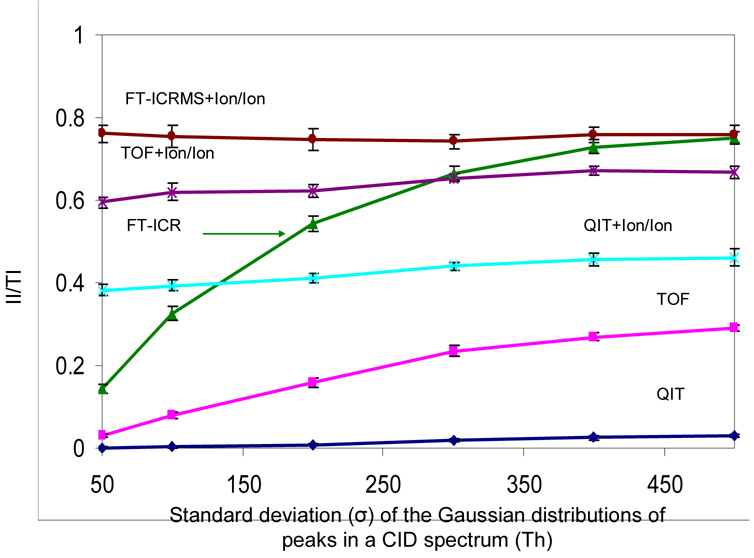
In practice, the effectiveness of an approach for deriving information from the ESI mass spectrum of a protein mixture or the CID spectrum of a multiply charged protein precursor ion is determined both by the number of resolving elements and by how the analyte fills the available m/z space. This is illustrated by the role played by the standard deviation of the distribution of product ion m/z ratios used in the CID simulations. Small standard deviations correlate with higher probabilities of peak overlap. Figure 7, for example shows the II/TI ratios determined from a series of simulations applied to a mixture of 300 product ions as a function of the product ion m/z standard deviation. The FT-ICR+Ion/Ion, TOF+Ion/Ion and QIT+Ion/Ion approaches are largely independent of the standard deviation of the initial product ion distribution of m/z values because the ion/ion reactions render the initial distributions into a distribution that much more resembles the true mass distribution, assuming most ions are converted to +1. Hence, with these methods, the final m/z distribution subjected to mass analysis is essentially independent of the initial distribution. On the other hand, the standard deviation of the product ion distribution is an important factor with the direct QIT, TOF, and FT-ICRMS approaches. The largest relative impact is noted for the FT-ICRMS approach because it best reflects the extent of peak overlap in the spectrum. The RP of the ICR is sufficiently high to determine product ion charge state for any ion that is separated from others whereas the other approaches may not be able to establish charge for a separated ion. Hence, while a larger standard deviation gives rise to more readily separated peaks for all three MS methods, the TOF and QIT may still not be able to establish product charge. This situation is clearly reflected in the modest change in II/TI ratio for the QIT case.

Figure 7.

The effect of peak distribution in a CID spectrum on the informing power of six mass spectrometry based approaches, QIT, TOF, FT-ICRMS, QIT coupled with ion/ion reaction, TOF coupled with ion/ion reaction and FT-ICRMS coupled with ion/ion reaction, in the context of the CID simulation. A mixture of 300 product ions was employed in the simulation. Data are averaged from 20 simulations and the error bar is the standard deviation of the repeated simulation results.

Conclusions

A number of factors are relevant to the overall performance of a mass spectrometry-based approach to whole protein mixture analysis. These include mass measurement accuracy, detection efficiency, the range of available activation methods, speed, etc. Included among these is informing power, which is related to the SP/TP and II/IT ratios determined here using simulations of the ESI-MS of protein mixtures and mass analysis of product ion spectra derived from CID of multiply charged proteins, respectively. As expected on the basis of resolving elements per component, of the three direct MS experiments intended to simulate QIT, TOF, and FT-ICR mass analysis, the FT-ICR experiment yielded, by far, the greatest information content of the three. Also as expected on the basis of resolving elements per component, the use of a charge reduction method, such as ion/ion proton-transfer reactions, can lead to significant enhancements of the informing powers, particularly for the QIT and TOF approaches. The inverse relationship between resolving power and m/z makes the implementation of a charge reduction strategy with the FT-ICR much less appealing for protein mixture analysis. However, even the FT-ICR approach can benefit from cases in which there is extensive overlap in m/z ratios of ions with difference masses and charges. Such a situation can occur in the CID of multiply charged protein ions. The greatest relative enhancement occurs for the QIT, which in the absence of ion/ion reactions, shows very limited performance for the ESI-MS of protein mixtures and MS/MS of whole protein ions. However, the combination of charge reduction with TOF provides superior performance relative to ion/ion reactions with the ion trap and was comparable to that of the FT-ICRMS approach (no charge reduction) with the assumptions used here.

The increase in informing power by the coupling of an ion/ion reaction in the ESI of protein mixtures results largely from the reduction of the number of peaks per component and, to a lesser degree, from dispersal of the ions over a wider m/z range. In the case of the protein CID experiment, the performance enhancement arises largely from the improved ability to establish product ion charge and from conversion of an approximately Gaussian product ion m/z distribution to a more evenly spaced distribution prior to mass analysis. The standard deviation of the product ion m/z distribution in the absence of charge state reduction plays a major role in determining the informing power of FT-ICRMS approach and a lesser role with the QIT and TOF approaches. The latter two approaches are limited in their ability to establish product ion charge in the absence of charge state reduction and therefore benefit less from a more widely distributed set of product ions.