Detecting Horizontally Transferred and Essential Genes Based on Dinucleotide Relative Abundance

Abstract

Various methods have been developed to detect horizontal gene transfer in bacteria, based on anomalous nucleotide composition, assuming that compositional features undergo amelioration in the host genome. Evolutionary theory predicts the inevitability of false positives when essential sequences are strongly conserved. Foreign genes could become more detectable on the basis of their higher order compositions if such features ameliorate more rapidly and uniformly than lower order features. This possibility is tested by comparing the heterogeneities of bacterial genomes with respect to strand-independent first- and second-order features, (i) G + C content and (ii) dinucleotide relative abundance, in 1 kb segments. Although statistical analysis confirms that (ii) is less inhomogeneous than (i) in all 12 species examined, extreme anomalies with respect to (ii) in the Escherichia coli K12 genome are typically co-located with essential genes.

1. Introduction

If biased mutational pressure is exerted globally and uniformly on all parts of the genome, then local differences in evolution rates can be explained by the negative selection principle of the neutral theory, which implies that ‘functionally less important parts in the genome evolve faster than more important ones’.¹ Recent progress in construction of single-gene knockout mutant collections makes it possible to determine the essentiality of each gene in any bacterium that can be cultured.² If evolution rates could be estimated in a defensible and consistent manner, the implication of the neutral theory might be tested by comparing estimates conditioned on essentiality. But if the evolutionary histories of bacterial genes were so transparent, then it would be easy to identify the ones acquired from foreign donors by horizontal gene transfer (HGT).

HGT detection has been pursued by phylogenetic methods, based on sequence alignment, and by composition-based methods^3,4 that involve alignment-free features such as G + C content, synonymous codon usage (SCU) and the frequencies of overlapping short oligomers. These species-specific features undergo amelioration, the process by which a foreign gene, acquired through HGT, evolves toward the composition of the host genome.⁵ Anomalous composition will be found in recently acquired genes, especially when they originate in distantly related species, but it will also be observed where amelioration has been retarded. Therefore, if genes are ranked according to dissimilarity with respect to global composition, the highest ranks will be awarded both to recent transfers and to relatively ancient coding sequences that have resisted mutational pressure. Composition-based methods have been criticized for falsely indicating HGT when highly conserved proteins have atypical amino acid compositions.⁶ The coding sequences of such proteins can undergo amelioration to the extent permitted by SCU—but not much farther. Therefore, we expect to find essential genes among false positives produced by HGT detection methods that operate on compositional features other than SCU.

Seminal investigations HGT in Escherichia coli examined G + C content and SCU to identify the ∼17.6% of genes most probably acquired since divergence from Salmonella ∼100 million years ago⁷ and to distinguish native genes from mobile elements (prophages and transposons).⁸ After refining the mathematical treatment of context-dependent SCU, Azad and Lawrence⁹ recently predicted 639 foreign genes in E. coli, reporting a false positive rate of 190/639 = 29.7% that was lower than for any competing method of comparable sensitivity. (False positives were genes >300 bp with homologs in S. enterica LT2.) SCU reflects species-specific preferences that are strongly correlated with gross cellular amounts of isoaccepting tRNAs,¹⁰ especially in highly expressed genes,⁸ without regard to function. Though driven by genome-wide mutational pressure on G + C, especially at the third codon position, these preferences are not selection-neutral,¹¹ and false positives may reflect the retarded amelioration of SCU in lowly expressed genes.

It has been theorized that higher order compositional features are inherently more species-specific than lower order features^12–14 and hence that tetranucleotide frequencies, computed without reference to a reading frame, convey more useful information than G + C content and SCU for purposes like fragment classification and HGT detection.^3,12–14 This claim could be reconciled with the implication of the neutral theory if higher order features ameliorate more rapidly and uniformly than lower order features. For example, dinucleotide composition can be mathematically decomposed into two parts: (i) the mononucleotide composition and (ii) the matrix of ‘odds ratios’ that compare the observed proportions of the individual dinucleotides to their expectations under the assumption of pure randomness.¹⁵ Nakashima et al.¹⁶ examined 10 complete genomes and concluded that part (ii) reflects phylogenetic relations better than part (i). The strand-invariant form of this feature is the dinucleotide relative abundance (DRA) profile which was called a ‘genomic signature’ by Karlin and Burge¹⁷ because an organism can generally be identified by computing it from any 50 kb or longer segment.¹⁸

DRA ratios thus exhibit species-specificity, approaching their global values in all sufficiently long segments of any single genome, but varying greatly between distant relatives. This phenomenon is unexplained¹⁹ but it could obviously be a consequence of the relatively rapid and uniform amelioration of genes with respect to DRA. The possibility of inferring HGT from anomalous dinucleotide composition was tested early on the path toward development of better methods and subsequent investigations have used this feature to establish a performance baseline.^3,9,20 We propose a new statistical procedure to assess the possibility that DRA ratios approach their global means more uniformly than G + C proportions in segments of bacterial genomes. If a compositional feature ameliorates uniformly, then its intra-genomic variability will be bounded within certain limits embodied in a null hypothesis of homogeneity as formulated below. After testing this hypothesis in several bacterial species, the most anomalous segments of the E. coli K12 sequence are subjected to a phylogenetic analysis to identify false positives (by the noted criteria¹⁰) which are subsequently checked for essentiality with reference to published data.²

2. Materials and methods

Let n_xy denote the number of overlapping xy dinucleotides in a coding sequence of length n + 1 = ΣΣn_xy + 1 so that f_xy = n_xyn is the corresponding (normalized) fraction. The mononucleotide count in the first place is n_x and the corresponding proportion is f_x. Symbol f is replaced by φ when the whole genome is considered. The dinucleotide odds ratios for the whole genome are defined as

The local value of this ratio (e.g. for a single gene) is denoted ρ_xy and obtained by substituting f for φ.

It is understood that the genomes are not perfectly homogeneous with respect to oligonucleotide compositions of any order. The present problem is to quantify the inhomogeneity with respect to dinucleotide composition and then apportion this total amount between parts (i) and (ii) defined above.¹⁶ Beginning with the mathematical identity

first take logarithms, then multiply through by n_xy and sum over all dinucleotides. The result is

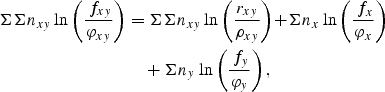1

in which each term is recognized as a deviance statistic that has a chi-squared (χ²) distribution for sufficiently large n under a particular hypothesis of compositional homogeneity.

In accordance with standard practice in genetics and many other fields,²¹ the deviance is replaced by its second order approximation, the χ² statistic, here denoted X, which converges in distribution more rapidly and monotonically to its large sample limit, subject to the usual proviso that each expected count is at least 5.²² This will almost guarantee a χ² distribution for n ≈ 1000 bp. On the left side of Equation (1), the deviance is

where the arrow says that it approaches χ² with 15 degrees of freedom under the hypothesis of (H₃:) homogeneity with respect to dinucleotide composition. On the right side of Equation (1) we have

where

is the expected value of n_xy under the hypothesis of (H₂:) homogeneity with respect to DRA. This hypothesis conforms to the saturated log-linear model defined by Agresti (chapter 5)²² in treating two-way contingency tables of Poisson-distributed counts. The last two terms on the right side of Equation (1) are added to obtain

under the hypothesis of (H₁:) homogeneity with respect to mononucleotide composition. Note that H₃ implies H₂ and H₁ (and conversely). Thus, Equation (1) becomes D₃ = D₂ + D₁, which leads to approximately the equivalent statement

2

in which the degrees of freedom add correctly (15 = 9 + 6).

Arbitrary segments (which may be intergenic or overlap more than one gene) can be handled similarly by averaging the dinucleotide counts of the sequence and its reverse complement. This step nullifies strand dependence and imposes counter-diagonal symmetry on the 4 × 4 matrix of dinucleotide proportions. The symmetrized dinucleotide odds ratios comprise the DRA profile, denoted ρ* by Karlin et al.,^17,18 who measured the distance between sequences g and h as

which they called delta-distance. When h is a segment of genome g, the intra-genomic delta-distances are log-normally distributed, with means approaching zero slightly slower than reciprocal square root of segment length.²³ But the statistical significance of large local delta-distances cannot be rigorously assessed.

Each quantity in Equation (1) has a strand-invariant analog, beginning with the symmetrized dinucleotide composition f*_xy, and the asterisk (*) can be appended to every one of the statistics in Equation (2) to indicate these substitutions. The degrees of freedom are changed as follows:

3

For example, the 10 non-redundant components of ρ* present 6 degrees of freedom, as remarked by Russell and Subak-Sharpe.²⁴ Note that the symmetrized mononucleotide composition is completely determined by the G + C proportions. Since χ²-tests are meaningless unless degrees of freedom are exact, we verified these claims [Equation (3)] by Monte Carlo calculations.²⁵ Each trial begins with random matrix [φ_xy], each count n_xy is a Poisson random number with expected value nφ_xy, and the three X* statistics are computed. After 2000 trials, the average value of each X* statistic is within ±0.15 of the specified degrees of freedom, and the probability integral transformations yield numbers that are uniformly distributed on the unit interval.

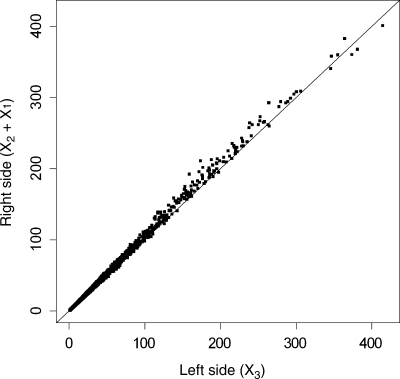
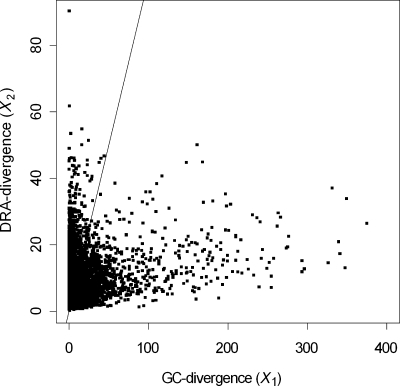
Starting with the published sequence of a bacterial chromosome, a window of length 1000 bp (1 kb) is displaced in increments of 1 kb from left to right (5′ to 3′), but not wrapping around to overlap the origin on the last displacement. Each window produces three X* statistics which obey Equation (2), as illustrated for the E. coli K12 sequence (NCBI reference sequence number NC_000913.2) in Fig. 1, where the sum of the two statistics on the right side of Equation (2) is evidently close to the value on the left, and the mean absolute difference (MAD) is only 3.4%. But each statistic commonly exceeds its null degrees of freedom (the expected value) by a large amount, as shown in Fig. 2, and many of them exceed the 99.5-percentile point of the χ²-distribution that describes the homogeneous case. Large values of X*₂ occur in segments with anomalous DRA. This statistic, henceforth called the DRA-divergence, exceeds the 99.5-percentile of its null distribution in 10.2% of segments. Large values of X*₁ occur in segments with anomalous G + C proportions. This statistic, the GC-divergence, exceeds the 99.5-percentile of its null distribution in 34.0% of segments. At the 95-percentile point, the exceedance rates (ERs) are 24.3% for the DRA-divergence and 46.4% for the GC-divergence. On this basis, we see that DRA is less inhomogeneous than G + C.

Figure 1.

Scatter plot of total chi-squared divergence, on the left side of Equation (2), versus the sum of the statistics on the right side, in 1 kb segments of the E. coli K12 genome. The line of unit slope through the origin is also drawn.

Figure 2.

Scatter plot of GC-divergence, describing fluctuations from the gross genomic G + C proportion, versus divergence with respect to DRA, in 1 kb segments of the E. coli K12 genome. The line of unit slope through the origin is also drawn.

A classic investigation of base compositional structure drew conclusions from two genomes, E. coli and human, and concluded that a viable stochastic model of both would probably fit ‘many or all of genomes’.²⁶ Subsequent research has shown that bacterial genomes have highly variable and idiosyncratic compositions. Thus it is important to examine some other species by the same methods. Escherichia coli is exceptional in having a nearly uniform mononucleotide composition. We select the linear chromosome of the spirochete Borrelia burgdorferi because it was found most homogeneous in G + C when viewed through windows of a certain size.²⁷ The cyanobacterium Synechocystis was judged to exhibit no detectable replication-associated strand bias.²⁸ Mycobacterium tuberculosis is included because it is AT-rich. Except for S. enterica, the other eight genomes in Table 1 are ad hoc choices. Summary statistics for these 12 bacteria are presented in Table 2.

Table 1.

Twelve selected bacterial genomes indexed by serial number (SN), identified by species, strain and reference sequence number (Ref.Seq.No)

SN	Species	Strain	NCBI Ref.Seq.No.	Length (kb)	G + C (%)
1	Bacillus subtilis	168	000964.2	4214	43
2	Borrelia burgdorferi	B31	001318.1	910	28
3	Campylobacter jejuni	RM221	003912.7	1777	30
4	Chlamydophilia pneumoniae	J138	002491.1	1226	42
5	Escherichia coli	K12	000913.2	4639	50
6	Haemophilus influenzae	Rd KW20	000907.1	1830	38
7	Helicobacter pylori	J99	000921.1	1643	39
8	Mycobacterium tuberculosis	CDC1551	002755.2	4403	65
9	Mycoplasma genitalium	G37	000908.2	580	31
10	Salmonella enterica	CT18	003198.1	4809	52
11	Staphylococcus aureus	N315	002745.2	2814	32
12	Synechocystis sp.	PC6803	000911.1	3573	47

Table 2.

Summary statistics for 12 selected bacterial genomes indexed by serial number (SN) as in Table 1

SN	Mean divergence			MAD	ER 95%			ER 99.5%
	Total	DRA	G + C		Total	DRA	G + C	TOTAL	DRA	G + C
1	25.8	10.8	15.9	2.9	47.2	27.9	43.2	32.4	13.4	32.2
2	21.3	9.7	12.0	3.9	42.2	22.7	39.6	25.2	7.8	28.4
3	21.7	10.4	12.0	3.9	45.1	26.2	40.2	28.0	10.9	27.4
4	15.6	9.6	5.9	1.7	34.8	22.7	26.4	17.2	8.1	14.0
5	27.1	9.8	18.4	3.4	48.0	24.3	46.4	33.5	10.2	34.0
5(n)	27.5	9.7	18.9	3.4	48.2	24.2	46.4	33.5	10.2	33.9
5(e)	20.4	11.4	9.5	2.9	45.5	14.6	37.5	21.6	4.3	23.2
6	19.9	10.6	10.2	3.6	37.0	27.1	31.0	23.2	11.6	20.3
7	19.1	11.4	9.2	5.5	39.7	29.4	32.0	25.0	14.3	21.7
8	20.2	9.5	10.3	2.4	32.1	20.1	27.8	19.1	8.4	18.4
9	26.2	11.3	14.0	3.4	49.3	28.6	41.4	33.6	13.9	30.7
10	30.4	10.8	21.9	5.2	52.8	28.3	49.3	38.2	12.8	38.2
11	21.7	11.3	10.2	2.6	40.7	28.6	32.9	25.6	12.9	21.2
12	24.4	10.0	16.6	5.7	43.8	22.2	44.6	28.6	9.8	32.4
Average	22.8	10.4	13.0	3.7	42.7	25.7	37.9	27.5	11.2	26.6

Mean values of the chi-squared divergence statistics in Equation (2) are shown with the MAD. ERs at two percentile points are listed. Averages across all species are shown in the last row.

Beyond statistical analysis by the method just described, we want to know if coding sequences undergo amelioration with respect to DRA at a rate that is relatively unaffected by essentiality. Accordingly, the 1 kb segments of the E. coli K12 sequence that are most anomalous in DRA-divergence are subjected to a phylogenetic analysis. The 20 highest ranking segments (largest DRA-divergences) are placed in serial order in Table 3. Each segment overlaps zero, one or two genes in the protein table of the current annotation. (We suppose that HGT typically involves segments longer than 1 kb.) Horizontal transfer (HT) is indicated by ‘M’ when the gene is pro-phage, phage-like, an insertion element or other documented Mobile element. Otherwise, the translated coding sequence is retrieved from EcoCyc²⁹ and its best alignment in S. enterica (all complete genomes) is found by tBLASTn (via the National Center for Biotechnology website with default parameters) and the corresponding E-value is noted.^30,31 If E > 0.1, the alignment is attributed to chance, and ‘+1’ is entered in the HT column to indicate true positive. If E ≤ 0.1 then the alignment is significant, the gene is assumed to have been inherited from the common ancestor, and the symbol ‘−1’ is entered in the HT column to indicate false positive. False positives are checked against the list of 302 essential gene candidates that were located on the chromosome of substrain MG1655 by testing knockout mutants.² When a false positive is an essential gene, ‘−1’ in the HT column is replaced by the abbreviated gene name (locus).

Table 3.

Characterizing the 20 most anomalous 1 kb segments of the E. coli K12 genome based on dinucleotide signature dissimilarity as measured by (a) DRA-divergence, (b) delta-distance, (c) Euclidean distance and (d) the quadratic discriminant

#	(a) chi-square		(b) delta-distance		(c) Euclidean		(d) quadratic		(e) G + C
	loc.	HT	loc.	HT	loc.	HT	loc.	HT	loc.	HT
1	200	yaeT	151	−1	151	−1	284	M	583	M
2	227	0	227	0	274	M	525	M	584	M
3	393	M	394	−1	575	M	526	M	1212	−1, −1
4	394	−1	526	M	777	−1	575	M	1636	M
5	526	M	777	−1	978	mukB	777	−1	2102	−1
6	777	−1	1287	−1	1142	rne	1142	rne	2105	+1
7	978	mukB	1427	M	1395	M	1427	M	2468	M
8	1142	rne	1465	0	1427	M	1465	0	2773	M
9	1465	0	1527	0	1465	0	1527	0	2783	0
10	1527	0	1707	−1	1527	0	1707	−1	2785	0
11	1707	−1	2071	M	2101	M	2104	+1	2989	+1
12	2071	M	2072	M	2104	+1	2105	+1	2990	−1
13	2072	M	2104	+1	2105	+1	2989	+1	2994	0
14	2104	+1	2994	0	2994	0	2990	−1	3267	+1, +1
15	3312	−1, infB	3312	−1, infB	3314	−1	2992	−1	3581	+1
16	3450	rplWD	3602	ftsY	3450	rplWD	2994	0	3797	+1,+1
17	3602	ftsY	3915	−1	3602	ftsY	3602	ftsY	3798	−1
18	3915	−1	4058	−1	4121	−1	3620	M	3803	−1, +1
19	4058	−1	4187	rpoC	4503	M	4503	M	4267	−1
20	4181	rpoB	4474	−1, +1	4504	M	4504	M, M	4475	+1
Genes	19		18		18		18		21
Errors	14(8)		12(3)		9(5)		6(2)		7(0)

Each segment, indexed by location (loc.) in kb from the published origin, overlaps zero, one or two genes in the protein table. Intergenic segments are classified as ‘0’. HT is indicated by ‘+1’ or by ‘M’ (if the gene is a mobile element). False positives are indicated by gene locus (if essential) or by ‘−1’ (if not). False positives account for total errors (bottom row) and the number of essential genes is given (in parentheses). The analysis is repeated for the 20 most anomalous segments with respect to (e) GC-divergence.

3. Results and discussion

3.1. Statistical analysis of compositional divergence in 12 bacterial species

Statistical analysis of 1 kb segments of the E. coli K12 sequence showed that DRA is more homogeneous than G + C. The same conclusion holds for the 11 other species in Table 1, as shown in Table 2, in so far as ERs at the 95- and 99.5-percentile points of the χ²-distributions are higher for GC-divergence than for DRA-divergence. This contrast holds in all 12 species despite the fact that mean GC-divergence is less than mean DRA-divergence in four of them. In every case, the χ² approximation of Equation (1) is defensible, as the MAD between the left and right sides of Equation (2) is <6%. But the variance of these results is wide and our sample is too small to argue that the contrast holds for all bacteria. By extending the analysis to a small, quasi-random sample of species, we have merely verified that the E. coli genome is not exceptional in this respect before exploring it more closely.

3.2. Phylogenetic analysis of extreme compositional anomalies in E. coli K12

The 20 segments having greatest DRA-divergences are characterized in the first pair (a) of data columns in Table 3. They overlap 19 genes of which 4 are mobile elements and 14 are false positives. The mobile elements include rhsD at location 256.³² (Location is the endpoint in kb from the start of the published sequence.) The one additional true positive, at location 2104, is the β-1,6-galactofuranosyltransferase gene wbbI (locus tag b2034) which leads transcription unit wbbIJK. This gene lacks a homolog in 283 completed genomes of other proteobacteria. The 14 false positives include eight essential genes: yaeT, mukB, rne, infB, rplW, rplD, ftsY and rpoB. The probability of finding one essential gene by chance in a sample of size 1 is 302/4639 ≈ 6.5%; but the binomial probability of finding eight or more essential genes in a sample of 19 is ∼10⁻⁵. Large DRA-divergence is thus a strong indicator of essentiality. On the other hand, if 17.6% of E. coli genes are foreign,⁷ the probability of finding five or more of these (four mobile elements plus one) by chance is roughly 10%, and large DRA-divergence is a weak indicator of HGT. Before attempting to reconcile this outcome with the conclusion drawn from compositional statistics, it seems important to consider some other mathematical discriminants as measures of DRA anomaly.

Delta-distance, introduced by Karlin et al. and defined above, has been used to establish a performance baseline as noted in the introduction. The 20 segments having greatest delta-distances from the global signature are characterized in the second pair (b) of data columns of Table 3. They overlap 18 genes of which 4 are mobile elements and 12 are false positives. An apparent contradiction arises in the 20th segment, ending 4474 kb from sequence start, which overlaps (by >300 bp each) two genes, yjgK (b4252) and yjgL (b4253), which encode hypothetical proteins. Classified as a conserved protein in EcoCyc, yjgK has homologs in S. enterica (E < 10⁻⁶⁵) and proteobacteria outside the gamma subdivision (E < 10⁻¹⁰); but yjgL is a true positive with no good alignments in other proteobacteria except three species of Shigella which we suppose to be descended from E. coli. The 12 false positives include three essential genes that were previously identified by large DRA-divergence. The probability of finding three or more essential genes in a random sample of size 18 is ∼11%.

Euclidean distance in 16-dimensional DRA space has been employed in several investigations. When Euclidean distance is computed in the 10-dimensional space of the non-redundant components of the strand-invariant DRA profile, the 20 most anomalous segments are listed in the third pair (c) of data columns in Table 3. They overlap 18 genes of which six are mobile elements and nine are false positives. Five false positives are essential genes that were previously identified by large DRA-divergence and the corresponding binomial P-value is ∼0.5%.

The species-specificity of a minimum Euclidean distance classifier was slightly enhanced by appropriately scaling the components.¹⁶ Applied to anomaly detection, a two-way classification problem, the effect of such scaling is to replace a spherical acceptance region with an ellipsoid. General principles of pattern recognition theory suggest that even greater specificity can be achieved by a quadratic discriminant classifier that inscribes more flexible boundaries in 10-dimensional DRA space. We constructed the anomaly detector using standard algorithms to form a quadratic discriminant³³ based on the logarithms of the strand-invariant DRA values (log-odds ratios). The 20 most anomalous segments, listed in the fourth pair (d) of data columns in Table 3, overlap 18 genes of which nine are mobile elements and six are false positives. Only two false positives are essential genes and the binomial P-value is 33%. Gene ftsY, which is essential for septation, is found anomalous by this and every discriminant considered previously. The true positives include adjacent, co-oriented genes wbbI and rfc and also yqeK (b2849) which was not discovered previously. Thus, the false positive rate of the most powerful discriminant is 33%, and 33% of false positives are essential. The 50 most anomalous segments identified by the quadratic discriminant contain 5 intergenic regions, 25 mobile elements and 8 essential genes including mukB, rplBWD, rfaK/waaU, ftsN and the two just noted. The binomial P-value for eight essential genes in 45 is <1%.

Last, the 20 highest ranking segments with respect to GC-divergence are analyzed. These segments, listed in the right-most pair (e) of columns in Table 3, overlap 21 genes of which five are mobile elements and six are false positives. Segment 4267 overlaps tyrB (b4054), a false positive and an RNA gene (b4621) which is not counted. Segment 3803 produces a contradiction, overlapping rfaB (false positive) and rfaS (true positive). (This is only the second such contradiction in all cases examined.) Segment 3798 contains false positive rfaZ in the AT-rich rfaQGPSBIJYZ-waaU transcription unit; but segment 3797 overlaps true positives waaU and rfaL that are oppositely oriented. The sole essential gene on this list is waaU (also known as rfaK) which has significant alignments in several proteobacteria outside the gamma subdivision. No essential genes are found among the six false positives. Large values of the GC-divergence thus predict HGT with the same false positive rate as the most powerful (quadratic) discriminant based on DRA-divergence but do not mistake essentiality for foreignness so often.

3.3. Compositional divergences in segments overlapping the essential genes

The 20 largest values of DRA-divergence in 1 kb segments of the E. coli K12 chromosome pointed to a significant number of essential gene candidates. Is DRA-divergence generally elevated in segments that contain essential genes? To answer this question, the mid-points of the coding sequences of essential gene candidates² are calculated, and each mid-point identifies a single segment. Mean divergences in these 302 ‘essential segments’ are shown in Table 4 and compared with corresponding genome-wide averages for all segments and for non-essential segments. Mean DRA-divergence is elevated, whereas the others are depressed, with reference to the third row where differences (n − e) are noted. The same pattern is followed by ER-95% and ER-99.5%. These ERs where higher for GC-divergence than for DRA-divergence, when all segments were considered, for all 12 species in Table 2; but this contrast disappears for the essential segments of E. coli.

Table 4.

Comparing essential segments of the E. coli sequence to all segments and to non-essential segments

Segments	Mean divergence			ER 95%			ER 99.5%
	Total	DRA	G + C	Total	DRA	G + C	Total	DRA	G + C
All segments	27.1	9.8	18.4	48.0	24.3	46.4	33.5	10.2	34.0
Non-essential (n)	27.6	9.7	19.0	48.2	23.7	47.2	34.1	9.8	35.0
Essential (e)	19.9	12.1	8.5	45.5	34.1	33.1	25.8	18.4	18.7
n − e	8.6	−2.4	10.5	2.7	−10.4	14.1	8.3	−8.6	16.3
	MSR			(MSR − 0.5)/SD			P-value
Essential	0.462	0.559	0.400	−2.29	+3.55	−6.02	0.011	0.0002	<10−9

Mean values and ERs of the divergence statistics are computed as in Table 2. The MSR of the divergence in essential segments is tested for significant departure from expected value (0.5) in the bottom row.

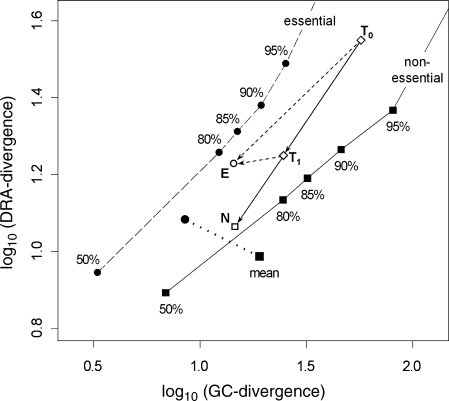
The statistical significance of the differences (n − e) in Table 4 is assessed by a non-parametric test procedure. All segments are ranked according to divergence. Under the null hypothesis, essentiality does not influence divergence, and hence the essential segments are uniformly distributed from rank 1 to 4639. Then the mean rank of essential segments is divided by 4639 to obtain the mean scaled rank (MSR) which is nearly normal with expected value equal to 1/2 and standard deviation (SD) = [(1/12)/302]^1/2 = 0.0166. The last row of Table 4 shows that MSR > 0.5 for DRA-divergence but <0.5 for the other two components. These differences are expressed in SDs from expected value and the normal P-values for one-sided tests are given. On this basis, DRA-divergence is significantly elevated, but GC-divergence is very significantly depressed, in the essential sample. This conclusion is reinforced by Fig. 3, which portrays the distributions of the divergence components on logarithmic axes. The non-essential sample is described by solid squares that mark the means, medians and labeled percentile points of the empirical distributions (not referred to χ²), whereas the essential sample is described by solid circles. As each circle lies above and to the left of the corresponding square, the essential sample distribution is evidently shifted lower with respect to GC-divergence, but higher with respect to DRA-divergence.

Figure 3.

Comparing observed distributions of compositional divergence components in segments of the E. coli K12 genome. Means, medians, and indicated percentile points are plotted for (circles) essential and (squares) non-essential segments. Arrows depict the inferred time course of amelioration as explained in Section 3.4.

3.4. Amelioration of compositional divergences

Proceeding from the initial proposition that higher order features ameliorate more rapidly and uniformly than lower order features, we predicted that bacterial genomes are more homogeneous with respect to (second order) DRA than with respect to (first order) G + C when viewed through 1 kb windows. After statistical analysis supported the prediction, we expected to detect recent HGT in segments of the E. coli K12 sequence that are most anomalous with respect to DRA. Instead, large DRA-divergence was a better indicator of essentiality. Can these results be reconciled with the initial proposition?

Lawrence and Ochman⁵ modeled the amelioration of G + C proportions at the three codon positions in accordance with the theory of mutation-selection equilibria.³⁴ Their assumption of constant substitution rates was reflected in the exponential time course of amelioration toward the equilibrium proportion. Amelioration rates are typically lower at the first two positions where mutations are more likely to degrade essential functionality. When the G + C proportions are averaged over three positions in a coding sequence, the average proportion, denoted P, approaches the gross genomic G + C proportion, Q. Then the logarithm of the squared difference D = (P − Q)² declines in three quasi-linear stages. After sufficiently long time, its rate of decrease falls to the lowest position-specific amelioration rate. GC-divergence, as derived above, evolves this way because

Relatively ancient coding sequences will have ameliorated to the extent that further reduction of GC-divergence is retarded by selective forces acting on the least neutral codon position.

DRA ratios approach species-specific constants in a manner that is formally analogous to the law of mass action by which the reversible reaction X + Y ↔ XY gives rise to chemical equilibrium with

The [bracketed] concentrations are analogous to the normalized frequencies and each whole genome DRA ratio plays the role of a formation constant. We suppose this analogy would be illuminated by a mathematical extension of the theory of mutation-selection equilibrium that has not been attempted. DRA-divergence is a weighted sum of squared differences between current values of the ratios and their ‘constant’ limits. If each term in the sum follows an exponential time course then DRA-divergence will obey the general rule stated above, ultimately declining at the rate of its least selection-neutral term; but now the minimum is taken from 10 terms instead of three. In old, essential coding sequences, this minimum may be extremely small, and DRA-divergence will decline more slowly than GC-divergence.

This argument is sketched on Fig. 3 where arrows extend from point T₀, representing the divergence coordinates at some time in the past, to points E (essential) and N (non-essential) with the same GC-divergence. In extreme cases, at least one DRA ratio resists mutational pressure so strongly that divergence drops to a floor level and goes no lower. This possibility is represented on Fig. 3 by the arrow branching to point E from T₁ that is attained after the less resistant ratios reach equilibrium. Extending this branch much farther will produce a coding sequence that closely matches gross genomic G + C but still exceeds the median of DRA-divergence. Gene ftsY fits this description in so far as its segment (3602) has small GC-divergence (X*₁=0.42) and its large DRA-divergence (X*₂=61.8) is half accounted for by three terms (for dinucleotides AT, TA and AG + CT).

Thus, the simplest explanation of our findings is that G + C typically ameliorates more rapidly than DRA, especially in older and essential parts of the genome, contrary to initial proposition. Finding DRA more homogeneous than G + C appears to contradict this explanation only if it is assumed DRA and G + C are equally divergent between donors and recipients of HT. In this re-interpretation of the data, we argue that the smaller intra-genomic range of DRA merely reflects its smaller inter-genomic range. For example, gross G + C fractions in E. coli and S. enterica differ by ∼2%, and segments of E. coli exhibit 19.9 average GC-divergence from the G + C fraction of S. enterica; but the average DRA-divergence relative to the genomic signature of S. enterica is only 12.4. These genomes appear to have diverged more rapidly in G + C than DRA.

3.5. Predicting essential genes based on dinucleotide composition

DRA-divergence was introduced to assess the statistical significance of local deviations from the genomic signature. Other discriminants found fewer essential genes among the 20 most anomalous segments, but none found as few as divergence with respect to G + C, which is not a reliable indicator of horizontal transmission.³⁵ It remains to be explained how HGT detection methods based on higher order signatures can overcome the failure mode predicted by the implication of the neutral theory. The difficulty is implicitly acknowledged when genes belonging to certain functional classes, such as ribosomal proteins, are ‘manually removed’⁶ from lists of HGT candidates produced by higher order methods.³ Our negative result highlights the challenge of reconciling such methods, which have advanced without explicitly addressing how essential genes impact performance, with principles of molecular evolution. Although we lack an a priori basis for extrapolating our result to higher order, it is evident that the performance level of a method based on DRA is an easy benchmark to exceed. Approaching the problem from the opposite perspective, it could be useful to screen out essential genes before proceeding with the search for HGT. Our analysis may suggest that DRA-divergence could serve this purpose. When all 1 kb segments of the E. coli K12 sequence are ranked by DRA-divergence, 42 essential segments are among the 302 highest ranks. The expected number is only (302)²/4639 ≈ 20 and the binomial P-value is ∼10⁻⁶. But the success rate of 42/302 ≈ 14% seems disappointing even though it is highly significant.

Various refinements could raise the success rate. The divergence quotient (DRA divided by GC) could be a stronger indicator of essentiality. A sliding window should improve the compositional contrast between essential and non-essential segments. (Our analysis used fixed length, non-overlapping windows to simplify statistical comparisons.) Essential coding sequences could become more detectable based on the 9 degrees of freedom divergence statistic (denoted by X₂ in Section 2) computed from the 16 strand-dependent odds ratios.

These suggestions aside, we doubt that any single composition-based method can reliably predict essential genes. DRA ratios are determined by the amino acid sequence and SCU. Our methods and results do not illuminate how much of the central tendency of DRA is explained by species-specific codon usage patterns nor how much of the variance is driven by differing expression levels that are independent of essentiality. Predicting essential genes may be as difficult as detecting HTs, but progress can be measured more directly, as new experimental methods identify essential genes without revealing their evolutionary histories.

Funding

This research was supported by the MKE (Ministry of Knowledge Economy), Korea, under the ITFSIP supervised by the IITA.