Neural Substrate of Modified and Unmodified Pathways for Learning in Monkey Vestibuloocular Reflex

Abstract

To understand how the brain learns, we need to identify the full neural circuit for a behavior; characterize how neural responses in the circuit change during behavioral learning; and understand the nature, location, and control of the cellular changes that are responsible for learning. This goal seems attainable for the vestibuloocular reflex (VOR), where the neural circuit basis for learning is already partially understood. The current hypothesis for VOR learning postulates cellular changes in the cerebellar cortex and the vestibular nucleus. It suggests that the brain stem contains two parallel pathways that have been modeled on the basis of extensive biological data as unmodified and modified VOR pathways with frequency-dependent internal gains and different time delays. We now show a correspondence between the responses of different groups of neurons in the vestibular nucleus and the signals emanating from the two pathways in the model. Floccular target neurons (FTNs) and position-vestibular-pause neurons (PVPs) were identified by their discharge during eye movements and by the presence or absence of inhibition by floccular stimulation. FTNs had response gains and phases that coincided with predictions for pathways that are modified in association with learning, whereas PVPs had responses in agreement with predictions for the unmodified pathways. The quantitative agreement of prior model predictions and new data supports the identity of FTNs and PVPs as brain stem interneurons in the modified and unmodified VOR pathways. Other aspects of the data make predictions about how vestibular inputs are transformed as they pass through the two pathways.

INTRODUCTION

One of the major questions in neuroscience is how groups of neurons work together to generate behavioral learning. We have many descriptions of behavioral learning and its representation in the responses of some neurons, as well as a detailed understanding of cellular and molecular events that are available in neurons to cause changes in synaptic and cellular function. Arguably, however, it has not yet been possible to link conclusively from synaptic plasticity to changes in neural circuit function that mediate changes in behavior, even though there are a few examples of impressive correlations between synaptic plasticity and behavioral learning (e.g., de Zeeuw et al. 1998; Jirenhed et al. 2007; Medina et al. 2000). Of all behaviors that have been studied, the vestibuloocular reflex (VOR) remains one of the most promising for revealing the neural and cellular basis for behavioral learning.

Normally, the VOR responds rapidly and accurately to compensate for head turns and allow the eyes to remain stationary with respect to the stationary visual surroundings. A variety of optical means have been used to increase, decrease, or even reverse the eye movements of the VOR (e.g., Gonshor and Melvill Jones 1976; Miles and Fuller 1974). In each instance, the changes in eye velocity are both learned and remembered in the sense that they are expressed in darkness even without the optical devices used to cause learning. The changes are adaptive—they always reduce the motion of images across the retina during head turns in the learning conditions.

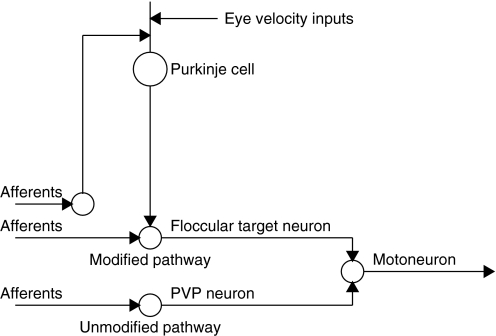
Prior studies have provided a plausible and testable hypothesis for the neural circuits that mediate the VOR and the sites of cellular changes that cause learning in the VOR (Blazquez et al. 2006; Lisberger 1994). The basic circuit is illustrated in Fig. 1. Vestibular inputs are transmitted by primary afferents to two kinds of VOR interneurons as well as to cerebellar projecting neurons in the vestibular nucleus. In turn, the VOR interneurons project to extraocular motoneurons while the cerebellar inputs are processed and returned over Purkinje cells to one of the VOR interneurons, known as “floccular target neurons” or FTNs (Lisberger et al. 1994a). The floccular complex also receives corollary discharge feedback reporting ongoing eye velocity as well as some visual inputs reporting visual image motion (Miles and Fuller 1975; Stone and Lisberger 1990).

FIG. 1.

Schematic diagram showing the current hypothesis for the organization of the modified and unmodified vestibuloocular reflex (VOR) pathways. The Purkinje cell is in the cerebellar floccular complex. The floccular target neuron (FTN), position-vestibular-pause (PVP) neuron, and floccular projecting neuron (not labeled as such) are in the vestibular nucleus. The motoneuron is in the abducens nucleus. In reality, PVP neurons and FTNs make excitatory and inhibitory connections on neurons in the contralateral and ipsilateral abducens nuclei, respectively.

In the current hypothesis for motor learning in the VOR, one of the brain stem pathways is not modified in association with learning and uses “position-vestibular-pause” or PVP neurons as its interneuron. The other brain stem pathway contains a locus of modifications that drive learning and uses “floccular target neurons” or FTNs as its brain stem interneuron (Lisberger et al. 1994b). In agreement with the cerebellar learning hypothesis (Albus 1971; Ito 1970; Marr 1969), an additional locus of learning is postulated to be in the vestibular pathways to floccular Purkinje cells (Lisberger et al. 1994c; Miles et al. 1980). Available data do not precisely localize the sites of molecular plasticity, but the current hypothesis holds that plasticity occurs in the vestibular inputs to FTNs and at the synapse between vestibular parallel fibers and Purkinje cells.

Current knowledge of the neural circuit basis for learning in the VOR is based on recording the responses of neurons in the VOR circuit before and after learning, in primates, and then using computational modeling to infer the loci of synaptic or cellular plasticity (Blazquez et al. 2006; Lisberger et al. 1994b,c). Our recent work has provided a new angle on the same question: two of our recent studies have used sinusoidal vestibular stimuli over a frequency range from 0.5 to 50 Hz and have studied the VOR before and after learning as well as the frequency responses of vestibular afferents and abducens neurons during the normal VOR. We used computer modeling to assemble the measures of behavior and neural responses into a model that made quantitative predictions about the response gain and phase shift of interneurons in the modified and unmodified VOR pathways as a function of stimulus frequency (Ramachandran and Lisberger 2005, 2006). The present study shows that during the normal VOR, FTNs and PVPs had response gains and phases in agreement with predictions for pathways that are and are not modified in association with learning. This finding provides an independent line of evidence in support of the assignment of these two brain stem interneurons to their respective pathways. We also use data obtained by varying the stimulus frequency to make some suggestions about how neural signals might be processed as they pass through each of the two brain stem VOR pathways.

METHODS

Data were collected from two male rhesus macaque monkeys (Macaca mulatta) that had been prepared for chronic experiments using techniques described in detail previously (Lisberger et al. 1994a; Ramachandran and Lisberger 2005, 2006). The monkeys had the VOR performance described in our earlier report (Ramachandran and Lisberger 2005). All procedures were approved by the Institutional Animal Care and Use Committee at UCSF and were in strict compliance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals.

Briefly, three surgical procedures were conducted using sterile procedure with isoflurane anesthesia to prepare monkeys for physiological experiments. First, we secured a stainless steel head post to the monkey's skull using materials developed for human orthopedic surgery: 5-mm-wide orthopedic strips and 8-mm-long screws, both made of titanium, as well as dental acrylic. We used the head post to fix the monkey's head to the chair during experiments, so that sinusoidal head velocity inputs could be imposed. Second, we sutured a 16-mm-diameter coil of extremely lightweight, Teflon-coated, stainless steel wire to the sclera (Ramachandran and Lisberger 2005) using techniques derived from human ophthalmologic surgery. Once they had recovered from the second surgery, monkeys were conditioned to head restraint and trained to fixate 0.1° spots of light for fluid reinforcement. In a final surgery, we trephined a hole in the skull and implanted a recording cylinder aimed at the vestibular nucleus (Lisberger et al. 1994a). Analgesics were administered for 3–4 days after surgery and we monitored the monkeys carefully to ensure that they were not experiencing pain or distress.

Vestibular stimulation

The physical setup for transmitting high-frequencies of vestibular stimulation from a turntable to the monkey's head has been described in detail previously (Ramachandran and Lisberger 2005, 2006). Briefly, monkeys were seated comfortably with their heads fixed to the ceiling of a specially-reinforced primate chair. The chair was bolted rigidly to a servo-controlled turntable (Contraves Goertz) and the field coils for monitoring eye position were secured to the floor so that they did not impose a load for the turntable. To assess the exact head stimulus applied to the vestibular apparatus, and the real eye movement response, we used two coils to measure the monkey's eye and head position with respect to the magnetic field (E_F and H_F). We differentiated the position output from each coil with analog circuits and then used equations derived previously (Ramachandran and Lisberger 2005) to compute the two parameters we needed to measure: eye velocity with respect to the head (Ė_H = Ė_F − Ḣ_F) and head velocity with respect to the world (Ḣ_W = Ḣ_F).

Data acquisition

In monkeys with normal VOR gains, glass-coated platinum–iridium electrodes were lowered into the brain stem to record from neurons in the vestibular nucleus. Voltage waveforms from the electrode were amplified conventionally and band-pass filtered, usually between 400 Hz and 8 kHz. We identified the relevant portion of the vestibular nucleus in relation to the location of the right abducens nucleus, which was distinguished by the characteristic singing activity associated with eye movements toward the right (Fuchs and Luschei 1970). In both monkeys, we had implanted a bipolar stimulating electrode (Rhodes Medical Instruments, Woodland Hills, CA) chronically in the floccular complex of the cerebellum, at a site where stimulation with single pulses or brief trains caused smooth eye velocity toward the side of stimulation with a latency of about 10 ms. Methods for implanting the stimulation electrode were described in detail before (Lisberger et al. 1994a). Briefly, we introduced a stimulating electrode through a small hole in the skull that had been prepared during sterile surgery and lowered the electrode under stereotaxic control until stimulation induced smooth eye movements toward the side of recording with a latency of about 10 ms. We then sedated the monkey, cemented the electrode in place, and soldered the leads to a connector that was cemented to the implant. During subsequent recording experiments, floccular stimulation was provided by biphasic, bipolar stimuli where each phase of the pulse had a duration of 100 μs and amplitude of 200 μA. We delivered single shocks to the floccular complex while we recorded from neurons in the vestibular nucleus to identify them according to whether they showed a clear inhibition at monosynaptic latencies.

We triggered action potentials with a dual-window discriminator (BAK Electronics) and recorded the time of the discriminator's recognition pulses at a 10-μs resolution. We also recorded the voltage waveforms from the electrode continuously at 25 or 40 kHz to allow off-line verification of the isolation of single units and, when deemed necessary, retriggering with an operator-controlled software time-window discriminator. After initial characterization according to their responses during smooth-pursuit eye movement and cancellation of the VOR with vestibular oscillation at 0.5 Hz, ±10°, both groups of neurons were studied during fixation of a stationary target with passive sinusoidal head oscillation at frequencies ranging from 0.5 to 50 Hz and head velocities of approximately ±15°/s. During recordings, monkeys were rewarded for keeping their eyes within 2° of the target.

Experiments were controlled by a custom real-time data-acquisition program that ran under Windows NT using the real-time kernel RTX (Ardence, Waltham, MA). The signals from the two coils were differentiated in real time by an analog differentiator with an upper-frequency cutoff at 100 Hz. As a side effect of its filtering properties, the analog differentiator also changed the gain and phase of the underlying signal at higher frequencies. We assessed these changes with pure sine-wave inputs and compensated for them by correcting the amplitude and phase of the filtered signals during data analysis. Signals related to coil position and velocity, as well as the head velocity signal from a tachometer on the shaft of the turntable, were sampled at 500 Hz per channel and stored on hard disk for later analysis.

Data analysis

The initial analysis of neural data involved estimating, for each neuron and each stimulus frequency, the sensitivity to head velocity and the phase shift between head velocity and firing rate. We used one of several analysis methods that were explained in detail and evaluated in our previous report (Ramachandran and Lisberger 2006). Method 1 allows every interspike interval (ISI) to contribute to the analysis and eliminates all averaging. For each cycle of stimulation and pair of spikes, we calculated firing rate as the inverse of ISI and plotted the firing rate for each interval as a function of the time of the center of the ISI relative to the start of the cycle (Angelaki and Dickman 2000), superimposing the responses to all stimulus cycles. We then fitted the envelope of firing rate and the head velocity for each stimulus frequency with a sine wave. We computed the sensitivity to head velocity as the ratio of the amplitudes of the sine waves and the phase shift from the temporal difference between the curves that fitted firing rate and head velocity. Method 2 relies on averages of firing rate accumulated in binned histograms. We divided each cycle of the stimulus into 16 equal-duration bins, counted the number of spikes in each bin, averaged across many cycles, and divided by the bin width to obtain estimates of firing rate. We then subjected the resulting histogram and the associated average of head velocity to a fast Fourier transform to estimate the amplitude and phase of the fundamental components of firing rate and head velocity. Method 3 estimated phase (but not amplitude) of the neural response by computing the value of phase that represented the center of mass of the spikes that occurred during the full set of stimulus cycles.

We found excellent agreement between the numbers provided by the three analysis methods whenever the distribution of spikes through a stimulus cycle allowed a given analysis to be used. When the neuron under study did not show phase locking, so that spikes occurred asynchronously through the stimulus cycle (e.g., Fig. 3, A–C), we used the numbers from the firing rate method (method 1) to estimate the sensitivity to head velocity and phase difference between firing rate and head velocity. When the afferent showed phase locking, we estimated phase by the center-of-mass method (method 3) and we did not attempt to estimate sensitivity to head velocity. We used the analysis based on binned histograms (method 2) only to validate the other methods and as a way of screening the data visually to determine whether the responses were phase locked or asynchronous, indicating whether the data should be analyzed with method 1 or method 3. Additional controls relevant to the analysis procedures appear in our previous study (Ramachandran and Lisberger 2006).

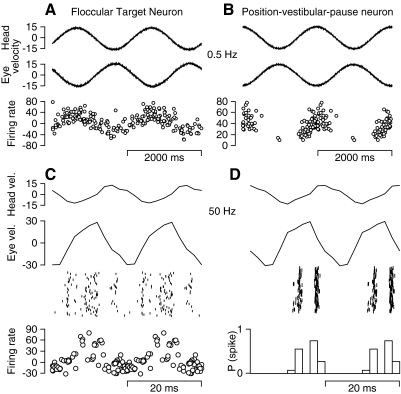
FIG. 3.

Responses of a typical FTN and PVP neuron during the VOR induced by sinusoidal whole body oscillation at low and high frequencies. The left and right columns show responses of an FTN and a PVP. A and B: oscillation at 0.5 Hz, ±15°/s. From top to bottom, the traces are head velocity, eye velocity, and firing rate. In the firing rate traces, each symbol plots the inverse of one interspike interval (ISI) as a function of where the middle of the interval falls on the stimulus cycle. Only one of every 10 symbols is shown to avoid an undistinguishable blob of points. C and D: oscillation at 50 Hz, ±15°/s. From top to bottom, the top 3 traces are head velocity, eye velocity, and a raster showing the responses on single cycles. In C, the bottom trace represents firing rate calculated in the same way as in A and B. In D, the bottom trace shows a histogram created by dividing the stimulus cycle into 16 bins, counting the spikes within each bin, and converting the counts to probabilities of spiking in each bin. A single cycle has been repeated in each panel to facilitate viewing of periodic events.

RESULTS

Identification of FTNs and PVP neurons

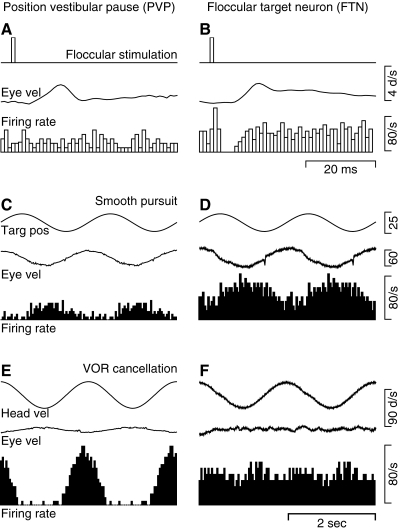
Position-vestibular-pause neurons (PVPs) showed a consistent relationship between steady firing rate and eye position (see later section) and paused during saccadic eye movements (Tomlinson and Robinson 1984). PVPs were not inhibited by stimulation of the floccular complex (Fig. 2A ) and showed weaker modulation of firing rate during pursuit with the head stationary (Fig. 2C) than during cancellation of the VOR with sinusoidal stimulation at 0.5 Hz (Fig. 2E): the mean sensitivity to eye and head velocity under these two behavioral conditions was 0.35 versus 1.05 spikes·s⁻¹ per deg·s⁻¹. Of our sample of 71 PVPs, 48 showed increased firing for eye motion away from the side of recording and head motion toward the side of recording; 23 showed increases for eye motion toward the side of recording and head motion away from the side of recording.

FIG. 2.

Response properties that define FTNs and PVPs. The left and right columns show responses of a PVP and an FTN. A and B: response to stimulation in the cerebellar floccular complex with single shocks. From top to bottom, the traces show the time of the stimulus, the average eye velocity evoked by the stimulation, and a histogram of the responses aligned on the time of electrical stimulation and averaged across 100 repetitions of the floccular stimulation. C and D: response during smooth-pursuit eye movements evoked by sinusoidal target motion at 0.5 Hz, ±10° with the head stationary. From top to bottom, the traces are target position, eye velocity, and a histogram of the neural responses accumulated by averaging across 20 cycles of pursuit. E and F: response during cancellation of the VOR induced by having the monkey track a target that moved exactly with him during sinusoidal head oscillation at 0.5 Hz, ±10°. From top to bottom, the traces are head velocity, eye velocity, and a histogram accumulated by averaging across 20 cycles of vestibular stimulation. A single cycle has been repeated in C–F to facilitate viewing of periodic events.

Floccular target neurons (FTNs) were identified by the clear pause in firing at monosynaptic latencies after application of single shocks in the cerebellar floccular complex (Fig. 2B). Across our population of 53 FTNs, the mean latency of the inhibition was 1.44 ms (range 1.0–2.5 ms). FTNs typically responded more strongly when the monkey used smooth-pursuit eye movements to track a target that moved sinusoidally (Fig. 2D) than when the monkey fixated a target that moved exactly with him and cancelled his VOR during sinusoidal vestibular stimulation at 0.5 Hz (Fig. 2F): the mean sensitivity to eye and head velocity under these two conditions was 0.90 versus 0.59 spikes·s⁻¹ per deg·s⁻¹. In agreement with Lisberger et al. (1994a), the saccadic responses of FTNs were quite varied and could comprise pauses, bursts, or no response at all. Of our sample of 53 FTNs, 33 showed increased firing for eye motion away from the side of recording during pursuit and head motion toward the side of recording during VOR cancellation; 20 showed increases for eye and head motion toward the side of recording.

Frequency response of FTNs and PVPs during the VOR

For each FTN and PVP we isolated, we recorded responses during the VOR induced by oscillation of head velocity at frequencies between 0.5 and 50 Hz, with the amplitude of head velocity held constant at approximately ±15°/s. Monkeys fixated a stationary spot to minimize saccadic eye movements. The responses of FTNs modulated strongly across the full range of frequencies, although the phase relationship between firing rate and head velocity was very different at 0.5 Hz (Fig. 3A) versus 50 Hz (Fig. 3C). The firing rates in Fig. 3 show what remains after using procedures outlined in our previous study (Ramachandran and Lisberger 2006) to remove the firing rate that was related to eye position. Removal of the eye position component has some impact on the gain and phase of the responses to low frequencies of vestibular oscillation because of the larger peak-to-peak excursion of head and eye position, but has little or no effect on the high-frequency data because of the very small amplitude of the position excursions with a stimulus velocity excursion of ±15°/s. In practice, the subtraction of the eye position component caused some of the traces to show negative values of firing rate (e.g., the FTN in Fig. 3), but shifts in the DC firing rate do not alter the sensitivity to head velocity, which is based on the strength of firing rate modulation. The responses of PVP neurons also modulated strongly across the full range of frequencies. The example illustrated on the right side of Fig. 3 exhibited cutoff at zero firing rate during the VOR at 0.5 Hz (Fig. 3B) and was strongly phase locked to the sinusoidal head velocity stimulus during the VOR at 50 Hz (Fig. 3D).

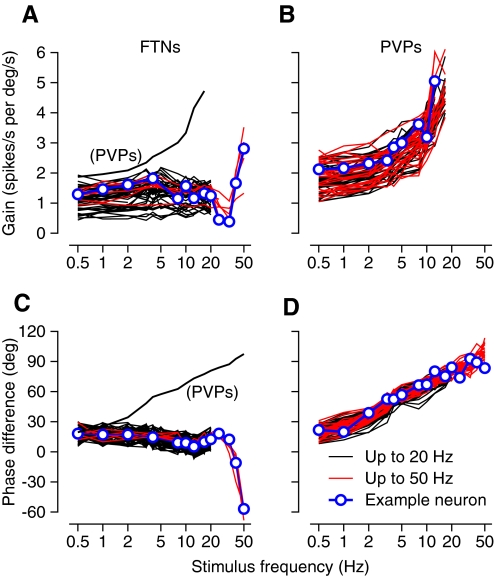
The sensitivity to head velocity (or response gain) and the phase difference between firing rate and head velocity were remarkably consistent within the FTNs and the PVPs, but showed large differences between the two groups. For FTNs, the gain defined in spikes·s⁻¹ per deg·s⁻¹ was quite flat across the frequency range from 0.5 to 20 Hz and then, for a small group studied at higher frequencies, showed a brief drop for vestibular oscillation at 25 and 33 Hz followed by a steep increase at 40 and 50 Hz (Fig. 4 A). Firing rate led head velocity by about 20° across the frequency range from 0.5 to 20 Hz and then showed a slight increase followed by an impressive phase lag that appeared at the highest frequencies of vestibular oscillation (Fig. 4C). The majority of our FTNs were studied only at frequencies ≤25 Hz (black traces). Still, the excellent agreement in the low-frequency responses of these and the six FTNs studied at frequencies ≤50 Hz (red traces) suggests that the data for the latter neurons are a good index of the high-frequency responses of the full population. For PVPs, the sensitivity to head velocity was higher than that for FTNs during the VOR at the lowest frequencies of vestibular stimulation. Sensitivity then increased progressively as frequency was increased (Fig. 4B). The firing rate of PVPs led head velocity by almost 30° for vestibular stimulation at 0.5 Hz and the phase lead increased steadily as a function of the frequency of vestibular oscillation (Fig. 4D). To emphasize the differences in the responses of the two groups of interneurons, we have plotted the averages of gain and phase of PVPs as a function of frequency as thin black curves in Fig. 4, A and C.

FIG. 4.

Gain and phase of responses of FTNs and PVPs during the VOR for stimulus frequencies over the range from 0.5 to 50 Hz. A and B: gain vs. stimulus frequency. C and D: the phase shift between firing rate and head velocity as a function of frequency, with positive values indicating that firing rate leads head velocity. Blue symbols and lines highlight data for single-example neurons. Red and black curves show data for neurons studied at frequencies from 0.5 to 50 Hz vs. those studied only for frequencies ≤20 Hz. The small number of FTNs studied at the highest frequencies is explained by the fact that one of our monkeys lacked a working floccular stimulating electrode for much of the time he was involved in brain stem recordings, whereas the other monkey had a stimulating electrode but was involved in experiments before we could retain isolation of FTNs during oscillation at 25–50 Hz. Thin black curves in A and C show the averages for the sample of PVPs; average gain is shown only for frequencies ≤12.5 Hz because many of the PVPs showed phase locking at higher frequencies.

We recorded neural responses during head rotation with a fixation point to induce the monkey to sit quietly as he worked for fluid rewards, increasing the likelihood that we would obtain enough quality data in the time we could retain isolation of neural signals. Even though visual motion was present during the recordings, two facts make us confident that the details of the neural responses at high frequencies reflect vestibular rather than visual inputs. First, visual motion neurons in extrastriate visual area MT do not respond periodically to oscillations of the visual stimulus at frequencies >10 Hz (Lisberger and Movshon 1999), meaning that no viable visual motion inputs are generated at higher frequencies. Second, we will show in the following text that the phase shifts of FTNs are compatible with time delays of 9 ms from the responses of vestibular afferents, not the 100-ms delays expected for visual inputs.

Phase-locking behavior of FTNs and PVPs at high stimulus frequencies

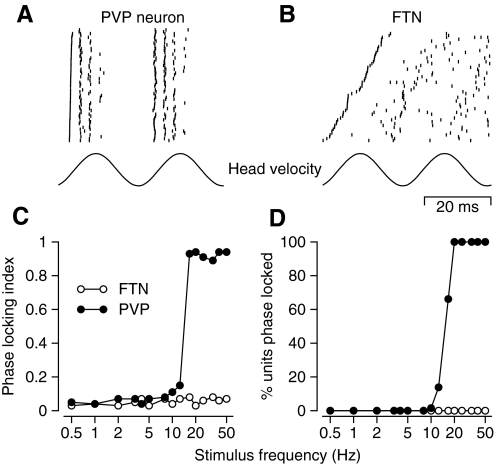
Quantitative analysis confirmed the examples of phase-locking behavior in Fig. 3, C and D: PVP neurons showed consistent phase locking during the VOR induced by the higher frequencies of vestibular oscillation whereas FTNs did not. To quantify phase locking, we performed the same analysis we had developed for analysis of phase-locking behavior in vestibular primary afferents and abducens neurons (Ramachandran and Lisberger 2006). For each neuron and each frequency of oscillation, we cut the continuous sequence of sinusoidal head velocities into single cycles and constructed rasters of the spike responses. Instead of keeping the cycles ordered according to time in the sequence of stimuli, we ordered them according to the time of the first spike during each cycle. Phase-locked responses had the appearance shown in Fig. 5 A for a recording from a typical PVP during vestibular oscillation at 20 Hz. The first spike in each cycle is synchronized, giving the appearance of a nearly vertical line of spikes, and the subsequent spikes in the two successive cycles remain quite well aligned with each other. Responses that were not phase locked had the appearance shown in Fig. 5B for a recording from a typical FTN during vestibular stimulation at the same frequency of 20 Hz. Here, the times of the first spikes are distributed across a wide range of times and the earliest of the second spikes occurs at about the time of the latest of the first spikes, meaning that the spikes form a rate-modulated train, seemingly oblivious to timing within the cycle.

FIG. 5.

Phase-locking behavior of FTNs and PVPs at high frequencies of sinusoidal oscillation. A and B: rasters of spike responses on many cycles of VOR induced by oscillation at 20 Hz for an example PVP (A) and FTN (B). Bottom trace shows angular head velocity. The lines of the rasters are ordered from bottom to top according to the time of occurrence of the first spike in each cycle. Two consecutive cycles are shown to facilitate viewing of periodic events, but each cycle in the data contributed a first cycle to the analysis. C: phase-locking index as a function of stimulus frequency for one example neuron from each group. D: the percentage of each interneuron population showing phase locking as a function of stimulus frequency. In C and D, open and filled symbols show data for FTNs and PVPs.

For each neuron and frequency of vestibular oscillation, we characterized the degree of phase locking by calculating the phase locking index (PLI) as

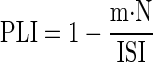(1)

where m is the slope of the relationship between the time of the first spike and the line number in the ordered rasters at the top of Fig. 5, N is the number of lines in the raster, and ISI is the mean interspike interval for spontaneous firing. This analysis computes the fraction of an average ISI covered by the range of times of the first spike in rasters like those of Fig. 5. Phase-locking behavior causes PLI to be approximately one, whereas a rate-modulated spike train will have PLI of approximately zero.

Plots of PLI as a function of frequency for representative FTNs and PVPs (Fig. 5C) show that the FTN (open symbols) continued to exhibit a rate-modulated spike train for stimulus frequencies ≤50 Hz, whereas the PVP (filled symbols) transitioned to phase-locking behavior just below 20 Hz. Across the full population (Fig. 5D), phase locking was very rare in FTNs for any frequency of vestibular oscillation and in PVPs at stimulus frequencies <10 Hz. At higher frequencies, PVP neurons transitioned abruptly to phase-locking behavior, so that all showed phase locking at frequencies of vestibular oscillation of ≥20 Hz.

Responses of FTNs and PVPs during fixation at different positions

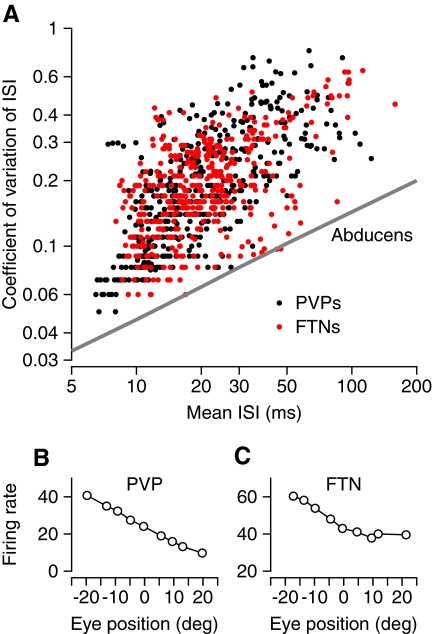
Our prior report documented the relationships between firing rate and steady eye position in FTNs and PVPs, and their subtle differences (Lisberger et al. 1994a). As shown in Fig. 6 B, PVPs showed linear rate-position curves. In contrast, FTNs tended to have a knee in their rate-position curves so that firing rate increased as a function of eye position only when the eye was positioned in the neuron's on direction (Fig. 6C). FTNs and PVPs have more irregular spike trains than do motoneurons, which also enjoy a relationship between firing rate and steady eye position. Figure 6A assembles data for many fixations of duration ≥600 ms across all the PVPs and FTNs we recorded. Each point was obtained from a single fixation and plots the coefficient of variation (CV) of the ISI as a function of the mean of the ISIs. The points form an elongated cluster, indicating a relationship between CV and ISI like that found for individual vestibular primary afferents (Goldberg et al. 1984) and for the population of abducens neurons (Ramachandran and Lisberger 2006). The spontaneous firing rates of FTNs (red symbols) and PVPs (black symbols) have statistics that are similar between the two groups, but quite different from those of abducens neurons (line taken from Fig. 6B of Ramachandran and Lisberger 2006). Unfortunately, it is not possible to make the same comparison with the spontaneous firing of vestibular primary afferents. Even though each individual afferent has a CV that is positively correlated with the mean ISI, the population nonetheless covers a wide range of values of CV even after normalization to a firing rate of 100 Hz (Goldberg et al. 1984). If plotted in Fig. 6, the distribution would not be meaningful.

FIG. 6.

Analysis of discharge of FTNs and PVPs during steady fixation with the head stationary. A: plot of coefficient of variation vs. mean ISI, where each symbol shows data from a single 600-ms interval of fixation. Data are pooled across the full sample of interneurons. Red and black symbols show data from FTNs and PVPs, respectively. The oblique line represents results of the same analysis on abducens neurons, taken from Fig. 6B of Ramachandran and Lisberger (2006). B and C: plot of average firing rate vs. eye position for an example PVP (B) and FTN (C).

DISCUSSION

We have conducted a detailed analysis of the neurophysiology of the VOR pathways in behaving primates to lay the groundwork for bridging from cellular plasticity mechanisms to learning at a systems level. Our goal is to elucidate this broad issue by asking detailed questions about the nature and mechanisms of signal processing within the VOR circuits. The present findings make progress by providing new evidence confirming the identity of the interneurons in the VOR pathways that do and do not undergo learning. Our analyses also make some suggestions about the location of time delays in the modified VOR pathways, the nature of the vestibular inputs to the two brain stem VOR pathways, and the downstream weighting of signals transmitted from FTNs and PVPs to motoneurons. Finally, our data raise questions about how continuous signals are processed in neurons that phase lock to a stimulus and about the potential functional importance of changes in discharge regularity along the VOR pathways. In this section, we treat each of these issues in turn.

Identity of interneurons in modified and unmodified brain stem VOR pathways

Vestibular inputs for the VOR seem to be processed in two sets of parallel pathways, one that is and one that is not modified in association with adaptive modification of the VOR (Lisberger 1984, 1994; Lisberger and Pavelko 1986; Ramachandran and Lisberger 2005). Prior evidence suggested that the unmodified pathway has a shorter latency from head turn to eye movement and uses PVPs as an interneuron and that the modified pathway has a longer latency and uses FTNs as an interneuron (Lisberger 1994). Importantly, changes in the gain of the VOR cause only small changes in the magnitude of PVP responses during the VOR, but large changes in the magnitude of FTN responses (Lisberger et al. 1994b). Both PVPs and FTNs project directly to motoneurons in the abducens nucleus (Scudder and Fuchs 1992).

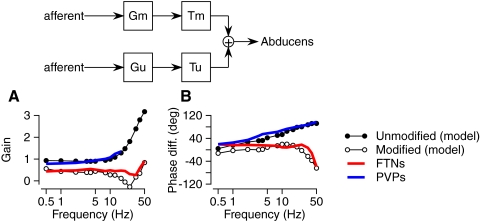
In our earlier reports (Ramachandran and Lisberger 2005, 2006), we developed a model (top panel of Fig. 7) of the parallel pathways that mediate the VOR and used the model to make quantitative predictions for the effect of stimulus frequency on the gain and phase shift of the vestibular signals transmitted through parallel modified and unmodified VOR pathways. Each of the model's pathways received vestibular inputs with gain and phase functions derived from our recordings of the responses of vestibular primary afferents (Ramachandran and Lisberger 2006). Each pathway adjusted its inputs from vestibular afferents with a frequency-dependent gain function (G_m, G_u) and a central time delay (T_m, T_u). Based on the values in the gain functions and time delays (T_m = 9.1 ms, T_u = 1.5 ms) that provided the best fit to measurements of the VOR before and after learning, Fig. 7, A and B shows the prediction of the model for the gain and phase shift of the outputs from the modified (open symbols) and unmodified (filled symbols) VOR pathways. We emphasize that the model predictions in Fig. 7 are taken from an analysis developed in our previous report (Ramachandran and Lisberger 2006) and that all details about the model and its parameters can be found there.

FIG. 7.

Comparison of the responses of FTNs and PVPs during the VOR with the predictions of a 2-pathway model of the VOR that took the responses of vestibular afferents as its inputs and predicted the responses of abducens neurons as its output. The inset at the top of the figure shows the model. G_x indicates the frequency-dependent gain of each pathway and T_x indicates the fixed time delay of each pathway, where “x” is “m” or “u” for the modified vs. unmodified pathway. A: predicted and actual gains for neurons in the unmodified and modified VOR pathways. B: predicted and actual phase shift with respect to head velocity as a function of stimulus frequency. Filled and open symbols show predictions for neurons in the unmodified and modified pathways, respectively. Red and blue curves show average responses for FTNs and PVPs, respectively.

We found excellent agreement between the average gains and phases of the predicted outputs of the two sets of parallel VOR pathways and the average responses of our samples of PVPs and FTNs (Fig. 7). The average responses of FTNs (red curves) agreed well with those predicted for the modified VOR pathways and the average responses of PVPs (blue curves) agreed well with those predicted for the unmodified VOR pathways. The agreement is emphasized by the high-frequency behavior of the model and data, but is present across the full range of frequencies used in our experiments. Thus the recordings reported here, as the culmination of a three-paper series using sinusoidal vestibular stimulation over a wide frequency range, add evidence supporting the assignment of FTNs and PVPs to the modified and unmodified VOR pathways.

Even though the recordings herein were made without changing the gain of the VOR, it is legitimate to draw conclusions about the role of the two interneurons in VOR learning because their responses were compared with a model of the VOR pathways that was constrained, itself, by measurements of the frequency response of the VOR before and after gain changes. Finally, it is important to appreciate that our experiment was designed to assign interneurons to the modified or unmodified pathway operationally, by simply measuring the neural responses as a function of frequency without making any assumptions about the mechanisms that give rise to the phase shifts of FTNs and PVPs. However, the success of the model in predicting the data suggests a number of mechanistic features of the VOR pathways that we now subsequently evaluate.

Sources of phase shifts of FTNs and PVPs

We have characterized the frequency responses of FTNs and PVPs in relation to a model that has parallel modified and unmodified pathways with different frequency-dependent gains and different time delays (Ramachandran and Lisberger 2006). Thus the agreement between the phase shifts in our data and those predicted by the model implies that the neural mechanisms modeled as gain functions and time delays, up to the final summing junction, all lie before the generation of spiking activity of the two interneuron groups we have studied, the PVPs and FTNs.

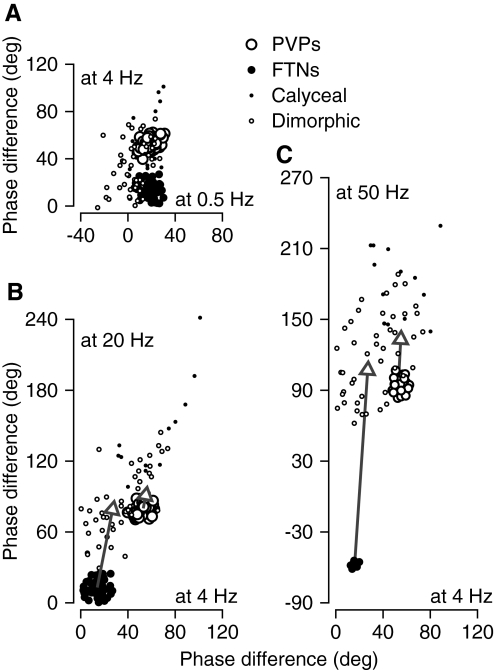
According to the model (Fig. 7), the phase shifts of PVPs and FTNs depend on two factors: the phase shifts of the vestibular afferents that provide their inputs and the time delays between afferent and interneuron firing. There are other possible explanations, but we start our analysis of this issue by comparing the phase shifts across the population of vestibular afferents (taken from Ramachandran and Lisberger 2006) with the phase shifts of the two groups of interneurons. For the afferents, plotting the phase shift at 20 or 50 Hz versus that at 4 Hz reveals a relationship that is characterized in Fig. 8, B and C. When the phase shifts from the present study for PVPs (large filled circles) and FTNs (large open circles) are plotted on the same graphs, they fall in two quite separate clusters, as expected from the frequency responses plotted in Fig. 4. The clusters for the PVPs lie close to but just outside the distribution of the primary afferents, whereas the clusters for the FTNs lie far outside the distribution for the afferents. We conclude that neither the PVPs nor the FTNs can inherit their phase shifts directly from primary afferents. Their afferent inputs must be subjected to additional processing that causes frequency- dependent phase lags, although the amount of additional phase lag is much larger for FTNs than that for PVPs.

FIG. 8.

Comparison of phase shifts with respect to head velocity of FTNs, PVPs, and different groups of vestibular primary afferents. A: phase shift at 4 Hz vs. that at 0.5 Hz. B: phase shift at 20 Hz vs. that at 4 Hz. C: phase shift at 50 Hz vs. that at 4 Hz. Positive values of phase difference indicate that firing rate led head velocity. Large filled and open symbols plot data from this study for FTNs and PVPs. Small filled and open symbols plot data from putative calyceal and bouton/dimorphic afferents, taken from Fig. 5 of Ramachandran and Lisberger (2006). Arrows show how removing the phase shift attributable to the delays in the 2 pathways of the model alters the mean phase shifts of the 2 populations.

Our prior model subjected the afferent inputs to PVPs and FTNs to different time delays that are large enough to cause fairly large phase lags at higher frequencies. Therefore we asked whether adjusting the phase of the interneurons for the time delays implied by our model would move the interneuron data in Fig. 8 into the distributions of phase shifts for vestibular primary afferents. If it did, we would conclude that the responses of interneurons could be accounted for by a model where each group of interneurons inherits the phase shift of its vestibular afferents, but adds phase lags due to a time delay. For each group of interneurons, we computed the mean phase shift of each population and corrected for the amount of phase shift that could be attributed to the time delays in the model, 9.1 ms for FTNs and 1.5 ms for PVPs. As shown by the arrows in Fig. 8, B and C, correcting for the contribution of time delays moved the average values of phase shift for both PVPs and FTNs into the distributions of phase shifts of vestibular afferents. After correction for the postulated time delays, the average phase of FTNs still leads head velocity by less than does that of PVPs at 4, 20, and 50 Hz. For vestibular oscillation at 0.5 Hz, there was little difference in the phase shift of FTNs and PVPs (Fig. 8A), perhaps because time delays of <10 ms would cause <2° of phase lag delay for a sine wave with a period of 2 s.

The time delays proposed by our model are biologically plausible and are in reasonable agreement with estimates obtained by other methods. For example, behavioral experiments suggest that the modified component of the VOR lags the unmodified component by about 5 ms for head accelerations in the physiological range (Lisberger 1984). Our model predicts a 7.6-ms difference between the responses of PVPs and FTNs as interneurons in the unmodified and modified pathways. Recordings from PVPs and FTNs during transient head turns revealed mean response latencies of 7.7 and 12.9 ms (Lisberger et al. 1994b). If we subtract a latency of 5 ms from the measured latencies of PVPs and FTNs, to account for the latency from head motion to the responses of vestibular afferents (Lisberger and Pavelko 1986), then we would expect central delays of 2.7 and 7.9 ms in the VOR pathways through PVPs and FTNs. Our model predicts central delays of 1.5 and 9.1 ms. Given that latency depends on the head motion stimulus (Maas et al. 1989), and that the latencies were estimated using different vestibular stimuli, the two estimates of the central delays in the modified and unmodified pathways are rather similar.

A relatively long delay of about 9 ms between vestibular inputs and FTN responses could result from neural processing in the cerebellum. The extra synapses that intervene in the cerebellar side loop make this an attractive explanation, but the relatively poor modulation of floccular Purkinje cells during the VOR makes this explanation seem unlikely. Although Purkinje cells have been studied only up to frequencies of 10 Hz (Raymond and Lisberger 1998), there is no evidence that they become more responsive at higher frequencies. Given that floccular Purkinje cells modulate relatively little during the VOR even at relatively high frequencies, it is difficult to explain the frequency responses of FTNs in terms of their floccular inputs, excluding the reasonable possibility that the phase lags of FTNs result from eye velocity signals passed through the cerebellum.

The agreement between our model and our data does not necessarily imply that the time delays used in the model exist in the brain. One alternate possibility is that the phase shifts of PVPs and FTNs are a consequence of unique dynamic response properties that are created by special properties of the cell membranes and would shift the phase of their inputs. Although this alternative is not excluded by available data showing that different vestibular neurons have different blends of potassium currents (Gittis and du Lac 2007), the cellular analyses designed to look directly at phase shifts have indicated that vestibular nucleus neurons would be expected to reliably transmit their vestibular inputs, without altering input dynamics (Sekirnjak and duLac 2006). One study found some phase shifts in the response to current injection in neurons that could have been FTNs, but the effect was phase lead rather than lag and, unfortunately, was tested only for frequencies ≤2 Hz (Sekirnjak and du Lac 2002). Further research is needed to fully evaluate this possibility.

A second alternate possibility is that some other combination of time delays and input phase shifts is responsible for the frequency-response characteristics in our data, and that the phase shift of the afferents to the two groups of interneurons plays an important role. In principle, time delay and input phase trade off, so that a wide range of parameters could explain the same frequency responses. For PVPs, the postulated time delay is small and we are suggesting that their phase shifts are determined primarily by the phase of their vestibular inputs. For FTNs, the range of possibilities is limited by the fact that the phase shifts of FTNs lie far outside the range of afferent phase shifts at 20 and 50 Hz. Some other factor must play a major role.

Prior analyses have suggested that the inputs to the VOR interneurons come from a diverse group of afferents (Highstein et al. 1987) that are centered roughly in the middle of the distribution of dynamic response properties (Bronte-Stewart and Lisberger 1994; Minor and Goldberg 1991). Further, prior data suggest that the vestibular inputs to the unmodified pathways may have somewhat more phase lead compared with inputs to the modified pathways (Lisberger and Pavelko 1986; Lisberger et al. 1994b). The analysis in Fig. 8 provides a tentative estimate of the average phase shifts of the afferents that provide inputs to PVPs and FTNs, supporting the prior suggestion (Lisberger and Pavelko 1986; Lisberger et al. 1994b) that the afferent inputs to PVPs show more phase lead than do those to FTNs on average.

The uniformity of phase shifts at a given stimulus frequency within each group of interneurons is striking, especially given the diversity of phase shifts across the afferent population. It seems unlikely that the narrow range of phase shifts in each interneuron group can be attributed to similar narrowness in the afferents to that group because of electrophysiological evidence indicating that each interneuron draws its inputs from a diversity of afferents (Highstein et al. 1987). Instead, there may be connections between members of each interneuron population that promote a narrowing of the range of phase shifts. As an alternative, each member of a given interneuron group might be receiving inputs from afferents with the same range of phases, allowing averaging to convert a diverse set of input phases into a narrow range of interneuron phase shifts.

Connection strengths of PVP and FTN synapses on motoneurons

If PVPs and FTNs provide most of the vestibular signals that drive the VOR, then our data suggest some conclusions about their relative effects on downstream neurons and circuits. Our previous study predicted the weights of signals on modified and unmodified pathways that would need to be combined to simulate the dynamic responses of abducens neurons during the VOR (Ramachandran and Lisberger 2006). Our recordings from FTNs and PVPs revealed the modulation of their firing rate during the VOR. These two sets of observations together allow us to compute the factors that would scale the responses of the VOR interneurons, in spikes·s⁻¹ per deg·s⁻¹ to match the predictions of the model for the relative contributions of the two pathways to eye movement. We found scale factors of 0.2 and 0.33 spikes·s⁻¹ per deg·s⁻¹ for PVPs and FTNs, suggesting that these two groups of neurons make different strength connections to abducens neurons. Of course, if future studies find other major groups of interneurons in the modified or unmodified VOR pathway, then our conclusions about the downstream connection strengths of PVPs and FTNs might be subject to change.

Phase locking and discharge regularity in the VOR pathways

Prior quantitative thinking about the VOR has been based mostly on rate models, where the discharge of groups of neurons is represented as an analog quantity that varies smoothly as a function of time. However, neurons in the VOR pathways signal with the digital code of action potentials. Further, they have spiking statistics that could have important effects on the operation of the circuit and that need to be taken into account in thinking both about normal VOR function and about how the activity within the neural circuit might deploy molecular mechanisms of plasticity and lead to learning in the VOR. First, phase locking is a feature of some vestibular afferents and all PVP neurons at frequencies of vestibular oscillation of ≥20 Hz. Yet the VOR functions quite smoothly at 20 Hz (Ramachandran and Lisberger 2005) and phase locking is absent from FTNs and neurons in the abducens nucleus (Ramachandran and Lisberger 2006). Second, there is a wide range of discharge variability within the VOR pathways. The vestibular afferents thought to provide inputs to the VOR have quite regular ISIs (Bronte-Stewart and Lisberger 1994; Minor and Goldberg 1991), yet both FTNs and PVPs have considerable irregularity in the duration of successive ISIs. When the final motor command comes together in abducens neurons, discharge regularity is restored (Ramachandran and Lisberger 2006). Perhaps the discharge of central neurons can be understood in terms of information transmission and/or their ability to discriminate vestibular stimuli that differ slightly (Sadeghi et al. 2007). Combined with evaluation of how phase-locked signals are processed, consideration of the impact of neural responses with different discharge regularities might provide new insights into the cellular and neural mechanisms of learning.

GRANTS

This work was supported by the Howard Hughes Medical Institute.