Low-Frequency Envelope Sensitivity Produces Asymmetric Binaural Tuning Curves

Abstract

Neurons in the auditory midbrain are sensitive to differences in the timing of sounds at the two ears—an important sound localization cue. We used broadband noise stimuli to investigate the interaural-delay sensitivity of low-frequency neurons in two midbrain nuclei: the inferior colliculus (IC) and the dorsal nucleus of the lateral lemniscus. Noise-delay functions showed asymmetries not predicted from a linear dependence on interaural correlation: a stretching along the firing-rate dimension (rate asymmetry), and a skewing along the interaural-delay dimension (delay asymmetry). These asymmetries were produced by an envelope-sensitive component to the response that could not entirely be accounted for by monaural or binaural nonlinearities, instead indicating an enhancement of envelope sensitivity at or after the level of the superior olivary complex. In IC, the skew-like asymmetry was consistent with intermediate-type responses produced by the convergence of ipsilateral peak-type inputs and contralateral trough-type inputs. This suggests a stereotyped pattern of input to the IC. In the course of this analysis, we were also able to determine the contribution of time and phase components to neurons' internal delays. These findings have important consequences for the neural representation of interaural timing differences and interaural correlation—cues critical to the perception of acoustic space.

INTRODUCTION

One cue used by human and animal listeners to determine the azimuthal location of a sound source is the time delay between the sounds received at the two ears (Rayleigh 1907). In mammals, the earliest point at which monaural pathways converge is the medial superior olive (MSO), a brain stem nucleus that shows submillisecond sensitivity to interaural time differences (ITDs) (Brand et al. 2002; Crow et al. 1978; Goldberg and Brown 1969; Moushegian et al. 1975; Spitzer and Semple 1995; Yin and Chan 1990). This exquisite sensitivity relies on the ability of earlier stages of the auditory system to preserve the temporal structure of frequency components in the sound by encoding them as precisely timed, high-fidelity trains of action potentials. These trains of action potentials from the left and right sides converge at principal neurons in the MSO. These neurons act as binaural coincidence detectors, showing a firing rate dependent on the correlation between the inputs from the two sides (the interaural correlation) (Yin and Chan 1990). As ITDs move the phase-locked inputs in and out of synchrony, they vary the interaural correlation, producing ITD sensitivity.

Despite the impressive ability of the peripheral auditory system to phase-lock to frequencies as high as 2 kHz (Johnson 1980; Joris et al. 1994), there is a limit to the frequencies that can be represented in this manner. Although auditory nerve fibers with high characteristic frequencies (CFs) cannot follow the carrier of high-frequency signals, they do show phase-locking to the envelope of amplitude-modulated signals (Joris et al. 2004). These envelope-locked spikes can serve as a substrate for coincidence detection in the MSO and high-CF neurons can show comparable sensitivity to envelope ITDs as low-CF neurons do to carrier ITDs (Batra et al. 1993; Griffin et al. 2005).

This suggests that carrier ITDs are used for localization at low frequencies, with envelope ITDs of primary relevance at higher frequencies. Here we demonstrate an envelope-sensitive component to the ITD sensitivity of low-CF (<1.5 kHz) neurons, in two midbrain nuclei that receive direct input from the MSO: the inferior colliculus (IC) and the dorsal nucleus of the lateral lemniscus (DNLL). This envelope sensitivity is responsible for asymmetry in the ITD-tuning curves in both IC and DNLL, with the strongest effect over the range of ITDs experienced under natural listening conditions (the range created by the size of the head). The presence of this envelope-sensitive component provides a mechanism by which envelope structure can influence sound localization at low frequencies (Bernstein and Trahiotis 1985).

METHODS

Surgical procedures

All experiments were carried out in accordance with the Animal (Scientific Procedures) Act 1986 of Great Britain and Northern Ireland. Young-adult guinea pigs (Cavia porcellus), with body masses ranging from 0.3 to 0.7 kg, were anesthetized with an intraperitoneal (ip) injection of urethane (1.0 g kg⁻¹, 25% solution); analgesia was induced with a 0.1-ml intramuscular injection of Hypnorm (fentanyl citrate/fluanisone; Janssen–Cilag, High Wycombe, UK). Anesthesia was monitored throughout the experiment via the withdrawal reflex and was maintained with supplementary 0.1-ml doses of Hypnorm as required. A 0.1-ml subcutaneous injection of atropine sulfate (0.6 mg ml⁻¹; Animalcare, York, UK) was used to reduce bronchial secretions and local anesthesia at surgical sites was produced using subcutaneous injections of lidocaine (2% solution). On completion of an experiment, animals were killed by a 1- to 2-ml ip injection of sodium pentobarbital (60 mg ml⁻¹, Pentoject, Animalcare).

A tracheotomy was performed to maintain airway patency and a homeothermic blanket was used to maintain body temperature at 36°C. The animal was positioned in a stereotaxic apparatus housed in a sound-attenuating chamber (IAC, Winchester, UK). Custom-made ear bars allowed positioning of the animal within the restraint so that the tympanic membranes could be clearly visualized. The skull was leveled stereotaxically and middle ear pressure was maintained throughout the experiment by ventilation through small cannulae sealed into the bullae with petroleum jelly. A craniotomy above the location of the right IC or the right DNLL was performed and the dura overlying the cortex was removed. A warm 4% agar solution was placed over the craniotomy and allowed to cool; this reduced brain pulsation and protected the cortical surface from desiccation.

Single-neuron recordings

An electrode was stereotaxically positioned in the brain above the site of either the right IC or the right DNLL. The DNLL and IC were located using stereotaxic coordinates that had previously been histologically verified to be accurate (McAlpine 2004; Medvedeva 1977). Either glass-coated tungsten electrodes (manufactured in house) or parylene-coated tungsten electrodes (World Precision Instruments, Stevenage, UK) were used. A brass screw, used as a ground, was positioned contralateral to the recording site, 1 mm anterior and 1 mm lateral of bregma.

Electrical signals were recorded using a Medusa preamp and RA16 base station (Tucker–Davis Technologies [TDT], Alachua, FL), which 16-bit quantized the signal at a 25-kHz sampling rate, high-pass filtered at 300 Hz and low-pass filtered at 10 kHz. The filtered signal was monitored both aurally (over a speaker) and visually (on an oscilloscope). Putative action potentials were isolated based on a template match to the voltage waveform, defined by a negative-threshold crossing, a positive-threshold crossing, and the time between the negative-threshold crossing and the peak of the waveform. The spike shape was continuously monitored to ensure a single-neuron recording.

Single neurons were isolated using tone pips with variable frequency and intensity. The characteristic frequency (CF) of a neuron was measured as the frequency of the pure-tone stimulus (at zero ITD) at the minimal sound level able to produce a detectable (audiovisual) change in discharge rate above spontaneous levels. The threshold of the neuron was measured as this minimum sound level. If the recorded response did not appear to be sensitive to changes in the ITDs of either tones or noise, the recording was abandoned.

Sound presentation

Acoustic stimuli were delivered via the ear bars using Beyerdynamic DT48 audiological speaker transducers (Beyerdynamic, Burgess Hill, UK). Small audiological microphones (FG3452, Knowles Europe, Burgess Hill, UK) were connected to the ear bar channels by high-impedance tubing, 1 to 2 mm from the tympanic membrane. The impulse response of these microphones had been previously calibrated with respect to the output of the speakers using a high quality 1/8-in. microphone (Type 4138, Brüel & Kjær, Stevenage, UK), 1/2-in. preamplifier (Type 2669, Brüel & Kjær) and measurement amplifier (Type 2610, Brüel & Kjær). On completion of surgery, these microphones were used to check the transfer function of the system and thereby assess the quality of acoustic coupling. In all experiments, the gain of the transfer function was flat to within ±5 dB over the frequency range 50 Hz to 2 kHz, and matched to ±2 dB between the ears. No interaural phase differences arose from differing transfer functions at frequencies relevant to this study.

Stimulus presentation and data collection were controlled by the Brainware program (TDT). Noise stimuli were generated using MATLAB (The MathWorks, Cambridge, UK) and presented via a custom Brainware interface we programmed in Delphi (Borland, Twyford, UK). Noise stimuli were then loaded onto signal processing hardware (RP2.1, TDT) and output at the maximum possible gain of the D/A converter, with digitally controlled analog attenuators used to control the sound intensity (PA5, TDT).

Recorded noise-delay functions

To investigate both envelope- and carrier-sensitive components of responses in IC and DNLL, responses were recorded to noise bursts that incorporated both interaural time delays (affecting both envelope and carrier) and interaural phase disparities (IPDs, affecting only the carrier) (Yin et al. 1987). Noise bursts of 300-ms duration were generated digitally via the inverse Fourier transform, at a sampling rate of 50 kHz. The power spectrum of each noise burst was flat, covering a frequency range of 50 Hz to 5 kHz, whereas the phase spectrum was randomly distributed from a uniform circular distribution. Stimuli were gated with 5-ms ramped-cosine windows, triggered synchronously to ensure no onset time differences between ipsilateral and contralateral stimuli. For each presentation, a new sample of noise was generated and presented ipsilaterally (the right ear). The contralateral (left ear) stimulus had a similarly flat power spectrum, but its phase spectrum θ_C(f) was formed from the ipsilateral phase spectrum θ_I(f) by taking each component with frequency f, time delaying it by τ milliseconds and phase delaying it by φ cycles (cyc)

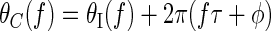(1)

Binaural presentation of this stimulus therefore resulted in a time difference and a phase difference between the spectra presented to the two ears: an ITD of τ milliseconds and an IPD of φ cyc. Positive ITDs corresponded to a time lead of the contralateral stimulus and IPDs in the range 0 to 0.5 cyc corresponded to a phase lead of the contralateral stimulus.

The presented range of ITDs varied between neurons, to account for CF-dependent changes in the width of tuning curves. The ITD was varied between ±1.5 periods of the CF (cyc re CF) in 0.05 cyc re CF steps, and the IPD ranged from −0.375 to 0.5 cyc in 0.125-cyc steps. Each ITD/IPD pair was repeated ten times, using a new sample of noise on each repeat (i.e., each noise was ever presented only once). On each repeat, all presentations of each ITD/IPD pair were randomly interleaved, to control for neural adaptation. The minimum interstimulus interval was 600 ms, although in practice it could be higher due to the computational overhead of uploading the stimulus to the hardware.

The sound pressure level (SPL) at which this noise stimulus was presented was determined for each neuron from its response to uncorrelated noise (for one neuron the response to correlated noise was used instead). Independent (i.e., uncorrelated) samples of noise were presented binaurally and the firing rate was recorded as the SPL (measured in dB SPL) was varied from 15 to 85 dB (−15 to 55 dB per spectral component). The delayed noise stimuli were presented at a level that was in the linear part of this rate–intensity function (to minimize any nonlinearity) and were sufficiently intense to ensure a response for all parameter conditions (so that the shape of the noise-delay function could be clearly seen). For neurons that showed saturation in their rate–intensity functions, the level used was the midpoint of the linear portion of the curve. If the rate–intensity function did not saturate over the range of levels tested, the level used was either the midpoint of the visible linear portion or a level 10 dB above threshold. One noise-delay function was recorded at a level 10 dB quieter than intended, although since it showed only mild rectification, the shape of the noise-delay function could still be seen. This resulted in stimulus intensities ranging from 35 to 80 dB in IC (5 to 50 dB per component) and from 40 to 60 dB in DNLL (10 to 30 dB per component).

To compare these levels for neurons with different sensitivities, neural thresholds to noise were estimated by finding the sound level above which mean spike rates were all significantly greater than the mean spike rate at the lowest sound level (P ≤ 0.05, permutation test). Estimated thresholds varied from 25 to 70 dB in IC and from 25 to 55 dB in DNLL. The range of stimulus sound levels was therefore 0 to 15 dB above threshold in DNLL and 10 to 35 dB above threshold in IC. However, for the majority of neurons, stimuli were 10 or 15 dB above threshold (DNLL: 12 of 15 neurons; IC: 14 of 20 neurons). Note that for the neuron whose noise-delay function was recorded at threshold, it is likely that the true threshold was lower but obscured by its high spontaneous firing rate.

Data analysis

QUANTIFYING THE ASYMMETRY.

The noise-delay function consists of a family of eight ITD tuning curves, one for each IPD (Fig. 1A; see appendix). Each IPD phase shifts the carrier of the noise-delay function, causing the family of curves to tile an area (shaded in Fig. 1A) that is constrained by upper and lower bounds. These upper and lower bounds are the maximum and minimum firing rates at each ITD. However, since only 8 data points are available at each ITD, the maximum and minimum firing rates could fall between data points. To find these extrema the IPD function at each ITD was interpolated up from 8 to 1,024 points (via the Fourier transform). The upper bounds were then measured from the maximum firing rate at each ITD and the lower bounds from the minimum firing rate at each ITD. To remove some of the noisiness, the bounds were then smoothed using the “robust loss” algorithm (smooth function, MATLAB). This used a robust least-squares method to fit a quadratic polynomial with a span of 25% of the entire data set around each data point. The value of the fitted polynomial at the central data point was then taken as the smoothed value of the bounds at that point.

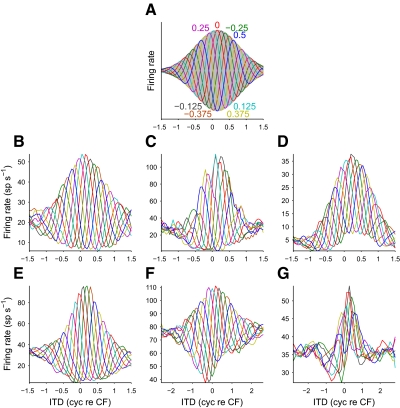
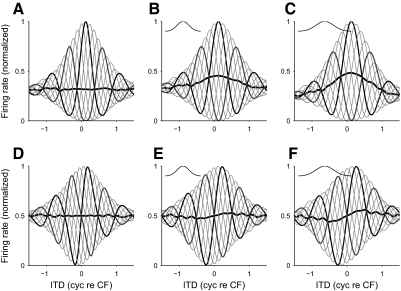
FIG. 1.

Noise-delay functions. A: an example of a noise-delay function predicted from the cross-correlation of narrowband-filtered stimuli. The response takes the form of a family of phase-delayed interaural time difference (ITD) functions; colored numbers indicate the interaural phase disparity (IPD, in cycles) for which the corresponding curve was predicted. The family of ITD functions tile an area (shaded) constrained by upper and lower bounds. Note that the upper and lower bounds are mirror images: modulated to the same depth and centered on the same ITD. B–G: noise-delay functions recorded from the dorsal nucleus of the lateral lemniscus (DNLL, B–D) and the inferior colliculus (IC, E–G). In contrast to the predicted responses (A), the bounds were asymmetric: upper and lower bounds were often different depths (B–E and G) and often centered on different delays (C–D and F–G). Characteristic frequencies were: B, 623 Hz; C, 337 Hz; D, 939 Hz; E, 337 Hz; F, 775 Hz; and G, 313 Hz. For ease of viewing, responses have been smoothed (over ITD) by a 3-point moving-average filter.

Linear sensitivity to interaural correlation predicts a symmetrical noise-delay function with identical upper and lower bounds (Fig. 1A). However, the recorded noise-delay functions showed distinct asymmetries. The upper and lower bounds could differ in their depth (rate asymmetry, Fig. 1B) and the ITD on which they were centered (delay asymmetry, Fig. 1F). The degree of rate asymmetry was quantified by determining how much of the total area within the upper and lower bounds was above (A₊) and below (A₋) the baseline firing rate (the response to uncorrelated noise, estimated from the average response to the most extreme ITDs). The rate asymmetry index (RAI) was then calculated as

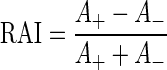(2)

Thus if the majority of the area enclosed by the bounds was above baseline then the RAI was positive (with a maximum of +1), whereas if the majority of the area was below the baseline then the RAI was negative (with a minimum of −1). If the area above baseline was equal to that below, then the RAI was zero.

The delay asymmetry was measured from the cross-correlogram of the upper and lower bounds by finding the delay that produced the most negative correlation. This usually, but not always, corresponded to the difference between the ITDs at the maximum of the upper bounds and the minimum of the lower bounds. Positive delay asymmetry indicated the upper bounds were shifted toward more positive ITDs than the lower bounds, whereas negative delay asymmetry indicated that the upper bounds were shifted to more negative ITDs than the lower bounds.

ANALYSIS OF IPD DEPENDENCE.

Noise-delay functions were decomposed into IPD-independent and IPD-dependent components using Fourier analysis (Fig. 3). Taking the Fourier transform of a noise-delay function r(τ, φ) over the IPD dimension resulted in eight frequency components: z₋₃(τ) through z₄(τ)

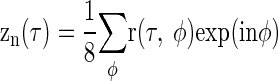(3)

Transforming these components back into the time domain and discarding the negative-frequency components (which were redundant) allowed the noise-delay functions to be expressed as the sum of five components, r₀(τ) through r₄(τ, φ), each of which had a different dependence on the IPD

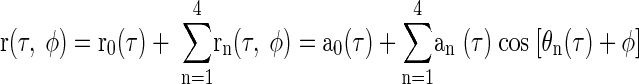(4)

where a_n(τ) is the absolute value of z_n(τ) (compensated for any power loss arising from a missing negative-frequency component)

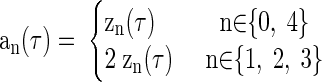(5)

and θ_n(τ) is the argument of the corresponding z_n(τ)

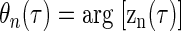(6)

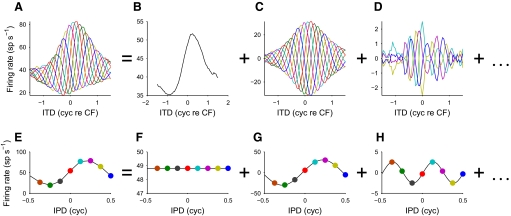
FIG. 3.

Fourier decomposition of a noise-delay function. The original noise-delay function (A) can be decomposed into several components (B–D) on the basis of the Fourier transform of the constituent IPD functions. For example, the responses to the 8 IPDs presented at zero ITD form a periodic function (E). Taking the Fourier decomposition of this yields several components: a DC offset (F), a fundamental (G), and a series of harmonics (of which only the second harmonic is shown, H). Each of these Fourier components is used to determine the IPD function at zero ITD in the corresponding noise-delay function component (B–D). Repeating this for the whole range of ITDs yields the complete components. Note that since the DC component is not modulated by IPD, the r₀(τ) component (B) will not show any IPD dependence. The data shown here are from a DNLL neuron with a characteristic frequency (CF) of 536 Hz.

TRIAL-TO-TRIAL VARIABILITY.

The trial-to-trial variability for each neuron was measured from the variance in firing rate at each point in the noise-delay function. This variability arose from a combination of both intrinsic variation and variation in the interaural correlation produced by the different noise stimuli used on each presentation. The mean response over all presentations of the same ITD and IPD pair was subtracted from the response on each individual presentation of that pair to produce an ensemble of residuals. The trial-to-trial variance was then calculated as the variance of these residuals as a proportion of the total variance of the recorded responses over all presentations of all ITD–IPD pairs. Thus the more consistent the recorded noise-delay function on each repeat, the lower the trial-to-trial variability.

BEST ITD.

Best and worst ITDs are traditionally measured for a correlated noise stimulus as the ITDs producing the maximum and minimum firing rates. To estimate best ITD and worst ITD from our noise-delay functions it was necessary to identify the location of maxima and minima in the noise-delay function recorded at 0 cyc IPD. These turning points were estimated from zero crossings in the first derivative of this response, using linear interpolation. The maximum was taken to be the positive-to-negative zero crossing corresponding to the highest firing rate and the minimum to be the negative-to-positive zero crossing corresponding to the lowest firing rate. The first derivative was estimated at each point from the gradient of the line between the two data points on either side of that point. Because of the sensitivity of this method to noise, recorded data analyzed in this way were first smoothed with a three-point moving-average filter before taking the derivative and identifying turning points.

Neurons were loosely identified as peak-type, trough-type, or intermediate-type on the basis of their characteristic phase (CP; see next section). For the analysis of best ITD and worst ITD neurons were classified according to whether their CP was nearer 0 cyc (peak-type) or 0.5 (trough-type). Elsewhere, exact classification was unnecessary since CP itself was used; in the text, we use peak-type to refer to neurons with CPs close to 0 cyc, trough-type to neurons with CPs close to 0.5 cyc, and intermediate-type to neurons with all other CPs.

CHARACTERISTIC DELAY AND CHARACTERISTIC PHASE.

The internal delays of ITD-sensitive neurons are often modeled as having a time component (the characteristic delay [CD]) and a phase component (the characteristic phase [CP]). Usually, these are extracted for a single neuron using pure-tone stimuli (Yin and Kuwada 1983) by regression using the model

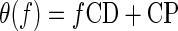(7)

where θ(f) is the best ITD (in cyc) measured using a pure-tone stimulus with frequency f.

The CD and CP can be similarly extracted by considering their effects on different frequencies when presented as a complex rather than individually. For a component with a linear dependence on interaural correlation, an internal ITD (the CD) will affect both carrier and envelope, translating the entire noise-delay function along the ITD axis. Any internal IPD (the CP) will phase-shift only the sinusoidal carrier, leaving the envelope untouched (see appendix).

The time and phase delays affecting the noise-delay function were measured from r₁(τ, φ) (Eq. 4). The CD was measured from the centroid of its amplitude envelope, a₁(τ) (Eq. 5)

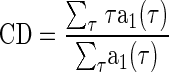(8)

whereas the CP was measured as the phase of the central peak relative to the envelope centroid. This was calculated by fitting the carrier θ₁(τ) (Eq. 6) to the model

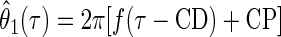(9)

where the parameters f (the frequency) and CP were found by holding CD constant and maximizing ɛ

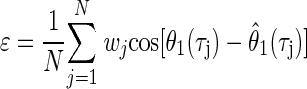(10)

where (w₀, w₁, …, w_N) are weighting factors. This minimized the mean angular deviation of the estimate from the recorded function. For residuals that are von Mises distributed, this estimate corresponds to the maximum-likelihood estimates of the parameters of Eq. 9 (Gould 1969; Mardia and Jupp 2000). Since the oscillations of the noise-delay function were damped at extreme ITDs, the contribution of noise was stronger around those ITDs, producing uncertainty in the measured phase response. To adjust for this, the square of the envelope of r₁(τ, φ) was used as a weighting factor at each ITD

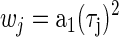(11)

This weighting factor also has the effect of making the regression equivalent to a conventional least-squares regression on the whole of r₁(τ, φ). The regression was performed using a subspace trust-region algorithm (fminunc, MATLAB). All parameters were unconstrained in the regression, with initial estimates determined from the dominant component in the Fourier transform of r₁(τ, φ) over ITD (at zero IPD).

The regression converged and was significant for all neurons (P ≤ 0.05, F-test). In the DNLL, the R² for the fits ranged from 0.94 to 1.00 (median 0.99, interquartile range 0.97 to 1.00) and in the IC, the R² ranged from 0.79 to 0.99 (median 0.96, interquartile range 0.90 to 0.98). For 13 neurons in DNLL and 15 neurons in IC, the residuals showed a systematic deviation with ITD (P ≤ 0.05, circular runs test; Mardia and Jupp 2000), indicating significant phase modulation, albeit with a weak effect. Visual inspection of θ₁(τ) revealed an increase in the instantaneous frequency at central ITDs, which was largely captured by the fits. The majority of unexplained variance arose from the slower instantaneous frequency at more extreme ITDs. Despite these errors, the high R² value indicated that this regression was a suitable method for measuring the phase of the central peak.

EQUIVALENCE CONTOURS.

To assess whether the observed rate asymmetry could be explained by a static nonlinear dependence on interaural correlation, we examined the line that marked the intersections of ITD functions corresponding to IPDs differing by 0.5 cyc (the equivalence contour, black line in Fig. 8A). A noise-delay function produced by a static nonlinear dependence on the interaural correlation will show a flat equivalence contour.

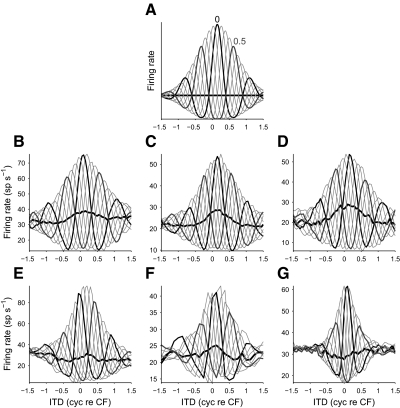
FIG. 8.

Equivalence contours of noise-delay functions. A: a rate-asymmetric noise-delay function simulated by passing the response in Fig. 1A through a quadratic nonlinearity. The nonlinearity produces positive rate asymmetry but no delay asymmetry. Responses obtained at 0 cyc IPD (black) and 0.5 cyc IPD (dark gray) are highlighted; those at all other IPDs are shown in light gray. The equivalence contour (thick black line), which describes the firing rate where antiphasic ITD-tuning curves intersect, is flat. B–G: rate-asymmetric responses recorded from the DNLL (B–D) and the IC (E–G). In contrast to the flat equivalence contour predicted from a nonlinear dependence on interaural correlation (A), the equivalence contours all showed significant ITD dependence (P ≤ 0.05, Wald–Wolfowitz runs test applied to the sign of the deviation from the median). CFs were: B, 460 Hz; C, 470 Hz; D, 623 Hz; E, 337 Hz; F, 215 Hz; and G, 210 Hz. For ease of viewing, responses were smoothed (over ITD) by a 3-point moving-average filter.

The coarse sampling of IPD meant that intersections were not present at every ITD, thus limiting the available data. To overcome this, the equivalence contour was not measured directly from the intersections but was instead obtained from the decomposed response by setting φ = φ_z(τ) in Eq. 4, where

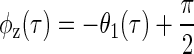(12)

(see appendix for derivation).

Modeling noise-delay functions

INCORPORATING HALF-WAVE RECTIFICATION.

Noise-delay functions predicted from half-wave rectification of the cochlear filtered input stimuli were generated as described elsewhere (Albeck and Konishi 1995). Briefly, white-noise stimuli were generated at a sampling rate of 100 kHz, band-pass filtered at 500 Hz using a rounded exponential (roex) filter, half-wave rectified, and then cross-correlated. To include the effect of IPDs, phase delays were introduced into the contralateral stimulus, as described earlier. A time delay was also introduced to produce a best ITD of 1/8 cyc re CF. Finally, the bandwidth of cochlear filtering was increased from that originally used to model noise-delay functions in owl to reproduce the narrower noise-delay functions in guinea pig (the P value of the roex filter was lowered from 20 to 4). To investigate the effect of additional low-pass filtering, responses were smoothed using a filter with a Gaussian impulse response. The degree of low-pass filtering was adjusted by varying the width of the filter.

INTERMEDIATE-TYPE RESPONSES.

Intermediate-type responses were modeled as a linear combination of an ipsilateral peak-type input and a contralateral trough-type input. Both sets of inputs were modeled using a delay-symmetric response recorded from DNLL that showed a characteristic delay around 1/8 cyc re CF and a characteristic phase around 0 cyc (Fig. 8B). The peak-type input was constructed from the r₀(τ) and r₁(τ, φ) components of this response (Eq. 4), with the degree of rate asymmetry adjusted by γ, the proportion of explained variance in r₀(τ)

(13)

The trough-type component was constructed by inverting the peak-type response (to reflect a preference for interaural anticorrelation) and reversing the ITD and IPD axes (to reflect a contralateral origin)

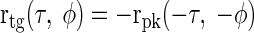(14)

Intermediate-type responses were then simply modeled as a linear combination of the two, with the mixing variable κ controlling the relative contribution of the inputs

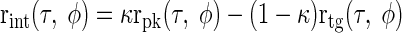(15)

Thus different characteristic phases could be produced by varying κ and different degrees of envelope sensitivity could be produced by changing γ. Although Eq. 15 can result in negative firing rates, it did not matter for the purposes of this model since only the shape of the response was of interest. Thus the contralateral input could be considered either an excitatory trough-type input or an inhibitory peak-type input and the ipsilateral input could be considered either an excitatory peak-type input or an inhibitory trough-type input.

The model was also tested using inputs generated from the responses of the model incorporating half-wave rectification. Instead of Eq. 13, the noise-delay function predicted by half-wave rectification was used as r_pk(τ, φ), and κ was fixed at 0.5 (γ was not used).

RESULTS

Responses were recorded from 35 isolated single neurons in 19 guinea pigs: 20 neurons were recorded in the IC and 15 in the DNLL. All recorded neurons had low CFs (<1.5 kHz) and were sensitive to ITDs in both pure-tone and noise stimuli. Noise-delay functions were recorded using both interaural time differences (ITDs) and interaural phase disparities (IPDs) (Yin et al. 1987). Since IPDs delay only the carrier of narrowband stimuli, the noise-delay function forms a family of phase-shifted ITD-tuning curves—one for each IPD (Fig. 1A).

Noise-delay functions in IC and DNLL are asymmetric

Noise-delay functions recorded from the IC and the DNLL (Fig. 1, B–G) differed from those predicted by a simple interaural-correlation model of MSO neurons (Fig. 1A; see appendix). Differences in details such as the degree of damping were expected because these can reflect differences in cochlear filtering. However, more fundamental differences were observed in the shape of the bounds of the noise-delay functions. The upper and lower bounds of the recorded noise-delay functions were similar but asymmetrical: one bound was often larger than the other (Fig. 1, B–E and G) and the maximum of the upper bounds and the minimum of the lower bounds sometimes occurred at different ITDs (Fig. 1, C and D, F and G), often on opposite sides of zero ITD. In contrast, the upper and lower bounds of the model noise-delay function have the same shape and size and both are centered at the same ITD. When the stimulus in one ear is inverted (i.e., by adding an additional 0.5 cyc IPD), the interaural correlation of a sound is similarly inverted. The noise-delay function in Fig. 1A therefore inherits this property by virtue of its linear dependence on interaural correlation. This produces reflectional symmetry between the upper and lower bounds. The asymmetry in the recorded data therefore indicated some process not captured in the model.

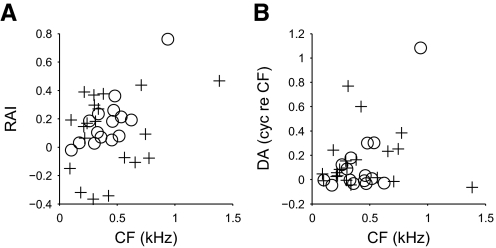
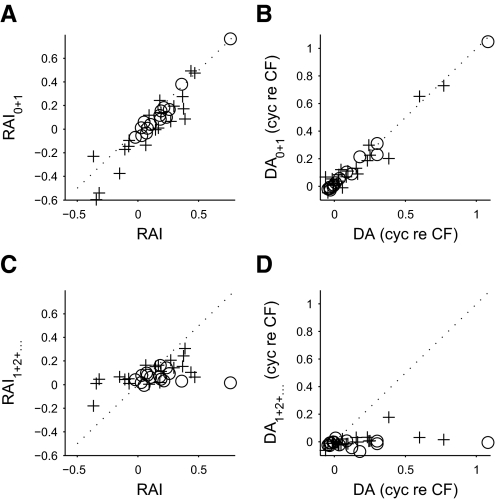
The rate asymmetry—the asymmetry in the size of the upper and lower bounds—was quantified using the rate asymmetry index (RAI; see methods). Positive RAI values indicated that the upper bounds were larger in area, whereas negative RAI values indicated that the lower bounds were larger. In the DNLL, RAIs were near zero at the lowest CFs, but increased with increasing CFs (Fig. 2A; r = 0.69, P = 0.006, Spearman's rank correlation coefficient). This indicated that the upper and lower bounds were roughly the same area for low-CF neurons, but that the upper bounds became larger as CF increased. In contrast, RAI values from IC were more often negative than those from DNLL (Fig. 2A; DNLL: one neuron; IC: seven neurons) and neither the RAI (P = 0.43) nor the absolute value of the RAI (P = 0.85) showed any correlation with CF. Thus rate asymmetry in IC responses was less stereotyped than that in DNLL.

FIG. 2.

The degree of rate (A) and delay (B) asymmetry for noise-delay functions in DNLL (circles) and IC (pluses).

The delay asymmetry—the asymmetry in the delays on which the upper and lower bounds were centered—was quantified using a cross-correlation measure (see methods). The delay asymmetry for most DNLL responses was small and negative (Fig. 2B), indicating upper bounds shifted toward slightly more negative ITDs than the lower bounds. However, six neurons showed large delay asymmetries, all of which were positive. For these neurons, the upper bounds were shifted toward more positive ITDs than the lower bounds and the size of the shift increased with the CF of the neuron. The pattern of delay asymmetry was similar in IC: some responses showed little delay asymmetry, whereas others showed a stronger, positive delay asymmetry. These delay-asymmetric neurons loosely matched the trend seen for the delay-asymmetric responses in DNLL, with delay asymmetry increasing with increasing CF.

Asymmetry is produced by a carrier-insensitive component

The deviation from linearity producing the asymmetric boundaries was investigated by decomposing noise-delay functions into IPD-independent and IPD-dependent components using Fourier analysis (Fig. 3; see methods). The response at each ITD was replotted as a function of IPD (e.g., Fig. 3E, which shows the IPD functions at 0 cyc re CF ITD) and decomposed into harmonic sinusoids (Fig. 3, F–H). This was repeated for each ITD and the components were recombined into several ITD functions, one for each harmonic (Fig. 3, B–D). The r₀(τ) component (Fig. 3B, produced by the DC term of the Fourier transform) was represented as a function independent of the IPD since the response at each IPD was identical.

The dominant component in the noise-delay functions was the r₁(τ, φ) component (Fig. 3C), which accounted for a median 90% of the total variance in DNLL and 73% in IC. The r₁(τ, φ) component arises from the fundamental component of the Fourier transform and so has a sinusoidal dependence on IPD. This is consistent with a linear dependence on the interaural correlation (Fig. 1A) and the dominance of this component reflects the fact that deviations from linearity were not extreme. The r₀(τ) component (Fig. 3B) accounted for a median 8% of the total variance in DNLL and 9% in IC. This component arises from the DC component of the Fourier transform and so is insensitive to phase shifts in the carrier. The r₂(τ, φ) (Fig. 3D) and higher components (not shown) arose from the second and higher harmonics in the Fourier transform. These made very little contribution in DNLL (median 2%), although they were stronger in IC (median 14%). This partially reflected a higher noise contribution in IC arising from the higher trial-to-trial variability (50%, IC; 25%, DNLL; P = 0.032, Wilcoxon rank-sum test). However, around half the neurons showed significant ITD-dependent variation in their r₂(τ, φ) components (IC: 11 neurons; DNLL: 6 neurons; P < 0.05, Wald–Wolfowitz runs test applied to the sign of the deviation from the median; Lehman 2006), which would not be expected if these components had arisen solely as a consequence of noise.

Since the component r₁(τ, φ) is necessarily both rate and delay symmetric due to its sinusoidal dependence on IPD, any asymmetry is produced by the other components. Removing the harmonic components from the responses produced little change in either the rate asymmetry (Fig. 4A) or the delay asymmetry (Fig. 4B), whereas removing the r₀(τ) component produced largely symmetrical responses (Fig. 4, C and D). Thus despite harmonic components making a significant contribution to the shape of many noise-delay functions, they made little contribution to the observed asymmetry. This indicated that the asymmetric responses in DNLL and IC could be well described by just two ITD-sensitive components: one sensitive to the phase of the carrier and the other insensitive to it. In DNLL, the weak harmonics meant that this approximation was close (median R² = 0.98, interquartile range 0.95 to 0.99), but the stronger harmonics in IC resulted in a poorer approximation (median R² = 0.87, interquartile range 0.78 to 0.89). In both nuclei, the quality of the approximation improved at higher CFs (DNLL: r = 0.59, P = 0.024; IC: r = 0.48, P = 0.033; Spearman's rank correlation coefficient), with R² values reaching around 0.99 in DNLL and 0.9 in IC. This reflected a decreasing contribution of the harmonic components with increasing CF.

FIG. 4.

The contribution of distortion components to the asymmetry. The asymmetry measures of the original noise-delay functions are plotted on the abscissas; the asymmetry measures of approximations of these noise-delay functions are plotted on the ordinates. In both DNLL (circles) and IC (pluses), removing the r₂(τ, φ) and higher components from noise-delay functions produced little change in either the rate asymmetry (A) or the delay asymmetry (B). Removing the IPD-insensitive r₀(τ) component, however, produced responses that were both rate symmetric (C) and delay symmetric (D).

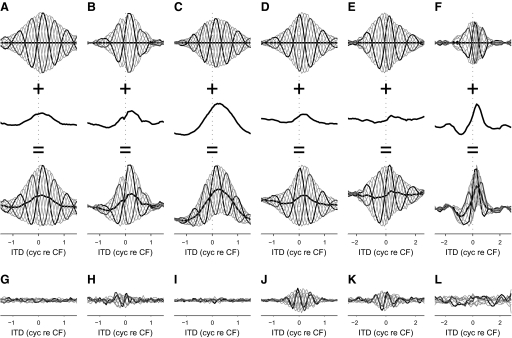
Figure 5 shows these approximations for the recorded noise-delay functions in Fig. 1, B–G. The bounds of each approximated noise-delay function result from the sum of the r₀(τ) component and the upper and lower bounds of the r₁(τ, φ) component. Rate asymmetric responses resulted from r₀(τ) directly increasing the size of one bound and decreasing the size of another. No delay asymmetry was produced if r₀(τ) was symmetrical with respect to the envelope of r₁(τ, φ) (Fig. 5, A and D), but delay asymmetry was produced if r₀(τ) was asymmetric with respect to the envelope (Fig. 5, B, C, E, and F). Finally, multimodal upper or lower bounds arose when r₀(τ) was large compared with the envelope of r₁(τ, φ) (Fig. 5, C and F). The asymmetry in the noise-delay functions was therefore entirely an effect of the carrier-insensitive component.

FIG. 5.

A–F: the creation of rate and delay asymmetry by an IPD-insensitive component. Bottom row: approximations of the noise-delay functions in Fig. 1, B–G, formed from the sum of the r₁(τ, φ) components (top row) and the r₀(τ) components (middle row). G–L: the residuals after subtracting the approximations in A–F from the original noise-delay functions (Fig. 1, B–G). Responses obtained at 0 cyc IPD (black) and 0.5 cyc IPD (dark gray) are highlighted; those at all other IPDs are shown in light gray. Equivalence contours are also shown (thick black lines). All components were smoothed (over ITD) by a 3-point moving-average filter for ease of viewing.

Best ITDs

Neurons in the MSO produce peak-type noise-delay functions (at zero IPD), with a large central peak (Yin and Chan 1990). The internal delay is indicated by the best ITD—the ITD producing the highest firing rate (at 0 cyc IPD). For these neurons, the best ITD compensates for the internal delay, bringing inputs into register, maximizing interaural correlation, and thereby producing a peak in the noise-delay function. In contrast, neurons in the lateral superior olive (LSO) produce trough-type noise-delay functions (at zero IPD), with a large central trough (Batra et al. 1997; Tollin and Yin 2005), due to a preference for interaural anticorrelation. For these neurons the internal delay is indicated by the worst ITD—that producing the lowest firing rate (at 0 cyc IPD).

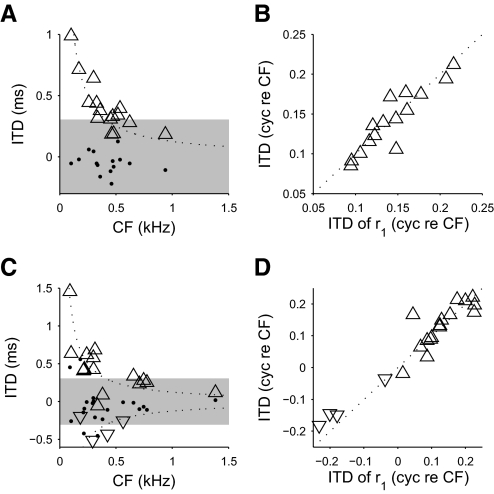
In agreement with previous reports (Hancock and Delgutte 2004; Joris et al. 2006; McAlpine et al. 2001), best ITDs of peak-type responses in IC showed a negative correlation with CF (Fig. 6C; r = −0.72, P = 0.002, Spearman's rank correlation coefficient) and were distributed roughly around 1/8 cyc re CF. Trough-type responses showed worst ITDs distributed roughly around −1/8 cyc re CF. In DNLL, best ITDs showed a similar dependence on CF (Fig. 6A; r = −0.78, P = 0.001), again distributed around roughly 1/8 cyc re CF (median: 0.14 cyc re CF; interquartile range: 0.11 to 0.17 cyc re CF). No trough-type responses were observed in DNLL, but this sampling difference between the DNLL and IC could have arisen by chance (P = 0.12, Fisher's exact test).

FIG. 6.

Best ITDs in DNLL and IC. A and C: best ITDs (upward triangles) of peak-type responses in DNLL (A) and IC (C). For trough-type responses, the worst ITDs are shown (downward triangles). The ITDs where first derivatives of the noise-delay functions (recorded at 0 cyc IPD) were maximal (most positive) are also shown (dots). Whereas the best ITDs were largely outside the physiological range (shaded area, ±300 μs; Sterbing et al. 2003), the ITDs of maximum slope were largely inside the physiological range. The dotted lines show the ITDs corresponding to ±1/8 cyc re CF. B and D: the best/worst ITDs of noise-delay functions (ordinates) plotted against the best/worst ITDs of the r₁(τ, φ) component (abscissas) for DNLL (B) and IC (D). The best/worst ITDs of the noise-delay function were determined by the best/worst ITDs of the r₁(τ, φ) components.

Characteristic delays and characteristic phases

Although a long-standing model suggested that internal delays are time delays arising from differences in axonal propagation time (Jeffress 1948), this does not always sufficiently describe the experimental data. Instead, internal delays are often modeled as having some dependence on the stimulus frequency with both a time component (the characteristic delay [CD]) and a phase component (the characteristic phase [CP]) (Yin and Kuwada 1983). A neuron's best ITD is therefore determined by both its CD and the CP

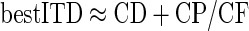(16)

where the best ITD and CD are measured in milliseconds and CP in cycles (in the range −0.5 to 0.5 cyc). We therefore sought to determine how the CD and CP contributed to the CF dependence of the internal delays.

Since the best ITD was determined by r₁(τ, φ) (Fig. 6, B and D), the CD and CP could be measured from their effects on that component alone. The CD was estimated from the centroid of the amplitude envelope a₁(τ), whereas the CP was estimated from the difference between the CD and the phase of its carrier θ₁(τ) (see methods). Although any internal ITD (CD) will translate the whole of r₁(τ, φ) along the ITD axis, any internal IPD (CP) will phase shift only the sinusoidal carrier θ₁(τ), leaving the envelope a₁(τ) untouched. This allows the effects of the CD and the CP to be distinguished. Note that since the phase of the carrier determines the best ITD, the CP was in effect the deviation of the CD from the best ITD, as suggested by Eq. 16.

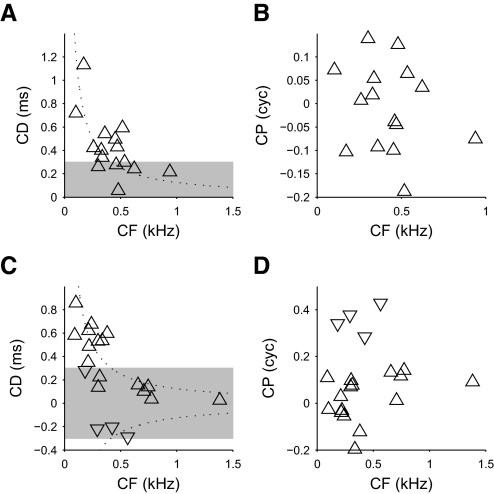
Similar to the best ITD, the CD of peak-type neurons was negatively correlated with the CF in both DNLL (Fig. 7A; r = −0.56, P = 0.032, Spearman's rank correlation coefficient) and IC (Fig. 7C; r = −0.74, P = 0.002). No significant difference was seen between CD and the best/worst ITD (DNLL: P = 1.00, IC: P = 0.82, sign test; see Fig. 6, A and C). Since the CP determines the deviation of the CD from the best ITD, the similarity between CD and best ITD reflected the lack of a systematic contribution from the CP. The CP showed a broad range of values with no dependence on the CF (Fig. 7, B and D; DNLL: P = 0.65, IC: P = 0.20). As expected from the lack of a significant difference between the CD and the best ITD, the CP of peak-type neurons showed no significant bias away from 0 cyc in either the DNLL (P = 1.00, sign test; median 0.00 cyc) or the IC (P = 0.45, median 0.08 cyc). Thus the inverse relationship we observed between best ITD and CF was chiefly determined by internal time delays (i.e., CD) that varied with the CF of the neuron, with no significant contribution from internal phase delays.

FIG. 7.

Time and phase contributions to the internal delay. A and C: the characteristic delay as a function of CF for both peak-type responses (upward triangles) and trough-type responses (downward triangles) in DNLL (A) and IC (C). The dotted lines show the characteristic delays (CDs) corresponding to ±1/8 cyc re CF and the shaded area shows the physiological range for the guinea pig (±300 μs). B and D: the characteristic phase (CP) as a function of CF for DNLL (B) and IC (D). CDs resemble the plots for best ITD (Fig. 6, A and C), whereas CPs are distributed around zero and have no systematic relationship with CF.

The lack of a significant CP contribution merely indicates that our sample of peak-type neurons contained about as many positive as negative CPs. The mean CP of peak-type neurons was −0.01 cyc in the DNLL (95% confidence interval, −0.06 to 0.04 cyc, bootstrap method), 0.03 cyc in the IC (95% confidence interval, −0.03 to 0.07 cyc), and 0.01 cyc for the DNLL and IC combined (95% confidence interval, −0.02 to 0.04 cyc). Thus we cannot exclude the possibility of some systematic contribution of CP for peak-type neurons. Nevertheless, it is clear that CF-dependent CDs strongly contribute to the best ITD.

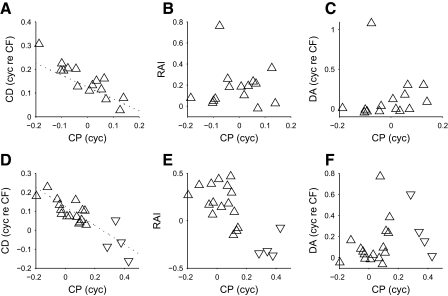
Equation 16 suggests that any best ITD is achievable with the right CP. However, this assumes that the CD and CP of a neuron are independent; in fact they covary. When the CD was normalized by the CF, a correlation between CP and CD was observed in both IC and DNLL (Fig. 11, A and D; DNLL: D_n = 0.44, P < 0.05; IC: D_n = 0.31, P < 0.05; Mardia's linear-circular rank correlation coefficient; Mardia 1976). This indicated different CDs for different classes of neurons: peak-type neurons had CDs around 1/8 cyc re CF, trough-type neurons had CDs around −1/8 cyc re CF, and intermediate-type neurons (those with CPs around 0.25 cyc) showed CDs around 0 cyc re CF.

This correlation indicates a more complex interaction of CD and CP than suggested by Eq. 16. This can be seen by approximating the relationship between CD and CP by

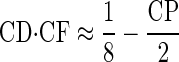(17)

for the range of CPs observed (−0.2 to 0.5 cyc). This corresponds to a linear transition from peak-type neurons with CDs of 1/8 cyc re CF to trough-type neurons with CDs of −1/8 cyc re CF. Linear regression produced the relationship y = 0.13(1 − 4.3x) for the grouped IC and DNLL data (R² = 0.78, P < 0.001, F-test), demonstrating that our approximation was reasonable. Incorporating Eq. 17 into Eq. 16 gives an expression that indicates how the CP of a neuron determines its best ITD

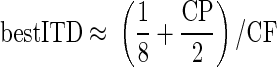(18)

which again applies only for the range of CPs observed (−0.2 to 0.5 cyc). Although only an approximation, Eq. 18 provides an understanding of how the CF-dependent best ITD depends on the range of CPs sampled.

Origin of rate asymmetry

We have shown that a carrier-insensitive component is responsible for the observed asymmetries in the noise-delay functions—but what is the source of this carrier insensitivity? One trivial explanation is the existence of a (static) nonlinear dependence on the interaural correlation. Neural responses to noise bursts with different degrees of statistical correlation between the two ears are nonlinear (Albeck and Konishi 1995; Coffey et al. 2006; Shackleton et al. 2005) and have previously been interpreted as reflecting a (static) nonlinear dependence on interaural correlation (Hancock and Delgutte 2004). Such nonlinearity could arise either directly in the MSO or through a transformation of the MSO response by the DNLL or IC. As demonstrated by the example in Fig. 8A, such a model can produce rate-asymmetric responses, although not delay-asymmetric responses. Furthermore, the r₀(τ) component of these responses will be carrier insensitive, similar to those in Fig. 5. Thus this model would appear to show an envelope-sensitive component, without requiring envelope sensitivity in the input to the MSO.

A simple prediction of this model is that antiphasic ITD-tuning curves will intersect each other at the same firing rate. At ITDs where two antiphasic ITD-tuning curves cross, inverting the carrier (by adding an additional 0.5 cyc IPD) produces no change in firing rate. For a response linearly dependent on the interaural correlation (Fig. 1A), the underlying interaural correlation at these points must be zero and these points will all sit along a line. Since a static nonlinearity is dependent only on the underlying interaural correlation, these intersections at zero interaural correlation will remain intersections in the nonlinearly transformed response and will be mapped onto the same firing rate. Thus for a noise-delay function with a (static) nonlinear dependence on the interaural correlation (Fig. 8A), the equivalence contour (the line along which these points sit) will be independent of the ITD. However, equivalence contours obtained in both IC and DNLL (see methods) were not constant, as predicted, but showed significant ITD dependence (Fig. 8, B–G; IC: 17 neurons; DNLL: 11 neurons, P ≤ 0.05, Wald–Wolfowitz runs test applied to the sign of the deviation from the median). Thus (static) nonlinear dependence on the interaural correlation cannot adequately describe the recorded responses, either because of their delay asymmetry or, even when delay symmetric, because of the ITD dependence of their equivalence contours.

Another possible explanation for the nonlinear dependence on interaural correlation is nonlinearity in the monaural pathways projecting to MSO. This nonlinearity (frequently modeled as half-wave rectification) will introduce carrier-insensitive distortion components into the input to MSO. In this model, carrier insensitivity in the noise-delay function arises from the interaural correlation of carrier-insensitive components in the input. Figure 9A shows a noise-delay function predicted by half-wave rectification of the filtered input stimuli (see methods). Similar to that in Fig. 8A, the noise-delay function shows rate asymmetry, but appears to have a flat equivalence contour. Thus envelope sensitivity introduced by half-wave rectification of stimuli at the cochlea cannot account for the envelope sensitivity observed in DNLL and IC.

FIG. 9.

Effect of peripheral nonlinearities. A: a noise-delay function simulated by cross-correlating half-wave rectified inputs. Similar to the response modeled by a post-MSO nonlinearity (Fig. 8A) there is clear rate asymmetry but the equivalence contour appears flat. B and C: the noise-delay function in A, low-pass filtered by smoothing with a Gaussian (inset). With smoothing the rate asymmetry persisted and the equivalence contour became elevated. D: a delay-asymmetric noise-delay function constructed from the convergence of peak- and trough-type inputs of the form in A. Again, note the flat equivalence contour. E and F: delay-asymmetric functions formed as in D, only with additional low-pass filtering (as for B and C). With smoothing the delay-asymmetry persisted but the equivalence contour became modulated. The CF of the model was 500 Hz and the full widths at half height of the Gaussian kernels were: B and E, 0.4 cyc re CF; C and F, 0.6 cyc re CF. All responses (including insets) have been normalized to facilitate comparison.

Similar to the preceding model, noise-delay functions predicted from the responses of low-CF auditory nerve fibers to noise showed flat equivalence contours (Joris 2003; Louage et al. 2004, 2006). Furthermore, noise-delay functions predicted for anteroventral cochlear nucleus (AVCN, the input nucleus to MSO) show a dip in the equivalence contour (Louage et al. 2005), which arises from an improvement in the phase-locking to the carrier (Joris et al. 1994; Louage et al. 2005). Thus peripheral processing cannot entirely account for the elevated equivalence contours observed in IC and DNLL.

Responses like those in Fig. 9A (and those predicted from auditory nerve and AVCN responses) contain the components r₀(τ), r₂(τ, φ), and higher, which are distortion components arising from nonlinearities such as half-wave rectification. As demonstrated in Fig. 5, if the r₂(τ, φ) and higher components are removed from the noise-delay function, the equivalence contour is completely determined by the r₀(τ) component. Thus the elevated equivalence contours can be produced from distorted responses by attenuating the higher components while leaving the r₀(τ) and r₁(τ, φ) components relatively unaffected. Figure 9B shows the same response as in Fig. 9A but smoothed with a Gaussian kernel. Such a smoothing process can arise from the convergence of heterogeneous MSO inputs in the DNLL or IC. If a given IC neuron receives input from several MSO neurons with a Gaussian selection of best ITDs, it would effectively low-pass filter the input in the manner illustrated. With the harmonic components attenuated, the equivalence contour is determined by r₀(τ) and so becomes elevated (Fig. 9B). Note that the rate asymmetry is unchanged due to the weak contribution of the harmonic components to the rate asymmetry (see Fig. 4A). As the cutoff of the low-pass filter shifts to lower frequencies (Fig. 9C), the r₁(τ, φ) component becomes more attenuated, increasing the relative contribution of r₀(τ) and thereby increasing both the rate asymmetry and the equivalence contour.

Low-pass filtering before cross-correlation has an equivalent effect: attenuating harmonic distortions in the input to MSO will attenuate the harmonic components in its output. This temporal low-pass filtering could arise from processes such as synaptic kinetics and membrane capacitance. Alternatively, it could arise from the heterogeneity of inputs to the MSO since multiple inputs phase-locked to a variety of preferred phases would broaden the spike-timing distribution compared with that of a single fiber.

Thus the elevated equivalence contours suggest additional processing unaccounted for in both the model incorporating half-wave rectification and the model based on the cross-correlation of peripheral responses. This processing must therefore occur either at the level of the MSO (cellular filtering, heterogeneous inputs) or above it (convergence in IC or DNLL).

Origin of delay asymmetry

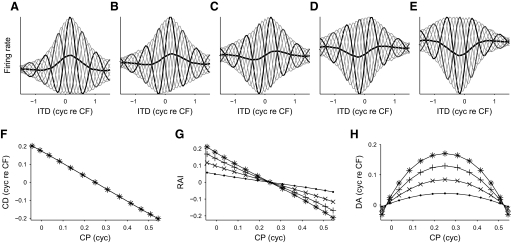
Intermediate-type responses in IC have previously been suggested to be formed from the combination of an ipsilateral peak-type input and a contralateral trough-type input (McAlpine et al. 1998; Shackleton et al. 2000), so it was of interest to see whether such a pattern of convergence could explain the observed delay asymmetry. Figure 10, A–E shows noise-delay functions produced by this model (see methods). When the peak-type input is dominant (Fig. 10A), the noise-delay function reflects that input, showing no delay asymmetry. As the trough-type input becomes stronger (Fig. 10C), delay asymmetry develops, only to disappear again when the trough-type input dominates (Fig. 10E). The relative strength of the inputs is reflected by the characteristic phase: responses dominated by a peak-type input will themselves be peak-type with a CP of 0 cyc, whereas those dominated by a trough-type input will be trough-type with a CP of 0.5 cyc. Responses where neither input dominates will be intermediate-type with CPs around 0.25 cyc. As the response shifts from a peak-type response to a trough-type response, the characteristic delay shifts from that observed for peak-type responses (1/8 cyc re CF) to that observed for trough-type responses (−1/8 cyc re CF). Thus this model predicts a negative correlation between the CP and the CD (Fig. 10F). It also predicts that rate asymmetry should be negatively correlated with the CP (Fig. 10G), with positive RAIs for peak-type responses falling to negative RAIs for trough-type responses. Finally, the delay asymmetry is expected to be zero for both peak- and trough-type responses, but higher for intermediate-type responses (Fig. 10H). Note that the exact degree of rate and delay asymmetry is dependent on the strength of the envelope-sensitive component to the response; if the inputs contain no envelope sensitivity (and therefore no rate asymmetry) then the resulting intermediate-type responses will show no envelope sensitivity (and hence no delay asymmetry). When the model incorporating half-wave rectification was used to generate inputs like that in Fig. 9A, delay asymmetry still resulted, although the equivalence contour appeared flat (Fig. 9D). Again, low-pass filtering was required to modulate the equivalence contours (Fig. 9, E and F).

FIG. 10.

Convergence of peak-type and trough-type responses. A–E: responses formed from the weighted sum of a peak-type input tuned to positive ITDs (A) and a trough-type input tuned to negative ITDs (E). Peak-type to trough-type mixture ratios were: A, 0%; B, 25%; C, 50%; D, 75%; E, 100%. The variance explained by the r₀(τ) component was 8%. F: the relationship between the CP of the modeled responses and their CD. G and H: the relationship between the CP of the modeled responses and their rate asymmetry (G) and their delay asymmetry (H). The variance explained by the r₀(τ) component was either 1% (points), 4% (pluses), 8% (crosses), or 12% (asterisks). These data points lay on top of each other in F.

To test whether this model of convergence could explain the observed responses, the correlations between the CP and the other parameters were examined. As discussed earlier, a strong negative correlation was observed between the CP and the CD in both DNLL and IC (Fig. 11, A and D), which was consistent with that predicted by the model. In IC, the RAI showed a strong negative correlation with the CP (Fig. 11E; D_n = 0.50, P < 0.01, Mardia's linear-circular rank correlation coefficient), with peak-type neurons showing large positive RAIs, and trough-type neurons showing large negative RAIs. The delay asymmetry was also correlated with CP (D_n = 0.34, P < 0.05), showing a correlation with the squared sine of the CP (Fig. 11F; r = 0.53, P = 0.018, Spearman's rank correlation coefficient). In the DNLL, the CP showed no relationship with the RAI (Fig. 11B; P > 0.1) and, although the CP appeared to be positively correlated with the delay asymmetry (Fig. 11C), this was not significant (P > 0.1).

FIG. 11.

Testing the model of convergence. The CD and CP are negatively correlated in both DNLL (A) and IC (D), matching the relationship predicted in Fig. 10F. The dotted line indicates the relationship y = 1/8 − x/2, which corresponds to a linear shift from a stereotypical peak-type neuron (CD = 1/8 cyc re CF, CP = 0 cyc) to a stereotypical trough-type neuron (CD = −1/8 cyc re CF, CP = 0.5 cyc). In DNLL, the CP is not correlated with the rate asymmetry (B) or the delay asymmetry (C). However, in IC, the CP is negatively correlated with the rate asymmetry index (RAI, E) and the delay asymmetry appears to show a dependence on the squared sine of the CP (F). This is a close match to the relationships shown in Fig. 10, G and H. Both peak-type responses (upward triangles) and trough-type responses (downward triangles) are shown.

Thus although the IC data showed good agreement with the convergence model, the similarity was less evident for the DNLL, possibly due to a lack of trough-type neurons. Neurons with CPs around 0.5 cyc have been previously observed in the DNLL (Kuwada et al. 2006; Siveke et al. 2006), suggesting that we undersampled trough-type neurons in this nucleus as a result of their weak response to our interaurally correlated search stimulus.

DISCUSSION

The main finding of this study is that low-CF neurons in both the IC and the DNLL show an envelope-sensitive component in their response to interaurally delayed noise. This component is enhanced over that seen in the monaural pathways and produces asymmetry in the noise-delay functions. In the course of analyzing these effects, we were also able to investigate factors contributing to the CF-dependent best ITDs in both the IC and DNLL. These findings have important consequences for the neural representation of interaural timing differences and interaural correlation.

Envelope sensitivity

Although a previous study (Joris 2003) suggested the existence of low-CF envelope sensitivity in IC, it could not address whether this was simply a side effect of neural firing rates having a nonlinear dependence on interaural correlation. In our study, measuring equivalence contours allowed us to demonstrate that this is not the case. Both the asymmetries and the elevated equivalence contours observed in this study can be seen in noise-delay functions recorded in other studies in cat IC (Joris et al. 2006; Louage et al. 2005), thus indicating that the low-CF envelope sensitivity is a general property of mammalian IC and DNLL. The existence of this envelope-sensitive component explains how envelope modulation biases the perceived lateral position of a sound at frequencies where ITD sensitivity was previously considered to be carried only by stimulus fine structure (Bernstein and Trahiotis 1985). With envelope modulation, the perceived lateralization space was broadened, producing more separation between different ITDs and potentially enhancing the spatial discriminability. Consistent with our findings, this influence of the envelope was greater at higher frequencies.

Envelope sensitivity in the peripheral auditory system is insufficient to explain the elevated equivalence contours observed in this study. Some enhancement of envelope sensitivity clearly occurs, as evidenced by the transition from carrier to envelope sensitivity in IC occurring at CFs roughly 1 kHz lower than those in auditory nerve (Joris 2003). However, it is unclear how much of this enhancement occurs at the level of the MSO and how much at the level of the IC and DNLL. The peaks of noise-delay functions in MSO (Yin and Chan 1990) appear smaller and broader than the very tall, very narrow peaks predicted from AVCN spike trains (Louage et al. 2005). However, phase-locking to monaural tones appears as precise in MSO (Yin and Chan 1990) as observed for AVCN (Joris et al. 1994). This suggests that, whereas low-pass processes at the MSO may have some effect, they are too weak to entirely account for the elevated equivalence contour. Thus convergence at the level of the IC and DNLL can account for both the enhanced envelope sensitivity and the delay asymmetry. A broad pattern of convergence from the MSO has been observed in the IC (Oliver et al. 2003). Although we modeled this using a Gaussian selection of ITDs (a Gaussian kernel), other patterns will also work. Consider a model with surround inhibition, receiving excitatory projections from similar ITDs but inhibitory projections from neighboring ITDs (a Mexican-hat kernel). This would result in band-pass and not low-pass filtering. However, this could still produce elevated equivalence contours, provided the band-pass selectivity was low-pass enough to attenuate the harmonic components but not so high-pass that it removed the r₀(τ) component.

Accounting for intermediate-type responses in the IC

In the IC, intermediate-type responses were delay asymmetric and consistent with the convergence of an excitatory input from ipsilateral MSO (peak-type, positive rate asymmetry) and an excitatory input from contralateral LSO (trough-type, negative rate asymmetry). This pattern of convergence has been previously demonstrated for some intermediate-type neurons in the inferior colliculus (McAlpine et al. 1998).

The trough-type input could alternatively be explained by a GABAergic inhibitory projection mediated by the contralateral DNLL or IC (originating from contralateral MSO) (Adams and Mugnaini 1984; Hernandez et al. 2006); this seems unlikely, however, because γ-aminobutyric acid (GABA) antagonists applied to intermediate-type neurons do not reveal peak-type inputs. For stimuli with time-varying ITDs, application of the GABA antagonist bicuculline can produce changes in best ITD (D'Angelo et al. 2005), but this is partially (if not wholly) attributable to depolarization block. Under bicuculline, depolarization block suppresses firing around what was the peak under the control condition, creating a “notch” (D'Angelo et al. 2005); thus peak firing inevitably occurs elsewhere, changing the best ITD. The effects of any inhibitory trough-type input are confounded with the effects of depolarization block (and its interaction with other temporal processes). This depolarization block may have been exacerbated by the loss of an adaptation current mediated by SK channels, of which bicuculline is also an antagonist (Debarbieux et al. 1998; Johnson and Seutin 1997). The use of stimuli with static ITDs and the specific antagonist SR95531 will reduce the effects of depolarization block (and other temporal processes) on the tuning curves. Under these conditions, depolarization block was not observed and the removal of GABAergic inhibition did not affect the shape of ITD-tuning curves in the IC, producing a change only in the gain (Ingham and McAlpine 2005).

Another possibility is that the convergence may not occur in the IC; instead, the intermediate-type responses may be inherited from an earlier processing stage. For example, a single MSO neuron may produce an intermediate-type response as a product of the inhibition in the MSO itself shaping the sensitivity (Batra et al. 1997). Coincidence detection of the two excitatory inputs would provide the peak-type component, whereas anticoincidence detection of an ipsilateral excitatory input and contralateral inhibitory input would supply the trough-type component. The combined effect of the excitatory and inhibitory inputs would therefore result in an intermediate-type response as suggested by the convergence model. However, in mammals the excitatory inputs are synchronous (Brand et al. 2002), meaning the peak-type components in the model would have CDs around zero. However, the relationship between CD and CP we observed requires peak-type inputs to have positive CDs. Thus the pattern of convergence we have suggested is unlikely to arise in the MSO.

Although the convergence model of intermediate-type responses provided a good qualitative description of the data, it could not account for the responses with negative CPs (−0.2 to 0 cyc). Although negative CPs could be produced from the convergence of an ipsilateral trough-type input and contralateral peak-type input, negative delay asymmetry would result. Instead, the delay asymmetry observed at negative CPs was positive (Fig. 11F). Inverting the envelope-sensitive components of both inputs would reproduce this relationship, but this would correspond to inputs from neurons sensitive to interaural correlation in the carrier but interaural anticorrelation in the envelope (and vice versa). The existence of such responses seems implausible. Negative CPs are observed in earlier nuclei such as the MSO (Yin and Chan 1990), so it is possible that they are directly inherited by the IC. Whether the asymmetry of these neurons is also inherited or arises from convergence is unclear. We hope that the model of convergence presented here can be developed to address such issues.

Composition of internal delays

The CF-dependent best ITD observed for noise-delay functions in IC was consistent with that observed in previous studies (Hancock and Delgutte 2004; Joris et al. 2006; McAlpine et al. 2001) and also with the CF-dependent best ITDs measured using pure tones at CF in the IC (McAlpine et al. 1996), DNLL (Siveke et al. 2006), and MSO (Brand et al. 2002). This study is the first to examine responses to noise in the DNLL and the observation of the same CF dependence further suggests that it is a property inherited from the MSO.

More significantly, the stimuli used in this study allowed us to investigate how this CF dependence is influenced by the CD and the CP. A previous study (Kuwada et al. 2006) has speculated that the CF dependence of the best ITDs chiefly arises from the range of CPs sampled. Since the best ITD (when measured in milliseconds) is given by

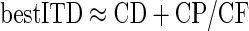(19)

the range of best ITDs for a fixed range of CPs will inevitably grow smaller as the CF increases. However, our findings indicate that CF dependence is observed in the CDs independent of the influence of the CP. Furthermore, we have demonstrated that accounting for the dependence of the CD on the CP produces the relationship

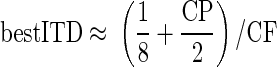(20)

Although neurons with CPs of 0 cyc will have best ITDs of 1/8 cyc re CF, neurons with CPs other than 0 cyc have best ITDs that show different inverse relationships with CF. Thus a mixture of different CPs will produce a spread in the recorded best ITDs. However, the mean best phase will be 1/8 cyc re CF, provided CPs are sampled uniformly around zero (for example, if analyzing neurons only where −0.25 ≤ CP ≤ 0.25). Thus differences in the CPs sampled by different experimenters may account for differences in the observed distributions of best ITDs. However, the value of 1/8 cyc re CF is only an approximation of the relationship between best ITD and CF (the use of 1/8 rather than 0.125 is an attempt to convey this lack of precision).

One explanation for the correlation between CD and CP is the model of convergence suggested for the IC. However, this correlation was also observed in the DNLL, which showed no other evidence for such a pattern for convergence. Although some other pattern of convergence may be at work, it is also possible that the correlation between CD and CP is inherited from the MSO. Various models have been proposed to explain the mechanism producing the internal delay in MSO. In the traditional Jeffress model (Jeffress 1948), internal delays arise from interaural differences in the length of axons projecting to MSO. In the stereausis model (Bonham and Lewis 1999; Shamma et al. 1989), internal delays are produced by interaurally mismatched latencies arising from interaural differences in CF. More recently, several biophysical MSO models have been proposed (Brand et al. 2002; Dodla et al. 2006; Zhou et al. 2005) that use inhibition to produce the internal delay (Brand et al. 2002; Pecka et al. 2008). So far, only the stereausis model has been demonstrated to produce a CF-dependent best ITD (Joris et al. 2006). However, in principle, the other models could similarly do so, by allowing key parameters to vary with a neuron's CF. If internal delays in DNLL reflect those in MSO, our findings set constraints on the candidate mechanisms: a model producing a CF-dependent best ITD should also produce a CF-dependent CD and the correlation between CD and CP that we observe. This may help differentiate these candidate mechanisms.

The CD and CP can be considered parameters of a model where the internal delay is composed of some time component (CD) and some phase component (CP). Traditionally, these parameters have been estimated from their effects on pure-tone stimuli (Yin and Kuwada 1983). Here, we have proposed another method that estimates CD and CP from their effects on noise stimuli (see appendix). This raises the question as to whether the CD and CP we measure using noise (CD_N and CP_N) are the same as those measured using tones (CD_T and CP_T). In theory they should be identical: both methods treat each frequency component in the stimulus as if it had been delayed by an interaural time component (CD) and an interaural phase component (CP). The tone method measures these components by looking at their effect on each frequency, whereas the noise method looks at their effect on the envelope and the carrier.

However, it is interesting to consider why these measures could differ in practice. One mundane possibility is measurement error: our method of estimation may result in some biased estimate of the true CD and CP. However, this is unlikely because we obtained the same results using other methods of extracting CD_N and CP_N (still from their effects on the envelope and the carrier). Another possibility is an error in our model: the CD and CP may not affect the noise-delay functions in the manner we expect. However, given that IPDs phase shift the response as expected, it seems reasonable that CPs would do likewise. It is worth noting that either source of error could also apply to the CD_T/CP_T as much as to the CD_N/CP_N.

A more intriguing difference between CD_T/CP_T and CD_N/CP_N would arise from an internal delay that depended on the stimulus: one that subjected pure-tone stimuli to delays different from those to the spectrally richer noise stimuli. This might conceivably arise from nonlinearity in the mechanism establishing the internal delay. However, even if this were so, it would not invalidate our findings: we use the CD_N and CP_N to make conclusions about responses to noise stimuli. Thus the delays are used for analysis under the same conditions in which they were measured. In contrast, CD_T and CP_T would not be relevant to the best ITD of noise stimuli. Furthermore, since natural stimuli are broadband, CD_N/CP_N would be more relevant to real-world listening than the CD_T/CP_T.

Our data permitted comparison of CD_N/CP_N and CD_T/CP_T for only a single neuron (the results were identical), so any difference is purely speculative. However, we can compare our findings to those obtained using tones. Similar to the CD_N, the CD_T in IC is CF dependent, and there is a correlation between CD_T and CP_T similar to that we observed for CD_N and CP_N (McAlpine et al. 1996). Thus the shaping of best ITD we observe for noise stimuli also appears to hold for tone stimuli.

Similarity to binocular-disparity sensitivity

Like ITD sensitivity, binocular-disparity tuning in primary visual cortex arises from a cross-correlation process (Ohzawa et al. 1990), with responses to broadband stimuli similar to the observed ITD-tuning curves (at 0 cyc IPD). When the contrast in one eye is reversed (an interocular phase disparity of 0.5 cyc), binocular-disparity–tuning curves undergo a phase shift of around 0.5 cyc and a reduction in amplitude (Cumming and Parker 1997), effects consistent with the rate asymmetry observed here. Additionally, the response of some complex cells show delay asymmetry. This has been proposed to arise from a combination of half-wave rectification of the monocular inputs to the cross-correlation processes (in simple cells), followed by binocular convergence (in complex cells) (Read et al. 2002). Envelope sensitivity has also been demonstrated to play a role in binocular disparity and this has been suggested to arise from a second stage of spatial filtering of the rectified monaural inputs (Tanaka and Ohzawa 2006). The similarities between these studies and our own suggest that a homologous model may underlie both binocular disparity and interaural time difference sensitivity.

GRANTS

This work was supported by a Wellcome Trust PhD Studentship (065419) to J. Agapiou and a Medical Research Council Grant (0300417) to D. McAlpine.

APPENDIX

Noise-delay functions predicted from the interaural correlation

After filtering by the cochleae, the interaural correlation ρ(τ, φ) produced by the (sufficiently white) noise stimulus s(t) with ITD τ and IPD φ would be expected to reflect the cross-correlation of the filtered input stimuli. If both cochlear filters are narrowband (i.e., the envelope of their impulse response contains no frequency content above their carrier frequency) then the interaural correlation will also be narrowband, of the form

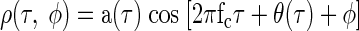(A1)

where the carrier frequency f_c, amplitude modulation a(τ), and phase modulation θ(τ) will depend on the CF of the cochlear filters.

If the firing rate in MSO, IC, and DNLL is proportional to the interaural correlation (Yin and Chan 1990), a noise-delay function r(τ, φ) should reflect Eq. A1

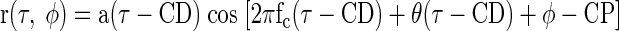(A2)

This will produce responses similar to those in Fig. 1A. For completeness, we have included the effects of the neuron's CD and CP (which compensate for the externally applied ITD and IPD). The assumption that cochlear filtering is narrowband restricts the effect of the IPD to a phase shift of the carrier. This is a reasonable assumption since the bandwidths of frequency-tuning curves recorded from guinea pig auditory nerve are narrow (Evans 2001). In addition, the phase shift of the carrier by IPDs, with no effect on the envelope of the response, is empirically demonstrated both here and in a previous study (Yin et al. 1987).

Equivalence contours

As shown in the previous section, the interaural correlation arising from the noise stimuli we use, ρ(τ, φ), can be expressed as an amplitude- and phase-modulated sinusoid (Eq. A1). If a neuron's firing rate is a function f(ρ) of the stimulus's interaural correlation ρ, then the noise-delay function will be some static nonlinear transformation of ρ(τ, φ)

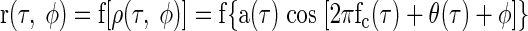(A3)

For simplicity, the CD and CP are subsumed into the τ and φ variables.

The equivalence contour of a noise-delay function at each ITD τ can be produced by finding φ_z(τ), the IPD necessary to produce an underlying interaural correlation of zero

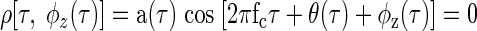(A4)

For a response of the form in Eq. A3, φ_z(τ) can be estimated from θ₁(τ), the phase of r₁(τ, φ) (see methods, Eq. 6). The nonlinearity f(ρ) will introduce distortions and every odd-powered term in the power series expansion f(ρ) will make a contribution to the r₁(τ, φ). For example, if f(ρ) is a cubic polynomial, f(ρ) = b₀ + b₁ρ + b₂ρ² + b₃ρ³, contributions to r₁(τ, φ) will arise from the linear and cubic terms. From the trigonometric formula

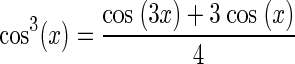(A5)

it can be seen that r₁(τ, φ) will be given by

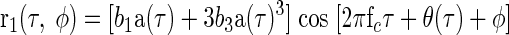(A6)

The polynomial term in Eq. A6 may be negative for some values of τ (e.g., if b₃ is negative). Since the envelope a₁(τ) extracted by the decomposition is an amplitude measure it reflects only the absolute value of the polynomial term. Thus the extracted phase θ₁(τ) will be shifted by π radians at ITDs where the polynomial is negative. However, θ₁(τ) will still be equivalent to the phase of the interaural correlation modulo π

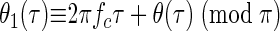(A7)

This line of logic can be extended to see that Eq. A7 will hold whatever the order of f(ρ). Thus setting φ_z(τ) = −θ₁(τ) + π/2 satisfies Eq. A4 and produces the equivalence contour f(0), which is independent of ITD (identical to the response to uncorrelated noise). Since antiphasic ITD-tuning curves intersect when the underlying interaural correlation is zero, the equivalence contour obtained using φ_z(τ) also describes the firing rate at these intersections.