Abstract
Brain stem signals that generate saccadic eye movements originate in the superior colliculus. They reach the pontine burst generator for horizontal saccades via short-latency pathways and a longer pathway through the oculomotor vermis (OMV) of the cerebellum. Lesion studies implicate the OMV in the adaptation of saccade amplitude that occurs when saccades become inaccurate because of extraocular muscle weakness or behavioral manipulations. We studied the nature of the possible error signal that might drive adaptation by examining the complex spike (CS) activity of vermis Purkinje (P-) cells in monkeys. We produced a saccade error by displacing the target as a saccade was made toward it; a corrective saccade ∼200 ms later eliminated the resulting error. In most P-cells, the probability of CS firing changed, but only in the error interval between the primary and corrective saccade. For most P-cells, CSs occurred in a tight cluster ∼100 ms after error onset. The probability of CS occurrence depended on both error direction and size. Across our sample, all error directions were represented; most had a horizontal component. In more than one half of our P-cells, the probability of CS occurrence was greatest for error sizes <5° and less for larger errors. In the remaining cells, there was a uniform increased probability of CS occurrence for all errors ≤7–9°. CS responses disappeared when the target was extinguished during a saccade. We discuss the properties of this putative CS error signal in the context of the characteristics of saccade adaptation produced by the target displacement paradigm.
INTRODUCTION
The monkey oculomotor system is capable of correcting the amplitudes of saccades, i.e., rapid shifts in the direction of gaze, when a dysmetria is caused by muscle weakness (Optican and Robinson 1980) or behavioral deceptions that cause saccades to seem to be inaccurate (Straube et al. 1997). The midline cerebellum, which is part of a parallel route for oculomotor information from the superior colliculus (SC) to reach the premotor brain stem generator for saccades (Harting 1977; Kralj-Hans et al. 2007; Noda et al. 1990; Yamada and Noda 1987), has been implicated as a structure where signals are adapted to reduce saccade dysmetria. It consists of the oculomotor vermis (lobules VIc and VII) and the caudal fastigial nucleus to which they project. After the oculomotor vermis is disabled, monkey saccades do not adapt when eye muscles are surgically weakened (Optican and Robinson 1980) or when dysmetrias are produced by behavioral paradigms (Barash et al. 1999).
How might the oculomotor vermis promote saccade amplitude adaptation? Based on a general model proposed by Marr (1969) and Albus (1971), Ito (1972, 1982) suggested a mechanism whereby the flocculus of the cerebellum might be involved with the motor adaptation of another oculomotor behavior, the vestibulo-ocular reflex (VOR). The VOR acts to stabilize the visual world on the retina when the head rotates. If the VOR becomes too large or small so that the visual world slips across the retina, Ito's model posits that a slip error signal is reported to floccular Purkinje cells by climbing fibers that originate in the contralateral inferior olive. The resultant complex spikes (CSs) that are produced would alter the discharge patterns of the other action potentials of the P-cell, the simple spikes (SSs). The modified SS activity would, in turn, descend to the brain stem where it would cause the appropriate alterations in the activity of VOR pathways to reduce the retinal slip (see Simpson et al. 1996 for a summary of the various roles proposed for CS activity in other behaviors). In the study described here, we use a behavioral paradigm that causes saccades to appear to be too large or small and ask whether CS activity in the oculomotor vermis changes according to the characteristics of the motor error and therefore might be used to drive saccade adaptation.
Because of the source of CS activity to the oculomotor vermis, we have some expectations about the nature of such a putative saccade error signal. CS activity to the oculomotor vermis originates in the b nucleus of the medial accessory olive (Kralj-Hans et al. 2007; Yamada and Noda 1987), which in turn, receives a strong input from the intermediate layer of the SC (Harting 1977; Huerta and Harting 1984). The intermediate layer of the SC contains neurons that have both visual receptive and motor movement fields, i.e., they discharge maximally for stimuli falling on a particular area of the contralateral hemifield and for contralateral saccades of a certain direction and size (for review, see Sparks and Hartwich-Young 1989). Therefore we hypothesize that CS activity recorded from the oculomotor vermis may also be specific for error direction and size.
To test this hypothesis, we recorded the CS activity of saccade-related P-cells in relation to different error directions and amplitudes. In our previous study (Soetedjo and Fuchs 2006), we reported that the CS activity in the interval between the end of dysmetric primary saccades and the onset of the subsequent corrective saccades either increased or decreased during saccade adaptation. Because of the limitations of the behavioral paradigm used in that experiment, we could only determine whether the CS activity preferred left- or rightward error directions, and we also were unable to control error size systematically. Here we tested CS responses to eight different error directions from 0 to 315°, 45° apart. Once we determined a direction that yielded the highest number of CSs on-line, we tested CS responses to different error sizes ≤9° along that direction. We also evaluated whether the error was visual or movement-related by turning off the target at the end of the primary saccades. These new data allow us to make inferences about the properties of saccade adaptation if these CS signals in the oculomotor vermis indeed drive motor learning.
METHODS
General procedures
Two rhesus monkeys were used in this study. We surgically implanted a scleral search coil on one eye to measure eye position with an electromagnetic technique (Fuchs and Robinson 1966; Robinson 1963) and stabilization lugs on the skull to prevent head movements. Once the monkeys had recovered from the surgery, they were placed in a dimly lit room and trained to make saccades to a jumping target spot that moved every 1–1.5 s and to fixate the target for from 0.4 to 1s, not including their reaction times, in return for an applesauce reward (Soetedjo and Fuchs 2006). The target was either the image of a red laser spot reflected from two mirror galvanometers (target diameter = 0.4°) onto a cylindrical drum surrounding the monkey or one of many light emitting diodes that were attached to a sphere facing the monkey. The LEDs, 0.25° in diameter, were placed every 1° along circumferential arcs positioned along eight directions, including right (0°), left (180°), up (90°) and down (270°), and along every 45° arc in between. The target was located either 44 (galvanometer-controlled display) or 61 cm (LED display) from the animal's eyes. The target always appeared within ±25° of straight-ahead.
After monkeys accurately tracked the jumping spot for ≥2 h, we implanted a vertical recording chamber on the mid-line, 14.5 mm posterior to the interaural axis to allow access to the oculomotor vermis, lobules VIc and VII. The oculomotor vermis could easily be identified by saccade-related activity recorded from presumptive afferent fibers. In the two monkeys, the responsive region was ∼3 mm long and 3 mm wide. We recorded the extracellular activity of vermal P-cells with homemade tungsten micro-electrodes, which we coated with iron particles to reduce the impedance measured at 100 Hz and 1 KHz to ∼150 and ∼100 kΩ, respectively. The unit recording was band-pass filtered between 30 Hz and 10 KHz. To qualify as a P-cell, a neuron had to have a clear CS that was visible during on-line recording. In our recording conditions, a CS was positive, ended in one or more wavelets that occurred at ∼1 ms intervals after an initial large spike and was followed by a brief pause in SS activity. Moreover, in this study, we considered only those P-cells that exhibited a transient change in SS activity, a burst, a pause or some combination of the two, for saccades in some, or often, all directions. We surmised that P-cells that already had SS activity related to saccades would be more likely to exhibit changes in CS activity during saccade errors than those that did not. Note that Catz et al. (2005) tested all P-cells in folia with oculomotor activity whether or not the P-cells exhibited a saccade-related change in SS activity. To test for saccade-related SS activity, we asked the monkey to make 15° saccades to target jumps that started straight ahead and landed along one of eight directions spaced at 45° intervals from 0 to 315° and chosen pseudo-randomly (Spike2 random number generator function). We sampled horizontal and vertical eye and target position at 1 kHz and unit activity at 50 kHz using a Power 1401 digitizer (Cambridge Electronic Design, Cambridge, UK). The raw digitized data were scrolled by on a computer monitor while, at the same time, the digitizer software, running in Spike2, performed several on-line analyses (Soetedjo and Fuchs 2006). It detected the occurrence of saccades by a velocity criterion (75°/s) and determined saccade amplitude and direction. After the saccade was detected, saccade onset and offset were marked for analysis when eye velocity first exceeded and later fell below 20°/s. It also identified the occurrence of a SS when the action potential exceeded a threshold set by the investigators and displayed SS histograms associated with 15° saccades in all eight directions on-line (Soetedjo and Fuchs 2006; their Fig. 3).
Identifying the CS preferred direction
After we had identified a P-cell with saccade-related SS activity, we caused the target to step backward during a targeting saccade so the eyes appeared to overshoot their goal (McLaughlin 1967). The resulting visual error elicited a change in CS activity (Soetedjo and Fuchs 2006); backward steps produced a more robust CS change than did forward steps (Soetedjo and Fuchs 2006). Therefore, as a monkey made a centrifugal saccade from the central target location to a 15° eccentric target located along one of the eight directions, we stepped the target backwards by 5° in the opposite direction (centripetally toward the central location).1
The computer triggered the backward step when vector eye velocity exceeded ∼70°/s. As shown in Fig. 1 for a sample of horizontal saccades, the backward step caused the primary centrifugal (leftward) saccade (from 0 to −15°) to overshoot (Fig. 1A) the final target position, and after a variable reaction time, the monkey made a rightward corrective saccade (from −15 to −10°) to bring the eyes on target. After a pseudo-random fixation interval, the target jumped by 15° to the right (from −10 to +5°). The resulting centripetal (rightward) saccade overshot the central location by 5° (Fig. 1B) but triggered a backward step that brought the target again to the central location. After a corrective saccade again brought the eyes to the central location, the centrifugal-centripetal sequence was initiated again in one of the eight directions, chosen pseudo-randomly. In Fig. 1, A and B, we merged all of the leftward (A) and rightward (B) saccades acquired pseudo-randomly and aligned them on the end of the saccade (dashed line).
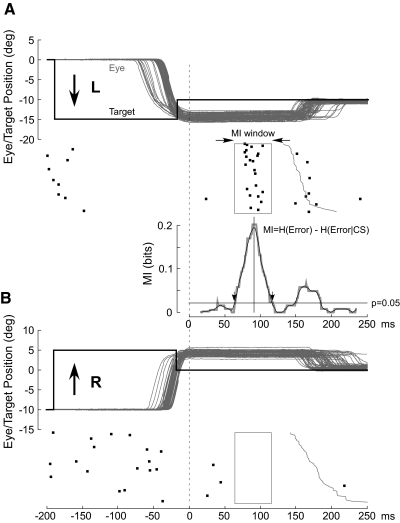
FIG. 1.
Examples of complex spike (CS) occurrences from a single P-cell to errors in opposite directions to show the mutual information (MI) analysis. A: 63 15° leftward target steps and 5° rightward intrasaccadic back steps produce 5° rightward errors, which are eliminated by rightward corrective saccades. B: 64 rightward target steps and leftward back steps cause a leftward error. In both A and B, all saccades are aligned on the end of the primary saccade and arranged from top to bottom in order of increasing latency of the corrective saccade (onset of the corrective saccade shown as jagged thin gray vertical curve). The initial target steps (black thick lines) were placed at the average saccade reaction time. Black dots represent the occurrence of CSs in relation to the associated eye and target movements immediately above. Beneath the CS rasters in A, we show the MI curve (gray) and its smoothed version (black) generated as described in detail in the text. Downward arrows, which mark the times when the smoothed MI curve crosses a probability threshold of 0.05 (black horizontal line), demarcate the width of the MI window (rectangles in CS rasters in A and B).
After we had collected 50 saccades in each of the eight directions, we counted the CSs associated with those saccade trials on-line by eye. This hand processing was necessary because CSs were not always recognizable by our spike-sorting algorithm; however, an experienced investigator using the three criteria mentioned earlier always could mark the CS reliably. For each of the eight directions, the computer displayed, on two 17-in monitors, a high-resolution, 200-ms segment of unit activity aligned on the end of the primary saccade for all 50 saccades (25 traces on each monitor) as shown in Fig. 2 for 16 saccades in the leftward (180°) and rightward (0°) directions, Fig. 2, A and B, respectively. We counted the number of CSs (identified by dots) in each direction to determine the direction of primary saccades associated with the most CSs. In the example in Fig. 2, there were 11 CSs for 180° (A) and 2 for 0° (B). Because we used a back step to generate the visual error, the actual direction of the error is opposite to the direction of the primary saccades; therefore, in this case, the preferred error (on error) direction was 0°. Because we collected only 50 saccades in each direction, little amplitude adaptation occurred; the maximum decrease of the error size was, on average, 0.79 ± 0.25° across all units.
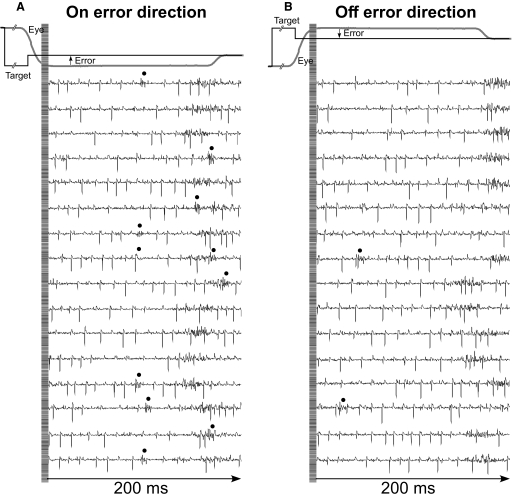
FIG. 2.
Raw extracellular unit records to show the identification of CSs. A and B: 200-ms segments of 16 raw extracellular recordings are aligned on the end of the primary saccade (single example, gray trace) in the on and off error directions, respectively. Black dots mark the locations of CSs, which we identified primarily by their multiple wavelets and the pause in simple spike (SS) activity that follows them. Even when the CS overlapped with an SS (like the 5th CS in A), it was still recognizable because of the subsequent pause in SS activity it caused.
For six neurons, we also tested whether the CS responses were visual. To do so, we ran the directional test paradigm again but did not trigger a 5° back step with the primary saccade. Instead, the occurrence of the primary saccade turned the spot off for 300 ms. Therefore when the saccade landed, there was no target and therefore no visual error present for ≥200 ms. If the CS response was visual, it should be different in the target-off and back-step conditions.
Determining the CS preferred error size
Once we identified on-line the direction of primary saccades associated with the highest incidence of CSs, we presented different size backward and forward steps during 15° primary saccades along that direction. Because we used back steps to identify the preferred error direction (recall above), we used a back step to produce positive (on-direction) errors and a forward step to produce negative (off-direction) errors. When we used mirror galvanometers to move the target spot, the back step sizes were 1.5, 3, 5, 7, and 9° and the forward steps were 1.5 and 3° relative to the target. When we used LED targets, the back step sizes were 1, 3, 5, 7, and 9° and the forward steps were 1 and 3°. We also used target steps without intrasaccadic steps, i.e., 0° back step. Because we randomized forward, 0°, and backward intra-saccadic steps, saccades did not undergo adaptation.
Off-line data analysis
The off-line quantitative analysis of CS activity was performed in two steps using custom programs running in Spike2 (Cambridge Electronic Design, Cambridge, UK). First, from the digitized unit data alone (no associated eye movement traces), we marked the occurrence of all CSs using the three criteria mentioned earlier. Marked CSs were placed in register with the associated eye and target position channels (Soetedjo and Fuchs 2006). The associated SSs also were identified and placed on another channel. Second, the data with the CS time stamp were analyzed using a program that measured the amplitude and timing of the targets and saccades. The program identified the 15° target step when target movement exceeded 300°/s and looked for a targeting saccade that occurred within 100–500 ms later. An eye movement was considered a saccade if the algebraic sum of the rectified peak velocities of the horizontal and vertical components was ≥75°/s. The beginning and end of the horizontal and vertical components of the saccade were marked when the velocity during acceleration and deceleration of each component crossed a threshold of 20°/s. The peak velocity of each component was the maximum velocity that occurred between the beginning and end of each saccade component. For oblique movements, the beginning and end of the saccades were the earliest beginning and the latest end of the two components, respectively. From these markings and the time of peak velocity, the program calculated both primary and corrective saccade metrics and timing attributes, such as saccade onset and end, saccade and target amplitude, saccade gain (saccade amplitude/target step amplitude), saccade duration and peak velocity, and saccade reaction times.
The eye position errors of the horizontal (H) and vertical (V) eye movement components were taken as the averages of (target position − eye position) over the interval from 45 to 53 ms (8 values taken every 1 ms) after the primary saccade of each individual H and V component. We did not measure eye position error right at the detected end of the saccades because the eyes were still moving at this time (recall that we used 20°/s threshold), and the saccades might end with glissades (Bahill et al. 1975). For the 45- to 53-ms interval, eye positions were more stable. The vector error direction was derived trigonometrically from the horizontal and vertical eye position errors.
Next, on the basis of these movement attributes, a Matlab program plotted the traces of eye and target position and CS occurrence. The program took only the trials in which eye position was within ±1.5° of the target position before the initial target step to ensure that the monkey had fixated the target. It also limited saccade duration to ≤90 ms, about twice the duration of normal 15° saccades, to eliminate trials in which the animal either blinked during the saccade or made “lazy” saccades. These restrictions eliminated <10% of the trials.
Finally, we grouped the data according to the direction and size of the error. To determine direction tuning, we created eight bins (±10° wide) straddling the eight average error directions. To determine error amplitude sensitivity, we created error size bins (±0.75°) that were centered on 9 and/or 7° and 5, 3, 1.5, 0, −1.5, and −3°. Positive errors indicate an on-direction error (generated by a back step). We analyzed only those trials in which the vector of the primary saccade was within ±10° of the direction that yielded the highest CS count on-line. For the six experiments in which we turned off the target during the primary saccade, we grouped the data according to the eight directions of the primary saccades because there was no visual error by which to group them. The analyses of these data were compared with those of the back-stepped data for the same unit. For further quantitative analyses (below), we aligned the data on the end of the primary saccade. We chose this moment in time because when CS activity was aligned on the start of the corrective saccade, it was much more broadly distributed (e.g., the cluster of CSs in Fig. 1A became broader).
Information theory analysis
How related is CS activity to error direction? In the example in Fig. 1A, CSs were clustered at ∼100 and ∼170 ms after the primary saccade. We required an objective measure to assess the magnitudes of these two clusters and their relation to error direction and size. Because CSs occur at extremely low rates and do not occur reliably on every trial (i.e., they occur stochastically), we used Shannon's information theory (see DeWeese and Meister 1999 for review) and G statistics (Sokal and Rohlf 1994; Wilks 1935) to create a probabilistic measure of direction selectivity. Because we tested eight error directions, the maximum uncertainty (entropy) of error direction, i.e., when all occurred with equal chance, is three bits (Eq. 1A). If the chance of CS occurrence increases more for some error directions than others, the occurrence of a CS gives us a better chance of predicting error direction. In other words, the uncertainty (entropy, H) of the error direction is reduced. To obtain this reduction of uncertainty, we next computed the remaining uncertainty about error direction if a CS did occur, i.e., H(Error|CS). The reduction of the uncertainty (entropy) of the error direction is simply the difference between the entropy of error direction, H(Error), and the conditional entropy of error direction given the occurrence of a CS, H(Error|CS). This difference is the mutual information (MI) between error direction and CS occurrences (Eq. 1). The higher the MI (i.e., the more uncertainty is reduced), the more correlated CS occurrence is with error direction. Because on each trial the CS represented two possible outcomes (exist or not), the theoretical maximum MI in this test is one bit.
To determine the time course of the MI measure, we computed it within a 30-ms window that slid in 1-ms increments from the end of the primary saccade to 250 ms later. For these analyses, we created 2 × 8 contingency tables in which the two rows indicated saccade trials either with (CS1) or without a CS (CS0) within the 30-ms window, and each column represented one of the eight error directions. We have never seen more than one CS within this 30-ms window. For each of the 220 (=250 − 30) tables, MI was computed using Eq. 1.
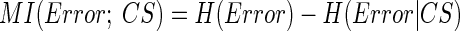 |
(1) |
where
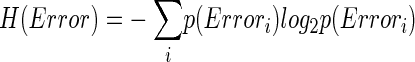 |
(1a) |
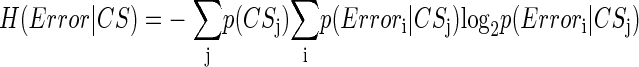 |
(1b) |
i = 1…8 and j = 0, 1.
The above analysis created an MI curve from t = 16 to t = 235 ms after the end of the primary saccade. As can be seen in Figs. 1 (middle) and 3 (bottom), MI curves (in gray) were noisy. Therefore we smoothed them with a 10-point running average (in black). The peak of such an MI curve (black vertical line in Figs. 1A and 3, A and B) indicates that point in time where CSs exhibited the highest correlation with error direction.
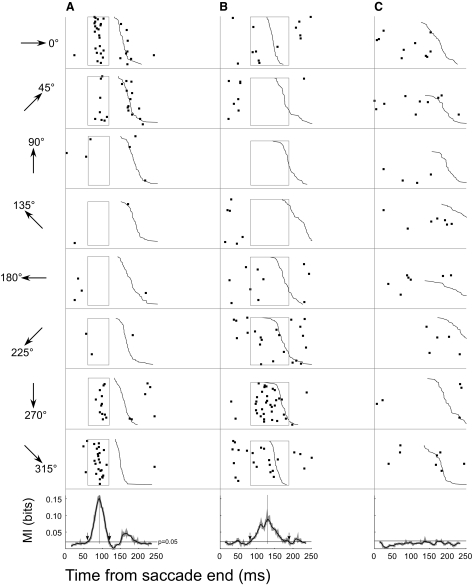
FIG. 3.
Examples of the directional selectivity of CS occurrence for 3 different P-cells (A–C). Each column shows a different neuron with CS rasters aligned on the end of the primary saccade at t = 0 and ordered from top to bottom according to increasing latency of the corrective saccade (jagged black curve). Those trials in which no corrective saccades occurred within the 250 ms were placed at the top, e.g., C, 180°. Each row shows the CS activity in 1 of the 8 directions indicated to the left by the arrows. In A and B, the rectangles mark MI windows where CS occurrence and error direction were significantly correlated (P < 0.05). Bottom panels show raw (gray) and smoothed (black) MI curves determined from data across all 8 directions. Downward arrows mark the threshold crossing times and identify the MI analysis window. Unit in A is the same as that shown in Fig. 1.
However, the MI curve does not tell us whether the correlation between an error and the occurrence of a CS is significant because Eq. 1 does not take into account both the total number of trials and the probability distribution, as is required in other statistical tests. Therefore we used G statistics to measure when in the error interval the MI curve was significant. The G statistic is a variant of a χ2 test and is closely related to MI by the following equation
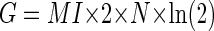 |
(2) |
where n is the grand total number of saccade trials for each unit during the error direction test. The derivation of this relation can be found in the appendix. The G statistic allows us to use the χ2 distribution to compute a P value. We took P < 0.05 as the criterion that the relation between the occurrence of a CS and an error direction was significant. The times where the smoothed MI curve crossed P = 0.05 (Figs. 1 and 3, black horizontal line) demarcated an MI window (downward arrows and vertical rectangles).
To illustrate the MI analysis further, we will construct contingency tables and probabilities for the data within the rectangular MI windows for the two directions in Fig. 1. In Table 1A, the rows indicate the number of trials with (CS1) and without (CS0) CSs for each direction. Based on Table 1A, Table 1B shows the probabilities of the two error directions given the occurrence of a CS, p(Error direction|CS). From Table 1A, p(Error180°) and p(Error0°) were 64/127 and 63/127, respectively. Therefore from Eq. 1A, H(Error direction) is 1.00 bit. Based on Table 1A, p(CS0) and p(CS1) are 105/127 and 22/127, respectively. By applying these CS probabilities and Table 1B to Eq. 1B, H(Error direction|CS) is 0.80 bits, which is the remaining uncertainty of error direction when you know a CS has occurred. Therefore knowing that a CS occurred reduces the entropy of the direction error by 0.20 bits, which is the MI value. The more correlated an error direction is with the occurrence of a CS, the higher the MI. Had a CS always occurred for 0° error (in this case, the CS0 and CS1 in the 0° column of Table 1A would be 0 and 63, respectively), the remaining uncertainty of error direction after knowing a CS had occurred, H(Error direction|CS), would be zero. Therefore MI would have a maximum of one bit, i.e., the occurrence of a CS would completely specify the error direction. On the other hand, if the CS occurred with equal chance in both the 0 and 180° error directions (in this case, the numbers in the cells of Table 1A would be 32, 32, 31, and 32, clockwise from the top left cell), MI would be zero bits. In this case, the occurrence of CSs would tell us nothing about error direction. Therefore the magnitude of MI indicates the tightness of the relation between CS occurrence and error direction.
TABLE 1.
Contingency tables and probabilities for the data within the rectangular MI windows for the two directions in Fig. 1
| Error180° | Error0° | Total | |
|---|---|---|---|
| A. Frequency contingency table | |||
| CS0 | 64 | 41 | 105 |
| CS1 | 0 | 22 | 22 |
| Total | 64 | 63 | 127 |
| B. Probability of error direction given CS, p(Error direction|CS) | |||
| CS0 | 64/105 | 41/105 | 1 |
| CS1 | 0/22 | 22/22 | 1 |
In Fig. 1A, the G value from the χ2 distribution for 1 df (the number of directions − 1) at P = 0.05 is 3.84. Therefore Eq. 2 indicates that the MI threshold for significance is 0.022 (horizontal line in Fig. 1). The intersection between the MI value at P = 0.05 and the smoothed MI curve demarcates an MI window (rectangle) within which the CS was significantly correlated with either the left (Fig. 1A) or right (Fig. 1B) error direction. If the MI curve of a unit did not rise above the MI threshold, we concluded that its CS activity was not correlated with that error direction. Like the unit in Fig. 1A, many units had MI curves with two peaks: one early and one later. However, the magnitude of the second peak varied considerably and did not always reach significance, so we considered only the first peak to determine the MI window.
Because the MI window was obtained by a technique similar to a moving average, the width of the MI window actually overestimated the actual jitter of CS occurrence relative to the end of primary saccades. We represented the jitter of CS occurrences within the MI window with the SD of CS timing relative to the end of the primary saccades. In the example in Fig. 1, the jitter of CS timing in the on-direction (A) was 8.24 (SD) ms.
Quantitative determination of preferred error direction
Once we had established a MI window for a particular unit, we applied the window to each error direction bin (Θ). We counted the number of CSs limited by this window and computed the probability of CSs for each error direction [prob(Θ)] and fit these eight data points with a Gaussian function
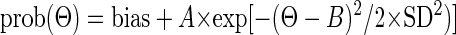 |
(3) |
where Θ is the angular error direction computed as the mean of error direction of each direction bin, B is the neuron's preferred direction, and SD, the SD of the Gaussian function, represents the tuning width. We used a Gaussian function because it fit the data better than a sine function.
In addition to using MI window analysis, we also computed the probability of CS occurrences within the whole error interval (the time between the end of primary saccades and the onset of corrective saccades), as we did in our former analysis (Soetedjo and Fuchs 2006). We plotted these probabilities against error direction and fit the data with Eq. 3. If the CS activity outside the MI window occurs at random, the preferred direction and tuning width determined by our former analysis would be similar to those calculated by the MI window-based analysis, but with a poorer goodness of fit. Such random CS activity may contribute to increasing the bias term in Eq. 3.
Quantitative determination of preferred error size
To determine the relation between CS activity and error size, we first plotted the probability of CS occurrence for different error sizes. For each unit, the probability of CS occurrence was computed within the same MI window established from the error direction analysis. Second, to measure how well CS occurrence was correlated with error size, we performed G statistics between the occurrence of CSs and positive (on-direction) error sizes (1.5, 3, 5, 7, and, for most units, 9°). The contingency table for this test was either 2 × 5 or 2 × 4 for the data with five and four error size bins, respectively. To eliminate the influence of directional selectivity, we did not include negative (off-direction) and “zero” error sizes, because some “zero error” trials had off-direction errors that could bias the average to be negative.
All experiments were performed in accordance with the recommendations of the National Research Council (1997–2003) and the Society for Neuroscience and exceeded the minimal requirements recommended by the Institute of Laboratory Animal Resources and the Association for Assessment and Accreditation of Laboratory Animal Care International. All procedures were evaluated and approved by the local Animal Care and Use Committee of the University of Washington.
RESULTS
We recorded the activity of 48 P-cells with saccade-related SS discharges from two monkeys. During 15° saccades in eight directions, 15 cells exhibited a burst in firing, 18 exhibited a pause, and 15 showed both a burst and pause in their SS discharge. The CSs of 39 of these cells were tuned for error direction. For 18 of these 39 cells, we held the isolation long enough to test their error amplitude sensitivity as well. We tested whether saccadic errors were induced by visual cues in 6/39 P-cells by turning off the target spot for 300 ms after the primary saccade was initiated. At the end of the experiments on each monkey, we placed lesions at sites that straddled an area with vigorous saccade-related activity. The retrieved lesion sites indicate that our recordings were made either from lobules VIc or VII.
Relation between CSs and error direction
Figure 3 shows the range of CS response patterns to error direction during the ∼250-ms error interval after the end of the primary saccade (time = 0). For each of the three representative P-cells, dots mark the time of occurrence of a CS. Each row indicates a trial (cf. Fig. 2), and trials are sorted from top to bottom in order of increasing latencies of corrective saccades (shown by the jagged black lines). For the neuron in Fig. 3A, the probability of CS occurrence was greatest for error directions of 0 and 315° and least for angles of 180 and 135° in the opposite direction. For the neuron in Fig. 3B, CSs occurred most often for an error direction of 270° and did not occur at all for angles of 90°. Note that even in a neuron's preferred error direction, a CS did not occur on every trial. The unit in C was unresponsive to error steps in any of the eight directions.
The neurons in Fig. 3, A and B, also show that the CS response for different P-cells can have different time courses. For the neuron in Fig. 3A, most of the CSs clustered tightly at ∼80 ms after the end of the primary saccade. At angles of 0 and 45°, there also was a second, smaller cluster around the time of the start of the corrective saccade. The occurrence and magnitude of the second response might have been limited by the occurrence of the corrective saccade because, for most P-cells, saccades are associated with a pause in CS activity in some directions (Soetedjo and Fuchs 2006; also Fig. 1A this paper). In contrast to the neuron in Fig. 3A whose CSs mostly were tightly clustered at ∼80 and ∼170 ms after the primary saccade, the CSs of the neuron in Fig. 3B were distributed broadly from ∼80 ms to essentially the time of the corrective saccade.
These two examples suggest that CS activity might fall into two subsets based on the timing of the response and the broadness of its distribution. Therefore we compared the time to the peak response and temporal duration (width) of the response across all 39 neurons. To determine these measures, we calculated an MI curve (Eq. 1) for each neuron by binning the data across all eight directions, e.g., across all rows in Fig. 3A, and moving a 30-ms window every millisecond along the 250-ms time span after the end of the primary saccade. As expected, the MI curve (gray curve in bottom panel) for the neuron in Fig. 3A showed double peaks at ∼80 and ∼170 ms. In contrast, the MI curve for the neuron in Fig. 3B showed a single, broad peak centered at ∼130 ms. This broad MI peak did not include any CSs that occurred within the first ∼80 ms after the end of the primary saccade, indicating that this early CS activity almost never reached significance. The unresponsive neuron in Fig. 3C had a flat MI curve. To calculate the width of the response, i.e., the MI window, we determined where the smoothed MI curve (black curves) exceeded a threshold level corresponding to a P < 0.05 (see methods). The MI thresholds for the neurons in Fig. 3, A–C, were 0.020, 0.021, and 0.024, respectively. The times where the smoothed MI curves crossed those thresholds were marked by downward arrows in Fig. 3, A and B. For neurons like that in Fig. 3A with double-peaked MI curves, we used only the first to determine the MI window because the timing and magnitude of the second peak was more variable, probably because of the spread of corrective saccade latencies. The MI windows for the units in Fig. 3, A and B, were 58 and 105 ms wide, respectively. The flat MI curve of the unit in Fig. 3C never exceeded its threshold.
The maximum point of the smoothed MI curve determined the magnitude and time of the peak MI. Where appropriate in later analyzes, we also considered the characteristics of the second peak.
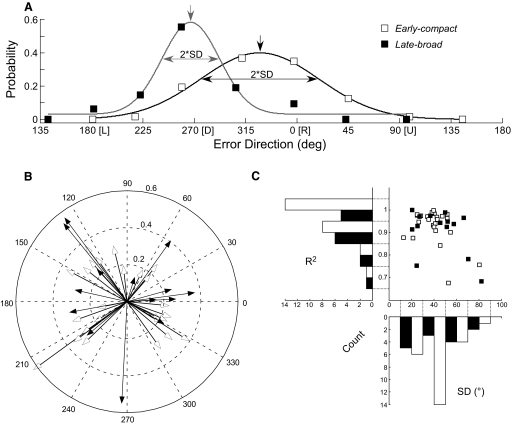
Neurons with the two temporal discharge patterns shown in Fig. 3, A and B, tend to fall in different parts of the response space defined by the times of their peak MI responses and the widths of their MI curves (Fig. 4 A). The peak times and widths of many units clustered between ∼85–115 and ∼28–70 ms, respectively (open squares within shaded rectangle). For those 25 neurons, MI curves had an average width of 51.12 ± 10.29 ms (range: 36–67 ms) and a peak that occurred, on average, 100.20 ± 5.85 ms (range: 92–114 ms) after the end of the primary saccade. When we considered the timing of CSs that occurred only in the preferred direction and within the MI window, the SD measures of the jitter of CS occurrence ranged from 4.64 to 18.11 ms (median: 9.41 ms). Therefore for this subset of neurons, CS occurrences in the preferred error direction were tightly clustered. Finally, the average magnitude of the peak MIs in this subset was 0.091 ± 0.03 bits. Eighteen of these 25 units had significant second MI peaks that occurred, on average, 69.11 ± 12.64 ms after the first peak. The average magnitude of the second peak was 0.052 ± 0.023 bits. We will show later that, whereas this subset of neurons was created somewhat arbitrarily, they show relations with error size that often are qualitatively different from those of the neurons outside the subset.
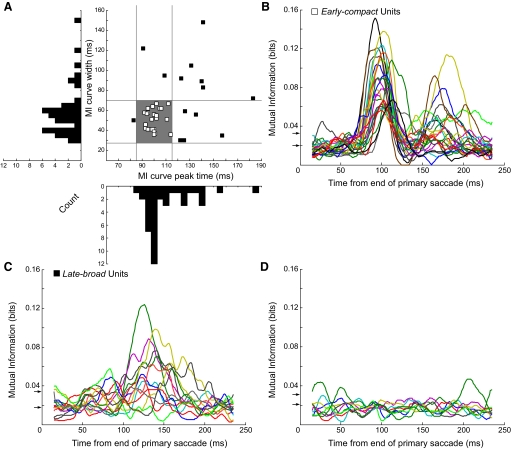
FIG. 4.
Identification of the different time courses of CS responses across all 39 directional neurons as revealed by their MI curves. A: distributions of responses according to the width and peak amplitude time of the MI curve. On the scatter plot, the vertical and horizontal lines were chosen to delimit the parts of each histogram with the highest number of counts. The shaded rectangle delimited by these lines identifies responses that all have short latencies with little variation. These early-compact neurons are identified here and in subsequent figures by open squares. Responses that fall outside the shaded rectangle tend to have both longer latencies and more variability. Such late-broad units are identified here and in subsequent figures by filled squares. B: smoothed MI curves for the 25 early-compact units. Significance thresholds (arrows) for these data ranged from 0.020 to 0.033 bits. C: smoothed MI curves for 14 late-broad units. Significance thresholds for these data ranged from 0.018 to 0.034 bits. D: smoothed MI curves for 9 units that did not show a correlation between CS occurrence and error direction. Significance thresholds for these data ranged from 0.021 to 0.031 bits.
For the remaining 14 neurons (Fig. 4A, ▪), the MI curves of 11 peaked later and 8 had greater widths (6 of 14 exhibited both properties). Not only did the peak occur later, on average (mean: 129.07 ± 24.14 ms), but its timing was more variable (range: 83–183 ms). The widths of the MI curves (30–148 ms; mean: 76.14 ± 35.38 ms) were ∼1.5 times broader than those of neurons in the other subset (cf. Fig. 4, B and C). Moreover, for this subset of neurons outside the shaded rectangle, the timing of the peak was 4–5 times more variable and the duration 3–4 times more variable. To provide an intuitive descriptor to aid the reader in following the subsequent analyses, we will refer to the neurons within the shaded rectangle in Fig. 4A as early-compact neurons and those outside as late-broad neurons. The third group (9 units) did not show any consistent peaks in their MI curves (Fig. 4D), and most parts of their MI curves were below the acceptance threshold. Therefore their CSs were not related to saccade error. Neither the early-compact nor late-broad neurons were preferentially located at a specific location in the recording grid or at a particular depth.
To plot direction-tuning curves, we next determined the probability of CS firing for each of the eight directions. For each direction, we counted the number of CSs within the MI window (Fig. 3, rectangles), divided by the number of trials to determine the average probability of CS occurrence and plotted average probability against the average direction. Figure 5 A shows such plots for our two related exemplar neurons (those in Fig. 3, A and B, shown as open and filled squares, respectively). The Gaussian curves, which fit both data sets well (R2 = 0.98 and 0.93, respectively), allowed us to characterize the direction tuning quantitatively. The tuning curves for the units in Fig. 3, A and B, had preferred directions of 327.7 and 267.1° and widths (as measured by the SD of the Gaussian fits) of 51.8 and 25.2°, respectively. The preferred error directions of 37 of our 38 directional units ranged from −60 to 230°; one unit preferred downward error (Fig. 5B). The characteristics of the direction tuning curves of the 25 early-compact (open squares, open histograms) and 14 late-broad (filled squares, black histograms) neurons obtained from fits like those in Fig. 5A are summarized in Fig. 5C. The Gaussian fits for all 39 neurons were quite good; R2 averaged 0.92 and only 2 neurons had an R2 < 0.7.
FIG. 5.
Directional tuning characteristics of CS occurrence for all 39 units. A: raw data and Gaussian fits of probability vs. mean error direction for the units in Fig. 3, A and B, here gray and black curves, respectively. The preferred directions are taken as the peak of the Gaussian curves (downward arrows; term Θ and A in Eq. 3). The width of direction tuning is indicated by ±SD from the Gaussian fits. B: summary of the preferred directions of both early-compact (open arrows) and late-broad (filled arrows) units. Length of the vector indicates the probability of firing from 0.0 to 0.6. C: distributions of goodness of fit (R2, histogram bin width 0.1) and width of tuning (SD, histogram bin width 20°) for both early-compact (open histogram) and late-broad (black histogram) units.
We also fitted the probabilities of CS occurrence within the whole error interval as a function of error direction and compared the fits with those determined from the MI interval analysis. For all units, the preferred directions of the fits obtained with the two analysis methods were not significantly different (P > 0.5) nor were the widths of the tuning curves (P > 0.3). The R2 values of the fits for the early-compact units were very significantly smaller with the whole error interval analysis (P < 0.001, mean difference: −0.15 ± 0.17), whereas they were not for the late-broad units (P > 0.1). This result was expected because the MI intervals for early-compact units were more consistent in their timings and widths than those for the late-broad units. In conclusion, the MI analysis accurately identified the part of the error interval within which the occurrence of a CS most reliably indicated the error direction.
It was impossible to determine with certainty whether the preferred direction of CS occurrence pointed ipsi- or contraversive to the recording side because the midline of the vermis in our histological material was unclear. However, we estimated the side of recording by using the location of the electrode penetration within the recording chamber. In the animal with the majority (32/39) of responsive units, we divided the data into two groups based on whether their CS on-directions had left- or rightward horizontal components. As shown in Fig. 5B, the majority of our neurons had on-directions between either ±60 or 120 and 240°. Only five neurons had preferred directions within ±30° of vertical. With the exclusion of those five vertical neurons, the averages of the horizontal coordinate locations of the recording sites in the chamber for the left- and rightward error groups were 0.91 ± 0.66 (to the right) and –0.40 ± 0.78 mm (to the left) relative to the center of the recording chamber, respectively (significantly different, P < 0.001). Therefore the preferred (on-) direction of CS occurrence was, on average, contraversive to the location coordinates of the recording.
The widths of the directional tuning curves of the early-compact (Fig. 5C, open histogram) were concentrated between 30 and 50° SD (56%), whereas the late-broad (black histogram) units had either broad tuning widths (>50° SD, 43%) or narrow tuning widths (<30°, 36%). On average, the tuning widths of the early-compact neurons were ∼12° narrower than those of the late-broad neurons (38.3 ± 13.6 vs. 50.1 ± 18.9° SD, respectively, P < 0.05).
The peak probabilities of occurrence of CSs with error direction (the A term in Eq. 3 and the length of the arrows in Fig. 5B) of the early-compact neurons were not statistically different from those of the late-broad neurons (0.29 ± 0.1 vs. 0.36 ± 0.13, respectively, P > 0.05). Note that the average peak probability of CS occurrence is approximately one third, so a CS occurs only about once every third trial even in the optimal error direction.
It is worth pointing out that the units in Fig. 3, A and B, did not produce any CSs within their MI windows in the off-directions (135 and 90°, respectively). The predicted probability of CSs in the off-direction is given by the bias term in Eq. 3. Based on the fits, the averages of the bias term for the early-compact and late-broad neurons was only 0.0031 ± 0.0059 and 0.0093 ± 0.012, respectively. These off-direction probabilities correspond to only 1.1 and 2.5% of their average peak probabilities, respectively. The average resting probability of the CS occurrence across all neurons (measured in the 100-ms window before the primary target step) was 0.1; therefore in the off-direction the CS probabilities were only 3.1 and 9.3% of the resting probability, respectively. Consequently, CS probabilities that were lower than the resting probability provide a sensitive indicator of a unit's off-direction and also suggest there may be an active inhibition of CSs in the off-direction.
Is the direction error signal visual? For six neurons, we also tested whether the CS responses to error direction were visual by turning off the target for 300 ms when the primary saccade occurred instead of causing the target to step backward (compare insets in Fig. 6, A and B). In this target-off condition, we grouped the trials according to the eight directions of the primary saccades to create the 2 × 8 contingency tables for the MI analysis. We binned the data according to the direction of the primary saccades because error direction is undefined during the target-off condition.
FIG. 6.
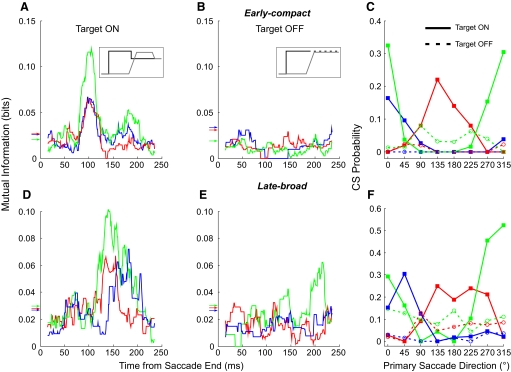
Demonstration that the information carried by a CS response depends on the presence of a visual error. A and D: MI curves in our normal target back-step paradigm (see inset in A) for 3 units with early-compact responses (A) and 3 with late-broad responses (D). B and E: MI curves of the same units to the left (matching colors) when the target is extinguished as the saccade is launched (inset in B). In this situation, CS mutual information is eliminated completely (B vs. A; 2 of 3 in E vs. D) or substantially altered (green response in E vs. D). Arrows indicate MI thresholds for significance (matching colors). C and F: CS probabilities within the MI windows during both target on (solid curves, filled squares) and off (dashed curves, open circles) plotted against the direction of the primary saccades for both early-compact (C) and late-broad (F) responses.
In the target-off condition, the MI curves for neither the three early-compact nor the three late-broad units (Fig. 6, B and E, respectively) exhibited the peaks that characterized the corresponding curves in the back-step condition (Fig. 6, A and D, respectively). The significant MI thresholds (horizontal arrows on ordinates) for the responses in Fig. 6A were 0.019, 0.031, and 0.033 bits, whereas in Fig. 6D, they were 0.027, 0.028, and 0.03 bits. In the target-off condition, the MIs of CS responses were below the threshold levels for significance for most of the error interval between 0 and 200 ms.
The low number of MI bits in the target-off condition could be because either the CSs ceased discharging completely or discharged randomly in all directions at the resting probability. To differentiate between these two possibilities, we plotted the CS probability within the MI window for each direction. In Fig. 6, C and F, we plotted the probability of CS occurrence during both target-on (solid curves) and -off (dashed curve) conditions against the direction of the primary saccades. When the target remained on, all six neurons exhibited clear increased CS probabilities for some primary saccade directions (solid curves). During the target-off condition, all six neurons no longer showed a tuning of CS probability with direction (dashed curves). Furthermore, the CS probabilities of all three early-compact neurons in the target-off condition (Fig. 6C) were lower than the average resting probability of 0.1. One of them (blue dashed line) had a zero probability of occurrence in all directions. On the other hand, CS occurrence for two of the three late-broad neurons (Fig. 6F, red and green dashed lines) showed no tuning, and the MI hovered near 0.1.
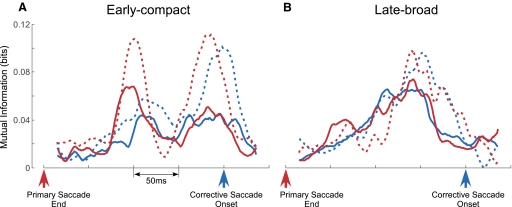
Although the absence of responses in the target-off conditions suggest that the CS response is visual, these data do not rule out the possibility that CSs encode information related to the corrective saccades, especially the second MI peaks, where CSs occurred close to the corrective saccades. If CSs encoded information for corrective saccades, the MI would be higher when the CSs were aligned on the onset of corrective saccades than on the end of primary saccades. However, to differentiate the MI curves produced by the two alignments, a wide distribution of corrective saccade latencies relative to the end of the primary saccade is needed. Therefore we selected units for which the SD of the average corrective saccade latency was >30 ms during the directional selectivity test. Only four early-compact units that had distinct second MI peaks and five late-broad units met the latency criterion.
The alignment comparison for two representative early-compact and late-broad CS response patterns is shown in Fig. 7, A and B, respectively. The other five units that met the latency criterion exhibited similar behaviors. When the CSs were aligned on corrective saccade onset (solid and dashed blue curves), the initial MI peaks of both early-compact units were substantially less than those with the CSs aligned on the end of primary saccades (solid and dashed red curves). Therefore the initial MI peaks were more tightly timed with the end of the primary than the onset of the corrective saccade. Differences in the second MI peaks for the two alignments are less obvious. For the early-compact neurons, the second MI peaks with the CSs aligned on the end of primary saccades appear to be slightly higher (both red curves) and narrower than those with CSs aligned on the start of corrective saccades (both blue curves). The MI curves of the late-broad units (Fig. 7B) also were quite similar for either alignment. However, diagnosis of the origin of the late response is confounded by two factors. First, the late response often has a broader distribution, especially for the late-broad neurons, than the early response. Second, the pause associated with the corrective saccade shapes the second response in unknown ways. Because the late response is not more robust when aligned on one saccade or the other, we conclude that the origin of the late response is ambiguous.
FIG. 7.
Comparison between MI curves produced with data aligned on the end of primary (red curves) and the onset of corrective (blue curves) saccades. A: 2 representative early-compact units (solid and dashed curves). B: 2 representative late-broad units (solid and dashed curves). Upward arrows are alignment times.
Taken together, the experiments shown in both Figs. 6 and 7 show that an enhanced CS response in the error interval requires a visual target. The initial response in early-compact neurons seems to be related to the visual error remaining after the dysmetric primary saccade. The late response also has a visual component, but our data do not allow us to determine whether it also has a motor component related to the corrective saccade itself. For some neurons, turning the target off after the primary saccade reduced the occurrence of CSs to below the resting probability.
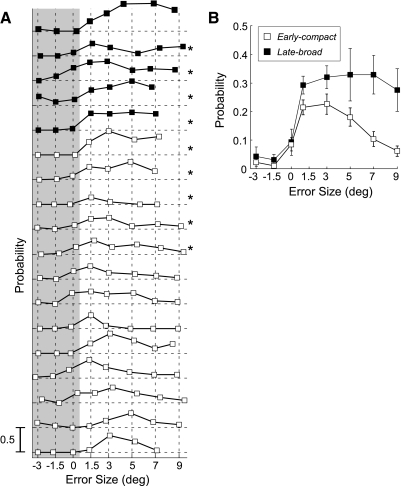
Error amplitude tuning
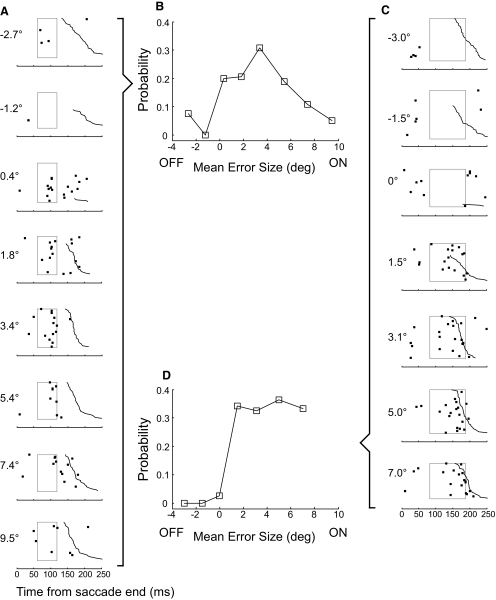
We maintained adequate isolation of 18/39 P-cells for sufficient time to test the influence of error size in the preferred direction. For 17, our on-line estimate of preferred direction was within ±45° of that obtained with the Gaussian fit (mean error: 15.6 ± 11.1°). Figure 8, A and C, shows the sensitivity of the units illustrated in Fig. 3, A and B, to error size with trials ordered from top to bottom according to increasing on-direction (decreasing off-direction) error. For both units, few CSs occurred for errors in the off-direction (negative values), whereas there were many for error sizes in the on-direction. The unit in Fig. 8A appeared to be tuned for error size, with most CSs occurring at an error of ∼3.4° and fewer for larger and smaller positive errors. In contrast, the CS activity of the unit in Fig. 8C appeared constant as on-direction error size increased. Both units had a weak response, if any, for errors near zero.
FIG. 8.
Examples of the sensitivity of CS occurrence with error size. A and C: data from units shown in Fig. 3, A and B, respectively. Numbers to the left of each column indicate the mean error size for the trials included in that data set; positive errors are in the preferred direction; negative errors in the opposite direction. As with similar data for direction tuning, trials are aligned on the end of the primary saccade (t = 0) and ordered from top to bottom according to increasing latency of the corrective saccade (jagged black curve). For small error amplitudes around 0, there often was no corrective saccade; as before, those trials were placed at the top of the raster. The rectangles represent MI windows determined from directional tuning data on the same unit. B and D: plots of probability of CS occurrence (within the MI window) against mean error amplitude for the units in A and C, respectively.
To show the sensitivity of each neuron to error size, we computed the probabilities of CS occurrence within the same MI windows used for the directional tuning analysis. Figure 8, B and D, shows plots of CS probability as a function of error size for the units in A and C, respectively. The tuning curve of the early-compact neuron in A peaked at ∼3.4° and decreased for larger errors in the on-direction and errors in the off-direction. For the late-broad neuron in C, in contrast, the probability of CS occurrence increased steeply for on-direction errors and saturated for errors from 1.5 to 7.0°.
The probability of firing as a function of error size for each of our early-compact (□) and late-broad (▪) neurons is shown in Fig. 9A. For all units, the probabilities of CS occurrence for negative (off-direction) error sizes were very low or zero. For average errors near zero, CS probability also was either zero or low. When the average error was > ∼1°, CS probabilities consistently were greater than zero. Qualitatively, the early-compact neurons (data of 11 lowest neurons plotted as open squares) appeared to exhibit amplitude tuning with higher probabilities for 1.5, 3, or 5° errors and decreasing probabilities for larger errors. In contrast, the five late-broad units (data of 5 highest plotted as solid squares) all discharged with high probability to errors of all sizes in the on-direction. Quantitatively, however, CS occurrence was not significantly different for different error sizes in the on-direction for 4 of the 5 late-broad neurons and 5 of the 13 early-compact neurons (G-statistics; methods; P > 0.05, neurons with *). Therefore 80% of late-broad neurons were not tuned for on-direction error amplitudes, whereas 62% of early-compact neurons were.
FIG. 9.
The relation between probability of CS occurrence and mean error size for all tested neurons. A: CS discharge probability as a function of error amplitude for each of 5 late-broad (filled squares) units and the 13 early-compact (open squares). Gray shading identifies data obtained for off-direction 3 and 1.5° errors and 0 error. *Neurons in which the relation between the CS occurrence and positive error sizes (unshaded data) was not significant (G statistics, P > 0.05). B: separate plots of the average probabilities with error size of the early-compact (open squares) and late-broad (filled squares) units. Error bars represent SE.
We compared the average CS sensitivities to error size for the early-compact (□) and late-broad (▪) neurons (Fig. 9B). For both response groups, negative error sizes produced little change in the averaged CS occurrence (Fig. 9A, shaded area). The averaged CS probability for both –3 and –1.5° errors was significantly smaller than the average resting probability of 0.1 (left-tail t-test, P < 0.05). For 0° error, the averaged CS probability was not significantly different from 0.1 (P > 0.05). For the population of early-compact neurons (□), the average CS probabilities for error sizes of 1.5, 3, and 5° were not significantly different from each other (P > 0.05), but the average probabilities for error sizes of 1.5 and 3° were significantly greater than those for error sizes of 7 and 9° (P < 0.05; 1-way ANOVA, multiple comparison with Bonferroni correction). In contrast, for the population of late-broad neurons, the average CS probability for all positive error sizes was not statistically different (P > 0.5; 1-way ANOVA). Therefore the average CS probability of many early-compact neurons was tuned for error size in the on-direction, whereas most late-broad neurons responded with equal probability, on average, to all error sizes ≤9° in the on-direction.
DISCUSSION
In this study, 39 of 48 P-cells in the oculomotor vermis with saccade-related SS activity also showed changes in CS activity when the eye was off target in the error interval between the end of a dysmetric primary saccade and the subsequent corrective saccade, which eliminated the error (Fig. 1). The paradigm that produced this dysmetria (McLaughlin 1967; our Figs. 1 and 2) causes adaptation of saccade amplitude in the monkey if the intrasaccadic adapting step has a roughly constant size and direction and is repeated for hundreds of trials (Scudder et al. 1998; Straube et al. 1997). In this study, however, we deliberately discouraged adaptation by randomizing both the direction and size of the error and gathering a maximum of only 50 saccades for each error condition. This strategy allowed us to obtain a range of relatively constant specific error sizes. Therefore we could study the properties of the error signal that would occur during a saccade adaptation, but with conditions under our control.
Two populations of CS responses
Our P-cells could be divided, somewhat arbitrarily, into two groups according to the timing of CS occurrence relative to the end of the primary saccade (time of error onset). An early-compact group exhibited an early response that peaked ∼100 ms after error onset (Fig. 4B) with very little scatter of timing across neurons. Many of these neurons also exhibited a smaller peak near the occurrence of the corrective saccade about 70 ms later. Because saccades often are associated with a pause in CS activity (Soetedjo and Fuchs 2006; Fig. 1A this paper), this later response might have been more probable (Fig. 4B) had the corrective saccade been delayed. A second CS seldom occurred on the same trial where one had occurred earlier.
Similar double peaks in CS discharge have been reported in response to stimulation of the cat forepaw (Bloedel and Ebner 1984). Cells in the inferior olive of the rat exhibit subthreshold membrane potential oscillations at 6–12 Hz, and when a spike occurred, it rode on the depolarization phase (Chorev et al. 2007). Therefore a similar subthreshold oscillation may cause our units to have two clusters of CSs separated by the period of the oscillation. Perhaps the occurrence of the primary saccade synchronizes the phase of the subthreshold oscillation, so that the first CSs occur with little jitter ∼100 ms after the saccades. Saccade occurrence could be signaled by the projection of the caudal fastigial nucleus to the inferior olive (Ikeda et al. 1989).
A late-broad group of P-cells exhibited only later responses with latencies scattered broadly across neurons. In this group, the response peaked an average of 128 ms after error onset. The average probability of CS occurrence was slightly higher for these late-broad (0.36 CSs/trial) than for the early-compact responses (0.29 CSs/trial).
These two groups, which can be differentiated on the basis of their temporal response patterns, also tend to show differential sensitivities to some characteristics of the intersaccadic error. With regard to direction tuning, the two groups show overlapping distributions of preferred error directions (Fig. 5B). There is a weak tendency, at best, for the majority of early-compact neurons to have a relatively narrow distribution of tuning half widths near 40°, whereas late-broad neurons show a broader distribution (Fig. 5C). With regard to sensitivity to error size, 80% of late-broad neurons did not show a significant relation to the size of on-direction error whereas 62% of early-compact neurons did. Therefore the majority of early-compact neurons were tuned for error size, whereas almost all late-broad neurons were not. However, more late-broad neurons will need to be examined to confirm this apparent dichotomy.
Our data raise the question of whether and how these error signals could be used for saccade adaptation. There is as yet no conclusive evidence that CS occurrence in the oculomotor vermis indeed provides an error signal for saccade adaptation. However, we could infer that it does if the selectivity of CSs for error size and direction matches the error selectivity, if any, of behavioral saccade adaptation.
Error signals and saccade adaptation
ERROR AMPLITUDE INFORMATION.
On average, the late-broad neurons had constant sensitivities to error sizes ≤9°. On the other hand, the early-compact neurons preferred errors of ≤3° (Fig. 9B). This relation resembles that describing the amount of behavioral adaptation associated with errors of different fixed sizes (Robinson et al. 2003: Fig. 4; their 12° data are nearest those from our 15° targets).
Perhaps the late-broad units that respond for errors of all sizes get the adaptation process started and the early-compact units provide a facilitating error signal once smaller dysmetrias have been achieved. In this scenario, errors near 3° would result in a greater, and perhaps faster, 15° saccade adaptation than that for other error sizes. If this were true, one might expect that during adaptation the speed of saccade gain change (caused by a 33% back step associated with a 15° target step) would increase with decreasing error. However, we have never seen evidence of a continual increase of adaptation speed in the middle of such an adaptation, in which case the decrease in saccade amplitude would have followed a polynomial instead of the often reported exponential time course. Perhaps the differential effect of small and large errors on the time course of adaptation can be observed only by comparing two adaptation sessions: one with a fixed small adapting error and a second with fixed large error (Robinson et al. 2003). Another possibility is that activity from the two CS populations are used selectively when dysmetrias result from different conditions. In this scenario, the untuned units might provide an emergency error signal in the case of a large dysmetria, such as that which occurs during the early months of development (Harris et al. 1993). In contrast, during the small gradual dysmetrias associated with aging (Munoz et al. 1998; Warabi et al. 1984), the tuned units might provide the error signal that drives adaptation.
ERROR DIRECTION INFORMATION.
The preferred error directions for CSs were distributed over all angles with fewer tuned for vertical directions (Fig. 5B). Few published studies have adapted saccade amplitudes in directions other than horizontal. If the CS activity described here drives adaptation, we predict that saccades should be able to adapt in all directions. Indeed, preliminary data gathered in our laboratory on one monkey indicate that saccade adaptation in all directions is very similar when the same error back-step is presented randomly for ≥250 trials in each of the eight directions tested in Fig. 3.
Because a single IO neuron projects to a limited number of P-cells (∼10 in the cat; Mlonyeni 1973), we suggest that only those P-cells targeted with CSs reporting a specific error vector (size and direction) could undergo plastic changes during saccade adaptation to that error signal. In this scenario, if we used the same error direction, say rightward, to adapt upward or leftward saccades, the same subset of P-cells would be active. They would be involved whenever a rightward error signal was used to drive adaptation of primary saccades in any direction. The tuning with error size and direction of one of our CS response groups is reminiscent of the characteristics of adaptation fields in both humans (Frens and van Opstal 1994) and monkeys (Noto et al. 1999). The term “adaptation field” describes the observation that adaptation of saccades of a particular vector transfers well to saccades with similar vectors but poorly, if at all, to saccades with vectors that are substantially different in either amplitude and/or direction. For example, the directional tuning of CS activity with a maximum SD of 90° (Fig. 5C) might underlie the lack of gain transfer to saccades orthogonal to the adapted direction (Noto et al. 1999).
The error information is visual. When we extinguished the target as the primary saccade landed, the CS response in the error interval of both early-compact and late-broad neurons largely disappeared (Fig. 6). Therefore the primary saccade per se was not responsible for the response, and the response was visual.
What are the possible sources of this signal? The intermediate layer of the SC projects to the b subnucleus of the caudal medial accessory olive (Frankfurter et al. 1976; Harting 1977; Huerta and Harting 1984), which, in turn, projects to lobule VII of the vermis (Kralj-Hans et al. 2007). Quasi-visual (QV) neurons in the SC (Mays and Sparks 1980), which start discharging 80–90 ms after a target step and cease firing only when the saccade is executed (and the error is eliminated), could be the source of this visual error signal. During adaptation, the discharges of the QV neurons for planning the corrective saccades may provide an error signal to the inferior olive. Moreover, the receptive fields of QV neurons could confer the directional and amplitude selectivity exhibited by CS responses. The CS preference of some of our units for small errors might be the result of the heavier projections from the rostral SC (Kyuhou and Matsuzaki 1991) to the inferior olive.
In summary, if the CS activity we reported here actually drives adaptation, our data suggest that behavioral adaptation should have certain properties. Indeed, the directional sensitivity of saccade adaptation seems to be consistent with the tuning widths of CS activity (Fig. 5A). Moreover, our preliminary (unpublished) experiments indicate that saccades can adapt equally well in eight directions, as might be expected by our observation that the CS responses of different P-cells represent all error directions (Fig. 5B). Because we have also documented the response characteristics of the putative error signal, e.g., its timing and probability of occurrence, a direct test of whether CS activity in the vermis actually is the error signal for adaptation would be to try to produce adaptation “artificially” by stimulating the b nucleus of the caudal medial accessory olive ∼100 ms after a saccade with the target turned off.
Comparison with other studies
Tuning of the magnitude of a putative CS error signal for adaptation also has been shown in another oculomotor behavior, the vestibulo-ocular reflex (VOR). The velocity at which the visual world slips across the retina when VOR gain is inappropriate is thought to be the signal that drives VOR adaptation (Miles and Lisberger 1981). Like our CS responses that favor small position errors, CS activity generated in the rabbit dorsal cap of Kooy of the inferior olive changes preferentially for very small horizontal slip velocities (Barmack and Hess 1980). However, not all slip directions are represented; the preferred axes are aligned with either the axes of the semicircular canals or the extraocular muscles (Leonard et al. 1988). In the somatosensory system, error direction for an intended arm movement is encoded by CSs in the cerebellar hemispheres (Kitazawa et al. 1998).
In our previous study, we concluded that CS occurrence indicated only the direction and not the magnitude of the error that induces behavioral adaptation. In that study, we examined only left- and rightward horizontal errors. Based on this study, we can say that CSs usually occurred more frequently for errors occurring in directions off the horizontal axis (Fig. 5B). In the previous paper, we also relied on the natural changes of error size produced by saccade adaptation, which restricted our error range to 1–5°. In this paper, we deliberately tested larger errors along the preferred error direction and showed that some units were tuned for error size. This property was not shown in our previous study because the maximum error we tested always was <5°.
One other group has examined the occurrence of CSs during saccade adaptation in the monkey. During backward adaptation, Catz et al. (2005) reported an increase in both the rate and duration of the average population CS response as adaptation evolved. The change began during the saccade and ended early in the intersaccadic error interval (their Fig. 4B). Our current data differ from theirs in three ways. First, during backward adaptation, we never observed an increase in CS occurrence earlier than 50 ms after the primary saccade (our Fig. 4, B and C); our peak CS activity occurred between 100 and 150 ms after the primary saccade, a time when their average activity already had returned to baseline. Second, their mean response rates (≤0.4 spikes/s) were only 40% of ours. Third, their data showed no change in CS activity at adaptation onset (when their error was ∼3°) and exhibited the maximum change only after adaptation had driven the error quite low. With a similar 3° initial error, the CS activity of our P-cells at the onset of adaptation would be elevated and would remain so throughout adaptation. Only after the error had been driven to zero would CS activity return to its resting levels. Further experiments will be necessary to explain the discrepancy between our data and theirs.
GRANTS
This study was supported by National Institutes of Health Grants EY-00745 and RR-00166 from the National Center for Research Resources (NCRR), a component of the National Institutes of Health. The contents of this paper are solely the responsibility of the authors and do not necessarily represent the official views of NCRR or National Institutes of Health.
Acknowledgments
We are grateful for the surgical assistance of B. Brown and the veterinary support of the staff of the Washington National Primate Research Center. We also benefited from the valuable comments of S. Bierer, C. Kaneko, J. Phillips, L. Ling, and A. Weiss on an earlier version of the manuscript.
APPENDIX
The MI and G statistics are statistical tests to measure the relation between two categorical random variables. MI measures the strength of the relation between the two variables, but to test the significance of the relation, a G test is required. The following derivation shows the relation between MI and the G test.
The G test compares the observed against the expected frequencies by the following formula
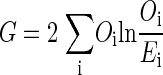 |
(4) |
where Oi is the observed frequency of cell i in the contingency table, and Ei is the expected frequency of cell i, which is the null hypothesis for this test, i.e., there is no relation between the two random variables.
For simplicity we will use 2 × 2 contingency table (Table 2) to derive the relation between MI and the G test, but the derivation can be generalized to an m × n table.
TABLE 2.
Two × two contingency tables used to show the calculation of the G statistic
| A1 | A0 | Total | |
|---|---|---|---|
| A. Observed frequency (Oi) table | |||
| B1 | a | b | a+b |
| B0 | c | d | c+d |
| Total | a+c | b+d | n |
| B. Expected frequency (Ei) table | |||
| B1 | (a+b)(a+c)/n | (a+b)(b+d)/n | a+b |
| B0 | (c+d)(a+c)/n | (c+d)(b+d)/n | c+d |
| Total | a+c | b+d | n |
| C. Probability of A given B [p(A|B)] table | |||
| B1 | a/(a+b) | b/(a+b) | 1 |
| B0 | c/(c+d) | d/(c+d) | 1 |
Using the observed (A) and expected (B) frequency tables, G is computed as
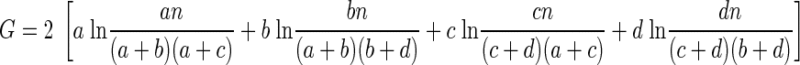 |
(5) |
Converting the natural log (ln) into log-base 2
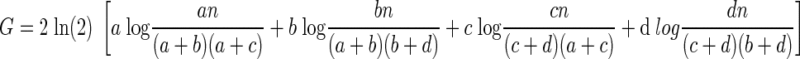 |
(6) |
The MI is based on Eqs. 1, 1A, and 1B and computed using the observed frequency (A) and p(A|B) tables (C)
The entropy of A
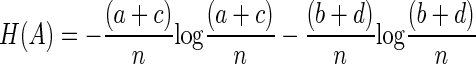 |
(7) |
which can be expanded to
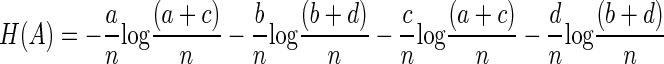 |
(8) |
The entropy of A given B is
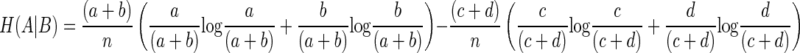 |
(9) |
Simplifying Eq. 9 by rearrangement
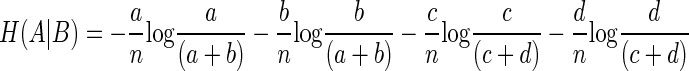 |
(10) |
Therefore the MI computed by subtracting Eq. 10 from Eq. 8 is
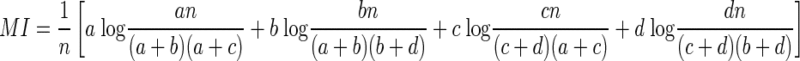 |
(11) |
By combining Eqs. 6 and 11, therefore
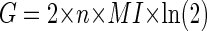 |
The costs of publication of this article were defrayed in part by the payment of page charges. The article must therefore be hereby marked “advertisement” in accordance with 18 U.S.C. Section 1734 solely to indicate this fact.
Footnotes
Because saccade size varied somewhat with direction, the error size after the back-step was not constant. For example, the error size for a typical experiment ranged, on average, from 3.0 ± 0.6 to 4.4 ± 0.7° across the eight directions. Such directional differences of error size should not have an impact on the evaluation of direction tuning because, as we will show later, the probability of CS for this range of error sizes was essentially constant.
REFERENCES
- Albus 1971.Albus J A theory of cerebellar function. Math Biosci 10: 25–61, 1971. [Google Scholar]
- Bahill et al. 1975.Bahill AT, Clark MR, Stark L. Dynamic overshoot in saccadic eye movements is caused by neurological control signed reversals. Exp Neurol 48: 107–122, 1975. [DOI] [PubMed] [Google Scholar]
- Barash et al. 1999.Barash S, Melikyan A, Sivakov A, Zhang M, Glickstein M, Thier P. Saccadic dysmetria and adaptation after lesions of the cerebellar cortex. J Neurosci 19: 10931–10939, 1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barmack and Hess 1980.Barmack NH, Hess DT. Multiple-unit activity evoked in dorsal cap of inferior olive of the rabbit by visual stimulation. J Neurophysiol 43: 151–164, 1980. [DOI] [PubMed] [Google Scholar]
- Bloedel and Ebner 1984.Bloedel JR, Ebner TJ. Rhythmic discharge of climbing fibre afferents in response to natural peripheral stimuli in the cat. J Physiol 352: 129–146, 1984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catz et al. 2005.Catz N, Dicke PW, Thier P. Cerebellar complex spike firing is suitable to induce as well as to stabilize motor learning. Curr Biol 15: 2179–2189, 2005. [DOI] [PubMed] [Google Scholar]
- Chorev et al. 2007.Chorev E, Yarom Y, Lampl I. Rhythmic episodes of subthreshold membrane potential oscillations in the rat inferior olive nuclei in vivo. J Neurosci 27: 5043–5052, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeWeese and Meister 1999.DeWeese MR, Meister M. How to measure the information gained from one symbol. Network 10: 325–340, 1999. [PubMed] [Google Scholar]
- Frankfurter et al. 1976.Frankfurter A, Weber JT, Royce GJ, Strominger NL, Harting JK. An autoradiographic analysis of the tecto-olivary projection in primates. Brain Res. 118: 245–257, 1976. [DOI] [PubMed] [Google Scholar]
- Frens and van Opstal 1994.Frens MA, van Opstal AJ. Transfer of short-term adaptation in human saccadic eye movements. Exp Brain Res 100: 293–306, 1994. [DOI] [PubMed] [Google Scholar]
- Fuchs and Robinson 1966.Fuchs AF, Robinson DA. A method for measuring horizontal and vertical eye movement chronically in the monkey. J Appl Physiol 21: 1068–1070, 1966. [DOI] [PubMed] [Google Scholar]
- Harris et al. 1993.Harris CM, Jacobs M, Shawkat F, Taylor D. The development of saccadic accuracy in the first seven months. Clin Vision Sci 8: 85–96, 1993. [Google Scholar]
- Harting 1977.Harting JK Descending pathways from the superior collicullus: an autoradiographic analysis in the rhesus monkey (Macaca mulatta). J Comp Neurol 173: 583–612, 1977. [DOI] [PubMed] [Google Scholar]
- Huerta and Harting 1984.Huerta MF, Harting JK. The mammalian superior colliculus: studies of its morphology and connections. In: Comparative Neurology of the Optic Tectum, edited by Vanegas H. New York: Plenum, 1984, p. 687–773.
- Ikeda et al. 1989.Ikeda Y, Noda H, Sugita S. Olivocerebellar and cerebelloolivary connections of the oculomotor region of the fastigial nucleus in the macaque monkey. J Comp Neurol 284: 463–488, 1989. [DOI] [PubMed] [Google Scholar]
- Ito 1972.Ito M Neural design of the cerebellar control system. Brain Res 40: 80–82, 1972. [DOI] [PubMed] [Google Scholar]
- Ito 1982.Ito M Cerebellar control of the vestibulo-ocular reflex–around the flocculus hypothesis. Annu Rev Neurosci 5: 275–296, 1982. [DOI] [PubMed] [Google Scholar]
- Kitazawa et al. 1998.Kitazawa S, Kimura T, Yin P-B. Cerebellar complex spikes encode both destinations and errors in arm movements. Nature 392: 494–497, 1998. [DOI] [PubMed] [Google Scholar]
- Kralj-Hans et al. 2007.Kralj-Hans I, Baizer JS, Swales C, Glickstein M. Independent roles for the dorsal paraflocculus and vermal lobule VII of the cerebellum in visuomotor coordination. Exp Brain Res 177: 209–222, 2007. [DOI] [PubMed] [Google Scholar]
- Kyuhou and Matsuzaki 1991.Kyuhou SI, Matsuzaki R. Topographical organization of the tecto-olivo-cerebellar projection in the cat. Neuroscience 41: 227–241, 1991. [DOI] [PubMed] [Google Scholar]
- Leonard et al. 1988.Leonard C, Simpson JI, Graf W. Spatial organization of visual messages of the rabbit's cerebellar flocculus. I. Typology of inferior olive neurons of the dorsal cap of Kooy. J Neurophysiol 60: 2073–2090, 1988. [DOI] [PubMed] [Google Scholar]
- Llinás, and Welsh 1993.Llinás R, Welsh JP. On the cerebellum and motor learning. Curr Opin Neurobiol 3: 958–965, 1993. [DOI] [PubMed] [Google Scholar]
- Marr 1969.Marr D A theory of cerebellar cortex. J Physiol 202: 437–470, 1969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mays and Sparks 1980.Mays LE, Sparks DL. Dissociation of visual and saccade-related responses in superior colliculus neurons. J Neurophysiol 43: 207–232, 1980. [DOI] [PubMed] [Google Scholar]
- McLaughlin 1967.McLaughlin SC Parametric adjustment in saccadic eye movements. Percept Psychol 2: 359–362, 1967. [Google Scholar]
- Miles and Lisberger 1981.Miles FA, Lisberger SG. Plasticity in the vestibulo-ocular reflex: a new hypothesis. Annu Rev Neurosci 4: 273–299, 1981. [DOI] [PubMed] [Google Scholar]
- Mlonyeni 1973.Mlonyeni M The number of Purkinje cells and inferior olivary neurones in the cat. J Comp Neurol 147: 1–10, 1973. [DOI] [PubMed] [Google Scholar]
- Munoz et al. 1998.Munoz DP, Broughton JR, Goldring JE, Armstrong IT. Age-related performance of human subjects on saccadic eye movement tasks. Exp Brain Res 121: 392–400, 1998. [DOI] [PubMed] [Google Scholar]
- Noda et al. 1990.Noda H, Sugita S, Ikeda Y. Afferent and efferent connections of the oculomotor region of the fastigial nucleus in the macaque monkey. J Comp Neurol 302: 330–348, 1990. [DOI] [PubMed] [Google Scholar]
- Noto et al. 1999.Noto C, Watanabe S, Fuchs AF. Characteristics of adaptation fields produced by behavioral changes in saccadic gain and direction. J Neurophysiol 81: 2798–2813, 1999. [DOI] [PubMed] [Google Scholar]
- Optican and Robinson 1980.Optican LM, Robinson DA. Cerebellar-dependent adaptive control of primate saccadic system. J Neurophysiol 44: 1058–1076, 1980. [DOI] [PubMed] [Google Scholar]
- Robinson 1963.Robinson DA A method of measuring eye movement using a scleral search coil in a magnetic field. IEEE Trans Biomed Eng 10: 137–145, 1963. [DOI] [PubMed] [Google Scholar]
- Robinson et al. 2003.Robinson FR, Noto CT, Bevans SE. Effect of visual error size on saccade adaptation in monkey. J Neurophysiol 90: 1235–1244, 2003. [DOI] [PubMed] [Google Scholar]
- Scudder et al. 1998.Scudder CA, Batourina EY, Tunder GS. Comparison of two methods of producing adaptation of saccade size and implications for the site of plasticity. J Neurophysiol 79: 704–715, 1998. [DOI] [PubMed] [Google Scholar]
- Simpson et al. 1996.Simpson JI, Wylie DR, De Zeeuw CI. On climbing fiber signals and their consequences. Behav Brain Sci 19: 384–398, 1996. [Google Scholar]
- Soetedjo and Fuchs 2006.Soetedjo R, Fuchs AF. Complex spike activity of Purkinje cells in the oculomotor vermis during behavioral adaptation of monkey saccades. J Neurosci 26: 7741–7755, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sokal and Rohlf 1994.Sokal RR, Rohlf FJ. Biometry: The Principles and Practice of Statistics in Biological Research (3rd ed.). New York: Freeman, 1994.
- Sparks and Hartwich-Young 1989.Sparks DL, Hartwich-Young R. The deep layers of the superior colliculus. Rev Oculomot Res 3: 213–255, 1989. [PubMed] [Google Scholar]
- Straube et al. 1997.Straube A, Fuchs AF, Usher S, Robinson FR. Characteristic of saccadic gain adaptation in rhesus macaques. J Neurophysiol 77: 874–895, 1997. [DOI] [PubMed] [Google Scholar]
- Warabi et al. 1984.Warabi T, Kase M, Kato T. Effect of aging on the accuracy of visually guided saccadic eye movement. Ann Neurol 16: 449–454, 1984. [DOI] [PubMed] [Google Scholar]
- Wilks 1935.Wilks SS The likelihood test of independence in contingency tables. Ann Math Statist 6: 190–196, 1935. [Google Scholar]
- Yamada and Noda 1987.Yamada J, Noda H. Afferent and efferent connections of the oculomotor cerebellar vermis in the macaque monkey. J Comp Neurol 265: 224–241, 1987. [DOI] [PubMed] [Google Scholar]