Dynamic Viscoelasticity of Actin Cross-Linked with Wild-Type and Disease-Causing Mutant α-Actinin-4

Abstract

The actin cross-linker α-actinin-4 has been found to be indispensable for the structural and functional integrity of podocytes; deficiency or alteration of this protein due to mutations results in kidney disease. To gain insight into the effect of the cross-linker on cytoskeletal mechanics, we studied the macroscopic rheological properties of actin networks cross-linked with wild-type and mutant α-actinin-4. The frequency-dependent viscoelasticity of the networks is characterized by an elastic plateau at intermediate frequencies, and relaxation toward fluid properties at low frequencies. The relaxation frequencies of networks with mutant α-actinin-4 are an order of magnitude lower than that with the wild-type, suggesting a slower reaction rate for the dissociation of actin and α-actinin for the mutant, consistent with a smaller observed equilibrium dissociation constant. This difference can be attributed to an additional binding site that is exposed as a result of the mutation, and can be interpreted as a difference in binding energy barriers. This is further supported by the Arrhenius-like temperature dependence of the relaxation frequencies.

INTRODUCTION

Rheological studies of biopolymer gels can make valuable contributions to our understanding of the cell as a material (1), and in particular the mechanical properties of the cytoskeleton. Research in recent years has focused on in vitro measurements of the viscoelastic properties of reconstituted cytoskeletal protein networks, which have been shown to resemble their in vivo counterparts in many aspects. Among the three major components of the cytoskeleton—actin, intermediate filaments, and microtubules—filamentous actin (F-actin) has been the most widely studied (2,3). F-actin is a polymer composed of 42 kDa globular monomeric subunits (G-actin) that assemble into double-stranded, helical, semiflexible microfilaments that measure ∼7 nm in diameter. The finely woven entangled networks typically formed by pure 1 mg/mL F-actin solutions behave like weak viscoelastic solids with an elastic modulus on the order of 0.1–1 Pa (4). The addition of cross-linking proteins strengthens these networks and can, at sufficiently high concentrations, bundle individual microfilaments into filaments of larger diameters, which in turn form networks of larger mesh size and often dramatically altered viscoelastic properties. Scruin, for instance, is a 102 kDa molecule that cross-links the network incompliantly, increasing its stiffness by two orders of magnitude at a monomer ratio to actin of 0.1 (5,6). The larger, more flexible 560 kDa dimer filamin affects the linear elasticity only weakly, but alters the nonlinear stiffness drastically (7,8). The cross-linker α-actinin, an antiparallel homodimer of 200 kDa and ∼40 nm in length, is similar to scruin in its structure, but cross-links actin reversibly as does filamin. Its various isoforms, which can be found in smooth muscle, skeletal muscle, and nonmuscle cells, result in networks of widely varying structure and stiffness (9–13).

In recent years, the nonmuscle isoform α-actinin-4 has been found to play a nonredundant role in the function of renal glomeruli (14,15). To date, five mutations in the actin-binding domain of α-actinin-4 have been shown to cause a progressive form of kidney dysfunction, characterized by a pattern of tissue injury termed focal and segmental glomerulosclerosis (FSGS) (15–17). An estimated 4% of familial FSGS in affected humans is accounted for by these mutations (17). The initial sites of injury are the glomerular epithelial cells, or podocytes, which are a major constituent in the filtration barrier and are exposed to significant mechanical stresses due to dynamic changes in glomerular capillary pressure. In these cells, α-actinin-4, which is believed to regulate the cells' highly organized actin cytoskeleton, is highly expressed. All disease-causing mutations increase the protein's actin binding affinity and lead to abnormal actin aggregation. Since the unique structure of podocytes renders them particularly susceptible to changes in the actin cytoskeleton, these α-actinin-4 mutations have drastic consequences for the kidney, even if they do not affect the phenotype of other organs and tissues.

One particular point mutation, which encodes a K255E amino acid exchange in the α-actinin-4 protein and is known to cause FSGS and kidney failure in humans, has been extensively investigated by Weins et al. (18). A mouse model homozygous for the mutation exhibits large actin/α-actinin-4 aggregates in the podocytes and subsequently develops a form of collapsing glomerulopathy. The actin cytoskeleton in podocytes is important for maintaining the structural integrity of these cells as mechanical support for the glomerular capillaries. Thus, it is likely that dysregulation of this intricate cytoskeleton is responsible for the collapsing phenotype. In standard cosedimentation assays of actin and α-actinin-4, the equilibrium dissociation constant for the mutant has been determined to be K_d,mut = 0.046 μM, almost six times lower than that of the wild-type, K_d,wt = 0.267 μM. Further, the mutant saturates actin at one dimer per two actin monomers, whereas the wild-type saturates at one dimer per four actin monomers. Weins et al. (18) attributed these differences to a conformational change in the protein. Each α-actinin monomer is composed of an N-terminal F-actin binding domain, four spectrin repeats, and a C-terminal Ca²⁺ binding domain. In wild-type α-actinin-4, the actin-binding domain contains two actin-binding sites, and its actin affinity can be regulated by Ca²⁺ binding to the neighboring N-terminal domain of the second α-actinin monomer (18). An additional actin-binding site is partially buried in the “closed” conformation of the wild-type. The K255E mutation is believed to lead to a higher propensity of the open conformation, which exposes the otherwise buried actin-binding site. The mutant has also been shown to be insensitive to regulation by Ca²⁺. This explanation is corroborated by the fact that inactivation of the additional binding site returns the affinity of the mutant to that of the wild-type, while leaving the affinity of the wild-type unaltered. Weins et al. (18) proposed that the different stoichiometric ratios of α-actinin-4 to actin can be ascribed to greater geometric flexibility of the mutant, which allows it to access every binding site along an actin filament. This flexibility also serves to explain their observation that actin polymerized in the presence of mutant α-actinin-4 forms networks of thin actin bundles, whereas the wild-type tends to connect actin into thicker, parallel bundles. Using miniature falling-ball viscometry, Weins et al. (18) found that the mutant results in an abrupt viscosity increase, signifying the gel point of the network, at a much lower cross-linker concentration than the wild-type. Further comparative investigations of the viscosity and elasticity of networks with wild-type and mutant α-actinin-4 could provide more insight into the disease-mediating characteristics of the mutant, especially in view of the pivotal role of the actin cytoskeleton in podocytes; however, to our knowledge, no systematic studies of actin networks cross-linked specifically with α-actinin-4 have been performed to date.

In this work we provide a detailed analysis of the viscoelastic properties of in vitro networks formed from actin with wild-type and K255E-mutant α-actinin-4, using rheological data. The difference between the two cross-linkers is most apparent in measurements of the elastic and viscous moduli as a function of the frequency of the applied oscillatory shear stress. We elucidate the effect of different binding affinities on the macroscopic network dynamics by contrasting it with the effect of varied cross-linker concentration and temperature.

MATERIALS AND METHODS

Materials

Actin was prepared from rabbit skeletal muscle in a polymerization-depolymerization cycle, and subsequently further purified by gel filtration. G-actin was stored in G-buffer (2 mM Tris-HCl, pH 7.4, 0.5 mM ATP, 0.5 mM 2-mercaptoethanol, 0.2 mM CaCl₂) at −80°C. Baculovirus-expressed recombinant wild-type and K255E mutant α-actinin-4 was generated from human cDNA sequences by ProteinOne (Bethesda, MD) (18) and stored in α-actinin buffer (20 mM Tris-HCl, pH 7.9, 20% glycerol, 100 mM NaCl, 1 mM DTT, 0.2 mM EDTA) at −80°C.

Network formation

Networks of various cross-linker concentrations were formed by mixing 23.8 μM (1 mg/mL) G-actin solution with α-actinin-4 solutions of concentrations ranging from 0.03 μM to 1.9 μM, corresponding to molar ratios of α-actinin to actin, R, between R = 0.00125 and R = 0.08. Polymerization was initiated by the addition of 5× polymerization buffer (50 mM Tris-HCl, pH 7.4, 500 mM KCl, 5mM MgCl, 2.5 mM EGTA, 2.5 mM ATP). The samples were then immediately transferred to a rheometer or confocal microscope, respectively.

Network visualization

Actin was fluorescently stained with 2 μM Alexa Fluor 488 phalloidin (Invitrogen, Carlsbad, CA). Samples of 10 μL in volume were confined between two glass coverslips spaced at ∼1 mm and examined under a Zeiss LSM 510-Meta confocal microscope with a 63× objective. Fluorescence was excited with an Argon laser at 488 nm, and the signal was filtered by a 505-nm-long-pass filter.

Bulk rheology

Oscillatory measurements of the elastic modulus G′ and the viscous modulus G″ were performed with a controlled stress AR-G2 rheometer (TA Instruments, New Castle, DE). The sample was loaded into a cone-plate geometry with a diameter of 20 mm, a cone angle of 2°, and a gap size of 50 μm (sample volume = 70 μL). A solvent trap was used to prevent drying. Immediately after the addition of polymerization buffer and sample transfer to the rheometer, polymerization was monitored for a period of 1–2 h through point measurements of the viscoelastic moduli in 5-min intervals at a strain of 0.5% and an oscillation frequency of 0.1 Hz. The frequency dependence of the linear viscoelastic moduli G′ and G″ was determined between 0.01 Hz and 10 Hz. To ensure that data were taken in the linear regime, where the network response is proportional to the amplitude of the imposed oscillatory stress, the instrument was operated in its strain-controlled mode at strains between 0.5% and 2%, depending on the strength of the network. For each measurement of the frequency dependence, the temperature was kept constant. If not stated otherwise, it was held at 25°C. To investigate the temperature dependence of the network dynamics, the temperatures for different measurements at the same sample were varied between 5°C and 40°C by means of the Peltier temperature control of the lower rheometer plate.

RESULTS AND DISCUSSION

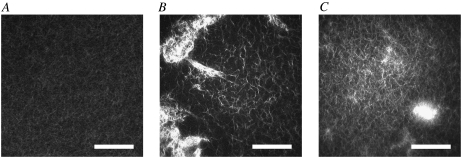
Actin polymerized in vitro forms finely meshed, homogeneous, isotropic three-dimensional networks (Fig. 1 A). The addition of cross-linking proteins often results in networks of larger mesh size, which consist of actin bundles comprising many individual filaments. We confirmed by confocal fluorescence microscopy that this general trend also holds for networks of actin with wild-type and mutant α-actinin-4 prepared in the same way as the samples used for our rheological measurements. At a concentration of one α-actinin-4 molecule per 100 actin monomers, R = 0.01, the wild-type cross-linker (Fig. 1 B) appears to form a coarser network than the mutant (Fig. 1 C), consistent with the larger bundle diameter reported by Weins et al. (18) for actin cross-linked with wild-type α-actinin-4. However, we find the cross-linked networks interspersed with large actin agglomerates (Fig. 1, B and C), whose size and number vary from sample to sample, and tend to increase with higher cross-linker concentration. Moreover, the homogeneous network regions vary in mesh size even within one sample, thus rendering a quantitative comparison of the effects of wild-type and mutant on the network structure unfeasible.

FIGURE 1.

Confocal images of networks formed of actin (1 mg/mL) (A) without cross-linker, (B) with wild-type α-actinin-4 (R = 0.01), and (C) with mutant α-actinin-4 (R = 0.01). Actin is fluorescently labeled with Alexa-Fluor-Phalloidin (excitation at 488 nm). Scale bar, 40 μm.

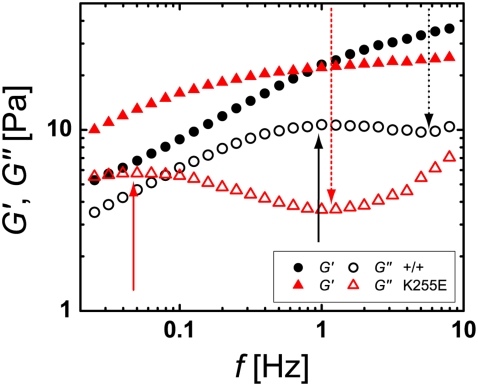
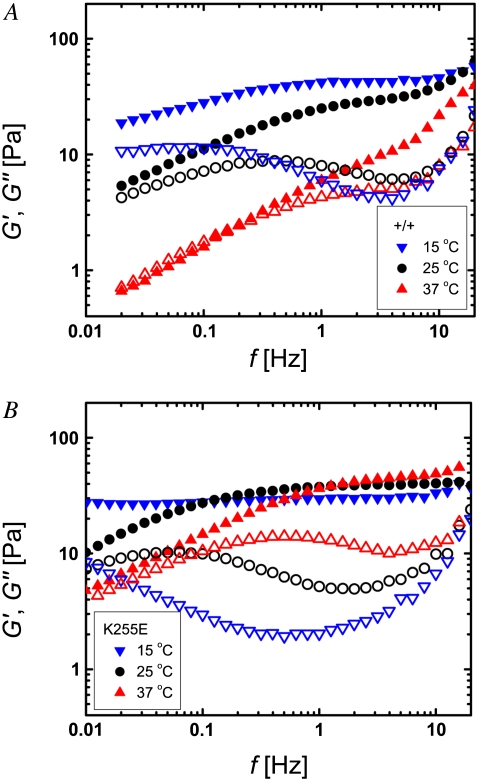
Despite the large sample-to-sample variations of the network structures and inhomogeneities at length scales of tens of micrometers, the cross-linked networks exhibit robust rheological properties, a consequence of sample averaging over larger dimensions. At a molar ratio of R = 0.01, cross-linking increases the network stiffness by about an order of magnitude. The elastic and viscous moduli vary greatly with the frequency of the applied oscillatory shear stress. At the intermediate frequencies that we can access through bulk rheological measurements, the linear viscoelasticity is characterized by a nearly frequency-independent plateau in the elastic modulus G′ and a corresponding minimum of the viscous modulus G″ (Fig. 2). A direct comparison of the effect of wild-type (circles) and mutant (triangles) cross-linker reveals that the latter results in a more distinct elastic plateau. Moreover, the characteristic frequency of the plateau, f_plateau, which we define as the frequency at which G″ assumes its local minimum, is smaller for the mutant than for the wild-type, as indicated by the dotted, downward pointing arrows in Fig. 2.

FIGURE 2.

Frequency dependence of the elastic modulus G′ (solid symbols) and the viscous modulus G″ (open symbols) of actin networks with wild-type (+/+, circles) and mutant (K255E, triangles) α-actinin-4 at a molar ratio of α-actinin-4 to actin of R = 0.01. The networks are characterized by an elastic plateau and a relaxation toward fluid properties at lower frequencies. The response for mutant α-actinin-4 appears shifted toward lower frequencies and exhibits a higher ratio G′/G″ at the plateau frequency. The dotted, downward-pointing arrows define the plateau frequency; the solid, upward-pointing arrows define the relaxation frequency of the networks.

In the high-frequency limit, we expect the network viscoelasticity to be dominated by the thermal bending fluctuations of individual filaments, leading to an increase of both moduli with frequency with a power of 3/4 (19,20). We cannot measure at frequencies high enough to confirm this dependence, but we observe for several samples the onset of an ascent of G′ and G″ with an increasing slope of up to 0.6 in a log-log plot.

At low frequencies, the networks carry the signature of a structural relaxation process: the viscous modulus G″ approaches the elastic modulus with decreasing frequency, passing through a maximum value and then decreasing along with G′. We expect G″ to eventually exceed G′, indicating a relaxation of the network behavior to fluid properties. Although for most data sets the range of our measurements does not extend to low enough frequencies to verify this crossover, we do observe it in a few cases. For comparisons of relaxation frequencies across samples, we take f_relax to be the well-defined frequency at which G″ reaches a local maximum, indicated by upward-pointing arrows in Fig. 2. In comparing networks with wild-type and mutant α-actinin-4, we find that f_relax is more than an order of magnitude lower for the mutant. Taken together with the smaller equilibrium dissociation constant of mutant α-actinin-4 (18), this observation suggests that the relaxation of the macroscopic network may be related to the microscopic unbinding of the cross-linker. When an α-actinin-4 dimer dissociates from actin at either binding site, the cross-link breaks, and filaments can locally slide with respect to each other. The cross-linker may bind again to actin at both ends, thereby reforming a link in the network. If this happens before other cross-linkers in the vicinity of the broken bond detach, a macroscopic relaxation of the network is not possible. However, our data suggest that enough cross-linkers unbind simultaneously to allow the network to structurally relax, becoming fluid-like at low frequencies.

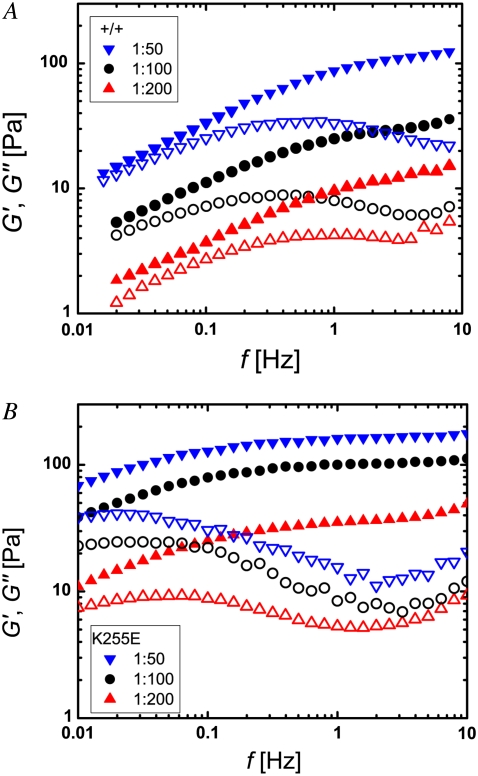
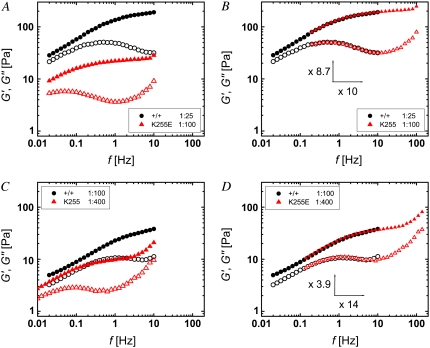
We extended our comparison of wild-type and mutant α-actinin-4 by investigating the effect of the cross-linker concentration on the frequency-dependent viscoelasticity of the networks. With increasing concentration of the wild-type or mutant cross-linker, G′ and G″ rise noticeably over the entire frequency range of our measurements. Although the elastic modulus is shifted upward without a change in its frequency dependence, an increase in concentration does alter the frequency dependence of the viscous modulus. At the plateau, the increase in G′ with concentration tends to be greater than that in G″. Thus, increasing the α-actinin-4 concentration enhances the plateau, pushing the network properties further toward that of a solid, as illustrated by representative network responses for relative α-actinin-4 concentrations of R = 0.005 (triangles), 0.01 (circles), and 0.02 (inverted triangles) in Fig. 3 A for the wild-type and in Fig. 3 B for the mutant cross-linker. Of interest, an increased amount of wild-type α-actinin-4 effects the shape of the viscoelasticity in the vicinity of the plateau qualitatively similarly to a replacement of wild-type by mutant cross-linker. In comparing the curves in Fig. 3, A and B, we see that the behavior of the wild-type cross-linker of the highest concentration shown resembles that of the mutant with the lowest concentration, albeit shifted along both axes. Based on this observation, we investigated whether the altered properties of the mutant can partly be compensated for by a decreased concentration. We found that this is indeed the case. The frequency-dependent viscoelasticity of a network with wild-type α-actinin-4 at a high concentration of R = 0.04 (circles) and a network with mutant α-actinin-4 at a four times lower concentration (R = 0.01, triangles), shown in Fig. 4 A, overlap remarkably well if the mutant curve is shifted toward higher frequencies and higher viscoelastic moduli, as illustrated in Fig. 4 B. Similarly, the curves for samples with a medium amount of wild-type (R = 0.01) and a low amount of mutant (R = 0.0025), which are shown in Fig. 4 C, can be scaled nearly perfectly (Fig. 4 D). This intriguing scaling behavior may have profound implications for understanding the effects of α-actinin-4 on the network properties.

FIGURE 3.

Frequency dependence of the elastic modulus G′ (solid symbols) and the viscous modulus G″ (open symbols) of actin networks with (A) wild-type and (B) mutant α-actinin-4 at molar ratios of α-actinin-4 to actin of R = 0.005 (triangles), R = 0.01 (circles), and R = 0.02 (inverted triangles). For both types of cross-linker, the elastic plateau modulus increases with concentration. Moreover, the plateau is more pronounced and appears at higher frequencies for increased concentration.

FIGURE 4.

Frequency dependence of G′ (solid symbols) and G″ (open symbols) of actin networks with wild-type (circles) and mutant (triangles) α-actinin-4 of different concentrations can be scaled onto one curve. For example, samples with wild-type at high concentration (R = 0.04) and mutant at medium concentration (R = 0.01), as shown in A, overlap if the mutant is shifted by a factor of 10 in frequency and by a factor of 8.7 in the moduli (B). Similarly, samples with wild-type at medium concentration (R = 0.01) and mutant at low concentration (R = 0.0025), shown in C, overlap if the mutant is shifted by a factor of 14 in frequency and by a factor of 3.9 in the moduli (D).

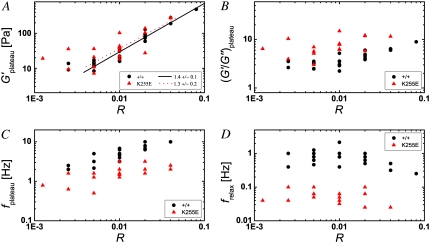
To test the statistical significance of our qualitative observations, we extracted several characteristic quantities from the frequency-dependent viscoelasticity of a larger set of samples, comprised of 24 networks with wild-type and 18 with mutant α-actinin-4, and containing the samples presented in Figs. 3 and 4, and plotted these quantities as a function of cross-linker concentration. We confirmed that the elastic modulus at the plateau frequency, G′_plateau, increases with cross-linker concentration for both wild-type (circles) and mutant (triangles), as shown in Fig. 5 A. Above relative α-actinin-4 concentrations of R = 0.005, the plateau modulus follows a power law of G_plateau ∼ R^4/3 (solid lines). A similar concentration dependence was previously observed for other cross-linkers (3,6). We infer from Fig. 5 that the values of G′_plateau for wild-type and mutant α-actinin-4 at the same concentration are comparable. This might at first seem surprising; however, if we assume a first-order binding reaction between actin and α-actinin-4, we calculate that at an actin monomer concentration of 23.8 μM, almost all cross-linkers are bound to actin. The higher binding affinity of the mutant therefore results in only a marginal increase of bound α-actinin-4 from 98.8% to 99.8% of the total cross-linker amount.

FIGURE 5.

Characteristic features of the frequency-dependent viscoelasticity as a function of the relative concentration R of wild-type (circles) and mutant (triangles) α-actinin-4. (A) The plateau modulus G′ _plateau has comparable values for wild-type and mutant, and increases with cross-linker concentration. Above R = 0.005, the plateau modulus follows a power law for both cross-linker types, as indicated by the solid line for the wild-type and the dotted line for the mutant, and their respective slopes (lower right). (B) The ratio of the plateau modulus and the corresponding viscous modulus, (G′/G″)_plateau, which indicates the solidness of the network, grows weakly with increasing cross-linker concentration, and is on average higher for the mutant than for the wild-type at the same concentration. (C) The frequency at which the elastic plateau occurs (minimum in G″) increases weakly with cross-linker concentration, and is systematically smaller for the mutant. (D) The relaxation frequency of the network (maximum in G″) appears to be independent of the cross-linker concentration, and is about an order of magnitude smaller for the mutant.

Although the mutant does not appear to increase the overall network strength, it does render the network more solid-like, as is evident from the consistently higher values for the ratio of G′ and G″ at the plateau, which is plotted in Fig. 5 B. As observed before and confirmed by the larger data set, this ratio increases slightly with concentration. In addition to G′/G″ at the plateau frequency, the prominence of the elastic plateau is characterized by the width of the frequency range spanned between f_relax and f_plateau. We find that the plateau frequency increases with cross-linker concentration (Fig. 5 C), whereas the relaxation frequency remains approximately constant (Fig. 5 D). As a result, the higher the amount of α-actinin-4, the wider the plateau tends to be. Furthermore, networks with the mutant cross-linker exhibit a slightly lower plateau and a significantly lower relaxation frequency. Consequently, the plateau width is greater for the mutant.

The networks with mutant α-actinin-4 differ most significantly from their wild-type counterparts in that their relaxation frequencies are consistently lower by at least an order of magnitude for concentrations ranging from R = 0.0025 to R = 0.04 (Fig. 5 D). We propose that this shift in timescales is a consequence of a smaller actin/α-actinin-4 unbinding rate for the mutant. Since the equilibrium dissociation constant K_d is the ratio of the dissociation rate, or off-rate k₋, and the association rate, or on-rate k₊, we cannot say with certainty which of the rates differs between wild-type and mutant. However, Weins et al. (18), following an argument of Wachsstock et al. (10), have explained their observation of a stronger tendency of wild-type α-actinin-4 to bundle actin partly by assuming a higher dissociation rate for the wild-type, consistent with the higher value they determined for K_d. If we adopt this assumption, the dissociation rate of the mutant follows to be ∼6 times smaller than that of the wild-type. Given that our practical definition of f_relax as the frequency at which G″ reaches a local maximum only approximates the frequency at which the relaxation actually occurs, this factor is consistent with the observed factor of slightly more than 10 between the relaxation frequencies of wild-type and mutant cross-linked networks (Figs. 2, 4, and 5 D).

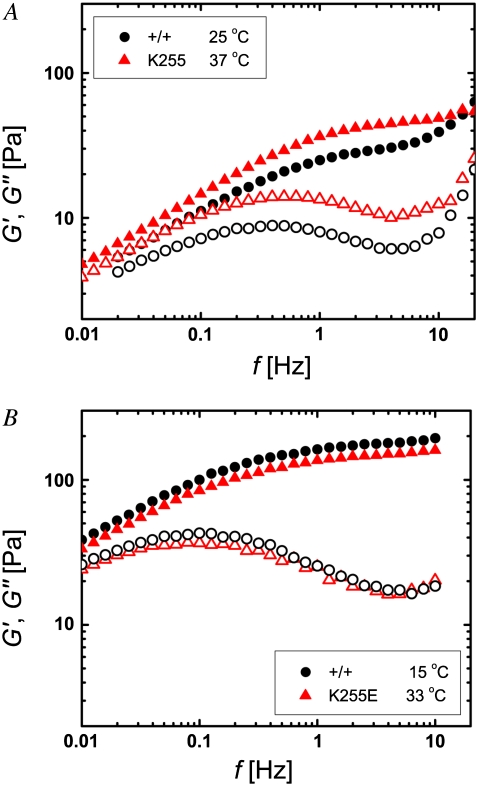
The proposed direct relationship between the characteristic relaxation frequency of the macroscopic network and the microscopic dissociation rates of its constituents is intriguing. One way to test whether the collective network relaxation is indeed related to the unbinding of cross-linkers is to control the microscopic dissociation rate. If we assume that this rate is limited by the fraction of cross-linkers with sufficient kinetic energies to overcome the activation energy barrier of the reaction, an obvious way to influence the dissociation rate is by means of the temperature. Based on our proposition, we expect that the characteristic frequencies of the networks increase with increasing temperature. Our measurements of the dynamic viscoelastic response of cross-linked networks for different temperatures verify this dependence, as demonstrated in Fig. 6 for networks with cross-linker concentrations of R = 0.01 at 15°C (inverted triangles), 25°C (circles), and 35°C (triangles). Since the relaxation frequency (f_relax) rises faster with temperature than the plateau frequency (f_plateau), the elastic plateau spans a wider frequency range at lower temperatures. Moreover, a decrease in temperature—similarly to an increase in α-actinin-4 concentration—increases the ratio of G′ to G″ at the plateau, rendering the network more solid-like. In contrast to a change in cross-linker concentration, which influences the prominence of the elastic plateau while leaving the relaxation frequency of the network unaltered, a change in temperature appears to influence both network features. We expect the effect of the mutation to be largely compensated for by an appropriate temperature increase, such that the viscoelasticity curves of networks with wild-type and mutant α-actinin-4 of different temperatures coincide without significant scaling in frequency or moduli. Our observations confirm this notion. For example, we find that the viscoelasticity of the network with wild-type α-actinin-4 at 25°C (circles in Fig. 6 A) agrees well with that of the network with mutant cross-linker at 37°C (triangles in Fig. 6 B), as illustrated in Fig. 7 A. Similarly, the viscoelastic responses of networks with wild-type (circles) and mutant (triangles) α-actinin-4 at R = 0.02 and temperatures of 15°C and 32.5°C nearly coincide, as illustrated in Fig. 7 B.

FIGURE 6.

Frequency dependence of the elastic modulus G′ (solid symbols) and the viscous modulus G″ (open symbols) of actin networks with (A) wild-type and (B) mutant α-actinin-4 (molar ratio of α-actinin-4 to actin R = 0.01) at 37°C (triangles), 25°C (circles), and 15°C (inverted triangles). Similarly to a high cross-linker concentration, a lower temperature results in a more pronounced elastic plateau. In addition, a temperature decrease shifts the network relaxation toward lower frequencies.

FIGURE 7.

Increase in temperature can return the viscoelasticity of networks with mutant α-actinin-4 (triangles) to that of networks with wild-type cross-linker (circles), as illustrated by the frequency dependence of G′ (solid symbols) and G″ (open symbols) for (A) R = 0.01, wild-type at 25°C, mutant at 37°C, and (B) R = 0.02, wild-type at 15°C, mutant at 32.5°C. In contrast to the scaling behavior for mutant and wild-type at different concentrations, a shift in frequency or moduli is not necessary.

To analyze the temperature dependence of the relaxation frequency more quantitatively, we measured the frequency-dependent viscoelasticity at temperatures between 5°C and 40°C for six samples of each cross-linker type with relative cross-linker concentrations ranging from R = 0.00125 to R = 0.08, and extracted f_relax from these curves. For a few samples, the relaxation frequency falls outside the range of our measurements (0.01–10 Hz) at the lowest temperatures (e.g., inverted triangles in Fig. 6 B), and the corresponding data are not included in our compilation. We assume that the temperature dependence of the dissociation rates of wild-type and mutant α-actinin-4 follows the Arrhenius equation:

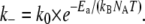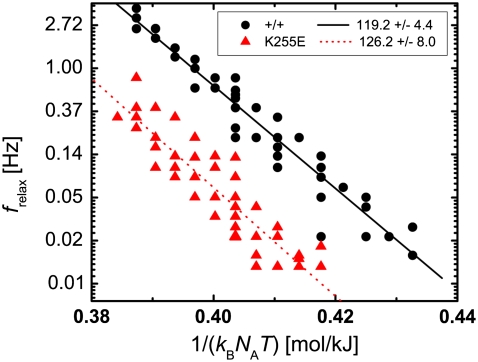
Herein, E_a denotes the molar activation energy that needs to be overcome for the dissociation reaction to take place, k₀ describes the rate at which unbinding is attempted, and k_B and N_A are the Boltzmann and Avogadro constants, respectively. To test whether the macroscopic relaxation frequencies of the networks exhibit the same temperature dependence, we plotted f_relax on a natural-logarithmic scale over the inverse of the thermal energy k_BN_AT, measured in kilojoules per mole. The relaxation frequencies for wild-type (circles) and mutant (triangles) α-actinin-4 form two distinct bands of data points, separated by about an order of magnitude, as shown in Fig. 8. The width of these bands can be attributed to the various cross-linker concentrations in the samples. However, since the concentration dependence of the relaxation frequency is very weak, we do not distinguish between different concentrations in our plot. The temperature-dependent relaxation frequencies of wild-type and mutant can indeed be described by the Arrhenius equation, as indicated by straight line fits with slopes of (119.2 ± 4.4) kJ/mol for the wild-type (solid) and (126.2 ± 8.0) kJ/mol for the mutant (dotted). These values are on the order of typical protein interaction energies, which allows us to identify them with the activation energies of the microscopic dissociation rates.

FIGURE 8.

Temperature dependence of the network relaxation frequency. The logarithm of the frequency is plotted as a function of the inverse thermal energy. For both wild-type (circles) and mutant (triangles) cross-linkers, the relaxation frequency follows the Arrhenius equation. The slopes (indicated by solid lines), which correspond to an activation energy barrier in the Arrhenius equation, are comparable. Relaxation frequencies for the mutant are consistently lower by about an order of magnitude.

The disparity in equilibrium dissociation constants K_d between wild-type and mutant α-actinin-4 can plausibly be accounted for by a difference in the activation energies. As Weins et al. (18) have established, the binding surface of the mutant cross-linker is extended by a third binding site, which is buried in the wild-type. This additional site could simply decrease the energy level of the bound state and thus increase the energy barrier E_a for unbinding. Since the activation energy appears in the exponential, a small difference E_a,mut-E_a,wt of 4.5 kJ/mol suffices to cause a six times lower dissociation rate k_−,mut consistent with the lower equilibrium dissociation constant observed for the mutant. This difference in activation energies is consistent with our data.

An alternative explanation lies in sequential binding of the two sites that the mutant α-actinin-4 has in common with the wild-type, and its additional binding site, as described by the following chemical reaction:

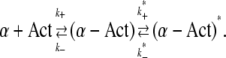We assume that the first reaction, including its association and dissociation rates, is identical for wild-type and mutant. The second reaction only applies to the mutant and describes its binding to actin at the third binding site, which results in a distinct, energetically favorable bound state. The overall concentration of mutant cross-linker, [α]_tot, is in this case:

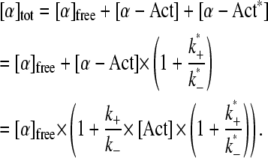The dissociation constant K_d,mut, as measured in a cosedimentation assay from the amount of free and bound cross-linker, can be calculated from the dissociation constant for the wild-type and the reaction rates for the second binding step:

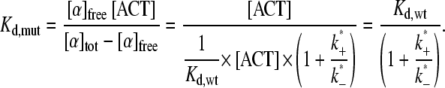To recover the experimentally determined factor of 6 between the binding affinities of mutant and wild-type, we need to assume a ratio k^*₊/k^*₋ = 5. This ratio also implies that most of the mutant is bound to actin at all three binding sites, and only one-sixth is in the weaker bound state. We can now explain the lower relaxation frequency of networks with mutant α-actinin-4 by relating it to the number of cross-linkers that unbind per unit time, which is the product of k₋, the rate at which weakly bound mutant α-actinin-4 dissociates completely from actin, and the number of mutant in this weaker binding state. With this interpretation, the shift in relaxation frequencies between wild-type and mutant stems from a lower prefactor for the mutant, which reflects the smaller fraction of cross-linker available for unbinding and is only weakly temperature dependent. The main temperature dependence of the relaxation frequency is determined by the exponential in k₋, which is the same for wild-type and mutant. Consequently, the slope of the natural logarithm of f_relax over 1/k_BN_AT, which is given by the corresponding activation energy E_a, is the same for both types of cross-linker as well. Our measurements of the temperature-dependent macroscopic relaxation frequencies of networks with wild-type and mutant do not provide a criterion by which to choose one of the proposed explanations over the other. Both are consistent with our data and support the suggested relationship between the network dynamics and the microscopic binding dynamics.

CONCLUSIONS

We have established through rheological measurements that the dynamic viscoelasticity of actin networks formed in vitro in the presence of the cross-linking protein α-actinin-4 is characterized by an elastic plateau in the frequency range between 0.1 Hz and 10 Hz, and a relaxation toward fluid properties at lower frequencies. These features result from a combination of the properties of individual actin filaments and the cross-linker dynamics. The high network elasticity at the plateau is a direct consequence of cross-linking, as evidenced by the increased elastic plateau modulus and greater prominence of the plateau at higher cross-linker concentration.

In contrasting the effects of the wild-type cross-linker and a mutant known to have a significantly higher actin-binding affinity, we find the network dynamics for the mutant to be shifted to longer timescales. In particular, networks with mutant α-actinin-4 undergo their relaxation at lower frequencies. We explain this phenomenon by proposing that the relaxation of the network on the macroscopic level results from the dissociation of α-actinin-4 from actin, which we assume to take place at a lower rate for the mutant, consistent with its smaller equilibrium dissociation constant. In strong support of this explanation, we show that the temperature dependence of the network relaxation frequency follows the Arrhenius equation for rate constants of chemical reactions, and allows us to extract a conceivable value of the energy implied in the dissociation reaction. Based on knowledge about an additional actin-binding site exposed in the mutant cross-linker, we suggest two different binding mechanisms: one-step binding with a lower energy level in the bound state for the mutant, and sequential two-step binding, which implies the same temperature dependence, but different prefactors for the dissociation of wild-type and mutant α-actinin-4 from actin.

In addition to shifting the relaxation to lower frequencies, the substitution of wild-type by mutant α-actinin-4 and a decrease in temperature both result in a more pronounced elastic plateau, thus rendering the network more solid-like. We find that a higher temperature compensated for the effect of the mutant. Of interest, an increase in cross-linker concentration likewise alters the frequency-dependent viscoelasticity in a manner remarkably similar to the change from wild-type to mutant, up to scaling factors in frequency and modulus. Whether there is a profound reason for this apparent scalability that could provide further insight into the properties of cross-linked networks remains a question for future investigations.

Our comparison of actin networks cross-linked with mutant and wild-type α-actinin-4 is not the first study of the effect of different binding affinities of actin cross-linkers on the dynamic rheological behavior of the resulting networks. Previous comparative studies have been performed, such as that by Wachsstock et al. (11), who related the different cross-linker dynamics of Acanthamoeba and chicken smooth muscle α-actinin to the mechanical properties of the networks. However, the difference between the two cross-linking proteins studied here is unique in that it results from the smallest possible variation in the underlying genetic code—a point mutation. It is interesting that we found this mutation to have a drastic effect on the properties of in vitro networks at shear frequencies around 1 Hz, close to the human heart rate. In vivo, the pathological consequences of the mutant cross-linker are most apparent in podocytes, which are subject to substantial shear stresses resulting from dynamic capillary pressure. The combination of these facts strongly suggests that altered viscoelastic properties of cross-linked actin networks contribute to the phenotypic changes in diseased kidneys.