Molecular Mechanism of Ion-Ion and Ion-Substrate Coupling in the Na⁺-Dependent Leucine Transporter LeuT

Abstract

Ion-coupled transport of neurotransmitter molecules by neurotransmitter:sodium symporters (NSS) play an important role in the regulation of neuronal signaling. One of the major events in the transport cycle is ion-substrate coupling and formation of the high-affinity occluded state with bound ions and substrate. Molecular mechanisms of ion-substrate coupling and the corresponding ion-substrate stoichiometry in NSS transporters has yet to be understood. The recent determination of a high-resolution structure for a bacterial homolog of Na⁺/Cl⁻-dependent neurotransmitter transporters, LeuT, offers a unique opportunity to analyze the functional roles of the multi-ion binding sites within the binding pocket. The binding pocket of LeuT contains two metal binding sites. The first ion in site NA1 is directly coupled to the bound substrate (Leu) with the second ion in the neighboring site (NA2) only ∼7 Å away. Extensive, fully atomistic, molecular dynamics, and free energy simulations of LeuT in an explicit lipid bilayer are performed to evaluate substrate-binding affinity as a function of the ion load (single versus double occupancy) and occupancy by specific monovalent cations. It was shown that double ion occupancy of the binding pocket is required to ensure substrate coupling to Na⁺ and not to Li⁺ or K⁺ cations. Furthermore, it was found that presence of the ion in site NA2 is required for structural stability of the binding pocket as well as amplified selectivity for Na⁺ in the case of double ion occupancy.

INTRODUCTION

Neurotransmitter transporters regulate the concentrations of specific neurotransmitters within the synaptic cleft (1,2). They are typically located in pre/post-synaptic and glial cell membranes and are responsible for rapidly clearing the neurotransmitters from the synapse. Many neurotransmitter transporters rely upon the electrochemical gradient of ions across the membrane (plasma or vesicular) to drive the uphill transport of neurotransmitters across membranes. A large set of transporters can be classified as neurotransmitter:sodium symporters (NSS), which utilize the sodium cation electrochemical gradient to drive transport. The NSS family represents some of the most well-studied transporters and contains proteins specific to dopamine, 5-HT, norepinephrine, glycine, and GABA. Transporters in this family have been associated with a large number of disorders including depression, schizophrenia, irritable bowel syndrome, and Parkinson's disease (3–5). These transporters (most notably the human serotonin transporter, hSERT) are also extremely common drug targets (3). For example, hSERT is targeted by a panel of antidepressant drugs as well as by narcotics such as MDMA (“ecstasy”) and cocaine, in addition to stimulants such as amphetamines. Much of the current knowledge about transporters comes from analysis of genetic data and from pharmacological studies (dose-response, binding, and transport assays).

In 2005, Yamashita et al. published the first crystal structure (PDB ID 2A65) of a bacterial homolog of Na⁺-Cl⁻-dependent neurotransmitter transporters (6) and opened a new avenue for discovering transporter structure/function relationships. The leucine transporter (LeuT) comes from the prokaryotic organism Aquifex aeolicus, which lives around deep sea vents where the temperatures average 97°C. The overall sequence identity between LeuT and related eukaryotic transporters (such as hSERT, NET, and DAT) ranges between 20 and 25%. Despite the low overall sequence identity, it has been shown that several functional regions (such as the active site) are highly conserved throughout the family (6,7). More recently, the same group published crystal structures (PDB IDs 2Q6H, 2Q72, 2QB4, and 2QEI) of LeuT in complex with three antidepressant drugs (clomipramine, imipramine, and desipramine) (6).

The active site of LeuT contains a substrate (leucine or alanine) binding site as well as two sodium-binding sites labeled NA1 and NA2 (8). One interesting aspect of the active site is how one of the sodium ions (NA1) is coordinated by the leucine substrate in addition to a transmembrane component (TM6). The other sodium ion (NA2) is coordinated by five residues that form part of a helix-break-helix motif of TM1. It is thought that the sodium ions are required to organize the substrate-binding site partially formed by flexible transmembrane helices (TM1 and TM6) (8). The crystal structures of LeuT show two bound sodium ions, suggesting that the binding stoichiometry is 2. We have yet to determine transport stoichiometry since it is difficult to accurately measure experimentally. It is therefore unknown whether both ions are required for both binding and transport. Some related transporters (GABA and glycine transporters) are known to transport two sodium ions with each substrate and others (SERT) are known to transport one sodium ion with each substrate molecule (4). The close proximity of the two ions to each other and to the substrate seems to play a major role in the observed coupling behavior between the ions (9–12).

The goal of this article is to further evaluate molecular mechanisms of ion coupling and its role in substrate binding and formation of the ion-selective motifs in similar membrane transporters. Special attention has also been given to the role of the specific ions in the formation of a high-affinity binding pocket and how different cations affect substrate-binding affinity for the transporter. In this study, molecular dynamics (MD) simulations performed for a full-atom system (see Fig. 1) were combined with free energy perturbation (FEP) techniques to evaluate effects of binding site composition and ion replacement on substrate binding affinity (9,13–15). The recently published crystal structure of LeuT complexed with clomipramine (a high-affinity drug) (8) was used as a followup to a previous study (9) with an aim to test robustness of the selectivity properties to sub-Ångstrom differences in the organization of the binding pocket. The computed root mean-square (RMS) deviations for heavy atoms forming the binding pocket differ by ∼1.3 Å between the two structures with and without drug bound, respectively. The FEP/MD techniques were used as well to measure absolute binding free energy of bound leucine in a few models of LeuT with different combinations of bound ions (Na⁺, Li⁺, and K⁺). Details on the role of the specific ions in the substrate binding site are particularly important for our understanding of the effects of Li⁺ on transport activity observed experimentally in various transporters (GAT-1, EAAT-3, Glt_Ph) (16–18). It was recently shown that one of the two ion-binding sites in homologous transporters (GAT-1, SERT, and DAT) was only slightly more selective for Na⁺ than for Li⁺, thus allowing transport of Li⁺ in some situations (16,19,20).

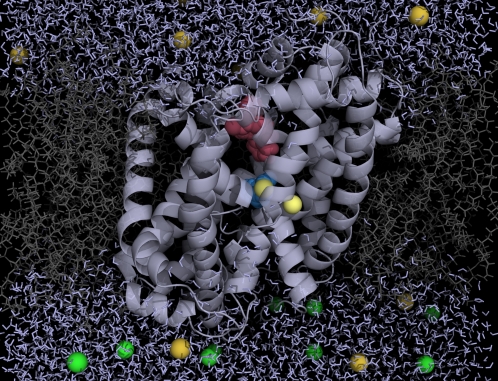
FIGURE 1.

Snapshot of full system of LeuT (PDB 2Q6H) embedded in a lipid membrane surrounded by water. Leucine substrate is shown in blue, bound clomipramine is shown in dark magenta, and the two sodium ions are shown in yellow. Site NA1 is the leftmost ion and NA2 is on the right.

METHODS

We used free energy perturbation molecular dynamics (FEP/MD) to carry out experiments on ion selectivity and substrate binding affinity in LeuT. For the ion selectivity FEP/MD experiments, all-atom simulations were carried out using the LeuT/clomipramine complex (PDB 2Q6H) embedded in a lipid membrane with explicit solvent. An initial system was built using a multistep membrane building procedure used in previous studies (9,21). The system contains the LeuT transporter, two bound sodium ions, one leucine substrate, one antidepressant (clomipramine, bound at the extracellular gate), and 148 DPPC molecules solvated by 100-mM NaCl aqueous salt solution. A snapshot of the full system is shown in Fig. 1. All computations were carried out by CHARMM Ver. c33b2 (22) using the CHARMM27 force fields for proteins and lipids. The simulation methods used are similar to those used in previous studies of membrane systems utilizing constant area/constant pressure algorithms (23,24). Pressure and temperature were kept constant (1 atm and 315 K, respectively). Electrostatic interactions were treated using a particle-mesh Ewald algorithm (25) and periodic boundary conditions were used. The initial system was equilibrated without any constraints for 5 ns. Two types of different systems were derived from the initial setup: one with only the ion in the NA1 site and the other with only an ion in the NA2 site. The three different cations were studied—Na⁺, Li⁺, and K⁺. All simulation systems were equilibrated for another 5 ns each without any constraints and were used for the free energy computations. The parameters for the bound clomipramine were developed using a protocol described before and are collected in the Supplementary Material, Table S1 and Fig. S1, in Data S1. The full set of parameters can be downloaded from http://www.ucalgary.ca/∼snoskov.

Interaction energies

Interaction energies were measured in all three models (single and double ion occupancy). Interaction energies were evaluated with an infinite cutoff. Interaction energy measurements were averaged over ∼7000 measurements taken from production trajectory frames. The averaged interactions were measured as between the leucine substrate and binding pocket side chains as well as between the ions and their corresponding interacting side chains.

Ion selectivity

FEP for ion selectivity was carried out using the CHARMM PERTurb command for 10 different simulations. Each FEP experiment was run in windowed mode with 22 windows (11 forward and 11 reverse) and 200 ps per window, with the thermodynamic coupling parameter (λ) varying between 0.0 and 1.0 by increments of 0.1. The integration timestep used was 2 fs. The FEP simulations had a total aggregate simulation time of 4.4 ns. The weighted histogram analysis method (15) was used to postprocess the FEP calculation data. All free energy simulations were performed without using soft-core potentials. The presence of soft-core potentials is thought to be important for absolute binding free energy computations. However, for the selectivity studies, e.g., evaluation of the relative free energy differences between two ionic species, where atomic radii never go to zero, the effect of the soft-core potentials is negligibly small (26,27). The usage of the weighted histogram analysis method enables robust evaluation of the free energies even with the use of equally spaced perturbation windows (28).

Binding affinity from free energy simulations

Substrate binding affinity experiments were carried out using the protocol described by Wang et al. (13). Briefly, the calculation of absolute free energy is decomposed into a series of sequential steps where specific interactions between the ligand and protein are turned on and off. In addition to this, repulsive and dispersive free energy contributions from nonbonded interactions between the ligand and binding site are calculated separately. While the decomposition is path-dependent, it has been shown that the results obtained by using this method are path-independent (13). To calculate absolute binding free energy we used the CHARMM PERT function with the additional CHEMPERT option. To decrease computational cost, only the atoms in and surrounding the binding site (within 20 of the bound leucine) are treated explicitly. All other atoms in the system are considered implicitly using a generalized solvent boundary potential (GSBP) generated for each system (29). It has also been shown that the effects of using GSBP significantly decrease the size of the system (in our case from ∼59,000 to ∼7,000 atoms) while keeping the statistical error relatively low (∼1–2 kcal/mol).

The original model system (with two ions, leucine and drug) as described above was used for these experiments. For each trial, the original model system file was modified according to the specific ion combination being tested. After this, the GSBP was generated and the reduced system minimized and equilibrated for 0.5 ns. Using the free energy decomposition protocol of Wang et al., electrostatic, dispersive, repulsive, and constraint forces were measured independently (13). All FEP/MD runs were equilibrated for 0.1 ns before collecting data during a 0.4 ns run. For the electrostatic, repulsive, and constraint components, 11 forward and 11 reverse windows, were used with λ varying between 0.0 and 1.0 by increments of 0.1. The dispersive component was measured through five forward windows with λ varying between 0.0 and 1.0 by increments of 0.125 (from 0 to 0.125 and 0.875 to 1.0) and 0.25 (from 0.125 to 0.875). Hydration free energy of leucine was calculated by FEP/MD using a model system of leucine (in zwitterionic form) solvated by 400 water molecules. The protocol used to determine hydration free energy is the same as that described above for the computation of absolute binding free energy. Equilibration without constraints was performed for 100 ps and window lengths for evaluation of free energy were 200 ps.

It should be noted that equally spaced λ-windows have been used for all computations. The use of equally spaced λ-windows is an easy way to ensure required overlap across a chosen reaction coordinate, provided that the energy landscape is not very rough and rugged. The convergence of the results could potentially be monitored via free energy change as a function of the chosen reaction coordinate (λ-values). The dependence of the computed relative free energies on λ-values is summarized in Fig. S2 in Data S1. The relatively small fluctuations (<5%) in the free energies (evaluated by the block-averages) and the smooth shape of the curves indicates good convergence of the results. Furthermore, an absence of large free energy changes across a single λ-window and the significant overlap between all λ-windows found in this and previous simulations of ion and substrate binding to LeuT (9,11) provides further justification for the usage of equally spaced windows across the reaction coordinate.

Binding affinity: method limitations

Absolute binding free energies calculated using FEP/MD methods are difficult to compare to experimentally determined values because the latter are a measured average of a large range of the protein's conformations (30,31), while FEP/MD results are measured from a single state (the equilibrated crystal structure). However, recent examination of the absolute binding free energy for leucine binding to LeuT shows that resulting affinity is likely to be overestimated (11). The partition function used to describe dynamics of the protein for the absolute free energy computations has to contain contribution from the open states of the transporter (32–34). The only known state is a very stable protein-substrate complex representing an occluded state in the transport cycle. It was shown that similar approach could be used with a higher degree of confidence to study relative binding free energies, e.g., the difference between binding affinities in presence of only minor perturbations of the transporter structure. Thus, in this article, we focus on the relative free energies or effect, e.g., relative to the native structure containing two Na⁺ ions in sites NA1 and NA2, respectively. It was shown both experimentally and theoretically that presence of competing cations such as Li⁺ or K⁺ is unlikely to cause large conformational changes in different amino-acid transporters (16,35), and thus, evaluation of relative binding free energies provide a useful route to evaluate different mechanisms of substrate binding and transport.

RESULTS

The results are collected in Tables 1 and 2 for the FEP/MD experiments that were performed to determine ion selectivity characteristics and substrate binding affinity in three initial LeuT models (single or double ion occupancy). One important result from studies done with the original LeuT structure (9) and current work is that selectivity characteristics of the transporter remain unaltered by the drug presence (see Table 2). Furthermore, selectivity characteristics appear to be robust despite the different structures used, displaying an intrinsic robustness of the ion selectivity to sub-Ångstrom level fluctuations of surrounding atoms.

TABLE 1.

The relative free energy of leucine binding to LeuT as function of the site occupancy

Site occupancy	0:NA2	NA1:0
ΔΔGelec	10.1	1.8
ΔΔGvdw	1.2	−1.3
ΔΔGconst	1.2	0.2
ΔΔGrot/trans	−0.2	−0.1
ΔΔGo	12.3	0.6

Relative energies are reported as difference in averages computed for single ion occupancy state (NA1:0 or 0:NA2) and double-ion occupancy state (NA1:NA2).

TABLE 2.

FEP/MD results (in kcal/mol) for the LeuT ion site selectivity (Na⁺/Li⁺/K⁺)

NA1 site	NA2 site	ΔGsite	ΔΔGselectivity	ΔΔΔGcoupling
K+	K+	47.9	11.5	4.9
Li+	Li+	−44.3	1.4	2.2
K+	—	22.2	4.0	—
Li+	—	−24.5	−1.6	—
—	K+	20.9	2.7	—
—	Li+	−22.1	0.8	—
Na+	K+	21.5	3.3	—
Na+	Li+	−20.9	1.9	—
K+	Na+	21.9	3.7	—
Li+	Na+	−22.8	0.0	—

Three different LeuT models were used: two ions; one ion in NA1 site; and one ion in NA2 site. Selectivity was calculated using Eqs. 1 or 2 with 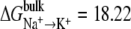kcal/mol and 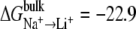kcal/mol. The results suggest that LeuT, when occupied by two ions, is selective for Na⁺ over Li⁺ and K⁺. Also, the NA1 site was found to be selective for Li⁺. The results also suggest that there is an ion coupling affect that amplifies selectivity.

We also present averaged interaction energies among ions, substrate, and protein in the same models. Uncertainties for the results of FEP/MD experiments are ∼±1 kcal/mol as determined in our previous studies (9,36). All experiments assume that the leucine substrate is in zwitterionic form, which is supported by both experimental and computational data (6,11). However, before discussing the results, it is important to outline the theoretical framework used to enable effective comparison to experimental data.

Ion-substrate binding stoichiometry

A number of free energy simulations were performed to evaluate the effect of ion occupancy on substrate binding affinity (see Table 1). These experiments can directly assess the role of the two ion-binding motifs in the formation of the leucine-binding pocket. The results of these simulations are collected in Table 1. Within statistical error (±1 kcal/mol), removal of the cation from the adjacent binding pocket (NA2) has little or no effect on the leucine binding affinity to LeuT. The small and unfavorable decrease in the electrostatic component of binding free energy is compensated by a small gain in the Lennard-Jones term. As expected, removal of the sodium from the site in direct contact with bound substrate (NA1) results in a very unfavorable relative binding free energy due to large loss in the electrostatic component.

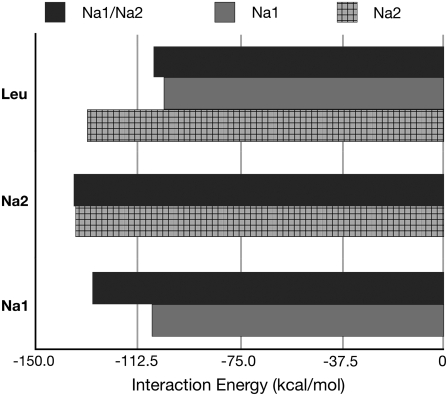
Interaction energy data are shown in Fig. 2. Standard error for each measurement is ±0.5 kcal/mol. The interaction energies between leucine and the protein become more favorable in the absence of NA1, while the removal of the NA2 ion makes the same interaction slightly less favorable. Interaction energies between the NA2 ion and the protein remain unchanged when NA1 is unoccupied. We also see a loss in favorable interactions between the NA1 ion and the protein when NA2 is removed. These are all expected results, as our previous work strongly supports the view of NA2 as a crucial structural cation for the stability of the binding pocket and not necessarily for direct stabilization of the substrate itself. Although the interaction energy results are illustrating only an enthalpic component of the binding free energy, they do provide evidence that the presence of the NA2 ion has a large effect on both NA1 and the leucine substrate. Celik et al. (10) reached a very similar conclusion using different methods and simulation strategies, suggesting that the results above are robust.

FIGURE 2.

Interaction energies between NA1/NA2/leucine and whole protein. All values are in kcal/mol, and are averages over 7000 measurements from production trajectory data. Standard error for each measurement is <0.5 kcal/mol.

Ion selectivity: single versus double occupancy

Assuming that monovalent cation selectivity of site A (i.e., NA1 or NA2) is uncoupled from the selectivity of site B, relative free energy characterizing single binding site selectivity could be defined as

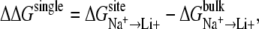(1)

where Li⁺ can also be K⁺. By convention, a positive ΔΔG means that the binding site is selective for Na⁺ over Li⁺ (or K⁺). Using this equation as a starting point, we can write an expression to evaluate contribution of the coupling between two ionic sites to overall ion selectivity of the transporter. This framework was previously defined and applied successfully to studies of single and double ion occupancy in the gramicidin channel (37). The collective relative monovalent cation selectivity of the binding pocket with double ion occupancy, such as that observed in LeuT, could be expressed as

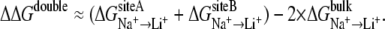(2)

We refer to ΔΔG^selectivity as the selectivity calculated by Eqs. 1 or 2 in the following text for the sake of simplicity, depending on the experiment (single or double ion occupancy). Using the same logic, it is easy to show that relative contribution of the coupling between two sites into ion selectivity can be expressed as

(3)

Results for ion selectivity experiments are shown in Table 2. As expected, LeuT is selective for Na⁺ over K⁺ in all cases. In addition to this, the perturbation of two Na⁺ ions into two K⁺ ions has an even more dramatic effect on selectivity in LeuT (ΔΔΔG^coupling is relatively high).

The results for Li⁺ selectivity are quite a bit different. The NA1 site showed weak selectivity for Li⁺ over Na⁺ when NA2 was unoccupied (−1.6 kcal/mol). In the case where the NA2 site is occupied by Na⁺, the selectivity of the NA1 site showed ambiguous selectivity for Na⁺ (+0.09 kcal/mol). This shows that presence of Na⁺ in the NA2 ion-binding site does have an effect on the NA1 site, presumably by affecting the structure and dynamics of the binding pocket. When both sites are perturbed to Li⁺, we see weak selectivity for Na⁺ (+1.4 kcal/mol). These results suggest an ion coupling effect that makes the transporter selective for Na⁺ overall.

Binding affinity

Absolute free energy of binding of a substrate is defined as the difference between the free energy of binding within site (G^protein) and that of hydration of the substrate (G^bulk):

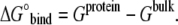(4)

Relative free energy of binding is defined as the difference in absolute free energies between two states (i.e.: between a system with two Li⁺ ions and one with two Na⁺ ions):

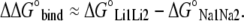(5)

The hydration free energy (G^hydration) of leucine was found (computationally) to be −63.1 kcal/mol, very close to a previously determined value of −62.8 kcal/mol (11). The small difference between the two values reflects the slightly different protocol used for MD simulations in this work, specifically the different window lengths. Nevertheless, the difference is well within statistical uncertainty for the computed property. The relative free energies of binding for the leucine substrate (in models with various ions) are shown in Table 3. The system with two bound Li⁺ cations resulted in the lowest free energy of binding at ∼1.4 kcal/mol lower than the two-Na⁺ system. Li⁺ in the NA2 site had a similar effect of decreasing binding free energy, but by a smaller amount (0.92 kcal/mol).

TABLE 3.

FEP/MD results in (kcal/mol) for relative free energy of leucine binding to LeuT with various cation occupancies

NA1 site	NA2 site	ΔΔG°bind	“Corrected” ΔΔG°bind
Na+	Na+	0.0	0.0
Li+	Li+	−1.4	0.0
Na+	Li+	−0.9	1.1
Li+	Na+	2.7	2.8
K+	K+	2.2	13.5
K+	Na+	1.9	5.6
Na+	K+	2.1	5.4

Absolute binding free energy (ΔG°_bind) was calculated using Eq. 4 with G^hydration of leucine of −63.1 kcal/mol and relative binding free energy ΔΔG°_bind calculated using Eq. 5. “Corrected” ΔΔG°_bind is calculated using Eq. 6.

On the other hand, Li⁺ in the NA1 site had the opposite effect of increasing binding free energy by ∼2.7 kcal/mol (less favorable binding). The low magnitude relative free energies (in conjunction with the uncertainty) make it difficult to say for sure whether one state results in stronger binding of leucine than another.

One important point has to be made to enable effective comparison to experimental results on ion-dependence of leucine binding to LeuT. Note that LeuT (outside of a lipid membrane) is unstable in the absence of sodium salts and so binding assays must be performed with small amounts of Na⁺ (S. K. Singh, Vollum Institute, Oregon Health and Science University, personal communication, 2008). Thus, to accurately compare results of the binding affinity computations to experimental data, one has to include the cost of replacement of Na⁺ by Li⁺ in the binding sites (which is essentially the selectivity measurement):

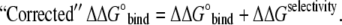(6)

The results collected in Tables 2 and 3 show that K⁺ is unlikely to support any binding. However, Li⁺ can support binding almost as efficiently as Na⁺.

DISCUSSION

The presence of multiple metal cation binding sites is a common feature of both soluble and membrane-bound proteins including NSS transporters (1,17,38–41). The functional significance of the ions is usually thought to be related to the catalytic activity or integrity of the structural elements of the protein. In membrane proteins, multi-ion structures could potentially be involved with optimization of the conduction rates, formation of gradients for substrate transport, or simply in the stabilization of particular structural elements. In fact, the very first mechanism explaining fast conduction of ion channels was based on the assumption that ion-ion repulsion in the pore optimizes conduction rates, now commonly known as the knock-on mechanism (42,43). Thus, ion-ion and ion-substrate interactions are some of the most important aspects relating to transport in biological channels (44). In potassium channels, multiple occupancy of the selectivity filter (which could be described as a multi-ion binding site) is required to optimize transport rates (44,45). In the following sections, we will discuss the roles of single and double ion occupancy of the binding pocket in LeuT in terms of the formation of a high-affinity binding pocket and monovalent cation selectivity.

Substrate binding affinity: dependence on the NA1-NA2 ion load

The relative binding free energies as a function of single ion occupancy are reported in Table 1. It should be stated that overall convergence in binding free energy simulations can potentially be slow. Furthermore, binding computations performed on the only known conformational state of the system will unavoidably lead to a strong overestimation in computed binding affinities, as mentioned above (since the structure itself is in a very stable state). Thus, our focus is on relative binding free energies, e.g., those relative to the LeuT-Leu complex with two Na⁺ ions. The relative free energies of leucine binding to LeuT suggest that removal of the ion from the directly coupled NA1 site will diminish any substrate binding to LeuT. At the same time, removal of the ion from the adjacent site NA2 leads to a relatively small decrease in binding affinity. However, the timescales of the simulations (λ-windows) were relatively short (200 ps to 1 ns per window) and the overall RMS values of the protein lacking an ion in the NA2 site are comparable to the model with two ions (1.3–1.7 Å). Despite these shortcomings, the data for monovalent cation selectivity and structural coupling between two binding sites provide important clues about the precise role of the NA2 site. The results literally provide a tantalizing clue that NA2 is a structural site, in accord with previous studies (10). However, further exploration about its ability to modulate function is warranted.

Na⁺/K⁺/Li⁺ selectivity: role of NA1-NA2 structural coupling

Molecular dynamics simulations performed on LeuT complexes show that replacement cations do not introduce significant conformational changes into the structure of the leucine-binding pocket. The RMS fluctuations of the positions of the heavy atoms forming the binding pocket are 1.8 and 1.1 Å for K⁺ and Li⁺ complexes with LeuT, respectively. The average ion-ligand distances are shown in Table 4. The change in the ion-ligand distances perfectly reflects the differences in the cation sizes. Thus, the absence of major conformational changes enables effective and accurate free energy perturbation simulations intended to highlight the role of NA1-NA2 coupling for monovalent cation selectivity.

TABLE 4.

The ion-oxygen distances for Na⁺, Li⁺, K⁺ in the NA1 and NA2 binding sites

Ion	Na+	Li+	K+
SITE NA1
A22 (O)	2.3	2.1	2.8
N27 (Oδ)	2.3	2.0	2.7
T254 (O)	2.6	2.3	2.8
T254 (Oγ)	2.5	2.1	2.65
N286 (Oδ)	2.6	2.4	2.8
LEU (OXT)*	2.6	2.1	2.7
SITE NA2
G20 (O)	2.3	1.95	2.7
V23 (O)	2.4	2.1	2.9
A351 (O)	2.5	2.3	2.8
T354 (Oγ)	2.4	2.0	2.9
S355 (Oγ)	2.4	2.0	2.65

All distances are in Ångstroms. Amino-acid residues and particular atoms forming the ion's coordination shells are shown.

^*Carboxylate oxygen from the zwitterionic substrate is part of the coordination shell in the site NA1.

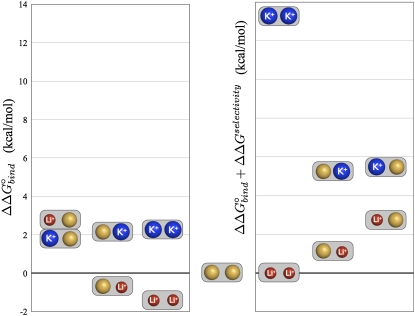
The results collected in Table 3 and pictured in Fig. 3 show that there are complex mechanisms by which the various ions affect the binding pocket, and thus binding affinity of the substrate. We addressed the molecular mechanism of monovalent cation selectivity of LeuT in our previous contribution (9). However, new data obtained from the FEP simulations performed with the two ions simultaneously (first two rows in Table 2) highlight the important effect of the structural coupling between the two sites. The simulation analysis provides some clues about the mechanisms behind Li⁺ binding to the primarily Na⁺-selective sites in LeuT. Again, we point out that the NA1 site alone is weakly selective for Li⁺. However, it was found that presence of Na⁺ in the structural site NA2 enables bias against Li⁺ binding to NA1. Importantly, the overall selectivity of LeuT for Na⁺ is not equal to the sum of the selectivities for the individual sites. The average contribution of the structural coupling effect between the two sites is ∼2–4 kcal/mol, enhancing selectivity of the transporter for Na⁺. This is especially important for Na⁺ /K⁺ selectivity, since the reverse K⁺ gradient could potentially drive outward transport of the substrate. The selectivity results show that the transporter is strongly selective for Na⁺ over K⁺ (for single and double ion occupancy), and weakly selective for Na⁺ over Li⁺ in all cases except one. For both single and double occupancy models, the NA1 site was less selective for Na⁺ than the NA2 site (by ∼2 kcal/mol). These theoretical findings are in excellent accord with recent experimental data (1,16). Taken together, theory and experiment support the idea that the NA2 ion has an essential role in stabilizing the binding pocket for another Na⁺ cation. It is likely that Na⁺ binds first to the most selective site (NA2), providing structural stabilization for the NA1 site and the substrate-binding pocket itself.

FIGURE 3.

Graphical representation of the data in Table 3. The data points represent the LeuT active site with double-ion occupancy combinations (Na⁺, Li⁺, and K⁺). Ion sizes are not drawn to scale. All data points are relative to the Na⁺/Na⁺ model (shown in the center). The leftmost chart shows ΔΔG°_bind data and the right shows the “Corrected” ΔΔG°_bind data. Li⁺ and K⁺ ions are labeled with text (red and blue, respectively); Na⁺ ions are unlabeled (orange). Ordering on the x axis is by ion occupancy.

Our results for ion selectivity show strong evidence that K⁺ ions are unable to replace Na⁺ ions and it is therefore highly unlikely that K⁺ ions are able to support transport. Data on the FEP/MD Na⁺/K⁺ selectivity could potentially be used to quantify this effect. We can calculate the substitution penalty by looking at the difference between the sum of the free energies of selectivity for single ion occupancy and that for double occupancy (for each ion type). We refer to this above as ΔΔΔG^coupling. The sum of the free energies of selectivity for single ion occupancy binding of K⁺ to the NA1 and NA2 sites individually (∼4.0 and ∼2.7, respectively) is 6.7 kcal/mol, while the result for double occupancy is ∼11.5 kcal/mol. The difference of 4.7 kcal/mol between these results shows that overall selectivity is not simply additive between the two ion-binding sites. We strongly suspect that an occupied NA2 site affects the conformation of the NA1 site, thus providing the observed amplification of selectivity.

Analysis of the dependence of ion-protein and ion-substrate interaction energies on site occupancy provide additional support for the predominantly structural role of the NA2 site. The data for the average ion-protein and substrate-protein interaction energies are collected in Fig. 2. The data show that removal of the ion from site NA1 leads to an increase in total interaction energy between the substrate and protein. Indeed, strong electrostatic interactions between the ion in the NA1 site and the charged carboxylate group of the substrate compensate for this loss in the protein-substrate interaction. Interestingly, presence of both ions shows less favorable interaction between the substrate and the protein, suggesting that direct coupling between the NA1 ion and the leucine substrate substantially restrict conformational dynamics of the substrate.

Cation-dependence of substrate binding: role of structural coupling between sites NA1 and NA2

The overwhelming evidence for cation-dependent substrate transport has motivated us to understand the molecular mechanisms of this effect. We know that LeuT is dependent on sodium for binding and transport. There is experimental evidence that (in some conditions) lithium directly affects substrate transport by related neurotransmitter transporters (GAT-1, EAAT-3) (16,17). In the bacterial glutamate transporter (Glt_Ph), lithium was shown to support weak transport (relative to sodium) (18). The effects of lithium on sodium-dependent transporters is worth studying, since Li⁺ salts have been used for many years to treat mood disorders without knowing specific mechanisms of action. The putative primary target of Li⁺ is inositol phosphatase, but it is possible that neurotransmitter transporters are also affected by therapeutic concentrations of the cation. There is evidence that lithium affects neurotransmitter concentrations in the synapse, but no single common target has been identified (46).

To study molecular mechanisms of ion-dependent substrate binding in LeuT, free energy simulations were performed with various models to estimate relative binding affinities of the leucine substrate to the transporter. The results of these simulations are collected in Table 3. Our theoretical data show that replacement of the two Na⁺ ions by Li⁺ leads to an enhancement of leucine binding to LeuT. This effect alone is relatively weak, given statistical error of ∼±1 kcal/mol. However, the theoretical relative binding free energy data lack one very important thermodynamic correction.

Theoretical evaluation of the binding free energy starts from a preequilibrated Li⁺-LeuT system. If we want to derive realistic conclusions from our data, we must consider the ion selectivity results together with the substrate binding affinity results when considering the replacement of ions. As mentioned above, experimental binding assays require small amounts of sodium to stabilize the protein. Therefore, we must account for the cost of ion replacement. Ion selectivity results showed preference for Na⁺ in all double ion occupancy states. Substrate binding affinity results showed that double ion occupancy by Li⁺ slightly increased the binding affinity of leucine. The inclusion of the relative free energy of Na⁺/Li⁺ selectivity as a correction factor results in an apparent cancellation of the increase in binding affinity.

The effect of K⁺ on leucine binding affinity follows a similar trend. The binding affinity (ΔΔG°_bind) of Leu to LeuT is slightly less favorable in the presence of K⁺, indicating a decrease in the substrate-ion interaction compared to that with Na⁺. However, applying the correction factor (selectivity relative free energy) to determine the “Corrected” term (ΔΔG°_bind + ΔΔG^selectivity) results in a dramatically less favorable effect of K⁺ on substrate binding. Our results indicate that presence of other cations (K⁺ or Li⁺) in the ion binding sites only slightly affects the binding affinity of leucine. It is the energetic penalty for the replacement of Na⁺ in the binding pocket that plays the major role in the observed inhibition of substrate binding in LeuT by monovalent cations. See Fig. 3 for a visual representation of cation-dependent binding affinities.

Tentative cotransport mechanism

Initially, the goal of this work was to study the possibility of coupling between the two ion-binding sites (and functional implications). However, computational studies unraveled an unexpected role of the NA2 ion as a selectivity enhancer for the nearby NA1 site. The extremely high specificity of site NA2 for Na⁺ over K⁺ supports the claim that presence of an ion in site NA2 is required to ensure proper directionality of uphill substrate transport (down the Na⁺ gradient). At the same time, specificity against cations seldom found in natural environments (Li⁺) remains marginal, providing a rationale for the Li⁺ currents observed in the absence of Na⁺ in many NSS transporters (1). Our findings suggest that there are serious deviations from the simplistic view of binding (and to some extent, transport) stoichiometry as a fixed property of the system. For example, in this system there seem to be various scenarios by which tight binding/occluded state stabilization can be achieved, depending on site occupancy. Therefore, these scenarios may exhibit very different substrate/ion ratios.

In principle, both ions could bind simultaneously to NA1 and NA2, and an ion leaving site NA2 will lead first to an apparent disruption of the selectivity of the site NA1 and then to a major disruption of neurotransmitter binding. Thus, these ions remain in the realm of fixed ion-substrate stoichiometry for both transport and binding (e.g., 2:1) for the leucine transporter studied. The computations performed here support another sequence of events leading to the formation of an occluded state. To illustrate this, we will discuss apparent differences in the absolute free energies of binding for Na⁺ to sites NA1 and NA2. We performed neutralizing free energy simulations using the protocol similar to that of the ion selectivity simulations. The ions were constrained with a weak harmonic force to avoid artifacts related to the absence of soft-core potentials. The absolute binding free energies for Na⁺ to sites NA1 and NA2 are −22.3 kcal/mol and −4.9 kcal/mol, respectively. Very similar results were obtained in the recent article by Shi et al. (47). The fivefold difference in the ion-binding free energy suggests that the site NA2 could readily exchange ions with the bulk phase, perhaps with the intracellular milieu, as suggested by Shi et al. (47). Furthermore, it is likely that ion binding at these sites occurs on vastly different timescales (perhaps even independently). This alternative binding/transport mechanism is supported by the indirect dependence of neurotransmitter binding on the occupancy of site NA2, which directly affects selectivity of the site NA1 that is directly coupled to the substrate. In reality, various binding/transport scenarios could coexist, thus challenging the oversimplified view of fixed binding and transport stoichiometry.

CONCLUSIONS

This computational study of structural coupling between two Na⁺ binding sites and its role in substrate binding to LeuT provides a good opportunity to broaden our perspective concerning the different microscopic factors affecting neurotransmitter uptake and transport. Combining FEP and MD simulations, we were able to analyze the role of different factors of binding inhibition in LeuT and draw general conclusions applicable (with some reservations) to a broad variety of multiple ion motifs in proteins. Of particular interest, this study reveals that binding inhibition by different cations is governed mainly by the penalty of the ion replacement in the two ion binding sites and only moderately depends on the modulation of protein-substrate interactions by different cations. Coupling between the two structural sites in LeuT provides the most effective and robust mechanism for ensuring that selectivity is maintained for Na⁺ over both Li⁺ and K⁺, as shown by recent experimental data. Furthermore, in the absence of this structural coupling, it is likely that Li⁺ will support substrate binding.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.