Anion-Cation Permeability Correlates with Hydrated Counterion Size in Glycine Receptor Channels

Abstract

The functional role of ligand-gated ion channels depends critically on whether they are predominantly permeable to cations or anions. However, these, and other ion channels, are not perfectly selective, allowing some counterions to also permeate. To address the mechanisms by which such counterion permeation occurs, we measured the anion-cation permeabilities of different alkali cations, Li⁺ Na⁺, and Cs⁺, relative to either Cl⁻ or anions in both a wild-type glycine receptor channel (GlyR) and a mutant GlyR with a wider pore diameter. We hypothesized and showed that counterion permeation in anionic channels correlated inversely with an equivalent or effective hydrated size of the cation relative to the channel pore radius, with larger counterion permeabilities being observed in the wider pore channel. We also showed that the anion component of conductance was independent of the nature of the cation. We suggest that anions and counterion cations can permeate through the pore as neutral ion pairs, to allow the cations to overcome the large energy barriers resulting from the positively charged selectivity filter in small GlyR channels, with the permeability of such ion pairs being dependent on the effective hydrated diameter of the ion pair relative to the pore diameter.

INTRODUCTION

The functional role of cys-loop ligand-gated ion channels, such as the cation-selective nicotinic acetylcholine receptor (nAChR) channel, the 5-hydroxytryptamine type 3 receptor channel, the anion-selective γ-aminobutyric acid types A and C receptor (GABA_AR and GABA_CR) channels, and the glycine receptor (GlyR) channel depends on their anion-cation selectivity. The excitatory channels are cation selective and the inhibitory ones anion selective (under typical adult Cl⁻ gradients) (1,2). However, these and other ion channels are not perfectly selective to only cations or anions, with, for example, the anion-selective glycine receptor channel allowing some permeation of counterion cations. Such observations have generated a certain amount of controversy since some Brownian dynamics (BD) simulations have appeared to suggest that counterions should not be able to permeate through very small charged channels. For example, BD modeling in the wild-type (WT) glycine receptor (GlyR) channel indicates that a single Na⁺ ion attempting to enter an empty GlyR channel would be effectively excluded from the channel (3).

Our experiments to investigate the molecular determinants of anion-cation selectivity in GlyRs have resulted in a set of mutant receptor-channels with well-characterized P_Cl/P_Na permeability ratios and minimum pore diameters (reviewed in Keramidas et al. (1)). The range of relative permeabilities of the counterions in this set of mutant GlyR channels was fairly large, with P_Cl/P_Na varying from ∼25 to 4 in anion-selective channels and from 0.34 down to 0.1 in the cation-selective channels (e.g., Table 1 of Keramidas et al. (1)), with P_Cl/P_Na, decreasing as the pore diameter increased. Given the modest anion-cation selectivity (P_Cl/P_Na ∼4 to ∼10) of a number of native anion channels, such as background Cl⁻ channels in neurons and skeletal muscle (4–8), and our set of single point mutated GlyRs with resultant changes in P_Cl/P_Na and pore diameter, it is timely to further explore the mechanisms of counterion permeation in anionic channels.

TABLE 1.

Permeability Ratios for Cl⁻ relative to Li⁺, Na⁺, and Cs⁺ at 22°C for both WT and mutant P−2′▵ GlyR channels

Channel	PCl/PLi	PCl/PNa	PCl/PCs	Ion selectivity
WT GlyR	23.4 ± 2.8 (6)	10.9 ± 0.3 (32)	5.0 ± 0.5 (6)	Anion
P−2′▵ GlyR	6.0 ± 0.4 (7)	3.3 ± 0.2 (8)	1.9 ± 0.1 (7)	Anion

The values were averaged from permeability ratios determined using the GHK equation from individual dilution potential experiments, and are given as the mean ± SE, with the number of observations shown in parenthesis.

To this end we have asked (see also Franciolini and Nonner (5,9) and Barry (10)): How do counterions permeate through such narrow ion channels where electrostatics plays such an important role? For example, how does a Na⁺ ion manage to pass through the positively charged selectivity filter region of an anion-selective GlyR channel? The aim of this article was therefore to investigate and test two hypotheses in GlyR channels: a), that counterion permeation in anionic channels depends on the equivalent hydrated size of the cation relative to the channel pore radius, with the equivalent hydrated size defined as the size of a nonhydratable ion with the same equivalent limiting conductivity, and b), that counterions permeate through charged selectivity filters by being chaperoned by the permeant anions.

We have thus explored the effects of different cation counterions on the magnitude of the chloride-to-cation permeability in two anion-selective GlyR channels with different minimum pore diameters: the WT α1 GlyR channel with a minimum pore diameter of 5.3 Å (11) and a mutant α1 GlyR channel with a proline deletion at the −2′ position (P−2′▵) and a minimum pore diameter of 6.9 Å (12). In both GlyR channels, the minimum pore diameter of the selectivity filter region was determined by measuring the relative anion permeabilities of a range of different sized organic anions that could permeate through the each channel (11,12), along the lines of similar measurements by Dwyer et al. (13) (see also Hille (14)) for the nAChR channel.

We also compared the relative cation-anion permeabilities measured under dilution conditions for two anions (Cl⁻ and 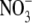) with different permeabilities (measured under biionic conditions) to determine if the cation counterion permeation depends on the anion permeability. Conversely, we also did slope conductance experiments in different salt solutions to investigate whether the anion conductance or permeability were dependent on the nature of the cation.

MATERIALS AND METHODS

Transient expression of recombinant wild-type and P−2′Δ α1 subunit GlyRs in HEK 293 cells

The proline residue at position 250 of the α1 human GlyR (GenBank accession No. X52009; (15)) was deleted by site-directed mutagenesis as described in Keramidas et al. (16). This mutation is represented as P−2′▵, using the M2 residue relative number system, where R252 is designated as 0′. The complementary DNA (cDNA) that encodes the α1 subunit of human GlyRs was subcloned into the pCis expression vector and transfected into HEK 293 cells using linear polyethyleneimine (jetPEI, Polyplus-transfection, Illkirch, France) according to the transfection conditions recommended by the manufacturer. The HEK 293 cells were also cotransfected with the cDNA that encodes the CD4 surface antigen, enabling them to be marked with “anti-CD4 beads” (Dynabeads M-450, CD-4; Invitrogen, Mount Waverley, Australia) to aid cell selection for the electrophysiological experiments.

Solutions

Dilution potential experiments were performed to determine the relative permeability of Cl⁻ to a selection of cations (P_Cl/P_cation). For NaCl, the standard intracellular (pipette) solution consisted of 145 mM NaCl, 10 mM HEPES, 2 mM CaCl₂, and 5 mM EGTA titrated to a pH of 7.4 with NaOH (∼18 mM). Three extracellular (bath) solutions were used for recording the dilution potential experiments. These were the standard extracellular solution, resulting in approximately symmetrical NaCl concentrations (and referred to as 1 NaCl), the solution where the concentration of NaCl was reduced to about half (0.5 NaCl), and the solution where the concentration of NaCl was reduced to about one quarter (0.25 NaCl). The 1 NaCl (approximately symmetrical) solution consisted of 145 mM NaCl, 10 mM HEPES, and 10 mM glucose; the 0.5 NaCl solution consisted of 75 mM NaCl, 10 mM HEPES, 10 mM glucose, and 136 mM sucrose; and the 0.25 NaCl solution consisted of 37.5 mM NaCl, 10 mM HEPES, 10 mM glucose, and 189 mM sucrose. All solutions were adjusted to pH 7.4 with measured amounts of NaOH (∼4 mM in each external solution) and the concentration of ionic HEPES⁻ at that pH was estimated to be 5.0 mM. The sucrose was present to maintain equiosmolar conditions. Similarly, dilution potential experiments were performed with solutions where LiCl or CsCl replaced NaCl in both the intracellular (pipette) solution and in the external solutions (at 1, 0.5, and 0.25 dilutions) with all other components remaining the same. In the LiCl and CsCl solutions, measured amounts of LiOH and CsOH (respectively) were used to titrate the solutions to a pH of 7.4 (again ∼18 mM in the pipette solution and 4 mM in each external solution). Biionic potential experiments were performed to determine the relative permeability of 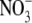with respect to Cl⁻. In this case, the internal (pipette) NaCl solution was the same as above, whereas the NaNO₃ external solution differed from the 1 NaCl solution only in the Cl⁻ being completely replaced by To determine the relative permeability of 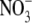with respect to Na⁺, P_NO3/P_Na, the dilution potential solutions for NaNO₃ (1, 0.5, 0.25) each contained 5 mM NaCl to provide for a well-defined and stable Ag/AgCl pipette potential. The remainder of the Cl⁻ was replaced by to give NaNO₃ concentrations of 140 mM, 70 mM, and 32.5 mM for the 1 NaNO₃, 0.5 NaNO₃, and 0.25 NaNO₃ extracellular solutions, respectively, and 140 mM NaNO₃ in the intracellular (pipette) solution. The concentrations of the other constituents were unchanged.

For the dilution potential measurements, the reference salt bridge concentrations had the same ionic composition as the initial bath solution (e.g., 1 NaCl, 1 LiCl, 1 CsCl, and 1 NaNO₃ for the NaCl, LiCl, CsCl, and NaNO₃ dilution potential measurements, respectively), whereas for the biionic experiments, they had the same composition as the initial 1 NaCl bath solution, in each case together with 3–4% agar to gel the salt bridge.

Glycine concentrations were prepared in each of the external solutions (1, 0.5, and 0.25) for activation of the GlyRs. A concentration of 100 μM glycine was used to activate the WT GlyRs and 10 mM to activate the P−2′▵ mutant. It should be noted that none of the external solutions contained any added CaCl₂ or MgCl₂. This is important when comparing the results with our previous P_Cl/P_Na measurements in WT GlyRs, which did contain both 2 mM CaCl₂ and 2 mM MgCl₂ (e.g., (17)). We have found that external Ca²⁺ ions at such concentrations increases the magnitude of P_Cl/P_Na in GlyR channels, suggesting that these divalent ions are mainly reducing the permeation of the Na⁺ counterions and to a lesser degree enhancing the permeation of Cl⁻ (S. Sugiharto, J. E. Carland, T. M. Lewis, A. J. Moorhouse, P. R. Schofield, and P. H. Barry, unpublished results).

Electrophysiology

All of the experiments used the whole-cell configuration of the patch-clamp recording technique and were performed at laboratory temperature (22 ± 1°C). Oval and bipolar single HEK 293 cells, lightly labeled with CD-4 Dynabeads, were chosen for electrophysiological recordings. Patch pipettes were made using borosilicate glass capillaries (Clark GC150F7.5; Harvard Apparatus, Middle Cove, Australia), pulled on a horizontal electrode puller (P-87 model, Sutter Instruments, Novato, CA) and fire-polished. Patch pipettes had resistances of 2–4 MΩ when filled with pipette solution. The series resistances ranged between 4 and 9 MΩ and were compensated by 60–70% with the Axopatch 1D Patch-clamp amplifier (Axon Instruments, now Molecular Devices, Sunnyvale, CA). Recordings were digitized with a Digidata 1200B A/D board using pClamp 8.03 (and in later experiments, by pClamp 9.0) data acquisition software (Molecular Devices) on a Pentium III 1.1 GHz computer (Intel, Santa Clara, CA). Currents were filtered at 2 kHz (−3 dB) and acquired at a sampling frequency of 10 kHz.

For the dilution potential and the biionic potential experiments with α1 WT and P−2′▵ GlyRs, current-voltage (I/V) curves were constructed from a computer-controlled voltage-step protocol generated by pClamp. The membrane voltage was stepped from −30 mV to 30 mV with 10 mV intervals and held for a duration of 100 ms at each voltage. The protocol was applied ∼2–3 s after the onset of the appropriate salt solution with added glycine. All glycine concentrations were applied directly onto the cell through a gravity-fed polyethylene U-tube. Since the current recorded during the voltage steps typically showed no obvious decay, the current amplitude was averaged over the duration of each step, excluding the capacitance transients. The voltage steps were first applied to the baseline current (in the absence of glycine), then to the glycine-activated current, and then again to the baseline current once the glycine had been washed out. The I/V data obtained in this way was determined sequentially in the 1, 0.5, and 0.25 dilutions of the particular salt solution (i.e., NaCl, LiCl, CsCl, or NaNO₃). In some cells, which remained viable for a long time, the complete set of dilutions potential measurements was repeated to check the consistency of the reversal potential measurements. After finishing each experiment, we tested for voltage drifts by breaking the tip of the electrode on the bottom of the chamber and measuring the zero-current potential. The voltage drifts in all experiments accepted for this article never exceeded ± 0.8 mV.

Macroscopic whole-cell glycine-activated I/V curves were measured for the WT GlyR channel in symmetrical NaCl solutions and again after exchange of the external solution for LiCl and then CsCl, and finally back in NaCl solution. Relative slope conductances were measured at −40 mV (between −35 mV and −45 mV) for this channel in each external solution.

Analysis

Clampfit (pClamp; Molecular Devices) was used to measure glycine-activated currents in all extracellular solutions (e.g., 1 NaCl, 0.5 NaCl, and 0.25 NaCl) by subtracting the averaged control and wash baseline currents from the currents measured in the presence of glycine at each membrane voltage. These glycine-activated currents were plotted against corresponding membrane voltage values (corrected for liquid junction potentials) to construct I/V curves using Sigma Plot 9 (Systat Software, Point Richmond, CA).

The liquid junction potential (LJP) corrections that arise from bath and pipette solutions were calculated using the Microsoft Windows version of JPCalc (18). Since there are significant changes in ionic strength in the dilution potential measurements, all liquid junction potential corrections were done using ion activities rather than ion concentrations (see later discussion in this subsection and in Appendix B). For example, the difference between the shift in the LJP corrections, ΔV_LJ, for the 0.25 LiCl dilution using concentrations was −11.0 mV, whereas the more correct approach using activities gave a slightly smaller ΔV_LJ correction of −10.2 mV. Using activities, the liquid junction potential corrections for 1 NaCl, 0.5 NaCl, and 0.25 NaCl solutions were 0.4, −2.7, and −5.9 mV, respectively. The corrections for the equivalent (1, 0.5, and 0.25) LiCl solutions were 0.2, −4.8, and −10.0 mV and for the (1, 0.5, and 0.25) CsCl solutions were 0.7, 0.8, and 0.8 mV, respectively. The V_LJ values for CsCl were similar at each dilution, since the relative Cs⁺ to Cl⁻ mobility ratio is close to unity (u_Cs/u_Cl = 1.011). It should be noted that these LJP corrections play a critical role in elucidating the relative permeability ratios. Although experimental measurements of LJPs can be technically difficult to do accurately and need some corrections, previous experimental measurements of LJPs for the same salts (LiCl, NaCl, and CsCl) under similar dilution conditions gave very similar results to the theoretical predictions (19), and were similar to the results in this article. The experimental (and corrected) LJPs for 150 mM: 75 mM dilutions of LiCl, NaCl, and CsCl (with 0.25 mM CaCl₂ and a lower HEPES concentration of 2 mM) were −6.0, −3.7, and 0.5 mV, respectively (19). The values are close to the theoretically calculated LJPs (calculated using activities) of −6.0, −3.7, and 0.1 mV (19); the signs of the quoted experimental and calculated values have been adjusted for the opposite sign convention now used for V_LJ (20,21). It should also be noted that Barry and Diamond (19) used specially prepared Ag/AgCl electrodes with fairly large corrections for Cl⁻ electrode potentials (the largest being with CsCl), so that the calculated value for CsCl is likely to be more accurate than the measured and corrected value, particularly since Cs⁺ and Cl⁻ ions have almost identical mobilities. In addition, the experimental and theoretical LJP values in that article (19) are close to the calculated LJP values in this article [V_LJ(0.5) − V_LJ(1) = −5.0, −3.1, and 0.1 mV for LiCl, NaCl, and CsCl respectively], taking into account the initial offset in the initial bathing solutions, and given the slightly different solution compositions compared to the earlier article (19). For the NaNO₃ solutions in this article, the LJP corrections, V_LJ, were 0.4, −2.1, and −4.8 mV for 1, 0.5, and 0.25 dilutions, respectively. For the biionic measurements, V_LJ = −0.7 mV. In each case, the corrected membrane potential, V_m, was determined from the pipette potential, V_p, and V_LJ by

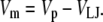(1)

All of the resultant corrected I/V data points were fitted with quadratic polynomials and the reversal potentials (the holding potential when current is zero, V_rev) were calculated for each of the dilution potential solutions (1, 0.5, and 0.25). These reversal potentials were then expressed as the change in reversal potential, ΔV_rev, with respect to the V_rev in the 1 (∼symmetrical) solution. The relative permeability of Cl⁻ with respect to the cation, P_Cl/P_cation, was determined by fitting the ΔV_rev values with the Goldman-Hodgkin-Katz (GHK) equation in SigmaPlot. In all calculations, the activities of the extracellular and intracellular cation (Na⁺, Li⁺, or Cs⁺) and anion (Cl⁻ or ) were used. For the cations, before being converted to an activity, the concentration was adjusted by the amount of the hydroxide required to titrate the solution to pH 7.4. The activities were determined by graphing and interpolating published values of activity coefficients for different ion concentrations obtained from Robinson and Stokes (22), taking account of the total ionic strength of the solution. To determine the individual ion activities in the appropriate solutions, the Guggenheim assumption was used in which individual activity coefficients are taken to be the same as the mean activity coefficient for the solution (see Barry and Diamond (19) and the discussion in Appendix B). The relative permeability ratios were calculated for each experiment and then averaged for the α1 WT and P−2′▵ mutant GlyRs.

For the dilution experiments using Cl⁻ as the anion, the GHK equation expressed in activities is given by

(2)

where ΔV_rev is the shift in reversal potential, R is the gas constant, T is the temperature in Kelvin, F is Faraday's constant, a is the activity of the ion, P is the permeability of the ion and superscripts “i” and “o” refer to the intracellular and extracellular solutions, respectively. For a justification of the use of this GHK equation in quantifying relative permeabilities and the use of the corrected activity version, see Barry (10) and Appendix B.

To determine the relative permeability of 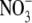with respect to Na⁺ and P_NO3/P_Na, the GHK equation is slightly modified to

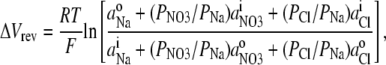(3)

where the small concentrations of Cl⁻ in both pipette and bath solutions are taken into account, using the value of P_Cl/P_Na determined in this study.

For the NaCl/NaNO₃ biionic potential measurements, Eq. 3 may be simplified and reorganized as

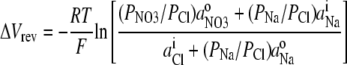(4)

since for these measurements there was no internal and no external Cl⁻. To evaluate P_NO3/P_Cl from Eq. 4, we used a value for P_Na/P_Cl, which is the reciprocal of the P_Cl/P_Na value determined in this study. However, it should be noted that the value of P_NO3/P_Cl is extremely insensitive to the value of P_Na/P_Cl used, especially for relatively small values, such as the ones similar to those measured.

All data are expressed as mean ± SE (n), where n is the number of experiments. To reduce the file size for presentation purposes, the current traces in Figs. 1, 2, and 4 were refiltered from 2000 Hz to 500 Hz and resampled from 10 kHz to 1.25 kHz by averaging every eight data points.

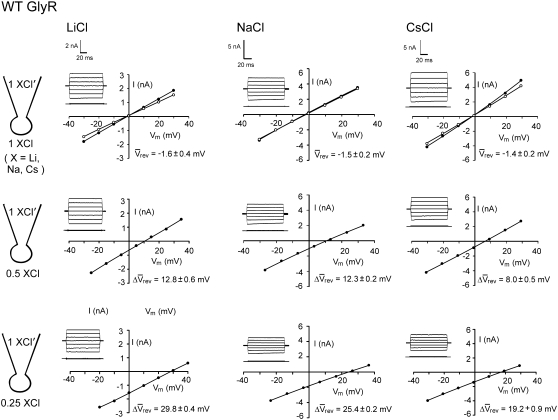
FIGURE 1.

Sample whole cell measurements of I/V curves for recombinant WT α1 GlyR channels in different dilutions of LiCl, NaCl, and CsCl solutions. Each column of I/Vs was recorded from the same cell, as the extracellular salt solution was diluted from its control concentration of ∼145 mM XCl, (1 XCl), where X represents Li, Na, and Cs, to ∼75 mM XCl (0.5 XCl), to 37.5 mM XCl (0.25 XCl), and then returned to the control concentration (1 XCl; points now shown as open circles; N.B., for the NaCl solution data shown; the before and after controls were almost identical). The pipette 1 XCl′ solution was almost the same as the 1 XCl solution except that it contained a small amount of CaCl₂ and EGTA to chelate the Ca²⁺ (full details of the solutions are given in Materials and Methods). Sets of current traces for voltage steps from 0 mV to −30 mV (bottom trace) and in increments of 10 mVs to +30 mV (top trace), in the presence (top) and absence (bottom) of glycine are shown in the inset of each graph. The potentials were all corrected for liquid junction potentials and the average reversal potentials (V_rev) and their shifts (ΔV_rev) for all the cells are shown with each graph (with bars over the top of the symbols to denote averaged values). The ΔV_rev values for all the diluted solutions are positive, indicating that the channel is anion-selective. However, the values are greater for the LiCl solutions, indicating that the relative counterion permeability for Li⁺ is less than it is for Na⁺. In contrast, the ΔV_revs are smaller for the CsCl solutions, indicating that the relative counterion permeability for Cs⁺ is greater than it is for Na⁺.

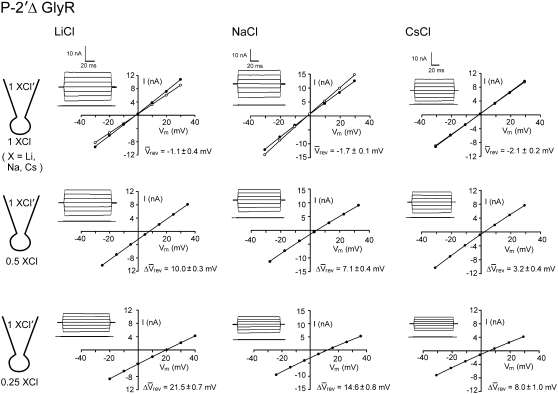
FIGURE 2.

Sample whole cell measurements of I/V curves for the larger P−2′Δ α1 GlyR channels in different dilutions of LiCl, NaCl, and CsCl solutions. The experimental procedures and solutions are identical to those described for Fig. 1. As in Fig. 1, the ΔV_rev values for all the diluted solutions are positive, indicating that this mutant GlyR channel is also anion-selective (but less so than the WT GlyR). Again, the ΔV_rev values are greatest for the LiCl solutions and least for the CsCl solutions, indicating that the relative sequence of counterion permeabilities is Li⁺ < Na⁺ < Cs⁺, as observed for WT GlyR channels, but note that all the ΔV_rev shifts are reduced compared to the values for the smaller diameter WT GlyR channel.

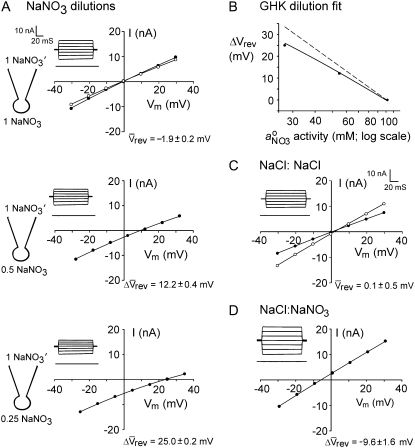
FIGURE 4.

Dilution potentials in NaNO₃ solutions and biionic NaCl:NaNO₃ solutions to determine relative P_NO3/P_Na and P_NO3/P_Cl values, respectively, for the WT α1 GlyR channel. (A) Sample whole cell measurements of I/V curves in different dilutions of NaNO₃ solutions to determine P_NO3/P_Na. The experimental procedures are identical to those described for Fig. 1 and the solution composition is given in Materials and Methods. As in Figs. 1 and 2, the ΔV_rev values for the 0.5 and 0.25 dilution solutions are both positive, indicating that the WT GlyR channel is still anion-selective when replaces Cl⁻. (B) Semilogarithmic plots of the averaged shifts in reversal potential versus external 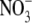activity (on a log scale). The solid lines show the fits of the GHK equation (Eq. 3) to these ΔV_rev values, as used to determine P_NO3/P_Na, averaged from individual experiments and shown in panel A. Again, as in Fig. 3, the dashed line indicates the ΔV_rev values expected if the counterion permeability had been zero. (C and D) Sample I/V curves in symmetrical NaCl solutions (C), before (solid circles) and after (open circles) measurements of biionic potentials in NaCl:NaNO₃ solutions (D). Both panels A and B are for the same cell, and panels C and D are for the same cell (though for a different one from that in panels A and B). The insets with the I/V curves show representative current traces in response to voltage steps (from 0 mV to −30 mV) (lower traces) through to +30 mV (top traces) in increments of 10 mV. The lower sets of current traces in each panel show control responses in the absence of glycine.

Calculations of equivalent or effective hydrated sizes of small ions

Our hypothesis is that the equivalent or effective hydrated size of ions can affect their permeation through small ion channels. Robinson and Stokes (22) used an empirical method to relate limiting equivalent conductivity and ionic size of a series of essentially nonhydratable tetra-alkyl ammonium ions. They then suggested that the method can be used to determine an equivalent hydrated size of an ion as the size as a nonhydratable ion with the same limiting equivalent conductivity. The methodology and results are outlined in Appendix A. We used this approach to determine the equivalent hydrated sizes of ions in this article. The validity of such an approach, in the light of more recent developments in the ion mobility field, is discussed in Appendix A.

RESULTS

HEK 293 cells transfected with WT α1 GlyRs produced glycine-activated currents (in “symmetrical” solutions of NaCl) of between ∼4,000 and 14,000 pA (+ 30 mV) and between ∼1,750 and 13,000 pA (+ 30 mV) for the mutant P−2′▵ GlyRs.

Relative permeability of the cations

For each salt (LiCl, NaCl, or CsCl), I/V curves of glycine-activated currents were determined sequentially in the 1, 0.5, and 0.25 solutions and then after returning to the 1 dilution potential solution. From these I/V curves, the zero current reversal potential, V_rev was calculated (see Materials and Methods). For cells expressing the α1 WT GlyR, the whole-cell currents were activated by 100 μM glycine and examples of I/V curves obtained for LiCl, NaCl, and CsCl are shown in Fig. 1. The mean V_rev values obtained in symmetrical conditions were −1.6 ± 0.4 mV (n = 6) for 1 LiCl, −1.5 ± 0.2 mV (n = 32) for 1 NaCl, and −1.4 ± 0.2 mV (n = 6) for 1 CsCl. In the presence of 0.5 and 0.25 LiCl, the mean ΔV_rev values were 12.8 ± 0.6 mV and 29.8 ± 0.4 mV (n = 6), respectively. By comparison, the mean values for 0.5 and 0.25 NaCl were smaller, being 12.3 ± 0.2 mV and 25.4 ± 0.2 mV (n = 32) respectively, whereas the mean values for CsCl were even smaller, being 8.0 ± 0.5 mV and 19.2 ± 0.9 mV (n = 6). The permeability values from individual experiments were determined in each case from fits of both the 0.5 and 0.25 dilutions, and then these permeability values were averaged and are shown with their mean ± SEs in Table 1.

In the same way, I/V curves of glycine-activated currents were also obtained from cells expressing the α1 P−2′▵ GlyR. In this case, the whole-cell currents were activated by 10 mM glycine. Given the large concentration of agonist required to activate these mutant receptors, controls were performed with the application of 10 mM glycine onto untransfected cells and also the application of 10 mM sucrose onto cells expressing the α1 P−2′▵ GlyR. These experiments confirmed that there were no osmotic contributions to the whole-cell currents recorded. Examples of I/V curves obtained for LiCl, NaCl, and CsCl are shown in Fig. 2. The mean V_rev values obtained in symmetrical conditions were −1.1 ± 0.4 mV (n = 7) for 1 LiCl, −1.7 ± 0.1 mV (n = 8) for 1 NaCl, and −2.1 ± 0.2 mV (n = 7) for 1 CsCl. In the presence of 0.5 and 0.25 LiCl, the mean ▵V_rev values were 10.0 ± 0.3 mV and 21.5 ± 0.7 mV. By comparison, the mean values for 0.5 and 0.25 NaCl were smaller, being 7.1 ± 0.4 mV and 14.6 ± 0.8 mV, respectively, whereas the mean values for CsCl were even smaller, being 3.2 ± 0.4 mV and 8.0 ± 1.0 mV. All these ▵V_rev values for the α1 P−2′▵ GlyR were smaller in comparison to those obtained with the α1 WT GlyR for the same salts.

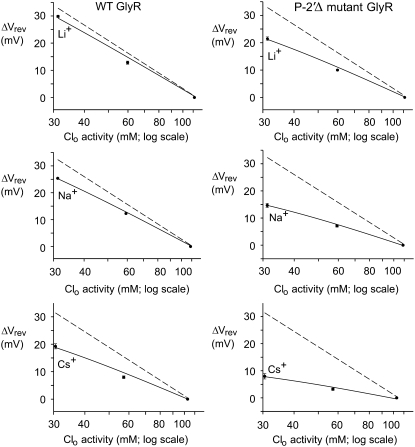
To determine the relative permeability of Cl⁻ with respect to Li⁺, Na⁺, or Cs⁺ (i.e., P_Cl/P_cation), the ▵V_rev values from each dilution potential experiment were plotted against the logarithm of the external Cl⁻ activity for each salt and fitted with the GHK equation (Eq. 2). The permeability ratios obtained were then averaged for each experimental condition and are summarized in Table 1. These results are also shown graphically in Fig. 3, where the mean ▵V_rev values obtained for the three salt solutions have been plotted against the logarithm of the external Cl⁻ activity and the GHK equation has been plotted using the mean permeability ratios from Table 1. For the WT GlyR, the relative permeability ratio is much larger when the counterion cation is Li⁺ (23.4 ± 2.8, n = 6) than with Na⁺ (10.9 ± 0.3, n = 32), and much smaller when it is Cs⁺ (5.0 ± 0.5, n = 6). This indicates that relative to P_Cl, the permeability sequence of the counterions is P_Li < P_Na < P_Cs. Although the α1 P−2′Δ GlyR channel exhibited the same relative permeability sequence for the counterions, each of the permeability ratios was reduced in magnitude compared to the WT values (Table 1). Specifically, the P_Cl/P_Li value is ∼3-fold larger than P_Cl/P_Cs for the P−2′▵ mutant GlyR, but for the WT GlyR it is almost fivefold larger. These results show that the α1 P−2′Δ GlyR channel is much less selective among the counterion cations.

FIGURE 3.

Semilogarithmic plots of the average shifts in reversal potential, ΔV_rev, versus external Cl⁻ activity (on a log scale) for the anion-selective WT and P−2′Δ GlyR channels in 1, 0.5 and 0.25 LiCl, NaCl, and CsCl solutions. The solid lines show fits of the GHK equation (Eq. 2) to the ΔV_rev values, as used to determine P_Cl/P_Na averaged from individual experiments and shown in Figs. 1 and 2. The dashed lines indicate the ΔV_rev values expected if the counterion permeability had been zero. The errors shown, when larger than symbols, are the SEs.

Changing the anion to nitrate

A set of additional experiments was undertaken with the predominantly permeant anion Cl⁻ being replaced with a more permeant anion. The purpose of these experiments was to determine whether the permeability of the anion had any influence upon the relative permeability of the counterion, as measured by P_anion/P_cation. Experiments by Franciolini and Nonner (5) with the neuronal chloride channel had suggested that the relative permeability ratio (P_anion/P_cation) was approximately constant for different anions. We chose the nitrate anion, 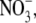which is similar in size to Cl⁻, but has a different permeability in WT α1 GlyR channels (e.g., (12)). We determined the relative permeability of 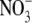with respect to Cl⁻ (P_NO3/P_Cl) under biionic conditions and obtained a value of 1.6 ± 0.1 (n = 8), confirming that 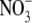is the more permeant of the two anions (Fig. 4, C and D). We next performed dilution potential experiments with the α1 WT GlyR in NaNO₃ solutions (1.0, 0.5, 0.25), using the same protocol as for the NaCl solutions. The reversal potential values obtained from the I/V curves were plotted against the 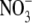activity and fitted with the GHK equation to determine the P_NO3/P_Na value. Typical I/V curves from these experiments are shown in Fig. 4 A, with the mean values of both reversal potential shifts and P_NO3/P_Na given in Table 2. The plot of the GHK equation with the mean P_NO3/P_Na and mean ΔV_rev values is shown in Fig. 4 B. As may be seen from Table 2, despite 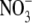being more permeant, the NaNO₃ dilution potential experiments showed no difference in the reversal potentials for the 0.5 and 0.25 dilutions compared to those in NaCl solutions. Consequently, the P_anion/P_Na values for 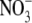and Cl⁻ were almost identical (11.3 ± 0.5 and 10.9 ± 0.3; Table 2).

TABLE 2.

average reversal potential shifts and permeability ratios for 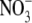Relative to Na⁺ at 22°C for WT GlyR channels

Anion	Vrev 1 NaX	ΔVrev 0.5 NaX	ΔVrev 0.25 NaX	Panion/PNa
Cl−	−1.5 ± 0.2 (32)	12.3 ± 0.2 (32)	25.4 ± 0.2 (32)	10.9 ± 0.3 (32)
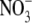	−1.9 ± 0.2 (7)	12.2 ± 0.4 (7)	25.0 ± 0.2 (7)	11.3 ± 0.5 (7)

Values are the mean ± SE, with the number of observations shown in parenthesis. V_rev and ΔV_rev values are in mV. X represents the anions Cl⁻ and 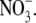The relative permeability ratio of 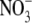or Cl⁻ to Na⁺ was averaged from permeability ratios determined using the GHK equation from individual dilution potential experiments.

Relative conductance experiments in WT GlyR channels

The aim of including these whole-cell experiments was to determine whether the macroscopic Cl⁻ conductance component was independent of the nature of the cation. Each set of experiments was done on the same cell with the intracellular solution of that cell constant (standard 145 mM NaCl pipette solution). The external solution initially contained 145 mM NaCl, then was sequentially changed to solutions containing 145 mM LiCl, 145 mM CsCl, and finally back to 145 mM NaCl, with I/V curves being determined in each solution. Example results are shown in Fig. 5. It can be seen that at positive potentials, which should represent the counterion component of current being dominated by the efflux of Na⁺ ions from the internal NaCl solution, the I/V curve was independent of the external cation. However, at negative potentials, when the counterion component of the current would be dominated by the influx of the external solution cation (Na⁺, Li⁺, of Cs⁺), there is clearly a small shift in the conductance in the different solutions, with a relative increase in the CsCl solution and a relative decrease in the LiCl solution compared to the NaCl one. The slope conductances were measured at −40 mV and the averaged results for different cells are given in Table 3. These small changes in inward current correlate well with the relative increases and decreases in Cs⁺ and Li⁺ permeability. If the counterion cation affected the anion conductance, we would predict much larger changes in the inward currents. To quantify this, we will make the assumption that at −40 mV, the counterion conductance component is being dominated by the external cation. If we then compare the conductances for the CsCl, NaCl, and LiCl solutions, we can split the total conductance, G, for each salt into its ionic conductance components, g, to give:

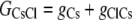(5)

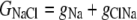(6)

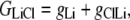(7)

where represents the Cl⁻ component of conductance in the CsCl solution, 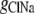represents the Cl⁻ component of conductance in the NaCl solution, and 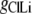the Cl⁻ component of conductance in the LiCl solution. Since the concentrations of CsCl, NaCl, and LiCl solutions were the same, we would expect ionic conductances to be proportional to permeabilities. We would like to consider two possible relationships between conductances of the cation counterion and the anion in the different salt solutions and, for brevity, will just consider a comparison of the CsCl and LiCl solution data.

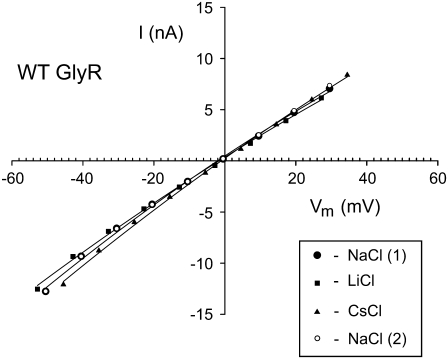
FIGURE 5.

Examples of whole cell I/V curves for the WT GlyR channel. The measurements were all made in the same cell in external solutions of control NaCl [NaCl(1)], then sequentially LiCl, CsCl, and finally back to NaCl [NaCl(2)], as indicated in the inset legend. Throughout each experiment, the NaCl composition of the cell was not changed. The V_m values were corrected for liquid junction potentials in each case. The aim was to measure the slope conductance at −40 mV for each solution (see Table 3 for averaged values), which should include a component of the conductance due to the cation counterions, anticipated at that potential to have a major contribution from the counterions in the external solution (see text). It may be seen that there is a small reduction in the slope conductance at −40 mV going from the external NaCl solution to the external LiCl solution and a small increase in slope conductance going to the external CsCl solution (see Table 3 for averaged values). The aim was to compare this relative shift in conductance with the prediction that the Cl⁻ conductance component was not dependent on the counterion.

TABLE 3.

Relative conductances in NaCl, LiCl, and CsCl solutions at V_m = −40 mV for WT GlyR channels at 22°C

NaCl(1)	LiCl	CsCl	NaCl(2)	n
1.01 ± 0.01	0.93 ± 0.01	1.04 ± 0.01	0.99 ± 0.01	5

Each value gives the averaged slope conductance from −35 mV to −45 mV (relative to the average NaCl (1) and NaCl (2) values) in each solution for n experiments. For each experiment, the measurements were done on the same cell, starting with NaCl [NaCl(1)], then going sequentially to LiCl, to CsCl, and back to NaCl [NaCl(2)]. V_m was corrected for liquid junction potentials before the conductances were measured.

Case 1: The Cl⁻ component of conductance is not affected by the nature of the counterion cation

In this situation, the Cl⁻ conductances are such that

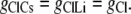(8)

From Eqs. 5 and 7, we have that

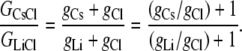(9)

Since the concentrations of cations and anions in each solution are both the same, then

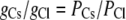(10)

(11)

Using the same data set from which the relative permeability values for P_Cl/P_Cs and P_ClP_Li are given in Table 1, the mean ± SE for the reciprocal P_Cs/P_Cl and P_Li/P_Cl were calculated from the individual permeabilities to be 0.208 ± 0.021 and 0.046 ± 0.005. Hence, using these mean values, the predicted value of G_CsCl/G_LiCl = (0.208 + 1)/(0.046 + 1) = 1.15 ± 0.02. The same mean ± SE values were obtained by taking the mean value of (P_Cs/P_C1 + 1)/(P_Cl/P_Li + 1) from the individual experiments.

Case 2: The anion component of conductance is affected by the cation, but the counterion conductance component is independent of the nature of the cation

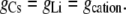(12)

From Eqs. 5 and 7, we now have that

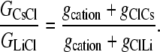(13)

Hence, from Eq. 11, we have that

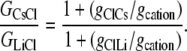(14)

Using the mean relative permeability values, P_Cl/P_Cs and P_Cl/P_Li, from Table 1, the predicted value for G_CsCl/G_LiCl = (1 + 5.0)/(1 + 23.4) = 0.25. Alternatively, if we calculate the mean value of G_CsCl/G_LiCl from the individual values of (1+P_Cl/P_Cs)/(1 + P_Cl/P_Li), we obtain a similar predicted value of 0.27 ± 0.04, which now also includes the mean ± SE for the mean.

The experimental value for G_CsCl/G_LiCl, determined from the mean experimental values of slope conductances in Table 3, was (1.04 ± 0.01)/(0.93 ± 0.01) = 1.12 ± 0.02. This result is virtually identical to the prediction of Case 1 (1.15 ± 0.02), and is very different from the predictions of Case 2 (0.27 ± 0.04). The experimental results therefore indicate that the anion component of conductance is independent of the nature of the cation (Case 1).

Estimates of equivalent hydration shell diameter

To help interpret the relative anion-cation permeability results obtained from the dilution potential experiments, estimates of equivalent or effective hydration shell radii and diameters for each of the cations and anions were determined. As indicated in Materials and Methods and Appendix A, these values were calculated from the limiting equivalent conductivities and Stokes' law radius data of Robinson and Stokes (22) for a range of effectively nonhydratable tetra-alkyl ammonium ions, to enable the determination of a correction factor for small ions (and are given in Table 4). The equivalent hydrated diameter of an ion is taken as the size of an essentially nonhydratable ion (as in the case of the tetra-alkyl ammonium ions) with the same limiting equivalent conductivity as the hydratable ion. Although ionic mobility within restricted regions, such as ion channel pores, may involve poorly defined microscopic interactions among ions, water molecules, and protein, we would interpret this effective diameter as slightly larger than the size of an ion with its tightly bound “primary hydration shell”, since interaction from its secondary water molecules would also be considered to have reduced its mobility (see discussion of hydrated sizes in Appendix A). The values of equivalent hydrated diameters for the cations Li⁺, Na⁺, and Cs⁺, together with the anions Cl⁻ and are shown in Fig. 6.

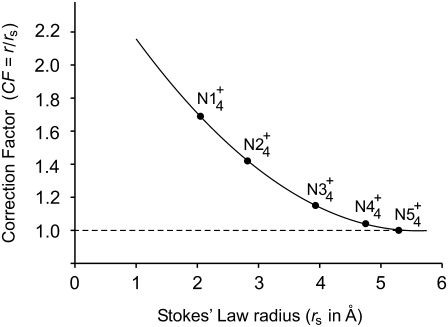
TABLE 4.

Ionic properties of the tetra-alkyl ammonium ions and the CF for the corrected Stokes' law radius of small ions

Ion	λ0	r (Å)	rs (Å)	r/rs = CF
	44.9	3.47	2.05	1.69
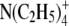	32.6	4.00	2.82	1.42
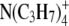	23.4	4.52	3.93	1.15
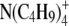	19.4	4.94	4.75	1.04
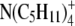	17.4	5.29	5.29	1.00

λ⁰ is in units of S.cm².equiv^.−1. The λ⁰ and r data are from Appendix 6.2 and Table 6.2, respectively, of Robinson and Stokes (22). However, r_s and r/r_s were calculated afresh, r_s from r_s = 0.820/(λ⁰ η^o), which, with η^o = 0.008903 poise for water at 25°C, gives r_s = 92.1/λ⁰.

FIGURE 6.

Schematic cartoon diagrams of the selectivity filter region and two of the M2 domains for the WT and P−2′Δ mutant GlyR channels, with measured minimum pore diameters (11,12) and associated counterion permeability data (n ≥ 6) from Tables 1 and 2. Although the diagrams are drawn to represent the minimum pore diameters of each channel and to indicate some relative putative protrusion of the residues from −3′ to 2′ into the lumen of the selectivity filter region and the proposed β-strand structure of this region (see text for discussion of this), they are not intended to accurately represent the positions of these residues in this region. The smaller “+” signs for the P−2′Δ mutant GlyR channels are intended to represent a weakened electric field in the channel lumen due to R0′ putatively protruding less into it (see text for discussion). The right inset gives the ionic diameter and calculated equivalent hydrated diameter (d_H) of the relevant permeant ions (from Table 5). For both Li⁺ and Na⁺, d_H has been newly recalculated and for Cs⁺, Cl^−, and the d_H values are de novo calculated ones, in each case from ionic sizes using other data from Robinson and Stokes (22), as outlined in Appendix A and Fig. 8. The pore diameters and ionic and equivalent hydrated radii have all been approximately drawn to scale.

DISCUSSION

We have previously suggested that counterions must permeate through the selectivity filter of the GlyR channels with permeant coions as a neutral ion pair (1). This was based upon the relatively low magnitude anion-cation permeability ratios obtained with some mutant GlyRs (e.g., (16)). Anion-cation chaperoning was observed by O'Mara and colleagues (3) in BD simulations of ion permeation in these channels, though they did not observe individual counterions transit the channels. However, in a different simulation on the same channels, Cheng and colleagues (23) did observe individual counterions transiting the channels.

The aim of this study was therefore to investigate and test two hypotheses: a), that counterion permeation in anionic channels depends on the size of the equivalent hydrated cation relative to the channel pore radius, and b), that counterions permeate through charged selectivity filters by being chaperoned by the permeant anions. To do this, we examined both the effect of counterions with different ionic diameters, and the effect of similar GlyR channels with different minimal pore diameters, on anion-cation permeability ratios. We therefore investigated the effects of Li⁺, Na⁺, and Cs⁺, on the relative anion-cation permeability in two anion-selective glycine channels: the WT GlyR (diameter 5.3 Å) and the larger diameter mutant P−2′Δ GlyR (diameter 6.9 Å). For both channels, we found that P_Cl/P_Li > P_Cl/P_Na > P_Cl/P_Cs, though the range of permeabilities was greatly reduced for the larger channel (Table 1). It should also be noted that the proline deletion in the mutant P−2′Δ GlyR, in addition to increasing the minimum pore diameter of the selectivity filter, could result in other structural changes in the pore. We have previously suggested that this mutation causes a positively charged arginine at 0′ to move back somewhat from the pore lumen, thus reducing its effective electrical field strength in the channel (1).

To more quantitatively explore the relationship between cation size and the relative anion-cation permeability results for both channels, the equivalent or effective hydration shell radii for each of the cations and anions was calculated (Appendix A), using limiting equivalent conductivities and Stokes' law radii for each ion (22). A correction factor was included that is particularly important for hydrated ions with a radius <∼5 Å (10 Å diameter). This correction factor was derived from measurements on essentially nonhydratable tetra-alkyl ammonium ions of known size, where their size was greater than predicted from the ion mobility using Stokes' law (Appendix A), because frictional forces over such small dimensions are less than is assumed in the derivation of Stokes' law. Although the hydrated size of an ion is considered to be a somewhat “fuzzy concept” (14), Robinson and Stokes (22) indicate that it does have some validity provided the sizes have been corrected (as outlined in Appendix A) and the hydrodynamic dimensions are not taken too literally as being equivalent to those of a rigid hydration shell. Using the data and approach of Robinson and Stokes ((22); see also Appendix A), the corrections were calculated from mobility measurements done on tetra-alkyl ammonium ions, which combine known molecular sizes of relevant dimensions (2–5 Å radius) and symmetrical shape, with low surface charge densities and hence minimal hydration shells of their own (see details in Appendix A). Hence, this corrected Stokes' law radius and diameter of a nonhydratable ion with the same limiting equivalent conductivity as the hydrated ion (e.g., alkali cation and halide anion) give an estimate of the equivalent hydrated diameters of these ions. We might expect this to be slightly larger than the size of an ion with its tightly bound hydration shell, since interaction from its secondary shell water molecules would also reduce its mobility (and therefore increase the estimate of its diameter). Robinson and Stokes (22) also showed that such equivalent hydrated sizes implied very reasonable ion hydration numbers (e.g., five water molecules for Na⁺ and seven for Li⁺). A consideration of hydrated sizes of ions is relevant for ligand-gated channels where ions do not seem to permeate in their fully dehydrated state. These calculations resulted in effective hydrated diameters for Li⁺, Na⁺, Cs⁺, Cl⁻, and 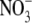of 7.5, 6.5, 5.0, 5.0, and 5.2 Å respectively, as indicated in Fig. 6 and Table 5.

TABLE 5.

Parameters for determining the equivalent hydrated radius, r_H, and equivalent hydrated diameter, d_H, for the three alkali cations, nitrate, and chloride

Ion	ri (Å)	di (Å)	λ0	rs (Å)	CF	rH (Å)	dH (Å)
Li+	0.60	1.2	38.6	2.39	1.57	3.74	7.5
Na+	0.95	1.9	50.10	1.84	1.77	3.26	6.5
Cs+	1.69	3.4	77.2	1.19	2.08	2.48	5.0
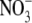	1.76	3.5	71.46	1.29	2.03	2.62	5.2
Cl−	1.81	3.6	76.35	1.21	2.07	2.50	5.0

Ionic radius, r_i, and ionic diameter, d_i, data for the alkali cations and Cl⁻ were from Pauling (43) (see also Table 3.1 in Robinson and Stokes (22)) and the 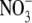value was from Grunwald and Effio (44). λ⁰ values were from Appendix 6.2 of Robinson and Stokes (22). The Stokes' law radius, r_s, calculated from limited equivalent conductivity using Eq. A7 in which r_s = 92.1/λ^o assuming the viscosity of water, η^o = 0.008903 poise. The CF, determined from the fit of the tetra-alkyl ammonium ion data in Fig. 8, was calculated from r_s using the fitted equation (A8) and the equivalent hydrated radius r_H was determined by multiplying r_s by CF (see text for details).

Before we discuss the experimental permeabilities of the WT and mutant glycine channels, it would be helpful to comment on the putative structure of the selectivity region of the GlyR channel. Much of this is covered in Keramidas et al. (1). Unlike both the cation-selective nAChR α1 and 5-HT_3AR subunits that have positive (K0′ or R0′) and negative (E-1′) amino acid residues at positions 0′ and −1′, the anion-selective GlyR α1 and GABA_AR α1 and GABA_CR ρ1 only have positive (R0′) and neutral (A−1′) amino acids at those two residues. For the nAChR α1 and 5-HT_3AR subunits, the evidence strongly suggests that the E−1′ glutamate controls conductance and selectivity, whereas the K0′ or R0′ does not. For whole-cell patch clamp experiments with the GlyR α1 channel in HEK 293 cells with the neutral −1′ residue mutated to a negative charge (A−1′E) and with the −2′ proline residue deleted (P−1′Δ), so as to make these residues equivalent to those in the nAChR α1 or 5-HT_3AR, the channel is clearly cation selective (P_Cl/P_Na = 0.13). This suggests that the electrostatic influence of the negative glutamate (A−1′E) is now greater than that of the R0′, suggesting that the −1′E now protrudes into the channel and that the R0′ in the GlyR does not (16). Without the proline deletion and with both negative (A−1′E) and positive (R0′) residues, the channel is only slightly cation-selective (P_Cl/P_Na = 0.34) and the WT GlyR with only the positive (R0′) residue is strongly anion selective (P_Cl/P_Na = 24.6) (16). With only the proline deletion (P−1′Δ), it becomes less anion-selective (P_Cl/P_Na = 0.34) (16). We would argue that in the WT GlyR α1, the electrostatic influence of the R0′ residue is protruding into the channel and that the proline deletion is affecting the relative exposure of R0′ (and the A−1′E, when present) there. BD simulations of these mutations in the GlyR by O'Mara et al. (3) and Cheng et al. (23) have been able to predict this permeability data and support these suggestions. Ideally, it would have been helpful to have been able to mutate the R0′ residue in the GlyR channel, but such mutations invariably resulted in the mutant channel not being expressed. Nevertheless, in microelectrode experiments in Xenopus oocytes by Wotring et al. (24) with GABA_CR ρ1 homomeric channels, mutating the positive R0′ residue to a negative residue (R0′E) resulted in this channel becoming weakly cation selective, whereas neutralizing the R0′ with either R0′M or R0′C also increased cation permeability, though the channel still remained predominantly anion selective. This residual anion selectivity in the absence of a charged 0′ residue may in part reflect the effect of pore size itself tending to favor anions over small cations (1) and the effect of external divalent ions reducing cation permeation in dilution potential experiments (S. Sugiharto, J. E. Carland, T. M. Lewis, A. J. Moorhouse, P. R. Schofield, and P. H. Barry, unpublished results). Wotring and Weiss (25) recently scanned this region in the GABA_CR ρ1 channel from −2′ to 5′ with glutamate substitutions. They showed that these glutamate substitutions displayed a significant increase in cation selectivity when made at the −2′, 0′, 2′ (see also Carland et al. (26)), 3′, and 5′ residues, with only small increases at −1′ and 1′. They suggested that this region may form a β-strand (25). In Fig. 6, we have shown R0′ as just protruding into the channel lumen for the WT GlyR and being slightly retracted for the P−1′Δ GlyR, to reflect the balance of experimental evidence, and have adjusted some of the other residues slightly in the light of the GABA_CR experiments, but we reiterate that the precise orientation of the residues in this selectivity filter region is unknown.

With the calculated equivalent hydrated ion sizes (Fig. 6; Table 5), we can now state that the cation permeability (P_Li < P_Na < P_Cs) correlates directly with ionic radii or inversely with the equivalent hydrated size of the cations, so that as the equivalent hydrated size increases, the cations became less permeant. This has the same sequence as free solution limiting equivalent conductivities, with the relative free solution mobilities of Li/Na/Cs ions being in the ratio of 0.5:0.65:1.0 (from Table 5), but the relative magnitudes of these cation permeabilities are quite different. For example, in the large pore diameter mutant P−2′Δ GlyR channel, P_Li/P_Na/P_Cs = 0.32:0.57:1.0 (from Table 1), so that compared to Cs⁺, the larger size equivalent hydrated Na⁺ ion is relatively reduced to ∼88% of its free solution mobility and the largest size equivalent hydrated ion Li⁺ is reduced to ∼64% of its free solution mobility. Comparable calculations for the small pore diameter WT GlyR channel, P_Li/P_Na/P_Cs = 0.21:0.46:1.0 (from Table 1), indicate that compared to Cs⁺, the larger equivalent hydrated Na⁺ ion is now only ∼71% of its free solution mobility and the largest equivalent hydrated ion Li⁺ is now only ∼42% of its free solution mobility. Clearly those cations with the larger equivalent hydrated radii have a slowed permeation through the channel pore, well below their relative free solution mobilities, the effect being accentuated in the smaller diameter channel. In addition, it should also be appreciated that the cation/anion permeabilities even for the most permeant cation, Cs⁺, (P_Cs/P_Cl = 0.5; Table 1) are far below their free solution mobility ratios (u_Cs/u_Cl = 1.01) for the P−2′Δ GlyR channel and even smaller (P_Cs/P_Cl = 0.20) for the small diameter WT GlyR channel (Table 1). Of course, we expect this reduction in cation/anion permeability because of the positively charged selectivity filter in both channels. In comparing permeation through the two channels, we also need to be aware, as previously mentioned, that in the large minimum pore diameter mutant P−2′Δ GlyR channel it seems likely that the arginine residue close by at 0′ also has a reduced field strength by virtue of its reduced exposure into the pore lumen compared to the WT GlyR, consistent with the P−2′Δ GlyR channel having a much reduced P_Cl/P_Na compared to the WT GlyR channel.

We would now like to explore the relationship among relative counter ion permeability of the cations, their calculated equivalent hydrated diameters, and the minimum channel pore diameter, in the light of our discussion in Appendix A about the validity of the concept of equivalent hydrated sizes. It has already been shown that selectivity among different anions in these anionic WT GlyR channels can be explained in terms of the energy difference among the anions interacting with charged (positive) sites within the channel and ion dehydration, as originally proposed by Eisenman (39) (see also the discussion in Hille (14)), and as acknowledged to describe relative anion permeability through GlyR channels by Bormann et al. (27) and others (1). However, such a model would not be expected to apply to cation counterions permeating through a positively charged selectivity filter region by themselves, where they would be electrostatically repelled by charged sites of the same sign. However, as we can see from Fig. 6, for the WT GlyR channel, there is clearly an inverse correlation between the equivalent hydrated size of the cations and the relative cation permeability. Without considering any detailed permeation mechanism for overcoming the electrostatic barrier to pass through the selectivity filter of the channel, the Cs⁺ ion would probably not need to be dehydrated to any significant extent, whereas the Na⁺ ion would have to be dehydrated from a diameter of 6.5 Å to at least 5Å and the Li⁺ ion to be further dehydrated from 7.5 Å again to at least 5 Å. The same principle would apply to the 6.9 Å mutant P−2′Δ GlyR channel, but the amount of dehydration for the Na⁺ ion would probably be quite small and the Li⁺ ion would need to reduce from 7.5 Å to at least 6.9 Å. For both channels, in each case, the decrease in relative cation permeability due to the required dehydration would need to be proportional to exp(−energy of required amount of dehydration/kT). Of course, the precise size of the hydration radius of each ion should not be taken too literally and the amount of dehydration need not be a complete spherical dehydration. Although additional factors can affect permeation, this partial dehydration effect may explain much of the relative cation permeability and its relationship to the difference between pore size and equivalent hydrated ion size.

Although the above data and analysis highlight the importance of the size of the equivalent hydrated radius relative to the pore size, one still needs to explain how cations can permeate through the positively charged selectivity filter region of small anion-selective channels. Corry (28) suggests from his BD modeling of permeation through channels of small radius with a charged selectivity filter that when the channel radius decreases to ∼3 Å (6 Å diameter), counterion permeation ceases (28). For example, BD modeling of ion permeation through the WT GlyR channel by O'Mara et al. (3) indicates that a single Cl⁻ ion entering an empty channel would experience a deep energy well of ∼−16 kT (due to the positively charged selectivity filter), facilitating its move into that region of the channel. Further Cl⁻ ion movement into the channel then needs a second Cl⁻ ion entering the channel vestibule to help the first ion move on out of that energy well. In contrast, a Na⁺ ion entering an empty channel faces an energy barrier of +27 kT, effectively excluding it from the channel (Fig. 2 of O'Mara et al. (3)). Nevertheless, experimental measurements of anion-cation permeability ratios show that cation counterions do permeate through such anion-selective channels. Anion-cation chaperoning has been observed in BD simulations (3) and we propose that the following must happen to overcome the large energy barrier for Na⁺ ions at the selectivity filter, particularly in the WT GlyR channel. We envisage that periodically Na⁺ and Cl⁻ ions will form an ion pair as they come close to the selectivity filter and that this neutral pair can pass through the selectivity filter. For the complex to permeate through the selectivity filter region, the larger hydrated ion (the cation) would at least have to lose some of its water of hydration as earlier described and as indicated by the data, but to completely dehydrate the ions is not necessary and would require a considerable amount of energy given the hydration energies of Na⁺ and Cl⁻.

For the larger diameter P−2′Δ GlyR channel with the weaker field strength sites, some of the counterion permeation may occur without the need for chaperoning, as the energy barrier for cation permeation is smaller and pore diameter larger. As already mentioned, our previous studies have revealed that the minimum pore diameter is not the only factor influencing the anion-cation selectivity (e.g., P_Cl/P_Na) of the channel, and that the sign of the electrostatic charge provided by amino acid side chains in the selectivity filter of the channel pore plays a dominant role in ion selectivity (e.g., (1)). This positive potential in the channel pore of anionic GlyRs would also influence P_Cl/P_cation values, and this can be best appreciated with hydrated Cs⁺ and hydrated Cl⁻ ions since they have similar ionic radii, similar equivalent hydrated diameters, but different valency. The preference of both channels for Cl⁻ (especially in the larger P−2′Δ GlyR) again illustrates the dominant effect of electrostatics in determining anion-cation selectivity. In addition, the cation counterion may still need some shielding to permeate through the larger channel. For example, it may permeate as a neutral ion pair to overcome the electrostatic energy barrier due to some positive residue charge at the selectivity filter.

If counterions do permeate through the selectivity filter as neutral ion pairs, as proposed above, then our hypothesis is that the rate of such pair formation should depend upon the local concentration of cations and anions close to the selectivity filter. In addition, it would seem reasonable that the local concentration of anions should be proportional to the rate at which the anions permeate. Further, the rate at which the neutral ion pairs permeate would be expected to be inversely proportional to the size of the larger hydrated ion of the pair (in our cases generally the cation) and, as indicated above, proportional to the permeability of the anion. This implies that for such a neutral pair permeation model, the permeability of different types of anions relative to the permeability of the same cation (P_anion/P_cation) should be a constant. In contrast, if the cations and anions permeated independently, the relative P_anion/P_cation would be expected to change as the anion permeability changed. Therefore, as a further test of the neutral pair permeation model for counterions, we investigated the P_anion/P_cation ratio using a different anion, As already noted, the effective hydrated diameter of 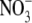of 5.2 Å (Table 5) is close to that of Cl⁻ (5.0 Å), which is not surprising given their similar bare ionic radii. The hydrated diameters of both anions are also much smaller than that of Na⁺. Biionic experiments (Fig. 4) indicated that was more permeant than Cl⁻, with P_NO3/P_Cl = 1.6 ± 0.1 (n = 8). However, measurement of P_anion/P_Na for both Cl⁻ and 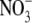gave virtually identical values of 10.9 ± 0.3 (n = 32) and 11.3 ± 0.5 (n = 7) (Table 2) or a ratio (P_NO3/P_Na)/(P_Cl/P_Na) of 1.04 ± 0.08. This strongly supports the neutral ion pair model, as opposed to the independent permeation of anions and counterion cations in GlyR channels. Similar results were obtained by Franciolini and Nonner (5) for the neuronal and skeletal muscle background Cl⁻ channels. Using Na⁺ salts of anions with different relative permeabilities and conductances (Cl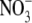⁻, propionate⁻, F⁻, Br⁻), they also found that dilution potential measurements gave essentially constant zero-current potentials (implying constant P_anion/P_Na values). They also suggested that the permeation of the cation was coupled to the anion in those channels. Such a proposition was further endorsed by Wang and colleagues (29) in their studies on cation-anion interactions in a predominantly anion-selective mutant GABA_A receptor Cl⁻ channel, in which they found that cation permeation could only be shown in the presence of a permeant anion. When they replaced internal Cl⁻ by a large organic impermeant anion (gluconate), they observed no inward single channel currents at very negative voltages.

In the WT GlyR conductance measurements in this article, although the data indicated that cation counterion permeability is coupled to anions so that they can permeate, the converse is not true. That is, anion permeation is independent of the nature of the cation counterion. The small changes in channel conductance in the presence of the different salts were shown to reflect the small and different contributions of the counterion cations in proportion to their relative permeabilities, so that the anion component of the macroscopic conductances was essentially unchanged.

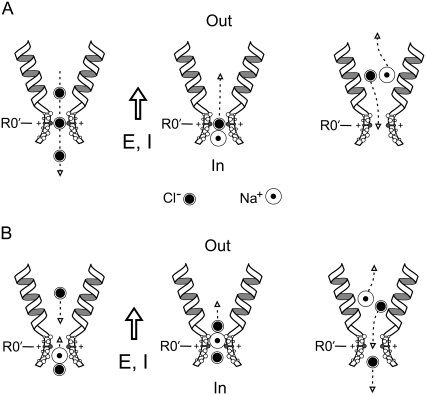
We suggest two possible models by which counterion permeation can occur as “neutral” ion pairs (see Fig. 7) that seem simple and fit the data very well. Both models involve the counterions being chaperoned by the permeant coion. The first model (Fig. 7 A; see also the figure legend), which we previously suggested (1), involves the counterions permeating by being chaperoned by the permeant coion as they pass through the selectivity filter as a “neutral” ion pair diffusing down its concentration gradient before dissociating in the external vestibule and the anion moving back through the selectivity filter. The cations with hydration shells larger than the pore radius will still need to lose an appropriate fraction of their hydration shell to permeate as a neutral ion pair. The second model (Fig. 7 B; see also the figure legend) is somewhat similar to that of Franciolini and Nonner ((9), Fig. 10 therein), except that we are assuming that the ions will carry with them about the same proportion of their hydration shells as in the case above and we have not specified any detailed interaction with particular channel sites lining the pore region. In this model, the internal solution anion does not permeate right through the channel with the cation, but just takes it to the internal end of the selectivity filter from where the cation is met by an anion on the external side, which then forms a neutral pair and allows the cation to move into the external vestibule before the new pair dissociates.

FIGURE 7.

Two possible schematic models (A and B) to explain counterion permeation through the selectivity filter (SF) region of GlyRs. In each case, the channel and equivalent hydrated ions are drawn approximately to scale for the dimensions of the SF region of the P−2′Δ mutant GlyR. As in Fig. 6, the relative protrusion into the channel lumen reflects the electrostatic contribution of the critical selectivity residues and the proposed β-strand structure of this region, rather than meaning to specify the precise orientation of these residues. The open arrows give the direction of the electric field (E) and net current (I). For these schematics, a positive potential (inside–outside) has been chosen such that the electrical gradient dominates the chemical activity gradient, which has been chosen such that it is from inside to outside. The electrical gradient (and electrochemical gradient) hence favors Na⁺ flux from inside to outside, and Cl⁻ flux from outside to inside (e.g., +30 mV, with an external 0.5 NaCl dilution). The predominant outward current is due to an inward movement of anions (e.g., as shown in the left panel of A). In panel A, it is proposed (as in the middle panel) that periodically an Na⁺-Cl⁻ ion pair is formed near the internal end of the SF region and that the “neutral” ion pair is able to diffuse through the SF region down its concentration gradient, with the Na⁺ counterion being effectively chaperoned. If the complex then dissociates once it has passed through the SF region, the Na⁺ ion should continue to move in the direction of the electric field, as indicated by the dashed arrow in the right panel, and so contribute to the net current flowing through the channel. The dissociated Cl⁻ ion should now move in the opposite direction to the electric field, back through the SF region, and so not contribute to the net current through the channel. Hence, the net result will be one Na⁺ ion moving through the channel (cf. Fig. 8, A and B, of Keramidas et al. (1)). Our panel B is somewhat similar to the model of Franciolini and Nonner (9) (see their Fig. 10), except that we are assuming that the ions will carry with them most of their hydration shells and we have not specified any detailed interaction with both polar and charged sites lining the SF region. We again assume that periodically an Na⁺-Cl⁻ ion pair is formed (as shown in the left panel) and is able to diffuse toward the SF region, with the Na⁺ ion (at least intermittently) aligned toward the SF. As Cl⁻ ions, which will be moving down their electrical gradient from outside to inside (also left panel), approach the SF region, they will make it easier for the Na⁺ ion to form a neutral ion pair with the Cl⁻ ion. The neutral ion pair can then diffuse away from the SF region, as in the middle panel. As it moves away from the constricted region, it will tend to dissociate and the Na⁺ ion will now move down its electrical gradient and the Cl⁻ ion is now free to again move toward the SF region (right panel).

CONCLUSIONS

We have made the case in this article that despite the development of successful new microscopic statistical ensemble theories to explain the relationship between ion mobility and ion size, that there is still some value in determining an equivalent hydrated size for small ions, particularly for investigating ion permeation through small diameter ion channels. We have then shown for ion permeation through anion-selective GlyRs that the physical properties of the cation counterion, in particular its equivalent hydrated diameter relative to the size of the ion channel, correlate inversely with the relative permeability of the counterion. The larger the equivalent hydrated diameter of the counterion, the smaller its relative permeability compared to the predominantly permeant anion. This effect is reduced in magnitude as the minimum pore diameter of the channel is increased. The data are also very consistent with the new estimates of the equivalent hydrated sizes of the ions and the measured minimum pore diameters of the two GlyR channels investigated and can be explained in terms of the additional energy barrier resulting from the relative amount of dehydration that the cation has to undergo to be able to pass through the selectivity filter region. We believe that the consistent explanation of these results adds to the validity of the approach. For two anions with different permeabilities, but both with smaller equivalent hydrated sizes than that of the cation (Na⁺), the value of P_anion/P_cation is the same in the WT GlyR channel, indicating that the counterion does not permeate independently of the anion in this channel. We have given a simple explanation as to why this could be the case, with the rate of anion-cation pair formation being proportional to the anion permeability and the permeation of the anion-cation pair being determined by the size of the larger equivalent hydrated size of the ion of the complex, in this case the cation. We have also shown from conductance measurements done for the WT GlyR channel that the data indicate that the anion conductance component is independent of the nature of the cation. Together our data strongly support a model where permeation of the cation counterions occurs as a neutral anion-cation pair, particularly in the case of the smaller diameter WT GlyR channel. We suggest two related models depicting how the counterion cation permeation could result in current flow through the channel, with the paired anion chaperoning the cation only across the selectivity filter before the cation dissociates from the pair.

APPENDIX A: CALCULATION OF EQUIVALENT HYDRATED SIZES OF THE SMALL ALKALI CATIONS LITHIUM, SODIUM, AND CESIUM, AND OF THE ANIONS CHLORIDE AND NITRATE

Empirically, the smallest alkali cation, Li⁺, has the smallest free solution mobility and requires the greatest energy to dehydrate it, whereas the largest, Cs⁺, is the most mobile and requires the least energy to dehydrate it. Since there is basically an inverse relationship between particle size and mobility, this suggested that such ions had some sort of a shell of water molecules surrounding them, with the hydration shell around Li⁺ being larger than that around Cs⁺. This is a helpful concept when considering ions moving through a small diameter ionic channel in a membrane, as such ions may need to be partially or fully dehydrated to pass through a selectivity filter region in the channel. In the past, it was usual to think of primary and secondary hydration shells around ions with the primary shell being most tightly bound. More recently, especially among physical chemists, the development of various theoretical approaches to model ion mobility in solutions that account for the interactions of an ion with polar water molecules has meant that a rigid hydration shell model has tended to go out of vogue. However, our hypothesis is that the above approaches are not mutually exclusive and that an equivalent or effective hydrated size of ions is still a useful concept that has some validity and value in helping to explain the permeation through small ion channels.

To defend this hypothesis, first of all, the relationship between Stokes' law radius and limiting equivalent conductivity will be outlined for nonhydratable tetra-alkyl ammonium ions based on empirical measurements. Then a short overview of the developing physical basis underlying the mobility of small ions in water will be presented, concluding with the results of a molecular dynamics study, which also supports the validity for a hydration shell type model especially for small Li ⁺ ions. Finally, in the light of such results, a case will be made for the value of calculating an equivalent or effective hydrated size for such small hydratable ions, as being equivalent to that of a predicted nonhydratable ion with the same limiting equivalent conductivity as the hydratable ion. These calculations will then be done for the ions in this article. The usefulness of the approach may then be judged on how well such equivalent hydrated sizes can explain the results in this article.

The relationship between Stokes' law radius and limiting equivalent conductivity for nonhydratable tetra-alkyl ammonium ions

The calculation of the Stokes' law radius, r_s, for small ions or molecules uses the relationship between terminal velocity, v, of an ion, or molecule, under a unit force F_x, which is given by

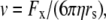(A1)

where η represents the viscosity of the medium (i.e., water) and r_s is the Stokes' law radius of the ion. Hence,

(A2)

and

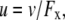(A3)

where u is the mobility of the ion (i.e., its velocity under a unit force), which is directly related to the limiting equivalent conductivity of the ion, λ^o, by

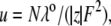(A4)

where N is Avogadro's number, F is the Faraday, and z is the valency of the ion. Thus, the Stokes' law radius, r_s, is related to λ^o by

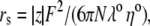(A5)

where η^o is the viscosity of pure water (22). Robinson and Stokes (22) indicate that for monovalent ions this becomes

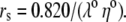(A6)

Using a value of η^o = 0.008903 poise (= 0.008903 × 10⁻⁵ N.s.cm⁻²) for water at 25°C, this then becomes

(A7)

where r_s is in Å when λ^o is measured in S.cm².equiv.⁻¹ at 25 °C. Although, the above equation is reliable for large molecules, the question arises as to whether it can be used for small molecules and ions. Robinson and Stokes (22) describe experiments to explore the relationship with a series of five tetra-alkyl ammonium ions and with radii, estimated from molecular volumes and models, increasing from ∼3.5 to 5.3 Å. These ions have the advantage that they combine a relatively large size with a symmetrical shape and low surface charge and so will not interact so strongly with water molecules. Robinson and Stokes (22) made the following point and described the method for determining ionic radii for the above ions as follows. They indicated that for “these ions the product λ^oη^o is very nearly constant over a fair range of temperatures in water” and suggested that “the mobilities of the tetra-substituted ammonium ions (could be used) to calculate correction factors for Stokes' law in water”. Their aim was then to use “these factors to calculate the size of the strongly hydrated ions from their mobilities”. To do this required knowing the sizes of the tetra-alkyl ammonium ions, which they suggested may be obtained, “to a fair approximation”, as follows:

1. The effective radius of the 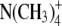ion can be estimated from the N-C internuclear distance of 1.47 Å to which is added Pauling's value of 2.0 Å for the van der Waals radius of the methyl group as a whole, giving 3.47 Å.

2. For the ion a similar calculation from bond lengths and angles indicates a maximum radius of ∼4.2 Å, whereas a scale model (using “Catalin” atomic models) suggests an average radius of 4.0 Å; The value is somewhat dependent on the configuration given to the C-C-H linkages. The latter value is probably preferable.

3. For the higher homologues, it is not easy to estimate a radius from bond lengths or models, as too many configurations exist. The following rather tentative method may be tried: the first two members of the series are structurally very similar to the symmetrical paraffins C(CH₃)₄ and C(C₂H₅)₄, which have molal volumes of 120 cm³ and 170 cm³, respectively. One would expect the radii to be directly proportional to the cube roots of the molecular volumes, and one finds, in fact, that the empirical relation

   

   (with r in Å and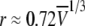 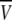in cm³ per mole) gives the first two members r = 3.55 Å and r = 3.99 Å in adequate agreement with the values given above. One may then estimate approximate radii for the higher members by this formula, assuming the density of the corresponding paraffins.

The ionic radii estimated from molecular volumes or models as outlined above are given in Table 4. The limiting equivalent conductance of these tetra-alkyl ammonium ions in water at 25 °C were “obtained from the latest values given by Kraus and his collaborators (30), obtained from measurements by the most fastidious techniques extending to concentrations as low as 10⁻⁴ molar, …” (22), and are also given in Table 4. From these values, the Stokes' law radius, r_s, was calculated for each ammonium ion and the values are given in Table 4.

Robinson and Stokes (22) thus showed (see Table 4) that for these ammonium ions, if they had a radius >∼5 Å, that the Stokes' radius, r_s, agreed well with the ionic radius, r. They thus suggested that the 6π constant (in Eq. A2) may not be so reliable for radii <5 Å and hence that a different constant should be used in Eq. A5. Using these equations, they therefore calculated the ratio (r/r_s) of the ionic or molecular radius (r) to the measured Stokes' radius (r_s) for the five tetra-alkyl ammonium ions (Table 4) and showed that all the data points could be very well fitted by a smooth curve. They further suggested that this correction factor (CF = r/r_s) for the tetra-alkyl ammonium ions could be used to correct Stokes' radii for small ions like Li⁺ and Na⁺. When they did this, they found that an estimate of the number of spherical water molecules that would fit within these corrected radii gave very reasonable hydration numbers. However, it should be noted that when they calculated the Stokes' radius, they used a slightly incorrect value for the ratio of 0.820/η^o at 25°C, getting a value of 91.5 instead of 92.1. We have recalculated their data for the tetra-alkyl ammonium ions (see Table 4), the differences from their values being generally <0.5%. We have replotted the recalculated values for these ammonium ions and fitted the data with a quadratic polynomial using SigmaPlot 9 and extrapolated the values for ions with Stokes' radii between 1 and 2 Å (Fig. 8) with the following equation used for fitting the data:

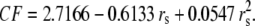(A8)

FIGURE 8.

Plot of the CF for small hydrated ions (≈≤5 Å), used for converting the Stokes' law hydrated radius, r_s, to the effective hydrated radius, r_H, for each ion. The Stokes' law radius was determined from measurements of limiting equivalent conductivity at 25°C using Eq. A7. This radius, r_H, has been measured as the radius, r, of equivalent small tetra-alkyl ammonium ions of known molecular size, as indicated by the solid circles. The data values (r/r_S) for these ions, where to represent 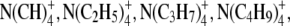and 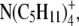were taken from Table 4. The Stokes' law radius, r_s, for these tetra-alkyl ammonium ions was recalculated using Eq. A7 from the limiting equivalent conductivity data at 25°C listed in Appendix 6.2 of Robinson and Stokes (22) (see text). The ionic radius, r, represents the actual radius of each ion estimated from molecular volumes or models and given in Table 6.2 of Robinson and Stokes (22). Note that above ∼5 Å, r ≅ r_s. The value of r/r_s can therefore be used as CF to determine the corrected equivalent Stokes' law radius for other ions, assumed to be the same as the ratio of the ionic radius determined from molecular models of the tetra-alkyl ammonium ions to their measured Stokes' law radius. The fitted curve was generated using SigmaPlot to enable the extrapolation of these values into the region required for ions of small hydrated size with an estimated Stokes law radius <2 Å. The graph therefore represents an extended and refitted version, with recalculated data (see text) of Fig. 6.1 of Robinson and Stokes (22).

These measurements have shown that for the nonhydrated tetra-alkyl ammonium ions <5 Å in radius that the Stokes' law radius calculated from the limiting equivalent conductivity underestimates the true molecular radius of the ion, by the correction factor given in Eq. A8. This is because of the breakdown of the Stokes' law relationship Eq. A5 over such small molecular dimensions.

A short overview of developments in the physical basis underlying the mobility of small ions in water

The developing picture of the physical basis of ionic mobility has been helpfully reviewed by Bagchi and Biswas (31) and some elements of this will be briefly considered. The classical picture to explain ionic mobility was one in which, just like the tetra-alkyl ammonium ions, as the ions increase in size, so their ionic mobility decreases, as predicted by Stokes' viscosity equation (Eqs. A4 and A5). However, this was found to be invalid for the case for small ions such as the alkali cations, where their mobility decreased as the ions got smaller (e.g., with u_Li ≪ u_Cs). Early on, it was suggested that this was due to a solvent-berg model (e.g., Glasstone (32), cited in Bagchi and Biswas (31)) in which the solvent molecules immediately adjacent to the ion are rigidly bound to it (33) and the smaller the bare ion, the larger the shell of water molecules surrounding it. Later it was also considered that, in practice, such a hydrated shell was not a rigid entity but was likely composed of both a more tightly bound inner core (“primary” hydration shell) and a less tightly bound and more fluid outer core (“secondary” hydration shell) (22).

As an early alternative to the solvent-berg model, a continuum model was suggested in which the total friction, ζ_total, experienced by an ion moving in solution was made up of two components: the bare friction, ζ_bare, due to the shear stress on the “bare” (crystallographic) ion as it moves through the fluid and the friction due to electrical interaction of the ion with the polar solvent molecules surrounding it (31). This latter component was considered to result from the ion having formed a polarization cloud of solvent molecules, which it leaves behind as it moves, and which then exerts a force retarding ion movement until the polarization cloud relaxes (33). This component of friction is referred to as dielectric friction (DF), ζ_DF (31). Hence, the total friction is given by

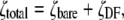(A9)

with the ion mobility being inversely related to the total friction, ζ_total. The early continuum models, in which it was assumed that there was continuous media right up to the surface of the ion, had difficulty reproducing the mobility of small ions, as they tended to overestimate the dielectric friction component (31). To overcome such a problem, microscopic theories were developed initially by Wolynes (33) and by Colonomos and Wolynes (34) that took into account the strong short range (hard) repulsive forces and the weaker long range (soft) attractive forces between the ions and solvent molecules, using a nonequilibrium statistical mechanics approach for an ensemble of solvent molecules around the ion (see also Wolynes (35)). Their basic equation for the dielectric friction, ζ_DF, was

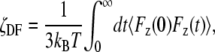(A10)

where F_z(t) is the z component of the force acting on a fixed ion by all of the solvent molecules at time t, k_B is Boltzmann's constant, T is the temperature (K), and 〈…〉 stands for the ensemble averaging over all the interactions of the solvent molecules with the ion and where the force includes both hard and soft force components (e.g., (31,33)). Further improvements to the theory included incorporating the ultrafast dynamics of dipolar solvents, like water, in which polarization relaxation was seen to have both an ultrafast Gaussian component with a time constant of 50–100 fs followed by a slow exponential-like decay with a 1 ps time constant, and also included the effect of the ion's own motion (e.g., (36)). The nonpolar friction contribution, ζ_bare, which comes from short-range ion-water forces, that are spherically symmetrical and primarily repulsive, was shown to be surprisingly well estimated from Stokes' law (cf. Eq. A5) from ζ_bare = 4πη r_ion, where r_ion is the radius of the bare ion and η is the zero frequency shear viscosity of the solvent (36,31). The polar dielectric friction component, ζ_DF, was shown to be dominated by the long wavelength solvent polarization fluctuations, primarily responsible for the ultrafast Gaussian solvation dynamics observed experimentally (36). It should be noted that the calculations to estimate ζ_DF are too involved to be outlined here (e.g., (31,36)). However, the result of such analyses is that as the size of the bare ion decreases, ζ_bare decreases, but ζ_DF increases rapidly (36). The limiting equivalent conductivity λ^o of an ion, a measure of its mobility in dilute solutions (see Eq. A4), is inversely related to ζ_total, as shown by

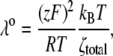(A11)

where the terms are as previously defined. It is also interesting to note that the ionic mobility is drastically reduced when the ultrafast polarization modes are not present (31). The physical reason for this is that the ultrafast component allows a rapid decay of the polarization disturbance caused by the ion's motion (31). This would radically increase the dissipation of the residual polarization cloud behind the moving ion that would otherwise retard ion movement (31,33).

One problem in the above theories is that the dielectric friction has largely ignored any solvent-berg component of solvent molecules traveling with the ion, though it is considered that for a small ion in a “slow” solvent, with a large viscosity (water is a “fast” solvent), the solvent-berg model should be valid (31). It was then shown how the solvent-berg model could be recovered from the microscopic dielectric friction theory in such cases (37). The physical picture is as follows (e.g., (31)): The polar solvent molecules close to the ion experience a strong electric field from the ion. The decay of this force depends on the mobility of the ion itself and the motion of the solvent molecules. If the rotational and translational motions of the solvent molecules are slow, then the dielectric friction term increases and slows the ion and increases the friction on the solvent molecules. When the size of the bare ion is small, the effect is enhanced and the solvent molecules next to the ion are essentially immobile (31) relative to the ion and hence tend to move with it. This solvent-berg model has been shown to be particularly valid for slow solvents like methanol, ethanol, and propanol (37), but how valid is it for a fast solvent like water, particularly with a very small ion? A recent computer simulation study by Lee and Rasaiah (38) using a molecular dynamics approach investigated the ionic mobilities of the alkali metal cations, Li⁺, Na⁺, K⁺, Rb⁺, and Cs⁺ in water at 25°C. Their study has shown that the water molecules (about six of them) in the first solvation shell around the very small Li⁺ ion “adhere” to the ion and move with it for about 190 ps, whereas the water molecules (∼6.6 of them) around the larger Na⁺ ion remain for ∼35 ps and water molecules (∼8–10 of them) around the large alkali cations only stay for ∼8–11 ps before significant exchange occurs with the surrounding water molecules (38). They estimate a radius of ∼2.2 Å in their modeling for the first solvation shell of Li⁺ (38) and suggest that as the cation size increases, so the water molecules in the first hydration shell are more weakly bound and their disruption and exchange with the surroundings occurs at a faster rate. Thus the classical solvent-berg model is seen to describe the mobility of Li⁺ ions in water adequately, with the mobility of Na⁺ ions being partly explained by these effects. This will be discussed further in the next section.

An equivalent hydrated shell model for small ions in water

Membrane biophysicists are interested in the movement of ions through small diameter selectivity filter regions of membrane channels. In particular, they are concerned at how ions with different ionic radii and degrees of solvation can permeate through such selectivity filter regions. The concept of primary and secondary hydration (or solvation) shells has been a very helpful one in this regard. Eisenman (39) was able to show that a simple static Coulombic calculation of the energy of interaction between an alkali cation and each of the charge centers of tripolar water molecules surrounding it, assuming ∼3.8 water molecules per ion could approximately account for the differences in hydration energies between each of these ions. Such energy considerations have been especially helpful in providing an understanding of the physical basis of ion selectivity in glasses and other membrane systems (39). Although we would expect different total numbers of water molecules for the primary hydrated shell around the different alkali cations, the principle is certainly supportive of a group of the closest water molecules being able to form some sort of inner hydrated shell around the ions and account for a major component of their hydration energies. More recent molecular dynamics modeling of ion mobilities in water have now also indicated that the Li⁺ ion behaves as existing in a hydrated shell of water molecules (38), thus satisfying the solvent-berg model, where the ion remains attached to the same water molecules for relatively long times, whereas for Na⁺ this would be for shorter times, and for Cs⁺, very much shorter. Qualitatively, it could be argued that Na⁺ and Cs⁺ are behaving respectively as if they had increasingly smaller time-averaged effective hydrated sizes. We would argue that it is of value and valid to calculate an equivalent or effective hydrated size for a test ion, such as Li⁺, Na⁺, and Cs⁺, as being of the same size as a nonhydratable ion (i.e., with zero ζ_DF) with the same limiting equivalent conductivity as the test ion. In further support of such a model, the hydrated radii estimated by Robinson and Stokes, for the ions that they considered, also gave reasonable estimates of measured hydration numbers (22).

Such an equivalent hydrated size for a hydratable ion would still need the same correction factor equation as required for the tetra-alkyl ammonium ions. If these values then indicated a sensible relationship to explain relative permeation of ions through a channel, that would clearly add validity to the concept of equivalent hydrated ion size.

We have now used this correction factor in Eq. A8 for all the monovalent ions in this article. For all these ions, the Stokes' radius can be calculated from the limiting equivalent conductivity for each ion using Eq. A7 with the constant value = 92.1. These r_s values are listed in Table 5. Then, using the correction factors (CF) obtained from the fitting of the graphed tetra-alkyl ammonium ion data (Fig. 8) in SigmaPlot, the equivalent (or effective) hydrated radius (r_H) for each of the ions in this article was calculated using the equation

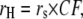(A12)

with the CF value determined from Eq. A8. The Stokes' law radii for Li⁺ and Na⁺ were slightly higher than Robinson and Stokes (22) had obtained from their limiting equivalent conductivities (being 2.39 instead of 2.37 and 1.84 instead of 1.83 for Li⁺ and Na⁺, respectively), and the resultant corrected r_H values using the numerical fitting procedure and Eqs. A7 and A8 are now also given at a slightly higher precision than would have been possible with their graphical fitting (22). In addition, values of r_s and r_H were calculated de novo from limiting equivalent conductivity data for Cs⁺, Cl⁻, and ions. All these values together with the equivalent hydrated diameters of each of the ions are given in Table 5.

APPENDIX B: DISCUSSION OF THE VALIDITY OF USING ACTIVITIES RATHER THAN CONCENTRATIONS IN DIFFUSION POTENTIAL EQUATIONS

The fundamental force, F_x, at a position x, underlying the movement of ions in solution, is the negative gradient of the electrochemical potential energy where the electrochemical potential energy, represents the free energy of a mole of ions. It is defined as

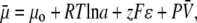(B1)

where μ_o is the standard state potential, ln is the natural log_e, a is the activity of the ion, ɛ is the electrical potential energy, P is the hydrostatic pressure, 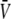is the partial molar volume of the ions, and R, T, z, and F are as previously defined in the article. In very dilute solutions (e.g., <1 mM), a can be approximated by the concentration, C, of the ions and the error will be <4% for typical salts. For ions, the hydrostatic pressure term is negligible in comparison to the electrical term. Hence, the force on a mole of ions within a particular state is given by

(B2)

From the definition of the mobility, u, of ions under a force F_x, their velocity, v, will be given by

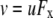(B3)

and the flux, J, of ions moving under such a force with a concentration, C, will then be given by

(B4)

For dilute solutions, a may be approximated by C and Eq. B4 simplifies to the form in which the Nernst-Planck flux equation is often written

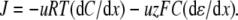(B5)

However, in most biological situations, this assumption is not valid unless the ionic strength is approximately the same throughout the solution(s). Alternatively, Eq. B4 may be rewritten as

(B6)

where γ = γ(x) is the activity coefficient, relating a(x) and C(x) by

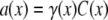(B7)

and where, in turn, γ is a function of the salt concentration, which itself varies with distance, x. E.g., for a simple salt dilution potential gradient and a simple monovalent salt, such as NaCl, if we denote the cation and anion by the subscripts “+” and “–”, respectively, then we have from Eq. B6 for the cation and anion fluxes that

(B8)

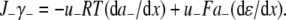(B9)

In this derivation, as in the rest of the article, the Guggenheim assumption (e.g., (40) and (19)) was used to relate single ion activities in solution to the mean activity of the salt. The assumption is that, for example, in a simple monovalent halide solution M⁺Cl⁻, the cation, anion, and mean activity coefficients are equal, so that γ_M = γ_Cl = γ_MCl. The alternative MacInnes assumption in this situation would be that the Cl⁻ activity coefficient, γ_Cl, is independent of the cation (40). He assumed that since K⁺ and Cl⁻ have “very similar electronic structures”, then γ_K ≅ γ_Cl ≅ γ_KCl, but that for other cations in halide salts γ_M ≠ γ_Cl (40). Since the deviation of the activity coefficient from unity arises from the interionic Coulombic interactions between the anions and cations, it would seem reasonable that the single activity coefficients of anion and cation would be codependent as suggested by the Guggenheim assumption. Furthermore, the Guggenheim assumption gave a better fit to measurements and calculations of salt bridge junction potentials and Ag/AgCl potentials than did the MacInnes assumption (19). Hence, from the Planck electroneutrality condition, at each point x in the solution, C₊(x) = C₋(x), combined with the Guggenheim assumption that anion and cation activity coefficients are equal at the same concentration, then at each point x, γ₊(x) = γ₋(x). In addition, in the zero current situation, the total current, I = J₊ − J₋ = 0, so that J₊ = J₋ . Hence, J₊γ₊(x) = J₋γ₋(x) under zero current conditions. We can thus equate Eqs. B8 and B9. After multiplying by −1, we have (see also Barry and Diamond (19)) that

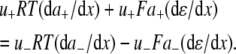(B10)

Thus the activity coefficient, with its dependence on concentration, has now disappeared from the equation. Actually, this principle of being able to drop out the concentration/distance dependent activity coefficient for each ion, can be extended to more than two ions at zero current, because of the Guggenheim assumption, which results from the activity coefficients being dependent on the ionic strength of the solution at that point, and being equal for monovalent anions and cations.

At each point a₊ = a₋ = a from electroneutrality conditions, where a is the salt activity. Eq. B10 therefore becomes

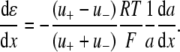(B11)

This is in the same form as in the case for the derivation of the standard concentration version of the Planck equation and it may be integrated with respect to x across the membrane (along the channel) and thus becomes

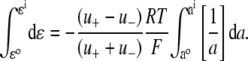(B12)

Integrating this equation results in the activity form of the Planck equation and can readily be shown to give an equation of the form

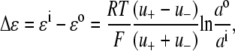(B13)

where a represents the activity of the salt, u₊ and u₋ the mobilities of cation and anion respectively, and superscripts “o” and “i” the values in the outside and inside solutions, respectively (19). It is relevant for the case of either a nonselective membrane or a simple liquid junction potential.

For a selective membrane, the mobilities in Eq. B13 are replaced by permeabilities, and the equation simply becomes (e.g., (41))

(B14)

Clearly, if one of the ions is impermeant, e.g., the anion, then the membrane potential difference becomes

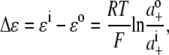(B15)

where a₊ refers to the activity of the cation, since, a₊ = a_- = a in this example with a simple monovalent salt. Note that Eq. B15 is the same as the Nernst equation for a cation in equilibrium across a membrane, and that the Nernst equation is derived directly from energy considerations in terms of activities and independent of any permeation model. The Planck equation must reduce to the Nernst equation when one of the ions is impermeant or else it is in error. However, the Planck equation will not necessarily reduce to the Nernst equation in such conditions if the Planck equation is defined in terms of concentrations, particularly in dilution potential measurements where the activity coefficients can be very different on both sides of the membrane. The same must be true of the GHK and any other diffusion potential equation. Note that even for a 1 mM NaCl solution, the activity coefficient, γ, is 0.97 (see Eq. B7) whereas for 100 mM NaCl γ is 0.78 (19), so the differences for dilution potential experiments are not trivial.

It should be noted that a biionic version of the Planck and Henderson equations, and other neutral site permeation models, have also been derived in terms of activities rather than concentrations (19,41), as has the Goldman-Hodgkin-Katz equation from nonequilibrium thermodynamics (42) and from the Ussing Flux equations (10). Furthermore, a comparison of relative permeabilities determined from either Planck or GHK equations with activity coefficients has been shown to give very similar permeability ratios (1,10), indicating that for zero-current membrane potential measurements, the permeabilities are really very model independent (10).

In addition, experimental validity arises from the fact that using activities in the Planck or GHK equations rather than concentrations generally gives much better fits to the data.