Phenomenological Model and Phase Behavior of Saturated and Unsaturated Lipids and Cholesterol

Abstract

We present a phenomenological theory for the phase behavior of ternary mixtures of cholesterol and saturated and unsaturated lipids, one that describes both liquid and gel phases. It leads to the following description of the mechanism of the phase behavior: In a binary system of the lipids, phase separation occurs when the saturated chains are well ordered, as in the gel phase, simply due to packing effects. In the liquid phase, the saturated ones are not sufficiently well ordered for separation to occur. The addition of cholesterol, however, increases the saturated lipid order to the point that phase separation is once again favorable. Our theory addresses this last mechanism—the means by which cholesterol-mediated ordering of membrane lipids leads to liquid-liquid immiscibility. It produces, for the system above the main chain transition of the saturated lipid, phase diagrams in which there can be liquid-liquid phase separation in the ternary system but not in any of the binary ones, while below that temperature it yields the more common phase diagram in which a gel phase, rich in saturated lipid, appears in addition to the two liquid phases.

INTRODUCTION

The hypothesis that the plasma membrane is not uniform, but consists of “rafts” rich in saturated lipids and cholesterol, which float in a sea of unsaturated lipids, remains extremely exciting and controversial (1–3). The extent to which one can define such entities in a biological membrane and the driving forces tending toward their formation is unclear. Much more certain are the results of studies on nonbiological bilayer membranes with compositions designed to mimic those of biological ones. They consist of a high-melting point lipid, usually saturated, a low-melting point lipid, usually unsaturated, and cholesterol (4). These systems readily display coexisting liquid phases.

One, the liquid-ordered (lo) phase (5), is rich in cholesterol and saturated lipids whose chains are relatively well ordered; the other, the liquid-disordered (ld) phase, is rich in unsaturated lipids whose chains are not so well ordered (4,6,7). In addition, at physiological temperatures, there is usually a gel phase rich in saturated lipids with chains that are very well ordered.

This phase behavior leads to the possibility that rafts in biological membranes are simply regions of one liquid phase in coexistence with, and surrounded by, the other liquid. A second scenario, engendered by the occurrence of a line of critical points in the system at which the two liquid phases become one, is that rafts are transient aggregates, manifestations of fluctuations that are particularly large near the critical line of a system that is effectively two-dimensional (8). A third interpretation is that such aggregates are the results of a line-active agent, perhaps cholesterol, which lowers the free energy of such aggregates and results in a liquid with much structure, as in a microemulsion of oil and water that is brought together by a surface-active agent.

It should be noted that not all ternary systems of lipids and cholesterol exhibit a gel and two liquid phases. Of particular interest is the system of diphytanoylphosphatidylcholine (diPhyPC), dipalmitoylphosphatidylcholine (DPPC), and cholesterol (9), which, at a temperature above the main-chain transition of the DPPC, exhibits a region of liquid-liquid coexistence in the middle of the Gibbs triangle; that is, at these temperatures none of the three binary systems undergo phase separation, whereas the ternary system does. This is unusual behavior in a liquid system, although other examples are cited in Francis (10). It is to be contrasted with that of most ternary liquid systems in which the existence of any phase separation is directly tied to the existence of such separation in one of the binary systems. Consequently, only two of the components are actually necessary to bring about the separation. A simple example is the ternary system of oil, water, and surfactant, which, for modest concentrations of surfactant, displays two liquid phases, one oil-rich, the other water-rich, with the surfactant partitioning between the two. Clearly, these phases evolve from the ones resulting from separation of oil and water in the binary system. It is conceivable that the existence of two liquid phases in the ternary cholesterol, saturated, and unsaturated lipid system, could be similarly directly tied to the existence of liquid-liquid phase separation in the cholesterol, saturated lipid system, a separation that had been reported earlier (11). However, there is now abundant experimental evidence (12) that such separation does not occur in this binary system. The significance of the phase diagram of the diPhyPC/DPPC/cholesterol system is that the existence of liquid-liquid phase separation in such ternary systems cannot be tied to phase separation in any of the binary systems, and must therefore be a consequence of the presence of all of the three components. This conclusion begs for theoretical understanding.

The simplest approach to a resolution of this puzzle would be to use regular solution theory that can, in fact, give rise to the kind of phase diagram described above (10,13,14), but to do so requires an attractive interaction between at least two of the components that is extremely large, and for the system of interest, inexplicably so. The failure of regular solution theory for this three-component system is most likely because it considers only the concentration of each component, and therefore ignores the many degrees of freedom of the lipid tails. These are certainly involved in the transition from the liquid to the gel phase, and might be involved in the liquid-liquid transition. Thus, one expects that a successful theory should include some explicit description of the degrees of freedom of the lipid tails.

There is surprisingly little theoretical work on the phase behavior of cholesterol and lipids, and most of that work concerns binary systems (5,15–17) that, as emphasized above, cannot explain the origin of liquid-liquid separation in the ternary systems of interest. Of the few articles on the phase behavior of ternary systems of saturated and unsaturated lipids and cholesterol (16,18,19), only that of Radhakrishnan and McConnell (18) has produced a phase diagram exhibiting liquid-liquid coexistence in the ternary system without phase separation in any of the three binary ones. Their theory posits that the cholesterol and saturated lipids form complexes, which then interact repulsively with the unsaturated lipids. The origin of this repulsion is not specified. In the explicit realization of this idea (18), the complexes are treated as a distinct, fourth component in the system, and the free energy is assumed to be well approximated by regular solution theory of a four-component system. The authors note that such complexes have never been isolated in bilayers, but stress that they should be considered as rapidly fluctuating entities. The evidence from simulation is mixed for such transitory complexation with a specific stoichiometry (20–22). Nevertheless, the authors emphasize the utility of the concept, as clearly demonstrated by its ability to reproduce the unusual phase diagram of the diPhyPC/DPPC/cholesterol system. The theory does not attempt to describe the more usual ternary mixtures of lipids and cholesterol that, in addition to two liquid phases, also display a gel phase.

Given the transitory nature of the posited complexes, it would be advantageous to formulate a theory that describes the system only in terms of the original three components, and that would provide further insight into the physics governing the system. In addition, one would also like it to describe systems exhibiting a gel phase. Lastly, it should be able to describe the evolution of the normal phase behavior into the more unusual one displayed by the diPhyPC/DPPC/cholesterol system.

The purpose of this article is to present such a theory, one that would highlight what we believe to be the basic physics of these ternary systems. This is easily stated. Saturated and unsaturated lipids undergo phase separation when the former are sufficiently ordered, as they are in the gel phase. The reason for this is a simple packing effect: the presence of one or more kinks in an unsaturated chain prevents the efficient packing, and free energy reduction, of the ordered, saturated, chains. Hence, the system lowers its free energy by separating into a gel phase rich in saturated lipids, and a liquid phase rich in unsaturated lipids. When the saturated and unsaturated lipids are in a liquid phase, the former are not sufficiently ordered to bring about a phase separation. The addition of cholesterol to the liquid phase, however, tends to increase the order of the saturated lipids, as is well known (23–26). With the addition of enough cholesterol, the saturated chains become sufficiently ordered that phase separation from the unsaturated chains becomes free-energetically favorable once again. The theory has been formulated to incorporate explicitly this physical mechanism while remaining sufficiently simple so that the manner in which the mechanism brings about the desired phase behavior is not obscured. The theory indeed produces phase diagrams in which there is only liquid-liquid coexistence in the middle of the Gibbs triangle, as in the diPhyPC system, as well as those that display two liquid phases and a gel, as seen more commonly.

THE MODEL

We consider a system of cholesterol, whose concentration is denoted c, a high melting-temperature lipid, henceforth referred to as “saturated,” whose concentration is s, and a low melting-temperature lipid, henceforth referred to as “unsaturated,” with concentration u = 1 – s – c. By describing the system in terms of two independent concentrations, rather than three independent areal densities, we are making the implicit simplifying assumption that the actual areal density of the system is not a crucial parameter in the description of its phase behavior, and can be treated as a constant. As a consequence, the free energy per area and free energy per molecule are related by this same constant so that there is no essential difference between them.

To incorporate into the theory the degrees of freedom of the saturated chains, we introduce an order parameter, δ, a single variable that can be thought of as a coarse-grained measure of the order of the entire saturated chain. Accordingly, it will be taken to be largest in the gel phase and smaller, but generally nonzero, in the liquid phases. We need not make explicit the relationship between δ and more conventional definitions of chain order parameters, such as those defined in nuclear magnetic resonance experiments. What will be important is that we require the free energy of a configuration involving a saturated chain to depend upon the order of the chain, and this order can be specified by δ. For simplicity, we do not introduce an order parameter describing the degrees of freedom of the unsaturated chains.

We begin with the observation that the transition between liquid and gel phases is a first-order one. Hence, for given values of the temperature and the two independent concentrations, the surface excess free energy of the system has, in general, two minima as a function of the order parameter δ representing the liquid and gel phases. It is convenient to expand the free energy about these two minima in turn. We first assume the system to be at a temperature, T, sufficiently high that there are only liquid phases. We write the surface free energy per particle of the system, in units of kT, in the form

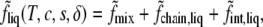(1)

where

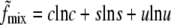(2)

is the usual entropy of mixing. The second term describes the interactions between the saturated lipids, and is therefore proportional to s²,

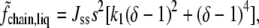(3)

with J_ss, a constant, dimensionless, interaction strength. Note that the magnitude of the interaction between saturated lipids depends upon their configuration, as is to be expected. The information about the configurations is encapsulated in the order parameter. Because of this interaction between saturated lipids, the free energy in the liquid phase has a single minimum as a function of δ. Taking advantage of the freedom to set the scale of the temperature and of the order parameter, we have used one of these degrees of freedom to assign δ the value unity in the pure saturated-lipid system. The constants J_ss and k₁ are positive. The last term in Eq. 1 is that due to the interaction between the saturated lipid and the other two components,

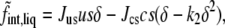(4)

with the constants J_us, J_cs, and k₂ all positive. The first term in Eq. 4 represents the repulsive interaction between saturated and unsaturated lipids due to the inability of the latter to pack well with the former. The strength of this repulsion depends, again, on the degree of order of the chains of the saturated lipids, a concept expressed in the earliest modeling of these systems (5). It is this term that encapsulates the idea that the interaction between unsaturated and saturated chains becomes more repulsive as the saturated chains become more ordered. The term brings about phase separation if its strength is sufficiently great. In the absence of cholesterol, however, it is not.

The second term in Eq. 4 expresses the idea that cholesterol increases the order of the saturated chains in the liquid phase. This attractive interaction, proportional to csδ, is crucial as it causes the addition of cholesterol to increase the chain order that thereby increases the magnitude of the repulsion between saturated and unsaturated lipids, expressed in the first term. As we have noted, when this first term is sufficiently large it brings about phase separation. One sees directly that the first two terms above express the physical ideas that lead to the phase behavior. They constitute the heart of our theory.

As it stands, however, the free energy is not bounded from below in the limit of vanishing s in which the contribution to the free energy of Eq. 3 vanishes so that the order parameter δ can grow without limit. Such growth decreases the free energy without limit due to the second term in Eq. 4. This uncontrolled increase of the order parameter is counter to the actual physical situation in which the order of the chains is finite; i.e., at some point, the chains are completely ordered and cannot be made more so. To ensure that the order parameter, and the free energy, remain bounded in this limit, we include the third term in Eq. 4.

Collecting the separate terms of Eq. 1 we have

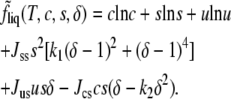(5)

Because the order parameter is not controlled externally, its value as a function of composition, δ_liq(T, c, s), is determined from the condition that it minimize the free energy,

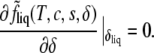(6)

Then the Helmholtz free energy per particle of the liquid phase, f_liq(T, c, s), is obtained from 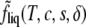according to

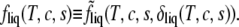(7)

Note that the term quartic in δ – 1 in the free energy of Eq. 5 affects the dependence of δ_liq(T, c, s) on the compositions and temperature and provides, therefore, an additional parameter to adjust so that the phase diagrams that we will obtain can be brought into even better agreement with experimental ones.

Two-phase coexistence is found in the usual way. Of the four unknowns, which are the two independent compositions in the two coexisting phases, three are determined by the conditions of equality of two independent chemical potentials and of the surface tension in each of the two phases. The surface tension is directly related to the Legendre transform, g, of the surface excess Helmholtz free energy per particle f_liq,

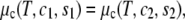(8)

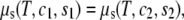(9)

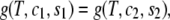(10)

where

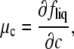(11)

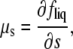(12)

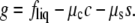(13)

Because one composition remains undetermined, there can be a region of concentrations over which two-phase coexistence occurs. We solve these equations numerically.

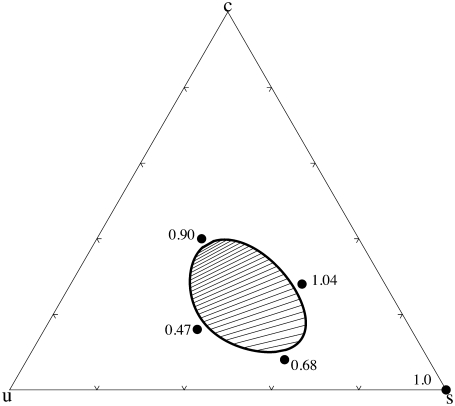
A phase diagram that results from this theory is shown in Fig. 1. It reproduces the kind of phase diagram found in the diPhyPC/DPPC/cholesterol system. We have indicated values of the order parameter at several concentrations. As expected, it is large in the regions in which the concentration of the saturated lipid is large, and tends to increase with the concentration of cholesterol due to its ordering effect. Further, because the cholesterol prefers the saturated lipid, there is more of it in the saturated-lipid rich lo phase than in the unsaturated-lipid rich ld phase. Hence, the tie lines connecting coexisting phases slope upward, a result that is in accord with many (9,27,28) experimental observations.

FIGURE 1.

Phase diagram of the ternary system at a temperature above the main chain transition of the saturated lipid. Values of the order parameter are shown at four composition marked by dots. The values of the parameters are as follows: J_ss = 1.0, k₁ = 1.0, J_us = 1.8, J_cs = 2.4, and k₂ = 0.21.

It may be helpful to consider how the presence of the order-parameter dependent terms in the free energy 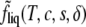affects the form of the Helmholtz free energy 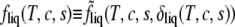To do this, we ignore for clarity the quartic term in δ − 1 in Eq. 5 so that the determination of the value of the order parameter that minimizes the free energy is immediate. We obtain

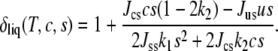(14)

This shows that the addition of cholesterol to the system of pure saturated lipid does tend to increase the magnitude of the order parameter due to the attractive interaction between cholesterol and saturated lipid J_cscs. We also note that while δ_liq can increase without limit as the pure unsaturated system is approached, the physical quantity is sδ_liq because there are no ordered chains without saturated lipid, and this quantity is well behaved everywhere. Substituting this result into the free energy of Eq. 5, one finds that the important interaction J_ususδ_liq contains

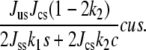(15)

This is a term that increases the free energy and is proportional to the product of the three concentrations. Hence, to lower its free energy, the system tends to avoid a one-phase region in which all components are present equally, and does so by undergoing phase separation. That this term is proportional to the product of the interactions between saturated lipid and the other two components, J_usJ_cs, is a manifestation of the basic idea that the key ingredient to the phase behavior is the combination of the ordering interaction between cholesterol and saturated lipid, and the repulsion between unsaturated lipid and ordered saturated lipid. It is not difficult to see analytically that this coexistence does not extend to the binary systems for the parameters chosen, but the argument is not sufficiently illuminating to warrant its presentation.

We now consider the system to be at a temperature at which it could exhibit a gel phase in addition to liquid phases. For the free energy of the gel phase, we write

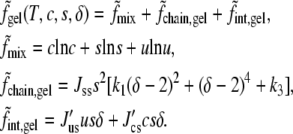(16)

We note the following. The form of has been taken to be of essentially the same form as for simplicity. We have set the single minimum of the free energy in the gel phase to occur at δ = 2 when the system consists only of the saturated lipid. In such a system the free energy of the gel phase exceeds that of the liquid phase by k₃J_ss; hence, k₃ is proportional to T – T*, with T* the liquid-gel transition temperature in the pure system. By changing k₃ from positive to negative values, we induce a liquid-to-gel transition in our system. The interaction strengths J′_us and J′_cs are positive so that the addition of cholesterol, as well as unsaturated lipid, reduces the order of the saturated lipid in the gel phase (11). The value of the order parameter, δ_gel(T, c, s), is determined by minimization of the above free energy, and the Helmholtz free energy in this phase is

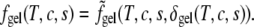(17)

The free energy of the entire system is now

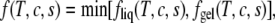(18)

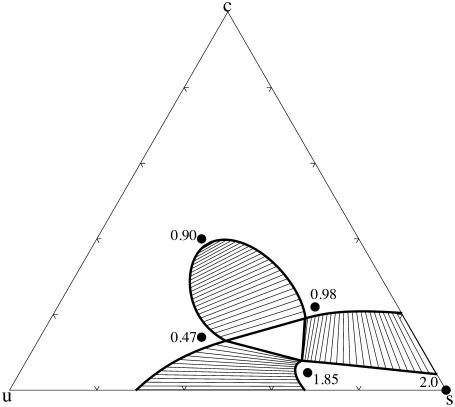
and phase coexistence is again found by the conditions of the equality of two chemical potentials and of the surface tension as in Eqs. 8–13 but with f_liq(T, c, s) replaced by f(T, c, s) above. A phase diagram that results when the temperature is below that of the gel transition of the saturated lipid is shown in Fig. 2. Values of the order parameter at various concentrations are shown. The phase diagram shows all the features of most of those observed experimentally. In particular, there are two liquid phases and a gel. Tie lines between the liquid phases indicate a greater presence of cholesterol in one liquid than the other. The values of the order parameter in the coexisting phases justify the designation of liquid-ordered (lo) for one phase, and liquid-disordered (ld) for the other phase. The order is greatest in the gel phase, of course. Little cholesterol, approximately a concentration of 0.04, is needed to destabilize this phase. This is in qualitative agreement with experiment (11), which also shows that a small concentration of cholesterol, ∼0.07, destabilizes the gel phase.

FIGURE 2.

Phase diagram of the ternary system as a temperature below the main chain transition of the saturated lipid. Values of the order parameter are shown at four compositions shown by dots. The values of the parameters are as follows: J_ss = 1.0, k₁ = 1.0, J_us = 1.8, J_cs = 2.4, k₂ = 0.21, k₃ = −0.25, J′_us = 0.7, and J′_cs = 0.0.

DISCUSSION

We have presented a simple phenomenological theory of ternary mixtures of cholesterol, a high-melting temperature (or saturated) lipid, and a low-melting temperature (or unsaturated) lipid. It is capable of producing the usual phase diagrams observed in this system in which there is a gel and two liquid phases, and also the unusual phase diagram of the DiPhyPC/DPPC/cholesterol system in which, for a range of temperatures, the ternary system exhibits phase separation even though none of the binary systems do. The model highlights the interesting physics of these systems; mixtures of high- and low-melting temperature lipids phase-separate when the chains of the former are sufficiently well ordered, as occurs in the gel phase. This is simply a result of packing constraints. In the liquid phase, the chains of the high-melting temperature lipid are not sufficiently ordered to induce phase separation from the more disordered low-melting temperature lipids. However, the addition of cholesterol tends to order the chains of the former until, with sufficient cholesterol, the chains have sufficient order to bring about phase separation.

The simple implementation of the above ideas we have provided illuminates many experimental observations. First, we note that the theory directly leads to a positive contribution to the free energy, Eq. 15, which is proportional to the product of the compositions of all three components. As a consequence, liquid-liquid phase separation is most likely to be found when this product is at maximum, i.e., at the canonical raft composition (2,29) of 1:1:1. Second, the theory highlights the importance of two interactions for phase separation. One of these interactions is the repulsion between unsaturated, or low melting point, and saturated, or high melting point, lipids. It is presumably due to this term that phase separation in the ternary system but not in any of the binaries was first observed in the system of DPPC and diPhyPC as the four methyl groups appended to the chains of the latter cause a strong repulsion between it and the saturated DPPC. One similarly understands the absence of liquid-liquid phase separation in the specific ternary mixture of cholesterol, DPPC, and POPC (30), because only one of the two chains in POPC is unsaturated. Hence, the repulsion between it and the DPPC is presumably weaker. The other important interaction is that which induces the cholesterol to order the saturated chains. Hence one expects, and observes, that sterols like ergosterol and cholesterol that strongly order lipid chains (31) also strongly induce phase separation (4,32), and those like lanosterol that do not strongly order the chains (31) do not strongly promote phase separation (33,34). One predicts that this correlation will be observed in systems using other sterols (35). Further, one can clearly predict results for various combinations of sterols, unsaturated, and saturated lipids.

As a result of the attractive interaction between cholesterol and saturated lipids in the liquid phase, we find the concentration of cholesterol to be greater in one of the liquid phases than in the other. This is reflected in the slope of the tie lines between liquid phases that, in the figures shown, would be horizontal in the absence of such a preference. The result agrees with most systems observed in experiment (9,27,28), but not all (36). Due to its preference for the saturated over the unsaturated lipids, cholesterol enhances their phase separation; i.e., it increases the temperature at which such separation occurs (13). This is clear from the phase diagram of Fig. 1. The binary lipid system is above its temperature of phase separation, but as cholesterol is added, that temperature increases until it exceeds the temperature for which the diagram is drawn. It follows from this that cholesterol is not expected to migrate to the interface between lo and ld phases and therefore is not expected to reduce the line tension between these phases. Thus, if one wants to think of the existence of rafts as indicating the formation of some sort of microemulsion, then one cannot attribute to cholesterol the role of a line active agent that brings it about. Rather, one must assign such a role to a protein (37), like N-Ras, that has two anchors, one of which prefers the lo environment, and the other the ld environment (38).

Our theory is sufficiently flexible to describe various possible evolutions of the phase diagram with temperature, or equivalently, with the interaction strengths as they are generally inversely proportional to temperature. With the parameters we have chosen in Figs. 1 and 2, liquid-liquid phase separation remains even above the main chain temperature of the saturated lipid. This can be traced to the large repulsion, J_us, between saturated and unsaturated lipids. Were the magnitude of this repulsion to be reduced, liquid-liquid coexistence would only be observed below the main chain transition of the saturated lipid. Additionally we note that the model is easily augmented with a repulsive interaction between cholesterol and unsaturated lipid so as to incorporate the strong antipathy between cholesterol and decosahexaenoic acid (39), and also to permit liquid-liquid coexistence to extend to the binary cholesterol, unsaturated lipid system as has been observed in some mixtures (40).

Finally we note that, while we have referred to the nonphospholipid component in the ternary system as cholesterol, it could equally be another molecule, such as a protein. The crucial ingredient of our theory is that the nonphospholipid component interacts with the saturated lipid in such a way as to increase its order parameter. If that were the case, then such a ternary system should exhibit a similar phase diagram to the one we have calculated here. Analogous conclusions also apply to a system consisting of such a protein and cholesterol and the unsaturated and saturated lipids.