Chirality-Based Signatures of Local Protein Environments in Two-Dimensional Optical Spectroscopy of Two Species Photosynthetic Complexes of Green Sulfur Bacteria: Simulation Study

Abstract

Two-dimensional electronic chirality-induced signals of excitons in the photosynthetic Fenna-Matthews-Olson complex from two species of green sulfur bacteria (Chlorobium tepidum and Prosthecochloris aestuarii) are compared. The spectra are predicted to provide sensitive probes of local protein environment of the constituent bacteriochlorophyll a chromophores and reflect electronic structure variations (site energies and couplings) of the two complexes. Pulse polarization configurations are designed that can separate the coherent and incoherent exciton dynamics contributions to the two-dimensional spectra.

INTRODUCTION

Coherent ultrafast two-dimensional (2D) electronic spectroscopy can provide valuable insights into the exciton structure and dynamics of chromophore aggregates (1–6). Recent applications to light-harvesting photosynthetic complexes revealed two energy transfer pathways (fast and slow) through the temporal evolution of crosspeaks (7–11). Oscillations provide information about quantum coherences (8). Photosynthetic antennae are pigment-protein complexes; the surrounding protein matrix affects the electronic structure properties of the pigments. The local protein environment is known to influence the initial electron transfer dynamics in the photosynthetic reaction centers of Rhodobacter sphaeroides (12). Interactions of the bacteriochlorophyll (BChl) a molecules in the Fenna-Matthews-Olson (FMO) complexes from green sulfur bacteria with the local environment are responsible for the differences in the site energies of these pigments. These variations determine the delocalization of the collective electronic states (excitons) as reflected in their temporal and spatial energy relaxation dynamics (13).

The role of the FMO complex in the photosynthetic apparatus is to mediate the transfer of excitation energy from the light-harvesting chlorosomes to the reaction center (14). The complex is a trimer made of seven identical BChl a subunits. FMO structures from different species of green sulfur bacteria are very similar, but their electronic spectra do vary. Chlorobium tepidum (C.t.) (15,16) and Prosthecochloris aestuarii (P.a.) are the two most thoroughly investigated species with known structures (17,18). The two structures are virtually identical, with minor differences in the positions and orientations of the BChls. However, differences in the local protein environment significantly affect the BChl site energies as shown in their optical spectra. The nature of these interactions is not fully understood. A recent electrostatic computation of the FMO site energy shifts in both species found that the major contributions to the shifts were from the charged amino acids and the ligands of the magnesium ions of the BChls (19). A combination of this method with quantum chemistry has enabled a more precise calculation of the site energies, revealing a strong influence of the backbone of α-helices (20).

The linear absorption, linear dichroism (LD), circular dichroism (CD), fluorescence, and pump-probe signals of the FMO complexes from the two species have been studied extensively (21–25). Hamiltonian parameters were first obtained by fittings of various one-dimensional (1D) spectra, and later refined for the C.t. species by fitting the 2D spectra (7). Excitonic CD spectra were found to be particularly sensitive to small variations in the site energies and the transition dipole orientations and the fluctuating environment (ligands or the protein matrix). This finding has been observed for the light-harvesting complex LH2 of the purple bacterium Rhodopseudomonas acidophila (26) and for the FMO complex from P.a. (24).

The information from all of these 1D spectroscopic techniques is limited by spectral congestion of broad line shapes. Coherent 2D nonlinear optical spectroscopy enhances the resolution by spreading the signals in two dimensions and by eliminating certain types of inhomogeneous broadening (4,5,27,28). We have recently proposed extensions of these techniques for probing system chirality (29–31). 2D electronic chirality-induced (2D ECI) signals were shown to be sensitive to structural changes of chiral systems and to provide higher resolution than conventional 2D electronic nonchiral (2D ENC) techniques, making 2D ECI most suitable for the determination of structural fluctuations. Other extensions of CD to the nonlinear regime have also been proposed (32,33).

2D signals are fourth-rank tensors that depend on the polarization configurations of the four laser beams. Linear combinations of various tensor components can interfere by suppressing diagonal and enhancing crosspeaks, thereby revealing information about structural dynamics through monitoring vibrational and electronic couplings (9,34,35). In a previous study, we used coherent control with an adaptive genetic algorithm to construct combinations of 2D CI tensor components that enhance otherwise weak, poorly resolved crosspeaks in 2D two-pulse photon echo spectra of a porphyrin dimer (36). Making use of the complex chirality and some fundamental symmetries of multidimensional optical signals, we identified pulse polarization configurations (PPC) that can separate coherent quantum oscillations and incoherent energy dissipation in the course of exciton relaxation and reveal their timescales (37).

In this study, we show that the 2D ECI signals are more sensitive than the 2D ENC to the electronic structure of the chiral FMO complexes from the C.t. and P.a. green sulfur bacteria. CI PPCs offer a better spatial resolution for coherent and incoherent exciton dynamics. Spectral changes are attributed to variations of the local protein environment. Simulations of the 2D ENC spectra are presented in the next section (Nonchiral Signals in the Dipole Approximation) and NC PPCs are shown in the section Separating Coherent and Incoherent Exciton Dynamics by Interference of NC Pulse-Polarization Configurations. The corresponding 2D ECI spectra are presented in the section Chirality-Induced 2D Photon Echoes, and finally the study results are discussed.

NONCHIRAL SIGNALS IN THE DIPOLE APPROXIMATION

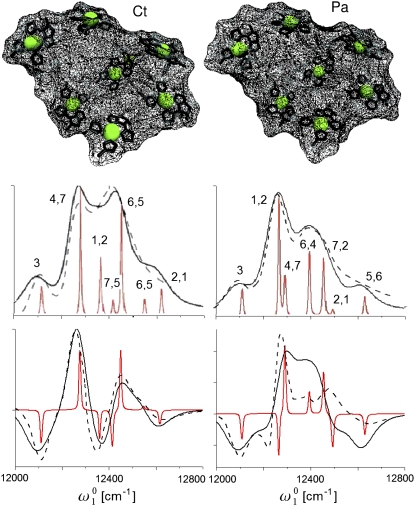
The electronic excitations of a single subunit of FMO containing seven BChl a chromophores may be described by the Frenkel exciton model. We use the parameter set described by Aartsma and colleagues (21,22,38) (refined for C.t. by Brixner et al. (7)); the data are provided in Tables 1 and 2. Atomic coordinates of the FMO complexes from C.t. (15,16) and P.a. (17,18) were taken from the Protein Data Bank (39). The Q_y electric transition dipoles were assumed to pass through the nitrogen b and d atoms according to the crystallographic nomenclature. The monomer electric dipole strength is 28.7 D² (magnetic dipole and electric quadrupole were neglected). The magnesium atoms, located at the centers of the BChl a molecules, were used as the reference points for the chromophore coordinates. The structures of the FMO complexes from the two species are shown in Fig. 1 (top). Surface wireframes around the BChl molecules reveal the differences in the protein environment. We show how these differences may be probed by 2D spectroscopic techniques.

TABLE 1.

One-exciton Hamiltonian matrix elements for FMO from C.t. (in cm⁻¹)

	BChl 1	BChl 2	BChl 3	BChl 4	BChl 5	BChl 6	BChl 7
BChl 1	280	−106	8	−5	6	−8	−4
BChl 2	−106	420	28	6	2	13	1
BChl 3	8	28	0	−62	−1	−9	17
BChl 4	−5	6	−62	175	−70	−19	−57
BChl 5	6	2	−1	−70	320	40	−2
BChl 6	−8	13	−9	−19	40	360	32
BChl 7	−4	1	17	−57	−2	32	260

TABLE 2.

One-exciton Hamiltonian matrix elements for FMO from P.a. (in cm⁻¹)

	BChl 1	BChl 2	BChl 3	BChl 4	BChl 5	BChl 6	BChl 7
BChl 1	−30	−94	5	−6	6	−14	−12
BChl 2	−94	85	30	7	2	12	5
BChl 3	5	30	−220	−51	−1	−9	1
BChl 4	−6	7	−51	−30	−63	−17	−59
BChl 5	6	2	−1	−63	220	88	−3
BChl 6	−14	12	−9	−17	88	100	38
BChl 7	−12	5	1	−59	−3	38	80

FIGURE 1.

Left column (top), structure of the FMO complex from the C.t. green sulfur bacteria. Surface wireframes around BChl molecules reveal the differences in the protein environment. Linear absorption (middle) and CD spectra (bottom): experimental (dashed line) and simulated (solid line) spectra. An overdamped Brownian oscillator model at 77 K (Λ⁻¹ = 100 fs, λ = 55 cm⁻¹) was used for the line broadening. Stick spectra are shown in red. The BChls with the largest contribution to each peak are indicated (in decreasing order of the contribution). The right column shows the same data for the P.a. green sulfur bacteria.

Each BChl chromophore is coupled to a bath characterized by an overdamped Brownian oscillator spectral density (2). Bath relaxation time Λ⁻¹ = 100 fs and reorganization energy λ = 55 cm⁻¹ of each BChl at T = 77 K were used to fit the absorption and CD spectra, shown in Fig. 1 (middle and bottom, respectively). The system has 7 one-exciton states, numbered in order of increasing energy (Table 3). At 77 K, the absorption spectra of both species show two overlapping peaks and two shoulders. Stick spectra, also shown in Fig. 1, reveal the transitions to all 7 one-exciton states. Previous analysis demonstrated the spatial delocalization of excitons (7,11,21,22,25). The lowest exciton state 1 in both species is mainly localized on BChl 3 (the numbering of BChls was introduced by Fenna and Matthews (17)). State 2 has similar oscillator strengths in both species, but it is slightly blue-shifted in C.t. The chromophore contributions to this state, however, are different. In C.t., the main contributions are from BChls 4 and 7, but they are from BChls 1 and 2 in P.a. BChls 1 and 2 contribute to state 3 in C.t., but BChl 4 primarily contributes in P.a. State 6 in P.a., which is formed by BChls 1 and 2, has negligible oscillator strength. The degree of delocalization of other states is also different. Delocalization patterns have clear signatures in the 2D spectra of the two species. The CD spectra shown in Fig. 1 can be analyzed in a similar way. The spectral differences can be attributed to the influence of environment on eigenvalues and exciton delocalization. A better fit is obtained for C.t., a finding that is in agreement with the previous work by Aartsma and colleagues (22,24).

TABLE 3.

Eigenvalues of the one-exciton Hamiltonians of FMO complexes (in cm⁻¹)

State	C.t.	P.a.
1	12116	12112
2	12279	12266
3	12364	12293
4	12416	12396
5	12452	12457
6	12548	12496
7	12620	12634

We have simulated the heterodyned 2D photon echo signals generated by three ultrashort laser pulses with wavevectors k_j and polarization directions ν_i (j = 1, 2, 3, 4). The signal is detected in the phase-matching direction k_s = −k₁ + k₂ + k₃ and Fourier-transformed with respect to the time delays between the first and the second (t₁) and between the third and the local oscillator (t₃) pulses. The corresponding conjugate frequency variables are denoted Ω₁ and Ω₃. There are three linearly independent ENC tensor components for isotropic systems in the dipole approximation: xyxy, xxyy, and xyyx (where x and y are the polarizations of the laser pulses) (31). The all parallel (xxxx) signal is given by the combination: xxxx = xyxy + xxyy + xyyx. Signals were simulated using the sum-over-states expressions (2) and the cumulant expansion of Gaussian fluctuations (CGF) (5). Orientational-averaging was made as described previously (31). Exciton transport was modeled using the Redfield equation within the secular approximation (40,41). All simulations were carried out at 77 K.

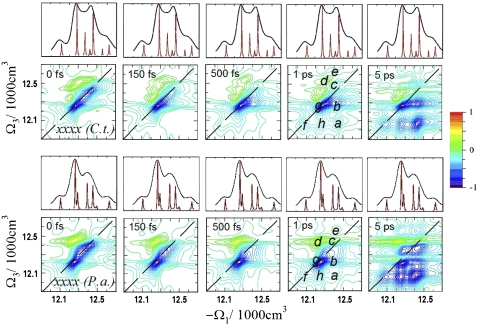
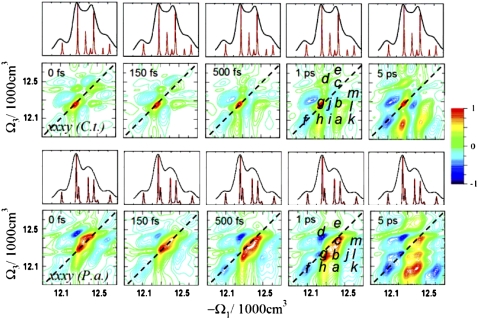
The xxxx signals (absorptive part) calculated using Eqs. 5.19–5.28 in the study by Mukamel and Abramavicius (5) of C.t. and P.a. complexes for different delay times t₂ are shown in Fig. 2. Electronic structure differences are apparent. The C.t. spectra closely resemble the recent measurements carried out by Brixner et al. (7) Similar diagonal and crosspeak patterns were observed (Fig. 2, a–h). As in the absorption, the main differences in the xxxx spectra at t₂ = 0 fs are the relative intensities of the two strongest diagonal peaks c and g. These peaks consist of exciton states with contributions of different BChls for different species. The xxxx signals at long t₂ (5 ps) show differences in the relative crosspeak intensities, h and a, which can be attributed to the fast energy transport pathway. Also, several weak crosspeaks appear above the diagonal line in the P.a. spectrum but not in C.t. Crosspeaks related to the slow energy transfer pathway are not resolved due to their weak intensities and spectral congestion. These include states 1, 3, and 7 in C.t., and states 1, 2, and 6 in P.a.

FIGURE 2.

Simulated 2D ENC xxxx spectra of FMO from C.t. and P.a. for several time delays t₂. The resolved diagonal and crosspeaks are illustrated (a–h). The linear absorption spectra (top) indicate the positions of single-exciton states.

At earlier time delays, the spectra of both species are very similar. Differences in coherent and incoherent dynamics are hardly noticeable due to the weak crosspeaks. Only the positive crosspeaks d show fast early dynamics, corresponding to excited-state absorption from the one- to the two-exciton states (FMO has 21 two-exciton states). The short (<150 fs) dynamics of the higher 5–7 one-exciton states are not resolved because the crosspeak e is too weak. Overall, both species reveal similar dynamics and timescales, even though different states with different delocalization patterns are involved. Isolated heterodimer delocalized over BChls 1 and 2 can be identified in C.t. (states 3 and 7). The corresponding BChls in P.a. contribute to more delocalized excitons with additional contributions of BChls 4 and 7 (state 2), and BChls 5–7 (state 6). Next, we demonstrate that 2D ECI signals contain much more pronounced signatures of chirality.

SEPARATING COHERENT AND INCOHERENT EXCITON DYNAMICS BY INTERFERENCE OF NC PULSE-POLARIZATION CONFIGURATIONS

By making use of some fundamental symmetries of the nonlinear signals, one can separate different phenomena through specific linear combinations of tensor components (37). Three NC signals were designed to highlight dynamical features. The signal A ≡ 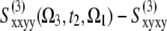(Ω₃, t₂, Ω₁) removes the static contributions that do not depend on t₂. It vanishes at t₂ = 0 fs due to the invariance of the response function to the interchange of the k₂ and k₃ laser pulses. When the timescales of various dynamical processes (coherent dynamics, dephasing, transport) are well-separated, they can be distinguished along t₂ in the signal A. The signal B ≡ 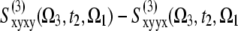) eliminates the population pathways and reveals the coherent quantum dynamics through oscillating crosspeaks. The signal C ≡ 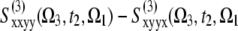) cancels the pathways with coherences in stimulated emission and thus highlights the population dynamics. This finding is observed as a redistribution of off-diagonal peak amplitudes. Note that the B and C signals are equal at t₂ = 0. These spectra show no populations (property of B) and no stimulated emission (property of C) contributions. Therefore, only excited state absorption (ESA) due to exciton intraband coherences is displayed by B and C signals at t₂ = 0.

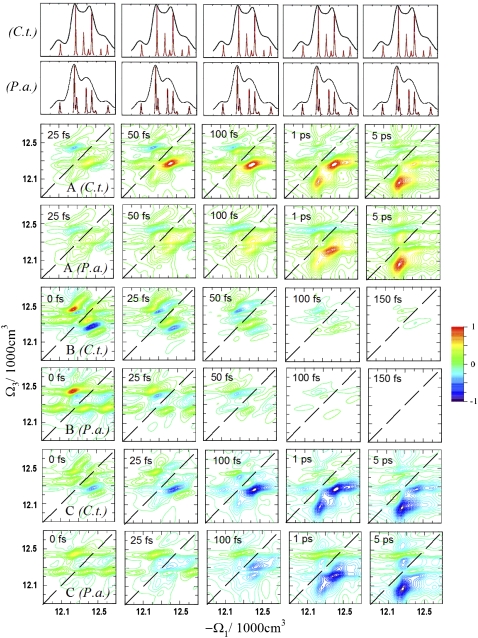
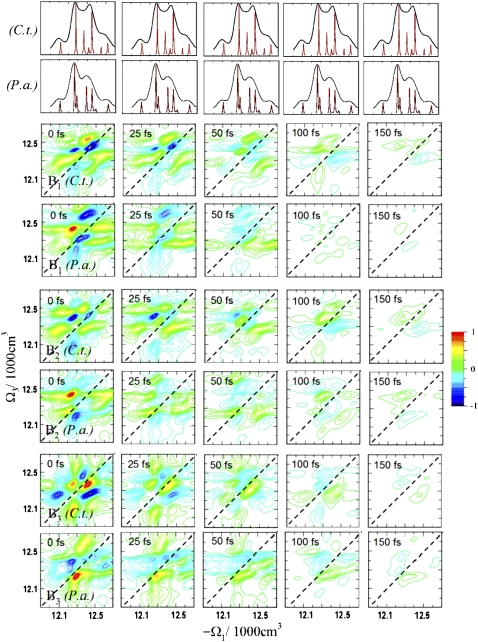
The 2D spectra of the A, B, and C signals for the C.t. and P.a. complexes are shown in Fig. 3. The B signals are normalized to the maximum intensity at t₂ = 0 fs, whereas the A and C signals are normalized to the maximum intensity at t₂ = 5 ps. These signals were previously simulated only for the C.t. species (37). Signal A reveals complex dynamics on different timescales that are not resolved in xxxx. Peaks oscillating on short timescales and other slow-varying peaks can be observed. The corresponding P.a. spectra are similar, but the crosspeaks grow more slowly than in C.t. Interference of fast and slow dynamics in the A signals complicates the interpretation of peaks. The B signals reveal ∼100 fs coherent evolution and ∼150 fs decay timescales in C.t. This decay is slightly faster in P.a. (∼100 fs). Distinct features in the P.a. spectra are the strong peaks at −Ω₁ = 12600 cm⁻¹, implying that state 7 is more delocalized in P.a. than in C.t. (note that localized excitons do not contribute to this signal). This information is not available from the xxxx or A signals alone. The C signals enhance the population pathways and reveal picosecond population redistribution dynamics, which are slightly slower in P.a. Due to spectral congestion, however, only features of the fast energy transfer pathway can be resolved. Overall, the C signals of both species are similar, reflecting the similarity of the population relaxation pathways.

FIGURE 3.

Simulated A, B, and C 2D ENC signals of FMO from C.t. and P.a. for several t₂ time delays. A and C spectra are normalized to the corresponding spectra at t₂ = 5 ps; B spectra are normalized to the spectra at t₂ = 0 fs. A shows how dynamics during t₂ breaks the t₂ = 0 symmetry; B reveals quantum oscillations of the density matrix; and C shows population relaxation (energy dissipation).

CHIRALITY-INDUCED 2D PHOTON ECHOES

Chirality-induced features

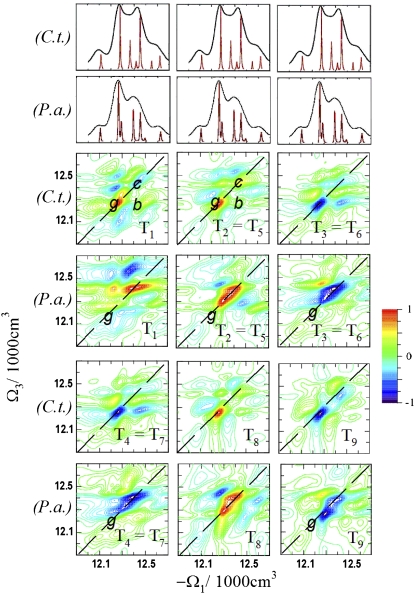
To resolve the congested spectral features in the 2D NC spectra and further highlight the electronic structure differences of the two species, we simulated chirality-sensitive PPC signals. The chirality-induced third-order nonlinear optical response vanishes in the dipole approximation and requires higher electric and magnetic multipoles (31). We simulated all nine linearly independent CI fifth-rank tensor components to first order in the wavevector: T₁ = R_xyzx(z,x,−x,−z), T₂ = R_xyxz(z,x,z,x), T₃ = R_xyxx(z,z,z,z), T₄ = R_xyxx (z,z,y,y), T₅ = R_xxyz(z,z,x,x), T₆ = R_xxyx(z,z,z,z), T₇ = R_xxyx(z,y,z,y), T₈ = R_xxxy(z,z,z,z), and T₉ = R_xxxy(z,y,−y,−z). Here R_ν4ν3ν2ν1(κ₄,κ₃,κ₂,κ₁) denotes the CI tensor component with polarization directions ν_j and wavevector κ_j, j = 1, 2, 3 and s (36). The simulation protocol has been described in detail previously (37).

The 2D ECI signals are more sensitive than the NC signals and provide new structural and dynamical information. Fig. 4 shows simulations of CI signals at t₂ = 0 fs. Here, T₂ = T₅, T₃ = T₆, and T₄ = T₇ because of the interchange symmetry of the second and third interactions at t₂ = 0 (31). The permutation of wavevectors and polarizations of the second and third interactions at t₂ = 0 causes the interchange of the excited state stimulated emission and ground-state bleaching contributions, but it does not change the overall signal. This symmetry breaks down at t₂ > 0 fs due to coherent dynamics, dephasing, and population relaxation (37). We have constructed the following A-type signals to probe these processes: A₁ ≡ T₆ – T₃, A₂ ≡ T₇ – T₄, A₃ ≡ T₅ – T₂.

FIGURE 4.

Simulated 2D ECI spectra (T₁ – T₉ tensor components) of FMO from C.t. and P.a. for t₂ = 0 fs. The shifted diagonal peaks g are marked in P.a. for comparison. The different signatures of chirality are revealed in the T₁ and the T₂ = T₅ signals of C.t. by the diagonal peaks c and g and the crosspeak b, as indicated.

The various 2D ECI spectra show different signs and relative intensities of the diagonal and the crosspeaks and so have different sensitivities to parts of the structure with opposite senses of chirality. A comparison of the T₁ and T₂ (T₅) signals from C.t. Fig. 4 shows that the diagonal peaks g and the crosspeaks b are positive in both cases, but the diagonal peaks c have different signs. Two states 4 and 5 in C.t. may contribute to the diagonal peaks c. Both states are delocalized on different BChls and have different spatial structures. In addition, the peaks c are slightly red-shifted in T₁ and blue-shifted in T₂ and T₅. Because of the shifts, we can assign these peaks to states c(T₁) = (4,4), c(T₂, T₅) = (5,5), and b(T₁) = (2,4) and b(T₂,T₅) = (2,5). These signals can resolve closely lying states and monitor small site energy shifts. In peaks c and g, other tensor components have the same signs.

Comparison of the T₁–T₉ signals from C.t. and P.a. at t₂ = 0 fs (Fig. 4) shows clear differences between the two species, much larger than the NC signals (Fig. 2). The strongest peak in C.t. is the diagonal g = (2,2). In P.a., this peak shows fine structure in T₈ due to interference of the closely lying states 2 and 3, and it is weaker in the T₁, T₃, T₄, T₆, and T₇ components. Interference also reduces the amplitude of g and leads to a better resolution of the neighboring crosspeaks b and h. The diagonal peaks g of the tensor components T₂, T₅, and T₉ from P.a. show blue shifts due to the larger contribution of state 3. In general, different pulse polarizations of 2D CI tensor components are sensitive to different states of the FMO complex.

The T₈ signals (xxxy, absorptive part) of C.t. and P.a. are shown in Fig. 5 for different delay times t₂. In contrast to the 2D ENC tensor components (xxxx in Fig. 2), the 2D ECI spectra of both species are very different, which reflects different exciton wave functions. For example, many new peaks (i–m) appear showing drastic differences in the signs and intensity pattern for the two species. Peaks a–h correspond to the same states as those in the xxxx spectra. The xxxy spectra show diagonal and crosspeaks with positive and negative signs, which is analogous to the CD spectra. This sign variation enhances the resolution. The diagonal peak f and the crosspeak h have the same signs in the xxxx spectra of C.t., but they have different signs in the xxxy spectra. Therefore, peak h is weak and not clearly resolved in xxxx at early t₂; this finding is in agreement with previous simulations and experiments (11). This peak is related to the coupling of states 1 and 2, and its intensity increases with t₂ due to energy transfer. In xxxy, the peak h has a different sign and is even stronger than peak a, which is the dominant crosspeak observed in xxxx.

FIGURE 5.

Simulated 2D ECI xxxy (T₈) spectra of FMO from C.t. and P.a. for several time delays t₂. Compared with the xxxx spectra in Fig. 2, these spectra reveal new well-resolved crosspeaks i–m. The electronic structure differences between C.t. and P.a. are thus amplified.

Large differences between the two species are seen in Fig. 5 in peaks g and h, which involve the closely lying states 2 and 3 in P.a. The two peaks overlap and have the same sign in the xxxx spectra. However, they have different signs in the 2D ECI spectra, and so peak h splits into a butterfly shape in P.a. There is a node at the center of the peak with a negative lower energy side and a positive higher energy side. The different signs of states 2 and 3 signify different delocalization patterns and reveal different senses of chirality. The complex chirality thus provides a better spectral resolution, which allows to better resolve the exciton states and, therefore, to follow the exciton dynamics. The time-resolved 2D spectra show predominant contributions of state 3 with the corresponding positive peaks at earlier time delays and the growth of the negative peaks involving state 2, due to the slow energy transfer pathway, at longer time delays. The split shape of crosspeak h for P.a. is especially pronounced in the xxxy t₂ = 5 ps spectrum. The single lowest energy diagonal peak g with a shoulder f in xxxx in Fig. 2 has been resolved in xxxy in Fig. 5 into three separate peaks with contributions of single exciton states. The splitting of peak g into two peaks with opposite signs is clearly seen at early t₂ = 150 fs or t₂ = 500 fs. For longer t₂, the diagonal peaks {1,1} and {2,2} are dominant in both species. These observations reflect the fast and slow energy transfer pathways, respectively. In xxxx, these peaks have the same signs, but they have the opposite signs in xxxy of C.t. In the xxxy spectra of P.a., they have the same sign, but peak {2,2} is distorted by interference with the closely lying opposite sign {3,3} peak.

Similarly, the two closely lying states 5 and 6 in P.a. result in split peaks. The position of the negative side of the butterfly-shaped crosspeak j corresponds to the very weak state 6, which also takes part in the slow energy transfer pathway. This peak has not been observed in any of the ENC spectra. Peak j corresponds to the crosspeaks {2,6} or {3,6}. Because both states 3 and 6 are localized mainly on the same BChls (2 and 6), this peak can be assigned to {3,6}. This peak also was not clearly resolved in any of the ENC spectra.

Coherent and incoherent dynamics of these states may be probed by constructing suitable linear combinations of tensor components, as demonstrated below.

Coherent dynamics and B-type signals

The following CI analogs of the B-type signals cancel population signatures and highlight coherent quantum dynamics: B₁ ≡ T₁ − T₂, B₂ ≡ T₃ − T₄, and B₃ ≡ T₇ − T₉ (37). These signals, shown in Fig. 6, reveal numerous new features that are not resolved in the ENC B signals. Similar to signal B, the B_j spectra of P.a. decay faster than C.t., but now all B_j show large differences. For example, B₁ of both species at t₂ = 0 fs show the strong negative crosspeaks h, but the crosspeaks e have different signs and shapes. The B₂ signal shows a crosspeak {6,7} in C.t. but not in P.a. The crosspeaks h in B₃ of both species are positive, but the crosspeaks b have opposite signs. Also, the crosspeak a is well-resolved in C.t. but is very weak in P.a. The lowest-energy exciton crosspeaks a or h are not resolved in the ENC B signals.

FIGURE 6.

Simulated 2D ECI signals B_j of FMO from C.t. and P.a. for several population time delays t₂, normalized to the spectra at t₂ = 0 fs. These signals are analogous to the 2D NC B signals shown in Fig. 3.

The new peaks make it possible to monitor the coherent quantum dynamics of various exciton states. Fig. 6 shows that some peaks decay very rapidly (∼50 fs), whereas others are slower (∼150 fs). In addition, the peaks oscillate with a frequency that corresponds to the energy differences of the relevant eigenstates. For example, the crosspeak l in the B₂ signal of P.a. changes sign at 25 fs compared to peak h at ∼100 fs. The various B_j signals are sensitive to different chiral regions of FMO and show characteristic crosspeak patterns. Crosspeak {6,7} in the B₂ spectra of C.t. is not resolved in the B₁ spectra.

Incoherent dynamics and C-type signals

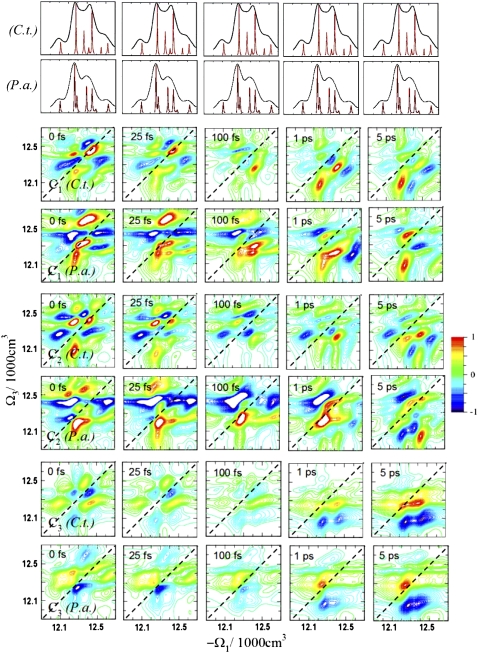
We examined the following CI C signals: C₁ ≡ T₅ – T₁, C₂ ≡ T₇ – T₆, C₃ ≡ T₉ – T₄ (37), designed to eliminate the stimulated emission coherent contributions and thus enhance the population relaxation pathways. Various linear combinations of CI tensor components control the interference of Liouville pathways and select various chirality-induced spectral features. Fig. 7 compares the incoherent energy dissipation within the FMO complexes of the C.t. and P.a. species. There are significant differences among the C_j signals of C.t. C₃ primarily shows the contributions from the fast energy transfer pathway at long t₂ (crosspeaks a and h). C₂ highlights the peaks due to the large contribution of the slow pathway (i and k). In C₁, the contributions from both pathways are clearly resolved — the intense crosspeak h results from the fast pathway, and the neighboring crosspeak i results from the slow pathway. Remarkably, the crosspeak a, which is the strongest in xxxx at t₂ = 5 ps and is also strong in T₈, is now suppressed due to the FMO chirality. This suppression allows to resolve the overlapping crosspeak i of the slow pathway. C₂, in contrast, suppresses the crosspeak h and resolves both peaks a and i.

FIGURE 7.

Simulated 2D ECI signals C_j of FMO from C.t. and P.a. for several time delays t₂, normalized to the spectra at t₂ = 5 ps. These signals are the chiral analogs to the 2D NC C signals shown in Fig. 3.

Similar behavior is observed for the P.a. species. Some peaks are split due to interference of closely lying states, as described in the previous section, and the P.a. spectra look very different. The C₁ signals of P.a. at t₂ = 5 ps reveal three crosspeaks of the lowest exciton state and the peaks due to the states taking part in the fast energy transfer pathway (a, h, and k). Peak a is very weak, which could be due either to interference with the neighboring crosspeak {1,6} or chirality. The latter mechanism is less probable, because the C₁ spectra at earlier t₂ show crosspeaks of state 6 with other states. The C₂ signals of P.a. reveal the splitting of a, and the resulting positive feature can be assigned to the {1,6} crosspeak. Similar to C.t., the C₃ signals of P.a. highlight the fast energy transfer pathway, revealing the a and h crosspeaks but not the expected k peak, which corresponds to the well-resolved crosspeak a = {1,5} in C.t.

The differences between the C₃ signals of C.t. and P.a. may be attributed to the change in chirality of the exciton states induced by the local protein environment of the participating BChl 5.

DISCUSSION

In this work, we have simulated the electronic 2D spectra of two species of FMO. Because the structure of C.t. and P.a. FMO complexes is very similar, the spectroscopic differences may be attributed to changes in the site energies and transition dipole orientations induced by the local protein environment. The electronic couplings and the influence of environment on coherent dynamics and incoherent energy transfer are directly observed. The crosspeaks in the 2D ENC signals of photosynthetic complexes are weak and poorly resolved due to spectral congestion (for example, the xxxx spectra in Fig. 2 at the ∼150 fs timescale).

2D ECI spectra are more sensitive to the electronic couplings and structure of the FMO complex than their NC counterparts, and they reveal richer peak patterns. For example, the xxxy (T₈) tensor component in Fig. 5 shows larger differences between the two species compared to the xxxx spectra. The dynamics are now better-resolved at earlier t₂ and show larger differences between the spectra of two species. These findings reflect different hydrogen bonding, ligand, and other environmental effects on the site energies and couplings between different exciton states. The magnitude of the 2D ECI signals is smaller than that of 2D ENC. The 2D ECI signals have an additional factor d/λ, where d is the exciton delocalization size and λ is the optical wavelength. The FMO size is ∼100× smaller than the center wavelength of the Q_y exciton band, and so the 2D ECI signals are estimated to be ∼100× weaker than 2D ENC. The same ratio exists between CD and linear absorption. Nonchiral B and C signals eliminate certain peaks in the 2D signals while leaving others unaffected. They have comparable magnitude to the NC xxyy, xyxy, and xyyx tensor components.

Resonant 2D signals may be interpreted using Feynman diagrams, which represent the various quantum pathways of the density matrix (27). Three types of contributions (excited state absorption (ESA), excited state stimulated emission (ESE), and ground-state bleaching) (GSB) interfere to produce the final signals. All pathways contribute to population dynamics, whereas ESA and ESE also contribute to the coherent evolution during the second interval t₂. By exploiting various symmetries of the multidimensional signals, we separated these processes through appropriate combinations of PPC (37). We thus obtained new families of 2D techniques aimed at studying coherent processes in photosynthetic systems. Coherent dynamics have been observed in energy transfer in the FMO complex of C.t. at 77 K (8). The PPC combinations can dramatically improve the resolution.

2D ECI spectra can also resolve peak splittings due to interferences of signals from closely lying states. This effect can also be observed in linear CD spectroscopy. However, the latter does not resolve the temporal evolution of these double peaks. For example, we clearly see that peak g is formed by two exciton states 2 and 3 in P.a. but only by one state 2 in C.t. Neither the linear absorption (Fig. 1) nor the 2D ENC spectra (Fig. 2) show any differences between peaks g of both species. The protein environment of FMO changes the pigment transition energies of the BChls 1, 2, 4, and 7, contributing to g in P.a. As shown in Fig. 1, only BChls 4 and 7 contribute to g in C.t. As a result, the exciton state 3 in P.a. moves closer to state 2 and is shifted to the red. Based on calculations of electrochromic shifts in site energies due to charged amino acids, the previous study by Adolphs and Renger (19) attributed the protein influence on the BChl 2 to be the largest among the four BChls contributing to peak g. The difference in the energy shifts of BChls 2 was attributed to the different structure of the water bridge between the chromophore and the Asn-79 amino acid. The resulting changes in the electronic structure of FMO are more significant for exciton states 3 and 7 in C.t. and for states 2 and 6 in P.a. (due to the large contribution of BChl 2). Site energy variations induce changes of the excited state delocalization and signature of chirality for each exciton. Analysis of the eigenfunctions shows that states 3 and 7 in C.t., which were predominantly delocalized on BChls 1 and 2 and formed an isolated dimer, become more delocalized over BChls 4 and 7 in P.a., and the corresponding relative contributions of BChls 1 and 2 also change. These differences in the 2D ECI spectra of the two species are more pronounced in the crosspeaks. For example, the crosspeak h, which corresponds to the diagonal peaks f and g, is similar in the xxxx spectra of both species (Fig. 1), but it has a different shape and intensity in xxxy (Fig. 5). It also has a butterfly-like shape in P.a., which is analogous to the diagonal peak g. The crosspeak b shows a similar behavior. These peaks result in a pronounced difference in the 2D ECI spectra of the two bacterial species.

Recent simulations of the site energies demonstrated that the largest difference between the two species was in BChl 5 (19). Its site energy shifts to the red for C.t. but to the blue in P.a. due to the contributions of different amino acids. This chromophore was found to be responsible for the changes in intensities of the main bands. We have demonstrated that these bands can be separated into different contributions in 2D spectra. The corresponding 2D ECI spectral differences provide information about the change in chirality of the associated exciton states. Our calculations demonstrate that the 2D ECI signals are very powerful probes of exciton coherent and relaxation properties and carry signatures of system structural properties.