Long Lasting Synchronization of Calcium Oscillations by Cholinergic Stimulation in Isolated Pancreatic Islets

Abstract

Individual mouse pancreatic islets exhibit oscillations in [Ca²⁺]_i and insulin secretion in response to glucose in vitro, but how the oscillations of a million islets are coordinated within the human pancreas in vivo is unclear. Islet to islet synchronization is necessary, however, for the pancreas to produce regular pulses of insulin. To determine whether neurohormone release within the pancreas might play a role in coordinating islet activity, [Ca²⁺]_i changes in 4–6 isolated mouse islets were simultaneously monitored before and after a transient pulse of a putative synchronizing agent. The degree of synchronicity was quantified using a novel analytical approach that yields a parameter that we call the “Synchronization Index”. Individual islets exhibited [Ca²⁺]_i oscillations with periods of 3–6 min, but were not synchronized under control conditions. However, raising islet [Ca²⁺]_i with a brief application of the cholinergic agonist carbachol (25 μM) or elevated KCl in glucose-containing saline rapidly synchronized islet [Ca²⁺]_i oscillations for ≥30 min, long after the synchronizing agent was removed. In contrast, the adrenergic agonists clonidine or norepinephrine, and the K_ATP channel inhibitor tolbutamide, failed to synchronize islets. Partial synchronization was observed, however, with the K_ATP channel opener diazoxide. The synchronizing action of carbachol depended on the glucose concentration used, suggesting that glucose metabolism was necessary for synchronization to occur. To understand how transiently perturbing islet [Ca²⁺]_i produced sustained synchronization, we used a mathematical model of islet oscillations in which complex oscillatory behavior results from the interaction between a fast electrical subsystem and a slower metabolic oscillator. Transient synchronization simulated by the model was mediated by resetting of the islet oscillators to a similar initial phase followed by transient “ringing” behavior, during which the model islets oscillated with a similar frequency. These results suggest that neurohormone release from intrapancreatic neurons could help synchronize islets in situ. Defects in this coordinating mechanism could contribute to the disrupted insulin secretion observed in Type 2 diabetes.

INTRODUCTION

Plasma insulin levels are pulsatile in many mammals, including humans (1,2), as is the secretion of insulin from the perfused pancreas (3,4) or groups of perfused isolated islets (2,5). The period of these oscillations varies but is generally in the range of 5–11 min, depending on the species (6–9). Insulin oscillations are physiologically relevant as it has been shown that the actions of insulin on its target tissues are more profound when the hormone is presented in a pulsatile versus a continuous manner (10–12). Additionally, insulin pulsatility is of clinical relevance to diabetes because patients with Type 2 diabetes and their first-degree relatives exhibit dysregulated pulsatility (13,14).

It is known that insulin secretion is driven by oscillations in [Ca²⁺]_i in the electrically coupled, well-synchronized network of β-cells within individual islets, and it has been recently shown that the periods of plasma insulin oscillations measured in mice in vivo match the periods of the [Ca²⁺]_i oscillations of isolated mouse islets measured in vitro (15). This is not surprising, as it is known that regulated insulin granule exocytosis is mediated by SNARE proteins in β-cells that require a rise in [Ca²⁺]_i for insulin granule fusion and release to occur (16,17).

Although details of the biophysical and biochemical mechanisms of islet [Ca²⁺]_i oscillations are being intensively investigated, and different models have been proposed, experimental studies have made it clear that islet [Ca²⁺]_i oscillations result from an interaction between ion channels and β-cell glucose metabolism, possibly via oscillations in both electrical and metabolic variables. As recently reviewed (18), these models can readily account for both the faster (e.g., <1 min period) and slower (e.g., 1–5 min period) types of oscillations.

However, as the human pancreas contains ∼1 million islets, the oscillatory activity of a majority of these islets must be closely coordinated or synchronized for pulses of secretion to occur from the whole pancreas, which in turn drives pulses of insulin (and other islet hormones) in the plasma. If this were not the case, and individual islet oscillations were out of phase, they would tend to cancel one another out, resulting in a loss of pulsatility. Although there has been progress in understanding the mechanisms that generate individual islet oscillations, the mechanisms involved in mediating islet-to-islet communication and synchronization are unknown. Thus, although it has been suggested that a neural network operating in vivo couples the activity of diverse islets together into a functional syncytium (19,20), there is little direct experimental evidence to support this hypothesis, and the functional characteristics of the network and its specific components remain unclear.

To address candidate mechanisms that may be involved in islet-to-islet synchronization, we focused our attention on several neurohormone systems known to reside in the pancreas in vivo that could conceivably help to synchronize islet activity. The pancreas is innervated by cholinergic fibers (21), ample amounts of choline acetyltransferase and acetylcholinesterase are in islets (22), and M₁ and M₃ type muscarinic receptors are expressed on islet β-cells (23). It is well established that parasympathetic stimulation of the pancreas potentiates insulin secretion both before and after glucose absorption from the gut (24), reinforcing the physiological importance of this system in glucose homeostasis. However, previous studies carried out in vivo using mainly pharmacological approaches to disrupt cholinergic input to the pancreas were generally unable to demonstrate a role for β-cell muscarinic receptors in insulin plasma pulsatility (19). Although vagotomy did shift the characteristics of insulin pulsatility, this was cited as evidence for other oscillatory drivers (25). However, besides concerns about nonspecific actions of the drugs used as probes and other effects of vagotomy (26), it can be difficult to quantify oscillation characteristics in vivo, which may also be subject to a variety of redundant control mechanisms in the intact animal.

Besides cholinergic input, we also tested whether sympathetic input to the pancreas will produce synchronization, as islets have extensive adrenergic innervation, and stimulation of the splanchnic or mixed autonomic nerves modifies islet insulin secretion by releasing noradrenaline and inhibiting glucose-stimulated insulin secretion by activating alpha receptors (27).

In this study, we utilized a simple experimental paradigm that allowed us to simultaneously measure [Ca²⁺]_i oscillations in multiple isolated mouse islets in vitro, using [Ca²⁺]_i as a surrogate measure of insulin secretion. We note that although oscillations in insulin secretion have been reported when [Ca²⁺]_i is not oscillatory (28), under most conditions oscillations in [Ca²⁺]_i act as the principal driver of islet insulin oscillations (15,29–31). An advantage of this experimental approach is that it provides information on the state of each islet, in contrast to in vivo and perfused pancreas experiments that only report the summed activity of all the islets.

The degree of synchronization among islets was quantified using a novel parameter we call the Synchronization Index (or SI; see Methods). We determined the SI before and after a very brief application of a putative synchronizing agent.

We found that the most efficacious synchronizing agent of those tested was the cholinergic agonist carbachol, which, acting through M-type receptors, briskly synchronized islet oscillatory activity and maintained synchrony for up to 30 min despite its being quickly washed out of the experimental chamber. The ability of carbachol to synchronize islets was glucose-dependent, as at concentrations <7 mM glucose, carbachol was ineffective. We also found that it was difficult to synchronize the activity of islets having divergent oscillation periods, in line with our recent proposal that the islets of individual mice may be close in their oscillatory characteristics to facilitate such synchronization (32). It is likely that synchronization was mediated by the perturbation of [Ca²⁺]_i after carbachol addition, as high KCl produced a similar degree of synchronization. In contrast, we did not observe significant synchronization after the application of norepinephrine or clonidine. Interestingly, the K_ATP opener diazoxide was partially effective in synchronizing islets.

To understand how a brief pulse of carbachol produced sustained synchronization, we used our recent Dual Oscillator Model (33) of islet oscillations, where oscillatory behavior is driven by interactions between fast ion channel-mediated oscillations using [Ca²⁺]_i as a negative feedback variable, and by a slower metabolic process, which in the present model is oscillatory glycolysis mediated by the allosteric enzyme phosphofructokinase-M (32,34). We performed simulations with five model islets, which varied in oscillation period due to heterogeneity in the value of one model parameter. Using this model, transient synchronization was observed when [Ca²⁺]_i was transiently elevated by the simulated application of carbachol or high KCl. The synchronization observed lasted for a time period much longer than the duration of the pulse of synchronizing agent. We show that the mechanism for this is twofold. First, the [Ca²⁺]_i perturbation resets the phases of the model islet oscillators, so that they are reset to an in-phase state. Second, a transient “ringing” or damped oscillation phase occurs during which the frequency of oscillation varies little from islet to islet. As a result, the model islets remain in phase, i.e., synchronized, for several minutes while the ringing persists. The implications of these findings and their novel theoretical basis are discussed.

MATERIALS AND METHODS

Islet preparation

Islets were isolated from the pancreata of Swiss-Webster mice using standard collagenase digestion (35). Islets were then put into 35-mm petri dishes and cultured in RPMI-1640 medium containing 11.1 mM glucose, fetal bovine serum, L-glutamine, and penicillin/streptomycin (Gibco, Grand Island, NY). Islets were kept for 1–3 days in an air/CO₂ incubator at 37°C.

Simultaneous measurements of [Ca²⁺]_i oscillations in multiple islets

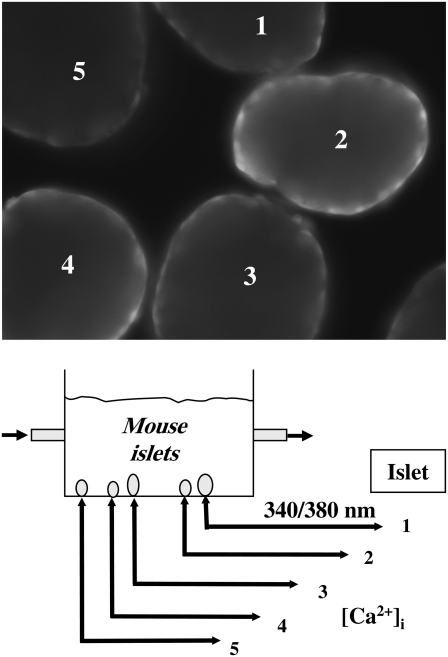
Islets were loaded with 5 μmol/l fura-2/AM and 0.01% pluronic acid (Invitrogen, Eugene, OR) and incubated at 37°C for 30 min in an incubator. Islets were then washed for 20 min. with a fura-2 free recording solution that contained (in mM): 115 NaCl, 3 CaCl₂, 5 KCl, 2 MgCl₂, 10 HEPES, and 11.1 mM glucose, unless the glucose sensitivity of the synchronization process was to be determined, as stated in the text (pH 7.2). Islet [Ca²⁺]_i was measured using an inverted fluorescence microscope-based (IX-50, Olympus, Tokyo, Japan) imaging system consisting of a Xe arc excitation source, a Ludl filter wheel (Ludl, Hawthorne, NY), and IPLab fluorescence imaging software (Scanalytics, Fairfax, VA). Using this setup, epifluorescence was simultaneously measured from 3–6 individual islets at 32–35°C in a 1 ml recording chamber continually perfused at 1 ml/min, and [Ca²⁺]_i values were expressed as the fluorescence ratio of Ca²⁺-bound (340 nm) to Ca²⁺-free (380 nm) fura-2, with emission collected at 510 nm. Parallel studies using dye-containing solutions with this system showed that complete solution exchange within the chamber occurred within 1–2 min. Healthy islets readily affixed themselves to the glass bottom of the recording chamber, above the fura objectives. The distance between the islets in this chamber ranged from 5 to 150 μm. A schematic of the experimental setup used is shown in Fig. 1.

FIGURE 1.

Schematic of experimental setup used. Small groups of islets were placed on the bottom of a small (1 ml) experimental chamber and islet fura-2 fluorescence was collected at 510 nm after alternate excitation at 340/380 nm. Saline was flowed through the bath at 1 ml/min. (Inset) Five islets loaded with fura-2 excited at 340 nm.

Synchronization index

To quantify the degree of islet-to-islet synchronization, we developed a measure of synchrony based on the recurrence of a calcium fluorescence trace to nearby values. This measure has been previously established for general chaotic dynamical systems (36) and is adept at detecting synchrony even when the traces are out of phase or nonstationary (i.e., the average value meanders). Given that a trace T is defined by its set of fluorescence values 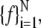the method follows three main steps:

1. Calculate the self-similarity matrix or recurrence matrix (R) for a given ɛ-neighborhood of trace T,

   

   where H(x) is 1 if x > 1 and 0 otherwise.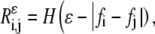
2. Construct the generalized autocorrelation function (P) from the recurrence matrix:

   
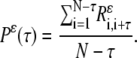
3. Calculate the pairwise correlation function of the mean-adjusted generalized autocorrelation functions:

   

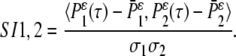
For the experiments with several islets, an average over the pairwise SI_ij, (i < j) values is taken to generate the SI. We pick the tunable parameter ɛ = 0.1.

Mathematical model

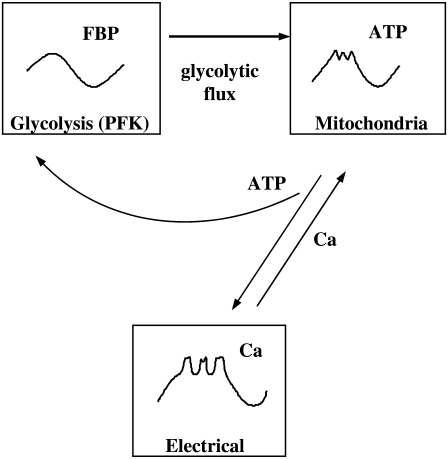
We use a mathematical model to simulate the effects of bath application of carbachol, KCl, and diazoxide. This “Dual Oscillator Model” has been described in detail in Bertram et al. (33), so it will only briefly be described here. The model has three compartments: for glycolysis, mitochondrial metabolism, and electrical activity and Ca²⁺ handling (Fig. 2). For appropriate values of the glucokinase rate, the glycolytic compartment can produce slow oscillations (a period of several minutes) in glycolysis, due to the action of the allosteric enzyme phosphofructokinase (PFK). This enzyme is stimulated by its product fructose 1,6-bisphosphate (FBP) and inhibited by ATP. It is the positive feedback of FBP that leads to oscillations, due to partial depletion of the PFK substrate fructose 6-phosphate (37). The negative ATP feedback onto PFK is modulatory and is not responsible for the oscillations in the model, although it is important for synchronization.

FIGURE 2.

Illustration of the three compartments of the Dual Oscillator Model (glycolytic, mitochondrial, and electrical/ionic).

The glycolytic compartment provides input to the mitochondrial respiration compartment. This compartment has equations for the mitochondrial inner membrane potential, mitochondrial Ca²⁺ concentration, mitochondrial NADH concentration, mitochondrial ATP and ADP concentrations, and oxygen consumption due to respiration. Mitochondrial ATP production can be oscillatory or nonoscillatory, reflecting the dynamics of the glycolytic compartment. The ATP produced by the mitochondria is transported into the cytosol, where it has two targets, PFK and the K_ATP channel in the plasma membrane. When the cytosolic ATP/ADP ratio is high, K_ATP channels are deactivated, and when ATP/ADP is low the channels are activated (38).

Data analysis

Data analysis and graphics were performed using IgorPro Software (Wavemetrics; Lake Oswego, OR) and statistical analysis was done using GraphPad Prism (GraphPad Software, San Diego, CA). Data shown are mean ± SE. Where paired Student's t-test was used to test for significance, p values <0.05 were considered significant and denoted by * in the figures; p < 0.01 is denoted by **, and p < 0.001 are denoted by *** in all figures.

RESULTS

Individual islets displayed regular slow oscillations in 11.1 mM glucose but were not synchronized to one another

Previous studies have suggested that mouse islet β-cells may synchronize with one another through a diffusible factor(s) released by the β-cell (39–44). To test this, we first tested whether synchrony could be observed between islets held in the common recording chamber and exposed to a continuous stream of saline. Thus, islets were affixed in the recording chamber, and their [Ca²⁺]_i oscillations were recorded simultaneously, with each islet surface designated as a region of interest in the software (Methods).

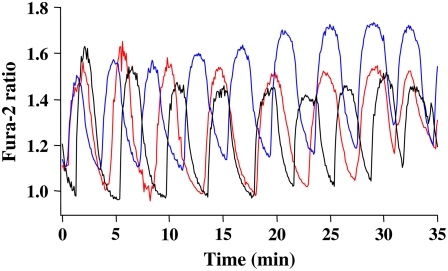
As shown in Fig. 3, in the presence of 11.1 mM glucose, islets exhibited regular slow [Ca²⁺]_i oscillations, typically having periods ranging from 3 to 5 min (15,32,35). From visual inspection it is clear that the oscillations of different islets in this case were not synchronized even after >30 min. This was confirmed by calculating the SI (see Methods) of the traces measured under control conditions, which was 0.31 ± 0.04, a relatively low value (n = 19 experiments; the number of islets tested per experiment was 4–6). Although individual islets did not synchronize under these conditions, we cannot rule out the possibility that the moving flow system we used may have prevented us from observing coupling mediated by diffusible factors released from the islets (see Discussion).

FIGURE 3.

Individual islets do not synchronize in 11.1 mM glucose. An example showing that the [Ca²⁺]_i oscillations from three different islets did not synchronize over a period of 35 min. Representative of 10 experiments.

The cholinergic agonist carbachol synchronized islet [Ca²⁺]_i oscillations in 11.1 mM glucose

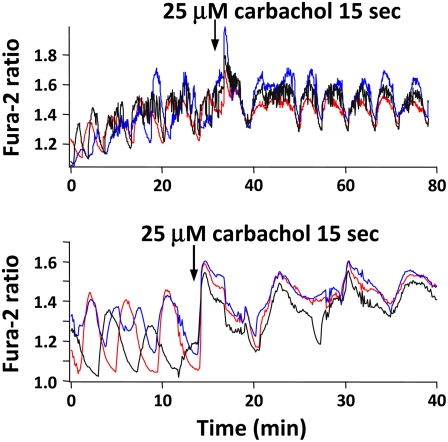
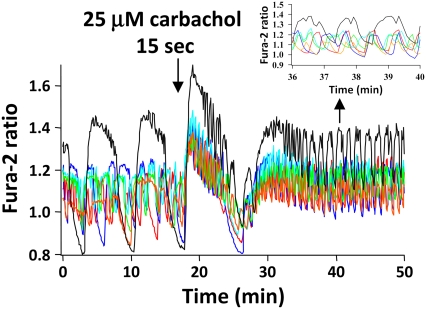
Acetylcholine (ACh), the major parasympathetic neurotransmitter, modulates pancreatic secretion through M₁ and M₃ muscarinic receptors (23,26,45,46). To test the hypothesis that β-cell muscarinic receptors could synchronize islet oscillations, we bath applied the cholinergic agonist carbachol to islets to mimic the effects of vagal nerve stimulation. As shown in Fig. 4 for two different groups of islets, under control conditions islets exhibited slow or mixed fast and slow [Ca²⁺]_i oscillations having periods of several minutes (35). However, exposing islets to 25 μM carbachol for as little as 15 s first elicited a transient peak in [Ca²⁺]_i in the islets, reflecting Ca²⁺ release from a cytosolic inositol trisphosphate (IP₃)-sensitive endoplasmic reticulum (ER) store (47–50). After this peak, the [Ca²⁺]_i oscillations of the individual islets became synchronized, resulting in an increase in the SI from a control level of 0.31 ± 0.04 to 0.62 ± 0.04 (p < 0.001). Fig. 4 is representative of data from 19 individual experiments, carried out using >80 islets. We also noted that carbachol tended to increase the periods of the [Ca²⁺]_i oscillations and increase mean [Ca²⁺]_i, consistent with the reported dual actions of ACh to release ER Ca²⁺ and also cause membrane depolarization (50,51). As for other potential synchronizing agents studied, the exposure time we chose was determined empirically so that intrinsic islet oscillations persisted. Exposing islets to certain agents for too long a time resulted in irreversible loss of the intrinsic islet oscillations.

FIGURE 4.

Exogenous carbachol synchronizes islet [Ca²⁺]_i oscillations in 11.1 mM glucose. Bath application of 25 μM carbachol for 15 s first initiated a peak in [Ca²⁺]_i, then synchronized the [Ca²⁺]_i signals from different islets. Representative of 19 experiments.

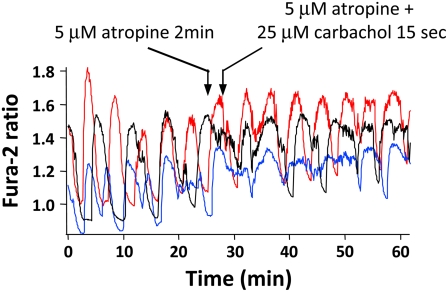
To confirm that the actions of carbachol were mediated by muscarinic receptors, we preexposed islets to the classic muscarine receptor antagonist atropine (at 5 μM) for 2 min before adding carbachol together with atropine. As can been seen in Fig. 5, atropine prevented the synchronizing action of carbachol (SI was 0.37 ± 0.06 before, and 0.27 ± 0.02 after adding carbachol in the presence of atropine, p > 0.05; n = 5) and also blunted the early peak in [Ca²⁺]_i. This indicates that the effect of ACh to synchronize islet [Ca²⁺]_i oscillations was mediated by muscarinic receptors.

FIGURE 5.

Atropine prevented the synchronizing effect of carbachol. To test whether the synchronizing action of carbachol occurred via muscarinic receptors, 5 μM atropine was added alone and then together with carbachol. As shown in the figure, atropine abolished the effect of carbachol on islet [Ca²⁺]_i synchronization.

Glucose alone does not cause prolonged synchronization but is required for islet synchronization by carbachol

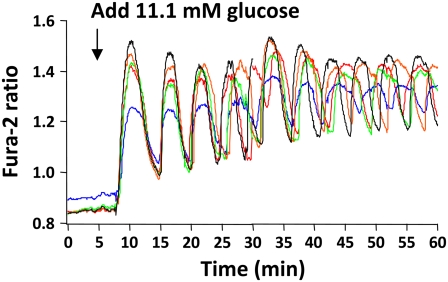
To test whether the concentration of glucose that islets were exposed to was a factor in carbachol-induced islet synchronization, [Ca²⁺]_i levels were recorded from islets before and after raising the glucose concentration from 2.8 to 11.1 mM. As shown in Fig. 6, no oscillatory activity was seen in 2.8 mM glucose, as expected, whereas switching to saline containing 11.1 mM glucose resulted in a rise in [Ca²⁺]_i and, initially, a few well-synchronized [Ca²⁺]_i oscillations (32,35). However, the oscillations became progressively desynchronized after the first few cycles (representative of three experiments carried out using a total of 13 islets), consistent with the data we observed in 11.1 mM glucose (shown in Fig. 3 under steady-state conditions). Thus, although raising glucose initially synchronized the islets, they quickly desynchronized over time, and glucose alone was unable to produce the prolonged synchronization characteristic of carbachol.

FIGURE 6.

Individual islets desynchronize after initially synchronizing, after glucose was increased from 2.8 to 11.1 mM.

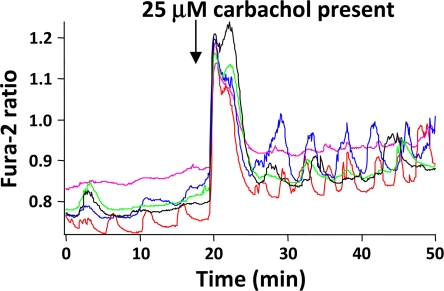
To determine how islet synchronization by carbachol depends on glucose concentration, islets were continuously exposed to 5.5, 7.5, 11.1, 15, or 20 mM glucose for 30 min after loading with fura-2/AM. As shown in Fig. 7, islets treated with saline containing 5.5 mM glucose, which is generally subthreshold for eliciting substantial rises in [Ca²⁺]_i and significant insulin secretion (32,52,53) responded to carbachol stimulation with an initial coordinated peak of [Ca²⁺]_i due to Ca²⁺ mobilization, but then exhibited unsynchronized oscillations. Interestingly, some of the islets exposed to 5.5 mM glucose appeared to oscillate more readily once carbachol was added. The degree of islet synchronization to carbachol progressively and quantitatively increased as a function of glucose concentration, as shown in Table 1. The results shown were representative of at least five experiments and suggest that cholinergic-mediated islet synchronization was glucose-dependent.

FIGURE 7.

Carbachol was unable to synchronize islets exposed to 5.5 mM glucose. Islets were preincubated with 5.5 mM glucose, then challenged with 25 μM carbachol, as shown in the figure. Carbachol potentiated [Ca²⁺]_i oscillations, but had no effect on islet synchronization unless glucose was sufficiently elevated.

TABLE 1.

Summary of synchronization indexes (SI) before and after treatment with different putative synchronizing agents. Mean ± SE, *P < 0.05, **P < 0.01

Glucose concentration (mM)	Number of experiments	SI before	SI after	P value
5.5	5	0.43 ± 0.14	0.45 ± 0.09	>0.05
7.5	7	0.39 ± 0.09	0.60 ± 0.11	>0.05
11.1	19	0.34 ± 0.04	0.58 ± 0.04	<0.001
15.0	7	0.47 ± 0.08	0.76 ± 0.05	<0.01
20.0	7	0.30 ± 0.08	0.58 ± 0.08	<0.05

Carbachol does not synchronize [Ca²⁺]_i oscillations in islets pre-exposed to different glucose concentrations to alter their oscillatory patterns

To test whether carbachol was able to synchronize islets having different [Ca²⁺] patterns, groups of islets were preexposed to 7, 11.1, or 15 mM glucose for 30 min after fura-2 loading, and then transferred to the recording chamber where they were all exposed to 11.1 mM glucose. This differential treatment was chosen to produce a fairly wide range of oscillatory patterns (32,35). The rationale for the approach is the well-documented action of different glucose concentrations to modify periods of mouse islet electrical or [Ca²⁺]_i oscillations (18,31,32,54,55). The protocol used here closely resembled the protocol shown previously (34) in which lowering glucose from 11.1 mM for several minutes and then adding 11.1 mM glucose back causes a maintained switch from slow to fast oscillations. Model simulations in Bertram et al. (34) show that such a maintained switch may be due to bistability in the dual oscillator system, which can be slow or fast at a given level of glucose.

As shown in Fig. 8, the islet [Ca²⁺]_i oscillations observed during the first 20 min before the addition of carbachol were very diverse and were clearly not well synchronized. Thus, some islets displayed fast, small amplitude oscillations whereas other islets had much slower, larger amplitude [Ca²⁺]_i oscillations. After being challenged with 25 μM carbachol for 15 s, all islets showed an initial and relatively prolonged [Ca²⁺]_i increase, but then generally only weak levels of synchronization. The data shown in the inset of Fig. 8 are on an expanded timescale and reflect the steady-state oscillatory behavior. These results are in accord with modeling from our own group showing that it is easier to synchronize islets having similar periods (15).

FIGURE 8.

Carbachol did not synchronize islets pretreated with unequal concentrations of glucose. Islets were incubated with different glucose concentrations (7.5, 11.1, or 15 mM) for 30 min before recording commenced, and then were exposed to saline containing 11.1 mM glucose. As shown in the figure, the islets had different patterns of [Ca²⁺]_i oscillations. The application of 25 μM carbachol still initiated a peak in [Ca²⁺]_i, but then failed to synchronize islet [Ca²⁺]_i signals.

Norepinephrine and clonidine failed to synchronize islets

Sympathetic fibers of the autonomic nervous system innervate the pancreas, directly influencing endocrine function (56,57). Many previous studies have shown that adrenergic agonists inhibit insulin secretion in various ways, including via inhibition of voltage-gated Ca²⁺ channels (58), activation of low-conductance BaCl₂-sensitive K⁺ channels (59), and direct inhibition of distal secretion via G-proteins coupled to α-receptors (60,61).

To test whether adrenergic agonists influence islet synchronization, norepinephrine (NE) or the α-receptor agonist clonidine were bath applied to islets in 11.1 mM glucose. It was found that neither 1–100 μg/mL NE nor 10 μM clonidine was capable of synchronizing mouse islet [Ca²⁺]_i oscillations. This was not due to their failure to act on the α-adrenergic receptor because NE initially lowered [Ca²⁺]_i and slowed islet [Ca²⁺]_i oscillations as expected from earlier reports (62,63). NE application actually tended to reduce SI from 0.35 ± 0.07 to 0.26 ± 0.07, although this was not significant (n = 6, p > 0.05). For clonidine, SI decreased from 0.40 ± 0.10 to 0.36 ± 0.11 after addition of the drug (n = 4, p > 0.05). The doses of these agonists used were consistent with those used in several previous reports (62,64,65).

The K_ATP channel opener diazoxide, which hyperpolarizes islets also caused partial islet-islet synchronization

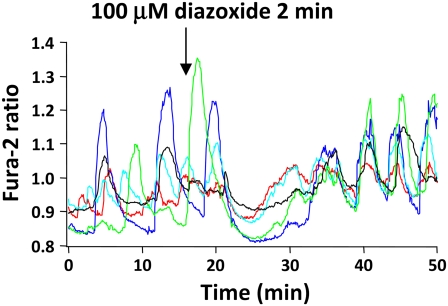
Diazoxide is a K_ATP channel opener that results in β-cell hyperpolarization, a lowering of [Ca²⁺]_i, and the cessation of glucose-stimulated insulin release (66–68). To test whether diazoxide could cause islet synchronization, we exposed islets to 100 μM diazoxide for 2 min in glucose-containing saline, as shown in Fig. 9. As can be seen in the figure, the addition of diazoxide resulted in a pronounced drop in [Ca²⁺]_i, which lasted for >10 min, followed by a resumption of islet [Ca²⁺]_i oscillations once the drug was washed out of the chamber. The SI values observed before and after diazoxide exposure were 0.33 ± 0.05 and 0.59 ± 0.06, respectively (n = 5, p < 0.05). These results thus suggest that hyperpolarization of the islet membrane potential resulting from K_ATP channel activation can also partially synchronize islet [Ca²⁺]_i oscillations. The slow dynamics of the action of diazoxide we observed here may reflect the time required for the drug to diffuse extensively enough through the islet to open a sufficiently large number of K_ATP channels to repolarize the islet.

FIGURE 9.

Hyperpolarizing islets with diazoxide modestly increased synchronization. Application of the K_ATP channel opener diazoxide to islets for 2 min first hyperpolarized islets, and then increased synchronization.

Depolarizing islets with high KCl but not tolbutamide also enhanced islet [Ca²⁺]_i synchronization

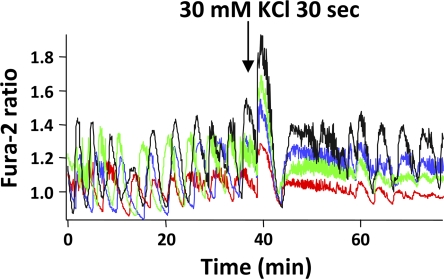
As carbachol increases [Ca²⁺]_i in islets, we tested whether other ways to increase islet [Ca²⁺]_i might also synchronize islet [Ca²⁺]_i oscillations. We thus exposed islets to 30 mM KCl for 30 s or to 100 μM tolbutamide for 2 min to test whether these agents, which provoke Ca²⁺ influx through β-cell Ca channels (55,69,70), were also capable of synchronizing islet oscillations. As shown in Fig. 10, KCl was able to synchronize islets, with the SI before and after KCl addition being 0.34 ± 0.04 and 0.63 ± 0.05, respectively (n = 10, p < 0.01). In contrast, the addition of tolbutamide did not lead to synchronization (data not shown) and the SI actually decreased from 0.46 ± 0.13 to 0.37 ± 0.13(n = 4, p > 0.05). These results suggest that Ca²⁺ influx produced by high KCl caused [Ca²⁺]_i synchronization. Fig. 11 compares SI values for all putative synchronizing agents tested in this study.

FIGURE 10.

Depolarizing islets with 30 mM KCl successfully synchronized islets.

FIGURE 11.

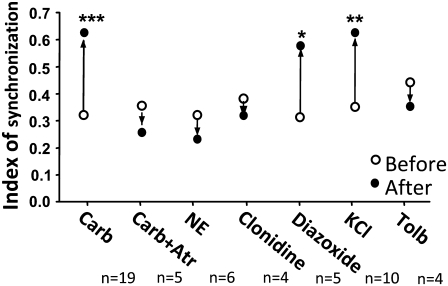
Summary of SI before and after treatment for all groups. SI was used to compare the efficacy of carbachol and other agents to synchronize islet [Ca²⁺]_i oscillations. As shown in the figure, carbachol, diazoxide, and KCl were able to significantly synchronize islet [Ca²⁺]_i oscillations. Open circles represent SI before treatments, solid circles represent SI after treatments. (*), (**), and (***) indicate p < 0.05, 0.01, and 0.001, respectively, versus before treatments. N represents the number of replicates.

Model simulations suggest a mechanism to account for synchronization

We use the Dual Oscillator Model (33) to understand the mechanism through which brief application of carbachol, KCl, or diazoxide can synchronize islet Ca²⁺ oscillations. The model is capable of producing a range of oscillatory patterns, including fast bursting (period ∼15 s), slow bursting (period ∼5 min), and compound bursting (fast bursts grouped into slower episodes). In the case of fast bursting, the glycolytic component of the model is nonoscillatory, and fast bursting oscillations are due to Ca²⁺ feedback onto Ca²⁺-activated K⁺ channels. However, glycolysis may be oscillatory, leading to slow oscillations in metabolism that have, as one target, the K_ATP channels. In this case, either slow or compound bursting is produced. The glycolytic compartment may be endogenously oscillatory, even if the plasma membrane potential is clamped (34). Alternatively, if the parameter values are modified, the glycolytic compartment may only be oscillatory when there are bursting electrical oscillations. In this case, clamping the membrane potential can terminate metabolic oscillations (18). For clarity, we refer to the first scenario, where the glycolytic compartment produces endogenous oscillations, as burst-independent glycolytic oscillations. We refer to the second scenario, where oscillations in glycolysis only occur in the presence of electrical bursting, as burst-dependent glycolytic oscillations.

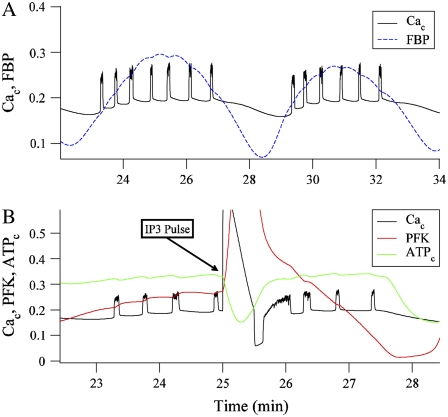
Fig. 12 A shows two episodes of compound Ca²⁺ oscillations, with oscillations in the glycolytic intermediary FBP superimposed. This is an example of burst-dependent glycolytic oscillations. The oscillating FBP reflects oscillations in glycolysis, which acts through mitochondrial respiration to ultimately produce oscillations in the cytosolic ATP/ADP ratio. This ratio regulates the activity of K_ATP channels so that the number of open K_ATP channels is reduced when the ratio is elevated (38). In this way, slow oscillations in glycolysis cause slow oscillations in the hyperpolarizing K_ATP current, which groups bursts of electrical activity into episodes, as shown in Fig. 12 A.

FIGURE 12.

(A) Two compound oscillations in cytosolic Ca²⁺ concentration (in μM). The FBP time course is superimposed and scaled to facilitate comparison with Ca_c. (B) Cytosolic Ca²⁺, ATP concentrations, and PFK reaction rate before, during, and after a 30 s pulse of IP₃ from 0 to 0.3 μM. Both ATP and the PFK rate have been scaled.

The oscillations in glycolysis are due to PFK, which is activated by its product FBP (71,72). Oscillations in the PFK reaction rate lead to oscillations in the glycolytic intermediates, including FBP, and ultimately to oscillations in mitochondrial ATP production. Fig. 12 B shows the effect of a simulated pulse of IP₃ on the PFK reaction rate, and the cytosolic Ca²⁺ and ATP concentrations. A 30 s pulse of IP₃ is used to simulate the bath application of carbachol, since carbachol leads to cytosolic IP₃ production. When IP₃ is applied in the model, the cytosolic Ca²⁺ concentration (Ca_c) immediately increases, due to release of Ca²⁺ from the ER. This Ca²⁺ must be pumped out of the cytosol, into the ER through Sarco-Endoplasmic Reticulum Ca²⁺ ATPases (SERCA pumps), or out of the cell through Ca²⁺ ATPases in the plasma membrane (PMCA pumps). Both types of pump hydrolyze ATP to perform the pumping, reducing the cytosolic ATP concentration. This is evident in Fig. 12 B, when Ca_c (black curve) rises during the IP₃ pulse whereas the cytosolic ATP concentration (ATP_c, green curve) declines. ATP is an inhibitor of PFK (73), so when ATP_c declines, the PFK will be disinhibited. This results in a spike in the PFK activity rate (red curve). In this way, the pulse of IP₃ due to a brief application of carbachol leads to a perturbation of the activity rate of PFK, and thus a perturbation in the time course of the glycolytic oscillator.

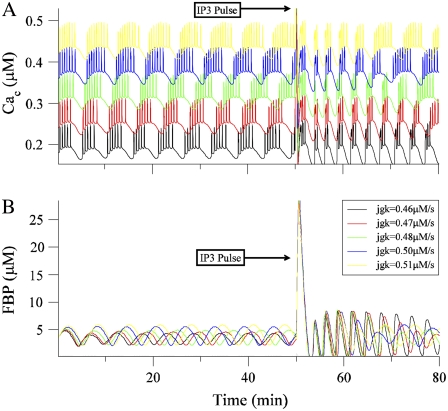
Fig. 13 A shows the time courses of Ca_c for five model islets, shown before and after an IP₃ pulse. The five traces are stacked to improve visibility. The model islets differ in a single parameter, J_GK, which is the glucokinase reaction rate. Because of differences in the value of this parameter, the islets have different oscillation periods. At the beginning of the simulation, all islets start from the same initial conditions, so they are initially synchronized. As time progresses, however, the islet oscillations drift apart due to their different periods. At 50 min after the start of the simulation, a 30 s IP₃ pulse is applied (IP₃ increased from 0 to 0.3 μM). This causes the expected spike in Ca_c in all islets. After the spike, the islets are synchronized, and remain synchronized for ∼20 min before beginning to drift apart. By the end of the simulation, the islets have mostly desynchronized.

FIGURE 13.

(A) Model simulation showing the Ca²⁺ time courses of five different islets, before and after a 30 s IP₃ pulse. Traces have been stacked to improve visibility. The islets differ from one another in the glucokinase reaction rate (the J_GK parameter). The model islets start with identical initial conditions, but drift apart since they have different intrinsic periods. The IP₃ pulse synchronizes them, although they have drifted apart again by the end of the simulation. (B) The FBP time courses of the five model islets are clearly out of phase before the IP₃ pulse. This pulse results in a spike of FBP, after which the FBP time courses are synchronized while the glycolytic oscillators are ringing (producing large amplitude FBP oscillations). As the oscillators return to their regular periodic motion, they desynchronize.

The mechanism for the IP₃-induced synchronization is more evident in Fig. 13 B, which shows the time course of the glycolytic variable FBP for each of the five islets. Although the model islets all start together, the FBP oscillations for the different islets quickly drift apart. As expected from Fig. 12 B, the IP₃ pulse causes a surge in FBP in all islets. The FBP surge resets the model oscillators to nearly the same phase, putting them all into an in-phase state. After this surge, the FBP concentrations for the model islets are largely synchronized with large amplitude. However, this is only transient behavior, as the FBP time courses for the different islets slowly drift apart, and the amplitudes for most islets decrease to much smaller values. That is, there is a transient “ringing” in the glycolytic oscillators after they are perturbed by the IP₃ pulse. This ringing reflects a transient phase of burst-independent glycolytic oscillations. During the ringing, the model islets oscillate with approximately the same frequency, since the frequency of bursting-independent glycolytic oscillations is relatively insensitive to parameter variations. Since the IP₃ pulse resets the oscillators to the in-phase state, and since they oscillate with the same frequency while the ringing persists, the FBP and Ca_c time courses are transiently synchronized among the model islet population. However, once the ringing ends and burst-independent glycolytic oscillations are replaced by burst-dependent glycolytic oscillations, the system returns to its regular periodic motion, and the FBP and Ca_c time courses for the different islets drift apart, just as they did at the beginning of the simulation.

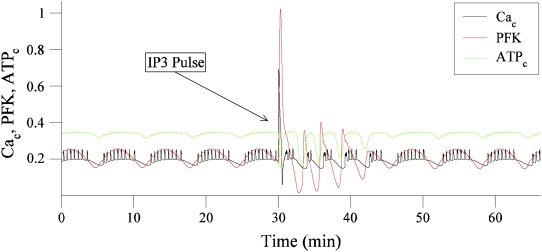
Another view of the ringing of the glycolytic oscillator is shown in Fig. 14. This shows Ca_c, ATP_c, and the PFK reaction rate before and after the IP₃ pulse. There is a clear spike in PFK during the pulse, followed by four large-amplitude ringing oscillations in PFK that persists for ∼10 min. This causes large downward spikes in the ATP concentration (when the PFK is at the bottom of an oscillation), which set the phase of the compound electrical and Ca²⁺ oscillations (a compound oscillation begins after each downward ATP spike). Although this figure shows only one of the five model islets, similar ringing occurs in each islet. In summary, the trigger for the synchronization is the IP₃-induced perturbation in the cytosolic Ca²⁺ concentration, which affects the glycolytic oscillator through ATP consumption, as illustrated in Fig. 12 B. The synchronization continues only during the transient ringing in the glycolytic oscillators (Figs. 13 B and 14).

FIGURE 14.

A 30 s IP₃ pulse induces a large spike in PFK activity, followed for 10 min by large-amplitude ringing, in a single model islet. This results in large downward spikes in the cytosolic ATP concentration, which sets the phase of the compound electrical and Ca²⁺ oscillations. While the PFK activity is ringing, the model islets are synchronized.

When the brief application of KCl is simulated by transiently increasing the K⁺ Nernst potential, the result is similar to an IP₃ pulse (simulation not shown). That is, the KCl causes an increase in Ca_c (this time due to depolarization and Ca²⁺ entry through L-type channels), which as before results in a lowering of the cytosolic ATP level due to extra ATP consumption, and a subsequent increase in the PFK reaction rate. Except for the membrane depolarization, the effect of a KCl pulse is similar to Fig. 13 B. Thus, as expected, a KCl pulse of sufficient size perturbs the PFK activity resulting in transient ringing, during which the model islets are synchronized. Smaller KCl pulses, which raise Ca²⁺ to a lesser extent, are less effective at synchronizing the model islets.

Simulated application of diazoxide works in a somewhat different way to synchronize the model islets (simulation not shown). This maneuver, simulated by setting the fraction of open K_ATP channels to 1, causes hyperpolarization of the model islet. This lowers Ca_c, causing ATP_c to increase, since its consumption by pumps is reduced. The end result is a transient reduction in PFK activity, which disturbs the glycolytic oscillator. Once the diazoxide is removed, the perturbation in PFK activity results in transient ringing, and while this continues the model islets are synchronized. In the simulations, the perturbation in PFK induced by hyperpolarizing the islets with diazoxide is not as great as the perturbation caused by increasing the Ca²⁺ concentration with an IP₃ pulse or KCl, so the ringing and accompanying islet synchronization do not last as long.

DISCUSSION

Individual islet oscillations can be synchronized by ACh

Individual β-cells within islets of Langerhans are synchronized through gap junctions (74–77), resulting in uniform electrical bursting, [Ca²⁺]_i oscillations and pulsatile insulin secretion (35,54,78,79). However, how these electrical and [Ca²⁺]_i signals are coordinated between islets in vivo to produce pulses of insulin in plasma is poorly understood.

It is known that parasympathetic and sympathetic nervous input to the pancreas play an important role in controlling insulin secretion and blood flow in islets (27,80,81), but the possible role of neurohormones in islet synchronization is unclear. Earlier studies conducted in vivo in canines and humans were done using either vagotomy or muscarinic receptor antagonist or agonists to alter cholinergic function. Although most of these early studies failed to convincingly demonstrate changes in pulsatility using these approaches (19,25), a shift in period was seen with vagotomy. Other studies have emphasized the importance of the nervous system for insulin secretion as the Na⁺ channel blocker TTX disrupted pulses of insulin in plasma when applied in vivo (19) and cholinergic agonists (82) and nicotinic antagonists (83) were effective as well. However, the interpretation of in vivo studies using pharmacologic approaches is complicated by actions of drugs on autonomic ganglia as well as β-cells and other targets (26). Of course, there may also be species differences in the mechanisms of synchronization of islet-to-islet oscillations within the pancreas (27).

To address the issue of islet-to-islet synchronization using a simplified in vitro approach, we used the [Ca²⁺]_i indicator fura-2 to monitor changes in islet [Ca²⁺]_i in groups of isolated islets exposed to various agents in real time. As shown in this article, carbachol was in fact capable of synchronizing islet [Ca²⁺]_i, whereas the adrenergic agonists NE and clonidine were not. In addition, this ability of carbachol depended on glucose concentration and presumably its metabolism.

Possible mechanisms involved in synchronization in vitro

It has long been known that ACh potentiates insulin release from islets by mobilizing Ca²⁺ from IP₃-sensitive stores (26), depolarizing β-cells by increasing their cationic conductance (51,84,85), and by increasing phospholipase C activation (86,87). Our results suggest that in addition, carbachol can have a synchronizing action on islets. The synchronizing effect of carbachol was mediated by muscarinic receptors because it was abolished by atropine, consistent with previous reports that the M₁ and M₃ subtypes of the muscarinic receptor are expressed on β-cells and are important functionally (26,45,88). Our finding that the action of carbachol to synchronize islets was glucose dependent could reflect the well-known glucose dependence of acetylcholine action on beta cells (50) and/or the fact that low glucose concentrations produced weaker Ca oscillations on their own. At present we have no data to separate these possibilities.

We also tested whether KCl or tolbutamide, which both depolarize β-cells and raise [Ca²⁺]_i, were similarly able to synchronize islets. We found that KCl was able to increase SI significantly (Fig. 10). Tolbutamide was generally unable to synchronize islets. We are unable to explain why KCl and tolbutamide differed in their ability to synchronize islets. On the other hand, hyperpolarization of the islets with diazoxide did enhance islet synchronization (Fig. 9).

How does a rise in cytosolic Ca²⁺ synchronize islets?

A striking feature of the experimental observations is that even transiently perturbing islet [Ca²⁺]_i is able to produce sustained synchronization of islet [Ca²⁺]_i oscillations, which we presume are fundamentally metabolic in origin. As a first step toward understanding how this might work, we used our Dual Oscillator Model ((33), Fig. 2) to carry out simulations of the experiments carried out here.

In the Dual Oscillator Model, the transient synchronization we observed experimentally was readily simulated by perturbing islet [Ca²⁺]_i to an extent that lowered ATP/ADP, resulting in the slow “ringing” of β-cell PFK activity, the source of the slow metabolic oscillations in this model. This ringing reflects a transient phase of burst-independent glycolytic oscillations, which are larger in amplitude than the burst-dependent oscillations. These oscillations are only modestly modulated by electrical bursting, unlike the burst-dependent glycolytic oscillations that require electrical bursting. The frequency of burst-independent oscillations is relatively insensitive to variations in parameter values that produce islet heterogeneity. Thus, during ringing, all model islets oscillate at almost the same frequency. The [Ca²⁺]_i perturbation also resets the model islets to an initial in-phase state. Therefore, while the ringing persists, the model islets remain in phase. Once the ringing stops, the model islets return to their original burst-dependent glycolytic oscillations and become desynchronized once again.

Interestingly, in the model simulations shown, the oscillations speed up during the ringing phase, immediately after the synchronizing phase. However, this was not observed in the experimental data. Although the reasons for this apparent discrepancy are not yet clear, using different parameter values, synchronization can be simulated using the model without this speeding up in period (data not shown). However, in these simulations, the islets desynchronize more quickly than in Fig. 13.

Physiological implications

These results suggest that acetylcholine release from intrapancreatic neurons within the pancreas may help synchronize islets in situ to mediate pulsatile pancreatic insulin secretion via a novel mechanism involving the dynamics of a metabolic oscillator intrinsic to islets. It is enticing to speculate that the release of ACh in the intact pancreas due to the activity of vagal neurons may provide sufficient stimulation of β-cell muscarine receptors to enable the synchronization of islet-to-islet oscillatory activity, even without ACh release itself being pulsatile. However, as discussed earlier, these results differ from those observed in vivo in humans (25) and in dog (19,82). Whether this reflects differences between the species under study, problems with the earlier studies, or the possibility that islet synchronization is a multiparameter redundant system remains to be established. Recent progress in carrying out glucose clamp studies and measurements of plasma insulin oscillations in mice suggests new in vivo studies might be feasible to directly address this (15,89).

An alternative to ACh as a synchronizing agent is ATP released from peptidergic, intrapancreatic neurons, as well as β-cells themselves. It has previously been reported that nitric oxide and ATP can synchronize isolated β-cells (40,41), which suggests that diffusible factors released by β-cells might synchronize islets. We note that others have failed to find this effect, however (90).

Nonetheless, a study by Salehi et al. (91) showed that pulsatility in the perfused rat pancreas was eliminated by the blockade of P2Y receptors using 2-deoxy-N-methyladenosine-3,5-bisphate (MRS 2179). Since MRS 2179 did not abolish oscillations in rat β-cell aggregates, in which gap junctional coupling presumably was able to maintain synchronization, it was concluded that the effect of purinergic blockade was specific to disrupt synchrony rather than the pulsatility of β-cells per se. However, as the drug showed an effect to depolarize both single β-cells and aggregates and the mean insulin release increased, it is difficult to rule out a primary effect to inhibit the pulsatility of the islets in the intact pancreas by depolarization beyond the oscillatory range. Nonetheless, this is an attractive alternative hypothesis to explore. Use of the in vitro preparation described here may be of value in separating effects on synchrony from effects on intrinsic pulsatility of islets. In limited experiments we did not observe effects of ATP to synchronize islets in vitro (L. Satin and M. Zhang, unpublished data), but further work in this direction is needed to reach a clear conclusion.

Defects in the coordinating mechanism could contribute to the disrupted insulin secretion characteristic of Type 2 diabetic patients. It is also intriguing to speculate that the synchronization of islet oscillations by diazoxide may contribute to the recently reported actions of diazoxide administration to increase glucose-induced insulin secretion in diabetics by mediating a period of “β-cell rest” (92). We were able to show that the synchronizing actions of diazoxide were also simulated by the model because even a drastic lowering of islet [Ca²⁺]_i resulted in the slow ringing of PFK activity after its pronounced drop via increased ATP/ADP.

In summary, we have demonstrated that cholinergic stimulation can synchronize a small group of mouse islets in vitro. In contrast, sympathetic agonists such as NE or the α₂-adrenoceptor agonist clonidine lacked this ability. The effects of carbachol may involve ER Ca²⁺ release as well as Ca²⁺ influx. The results could be accounted for by a mathematical model where the slow dynamics of mouse islets and the regulation of the oscillatory processes by Ca²⁺ led to slow damped oscillations during which islet Ca²⁺ cycles were in phase. We thus suggest that neurohormones released within the pancreas may in turn help synchronize islets by periodically pacing distant islets by detuning the slow oscillatory processes that are intrinsic to each islet. Specifically, parasympathetic nerve input to the pancreas, by periodically releasing ACh onto β-cells, might contribute to islet-to-islet communication and therefore help maintain the coordinated activity of the system. If this was the case, it would be interesting to test whether insulin pulsatility is modified in islets from M₃-receptor knockout mice, or after vagotomy.