Membrane Deformation under Local pH Gradient: Mimicking Mitochondrial Cristae Dynamics

Abstract

Mitochondria are cell substructures (organelles) critical for cell life, because biological fuel production, the ATP synthesis by oxidative phosphorylation, occurs in them driven by acidity (pH) gradients. Mitochondria play a key role as well in the cell death and in various fatigue and exercise intolerance syndromes. It is clear now that mitochondria present an astonishing variety of inner membrane morphologies, dynamically correlated with their functional state, coupled with the rate of the ATP synthesis, and characteristic for normal as well as for pathological cases. Our work offers some original insights into the factors that determine the dynamical tubular structures of the inner membrane cristae. We show the possibility to induce, by localized proton flow, a macroscopic cristae-like shape remodeling of an only-lipid membrane. We designed a minimal membrane system (GUV) and experimentally showed that the directional modulation of local pH gradient at membrane level of cardiolipin-containing vesicles induces dynamic cristae-like membrane invaginations. We propose a mechanism and theoretical model to explain the observed tubular membrane morphology and suggest the underlying role of cardiolipin. Our results support the hypothesis of localized bioenergetic transduction and contribute to showing the inherent capacity of cristae morphology to become self-maintaining and to optimize the ATP synthesis.

INTRODUCTION

Mitochondria are cellular organelles having a key role in life because biological fuel production, the ATP synthesis by oxidative phosphorylation, occurs in the mitochondrion (1). Mitochondria have a key role as well in cell death—they were recently recognized as central regulators of the apoptotic program (the programmed cell death) of eukaryotes (2,3). Mitochondria-related diseases as mitochondrial myopathy (4) and various fatigue and exercise intolerance syndromes still need cures. Mitochondria are usually tubular, 1–2 μm long and 0.1–0.5 μm large. A mitochondrion is made of two membranes, the OM and the IM, separated by the intermembrane space. The IM surrounds protein-rich medium called mitochondrial matrix. The IM is made of proteins and lipids 80/20 w/w (5). The lipid composition of IM represents a remarkably conservative feature: large amounts (10–20 mol % of the total lipid) of specific lipid, diphosphatidylglycerol, also known as CL that is not found in other cellular membranes; PC ∼40 mol %; PE ∼30 mol %; PI ∼5 mol %; PS ∼3 mol %; and sterol <0.5 mol % (6). It was shown that CL plays a critical role in mitochondrial function and diseases including ischemia, hypothyroidism, aging, and heart failure (7). The OM contains particular proteins (porins) that make it freely permeable to ions and other molecules smaller than 10 kDa, whereas the IM is impermeable even to protons (8). The area of the IM is much larger than the one of the OM. This implies the presence of an important number of IM inward invaginations termed cristae (9,10). The real 3D structure of mitochondrion became accessible only over the course of the last 10 years due to the techniques of the high resolution scanning electron microscopy (11) and that of electron microscopy tomography (12,13) (for review, see Mannella (14) and the articles therein). They allow for ∼3-nm resolution when looking at an object the size of a mitochondrion and clearly show that the cristae have a predominantly tubular nature (Figs. 1 and 2). For example, the tubular parts of cristae in human liver mitochondria are 30–40 nm in diameter and up to several hundred nanometers long (11).

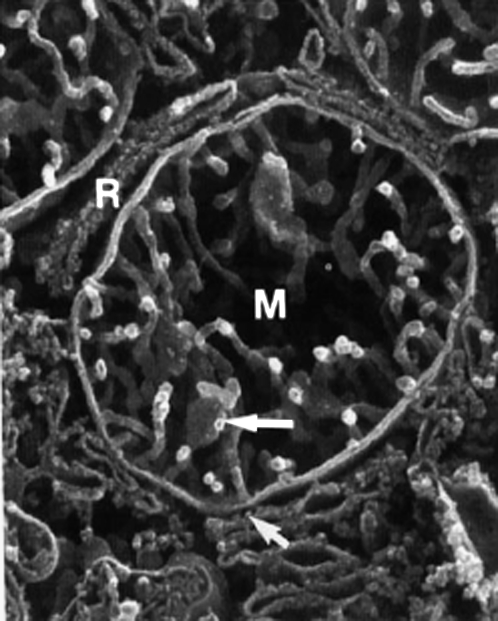
FIGURE 1.

High resolution scanning electron microscopy micrograph of human liver mitochondrion (M), in close proximity to rough endoplasmic reticulum (R). The cristae are tubular, several hundred nanometers long and ∼30 nm in diameter, × 40,500. Reprinted from Lea et al. (11) with permission of Wiley-Liss. In living cells, mitochondria are usually tubular (1–2 μm long and 0.1–0.5 μm large) and interact with other cellular components, especially with the cytoskeleton and endoplasmic reticulum (59,60).

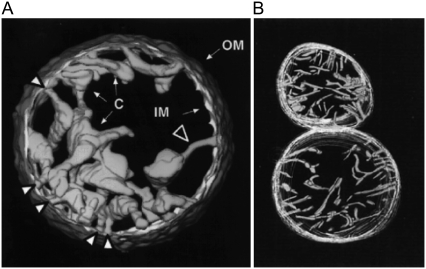
FIGURE 2.

Electron microscopy tomography images of mitochondria. Normally functioning mitochondria are going from (A) condensed to (B) orthodox state morphology, back and forth, depending on their respiratory rate. Mitochondria carrying out maximum respiratory rate (in excess ADP and respiratory substrate) present condensed (matrix contracted) morphology (A). Their cristae are swollen cisterns or sacs connected to the peripheral part to the IM by narrow tubular segments (cristae junctions) (A, large white arrow). The cristae in orthodox (matrix expanded) morphology are narrow, flattened, or almost tubular (b). OM diameter: (A) 1.5 μm; (B) lower, 1.2 μm. (A) Reprinted from Mannella et al. (13), with permission of IOS Press. (B) Reprinted from Mannella et al. (12) with permission of Wiley-Liss.

Respiratory chain proteins (proteins involved in oxidative phosphorylation) reside within the mitochondrial IM, mostly within the cristae compartments (15–19), and comprise the electron transport chain proteins, and the ATP synthase complex. During cellular respiration, electron transport chain proteins pump protons from the matrix into the intermembrane space, generating a proton concentration difference (ΔpH) across the IM. The proton concentration difference allows the ATP synthase complex to synthesize the ATP (20). The bulk mean pH, measured by pH dependent fluorescence (21), proved to be ∼8 in the matrix, whereas in the intermembrane space it was estimated to be ∼7.4 (as the pH in the cytosol) because of rapid diffusion of protons through the numerous pores in the OM. On the other hand, it was suggested that the local pH in the intracristal compartments might be much lower then 7.4 (the bulk pH of the intermembrane space). This hypothesis (the local pH gradient hypothesis) is based on at least three reasons for the existence of local proton concentration gradients within the intracristal compartments: i), the restricted diffusion of protons between the intracristal and peripheral spaces (22–25) along the cristae nanotubular structures; ii), the presence of the negatively charged membrane, and, iii), the CL capacity as a “proton trap” (26,27). In particular, the mini review of Haines and Dencher (27) supports the idea that “the CL may aggregate the oxidative phosphorylation proteins into a patch while it restricts pumped protons within its headgroup domain—supplying protons to the ATP synthase with minimal changes in the bulk phase pH”. It was shown (28) that the mitochondrial membrane potential is decreased in mutant cells having no CL in mitochondrial membranes as, for example, the Saccharomyces cerevisiae cells (containing a disruption of the structural gene encoding CL synthase). Jiang et al. (28) proposed “that CL is required for maintaining the mitochondrial membrane potential and that reduced membrane potential in the absence of CL leads to defects in protein import and other mitochondrial functions.” In any case, one should keep in mind that the direct measurement of local proton concentrations at the nanometric scale of mitochondrial cristae still encounters substantial difficulties.

We believe it is now obvious that mitochondria present an astonishing variety of IM morphologies (IM pleomorphism). Moreover, the shape of the inner membrane of a mitochondrion is dynamic, changing in correlation with its functional state (3,4) and characteristic for normal (Figs. 1 and 2) as well as for pathological cases. Normally functioning mitochondria are going from condensed (matrix contracted) to orthodox (matrix expanded) state morphology, back and forth, depending on their respiratory rate (Fig. 2). Mitochondria carrying out maximum respiratory rate (in excess ADP and respiratory substrate) present condensed morphology (Fig. 2 A). Their cristae are swollen cisterns or sacs connected to the peripheral part to the IM by narrow tubular segments (cristae junctions) (Fig. 2 A, large white arrow). The narrow cristae junctions might have a special function—restricting the diffusion between intracristal compartments and intermembrane space (25). The reduction in respiration due to the ADP depletion makes the mitochondria to reverse to the orthodox morphology. The cristae in that state being narrow, flattened or almost tubular (Fig. 2 B). On the other hand, the pathological functions of mitochondria are correlated with particular morphologies, for example, the mitochondrial myopathy is coupled with highly abnormal vesicular cristae (4). The anaerobic pathogen Cryptosporidium parvum, having a single (relict) mitochondrion and a deficient respiratory chain, presents one of the very few cases of highly folded inner membrane that lacks the typical cristae-like morphology (29).

Looking at 3D images of mitochondria, one is logically led to the question how mitochondria function factors determine IM morphology and, conversely, how the IM morphology can influence mitochondrial functions (14,20,30)? What are the factors that determine IM morphology? The common view has focused on the role of proteins, in particular on those inducing membrane curvature by their conic-like shape as the ATP synthase dimers (16). The role of tBID protein (31,32), mitofilin multimeric complexes (33), and that of the generated reactive oxygen species as functional factors for the IM morphology has been widely recognized as well (2,3). It remains unclear, however, if the inner membrane morphology and dynamics are governed by specific mitochondrial proteins only, or, if lipid mediated processes take place as well. In fact, quite limited attention was paid so far to the purely physical, membrane mechanics aspects. Even if it was the case, the consideration was limited to the evident one: IM has much larger area then the OM and therefore it is under simple mechanical (space) constraint that causes it to fold. But simple folds do not account for the typical cristae-like functioning morphology. On the other hand, several studies (e.g., Ponnuswamy et al. (34)) suggested some thermodynamic considerations of cristae morphology, but these studies remain partial and far from any dynamics perspective.

Our approach consists in looking for a minimal physicochemical system that model the dynamic morphology of mitochondrial IM. It involves GUV as model membrane system (35–38) and micropipette manipulations (39–42) for local pH modulation. In this study, we show experimentally that proton flow localized at membrane level of CL containing vesicles induces cristae-like membrane invaginations, and that the morphology of these invaginations is dynamic: one can make the induced invaginations progress or regress by modulating the local pH. We propose a mechanism and theoretical model to explain the observed tubular, cristae-like, membrane invaginations of GUV. We relate our model membrane studies to the dynamics of mitochondrial inner membrane morphology and also suggest the underlying role of mitochondrial lipids, especially that of the cardiolipin. Finally, our results support the hypothesis of localized bioenergetic transduction as far as it permits to explain how the IM morphology becomes self-maintaining while optimizing the synthesis of biological energy.

MATERIALS AND METHODS

Chemicals

Lipids were obtained and used without further purification as follows: egg yolk L-α-phosphatidylcholine (PC), Sigma-Aldrich, Lyon, Rhône, France; egg L-α-phosphatidylethanolamine (PE), heart bovine 1,3-bis(sn-3-phosphatidyl)-sn-glycerol diphosphatidylglycerol (CL), brain porcine L-α-phosphatidylserine (PS), Avanti Polar Lipids, Alabaster, AL; HEPES, Interchim, Montluçon, Allier, France; EDTA, Sigma.

GUV

GUV were formed by the liposome electroformation method (35–37) in a thermostated chamber. The particular electroformation protocol established in this work was as follows: single lipids as well as lipid mixture solutions were prepared in chloroform/diethyl ether/methanol (2:7:1) at 1 mg/ml of total lipid. A droplet of lipid solution (1 μl) was deposited (avoiding sliding) on each of the two parallel platinum wires (diameter, 0.8 mm; distance between axes, 3 mm) and dried under vacuum for 15 min. An AC electrical field, 10 Hz, 0.26 V pp, was applied to the electrodes. Buffer solution (2 ml, pH 8, HEPES 0.5 mM, EDTA 0.5 mM, temperature ∼25°C) was added (avoiding agitation) to the working chamber. The voltage was gradually increased (>2 h) up to 1 V pp and kept for 15 more min before switching the AC field off. The GUV were ready for further use. In each preparation at least 10 GUV of diameter 50–80 μm were available.

Imaging GUV

We use a Zeiss Axiovert 200M microscope, equipped with a charge-coupled device camera (Cool SNAP HQ). The experiments were computer controlled using the Metamorph software (Molecular Devices, Downington, PA). The morphological transformation and dynamics of the membrane were followed by phase contrast microscopy.

Microinjection

We made our micropipettes with internal diameter 0.3 μm, by pulling borosilicate glass capillaries using Narichige pipette puller PC-10. We used an Eppendorf FemtoJet for the local microinjection. The injection pressure was 15–25 hPa, and the initial distance from the GUV membrane was ∼10 μm. The hydrodynamics of the solution injected by the micropipette could be visualized and thereby we could estimate that the part of the GUV membrane directly affected by the microinjection was ∼10%. Visualizing the flux from the micropipette allows estimating as well the dilution of acid solution after injection. We calibrated the pH in function of the dilution of 100 mM HCl pH 1.6 in the buffer in which the GUV were formed (HEPES 0.5 mM, EDTA 0.5 mM, pH 8). That allowed us to estimate the local pH value effectively created at the GUV membrane during the HCl delivery to be about pH 4–5. In fact, we aimed modulating locally the proton concentration to be phemenologically coherent with the local pH gradient hypothesis, as stated in the Introduction.

LUV

LUV were prepared using the extrusion method (43). Samples were prepared by dissolving and mixing the indicated lipids in chloroform/methanol (9.4:0.6) to obtain the desired compositions. Thereafter the solvent was removed under a stream of oxygen-free dry nitrogen (30 min). The residues were subsequently maintained under vacuum for 2 h and then HEPES buffer, pH 8 or 4 respectively (HEPES 5 mM, EDTA 0.1 mM, 1 mM NaCl) was added at room temperature (23°C) to yield a lipid concentration of 1 mM. The samples were heated at 30°C for 30 min, vortexed for 2 min and left in a sonication bath for 30 min, vortexed again for 1 min to ensure more uniform vesicle dispersion, and incubated again at 30°C for 15 min. The multilamellar vesicles were then extruded with a LiposoFast small-volume extruder equipped with polycarbonate filters (Avestin, Ottawa, Canada) as follows: 10 extrusions through 800 nm, and after that 21 extrusions through 100 nm filters. LUV average size for PC/CL 90:10 mol/mol was 108 nm at pH 8 and 122 nm at pH 4. The size was decreased with increasing CL concentration. LUV samples were kept at 4°C, and used for measurements the day after.

Thin layer chromatography

The possible chemical degradation of lipids due to the acid was checked as follows: LUV made of PC or PC/CL 90:10 mol/mol in HEPES buffer at pH 8 were incubated in HCl solution (final concentration 1 mM in total lipid and 100 mM in HCl, pH 1.4, 25°C) during 1 h, and then checked for degradation products by thin layer chromatography (TLC). The organic compounds were visualized by exposing the TLC plates to iodine vapor during 20 min to 3 h. No chemical degradation was observed.

LUV size and ζ-potential

The size were obtained by dynamic light scattering, and the ζ-potential was obtained by electrophoretic mobility (applying the Henry equation and Smoluchowski model) from LUV suspensions (0.2 mM total lipid) using Nano-ZS (Red badge) ZEN 3600 (Malvern Instruments, Malvern, UK).

Mean area per lipid molecule

Surface pressure versus molecular area (π − A) isotherms were recorded on a Langmuir mini trough (Riegler and Kirstein, Potsdam, Germany) equipped with two movable barriers. The surface pressure was measured by using the Wilhelmy plate method. The trough was enclosed in a thermostated box. The temperature was regulated to 25 ± 0.5°C. Lipid solution (25 μl, chloroform/methanol 95:5) was spread on the buffer surface (pH 8 or 4 respectively, HEPES 0.5 mM, EDTA 0.1 mM) using a Hamilton syringe. After a minimum of 10 min for solvent evaporation, lipids at air-water interface were compressed at constant rate of 2.4 cm² × min⁻¹ corresponding to ∼3.25 Ų × molecule⁻¹ × min⁻¹. Compression rates of <4 Ų × molecule⁻¹ × min⁻¹ are considered as suitable for thermodynamic analysis (44). The errors in π and A were estimated as ±1 mN m⁻¹ and ±1 Ų, respectively.

RESULTS

Design of a minimal model membrane system exhibiting dynamic cristae-like morphologies

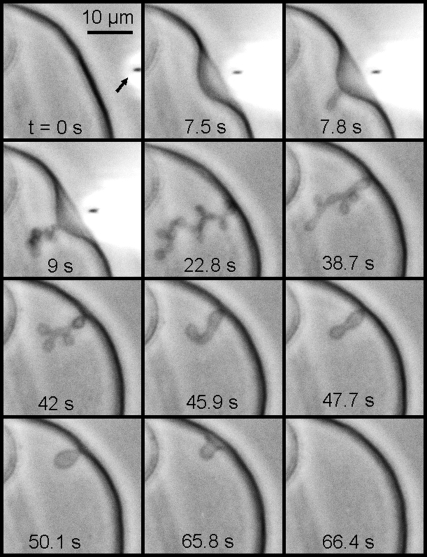
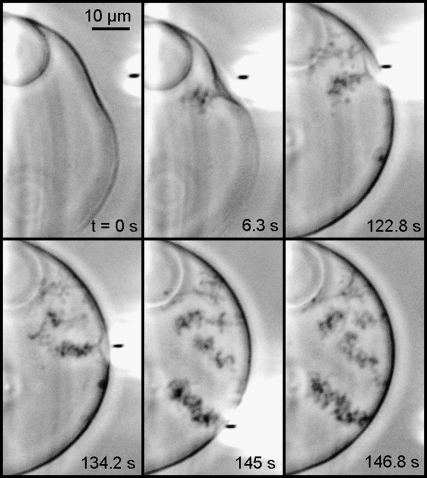
The main lipids of mitochondrial IM (presenting >90 mol % of the total lipid) are the CL, the PC, and the PE. In addition, it was Kagawa et al. (45) showed that PC and PE were both required for the reconstitution of vesicles with high ³²P_i-ATP exchange activity, and the activity was markedly accelerated by low amounts of CL. Therefore we made our GUV from PC/PE/CL 60:30:10 mol/mol (unless otherwise stated) in buffer at pH 8 (similar to the bulk pH in the matrix). pH was locally modulated in real time, (lowered and then let to rise to the initial bulk value) by a micropipette delivering (or not) an acid solution at the outer side of the GUV membrane. The microinjection parameters were the same for the vesicles shown in Figs. 3–6 and the corresponding Supplementary Material (Movie S1, Movie S2, Movie S3, Movie S4, and Movie S5). One can see in Fig. 3 (frame 0 s) the micropipette (inner diameter, 0.3 μm; injection pressure, 15–25 hPa) delivering 100 mM HCl solution from a distance ∼10 μm from the GUV. It is possible to follow directly the induced membrane invagination (Fig. 3, frame 7.5 s) and the development of characteristic morphology (Fig. 3, frames 7.8 s–22.8 s). We identified this morphology as “cristae-like” as it mimics very well the mitochondrial IM morphology shown by 3D electron microscopy (see Figs. 1 and 2). This cristae-like morphology is dynamic, reversible, and modulated by local pH. As soon as the acid delivery is off, the cristae-like membrane invagination regresses and completely disappears when the local pH gradient vanishes (Fig. 3, frames 38.7 s–66.4 s, and Fig. 4). We could make our GUV produce several (e.g., four) crista-like deformations coexisting dynamically within the same GUV as shown in Fig. 5. Invaginations shapes, their typical sizes, and characteristic times of regress are dependent on the GUV initial states: either deflated or quasi-spherical. Deflated GUV yield cristae-like morphology with large tubes and vesicular shape segments (Figs. 3, 4, and 6 A), disappearing within a few tens of seconds after the acid delivery is off. Conversely, the quasi-spherical ones yield morphology with thin and long tubes quite often winding themselves, and being present a long time (up to several tens of minutes) after the acid delivery is off (typical examples are shown in Fig. 5). The much longer “lifetime” of the long thin tubular structures might be a sign of restricted proton backward diffusion along the tube. In consequence, the equilibration of local pH with that of the bulk might be slowed down due to space factors. We found experimentally that the possibility of triggering the pH-induced membrane invagination and the development of cristae-like morphology occurs only by creating a sufficient pH gradient. For example, injecting 10 mM HCl solution instead of 100 mM (other microinjection parameters being the same) did not trigger the cristae-like deformation. On the other hand, abrupt local delivery of large amounts of acid (e.g., injecting 6 M HCl solution instead of 100 mM) led to GUV destruction.

FIGURE 3.

Modulation of local pH gradient at membrane level of a cardiolipin containing vesicle induces dynamic cristae-like membrane invaginations. GUV is made of PC/PE/CL 60:30:10 mol/mol in buffer at pH 8. The local delivery of HCl (100 mM pH 1.6), which lowers the local pH, is carried out by a micropipette (its position is pointed by the arrow in frame t = 0 s).The induced membrane invagination (frame 22.8 s) is completely reversible (frames 38.7–66.4) as far as the acid delivery is stopped. Deflated GUV yield cristae-like morphology with large tubes and vesicular shape segments. (See Movie S1.)

FIGURE 4.

As soon as the acid delivery is off, the cristae-like membrane invagination regresses and completely disappears when the local pH gradient vanishes. The GUV is made of PC/PE/CL 60:30:10 mol/mol in buffer at pH 8. The HCl delivery conditions are as in Fig. 3. (See Movie S2.)

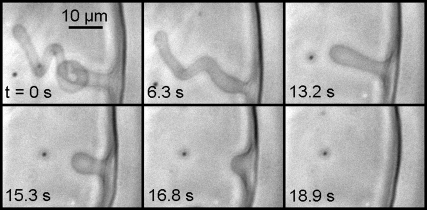
FIGURE 5.

We could make our GUV produce several (e.g., four) crista-like deformations coexisting dynamically within the same GUV. The GUV is made of PC/PE/CL 60:30:10 mol/mol in buffer at pH 8. The HCl delivery conditions are as in Fig. 3. The quasi-spherical GUV yield morphology with thin and long tubes quite often winding themselves, and being present a long time (up to several tens of minutes) after the acid delivery is off. (See Movie S3.)

FIGURE 6.

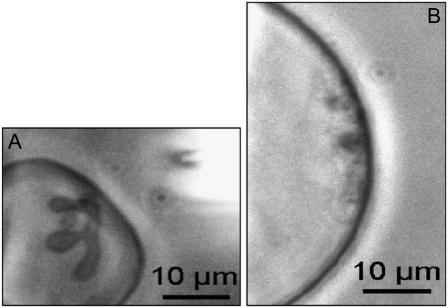
CL plays a crucial role in the development of the specific cristae-like tubular morphology in our GUV model membranes. (A) A very deflated GUV made of PC/CL 90:10 mol/mol in buffer at pH 8. The local microinjection of HCl induced cristae-like morphology similar to that observed with the two deflated GUV, made of PC /PE/CL 60:30:10 mol/mol, presented in Figs. 3 and 4. (B) A quasi-spherical GUV made of PC/PS 90:10 mol/mol, no cristae-like morphology, no tubular invagination protruding into the GUV internal space, were developed on the local microinjection of HCl. In addition, no vesicle shape changes were observed when HCl was locally microinjected to GUV made only of PC or PC/PE 66:34 mol/mol. (See Movie S4 and Movie S5.)

Control experiments

We microinjected buffer solution only to check for any eventual hydrodynamic effects, as well as a salt solution (100 mM NaCl) to verify if the observed effects were not simply due to charge screening and/or osmotic effects (all other conditions being similar). The characteristic cristae-like invaginations and morphology were not observed. Injecting another acid, the weak acetic acid (100 mM), induced cristae-like structures similar to those described in the case of HCl. Finally, we checked the importance of creating a local pH gradient: in a control experiment we slowly decreased globally the pH of the buffer (from pH 8 to pH 4) in the whole chamber containing GUV. We observed obvious dumping of membrane thermal fluctuations and transition to spherical shape of some initially flat vesicles (due probably to an increased membrane tension). Some GUV ruptured and transformed in multilamellar ones. No cristae-like tubular structures were observed inside the GUV.

The role of CL in the development of cristae-like morphology

We carried out experiments with GUV containing only PC and CL (PC/CL 90:10 mol/mol %), i.e., without PE (Fig. 6 A). The effects of local pH modulations were similar to those observed with GUV made of PC/PE/CL 60:30:10 mol/mol. We tested the effect of HCl microinjection on GUV that do not contain CL (made only of PC, or PC/PE 66:34 mol/mol). No morphology transformation was observed in these cases. But was the pH effect, observed with CL containing GUV, only due to the presence of a negatively charged lipid component? To answer this question we carried out similar experiments with GUV made of PC/PS 90:10 mol/mol and PC/PI 90:10 mol/mol (having in mind the presence of PS and PI in the mitochondrial IM). The morphology induced by the local microinjection of acid in these cases was very different (Fig. 6 B). Multiple membrane invaginations were triggered from different points of the zone exposed to the acid delivery and led to formation on the internal side of the GUV membrane of a large number of small, spherical structures at the limit of optical resolution. No cristae-like morphology and no tubular invagination protruding into the GUV internal space were developed. All these results indicate that CL plays a crucial role in the development of the specific cristae-like tubular morphology in our GUV model membranes.

pH effects on CL-containing model lipid membranes

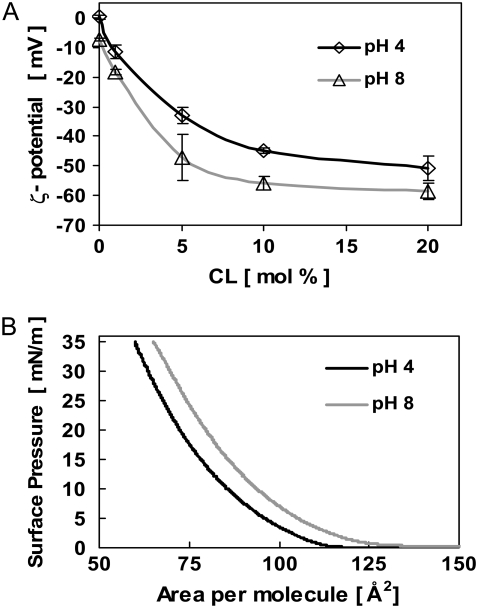
The hydrodynamics of the solution injected by the micropipette could be visualized. This allowed us to estimate that the part of GUV membrane directly affected by the microinjection was ∼10%. The local pH value effectively created at the GUV membrane was roughly estimated to be about pH 4–5. The possibility of chemical degradation of lipids due to the effect of the acid was checked using LUV and TLC. No chemical degradation was observed. We studied the effect of pH on the ζ-potential of LUV made of PC/CL for different CL concentrations (0, 1, 5, 10, and 20 mol % of CL) as well as on the mean area per lipid molecule (A) in monolayers spread at the air-water interface, using PC/CL 90:10 mol/mol mixtures. We made measurements for pH 8 and pH 4, as far as that corresponds to a possible (maximum) pH change induced at the GUV membrane. The corresponding ζ-potentials for LUV (PC/CL 90:10 mol/mol) change from −56 mV to −45 mV (∼20% change) (Fig. 7 A). The mean area per molecule (A) in monolayers made of PC/CL 90:10 mol/mol decreases (at surface pressure 30 mN/m), from 70 Ų at pH 8 to 64 Ų at pH 4 (∼8.6% decrease) (Fig. 7 B). These changes should be due to the pH effect mostly on the CL as far as no significant difference was observed in the case of only PC monolayers for similar pH intervals (46). We conclude that due to the presence of CL, the pH affects: i), the actual charge of the lipids, and ii), the mean area per molecule. Note that both effects are probably linked, the lipids interacting electrostatically.

FIGURE 7.

Effect of pH on CL containing vesicles. (A) ζ-potential of LUV made of PC/CL as a function of CL concentration at pH 8 and pH 4, respectively. The corresponding ζ-potential change for PC/CL 90:10 is ∼20% (from −56 mV at pH 8 to −45 mV at pH 4). LUV average size was 108 and 122 nm at pH 8 and pH 4, respectively. (B) Mean area per lipid molecule (A) of LUV made of PC/CL 90:10 mol/mol at pH 8 and pH 4, respectively. A decrease of A of ∼8.6% (from 70 Ų at pH 8 to 64 Ų at pH 4) is observed at surface pressure 30 mN/m. The errors in π and A were estimated as ±1 mN m⁻¹ and ±1 Ų, respectively.

A mechanism and a model to explain the observed tubular GUV membrane invaginations

Our experiments suggest that delivering protons onto CL-containing membrane leads to a partial charge neutralization and area reduction of the exposed monolayer. The induced area mismatch between the inner and outer monolayers of the membrane will create a mechanical stress and induce some deformation. In the following, we show theoretically that the tubular, cristae-like, invaginations satisfy the various area, volume, and energy requirements, and that their predicted length and width agree well with the experiments reported in the Results section.

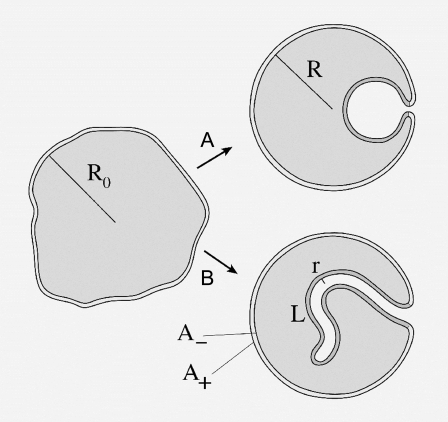
The GUV used in our experiments are schematically presented in Fig. 8. Their typical radius is R₀ and they are more or less deflated. Calling A the midplane area of the vesicle and V its volume, R₀ can be defined through the relation A = 4π 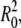and the reduced volume v (0 < v < 1) is then defined through V = (4/3)π 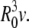In our experiments, v ≈ 0.75 corresponds to a much deflated vesicle and v ≈ 0.95 to a quasi-spherical one. The reduced volume v of a GUV could be roughly evaluated by comparing the observed vesicle shape with the shape phase diagrams obtained by the generalized bilayer-couple model in Heinrich et al. (47) and by the area difference elasticity model (48).

FIGURE 8.

Sketch of deflated vesicle undergoing (A) a spherical invagination or (B) a tubular invagination.

Initially, the relative area difference δA/A ≈ 8π R₀d/A between the outer and inner monolayers is positive and of order ≈0.03% (with bilayer thickness d ≈ 5 nm, R₀ ≈ 30 μm, and taking into account the fact that 2d/R₀ « 1). From our experiments, we assume that the acid delivery may yield a reduction of the outer monolayer area as large as a few 0.1% (indeed, starting from the raw value ≈8.6% at pH 4 (Fig. 7 B), we multiply by 0.1 to take into account that only ∼10% of the vesicle area is concerned and we further reduce this estimation by a factor ∼5 to account for bulk dilution and pH nonlinearity effects). It follows that due to the acid injection, δA/A may change sign, going from ≈0.03% to ≈−0.1%. The ratio λ between the new value and the old value of δA/A thus varies typically in the interval −3 ≤ λ ≤ 1 (λ =1 corresponds to the initial or the final (relaxed) state; the lower λ, the stronger acid effect).

Let us assume, as experimentally observed, that the invagination has a tubular shape with length L and radius r (roughly spherical invaginations may be taken into account by assuming L ≈ r). Neglecting the curvature of the vesicle at the tube foot (r « R₀) and the area of the tube end-cap (r « L), one may write the monolayer areas in the final state as

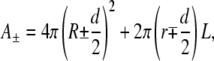(1)

where A₊ and A₋ denote the area of the outer and inner monolayers, respectively, and R denotes the average radius of the vesicle in the final state. Because on the timescale of our experiment one may neglect any lipid exchange between the two monolayers and any volume variation of the vesicle, we require that A₊, A₋, and V each remain equal to their initial value. This yields for the unknown r, L, and R the following system:

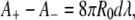(2)

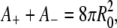(3)

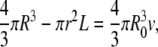(4)

The solution consistent with the approximations made above is:

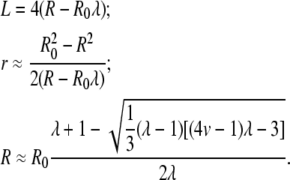(5)

For instance, for a GUV with R₀ ≈ 30 μm and v = 0.75 (relevant to the deflated vesicles in our experiments), our model yields for λ = −1 a long thread-like tube of radius r ≈ 1.3 μm and length L ≈ 230 μm.

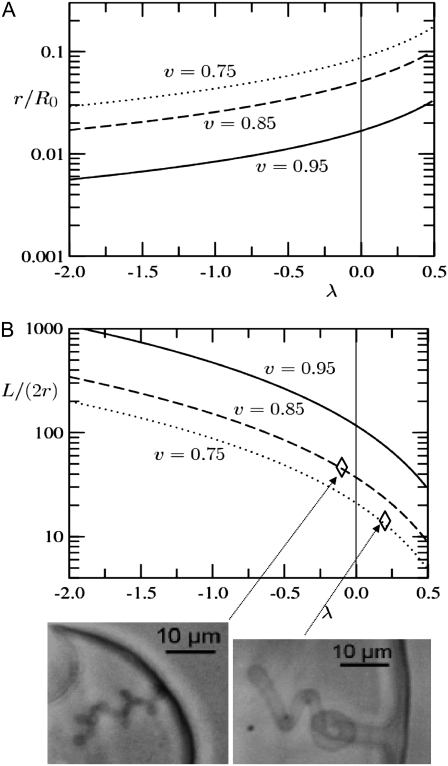
Fig. 9, A and B, present the geometrical features of the tubular invagination calculated from our model (see Eq. 5) as a function of the area reduction factor λ that is controlled by the acid delivery. Note that λ = 1 corresponds to the initial state (and also to the late, completely relaxed state). The lower λ, the stronger acid effect. The radius of the tube normalized by the radius of the initial vesicle (r/R₀) is plotted in Fig. 9 A. The aspect ratio of the tube (the ratio between the tube length and the tube diameter, L/(2r) is plotted in Fig. 9 B. As shown in Fig. 9, A and B, we obtain, in agreement with the experimental results, long and thin tubes (aspect ratio of the tube L/(2r) ≥ 100) for λ < −1 (strong effect of the acid) and large and short tubes (aspect ratio of the tube L/(2r) ∼5–50) for λ > 0 (weak effect of the acid); we find also that the tenser the vesicle (v closer to unity) the thinner and longer the tubes. The experimental measurement of L/(2r) being restricted by the optical resolution and by the 2D projection, we made only two rough quantitative estimations corresponding to the experimental situations shown in Fig. 9 B.

FIGURE 9.

Geometrical features of the tubular invagination calculated from our model (Eq. 5) as a function of the area reduction factor λ that is controlled by the acid delivery (λ = 1 corresponds to the initial or the final (relaxed) state; the lower λ, the stronger acid effect). (A) Radius of the tube normalized by the radius of the initial vesicle. (B) Aspect ratio of the tube. Both are given for three experimentally relevant values of the reduced volume v of the initial vesicle. Two experimental illustrations are given for v = 0.85 and 0.75 and L/(2r) ratios ∼40 and 14, respectively: thin and long tube at decreasing local concentration of acid (i.e., weak effect of the acid, λ ≈ −0.1), and, large and short tube at vanishing affect of the acid (λ ≈ 0.2).

Let us now envisage the case of mitochondria. For a vesicle of initial size R₀ ≈ 1 μm, relevant to typical mitochondria sizes, our approximations (e.g., 2d/R₀ « 1) still hold. With λ = −1 and v = 0.75 we get r ≈ 40 nm and L ≈ 7 μm. This agrees well with the IM cristae of mitochondria in the orthodox conformation, which are several hundred of nanometers long and 20–40 nm in diameter (11,12).

Our model shows that when an invagination forms a single structure, it must generically be tubular. The case of a spherical invagination might appear in the case of a much deflated vesicle subject to a very weak effect of acid (λ > 0.5, v < 0.75). Note that a large number of n disconnected spherical structures could also satisfy the constraints: similar calculations as above yields for r a similar result and gives n ≈ L/r. Our model does not explain why isolated long tubes are more favored than numerous small spherical invaginations. However, two explanations might be relevant: i), dynamically, once an invagination starts, the quicker pathway is probably to let it elongate; and ii), energetically, lipids with elongated polar heads (such as CL that have a very peculiar double phosphate elongated polar head to which are attached four aliphatic chains) were predicted to have a susceptibility toward an in-plane orientational ordering of the polar heads that stabilizes cylindrically curved structures (49).

Let us finally check the consistency of the invagination process by estimating the orders of magnitude of the energies involved. We considered above the case R₀ ≈ 30 μm, λ = −1 and v = 0.75 (relevant to the deflated vesicles in our experiments). Our model yielded then a long thread-like tube of radius r ≈ 1.3 μm and length L ≈ 230 μm. The area reduction of the outer monolayer is α ≈ 2d λ/R₀ ≈ −0.03%. Would the invagination not take place, the new preferred area per lipid in the outer monolayer would be unsatisfied, yielding an expansion energy 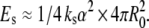With k_s ≈ 0.2 J/m², this gives E_s ≈ 6 × 10⁻¹⁷ J (of order ≅ 10⁴ k_BT). On the other hand, the creation of the tube costs the curvature energy E_c ≈ (k_c/2r²) × 2πrL, where k_c ≈ 10⁻¹⁹ J, yielding E_c ≈ 5 × 10⁻¹⁷ J, i.e., E_c ≈ E_s. This means that the tube creation process is energetically viable.

CONCLUSION

Our results allow us to suggest that mitochondrial lipids, in particular the cardiolipin, play specific role in IM morphology and dynamics. In this study, we elaborated a minimal model system displaying cristae-like morphology. It involves two major elements: i), a lipid bilayer membrane containing cardiolipin (a specific mitochondria inner membrane lipid), and ii), the creation of a localized pH gradient at the membrane level.

Our results make us suggesting an original view for explaining the coupling of mitochondrial function with the typical cristae morphology: the electron transport chain proteins create the pH difference across the IM; the proton gradient is “kept” localized in the vicinity of the electron transport chain proteins due to the presence of CL headgroups acting as proton “traps”, as suggested by Haines and Dencher (27); the CL containing bilayer bends starting a tube like invagination, thereby initiating the cristae-like shape; the cone-like ATP synthase dimers localization is coupling with the initiated curvature; that leads to further stabilization of the curvature and development of cristae morphology; as a result, the ATP synthase and the electron transport chain proteins get colocalized within the extremities (the most curved parts) of cristae compartment. Once established, the cristae morphology becomes self-maintaining, as far as it limits the lateral diffusion of membrane inclusions (the oxidative phosphorylation protein complexes) as well as of protons in the vicinity of those protein complexes.

We carried out our model experiments using GUV of sizes ∼50 μm that permeated the direct microscope observation of the cristae-like deformation dynamics. Then, we proposed a mechanism and a simple geometric model to describe our experimental observations. For example, considering a deflated vesicles of initial radius ∼30 μm, our model yields a long thread-like tube of radius ∼1.3 μm and length ∼230 μm that is coherent with our experimental observations. The analytical model approximations still hold for the mitochondria length scale (typically ∼1 μm) giving in this case long tube of radius ∼40 nm and length ∼7 μm. This agrees well with the IM cristae of mitochondria in the orthodox conformation, which are several hundred of nanometers long and 20–40 nm in diameter (11,12). On the other hand, the verification that our model membrane experiments scale down to the typical mitochondrial sizes represents still a real challenge. The technical details to be worked out imply creating pH gradients and simultaneously visualizing membrane shape transformation at the scales of 100 nm and several seconds.

Our model suggests large and short (cistern-like) cristae for mitochondria in condensed state and long and thin tubes for the cristae of mitochondria in the orthodox state. Indeed, in the condensed state the ATP synthase activity (and therefore the proton gradient consumption) is maximal due to the excess ADP. That might lead to decreased local proton concentrations, less local charge neutralization effect, increasing parameter λ (Fig. 9, A and B), and lower ratio L/(2r). On the other hand, in the orthodox state the ATP synthase activity (and therefore the proton gradient consumption) is reduced due to the ADP depletion. That might lead to increased local proton concentrations (supposing that the flow of protons is kinetically controlled in local regions and limited by diffusion). The higher the proton gradient, the bigger the local charge neutralization effect. That corresponds to a decreasing λ-parameter (Fig. 9 B) that leads to a higher L/(2r) ratio.

Outside tubules can be formed from giant vesicles applying external forces, using either hydrodynamical flows (50), micropipettes (51), optical tweezers (52), or molecular motors (53). Development of inside tubular membrane deformations was reported earlier by one of us: that was a result of local interactions between DNA and cationic GUV (39). Some studies involving giant lipid vesicles subjected to transmembrane global pH differences (achieved by transferring the vesicles from an acidic to a basic buffer solution) were carried out before (54,55). They reported about global vesicle transformations equivocal with the pH difference applied across the membrane. Neither particular localization of the deformation was observed, nor particular new membrane shape was favored by the global transmembrane ΔpH. In this study, we point out that involving localized pH gradients in our model experiments was crucial for developing tubular, cristae-like morphology inside the vesicles.

Historically, two alternative theories, explaining the background of energy transduction for ATP synthesis in mitochondria were put forward in the early 1960s. The one generally stated is the Mitchell's theory (56) of “chemiosmosis”. This theory is based on an equilibrium approach and considers the mitochondrial inner membrane as a vesicular closed surface separating the generalized inside from the generalized outside. The proton distribution is homogeneous within these two spaces and is characterized by a “jump” at the delimiting surface (the IM) defining the proton potential between the inside and the outside. The alternative theory proposed simultaneously by Williams (22–24) is “that the flow of protons kinetically controlled in local regions and limited by diffusion, although not necessarily in an enclosed space, could represent the intermediate of energy transduction” operating in accordance with the very close positioning of the generating units for proton gradient and ATP synthesis. Experimental verification of the two alternative theories is still a challenge as far as the direct measurement of proton concentration at the nanometric scale of mitochondrial cristae still meets substantial difficulties. Therefore any experimental evidence helping to elucidate the fundamental assumptions of the two hypotheses contributes to explaining the mechanisms of energy transduction in oxidative phosphorylation.

Our results support the hypothesis of a localized bioenergetic transduction forwarded by Williams (22–24) and developed in Cherepanov et al. (57) and the review articles (14,58). The characteristic cristae morphology and the resulting nanocompartmentation of protons might lead to locally greater pH differences across the crista membrane as suggested by Mannella et al. (25). According to our model studies, the localized pH gradients would be in their turn the driving force stabilizing the cristae morphology, thereby enhancing themselves. The system thus becomes self-maintaining, which optimizes the synthesis of biological energy.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.