Influence of Liquid-Layer Thickness on Pulmonary Surfactant Spreading and Collapse

Abstract

Pulmonary surfactant spreads on the thin (∼0.1 μm) liquid layer that lines the alveoli, forming a film that reduces surface tension and allows normal respiration. Pulmonary surfactant deposited in vitro on liquid layers that are several orders of magnitude thicker, however, does not reach the low surface tensions (∼0.001 N/m) achieved in the lungs during exhalation when the surfactant film compresses. This is due to collapse, a surface phase transition during which the surfactant film, rather than decreasing surface tension by increasing its surface density, becomes thicker at constant surface tension (∼0.024 N/m). Formation of the collapse phase requires transport of surfactant to collapse sites, and this transport can be hindered in thinner liquid layers by viscous resistance to motion. Our objective is to determine the effect of the liquid-layer thickness on surfactant transport, which might affect surfactant collapse. To this end, we developed a mathematical model that accounts for the effect of the liquid-layer thickness on surfactant transport, and focused on surfactant spreading and collapse. Model simulations showed a marked decrease in collapse rates for thinner liquid layers, but this decrease was not enough to completely explain differences in surfactant film behavior between in vitro and in situ experiments.

INTRODUCTION

The role of pulmonary surfactant is critical to the mechanics of the lungs. Pulmonary surfactant forms a film at the air-liquid interface of a thin layer of fluid lining the alveoli, and this film lowers surface tension. Without surfactant, the air-liquid surface tension would be too high and the lungs would collapse during exhalation, as is the case with premature babies who develop respiratory distress syndrome because they lack a sufficient amount of pulmonary surfactant (1).

Surfactant deposition on a liquid layer leads to the spreading of surfactant due to surface tension gradients. This self-spreading phenomenon is of interest for applications such as surfactant replacement therapy in infants suffering from respiratory distress syndrome and for drug delivery, and also occurs naturally in the alveoli after vesicles containing pulmonary surfactant are adsorbed at the air-liquid interface (1,2). Changes in surfactant concentration and surface tension also occur in the lungs during respiration.

The surface area of the pulmonary-surfactant film changes as alveoli expand and contract during respiration. Assuming that the surfactant film is a monolayer and that the surfactant is insoluble in the liquid and gas phases it separates, a decrease in the monolayer area should result in a higher surfactant concentration and lower surface tension (1,3). Experiments with excised lungs indeed have shown that the surface tension of the alveolar lining layer changes with lung inflation and that surface tensions in the alveoli of deflated lungs become as low as 0.001 N/m, even when applied rates of lung deflation are extremely slow (4). Moreover, these low surface tensions can be maintained for >20 min (4). Experiments in vitro, however, show that pulmonary surfactant monolayers under a slow rate of compression do not reach surface tensions below ∼0.024 N/m, the equilibrium spreading tension for pulmonary surfactant (3,5,6). This is because at ∼0.024 N/m, the surfactant monolayer starts to thicken at constant surface tension, forming collapsed three-dimensional structures that are composed of several layers of surfactant molecules (3,6–10).

The low surface tensions achieved in in situ experiments with excised lungs (4) suggest that pulmonary surfactant films in the lungs may resist (or avoid) collapse. Although many researchers have tried to explain this discrepancy, few have addressed the effect of the alveolar liquid-layer thickness on collapse. Measurements of the alveolar lining layer thickness in rat lungs by electron microscopy after rapid freezing ranged from 0.09 to 0.89 μm (11), whereas the typical liquid-layer thickness used for in vitro studies is no thinner than 5 mm (12). Since a thinner liquid layer is associated with a higher resistance to transport due to an increase in the effect of viscous fluid forces, this difference in thickness between in vitro and in situ experiments may significantly affect how quickly surfactant in the monolayer can be transported to the interface between the monolayer and collapse phases, from where surfactant transfers to the collapse phase. Therefore, the speed of surfactant transport within the monolayer may in turn affect how fast the surfactant monolayer can collapse.

In this article, we investigate the influence of the liquid-layer thickness on monolayer transport and surfactant transfer rates to the collapse phase. To this end, and due to the many technical challenges of achieving liquid layers as thin as 0.1 μm in vitro, we have developed a mathematical thin layer model. Simulations of the model were used to quantify the effect of liquid-layer thickness in surfactant transport during surfactant collapse. Since surfactant spreading and its dependence on liquid-layer thickness have been investigated by other researchers (e.g., (1,2,13–16)), simulations involving spreading were used mainly as a validation of our model. To estimate the influence of liquid-layer thickness on collapse, simulations of monolayer transport were performed for different initial liquid-layer thicknesses ranging from 0.025 to 5 μm.

Monolayer compression and collapse

Pulmonary surfactant is primarily composed of phospholipids, of which the most abundant are phosphatidylcholine, phosphatidylinositol, and phosphatidylglycerol, and other compounds, including cholesterol and surfactant proteins (17). This mixture of compounds typically forms a monolayer at the air-liquid interface. Further, pulmonary surfactant can form monolayers with coexisting liquid-expanded (LE) and liquid-condensed (LC) phases (8), with molecules in the LC phase more tightly packed than those in the LE phase. Although monolayer collapse can occur in both the LE and LC phases, it proceeds much more quickly in the LE phase.

Early experiments with pulmonary surfactant constituents (e.g., (3)) showed that dipalmitoyl-phosphatidylcholine (DPPC) was the only component of pulmonary surfactant present in significant amounts that could be easily compressed to surface tensions as low as 0.001 N/m and could remain at those surface tensions, without collapsing significantly, for hours. The mixture of extracted pulmonary surfactant, however, collapsed at ∼0.024 N/m at 37°C (6). DPPC forms LC films, and the stability of DPPC films is associated with the LC phase. The surface shear viscosity of the more solidlike LC domains is markedly higher than that of the LE regions. A high surface shear viscosity may influence surfactant transport and collapse, and explain the tendency of LE films to collapse faster than LC films (18). The stability properties of DPPC, which are very similar to the stability properties of surfactant films in the lungs, lead to the hypothesis that in the lungs, surfactant films contain more DPPC than the secreted pulmonary surfactant. However, no mechanism that could explain the change in composition in the surface films has been found (see (19)), and, moreover, the presence of cholesterol in pulmonary surfactant causes a marked decrease in the surface shear viscosity of LC regions, thus reducing its effect on surfactant transport and collapse (20–22).

Recent experimental evidence shows that stability of pulmonary surfactant films is also achieved with high concentrations of vesicles in the subphase—the liquid layer (23). In this case, collapse seems to occur at surface tensions much lower than the equilibrium spreading tension, σ_eq (24,25). The mechanism by which vesicles could stabilize the films is not known, and the concentration of vesicles in the liquid-lining layers of the lungs is difficult to estimate. We focused here on the effect of subphase thickness on collapse, assuming a low concentration of vesicles in the subphase. However, the model could also be applied, with similar results, for the case in which collapse occurs at lower surface tensions.

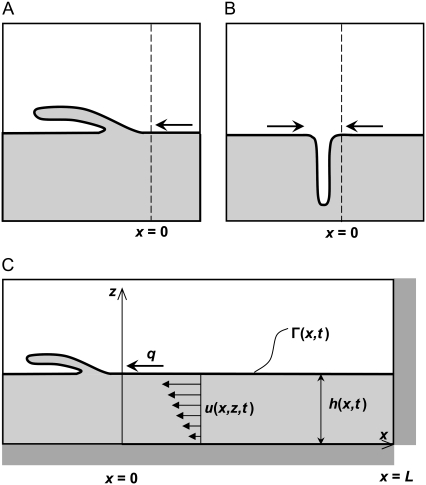
Collapse is a phase transition of the monolayer film (9) that can occur due to changes in surface tension. The monolayer and collapse phases coexist at the equilibrium spreading tension, σ_eq, and collapse proceeds spontaneously when surface tension is below σ_eq. Like other phase transitions, collapse has been observed to start at nucleation sites (usually defects in the surfactant film). In surfactants composed mainly of phospholipids (such as pulmonary surfactant), collapse is generally thought to occur by a “sliding mechanism”, in which lamellae of surfactant slide over (or below) the monolayer, adding two additional layers to the film (see Fig. 1 A) (7,26). By this mechanism, regions of collapse can also be created when monolayers flow as continuous lamellae into bilayer disc structures through a narrow line or point on the edge of the disc (26). Other researchers have observed that collapse in monolayers that have a continuous LE phase network with islands of LC phase is due to the buckling or fracturing of the monolayers, and that both LE and LC regions may be included in the buckled section (see Fig. 1 B) (8,10). In all of these cases, however, the progression of collapse at constant film area requires the transport of surfactant molecules to the interface between the collapsed structures and the monolayer (Fig. 1, x = 0).

FIGURE 1.

Mechanisms of collapse for a surfactant phospholipid monolayer. (A) Monolayer slides into a multilayer collapsed structure. (B) Monolayer buckles into the liquid subphase. (C) One of the possible model geometries for the collapsed phase scenario. q, rate of mass transport into the collapsed phase; h, fluid height; u, fluid velocity in the x direction; Γ, surfactant surface concentration. x = 0 represents the interface between the monolayer and collapse phases.

Considering the rate at which collapse typically occurs (26,27), transport of molecules within the monolayer by diffusion is not enough to sustain collapse, so convective transport that involves motion of surfactant molecules toward the interface between the monolayer and collapse phases at a certain velocity is necessary. Since surfactant molecules have to move at the same velocity as the adjacent liquid molecules at the air-liquid interface, this surface motion creates a viscous boundary layer in the fluid that provides a resistance to the surfactant movement. This viscous resistance is more important in “thin” than in “thick” liquid layers. In this article, we will investigate how film thickness affects surfactant transport and collapse, with the objective of determining whether the difference in liquid-layer thickness between in situ (<1 μm) and in vitro (∼5 mm) experiments could explain the presumably higher resistance of films to collapse in situ than in vitro.

MODEL DEVELOPMENT

Introduction

To investigate the effect of liquid-layer thickness on pulmonary surfactant collapse, we developed a mathematical model of surfactant transport based on lubrication theory. Using this model, we first simulated spreading rates over a range of liquid-layer thicknesses and compared our results with those of other researchers (e.g., (13)). As the range of surfactant concentrations considered for the surfactant spreading scenario (0–2.5 × 10⁻⁷ kg/m²) was lower than that at which an LC phase is first observed (2.7 × 10⁻⁶ kg/m²), we neglected the effects of surface shear viscosity and dilatational viscosity on surfactant movement.

We also simulated the collapse of a surfactant monolayer that is initially at a surface tension lower than the equilibrium surface tension, σ_eq, below which collapse progresses. This corresponds to an initial surfactant surface concentration, Γ, above the equilibrium concentration, Γ_eq. To accommodate the different theories for mechanisms of monolayer collapse, rather than developing a geometrically explicit model of the collapse process, we focused here on the influence of liquid-layer thickness on the rate of surfactant mass transport to the interface between the monolayer and collapse phases. To represent the transfer of surfactant molecules from the monolayer to the collapse phase, we applied a boundary condition to one end of the model (x = 0), which corresponds to the interface of the collapse phase with the surfactant monolayer (see Fig. 1). Since this boundary condition is imposed at the interface between the surfactant monolayer and the collapse phase, our simple model is applicable regardless of the specific geometry of the collapse-phase formation. Fig. 1 C illustrates one possible mechanism for the collapse-phase formation; as our model simulates the region x > 0, it would make no difference to the simulation outcome if the collapsed structure were to protrude into the aqueous phase instead of the air. Based on this scenario, we compared the changes in monolayer surface tension with time to previously reported results (27) in which collapse proceeded at constant surface area, and we evaluated the rates of surfactant transport into the collapsed phase for a range of initial fluid heights.

Assuming that the fluid thickness does not affect the mechanism by which collapse proceeds, and taking into account that the goal of our model was to determine the effect of the liquid-layer thickness on surfactant transport, we neglected the influence of surface effects such as surface viscosity and the thickness and composition of the surfactant monolayer and collapsed structure in this model. Such surface effects will have a comparable level of impact on surfactant transport regardless of changes in liquid-layer thickness, so incorporating these factors into our model is not necessary to address our fundamental concern, the effect of liquid-layer resistance on surfactant transport to the interface with the collapse phase.

Physical parameters

Consider a thin layer of fluid contained within a trough with vertical walls at x = L and x = −L, where L is the length of the monolayer. The height of the fluid is h(x,t) for a given position x and time t (Fig. 1 C). A surfactant monolayer on top of the liquid layer has surface concentration Γ(x,t). Fluid velocity is u(x,z,t) in the x direction and w(x,z,t) in the z direction, and we assume a unit width of 1 mm in the y direction.

At the air-fluid interface, a linear relationship between surface tension, σ, and surface concentration was assumed:

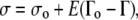(1)

where E is the surface dilatational modulus, ɛ, divided by a reference surfactant concentration, Γ_o, and σ_o is the surface tension at surfactant concentration Γ_o. This linear relationship is suitable, given the small surface tension ranges considered in the surfactant spreading simulations (0.0658–0.070 N/m) (28). Although the surface tension range for the collapsed phase model was somewhat larger (0.00513–0.024 N/m), our sensitivity analyses for the model demonstrated that the surfactant distribution and liquid-layer height were insensitive to 100-fold changes in E, so an assumption of linearity did not significantly affect model results.

The surfactant is considered to be perfectly insoluble with respect to the fluid and air, so that the surfactant mass remains at the interface at all times.

Governing equations

A detailed derivation of the equations that govern the motion of the surfactant at the air-fluid interface is given in the Appendix. Because the motion of the surfactant affects the motion of the liquid layer underneath, surfactant motion locally alters the height of the liquid layer. Applying the typical assumptions based on lubrication theory to conservation of mass and momentum for the liquid layer and the surfactant monolayer (see, e.g., (13–15)), and using Eq. 1, the key equation for fluid height takes the form (Eq. A17 of the Appendix)

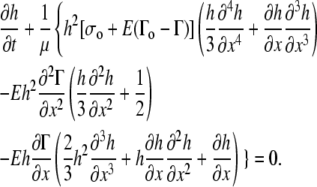(2)

The key equation for surfactant transport (Eq. A19 of the Appendix) is

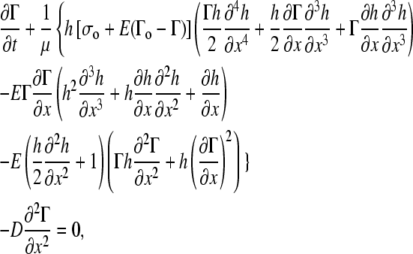(3)

where μ is the dynamic viscosity of the liquid layer and D is the surface diffusion coefficient for the surfactant in the fluid.

To solve Eqs. 2 and 3, a finite difference scheme was implemented in which the initial fluid height and surfactant distributions were used in a series of successive substitutions to numerically integrate the coupled partial differential equations with respect to time (29).

Surfactant spreading scenarios

To compare surfactant spreading rates over a range of liquid-layer thicknesses, we simulated a surfactant drop located at x = 0 spreading over a clean surface (Γ_init = 0) and over a surface with endogenous surfactant already present (Γ_init = 1 × 10⁻⁸ kg/m²). We began our simulations with an initially flat layer of fluid (thickness range 0.05–5 μm) and modeled the surfactant drop as a step function for surfactant concentration:

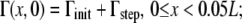(4)

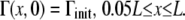(5)

The model parameters used for the surfactant spreading scenarios are listed in Table 1. The surfactant step magnitude, Γ_step, was selected to fall within the LE phase of pulmonary phospholipids, and the endogenous surfactant level is 4% of Γ_step. The dilatational elasticity, E, was estimated by fitting Eq. 1 to two reference points: clean water at a physiological temperature of 37°C (Γ = 0, σ = 0.07 N/m) (30), and the pulmonary phospholipid concentration equivalent to a surface tension of 0.065 N/m (Γ = 1.26 × 10⁻⁶ kg/m²) (31). The fluid dynamic viscosity, μ, was that of water at 37°C (30), and the diffusion coefficient, D, was based on experimental measurements in pulmonary phospholipid monolayers in the LE phase at σ = 0.07 N/m (32). Boundary conditions, which correspond to symmetry at x = 0 and an impermeable wall at x = L, can be found in the Appendix (Eqs. A20–A25).

TABLE 1.

Model parameters for surfactant spreading and collapsed phase scenarios

Surfactant spreading scenario
Surfactant concentration step magnitude	Γstep	2.5 × 10−7	kg/m2
Baseline surfactant concentration	Γinit	0 or 1.0 × 10−8	kg/m2
Dilatational elasticity	E	3.97 × 104	N·m/kg
Reference surfactant concentration	Γo	0.0	kg/m2
Reference surface tension	σo	0.07	N/m
Dynamic viscosity	μ	7.0 × 10−4	kg/m·s
Surface diffusion coefficient	D	1.0 × 10−10	m2/s
Liquid layer length	L	0.001	m
Collapsed phase scenario
Initial surfactant concentration	Γinit	3.0 × 10−6	kg/m2
Equilibrium spreading concentration	Γeq	2.7 × 10−6	kg/m2
Dilatational elasticity	E	6.29 × 104	N·m/kg
Reference surfactant concentration	Γo	2.7 × 10−6	kg/m2
Reference surface tension	σo	0.024	N/m
Mass transfer coefficient	k	1.0 × 10−5 to 100	m/s
Dynamic viscosity	μ	7.0 × 10−4	kg/m·s
Surface diffusion coefficient	D	1.0 × 10−11	m2/s
Liquid layer length	L	0.001	m

To compare surfactant spreading rates across the range of liquid-layer thicknesses, and between the clean surfaces and those with endogenous surfactant, we determined the time required for the surfactant front to reach x = 0.5 mm = 0.5L. This characteristic spreading time, t_c, was more specifically defined as the time at which the condition Γ > Γ_init + 0.001Γ_step is first satisfied at position x = 0.505 mm. This criterion correlated well with a visual assessment of the leading edge of the surfactant wave.

Collapsed phase scenarios

The viscous resistance of thin liquid layers to fluid movement may affect how quickly surfactant is transported to the interface between the monolayer and collapse phases and, therefore, how quickly collapse can proceed. To investigate this phenomenon, we modeled a region of the surfactant film on a thin liquid layer. In our model, the interface between the monolayer and the collapse phase was at x = 0, and the collapse transition was modeled as a transfer of surfactant from the monolayer into the collapsed structure (26), as shown in Fig. 1 C. Collapse occurs when surface tension decreases below the equilibrium spreading tension σ_eq, which corresponds to an equilibrium monolayer surfactant concentration Γ_eq. Within the collapsed phase, surface tension is considered uniform at σ_eq (6). For small deviations from equilibrium conditions, the speed of transport of surfactant molecules from the unstable monolayer phase (σ < σ_eq) to the stable collapse phase (σ = σ_eq) can be assumed to be proportional to the surface tension difference between the monolayer and the collapsed phase at x = 0 (26). Thus, using Eq. 1 to relate surface tension to surfactant concentration, the surfactant mass flow rate, q, is given by

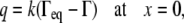(6)

where k is the mass transfer coefficient, which was assumed to be constant. To mimic the conditions under which collapsed structures are typically observed, the starting condition for the collapsed phase scenario is a uniform surfactant distribution at an initial concentration Γ_init > Γ_eq, as if the surfactant monolayer has just been rapidly compressed. The initial fluid height is also constant with respect to x.

Table 1 includes the model parameters used in the collapsed phase scenarios. E was estimated from experimental data for pulmonary phospholipids collected over a range of concentrations close to Γ_eq (6,12), and the reference surfactant concentration, Γ_o, and reference surface tension, σ_o, correspond to the equilibrium point. The mass transfer coefficient, k, was estimated to be 1 × 10⁻⁴ m/s using Eq. 6, which is independent of liquid-layer thickness, and the surface tension changes reported during the collapse of purified pulmonary surfactant phospholipids at constant interfacial area (27), assuming that monolayer surface tension was uniformly distributed. We also conducted simulations in which k was varied over a fairly large range (1 × 10⁻⁶ to 100 m/s) to investigate how the overall mass transfer rate (which could account, in a lumped manner, for the number of collapse nucleation sites) would affect collapse rates. We considered a smaller surface diffusion coefficient, D, than in the surfactant spreading case to reflect the decrease in lateral movement within the surfactant monolayer at concentrations close to Γ_eq (32,33). Initial fluid thickness varied from 0.025 to 5 μm, and the fluid dynamic viscosity used was that for water at 37°C (30). At physiological temperature, σ_eq is ∼0.024 N/m (6).

Collapse phase boundary conditions

At x = L, the same boundary conditions applied for the surfactant spreading scenario, an impermeable wall (Eqs. A23–A25) apply. At x = 0, surfactant is transferred into the collapsed phase at the rate given in Eq. 6. Due to the morphology of the collapsed structure (26), we assumed that the liquid layer immediately adjacent to the collapsed phase was flat, with

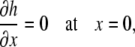(7)

and that this locally flat geometry was also reflected by a lack of curvature at this boundary, denoted by

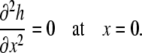(8)

Combining Eq. 8 with Eq. 6 and Eq. A27 (see Appendix) yields the boundary condition for surfactant transfer to the collapsed phase

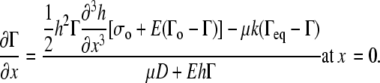(9)

(A detailed derivation of this boundary condition is given in the Appendix (Eqs. A26–A28).)

Collapsed phase analysis

We used the time required for surfactant concentration to reach equilibrium within the monolayer, t_e, as a point of comparison between liquid-layer thicknesses. This quantity was defined as the minimum time at which all surfactant concentrations for 0 < x < L were within 1% of Γ_eq.

RESULTS AND DISCUSSION

Although pulmonary surfactant films can reach very low surface tensions (< 0.005 N/m) in the lungs, and sustain them for >20 min (4), surfactant films in vitro do not reach surface tensions lower than σ_eq (0.024 N/m) under slow compression. The fundamental question that we address in this article is whether differences in pulmonary surfactant behavior in vitro and in situ could be attributed to the effect of the liquid-layer thickness, which is considerably thinner in the lungs (<1 μm) than in vitro (∼5 mm) experiments (11,12,34). Thinner liquid layers provide an increased resistance to surfactant motion that could slow transport of surfactant molecules. This diminished motion could slow collapse, and even stop it, if molecules cannot reach the interface from where they transfer to the collapse phase (x = 0 in our model). Thus, to establish the importance of liquid-layer thickness, we concentrated here on a model of surfactant transport that neglected several characteristics of the surfactant films, such as bending elasticity and surface viscosity, that would produce similar effects in situ and in vitro. Other factors, such as the interaction between surfactant layers within the collapsed structure, and resistance to collapse due to the geometry of the collapse phase, were also neglected according to similar reasoning. We also neglected, in this first analysis, the undulating nature of the liquid-layer thickness in the lungs due to the irregularity of cell surfaces and cell geometry, since we would like to establish a limiting behavior. In this way, we isolated the effects of liquid-layer thickness on transport and concentrated on the availability of surfactant at the interface between the collapse and monolayer phases, which could affect collapse rates.

Surfactant spreading

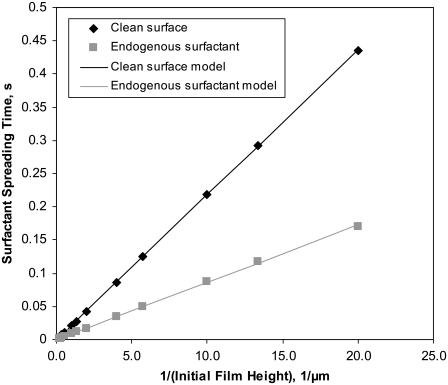
We first simulated the spreading of a surfactant drop along the surface of a thin liquid layer for various initial fluid heights. As noted by Grotberg et al. (16), a comparison of surfactant spreading in the presence or absence of endogenous surfactant depends on how the leading edge of the surfactant front is defined. Here, we defined the characteristic spreading time, t_c, based on the elevation of the surfactant concentration to Γ_init + 0.001Γ_step at a landmark point, x = 0.505L, as described in the Model Development section. This is similar to the definition used by Espinosa et al. (13), and our simulation results are in agreement with their observation that t_c is smaller in the presence of endogenous surfactant than on a clean fluid surface, as shown in Fig. 2. Briefly, this increase in surfactant spreading rate can be attributed to the concentration increase in the endogenous surfactant due to the surface area compression of the fluid surface ahead of the surfactant front, which creates an area of elevated surfactant concentration that actually extends farther than the distance traveled by the newly added exogenous surfactant (16).

FIGURE 2.

Characteristic spreading time, t_c, required for the surfactant front to reach x = 0.5 mm at various initial fluid heights for a clean interface (Γ_init = 0) and one with endogenous surfactant (Γ_init = 1.0 × 10⁻⁸ kg/m²). Model curves were fitted to the numerical data according to the function t_c = C₁/h_o (solid lines). Model parameters are listed in Table 1.

Espinosa et al. (13) reported a relationship for surfactant spreading in their model that, when applied to the model described here, implies that initial fluid height, h_o, and t_c are inversely proportional:

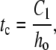(10)

where the slope C₁ is a constant that depends on the viscosity of the liquid layer, the length over which the surfactant is spreading, the amount of surfactant added (in the drop), and the surfactant dilatational modulus. Fig. 2 shows our calculated values of t_c versus 1/h_o, both for a clean surface and for one with endogenous surfactant. Our model correctly captures the linear relationship between t_c and 1/h_o.

Results obtained for t_c can be explained in terms of two forces that act in opposition in this system: Marangoni forces, which cause fluid flow due to surface tension gradients, and liquid-layer viscous forces, which offer resistance to fluid flow. Initially, Marangoni forces in our simulations result from the jump in surface tension at x = 0.05L. This initial discontinuity was independent of fluid thickness. Viscous forces in the liquid layer, which oppose Marangoni forces, increase as fluid thickness decreases. This explains the relatively large t_c observed when we simulated very thin liquid layers.

Collapse phase

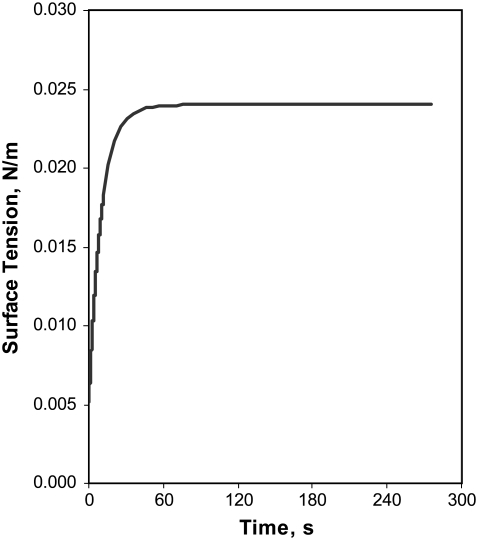
For the collapsed-phase scenario, we modeled the changes in surfactant distribution for a monolayer just after it has been subjected to a fast compression resulting in a uniform surface tension lower than the equilibrium spreading tension σ_eq. Fig. 3 shows the surface tension, averaged over the length of the liquid layer, versus elapsed time for the collapsed-phase scenario with k = 1 × 10⁻⁴ m/s and h_o = 1.0 μm. As surfactant is transferred into the collapsed phase, the corresponding decrease in surface concentration within the monolayer is reflected by the increased surface tension, which levels off as the system approaches equilibrium. Initially, the surface tension rises relatively quickly in response to the surface tension difference between the surfactant monolayer and the equilibrium spreading tension of the collapsed phase. This behavior and the time required to reach equilibrium follow the same trends as the experimental results reported by Yan et al. (27), who compressed monolayers of purified pulmonary surfactant phospholipids to a low surface tension (0.018 N/m) and then allowed the monolayers to relax while interfacial area was held constant.

FIGURE 3.

Surface tension (averaged along the length of the fluid layer) versus elapsed time for collapsed phase scenario with k = 1 × 10⁻⁴ m/s and h_o = 1.0 μm. Additional model parameters are listed in Table 1.

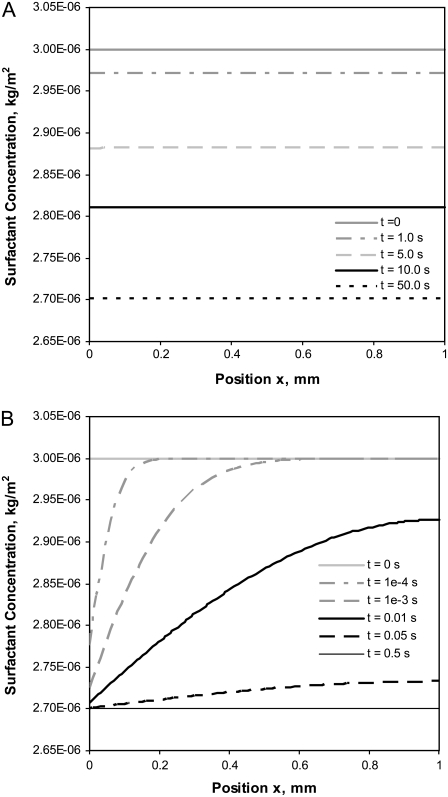
The surfactant concentration distributions at several different elapsed times are shown in Fig. 4 for two values of k (k = 1 × 10⁻⁴ m/s and k = 1.0 m/s) with an initial fluid thickness of h_o = 0.1 μm. Exploring trends for larger values of k allows us to visualize how collapse might proceed if overall mass transfer rates were much higher or if additional nucleation sites were present. For the smaller mass transfer coefficient, k = 1 × 10⁻⁴ m/s, the surfactant is distributed uniformly across the fluid surface at all times (Fig. 4 A). When the mass transfer coefficient is increased to 1.0 m/s, as seen in Fig. 4 B, surfactant concentrations are lower near the collapsed-phase boundary than at the opposite end of the liquid layer. This difference in the concentration distributions reflects the balance between 1), the surfactant mass transfer into the collapsed phase, which is a function of k and the concentration difference at x = 0 (Eq. 6), and 2), the movement of the surfactant on the liquid-layer surface due to Marangoni forces opposed by viscous forces. The uniform surfactant concentrations observed when k = 1 × 10⁻⁴ m/s suggest that the mass transfer into the collapsed phase proceeds slowly enough that the remaining surfactant in the monolayer can be redistributed uniformly, and therefore, collapse rates are limited by transfer of surfactant into the collapsed phase. In contrast, when k = 1.0 m/s, the rate of transfer into the collapsed phase is rapid enough that a localized depletion of surfactant occurs. In this case, Marangoni forces are not large enough to supply surfactant to the depleted zone, and the rate of collapse is limited by surfactant transport within the monolayer. Similar behavior occurs if k is held constant while h_o is decreased (data not shown); the reduction in h_o leads to a localized depletion of surfactant near the interface with the collapsed phase. This reflects the increase in the resistance to surfactant motion due to viscous forces at decreased fluid thicknesses.

FIGURE 4.

Surfactant concentration distributions on a thin layer of fluid (h_o = 0.1 μm) at several elapsed times when the mass transfer coefficient is (A) k = 1 x 10⁻⁴ m/s and (B) k = 1.0 m/s. Additional model parameters are listed in Table 1.

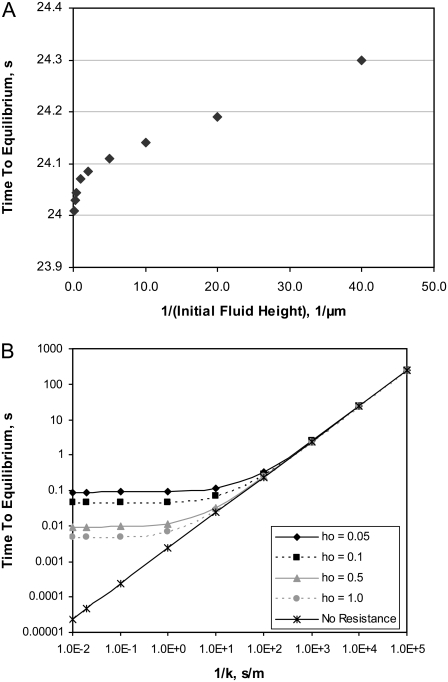
When the time to equilibrium, t_e, at which all surfactant concentrations along the monolayer are within 1% of Γ_eq, is plotted versus the inverse of the initial fluid height, h_o, when k = 1 × 10⁻⁴ m/s (Fig. 5 A), the resulting trend for the thinner heights considered (larger 1/h_o) is quite similar to the curve for surfactant spreading times versus 1/h_o in Fig. 2: the slope of t_e versus 1/h_o is linear for thinner liquid layers. As in the surfactant spreading scenario, the larger t_e obtained for thinner liquid layers reflects the increased viscous resistance of thinner liquid layers to transport of surfactant molecules along the fluid surface. This trend, however, is not reproduced for thicker liquid layers. Similarly, when t_e is plotted versus 1/k for several different initial fluid heights (Fig. 5 B), t_e increases as h_o decreases for a given value of k, particularly for k > 0.1 m/s. Again, this reflects the increased viscous resistance of the thinner liquid layers. Fig. 5 B shows two limiting regions: 1), a region of large k (small 1/k), in which collapse rates are limited by transport of surfactant within the monolayer, and therefore collapse rates are sensitive to h_o; and 2), a region of smaller k (large 1/k) in which collapse rates are limited by transfer of surfactant to the collapsed structures (given by the value of k) and are therefore almost independent of h_o. The difference in t_e between the thinnest liquid layer considered (h_o = 0.025 μm) and the thickest (h_o = 5.0 μm) is less than half a second for all values of k considered.

FIGURE 5.

Time for monolayer to reach equilibrium, t_e, during collapse from an initial surface tension of 0.00513 N/m. (A) t_e versus 1/h_o (inverse of initial fluid height) for k = 1 × 10⁻⁴ m/s. The reported t_e is the time required for surfactant concentration at all points along a thin fluid surface to decrease to within 1% of the equilibrium spreading concentration. (B) t_e versus 1/k (inverse of mass transfer coefficient) for four different initial fluid heights h_o (log-log plot, in μm). Model parameters are listed in Table 1. The curve denoted as “no resistance” shows the theoretical trend for t_e (from Eq. 11) assuming that the liquid layer thickness does not influence surfactant transport within the monolayer.

The viscous resistance of the liquid layer to surfactant transport along the fluid interface can be changed not only by adjusting the initial fluid height, but also by changing the dynamic viscosity of the fluid, μ. In an analysis of model sensitivity to μ, we found that reducing μ to 10% of its original value (7.0 × 10⁻⁵ kg/m·s) reduced t_e by <1% when k = 1 × 10⁻⁴ m/s and h_o = 0.1 or 1.0 μm. Increasing μ by 10-fold (to 7.0 × 10⁻³ kg/m·s) caused an increase of ∼1.5% in t_e when h_o = 0.1 μm, but t_e increased by only 0.12% when h_o = 1.0 μm, as compared to the t_e values at each initial fluid height obtained with k = 1 × 10⁻⁴ m/s and μ = 7.0 × 10⁻⁴ kg/m·s. It is interesting to note that although a 10-fold increase or decrease in μ resulted in a relatively small change in t_e for either of these initial fluid heights, the changes were greater for the smaller liquid thickness, reflecting the increased importance of viscosity for thinner liquid layers. In the limiting case in which the liquid layer does not resist the motion of the surfactant molecules, and in which the effects of surfactant diffusion are ignored, surfactant loss from the monolayer to the collapse phase can be expressed as

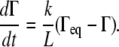(11)

Equation 11 implies that surfactant is homogeneously distributed along the monolayer at all times. Further, because the liquid-layer thickness does not affect surfactant transfer to the collapsed phase, Eq. 11 approximately captures the decay of surfactant in thick liquid layers. Fig. 5 B shows that the time for equilibrium, t_e, calculated from Eq. 11 (“no resistance” curve) and from our model, only differ significantly for the larger values of k considered (>0.1 m/s). This suggests that if the effective k for collapse is <∼0.1 m/s, the thickness of the liquid layer does not have a large effect on transport and collapse rates.

Focusing solely on the effects of liquid-layer thickness on surfactant transport, we found that regardless of the value of k, our model predicts differences in the time for the monolayer to reach equilibrium, t_e, between thick and thin liquid layers. These differences, however, were relatively small (<0.5 s) compared to differences observed between in vitro and in situ experiments (>20 min). Although the ratio of t_e between thin and thick liquid layers could be relatively large (several orders of magnitude for the largest values of k considered), t_e was quite small (<0.1 s), suggesting that the smaller values of k better represent the transfer of surfactant molecules to the collapsed structures, in agreement with the calculated value of k = 10⁻⁴ m/s estimated from experimental results (27). Therefore, our model results do not seem to completely explain differences in surfactant behavior between in vitro and in situ experiments. The presumably larger resistance of pulmonary surfactant films to collapse in the lungs is likely not only the result of an increased resistance to surfactant motion due to a thinner lining layer. A more realistic surface model of collapse nuclei formation, which includes the resistance to collapse due to the geometry of the collapsed structure and the subphase into which it protrudes, might be the key to complete understanding of the role of the liquid-layer thickness in collapse, and could constitute possible directions for further refinement of the model.

CONCLUSIONS

Our model of surfactant mass transfer from a monolayer into a collapsed phase agreed well with previously published experimental results of changes in surface tension versus time for collapse at constant area. Concentration profiles were relatively flat when the mass transfer rate was comparable to the Marangoni flow along the fluid surface, but showed some depletion local to the collapsed-phase boundary when the mass transfer rate exceeded the surface transport rate due to Marangoni flow. This local depletion was observed when 1), the mass transfer coefficient k was large, and/or 2), initial fluid thickness h_o was small. In the latter case, results suggest that the resistance to flow due to viscous forces was more influential than the Marangoni forces. Although the time for the surfactant monolayer to reach equilibrium with the collapsed phase, t_e, did increase for smaller fluid thicknesses, the overall differences in t_e were quite small, suggesting that our simplified collapse model does not completely explain the presumably much slower formation of a collapsed phase observed in in situ versus in vitro experiments.

APPENDIX: SIMPLIFYING ASSUMPTIONS

From lubrication theory, assuming that fluid height h ≪ L continuity gives

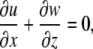(A1)

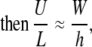(A2)

where L, h, U, and W are the characteristic length, fluid height, horizontal velocity (x direction), and vertical velocity (z direction) for the system. Rearranging the terms in Eq. A2 and comparing them to the assumption h ≪ L gives

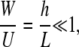(A3)

so that vertical velocity w(x,z,t) can be considered small relative to horizontal velocity u(x,z,t). Also, assume that

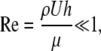(A4)

where Re is the Reynolds number, so that inertial terms can also be neglected. For thin liquid layers, gravitational effects are also negligible. The normal stress balance at the fluid surface, which depends on surface tension, the curvature of the fluid surface, and fluid pressure, is

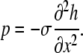(A5)

Governing equations

Applying the abovementioned simplifications to the 2D Navier-Stokes equation for fluid dynamics in the x direction, the full equation

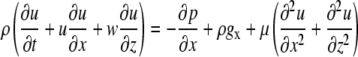(A6)

reduces to

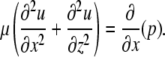(A7)

However, since

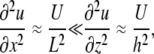(A8)

Eq. A7 can be simplified further to

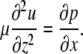(A9)

The full 2D Navier-Stokes equation for fluid dynamics in the z direction is

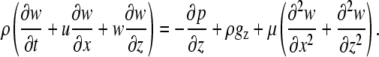(A10)

As the vertical velocity component, w, is much less than the horizontal component, u, Eq. A10 can be reduced to

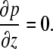(A11)

Thus, p has no dependence on z, i.e., p = p(x,t).

Integrating Eq. A9 with respect to z and subject to equilibrium of forces (fluid viscous forces and Marangoni surface forces) at the fluid surface,

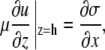(A12)

and the no-slip boundary condition,

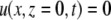(A13)

results in an equation for the horizontal velocity of the fluid:

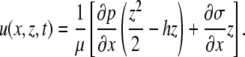(A14)

Mass conservation of fluid dictates that

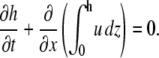(A15)

After integrating u(x,z,t) over the fluid height, Eq. A15 becomes

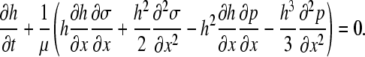(A16)

When the surface tension (σ) and pressure (p) terms are expressed in terms of surfactant concentration (Eq. 1 from the article text) and fluid height (Eq. A5), the key equation for fluid height takes the form

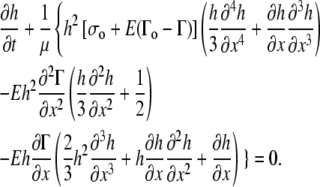(A17)

At the surface, conservation of surfactant mass gives

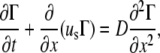(A18)

where u_s is the surface velocity u(x,h,t) and D is the diffusion coefficient for the surfactant. Expressing Eq. A18 in terms of surfactant concentration and fluid height, the key equation for surfactant transport is

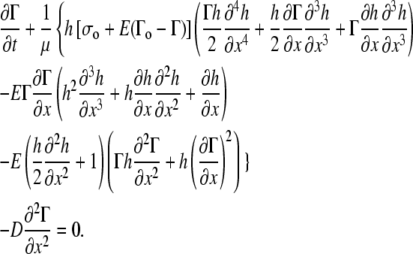(A19)

Surfactant spreading boundary conditions

Because the surfactant drop spreads symmetrically about the z axis, we modeled the section from x = 0 to x = L. Applying symmetry boundary conditions for both the liquid layer and the surfactant monolayer at x = 0,

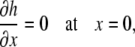(A20)

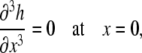(A21)

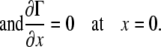(A22)

The boundary conditions at x = L result from assuming that there was an impermeable wall at x = L, and therefore there is no surfactant flux at that boundary:

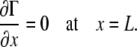(A23)

We also assumed that the pressure within the fluid is in equilibrium with the air pressure (p_air=0) at x = L; thus, based on Eq. A5,

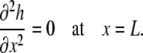(A24)

At x = L, the horizontal fluid velocity u(x = L,z,t) is zero. In our model (see Eq. 1), 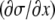is directly proportional to 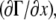which is zero at this boundary, and therefore, from Eq. A14,

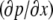must equal zero. Thus, using Eq. A5,

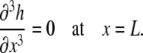(A25)

Since our simulations terminated before the surfactant reached x = L, these boundary conditions (Eqs. A23–A25) did not affect the spreading behavior.

Collapsed phase boundary conditions

Assuming that the surfactant mass flow rate into the collapsed phase is

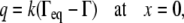(A26)

this must match the surfactant mass flow due to convection and diffusion at that point:

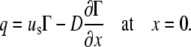(A27)

Taking Eqs. A26 and A27 to be equal, rewriting them in terms of Γ and h, applying the boundary condition 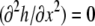at x = 0 (see Eq. 8 from the article text), and solving for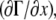

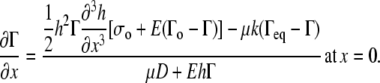(A28)