Monte Carlo Simulations of Protein Assembly, Disassembly, and Linear Motion on DNA

Abstract

We use Monte Carlo simulations to analyze the simultaneous interactions of multiple proteins to a long DNA molecule. We study the time dependence of protein organization on DNA for different regimes that comprise (non)cooperative sequence-independent protein assembly, dissociation, and linear motion. A range of different behaviors is observed for the dynamics, final coverage, and cluster size distributions. We observe that the DNA substrate is almost never completely covered by protein when taking into account only (non)cooperative binding, because gaps remain on the substrate that are smaller than the binding site size of the protein. Due to these gaps, the apparent binding size of a protein during noncooperative binding can be overestimated by up to 30%. During dissociation of cooperatively bound proteins, the dissociation curve can be exponentially shaped even when allowing only end-dependent dissociation. We discuss the potential of our method for the analysis of a number of single-molecule experiments, for example, the binding of the DNA-repair proteins RecA and Rad51 to DNA.

INTRODUCTION

In the last decade, new experimental techniques have opened the way to study protein-DNA or protein-protein interactions at the level of single molecules. In contrast to bulk experiments, single-molecule experiments do not suffer from averaging multiple events, thereby allowing much more detailed characterization. The interaction between proteins and DNA involves a variety of relevant processes, e.g., binding, dissociation, translocation, shape deformation, etc. To describe the dynamic interactions between a protein and DNA, one can study systems where the protein-DNA interaction is restricted to a specific site, e.g., a recognition sequence for a restriction enzyme (1). For this type of experiment with a single protein interacting with DNA, models were developed to extract the relevant kinetic interaction rates.

For proteins that bind nonspecifically to DNA, however, the situation may be much more complex. Often, many proteins interact with DNA and other proteins simultaneously. One approach to study these systems in detail has been to avoid multiple events by severely reducing the amount of target area. For example, the length of available DNA substrate can be limited to only tens of bases, or the concentration of protein present in the reaction can be substantially lowered with respect to the target area. Another approach to study the dynamics of multiple nonspecific interactions of proteins with DNA or other proteins is to develop models that go beyond the description of single-entity binding.

In the classic protein-binding model of McGhee and von Hippel (MVH) (2), two cases of nonspecific protein-DNA binding are addressed: noncooperative and cooperative binding. In the former, proteins bind randomly to the lattice without any preference to bind adjacent to an already bound protein. In cooperative binding, however, a nucleation event is followed by an extension phase where proteins preferably bind next to an occupied lattice position (Fig. 1 A). In their analytical approach, MVH assumed an infinite lattice to which proteins can bind (non)cooperatively, without taking into account disassembly. Depending on the protein concentration and the strength of the cooperativity, the fractional final coverage was deduced at equilibrium—yielding a value for the binding constant of the protein to the lattice.

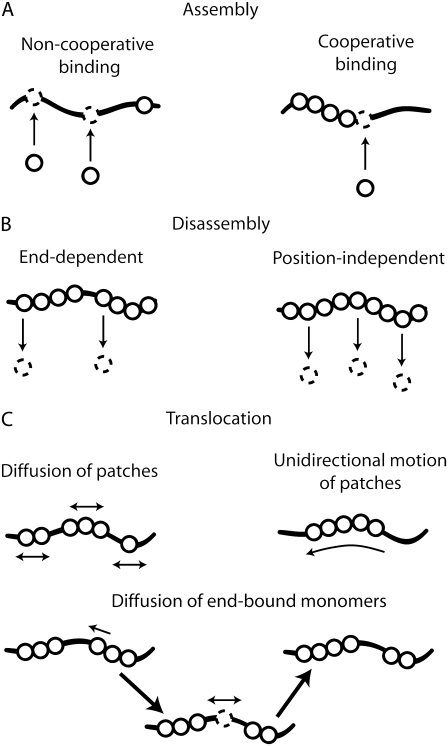
FIGURE 1.

Schematic drawings of different pathways for protein-DNA kinetics. (A) Assembly of a nonspecifically binding protein on its DNA substrate can be divided into two modes, noncooperative and cooperative. In the former (left panel), the protein binds randomly, whereas, in the latter (right panel), a preference exists to bind next to an already bound protein. (B) Disassembly of bound proteins can also be divided into two different modes, end-dependent and position-independent dissociation. In the first case (left), only proteins located at the end of a protein complex can dissociate, whereas, in the second case (right), all bound proteins, regardless of their position within the protein complex, have the same probability to dissociate. (C) Linear motion of a protein patch can be described by either a diffusive (left) or a unidirectional (right) mode. In the mode depicted at the bottom of the panel, end-bound monomers are allowed to detach from a protein patch and move diffusively toward a neighboring protein patch.

Although this model is valuable and widely used to determine the magnitude of cooperativity for a certain protein-DNA system (3–5), it has certain limitations. In a single-molecule experiment, one can measure the fractional coverage as it develops in time. The approach of MVH does not allow us to describe this dynamics or to extract kinetic parameters from the experimental single-molecule data, because it restricts the description to the final equilibrated system. Furthermore, the model proposed by MVH assumes that for B proteins that bind noncooperatively to the lattice, there are B + 1 gaps of bare DNA in between the bound proteins. This is a priori not true, because even in the noncooperative case, proteins can bind next to an already bound protein. Finally, the obtained coverage for cooperative binding in the MVH model is always complete. This outcome is incorrect because gaps smaller than the binding size of the protein remain on the lattice due to the random nucleation of proteins along the lattice.

Recently, an analytical tool based upon hidden Markov modeling was developed and applied to extract kinetic rates from single-molecule fluorescence data (6,7) and ion-channel data (8,9). A regular Markov model consists of a series of states where, at each time, the system may change from the state it was in the moment before, or may stay in the same state. These states are directly visible to the observer. In a hidden Markov model, however, the model contains an underlying stochastic process that is not observable (it is hidden) (10). A correct interpretation of single-molecule data using hidden Markov modeling depends on the number of states in the model and the corresponding probabilities involved (11). Furthermore, the states within the model should be independent of each other. For example, hidden Markov modeling does not work well for RNA secondary-structure analysis (10). Studying protein binding to a lattice using hidden Markov modeling causes a similar problem, because an already bound protein can influence a different protein cluster.

Here, we develop a new analysis method based upon Monte Carlo simulations that allows a description of both the dynamics and the final states of systems with multiple protein-DNA or protein-protein interactions via nonspecific target areas. In these Monte Carlo simulations, a Markov chain of different states is calculated. The simulations allow following the interaction of multiple proteins with a single DNA or protein substrate modeled as a one-dimensional lattice in time. We separately show the results for proteins that bind noncooperatively or cooperatively, dissociate, or reorganize along the DNA substrate. Furthermore, combinations of these three different interaction modes are implemented in the Monte Carlo simulations. The usefulness of our method was recently illustrated with a comparison to the interaction between the recombinase Rad51 with single- and double-stranded DNA, where a fit of the model to the experimental data allows us to extract a variety of protein-DNA interaction parameters that could not be obtained otherwise (12). Finally, we suggest a number of different systems to which this method can be applied.

Description of the model

We model protein-DNA interaction using Monte Carlo simulations (13–16). In our Monte Carlo simulations, we model the interaction between protein and DNA with a Markov chain where the next state of the protein-DNA complex depends on the current state. The transition probabilities between different states are given, and a certain stochastic pathway results. The Monte Carlo approach allows us to study both the dynamics as well as equilibrium states.

We first describe the concept for simulating the simplest two-state process that can be written as

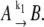(1)

The reaction rate k₁ is coupled to a transition probability p₁ in a Markov Chain as

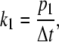(2)

where Δt is the duration of a single simulation step in the Monte Carlo simulations. The duration of a simulation step is taken such that 1), the transition probability within a single simulation step is always much smaller than unity; and 2), the chance of having two local transitions within a single simulation step is negligible. In the Monte Carlo simulations, a transition to the new state occurs when the transition probability is larger than a random value extracted from a uniform distribution between 0 and 1.

The interaction between proteins and DNA is implemented as follows in the Monte Carlo simulations (for details, see Methods). The DNA substrate is represented as a long one-dimensional array with the number of elements equivalent to the number of nucleotides or basepairs available. Upon binding, a protein occupies a certain number of elements corresponding to its binding site size corresponding to the most simple model of irreversible adsorption known as random sequential adsorption. The random sequential adsorption model has proven to be quite successful in describing a number of systems (17), lattice and continuum limits have been studied (18,19). Subsequently, the protein can dissociate or move along the substrate, respectively freeing or occupying other elements of the array. The protocol for binding, dissociating, and moving is repeated for each protein interacting with the DNA. Monitoring the transitions in time can be done by evaluating observables such as the lattice occupancy, contour length, or stepping of a single labeled protein.

METHODS

Binding of protein onto a DNA substrate was modeled using Monte Carlo simulations implemented in Interactive Data Language (RSI, Boulder, CO). A one-dimensional array was used to represent the DNA substrate containing a number of elements equivalent to the number of nucleotides or basepairs of the DNA molecule of interest. Simulations were done with various binding sizes for the protein. Cooperative binding was described by nucleation followed by growth that extended the nucleation point, whereas noncooperative binding involved nucleation only.

Nucleation was allowed to occur at any point along the entire molecule. In the Monte Carlo simulations, the nucleation step was simulated as follows: a value was randomly extracted from a uniform distribution yielding a value between 0 and 1. If this value was smaller than a given threshold corresponding to the set nucleation rate for the entire molecule, a protein was bound. The binding location was deduced from a second random number between 0 and 1, which was extracted from a uniform distribution that was multiplied by the number of elements in the one-dimensional array. Binding occurred only when this site plus the following n – 1 sites were not covered by another protein, to account for the fact that each protein covers n nucleotides or basepairs.

For cooperative binding, we evaluated all nucleation sites where protein patch extension could occur. For each site, a value was extracted from a uniform distribution and compared to a given threshold corresponding to the set rate of extension for a single protein patch. If this value was smaller than the threshold, the protein patch was extended if the next n nucleotides or basepairs were not already covered by protein. Extension was only permitted into the direction of higher numbers in the one-dimensional array.

The probabilities for nucleation and growth per time step were taken so small, that the chance of two binding events within a single Monte Carlo step was negligible. For comparison to experiments, the threshold values, which are rates expressed in units (Monte Carlo step)⁻¹, can convert into kinetic rates expressed in s⁻¹ by adjusting the time axis of the Monte Carlo growth curve to the experimental growth data. Whereas our simple modeling involved protein patch extension and disassembly in a unidirectional fashion, the model can be extended using protein patch extension and/or disassembly in both directions. Essentially the same results are found if extension and disassembly occur in both directions, albeit with two slightly different values for the rates that change by a factor up to 2.

In those cases where disassembly was considered, we additionally allowed dissociation to occur after the protein patch extension step. At each end of a protein patch (i.e., a protein cluster consisting of m protein monomers, with m ≥ 1) opposite to the protein-patch-extension end (i.e., toward lower numbers in the array), a value was extracted from a uniform distribution and if this value was smaller than the threshold set by the dissociation rate, the protein dissociated and a vacancy was created. In the case of diffusion of these end-bound monomers, the protein remained bound to the lattice. Alternatively, a second route was considered where dissociation was allowed at all monomer sites i.e., also in the middle of protein patches. Here, the above procedure was extended to all bound proteins.

Reorganization of individual proteins or protein patches along the DNA substrate was incorporated as follows: a value was randomly extracted from a uniform distribution yielding a value between 0 and 1. If this value was smaller than a given threshold corresponding to the reorganization rate, a step of the protein patch was made of one nucleotide or basepair. For unidirectional translocation, the direction was chosen uniformly, toward lower numbers in the array. For diffusive motion, the stepping direction was randomly toward higher/lower numbers in the array, when an extracted value from a uniform distribution was larger/smaller than 0.5. Diffusive motion of end-bound monomers after detachment was done similarly. Upon collision with individual proteins or protein patches, the diffusive motion was stopped.

To ensure the robustness of the code, all simulations were run a number of times (with different seeds) to validate that the outcome was similar for different runs. Typical data of the different scenarios is shown in the corresponding figures.

RESULTS

We modeled the interaction between proteins and DNA for a variety of processes, i.e., binding, dissociation, reorganization, and combinations of these. Protein-DNA binding can be divided into two different schemes—noncooperative and cooperative binding (see Fig. 1 A) (20–23). We first present the results for noncooperative binding of proteins to DNA.

Noncooperative binding

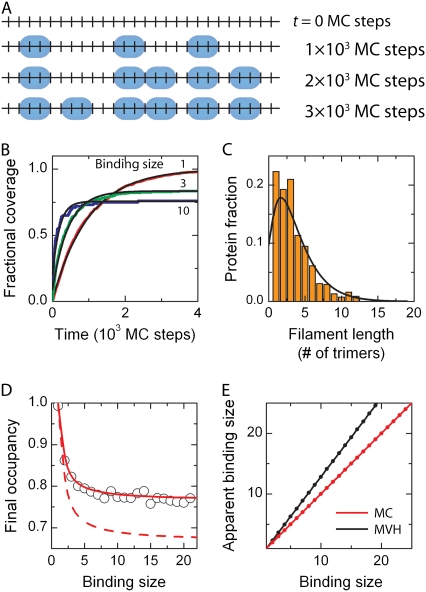
Noncooperative binding of proteins to a DNA molecule is modeled in the Monte Carlo simulations as random binding to a one-dimensional lattice. Upon binding, the protein covers a binding site of multiple nucleotides or basepairs. First, only binding is considered; i.e., once bound, a protein does not disassemble or rearrange. The occupancy of the lattice is followed in time (see Fig. 2 A). The resulting protein coverage displays an exponential growth profile, independent of the binding site size of the protein (see Fig. 2 B). The final occupancy, however, varies with respect to the chosen size of the binding site of the protein (see Fig. 2 D). For a binding site size of 1 nt, full occupancy is obtained, as expected. However, the fractional occupancy decreases for an increasing binding site size, reaching a plateau of ∼0.76 (Fig. 2 D). Due to the finite size of the binding site, gaps of unoccupied lattice elements with a size smaller than the binding site remain throughout the lattice (see bottom panel in Fig. 2 A for an example). The actual number of bound proteins to the lattice is therefore smaller than when all proteins would mutually align such that no gaps would remain on the lattice. Division of the length of the lattice by the number of bound proteins yields the apparent binding size for the protein, which is larger than its intrinsic binding size due to the existence of gaps. This leads to an increase in the apparent binding size of 29.5 ± 0.2% compared to the actual binding size (see Fig. 2 E).

FIGURE 2.

Noncooperative binding. (A) Snapshots of the DNA occupation by proteins at different times during a Monte Carlo simulation for noncooperative protein binding. This simulation is carried out for k = 5 × 10⁻⁶ site⁻¹ (MC step)⁻¹. As a protein covers 3 nt or 3 bp upon binding, binding can only occur if sufficient space is available. In the bottom panel, the simulation has reached its final state since no further proteins can bind. Gaps of 1 or 2 nt/bp are clear. (B) Time-dependent binding profiles are simulated for different binding sizes, i.e., n = 1, 3, and 10 (respectively red, green, and blue lines), showing an exponentially shaped growth curve (red line). Only for n = 1, full coverage is obtained. (C) The protein-patch length distribution of bound proteins in the saturated state has a maximum around a dimeric protein-patch length. The solid black line denotes the fit of Eq. 6 yielding a cooperativity number of 1.0 ± 0.3. (D) After protein coverage has saturated, the final occupancy of the substrate was determined. With increasing binding site size of the protein, the final occupancy decreased and finally reaches a plateau of ∼76%. The dependence is quite well described by Eq. 5 (red line). The dashed red line indicates the dependence when the gap size corresponds to 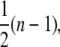which clearly fails to describe the data. (E) The apparent binding site size of the protein can deviate from the actual binding site size due to the existence of gaps between bound proteins. In the Monte Carlo simulations the apparent binding site size is equivalent to the real size (red line). The obtained values in the MVH model overestimate the actual value by ∼30% (black line).

The kinetics of simple noncooperative binding can be described analytically as follows (21). The binding process is limited by the amount of free basepairs available on the DNA molecule (see Fig. 2 A). During growth the amount of free basepairs N_free decreases according to dN_free/dt=−aN_free, where a is the binding rate of the protein to the lattice, which together with the boundary condition of N_free(0) = N yields N_free = Ne^−at. The time-dependent occupancy θ becomes

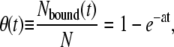(3)

showing an exponential binding profile in excellent agreement with the profiles obtained in the Monte Carlo simulations (see black lines in Fig. 2 B).

The final occupancy depends on the binding size n of the protein. A lattice that consists of N possible binding sites allows binding up to (N/n) proteins. During a noncooperative binding process, gaps of size i (1 ≤ i ≤ n – 1) are created throughout the entire lattice reducing the final amount of proteins on the DNA. For the final state, an effective binding size n* = n + s_gap can be defined, where s_gap is the average gap size between proteins. This average gap size between proteins is not equivalent to 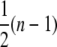but instead 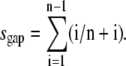When the binding size increases, the possible gap sizes increase accordingly. Therefore, one needs to take into account the actual number of proteins with an adjacent gap size i that is bound to the lattice decreasing as (n + i)⁻¹ and not as n⁻¹. Together, this yields for the fractional occupancy

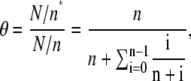(4)

which can be simplified into

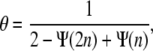(5)

where 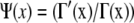and Γ(x) is the γ-function. This relation between fractional coverage and binding site indeed describes the observed behavior from our Monte Carlo simulations well; see the solid red line in Fig. 2 D. The fractional coverage for a protein covering two sites (n = 2) is 0.857, close to the result of 0.865 derived by Flory (24) using combinatorial techniques. For large binding sites, noncooperative binding is similar to the car-parking problem, where one-dimensional cars are parked randomly in a linear array (25,26). Equation 5 yields a fractional coverage of 0.765 for n → ∞ in fairly good agreement with the result of 0.748 obtained for the car-parking problem (25).

Cooperative binding

Cooperative binding of proteins to a DNA molecule is modeled in the Monte Carlo simulations in two steps: nucleation followed by extension. “Nucleation” denotes protein binding at an unoccupied DNA position not adjacent to already bound proteins, whereas we define “extension” as binding to a site directly adjacent to one that is already occupied. We can follow the binding process to the lattice in the Monte Carlo simulations in time by visualizing the binding of every individual protein (or protein cluster if binding occurs via multimers); see Fig. 3, A and B. Using these simulations, we obtained lattice occupancy profiles at different ratios between extension and nucleation (Fig. 3, C and D). Different qualitative behavior is observed, depending on the ratio between rates for extension and nucleation, henceforth called the cooperativity number ω. For a high cooperativity number (i.e., when nucleation is rare; see solid line in Fig. 3, A and B), nothing happens until a first nucleation event occurs, after which the coverage of the DNA molecule increases linearly due to the extension of the protein patch. By contrast, at low cooperativity numbers, many nucleation loci are created followed by extension into multiple protein patches. The process ends when the molecule has no more free binding sites that are large enough to accommodate binding of another protein or protein cluster. With increasing cooperativity numbers, the obtained time-dependent binding profiles change from an exponential (for a ratio of zero, equivalent to noncooperative binding) to a linear relationship (for ratios >10⁶) (see Fig. 3, C and D). The final fractional coverage of the lattice increases for increasing cooperativity values, because the final amount of gaps is reduced (Fig. 3 G) (20,27). Although extension can be orders-of-magnitude larger than nucleation, full coverage is hardly ever obtained for n ≥ 2.

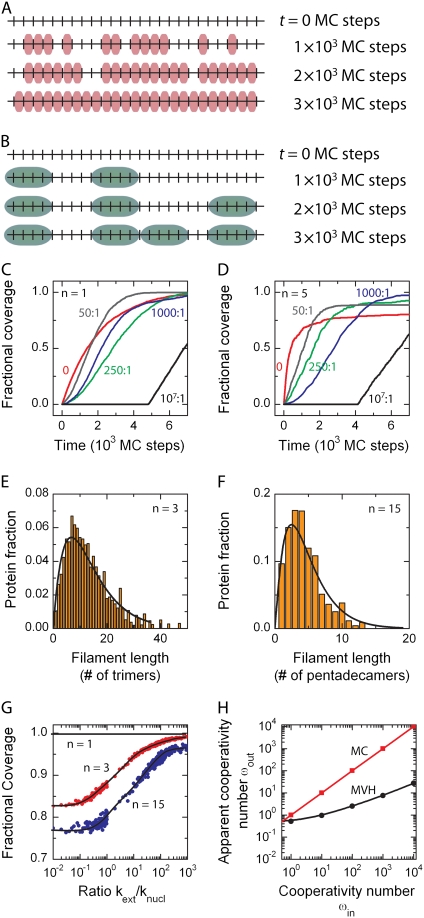
FIGURE 3.

Cooperative binding. (A) Snapshots of the DNA occupation by protein at different times during a Monte Carlo simulation for cooperative protein binding. This simulation is carried out for k_nucl = 1 × 10⁻⁶ site⁻¹ (MC step)⁻¹, k_ext = 5 × 10⁻⁵ (MC step)⁻¹, and a binding size n = 1. Due to the fast nucleation rate, multiple protein patches are formed along the DNA substrate. Because the protein covers only a single nucleotide or basepair, the final state (bottom panel) is a fully saturated lattice. (B) For a binding size >1, here n = 5, a similar intermediate state is observed for equivalent binding rates, but the final state contains gaps since no further proteins can bind. (C) Time-dependent lattice occupancy profiles are obtained from the simulations for different levels of cooperativity. If only random binding (nucleation) occurs along the contour length of the DNA molecule (noncooperative binding; see top left), an exponential lattice occupancy profile is obtained. However, if protein-patch extension is fast compared to nucleation, e.g., for a ratio >10⁶ (strong cooperative binding; see bottom right), the lattice occupancy profile becomes linear and the molecule can be fully covered by the protein. For intermediate ratios between protein-patch extension and nucleation, sigmoidally shaped lattice occupancy profiles are observed. All lattice occupancy profiles reach complete saturation because the binding site size of the protein is one nucleotide or basepair in this case. (D) For n = 5 a similar change in binding profiles is observed, but complete saturation is not obtained. (E) The protein patch-length distribution for a protein with a binding-site size of three nucleotides or basepairs at a cooperativity number of ω_in = 100. The solid line denotes the best fit obtained with Eq. 6, yielding a cooperativity ω_out of 2.3 ± 0.3. (F) Similar scheme, but for a protein with a binding site size of 15 nucleotides or basepairs, yielded a cooperativity number of 10.8 ± 1.0 using Eq. 6. (G) Final occupancy of the substrate for varying numbers of cooperativity. If the binding site size is one nucleotide or basepair, full coverage is always obtained. For larger binding site sizes, the final occupancy increases with the applied cooperativity number approaching the full 100% at very high k_ext/k_nucl. (H) Apparent cooperativity number ω_out versus actual cooperativity number ω_in. For varying cooperativity numbers (ω_in), the protein patch-length distribution is determined for n = 3. Subsequently, the simulated distributions are fit with Eq. 6 to obtain a measure for the apparent cooperativity number (ω_out). For nucleation-driven reactions (ω_in = 1), the fit yields a value close to 1. For extension-driven reactions where the cooperativity number is >1, however, the obtained value ω_out deviates significantly from the input value ω_in.

The final distribution of protein clusters along the lattice can be quantified. Different protein-patch length distributions can be obtained depending on the size of the protein cluster that binds during nucleation and extension and the ratio between nucleation and extension rate (see Fig. 3, E and F). For the noncooperative case, the distribution of protein patch sizes peaks around the size of the binding unit with a long tail toward longer protein patches (see Fig. 2 C). An analytical expression for the protein-patch-length distribution F_c has been proposed by (27)

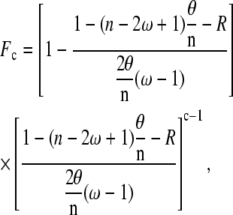(6)

where

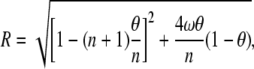(7)

and c the length of the protein patch. In the saturated state (θ = 1), the cluster size approaches infinity, independent of the binding site of the protein (27). This prediction for the noncooperative case of ω = 1 is not in agreement with the observed behavior where the distribution shows a Poissonian profile (see Fig. 2 C) due to the existence of gaps. We can fit the distributions for n ≥ 2 with Eq. 6, where one can reduce the number of free parameters to one, i.e., the cooperativity number ω, because the relative coverage θ is given by 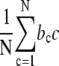with b_c the number of appearances of a protein patch with length c. Protein patch length distributions for n = 3 were fit for varying cooperativity numbers (ω_in) with Eq. 6 to obtain an apparent value for the cooperativity number (ω_out). Interestingly, the fits yield significant differences—even by orders of magnitude—between the values entered (ω_in) and obtained after fitting (ω_out) for the cooperativity number (see Fig. 3 H). Due to the finite lattice length and incomplete coverage, the fit severely underestimated the cooperativity number in all cases.

Multimeric binding and Hill coefficient

In the MVH model, it is assumed that the binding unit of the protein during nucleation and extension is the same. Both processes, however, in principle, can involve different protein multimers. The binding unit can be determined from concentration-dependent binding reactions where the binding rate in either nucleation or extension, is determined with respect to the protein concentration (see Fig. 4 A). This behavior can be described by the Hill equation

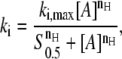(8)

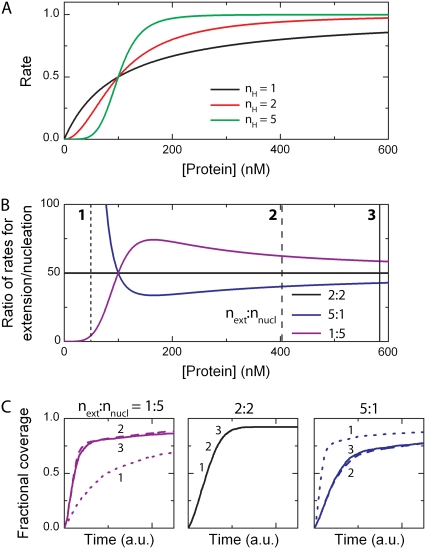
where n_H is the Hill coefficient and S_0.5 the concentration where half-maximum activity occurs. The Hill coefficient can be interpreted as the minimal size of the binding unit, i.e., for n_H = 1, the protein binds as a monomer to the lattice, whereas for larger values of n_H, the protein binds as a n_H-mer (28). This coordination between proteins, for example by binding of preformed multimers, is sometimes called cooperative binding, but this is entirely unrelated to the cooperative binding defined above (the ratio between extension and nucleation in protein patch formation). Within the Monte Carlo simulations, the binding unit in nucleation and extension can be varied independently. In the case where the binding units for nucleation and extension are equivalent, i.e., when the Hill coefficients are identical, the lattice occupancy profiles remain the same independent of protein concentration. On the other hand, if the binding units are not equivalent, the growth profiles and final occupancy change depending on the protein concentration (see Fig. 4 C).

FIGURE 4.

Influence of the Hill coefficient on the kinetic interaction between protein and DNA. (A) Concentration dependence of the binding rates. If the protein interacts as a monomer with the DNA substrate, the curve follows a Michaelis-Menten dependence (black). However, for larger complexes (Hill coefficient n_H ≥ 2), the profiles become sigmoidal (red and green for, respectively, a dimer and pentamer). (B) The ratio between extension and nucleation is concentration-dependent when the Hill coefficients differ for extension and nucleation. Blue and magenta denote the ratio between pentameric-monomeric and monomeric-pentameric binding units, respectively. (C) At three different concentrations (in order of increasing concentrations denoted by 1, 2, and 3 in the inset of panel A), the lattice occupancy profiles for the three independent cases are depicted. The black curves for n_H = 2 (middle panel) in both nucleation and extension are the same for various protein concentrations. The magenta and blue curves, for n_ext: n_nucl = 1:5 and 5:1, respectively, are protein-concentration dependent. It is clear that the lattice occupancy profiles change when the ratio is not constant in the applied concentration regime.

Dissociation

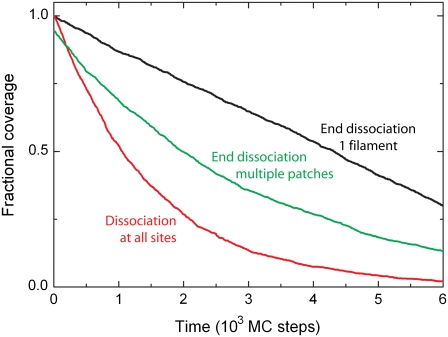
In the above binding schemes, the binding was taken to be irreversible. However, proteins bound to a lattice can have a probability to detach from the lattice, i.e., they dissociate (22). Two different scenarios can be envisioned (see Fig. 1 B). As longer protein patches are formed on the lattice, 1), only proteins located at an end of a patch are allowed to dissociate (29,30); or 2), all proteins are allowed to dissociate regardless of their position within the patch (31). For the latter, the Monte Carlo simulations show an exponentially shaped disassembly curve (see red line in Fig. 5), as expected. This dissociation behavior is independent of the assembly history. Dissociation is, however, linear when dissociation occurs only at the end of a single protein patch (see black line in Fig. 5). If growth has resulted in a multitude of small patches, end dissociation, however, also leads to an exponentially shaped profile (see green line in Fig. 5) (30).

FIGURE 5.

Protein dissociation. After proteins have formed a single continuous filament on the DNA substrate, a linear decrease is observed when the protein disassembles from one end with k_dis = 0.2 (MC step)⁻¹ (black line). When all bound proteins have the same probability to dissociate irrespective of their position in the protein complex, an exponentially shaped disassembly curved is obtained with k_dis = 6.7 × 10⁻⁴ (MC step)⁻¹ (red line). If the proteins form multiple short protein patches on the DNA substrate with bare DNA in between, end-dependent disassembly shows again an exponentially shaped disassembly profile with k_dis = 2.2 × 10⁻³ (MC step)⁻¹ (green line).

These observations can be understood straightforwardly. For noncooperative binding, bound proteins do not gain from protein-protein interactions and equivalently, once bound, every protein has an equal probability to dissociate. Following a similar reasoning as above for binding (Eq. 3), this yields an exponential dissociation profile, in agreement with the Monte Carlo simulations. In the case of cooperatively bound proteins, dissociation results in a linear profile only if a single protein patch exists on the lattice, because the proteins can only dissociate from one end, as indeed observed in the Monte Carlo simulations. Multiple patches result in multiple end-dissociation points, and the broad size distribution of the patches then leads to an approximately exponential dissociation curve (29,30).

Rearrangements

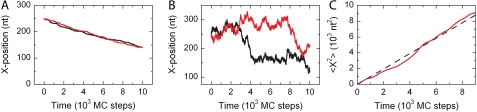
We also consider in our simulations the spatial rearrangement of proteins on the DNA, where bound proteins can move linearly along the DNA. This is modeled by three different pathways (see Fig. 1 C): 1), the protein cluster moves diffusively; or 2), the protein cluster translocates unidirectionally along the DNA molecule; or 3), end-bound monomers detach and move diffusively toward the neighboring protein cluster. Diffusive movement of the protein leads to a random walk in the Monte Carlo simulations (Fig. 6 B). Unidirectional motion leads to an approximately linear relation between traveled distance and time, as expected (see Fig. 6 A). Unidirectional motion is of course only possible at the expense of an available energy source, e.g., ATP hydrolysis.

FIGURE 6.

Linear motion of a protein. (A) The position of a protein bound to the DNA substrate is followed while allowing unidirectional motion with k_uni = 0.01 (MC step)⁻¹. This yields an approximately linear decrease in time. (B) For a diffusive process with k_dif = 0.01 (MC step)⁻¹, the position of the protein along the DNA substrate displays a random walk. (C) As expected for a diffusive process, the mean-square displacement of a protein increases approximately linearly in time. The obtained diffusion constant is 0.0049 nt² (MC step)⁻¹ in excellent agreement with the expected rate of diffusion, 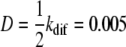nt² (MC step)⁻¹.

One-dimensional diffusive motion of a protein cluster along the lattice can be written as 〈x²〉 = 2Dt, where 〈x²〉 is the average mean-square displacement, D the diffusion coefficient, and t the time that the protein is moving along the lattice. As shown in Fig. 6 C, the average mean-square displacement of a single protein over a given time window indeed follows this relation.

So far, we have considered that, upon dissociation, an end-bound monomer detaches from the protein cluster on the DNA and vanishes to bulk solution. Instead of dissociation into the bulk solution, the detached monomer can also remain bound to the DNA molecule as sketched in scenario 3 (lower mode in Fig. 1 C). After end detachment, the monomer diffuses freely between two protein clusters (32). When the monomer reaches either protein cluster, it will bind.

Combination of processes

Above we have shown different interaction modes for a protein with the DNA substrate, i.e., (non)cooperative binding, dissociation, and reorganization. In the simulations, these modes can be combined in various ways to sort out the different processes that contribute to the occupancy of the lattice. Combination of these pathways can yield very different results. Here, we visualize these using kymographs, graphs that represent the one-dimensional lattice occupancy on one axis and time on the other (33).

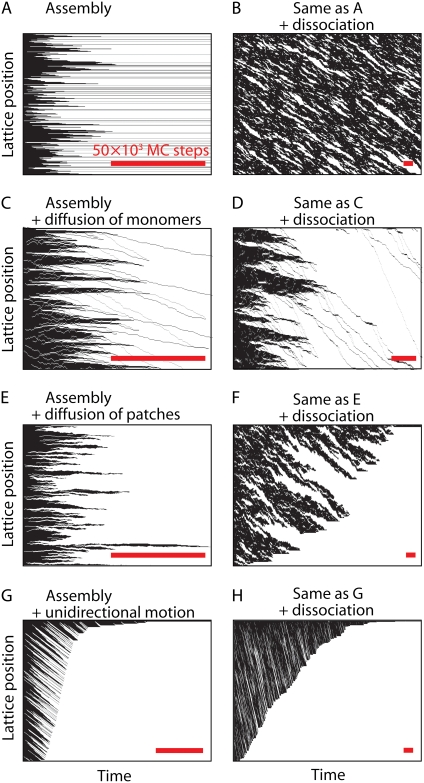
Fig. 7 A shows a kymograph for cooperative binding, where the final lattice is not completely covered because gaps between protein clusters remain on the lattice. The grayscale in the kymographs indicate protein-bound (open) and protein-free (solid) DNA substrate. The permanent gaps in Fig. 7 A thus are seen as the solid horizontal lines that persist over time. Cooperative binding in the presence of end-dependent disassembly yields a different behavior (Fig. 7 B). As can be seen in Fig. 7 B, protein patches appear and disappear in time at different positions on the lattice. The dissociation rate is chosen such that the fractional coverage on the lattice remains approximately constant in time.

FIGURE 7.

Kymographs for various combinations of protein-DNA interactions. (A) Cooperative protein binding is visualized in time, where open representation corresponds to proteins occupying lattice sites and solid representation denotes unoccupied lattice positions. The simulation is carried out for n = 3, k_nucl =3× 10⁻⁵ site⁻¹ (MC step)⁻¹, and k_ext = 5 × 10⁻⁴ (MC step)⁻¹. In the final saturated state, gaps remain smaller than the binding size of the protein. (B) In the presence of end-dependent disassembly, k_dis = 7 × 10⁻⁴ (cluster end)⁻¹ (MC step)⁻¹, protein patches appear and disappear on the lattice. (C) Cooperative binding and diffusive motion of detached end-bound monomers, k_det = 0.01 (MC step)⁻¹, and k_step = 0.1 (MC step)⁻¹, yields a completely covered lattice. (D) In the presence of dissociation of detached monomers, k_dis = 7 × 10⁻⁴ (detached monomer)⁻¹ (MC step)⁻¹, a combination of cooperative binding, dissociation, and diffusive motion of detached end-bound monomers also yields a completely covered lattice albeit on a longer timescale. (E) Cooperative binding and diffusive motion of protein patches, k_dif = 0.01 (MC step)⁻¹, yields a single continuous protein complex. (F) A combination of cooperative binding, dissociation, and diffusive motion leads to the formation of single continuous protein complex albeit on a longer timescale. (G) A similar saturated end state is observed for cooperative binding and unidirectional motion of protein patches, k_uni = 0.01 (MC step)⁻¹. (H) Same as panel F, but with unidirectional instead of diffusive motion. This also eventually leads to the formation of a single continuous protein complex.

Upon allowing reorganization of detached end-bound monomers or bound protein patches either by diffusive or unidirectional motion, a completely covered lattice is obtained (see Fig. 7, C, E, and G, respectively). Unidirectional movement of the protein patches is observed in the kymographs by linear stripes in the downward direction (Fig. 7 G), which represent protein patches that shift and fuse with other patches at the bottom. Diffusive motion of monomers or protein patches leads to a more strongly fluctuating behavior (Fig. 7, C and E). Also, upon combining all three modes—cooperative growth, rearrangement, and end-dependent disassembly—the final lattice is completely covered (Fig. 7, D, F, and H). Note that the timescale now has significantly increased due to the presence of protein dissociation before saturation is obtained. The downward motion observed for one-dimensional diffusion is caused by protein monomers that erode from patches and after a diffusive walk, end up at the next patch. A similar behavior is observed in Fig. 7 B.

DISCUSSION

Using Monte Carlo simulations, we have modeled different interactions between protein and DNA, i.e., (non)cooperative binding, dissociation, and reorganization. The flexibility of the Monte Carlo simulations allows our using different binding-site sizes of the protein during nucleation, filament extension, or dissociation. The Monte Carlo simulations of the different interactions yielded interesting results. First, the DNA substrate is almost never completely covered by protein when taking binding only, into account. Gaps remain on the substrate smaller than the binding site size of the protein. Second, the apparent binding size of a protein during noncooperative binding can be overestimated by up to 30% due to the existence of gaps. Furthermore, the fractional coverage increases for higher numbers of cooperativity. Finally, the dissociation behavior of cooperatively bound protein can lead to an exponentially shaped dissociation curve even when allowing only end-dependent dissociation (30,31).

We can compare the benefits of our Monte Carlo simulations to the MVH model and hidden Markov modeling. MVH derived equations to describe the binding of a protein to a lattice while taking into account cooperativity. This model has been applied numerous times in equilibrium studies to extract binding constants and the cooperativity number. The model fails, however, to address the kinetics of individual proteins when dissociation and translocation of bound proteins are relevant. Furthermore, the final occupancy of the lattice is (incorrectly) always complete despite the finite binding site size of the protein involved. Indeed, our Monte Carlo results show that the MVH cooperativity number extracted from filament length distributions did not correspond to the input value. Finally, the binding site sizes of the protein during nucleation and protein patch extension in the original MVH model are identical, whereas in an experiment they can be different.

In contrast to the MVH model, hidden Markov modeling allows addressing the reaction kinetics. Due to the modular setup of a Markov chain, different interaction pathways can be modeled. However, hidden Markov modeling cannot cope with systems where different pathways influence the outcome of each other.

With Monte Carlo simulations, protein-DNA interactions can be followed in time for each protein involved. A disadvantage is that it takes a fair amount of computational power to simulate the kinetics of complex pathways in Monte Carlo simulations, but not unreasonably so. (The current results were obtained on a PC with an integrated computation time of three weeks.)

Application of Monte Carlo modeling

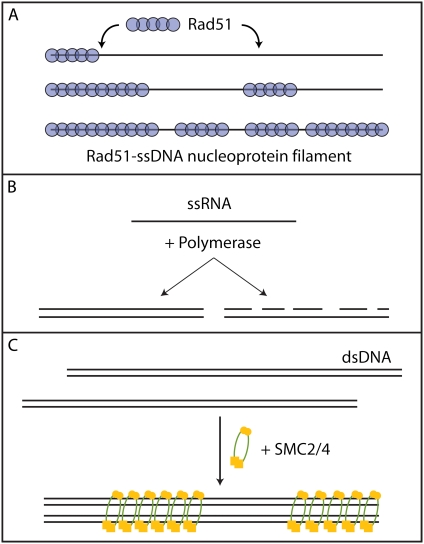
The Monte Carlo simulations described here can be applied to a variety of experimental systems. We briefly mention a few examples. A system to which this method was applied, was the interaction between the RecA-like recombinase RAD51 and DNA (12) (see Fig. 8 A). Using magnetic tweezers, the end-to-end distance of a tethered DNA molecule was followed in time while RAD51 was allowed to bind forming a nucleoprotein filament. Upon binding to the DNA substrate, RAD51 induces a change in end-to-end distance yielding a measure for the lattice occupancy. The induced changes in end-to-end distance were fit with Monte Carlo simulated binding profiles yielding all relevant single RAD51 (dis)assembly rates.

FIGURE 8.

Different biological systems to which the current Monte Carlo simulations can be applied. (A) The interaction between the RecA-like recombinase RAD51 and DNA was successfully modeled using the analysis described. This showed that RAD51 binds cooperatively to DNA forming short nucleoprotein filaments (12). (B) RNA polymerase transforms a single-stranded template into a double-stranded substrate in the presence of free nucleotides. Two different pathways exist. In the most common pathway, the polymerase creates full-length templates, whereas in the other case, known as abortive initiation, the polymerase forms short oligomers. The pathways are similar to, respectively, a high- and low-cooperative binding mode. (C) Structural maintenance of chromosomes (SMC) proteins form condensed DNA structures by binding cooperatively to DNA holding two DNA molecules in close proximity.

Another useful application would be RNA-dependent RNA polymerases. These polymerases can either generate template-long duplexes by synthesizing full-length RNA chains in one run, or generate many short duplexes by synthesizing short complementary RNA oligonucleotides scattered along the RNA template, known as abortive initiation (see Fig. 8 B) (34). The former is a highly cooperative binding mode, whereas abortive initiation corresponds to a low-cooperative binding mode. This can be experimentally measured because the creation of duplex RNA from a single strand template increases the stiffness of the RNA molecule yielding a change in end-to-end distance of a tethered molecule in, e.g., a tweezers setup. These changes in end-to-end distance can be analyzed with the Monte Carlo simulations yielding values for the rates of initiation and duplex extension.

Other protein-DNA binding reactions can be analyzed as well. The case of single-stranded binding proteins like SSB and RPA, or nucleosome binding to DNA, is conceptually very similar to the RAD51 binding that we have already described. Another example is structural maintenance of chromosome (SMC) proteins, which are the central components of several multiprotein complexes that help to organize chromosomes throughout the cell cycle (35) (Fig. 8 C). The analysis presented here provides a basis for quantification of, for example, the binding size, the presence of any cooperativity involved, or possible reorganization during binding of SMC proteins with DNA.

CONCLUSION

To overcome certain limitations of the classic MVH model and the hidden Markov model, we have used Monte Carlo simulations to model ligand-lattice interaction. These Monte Carlo simulations allow determination of protein-related binding rates even when multiple proteins interact simultaneously with the lattice. This tool was applied to understand RAD51-DNA interaction. Application of this analytical tool can be extended to other systems where cooperativity plays a crucial role, like single-stranded binding proteins, polymerases, and SMC proteins.