Abstract
Recently, electron microscopy measurement of single particles has enabled us to reconstruct a low-resolution 3D density map of large biomolecular complexes. If structures of the complex subunits can be solved by x-ray crystallography at atomic resolution, fitting these models into the 3D density map can generate an atomic resolution model of the entire large complex. The fitting of multiple subunits, however, generally requires large computational costs; therefore, development of an efficient algorithm is required. We developed a fast fitting program, “gmfit”, which employs a Gaussian mixture model (GMM) to represent approximated shapes of the 3D density map and the atomic models. A GMM is a distribution function composed by adding together several 3D Gaussian density functions. Because our model analytically provides an integral of a product of two distribution functions, it enables us to quickly calculate the fitness of the density map and the atomic models. Using the integral, two types of potential energy function are introduced: the attraction potential energy between a 3D density map and each subunit, and the repulsion potential energy between subunits. The restraint energy for symmetry is also employed to build symmetrical origomeric complexes. To find the optimal configuration of subunits, we randomly generated initial configurations of subunit models, and performed a steepest-descent method using forces and torques of the three potential energies. Comparison between an original density map and its GMM showed that the required number of Gaussian distribution functions for a given accuracy depended on both resolution and molecular size. We then performed test fitting calculations for simulated low-resolution density maps of atomic models of homodimer, trimer, and hexamer, using different search parameters. The results indicated that our method was able to rebuild atomic models of a complex even for maps of 30 Å resolution if sufficient numbers (eight or more) of Gaussian distribution functions were employed for each subunit, and the symmetric restraints were assigned for complexes with more than three subunits. As a more realistic test, we tried to build an atomic model of the GroEL/ES complex by fitting 21-subunit atomic models into the 3D density map obtained by cryoelectron microscopy using the C7 symmetric restraints. A model with low root mean-square deviations (14.7 Å) was obtained as the lowest-energy model, showing that our fitting method was reasonably accurate. Inclusion of other restraints from biological and biochemical experiments could further enhance the accuracy.
INTRODUCTION
Protein-protein interactions support a wide range of cellular processes in all forms of life, from bacterial cell division to mammalian immunity (1). Recently, high-throughput screening methods, such as the yeast-two-hybrid method and tandem affinity purification, have generated large datasets of protein-protein interactions (2,3). Although these data provide a wealth of information about cellular processes, they do not elucidate either how these proteins interact or how they are spatially arranged within a complex. X-ray crystallography is the most accurate method for solving the 3D structure of protein-protein complexes; however, it is suitable only for molecules that can be purified in sufficient quantity and crystallized. The gap between high-throughput screening method and x-ray crystallography is now being closed with the aid of new experimental techniques such as cryoelectron microscopy (cryo-EM; for reviews, see (4–7)). An electron microscopy measurement of single particles can provide a low-resolution 3D density map of a large biomolecular complex composed of many proteins, although its resolution is in the medium range. These 3D density map data have been accumulated in the electron microscopy database (EMDB) (8,9). The number of registered data of the EMDB is now ∼500; their resolutions range from 3.8 to 85.0 Å, with an average value of 18.6 Å. If atomic models of subunit structures in the complex are available from x-ray crystallography or homology modeling studies, fitting these atomic models into cryoelectron-microscopy maps has yielded pseudoatomic models of macromolecular complexes. Recently, many macromolecular models have been proposed by this fitting technique: viral subunits (10), ribosome and ribosome-interacting proteins (11), clathrin lattice (12), and clamp-loading complex (13).
Initially, the fitting of atomic models into the low-resolution density map was performed by manual docking, in which expert researchers placed atomic models “by hand” using molecular graphic programs. The manual docking method is considered to be reliable, but it has weaknesses; it cannot show all the alternative solutions, and its solutions may lack objectivity. To overcome the limitations of manual docking, a variety of computational methods have been proposed (see reviews by (14,15)). We can characterize various proposed methods from two perspectives: scoring function and search method. The most popular scoring function is a correlation coefficient between a given density map and an expected low-resolution density map of atomic models. A locally normalized correlation function has also been proposed for cases in which an atomic model represents only a part of the density map (16). Matching with the contour-enhanced density maps has been employed by several researchers (17,18). Chacon and Wriggers showed that contour matching with a Laplacian filter was effective for fitting into the density map with ∼30 Å resolution (17). A search method is also important for correct modeling. The difficulty of searching depends on the number of subunits to be optimized; six degrees of freedom are required for each subunit. The most primitive search method is an exhaustive search, in which all the parameters are equally sampled using a given step size. This method is practical if only one rigid subunit is to be optimized (six degrees of freedom are required). Stochastic search methods, such as Monte Carlo and simulated annealing methods were employed to enhance sampling efficiencies (19–21). The fast Fourier transfer algorithm was also applied to reduce the computational cost of searching translation (17) and rotation (22). The vector quantization method was unique in both scoring function and search method (23,24). This method employed the set of 3D points as approximations for both the atomic models and 3D density map; all the possible matches between the two sets of points were exhaustively examined. The difference in distances between the corresponding points was employed as a scoring function.
Fitting subunits into a low-resolution density map presents three major problems. The first problem is the large computational cost of searching, especially for multiple-subunit complexes. The more subunits there are to be optimized, the harder it becomes to find the optimal position for each subunit. For this reason, most existing programs fit only one subunit into a density map. For a multiple-subunit complex, these programs often optimize subunits one by one, sequentially, avoiding spaces occupied by the previous subunits (17,19). However, this sequential strategy may not always find the best solutions, because the position of first subunit is not modified by following optimizations. The second problem is that some low-resolution 3D density maps have insufficient information for determining one optimal configuration of subunits. In these cases, multiple different subunit configurations yield similar fitness scores, and additional biochemical or biophysical information must be introduced to help decide the true configuration. Recently, Alber et al. (2007) tackled the modeling of the nuclear pore complex, assembling 456 subunit proteins into a low-resolution density map (21). Because of the large number of subunits, they used many spatial restraints adapted from a wide range of experimental data. Their approach demonstrates that a fitting program should be extendable, so that many kinds of experimental information can be included. The third problem is that subunits can undergo conformational changes upon association. To simulate realistic conformational changes, several approaches have been proposed. In some studies, the subunit is divided into domains, which are independently fitted as separate rigid bodies (11). Wriggers et al. employed a full-atomic molecular mechanics with a constraint energy that penalizes the distance between centroids of atoms in the Voronoi cell and the corresponding codebook vectors (25–27). Recently, normal-mode analysis based on elastic models has been applied for flexible fitting (28,29). Even employing these methods, however, it is still difficult to simulate realistic large conformational changes.
In this study, we mainly focus on the first problem, i.e., the large computational cost of modeling multiple-subunit complexes. To reduce the computational costs, we propose a new, to our knowledge, representation of molecules using a Gaussian mixture model (GMM). The GMM is a probability distribution function consisting of linear combinations of several Gaussian functions. It was first proposed in the 1930s as a means for estimating the probability distribution functions from large amounts of observed data; in the 1980s, the expectation maximization algorithm was proposed to efficiently estimate the parameters of the model (30). Because of its flexibility, the GMM has been applied to various problems involving clustering and probabilistic modeling. In the field of molecular biology, it has been applied to the clustering of microarray expression data (31,32), as well as to the spatial probability distribution of protein atoms around a binding ligand (33). We used a Gaussian distribution function (GDF) for approximating the geometry of complicated atomic structures and density maps of macromolecular complexes. As far as we know, this is the first study in which the GMM has been applied for reducing representation of 3D macromolecular shapes. The model has at least four advantages. First, the GMM has the ability to express any type of distribution using a reasonably small number of parameters. Second, a low-resolution density map often does not have a clear boundary between molecules and empty space; therefore, it is suitable to represent it by a probability density function. Third, the GMM enables us to quickly calculate the fitness of the density map and the subunit models, because the overlap of the product of two GDFs can be analytically obtained. Fourth, the gradient and the torque of the overlap can also be analytically calculated, and various gradient-based local optimization methods can be applied. In this article, we first explain the concepts of the GMM and our method of estimating parameters; concomitantly, we introduce three energy functions between the models, as well as methods for optimization. The ability of our method to approximate a density map is evaluated on a homotrimer and the GroEL/ES complex. As simple test cases, simulated low-resolution density maps of atomic models of a homodimer, a trimer, and a hexamer were generated, and their subunits were fitted using the GMM. As a more realistic test, we tried to build an atomic model of the GroEL/ES complex by fitting 21-subunit atomic models into the 3D density map obtained by cryo-EM, using C7 symmetric restraints.
FITTING PROCEDURES
Overview of the fitting procedures
The aim of this study was to build atomic models of complex structures by fitting atomic models of subunits into a low-resolution 3D density map of their complex structure. Both the atomic models and the 3D density map are first changed to GMMs. Fitting of the subunit GMMs into the complex GMMs is performed using random generation of initial configurations and steepest-descent local searches using gradients and torques of the energy. Finally, the atomic model of the complex structure is obtained by transforming the subunit atomic models, with the optimal positions and orientations obtained by the fitting calculation driven by the GMMs. This procedure is shown schematically in Fig. 1. We call our fitting program “gmfit” (Gaussian Mixture macromolecule FITting). The program was mainly implemented in C.
FIGURE 1.
Outline of fitting of subunit atomic models into a 3D density map of their complex, using a GMM.
Gaussian mixture model
The GMM was developed to estimate a putative probabilistic distribution function (30). We suppose that the density of a molecule can be written in the form
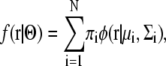 |
where r is the observed probabilistic variable, N is the number of GDFs, φ(r|μi,Σi) is the ith GDF in 3D space, πi is its weight, and Θ indicates the set of parameters for describing N GDFs. The sum of the weights πi should be 1:
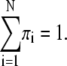 |
The GDF in 3D space is written as
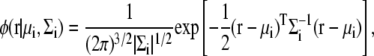 |
where μi is the mean position, Σi is the covariance matrix of the distribution, and |Σi| is the determinant of the matrix Σi.
Parameter estimation from a set of atom positions
The expectation maximization algorithm is widely used for estimating probable parameters of the GMM for a given set of observed data points (30). In this study, a set of 3D coordinates of L heavy atoms (r1,r2,…,rL) for a subunit atomic model is taken as the observed data points (schematically shown in Fig. 2). To estimate the most probable density function for generating the observed points, the following log-likelihood log Latom should be maximized by changing the parameter set Θ:
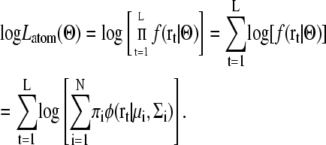 |
FIGURE 2.
Expectation maximization algorithm (EM algorithm) estimates a GMM from observed 3D data points.
For maximizing the likelihood log Latom(Θ), the expectation maximization algorithm iteratively updates each parameter according to the equations (30,34)
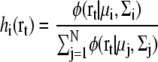 |
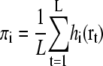 |
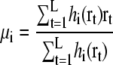 |
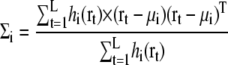 |
In this study, the initial parameters are derived using K-means clustering method (34). The number of GDFs, N, controls the resolution of the GMM. A larger N generates a more detailed density functions, but requires larger computational time for the estimation of parameters, and for the optimal configuration search. The log-likelihood log Latom assumes that all the heavy atoms have approximately equal atomic weights. This approximation will not be serious for modeling protein complexes, because atomic numbers for protein heavy atoms are relatively uniform.
Parameter estimation from a set of grid points with densities
A GMM for the 3D density map can be obtained using a similar expectation maximization algorithm. Let us assume that a 3D density map is represented by L grid points (r1,r2,…,rL), and that each grid point rt has its own density ρ(rt). To estimate a GMM for the 3D density map, we modified the likelihood as follows:
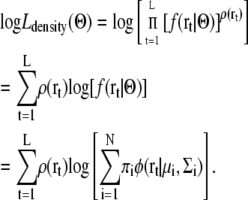 |
We assume that the number of observations at a grid point r is proportional to its density ρ(r). The expectation maximization algorithm for maximizing this likelihood Ldensity(Θ) is modified as follows:
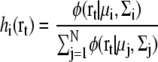 |
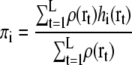 |
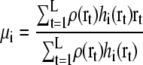 |
 |
Overlap function between Gaussian mixture models
An overlap function ov is introduced to define interaction energies between GMMs. ov is the integral of the product of two distribution functions fA and fB over all space:
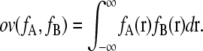 |
The overlap function between two GDFs φA(r) = φ(r|μA,ΣA) and φB(r)=φ(r|μB,ΣB) can be analytically obtained as follows:
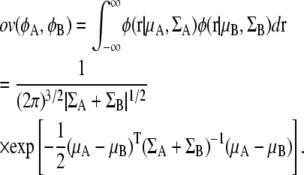 |
Using this equation, the overlap function between two Gaussian mixture functions also can be calculated analytically. Let us assume that two Gaussian mixture distributions fA and fB are defined as
 |
The overlap function for the two Gaussian mixture distributions fA and fB is obtained by the sum of the overlap function of two Gaussian distributions:
 |
Fitness energy and repulsion energy
At least two types of energies are required to generate a good complex model: fitness energy between the complex density map and subunits, and repulsion energy between subunits. Because both the complex density map and the subunit atomic models are represented by the sum of GDFs, the fitness energy and repulsion energy can be described by the sum of the overlap function ov of two GDFs. To begin with, we describe notations of GMMs of the complex image and the subunit atomic models. Let us assume that the distribution function fC(r) of the complex 3D density map and the distribution function fSa(r) of the ath subunit atomic model are represented by the sum of GDFs:
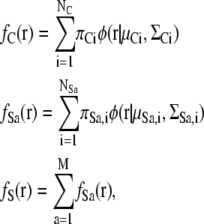 |
where M is the number of subunits. The center of gravity gSa of the Gaussian mixture distribution for the subunit Sa is defined as the weighted center of each GDF:
 |
Using the overlap function ov, the attractive fitness energy, Efit, between the 3D density map and the subunits, and the repulsive energy, Erep, between subunits can be described:
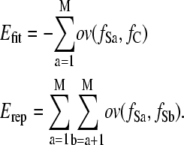 |
The energy Efit is similar to a correlation coefficient between the 3D density map and the subunits employed by many other previous studies, although our energy is independent of the variance of the distribution of subunits.
Restraint energy for symmetry
Macromolecules often contain identical subunits, and most of them are symmetrical oligomeric complexes (35). A restraint of symmetrical configuration will reduce the computational costs for finding the optimal configuration for complexes containing identical units. Among several proposed methods for prediction of symmetrical protein complexes, we chose the restraint energy for symmetry, which is similar to the method employed by Alber et al. (36). We assume that the types of point group symmetries (such as C3, C4, D2) for the target complex are given, and the initial configuration is generated to satisfy the given symmetry. The restraint energy for symmetry Esym is introduced for the corresponding pair of the models to keep the given symmetry:
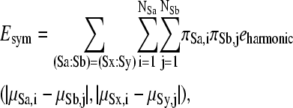 |
where (Sa:Sb) = (Sx:Sy) means that the geometry of subunit Sa relative to subunit Sb is equivalent to the geometry of the subunit Sx relative to the subunit Sy. The examples of corresponding geometric pairs for the typical point symmetries are shown in Fig. 3. The function eharmonic is the harmonic restraint function of two distances, defined as follows:
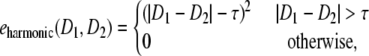 |
where D1 and D2 are distances and τ is the tolerance constant for restraint. We used τ = 5.0 Å in this study.
FIGURE 3.
Configurations (A–C) and corresponding pair tables (D–F) of subunits for typical point symmetric groups C3 (A and D), C4 (B and E), and D2 (C and F). A pair with the same letter code (a, b, or c) in the tables is a corresponding pair. Geometry of one subunit viewed from another subunit is equivalent to that of its corresponding pair.
Total energy Etotal can be described by the sum of Efit, Erep and Esym with weighting constants wfit, wrep and wsym:
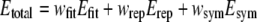 |
In this study, we employed wfit = wrep = 1.0 and wsym =10.0. As shown in the next section, this sets of weights yielded reasonably good fitting results, although we did not check performances of other weights systematically.
Searching procedures
Parameters to be optimized by the fitting calculations for each subunit Sa are the translation 3D vector ta and rotational 3D vector wa; the pose of the distribution function for complex density map fC(r) is fixed (shown in Fig. 4). To find the lowest-energy configuration, many initial configurations are randomly generated, and the steepest-descent local search is performed for each of them. For finding the global minimum, it will be sufficient to perform the local search only for the best part of the initially generated configurations, since the energy values of the initial configuration and its locally optimized configuration are correlated. We thus employ the following procedure: after Ninit random initial configurations are generated, they are sorted by their value of total energy, and only the best Ninit_locsch initial configurations are selected for the steepest-descent search. The ratio of Ninit_locsch and Ninit is empirically determined, and ranges between 0.1 and 1.0.
FIGURE 4.
Optimization of position and orientation of subunits (GMMs S1 and S2) to fit them into the fixed 3D density map of their complex (GMM C).
Generating random initial configurations is an important step in an efficient search for the optimal configuration. We decide the center of each subunit based on randomly chosen points from the GMM of the complex 3D density map. One GDF is randomly chosen using a πi-weighted uniform random number; a random 3D position from the chosen GDF is generated with three uniform random numbers and a triangular matrix of the covariance matrix (37). A rotation matrix for each subunit is randomly determined using a quaternion (38).
When symmetry of subunits is known, a random initial configuration is generated that satisfies the given symmetry: the configuration of the first subunit is randomly generated; those of the others are generated by rotational transformations of the first subunit. The rotational axis is chosen from the principal axes of the GMM of the 3D density map of the complex (39).
After generating many initial configurations, a steepest-descent search is performed. From the initial configuration of atomic models, the configuration of atomic models is repeatedly updated using the following equations:
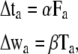 |
where Δta is the translational vector and Δwa is the rotational vector, Fa is the force for subunit a, and Ta is the torque for subunit a. The parameters α and β are determined by the linear search (40). Using the vectors Δta and Δwa, the center position μSa,i and covariance matrix ΣSa,i are updated as follows:
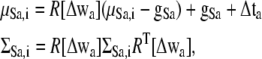 |
where gSa is the center of gravity of the subunit GMM Sa, and the matrix R[Δwa] is a rotational matrix obtained by the rotational vector Δwa. The mathematical formulas for Fa and Ta of the fitness energy are described in the Appendix. They are somewhat complicated, but can be calculated at low computational cost.
TEST CALCULATIONS
Required number of GDFs to approximate a 3D density map
We first estimated the required number of GDFs for approximating a low-resolution 3D density map with sufficient accuracy. A simulated low-resolution 3D density map was generated from an atomic model of the complex by placing the isotropic GDFs at the centers of heavy atoms of the model, assuming all the heavy atoms have equal atomic weights. The standard deviation of the isotropic Gaussian function for each atom was equal to half of the resolution of the 3D density map. Four types of low-resolution 3D density map (10, 15, 20, and 30 Å) were generated with the following grid widths: 2 Å for resolution values r ≤ 8 Å, 3 Å for resolutions 8 < r < 12 Å, and 4 Å for r > 12 Å (17,24). For each of the density maps, GMMs with different numbers of Gaussian functions were generated using the expectation maximization algorithm.
As the first example, we used a homotrimeric complex of nitrite reductase (41) (Protein Data Bank (PDB) code: 1nic). Fig. 5 summarizes the correlation coefficient values between the generated low-resolution density maps and their GMMs, plotted against the number of GDFs. The figure demonstrates that better resolution maps required a larger number of GDFs to achieve a given value of the correlation coefficient. For example, to obtain a correlation coefficient >0.98, only three GDFs were required for a density map of 30 Å resolution; however, 6 and 11 GDFs were required for 20 and 15 Å resolution, respectively. Fig. 6 graphically shows the density maps of simulated low-resolution data and corresponding GMMs having correlation coefficients >0.98.
FIGURE 5.
Correlation coefficient between the simulated low-resolution density map for the homotrimeric complex structure (PDB code: 1nic) and its GMM. The thick solid line, long-dashed line, thin solid line, and short-dashed line correspond to density maps of 10 Å, 15 Å, 20 Å, and 30 Å resolution, respectively.
FIGURE 6.
Simulated low-resolution density maps and GMMs for the homotrimeric complex structure. (A) Atomic model of the complex (PDB code: 1nic). (B–D) Simulated density maps with 30 Å, 20 Å, and 15 Å resolutions, respectively. (E) GMM using three GDFs generated from the 30-Å map (B). (F) GMM using six GDFs generated from the 20-Å map (C). (G) GMM using 11 GDFs generated from the 15-Å map (D). Correlation coefficients for the corresponding density pairs (B and E, C and F, and D and G) are >0.98.
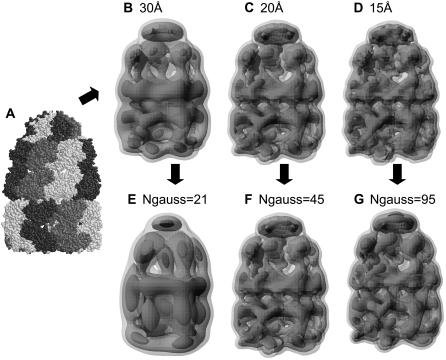
For a 21-subunit heterocomplex, GroEL/ES (42) (PDB code: 1aon), the same types of correlation coefficient plot are shown in Fig. 7, and density maps are shown in Fig. 8. To obtain correlation coefficients >0.98 for the 21-subunit complex, 21, 45, and 95 GDFs were required for density maps of 30, 20, and 15 Å resolution, respectively. Taken together with the results described above, these results show that the number of GDFs required also depends on the size of the complex, not only its resolution. From the five oligomer data (1afw, 1nic, 7cat, 1euz, and 1aon), we observed that the number of GDFs required for a given correlation coefficient was approximately proportional to the molecular size of the complex and the inverse of the resolution of the density map (data not shown). A correlation coefficient plot for the cryo-EM density map of the GroEL/ES complex (43) (EMDB code: emd_1046, resolution 23.5 Å) was also plotted in Fig. 7. It is of interest that the plot of the cryo-EM density map of 23.5 Å was similar to that of the simulated map of 20 Å, indicating that our simulated density maps were generated realistically.
FIGURE 7.
Correlation coefficient between the simulated low-resolution density map for the 21-subunit heterocomplex structure (PDB code: 1aon) and its GMM. The thick solid line, long-dashed line, thin solid line, and short-dashed line correspond to density maps of 10 Å, 15 Å, 20 Å, and 30 Å resolution, respectively. A thin dotted line corresponds to the correlation coefficients for the cryo-EM density map of the complex (EMDB code: emd_1046, resolution:23.5 Å).
FIGURE 8.
Simulated low-resolution density maps and GMMs for the 21-subunits heterocomplex structure. (A) Atomic model of the complex (PDB code:1 aon). (B–D) Simulated density maps with 30 Å, 20 Å, and 15 Å resolutions, respectively. (E) GMM using 21 GDFs generated from the 30-Å map (B). (F) GMM using 45 GDFs generated from the 20-Å map (C). (G) GMM using 95 GDFs generated from the 15-Å map (D). Correlation coefficients for the corresponding density pairs (B and E, C and F, and D and G) are >0.98.
Fitting calculation for the simulated low-resolution 3D density map
We next performed the fitting calculation, in this case, fitting subunit atomic models into a simulated density map generated from a known atomic model of a complex structure. The aim of the calculation was to test the performance of our fitting method and to find the 3D density map resolution and the number of GDFs required for accurate remodeling of the complex. We applied our fitting method to four symmetric homooligomers used in previous studies (17,24). The PDB codes for the four oligomers were 1afw (44) (homodimer, D2 symmetry), 1nic (41) (homotrimer, C3 symmetry), 7cat (45) (homotetramer, D2 symmetry), and 2rec (46) (homohexamer, C6 symmetry). We performed fitting calculations using 168 different parameter sets: three resolutions of the simulated 3D density map (10, 20, and 30 Å), seven different numbers of GDFs for the complex (2, 3, 4, 6, 12, 18, and 24 GDFs), four numbers for the subunit (4, 8, 16, and 32 GDFs), with and without the symmetric restraint. After generating Ninit = 1000 random initial configurations, only the best Ninit_locsch = 100 initial configurations were selected for the steepest-descent search.
Tables 1–4 summarize root mean-square deviations (RMSDs) between minimum-energy atomic structures and the original atomic structures registered in the PDB. No translation and rotation were performed for calculating the RMSD between two structures. Corresponding pairs of subunits for two homooligomers were decided to obtain the minimum RMSD value. Values of mean-square deviation were calculated for all the possible M! correspondences (M is the number of subunits), and the correspondence with the minimum mean-square deviation was chosen.
TABLE 1.
RMSD (Å) between modeled structures and the correct structure for the homodimer (PDB code: 1afw, C2 symmetry)
| Resolution (Å)† | No. of GDFs‡ | No. of GDFs per complex map§
|
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Symmetry* | 2 | 3 | 4 | 6 | 12 | 18 | 24 | ||
| False | 10 | 4 | 2 | 1 | 2 | 2 | 2 | 2 | 2 |
| 20 | 4 | 2 | 1 | 1 | 2 | 1 | 1 | 1 | |
| 30 | 4 | 2 | 3 | 2 | 1 | 1 | 2 | 2 | |
| 10 | 8 | 1 | 1 | 1 | 1 | 2 | 1 | 2 | |
| 20 | 8 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 30 | 8 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 10 | 16 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 20 | 16 | 1 | 2 | 1 | 1 | 1 | 1 | 1 | |
| 30 | 16 | 3 | 2 | 1 | 1 | 1 | 1 | 1 | |
| 10 | 32 | 2 | 2 | 2 | 2 | 1 | 0 | 0 | |
| 20 | 32 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 30 | 32 | 2 | 2 | 2 | 1 | 2 | 1 | 1 | |
| True | 10 | 4 | 2 | 1 | 2 | 2 | 2 | 2 | 2 |
| 20 | 4 | 2 | 1 | 1 | 2 | 1 | 1 | 1 | |
| 30 | 4 | 2 | 3 | 1 | 2 | 1 | 2 | 2 | |
| 10 | 8 | 1 | 1 | 2 | 1 | 2 | 1 | 2 | |
| 20 | 8 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 30 | 8 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 10 | 16 | 1 | 2 | 1 | 1 | 1 | 1 | 1 | |
| 20 | 16 | 1 | 1 | 1 | 2 | 1 | 1 | 1 | |
| 30 | 16 | 1 | 2 | 1 | 1 | 1 | 1 | 2 | |
| 10 | 32 | 1 | 2 | 2 | 2 | 1 | 1 | 0 | |
| 20 | 32 | 1 | 1 | 2 | 2 | 2 | 1 | 1 | |
| 30 | 32 | 2 | 2 | 1 | 2 | 1 | 2 | 2 | |
“True” indicates that the search was performed using a random symmetric initial configuration and restraint energy of symmetry. “False” indicates that these were not used.
A resolution value (Å) of a simulated 3D density map.
Number of GDFs for each subunit atomic model.
Number of GDFs for a 3D density map of the complex.
TABLE 2.
RMSD (Å) between modeled structures and the correct structure for the homotrimer (PDB code: 1nic, C3 symmetry)
| Resolution (Å)† | No. of GDFs‡ | No. of GDFs per complex map§
|
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Symmetry* | 2 | 3 | 4 | 6 | 2 | 18 | 24 | ||
| False | 10 | 4 | 29 | 13 | 11 | 9 | 2 | 2 | 3 |
| 20 | 4 | 29 | 12 | 10 | 9 | 2 | 3 | 3 | |
| 30 | 4 | 32 | 12 | 11 | 10 | 9 | 9 | 9 | |
| 10 | 8 | 22 | 2 | 3 | 2 | 2 | 2 | 2 | |
| 20 | 8 | 20 | 4 | 3 | 3 | 2 | 3 | 2 | |
| 30 | 8 | 29 | 5 | 6 | 4 | 4 | 3 | 3 | |
| 10 | 16 | 4 | 3 | 3 | 2 | 2 | 2 | 2 | |
| 20 | 16 | 28 | 3 | 4 | 3 | 2 | 2 | 2 | |
| 30 | 16 | 28 | 5 | 6 | 4 | 7 | 3 | 2 | |
| 10 | 32 | 24 | 18 | 3 | 1 | 2 | 2 | 1 | |
| 20 | 32 | 28 | 5 | 3 | 3 | 2 | 3 | 2 | |
| 30 | 32 | 28 | 3 | 8 | 4 | 4 | 7 | 5 | |
| True | 10 | 4 | 30 | 13 | 10 | 8 | 2 | 3 | 3 |
| 20 | 4 | 29 | 11 | 10 | 9 | 2 | 3 | 3 | |
| 30 | 4 | 12 | 12 | 11 | 10 | 9 | 9 | 9 | |
| 10 | 8 | 31 | 2 | 4 | 2 | 2 | 2 | 2 | |
| 20 | 8 | 32 | 2 | 3 | 2 | 2 | 2 | 2 | |
| 30 | 8 | 2 | 3 | 3 | 3 | 2 | 2 | 2 | |
| 10 | 16 | 31 | 2 | 3 | 2 | 2 | 1 | 2 | |
| 20 | 16 | 31 | 2 | 3 | 2 | 2 | 2 | 2 | |
| 30 | 16 | 3 | 3 | 3 | 3 | 3 | 2 | 2 | |
| 10 | 32 | 36 | 2 | 3 | 2 | 1 | 2 | 1 | |
| 20 | 32 | 36 | 2 | 3 | 2 | 3 | 2 | 2 | |
| 30 | 32 | 3 | 3 | 2 | 2 | 2 | 2 | ||
Notes are the same as for Table 1.
TABLE 3.
RMSD (Å) between modeled structures and the correct structure for the homotetramer (PDB code: 7cat, D2 symmetry)
| Resolution (Å)† | No. of GDFs‡ | No. of GDFs per complex map§
|
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Symmetry* | 2 | 3 | 4 | 6 | 2 | 18 | 24 | ||
| False | 10 | 4 | 39 | 42 | 32 | 39 | 44 | 38 | 29 |
| 20 | 4 | 44 | 43 | 42 | 34 | 38 | 33 | 30 | |
| 30 | 4 | 43 | 39 | 42 | 37 | 43 | 43 | 37 | |
| 10 | 8 | 44 | 41 | 43 | 46 | 41 | 45 | 39 | |
| 20 | 8 | 40 | 46 | 38 | 44 | 40 | 38 | 41 | |
| 30 | 8 | 41 | 41 | 41 | 42 | 40 | 46 | 39 | |
| 10 | 16 | 41 | 42 | 42 | 43 | 44 | 45 | 40 | |
| 20 | 16 | 46 | 43 | 43 | 41 | 38 | 41 | 38 | |
| 30 | 16 | 41 | 42 | 38 | 41 | 39 | 29 | 38 | |
| 10 | 32 | 40 | 42 | 35 | 37 | 44 | 40 | 41 | |
| 20 | 32 | 46 | 45 | 43 | 42 | 45 | 41 | 43 | |
| 30 | 32 | 42 | 48 | 42 | 40 | 42 | 45 | 44 | |
| True | 10 | 4 | 37 | 44 | 47 | 42 | 9 | 11 | 11 |
| 20 | 4 | 42 | 46 | 41 | 42 | 42 | 11 | 11 | |
| 30 | 4 | 39 | 39 | 42 | 39 | 39 | 39 | 39 | |
| 10 | 8 | 42 | 46 | 42 | 45 | 43 | 45 | 3 | |
| 20 | 8 | 42 | 42 | 42 | 45 | 42 | 45 | 42 | |
| 30 | 8 | 42 | 47 | 42 | 39 | 42 | 42 | 42 | |
| 10 | 16 | 42 | 42 | 42 | 41 | 3 | 1 | 2 | |
| 20 | 16 | 40 | 42 | 42 | 41 | 2 | 4 | 2 | |
| 30 | 16 | 42 | 42 | 42 | 42 | 38 | 42 | 4 | |
| 10 | 32 | 40 | 42 | 42 | 3 | 3 | 1 | 1 | |
| 20 | 32 | 41 | 2 | 42 | 1 | 2 | 4 | 1 | |
| 30 | 32 | 42 | 3 | 42 | 41 | 3 | 3 | 2 | |
Notes are the same as for Table 1.
TABLE 4.
RMSD (Å) between modeled structures and the correct structure for the homohexamer (PDB code: 2rec, C6 symmetry)
| Resolution (Å)† | No. of GDFs‡ | No. of GDFs per complex map§
|
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Symmetry* | 2 | 3 | 4 | 6 | 2 | 18 | 24 | ||
| False | 10 | 4 | 28 | 30 | 28 | 29 | 20 | 19 | 18 |
| 20 | 4 | 27 | 28 | 30 | 27 | 22 | 24 | 24 | |
| 30 | 4 | 32 | 24 | 23 | 23 | 10 | 20 | 14 | |
| 10 | 8 | 30 | 24 | 27 | 16 | 29 | 14 | 16 | |
| 20 | 8 | 27 | 24 | 26 | 20 | 23 | 19 | 11 | |
| 30 | 8 | 28 | 22 | 26 | 19 | 18 | 24 | 25 | |
| 10 | 16 | 28 | 27 | 15 | 9 | 18 | 14 | 20 | |
| 20 | 16 | 25 | 30 | 23 | 17 | 23 | 20 | 22 | |
| 30 | 16 | 31 | 28 | 20 | 28 | 27 | 19 | 19 | |
| 10 | 32 | 30 | 24 | 15 | 24 | 15 | 14 | 24 | |
| 20 | 32 | 30 | 30 | 24 | 18 | 23 | 21 | 21 | |
| 30 | 32 | 35 | 29 | 27 | 22 | 17 | 22 | 24 | |
| True | 10 | 4 | 5 | 4 | 5 | 29 | 29 | 1 | 2 |
| 20 | 4 | 27 | 7 | 8 | 29 | 29 | 2 | 2 | |
| 30 | 4 | 28 | 33 | 33 | 29 | 29 | 29 | 28 | |
| 10 | 8 | 22 | 5 | 6 | 5 | 3 | 2 | 2 | |
| 20 | 8 | 22 | 9 | 4 | 4 | 3 | 2 | 2 | |
| 30 | 8 | 21 | 9 | 5 | 15 | 3 | 3 | 3 | |
| 10 | 16 | 21 | 4 | 3 | 4 | 4 | 2 | 3 | |
| 20 | 16 | 28 | 7 | 6 | 4 | 2 | 2 | 2 | |
| 30 | 16 | 26 | 9 | 5 | 4 | 2 | 2 | 2 | |
| 10 | 32 | 20 | 4 | 3 | 4 | 2 | 1 | 2 | |
| 20 | 32 | 26 | 7 | 4 | 4 | 3 | 2 | 2 | |
| 30 | 32 | 26 | 12 | 5 | 5 | 5 | 3 | 4 | |
Notes are the same as for Table 1.
In general, the difficulty of finding the correct configuration depended on the number of subunits. RMSD values of the dimer were generally smaller than those of the trimer, tetramer, and hexamer. A reason why RMSD values of the tetramer were higher than those of the hexamer might be that the tetramer 7cat has a D2 symmetry, which has two rotational axes, whereas C6 symmetry has only one axis. For correct modeling, the minimum number of GDFs for a complex was about two for the dimer, three for the trimer, three to six for the tetramer, and four to six for the hexamer. The number of GDFs for each subunit was also important. For correct modeling of the trimer 1nic and hexamer 2rec, at least eight Gaussian functions were required for one subunit. For the D2 tetramer 7cat, at least 16 Gaussian functions were required. The importance of a sufficient number of GDFs for each subunit is illustrated in Fig. 9. Symmetrical restraints were necessary for correct modeling of the D2 tetramer and the C6 hexamer, but not really necessary for that of the dimer and trimer. Fitted atomic models with and without C6 symmetric restraint are shown in Fig. 10. It was a surprise that resolutions of the simulated density maps did not correlate well with the RMSDs, although some failures were observed for the tetramer and hexamer using 30 Å resolution maps (Table 3 and 4). We can say that correct modeling is possible for the 30 Å resolution density map if sufficient GDFs and symmetric constraints are used, which means that our method for creating low-resolution maps performs comparably to those used in previous studies (17,24).
FIGURE 9.
Fitting models and 3D density maps for the homotrimer (PDB code: 1nic) showing the effect of the number of GDFs representing each subunit. (A) GMM using three GDFs generated from the 20-Å simulated low-resolution density map of the complex. (B) Energy-minimum GMMs using four GDFs for each subunit. (C) Energy-minimum GMMs using eight GDFs for each subunit. (D) Crystal structure for the homotrimer (PDB code: 1nic). (E) Atomic model of the complex structure corresponding to the model using four GDFs for each subunit (B). Its RMSD from the crystal structure (D) was 11.6 Å. (F) Atomic model of the complex structure corresponding to the model using eight GDFs for each subunit (C). Its RMSD from the crystal structure (D) was 3.5 Å. Both energy minimum structures were generated without the symmetric restraint.
FIGURE 10.
Fitting models and 3D density maps for the homohexamer (PDB code: (2rec) showing the effect of the symmetric restraint. (A) GMM using six GDFs generated from the 20-Å simulated low-resolution density map of the complex. (B) Energy-minimum GMMs without using the symmetric restraint. (C) Energy-minimum GMMs using the symmetric restraint. (D) Crystal structure for the homohexamer (PDB code: 2rec). (E) Atomic model of the complex structure corresponding to the model without the symmetric restraint (B). Its RMSD from the crystal structure (D) was 19.7 Å. (F) Atomic model of the complex structure corresponding to the model using the symmetric restraint (C). Its RMSD from the crystal structure (D) was 4.2 Å. Both energy-minimum structures were generated using eight GDFs for each subunit.
Performance comparison between gmfit and colores
For a more explicit comparison with other approaches, we compared the performance of our gmfit program with that of the program colores, which is a part of the most popular program package SITUS (27) for fitting atomic models into density maps. The SITUS package includes two fitting programs, qdock and colores. The qdock program is based on the vector quantization approach, and the colores employs the fast Fourier transfer translational search and the exhaustive rotational search, using Lapracian-filtered density maps. Our main purpose is for modeling a complex with multiple subunits, but the qdock program cannot model more than one subunit. The colores program is able to superimpose a subunit atomic model into a part of the density map, and to output multiple candidate configurations for the subunit. By assembling these multiple configurations, a homooligomeric structure can be modeled.
To test the performance of the program colores and gmfit, we used the simulated density map with 20 Å resolution for the four complex atomic structures (1afw, 1nic, 7cat, and 2rec). The colores program of SITUS (version 2.3) was executed with the default options. For the gmfit program, of the Ninit = 1000 random initial configurations generated, only the best Ninit_locsch = 100 initial configurations were selected for the steepest-descent search with symmetric restraints. The number of GDFs for the density map is 12. We tested two different numbers of GDFs, 8 and 16, for subunit atomic models. Both programs were executed using a single CPU (Intel Xeon, 3.00 GHz).
Table 5 summarizes the performances of the colores and gmfit programs in view of their computational time and prediction accuracy (RMSD). The computational times of the colores program were ∼1 or 2 min, and the RMSDs between the correct and modeled structures were very low (∼1 Å). The computation times of gmfit using eight GDFs for each subunit were <1 min, much smaller than those of colores. The gmfit RMSDs were slightly higher than those of colores, except for the complex 7cat, which was not successfully fitted. In the case of the fitting calculations using 16 GDFs for each subunit, RMSDs were improved, especially for the complex 7cat; computational times became longer, but were still shorter than those of colores.
TABLE 5.
Comparison of the programs colores and gmfit in terms of computation time and RMSD (Å)
|
colores
|
gmfit*
|
gmfit†
|
||||||
|---|---|---|---|---|---|---|---|---|
| PDB code | Time (s)‡ | RMSD (Å) | Times for each step (s)§ | Time (s)‡ | RMSD (Å) | Times for each step (s)§ | Time (s)‡ | RMSD (Å) |
| 1afw | 107.8 | 0.65 | 1.0, 2.7, 1.4 | 5.1 | 1.16 | 5.4, 2.7, 7.1 | 15.2 | 1.03 |
| 1nic | 94.6 | 1.85 | 1.2, 5.9, 4.9 | 12.0 | 1.89 | 5.6, 5.9, 16.0 | 27.5 | 1.77 |
| 7cat | 77.0 | 0.61 | 4.6, 12.9, 10.6 | 28.0 | 41.83 | 6.0, 12.9, 46.0 | 64.9 | 2.27 |
| 2rec | 142.8 | 0.33 | 0.1, 3.8, 37.7 | 41.6 | 2.91 | 0.1, 3.8, 110.9 | 114.8 | 2.29 |
Performance of the gmfit program using 8 GDFs for each subunit and 12 GDFs for a density map.
Performance of the gmfit program using 16 GDFs for each subunit and 12 GDFs for a density map.
Total computation time.
Computation times for the three steps of gmfit: estimating the GMM from a subunit atomic model; estimating the GMM from a density map of the complex; and searching for the optimal configuration.
We can summarize the performance of colores and gmfit as follows. The prediction accuracy of gmfit is sufficiently high, but that of colores is higher. The colores program achieves its high prediction accuracy without any knowledge of symmetry; in contrast, the gmfit program requires symmetric restraints for the tetramer and hexamer. The advantage of gmfit is its fast computation, implying a potential to model a complex composed of larger numbers of subunits.
Fitting calculation for the cryo-EM density map of GroEL/ES complex
For a more realistic and large-scale test, we performed a fitting calculation for the cryo-EM density map of the GroEL/ES complex, registered as the ID code emd_1046 in the EMDB (43) (shown in Fig. 11 A at 23.5 Å resolution). Because an accuracy evaluation of fitting is feasible by comparison with the crystal atomic structure registered in the PDB (42) (PDB code: 1aon), other researchers have also tested their methods using this complex (18,22). The GroEL/ES complex was composed of three C7 symmetric rings: seven ADP-bound GroELs (cis ring), seven ADP-free GroELs (trans ring), and seven GroESs. For our fitting calculation, we picked up three types of subunit from the complex atomic structure (1aon): the cis ring form of GroEL (chain A), the trans ring form of GroEL(chain H), and the GroES (chain O). We prepared seven copies for each type of subunit (in total, 21 subunits), and assigned the three C7-symmetric restraints assuming that subunits of the same types assembled into a C7 symmetric ring. Forty-five GDFs were used for the density map of the complex GroEL/ES, and eight functions were used for each subunit atomic model. We repeated the fitting run eight times. In each run, Ninit = 106 random initial configurations are generated, and only the best Ninit_locsch = 104 initial configurations were selected for the steepest-descent search. Each run took ∼20 h using the single CPU. To find the correct standard position, the fitted complex atomic model was generated by a Gaussian fitting calculation of the entire complex atomic model into the 3D density map (Fig. 11 B). The lowest-energy model is shown in Fig. 11 C; its RMSD from the fitted complex atomic model is 14.7 Å. The positions and orientations of the cis ring and trans ring GroEL subunits were built almost correctly, but the orientations of GroES subunits were not correct. The failure to fit the GroES subunits was also reported in previous studies (18,22), suggesting that the cryo-EM density map may not have sufficient information to determine the orientation of GroES correctly, and that the prediction accuracy of our method is in fact relatively high. For a more accurate modeling of the GroEL/ES, additional experimental data will be necessary.
FIGURE 11.
(A) 3D density map of the complex (ID code: emd_1046). (B) Atomic model of the complex (PDB code: 1aon) fitted into the 3D density map. (C) Energy-minimum model obtained by the Gaussian mixture fitting method. Its RMSD from the atomic complex model (B) was 14.7 Å.
DISCUSSION
Our Gaussian mixture molecular model can represent rough features of macromolecules by using several GDFs. The concept of our Gaussian mixture molecular model is similar to that of the vector quantization method (23,24). The vector quantization method represents a macromolecule as a set of 3D points, whereas our model represents it as a set of 3D GDFs. Our GMM is a kind of density distribution function, and is therefore more suitable to represent a low-resolution density of molecule whose boundaries are not clearly determined. Figs. 5–8 show that reasonably small numbers of GDFs are sufficient to approximate low-resolution density maps.
In this study, we assumed that all the heavy atoms had approximately equal atomic weights, for deriving GMMs and simulated density maps for atomic models. This approximation will not be critical for modeling protein complexes, but it may make a difference in modeling complexes containing nucleic acids, because atomic numbers of heavy atoms in nucleic acids are far from uniform. We now plan to implement a modified expectation maximization algorithm to consider different atomic weights, which is similar to the estimation algorithm from a set of grid points with densities, described in this article.
One of the problems of fitting multiple subunits into a density map is the large computational cost. The GMM enables us to develop a fast fitting method, because the overlap of two GMMs can be more quickly calculated than the overlap of a grid-represented density map and a sphere-represented subunit. Another advantage of our model is its fast calculation of gradient and torque of overlap energy allowing an efficient gradient-based local search to be easily implemented. Tables 1–5 show that our method is fast and accurate enough to model the typical homo oligomeric structures. The comparison of the popular program colores (shown in Table 5) showed that the colores program provided more accurate predictions, but the gmfit program was faster than the colores. Considering the fast computation and flexibility to include the various restraints, the program gmfit has a potential to model a complex composed of large number of subunits.
Because we employed the general formalism of energy optimization, we can easily include additional information from a variety of biological or biochemical resources by adding additional restraint energies. In this study, the symmetric energy was implemented as harmonic restraints on distances between equivalent subunit pairs. As shown in Tables 1–4 and in Fig. 10, the symmetric restraint was really necessary for building complexes with larger numbers of subunits. Other types of restraints, such as proximities of subunits, can be implemented as upper and lower limits on the distance between subunits (36).
The problem of conformational change cannot be solved by our proposed method. Our Gaussian mixture molecular model was a rigid body; the relative geometry between each GDF was strictly fixed. Small conformational changes (such as side-chain rotations) upon binding are not of critical importance for our method, because our GMM has a soft boundary. To incorporate domain-level conformational changes, combinations with other programs might be useful. Our method can provide good initial configurations to the program dealing with conformational changes, such as normal-mode flexible fitting.
Our method of representing a molecule by the GMM can be applied to other fields, such as docking and molecular shape comparison. Grant et al. proposed the shape comparison of small molecules using the sum of isotropic GDFs (47). Our GMM has a higher capacity than their isotopic functions to approximate molecular shapes. We now plan to develop shape comparisons of macromolecules using our Gaussian mixture molecular model.
CONCLUSION
In this study, we proposed a molecular representation using GMMs, and a fitting method using random search and successive gradient-based local search. Because our fitting method is computationally fast, and its prediction accuracy is reasonably high, it can serve as a practical tool for electron microscopy researchers. Our Gaussian mixture molecular model has the potential to be applied to a wide range of research in macromolecular structural biology. We now plan to release our source codes as academic freeware, and we encourage readers who wish to use our program to contact us via email.
Acknowledgments
We are grateful to Dr. Kei Yura for his general supervision of the CREST project, and for checking our manuscript. We also thank Drs. Hisashi Ishida and Atsushi Matsumoto for their helpful advice about theoretical problems. Drs. Kenji Iwasaki and Hirofumi Suzuki kindly advised us from the experimentalists' viewpoint.
APPENDIX
Force and torque by attractive interaction energy between two distribution functions
To perform the steepest-descent search method, we must know the force and torque vector of the energy for each subunit. To simplify the problem, we focus on the attractive overlap energy between two distribution functions, fA and fB, illustrated in Fig. 12. We define the attractive fitness energy E(r) at a point r as follow:
 |
FIGURE 12.
Local force FA(r) and a total force FA for a distribution fA, by the attractive overlap energy, E, of two GMMs, fA and fB.
The total fitness energy, E, is obtained by the integral of E(r) for the entire space as follow:
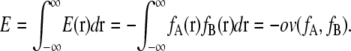 |
A local force FA(r) for the distribution fA at point r is defined as the derivative of energy E(r) by the center position gA of distribution fA:
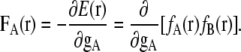 |
A total force FA for the distribution fA at the center point gA is obtained by the integral of FA(r) for the entire space:
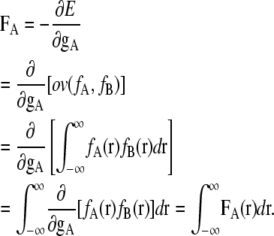 |
A torque around the point gA is described as the integral of the outer product between the positional vector r and the local force FA(r):
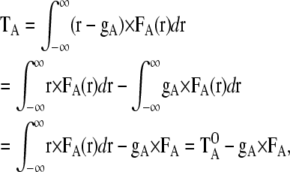 |
where
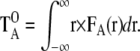 |
Force and torque of fitness energy for two Gaussian mixture models
Let us assume that distributions fA and fB are described as the GMMs:
 |
The centers of gravity, gA and gB, are defined as follows:
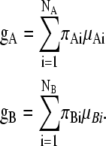 |
Then, the force FA for distribution fA is analytically obtained as follows:
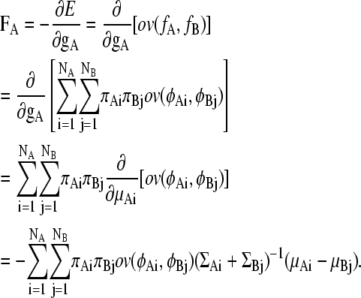 |
The partial differential by the center of gravity, gA, is equivalent to the differential by the center of each Gaussian distribution, μAi, because we assume that each GMM is a rigid body.
Next, the torque 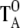 has to be obtained to calculate the torque, TA, for distribution fA.
has to be obtained to calculate the torque, TA, for distribution fA.
 |
where
 |
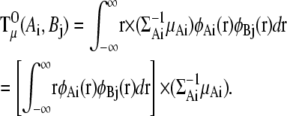 |
Then, the torque for distribution fA can be described as the sum of the three terms 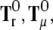 and gA × FA:
and gA × FA:
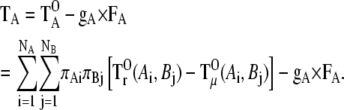 |
To calculate  (Ai,Bj), we need the integral
(Ai,Bj), we need the integral
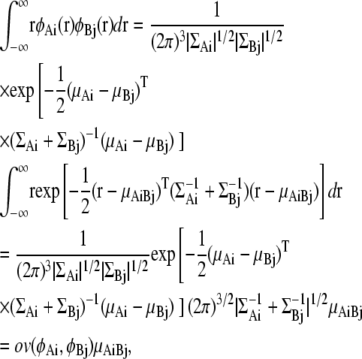 |
where
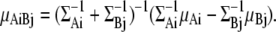 |
Then, the torque  is described as
is described as
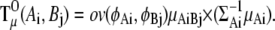 |
Calculation of the term  is more complicated. First, we obtain the second-moment matrix Q for the product of φAι(r) and φBj(r):
is more complicated. First, we obtain the second-moment matrix Q for the product of φAι(r) and φBj(r):
 |
Using matrix Q, the term 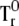 is described as
is described as
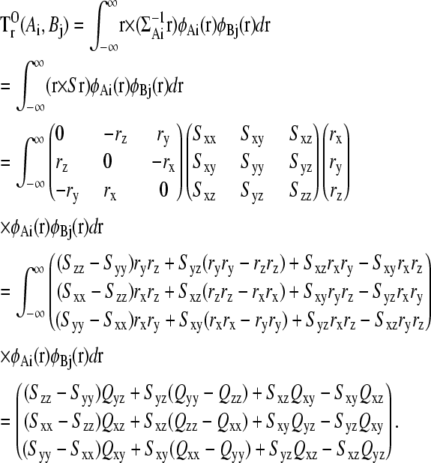 |
For a simpler notation here, we replace the covariance matrix  with the matrix S.
with the matrix S.
Editor: Klaus Schulten.
References
- 1.Kleanthous, C. (Editor.). 2000. Protein-Protein Recognition. Oxford University Press, Oxford, UK.
- 2.Pandey, A., and M. Mann. 2000. Proteomics to study genes and genomes. Nature. 405:837–846. [DOI] [PubMed] [Google Scholar]
- 3.von Mering, C., R. Krause, B. Snel, M. Cornell, S. G. Oliver, S. Fields, and P. Bork. 2002. Comparative assessment of large-scale data sets of protein-protein interactions. Nature. 417:399–403. [DOI] [PubMed] [Google Scholar]
- 4.Frank, J. 2002. Single-particle imaging of macromolecules by cryo-electron microscopy. Annu. Rev. Biophys. Biomol. Struct. 31:303–319. [DOI] [PubMed] [Google Scholar]
- 5.Sali, A., R. Glaeser, T. Earnest, and W. Baumeister. 2003. From words to literature in structural proteomics. Nature. 422:216–225. [DOI] [PubMed] [Google Scholar]
- 6.Frank, J. 2006. Three-Dimensional Electron Microscopy of Macromolecular Assemblies. Oxford University Press, Oxford, UK.
- 7.Robinson, C. V., A. Sali, and W. Baumeister. 2007. The molecular sociology of the cell. Nature. 450:973–982. [DOI] [PubMed] [Google Scholar]
- 8.Tagari, M., R. Newman, M. Chagoyen, J. M. Carazo, and K. Henrick. 2002. New electron microscopy database and deposition system. Trends Biochem. Sci. 27:589. [DOI] [PubMed] [Google Scholar]
- 9.Henrick, K., R. Newman, M. Tagari, and M. Chagoyen. 2003. EMDep: a web-based system for the deposition and validation of high-resolution electron microscopy macromolecular structural information. J. Struct. Biol. 144:228–237. [DOI] [PubMed] [Google Scholar]
- 10.Stewart, P., S. D. Fuller, and R. M. Burnett. 1993. Difference imaging of adenovirus: bridging the resolution gap between X-ray crystallography and electron microscopy. EMBO J. 12:2589–2599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gao, H., and J. Frank. 2005. Molding atomic structures into intermediate-resolution cryo-EM density maps of ribosomal complexes using real-space refinement. Structure. 13:401–406. [DOI] [PubMed] [Google Scholar]
- 12.Fotin, A., Y. Cheng, P. Sliz, N. Grigorieff, S. C. Harrison, T. Kirchhausen, and T. Walz. 2004. Molecular model for a complete clathrin lattice from electron cryomicroscopy. Nature. 432:573–579. [DOI] [PubMed] [Google Scholar]
- 13.Miyata, T., H. Suzuki, T. Oyama, K. Mayanagi, Y. Ishino, and K. Morikawa. 2005. Open clamp structure in the clamp-loading complex visualized by electron microscopic image analysis. Proc. Natl. Acad. Sci. USA. 102:13795–13800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wriggers, W., and P. Chacon. 2001. Modeling tricks and fitting techniques for multiresolution structures. Structure. 9:779–788. [DOI] [PubMed] [Google Scholar]
- 15.Volkmann, N., and D. Hanein. 2003. Docking of atomic models into reconstructions from electron microscopy. Methods Enzymol. 374:204–225. [DOI] [PubMed] [Google Scholar]
- 16.Roseman, A. M. 2000. Docking structures of domains into maps from cryo-electron microscopy using local correlation. Acta Crystallogr. D Biol. Crystallogr. 56:1332–1340. [DOI] [PubMed] [Google Scholar]
- 17.Chacon, P., and W. Wriggers. 2002. Multi-resolution contour-based fitting of macromolecular structures. J. Mol. Biol. 317:375–384. [DOI] [PubMed] [Google Scholar]
- 18.Ceulemans, H., and R. B. Russell. 2004. Fast fitting of atomic structures to low-resolution electron density maps by surface overlap maximization. J. Mol. Biol. 338:783–793. [DOI] [PubMed] [Google Scholar]
- 19.Wu, X., J. L. S. Milne, J. Borgnia, A. V. Rostapshov, S. Subramaniam, and B. R. Brooks. 2003. A core-weighted fitting method for docking atomic structures into low-resolution maps: application to cryo-electron microscopy. J. Struct. Biol. 141:63–76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Topf, M., M. L. Baker, B. John, W. Chiu, and A. Sali. 2005. Structural characterization of components of protein assemblies by comparative modeling and electron cryo-microscopy. J. Struct. Biol. 149:191–203. [DOI] [PubMed] [Google Scholar]
- 21.Alber, F., S. Dokudovskaya, L. M. Veenhoff, W. Zhang, J. Kipper, D. Devos, A. Suprapto, O. Karni-Schmidt, R. Williams, B. T. Chait, M. P. Rout, and A. Sali. 2007. Determining the architectures of macromolecular assemblies. Nature. 450:683–694. [DOI] [PubMed] [Google Scholar]
- 22.Garzon, J. I., J. Kovacs, R. Abagyan, and P. Chacon. 2007. ADP_EM: fast exhaustive multi-resolution docking for high-throughput coverage. Bioinformatics. 23:427–433. [DOI] [PubMed] [Google Scholar]
- 23.Wriggers, W., R. A. Milligan, K. Schulten, and J. A. McCammon. 1998. Self-organizing neural networks bridge the biomolecular resolution gap. J. Mol. Biol. 284:1247–1254. [DOI] [PubMed] [Google Scholar]
- 24.Birmanns, S., and W. Wriggers. 2007. Multi-resolution anchor-point registration of biomolecular assemblies and their components. J. Struct. Biol. 157:271–280. [DOI] [PubMed] [Google Scholar]
- 25.Wriggers,S., R. A. Agrawal, D. L. Drew, A. McCammon, and J. Frank. 2000. Domain motions of EG-G bound to the 70S ribosome: insights from a hand-shaking between multi-resolution structures. Biophys. J. 79:1670–1678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Darst, S. A., N. Opalka, P. Chacon, A. Polyakov, C. Richter, G. Zhang, and W. Wriggers. 2002. Conformational flexibility of bacterial RNA polymerase. Proc. Natl. Acad. Sci. USA. 99:4296–4301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wriggers, W., and S. Birmanns. 2001. Using situs for flexible and rigid-body fitting of multiresolution single-molecule data. J. Struct. Biol. 133:193–202. [DOI] [PubMed] [Google Scholar]
- 28.Tama, F., O. Miyashita, and C. L. Brooks III. 2004. Normal mode based flexible fitting of high-resolution structure into low-resolution experimental data from cryo-EM. J. Struct. Biol. 147:315–326. [DOI] [PubMed] [Google Scholar]
- 29.Hinsen, K., N. Reuter, J. Navaza, D. L. Stokes, and J.-J. Lacapere. 2005. Normal mode-based fitting of atomic structure into electron density maps: application to sarcoplasmic reticulum Ca-ATPase. Biophys. J. 88:818–827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.McLachlan, G., and D. Peel. 2000. Finite mixture models. John Wiley & Sons, New York.
- 31.Yenung, K. Y., C. Fraley, A. Murua, A. E. Raftery, and W. L. Ruzzo. 2001. Model-based clustering data transformations to gene expression data. Bioinformatics. 17:977–987. [DOI] [PubMed] [Google Scholar]
- 32.McLachlan, G. J., R. W. Bean, and D. Peel. 2002. A mixture-model based approach to the clustering of microarray expression data. Bioinformatics. 18:413–422. [DOI] [PubMed] [Google Scholar]
- 33.Rantanen, V.-V., K. A. Denessiouk, M. Gyllenberg, T. Kosk, and M. S. Johnson. 2001. A fragment library based on Gaussian mixtures predicting favorable molecular interactions. J. Mol. Biol. 313:197–214. [DOI] [PubMed] [Google Scholar]
- 34.Press, W. H., S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery. 2007. Gaussian mixture models and K-means clustering. In Numerical Recipes: The Art of Scientific Computing, 3rd ed. Cambridge University Press, New York. 842–850.
- 35.Goodsell, D. S., and A. J. Olson. 2000. Structural symmetry and protein function. Annu. Rev. Biophys. Biomol. Struct. 29:105–153. [DOI] [PubMed] [Google Scholar]
- 36.Alber, F., M. F. Kim, and A. Sali. 2005. Structural characterization of assemblies from overall shape and subcomplex compositions. Structure. 13:435–445. [DOI] [PubMed] [Google Scholar]
- 37.Press, W. H., S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery. 2007. Multivariate normal deviates. In Numerical Recipes: The Art of Scientific Computing, 3rd ed. Cambridge University Press, New York. 378–379.
- 38.Leech, A. R. 2001. Molecular Modeling: Principles and Applications. Prentice Hall, Upper Saddle River, NJ. 420–422.
- 39.Lasker, K., O. Dror, M. Shatsky, R. Nussinov, and H. J. Wolfson. 2007. EMatch: discovery of high resolution structural homologues of protein domains in intermediate resolution cyro-EM maps. IEEE/ACM Trans. Comput. Biol. Bioinform. 4:28–39. [DOI] [PubMed] [Google Scholar]
- 40.Press, W. H., S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery. 2007. Golden section search in one dimension. In Numerical Recipes: The Art of Scientific Computing, 3rd ed. Cambridge University Press, New York. 492–496.
- 41.Adman, E. T., J. W. Godden, and S. Turley. 1995. The structure of copper-nitrite reductase from Achromobacter cycloclastes at five pH values, with NO2− bound and with type II copper depleted. J. Biol. Chem. 270:27458–27474. [DOI] [PubMed] [Google Scholar]
- 42.Xu, Z., A. L. Horwich, and P. B. Sigler. 1997. The crystal structure of the asymmetric GroEL-ES-(ADP)7 chaperonin complex. Nature. 388:741–750. [DOI] [PubMed] [Google Scholar]
- 43.Ranson, N. A., G. W. Farr, A. M. Roseman, B. Gowen, W. A. Fenton, A. L. Horwich, and H. R. Saibil. 2001. ATP-bound states of GroEL captured by cryo-electron microscopy. Cell. 107:869–879. [DOI] [PubMed] [Google Scholar]
- 44.Mathieu, M., Y. Modis, J. Ph. Zeelen, C. K. Engel, R. A. Abagyan, A. Ahlberg, B. Rasmussen, V. S. Lamzin, H. Wolf, W. H. Kunau, and R. K. Wierenga. 1997. The 1.8 Å crystal structure of the dimeric peroxisomal 3-ketoacyl-CoA thiolase of Saccharomyces cerevisiae: implications for substrate binding and reaction mechanism. J. Mol. Biol. 273:714–728. [DOI] [PubMed] [Google Scholar]
- 45.Fita, I., and M. G. Rossmann. 1986. The NADPH binding site on beef liver catalase. Proc. Natl. Acad. Sci. USA. 82:1604–1608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Yu, X., and E. H. Egelman. 1997. The RecA hexamer is a structural homologue of ring helicases. Nat. Struct. Biol. 4:101–104. [DOI] [PubMed] [Google Scholar]
- 47.Grant, J. A., M. A. Gallardo, and B. T. Pickup. 1996. A fast method of molecular shape comparison: a simple application of a Gaussian description of molecular shape. J. Comput. Chem. 17:1653–1666. [Google Scholar]