Kinetics of Reduction of Fe(III) Complexes by Outer Membrane Cytochromes MtrC and OmcA of Shewanella oneidensis MR-1

Abstract

Because of their cell surface locations, the outer membrane c-type cytochromes MtrC and OmcA of Shewanella oneidensis MR-1 have been suggested to be the terminal reductases for a range of redox-reactive metals that form poorly soluble solids or that do not readily cross the outer membrane. In this work, we determined the kinetics of reduction of a series of Fe(III) complexes with citrate, nitrilotriacetic acid (NTA), and EDTA by MtrC and OmcA using a stopped-flow technique in combination with theoretical computation methods. Stopped-flow kinetic data showed that the reaction proceeded in two stages, a fast stage that was completed in less than 1 s, followed by a second, relatively slower stage. For a given complex, electron transfer by MtrC was faster than that by OmcA. For a given cytochrome, the reaction was completed in the order Fe-EDTA > Fe-NTA > Fe-citrate. The kinetic data could be modeled by two parallel second-order bimolecular redox reactions with second-order rate constants ranging from 0.872 μM⁻¹ s⁻¹ for the reaction between MtrC and the Fe-EDTA complex to 0.012 μM⁻¹ s⁻¹ for the reaction between OmcA and Fe-citrate. The biphasic reaction kinetics was attributed to redox potential differences among the heme groups or redox site heterogeneity within the cytochromes. The results of redox potential and reorganization energy calculations showed that the reaction rate was influenced mostly by the relatively large reorganization energy. The results demonstrate that ligand complexation plays an important role in microbial dissimilatory reduction and mineral transformation of iron, as well as other redox-sensitive metal species in nature.

Metal ion speciation depends on conditions in the chemical environment. In nature, metal ions rarely exist as free (hydrated) ions. They are either hydrolyzed or complexed with various inorganic or organic ligands. Typical sources of ligands include mineral dissolution, biological processes such as decomposition of plants, and chemical processes involved in agricultural, detergent, and nuclear industries (7, 44, 61), in which ligands such as phosphate, citrate, nitrilotriacetic acid (NTA), and EDTA are released. Of particular environmental concern are the former nuclear weapons sites across the United States where large quantities of radioactive contaminants (e.g., U and Tc) were disposed or leaked along with high concentrations of phosphate, NTA, and EDTA into the underlying soils and sediments (7, 19). Any effective remediation strategy for the contaminated sediments has to take into consideration the effect of ligand complexation of the target radioactive contaminants.

Members of the genera Shewanella and Geobacter, including well-studied models such as Shewanella oneidensis MR-1 and Geobacter sulfurreducens, are capable of respiration with a wide range of electron acceptors, including soluble Fe(III) and Mn(III), insoluble Fe(III) and Mn(III,IV) oxides, and radionuclide contaminants, such as U(VI) and Tc(VII) (13, 14, 23, 35, 37, 38, 57). Dissimilatory metal reduction by bacteria (DMRB) has profound consequences for the reductive dissolution of metal oxide solids and mineral phase transformation. For iron, the generation of ferrous ions upon microbial reduction can promote the formation of either ferrous or mixed ferric-ferrous minerals (12, 59). For U and Tc, DMRB has the potential to convert UO₂²⁺ and TcO₄⁻, which are highly soluble and thus mobile in subsurface soils and sediments, into the sparingly soluble oxide solids TcO₂(s) and UO₂(s) (11, 14, 24, 35, 36, 41). Since ligand complexation not only affects the solubility and transport behavior of metal ions but also modifies the redox properties of metal ions (28), microbial reduction of metal ions is influenced by ligand complexation.

To date, there have been only limited studies of the reduction kinetics of aqueous metal complexes by microorganisms (21, 32, 33, 41), and even fewer studies have focused on the reduction kinetics of these complexes using purified ferric reductases (e.g., c-type cytochromes) (2, 34, 55). Liu et al. (32) showed that the rate of reduction of metal complexes in cultures of several dissimilatory metal-reducing bacteria was metal specific and electron donor dependent. Investigations of Fe(III)-organic ligand complex reduction by Shewanella putrefaciens under anaerobic conditions demonstrated that the pseudo-first-order ferric reduction rate was related mostly to the thermodynamic stability constant of the 1:1 Fe(III)-ligand complex, even though thermodynamic calculation indicated that primarily higher complexes were formed under the experimental conditions (21). However, work on dissimilatory metal reduction by S. oneidensis MR-1 (5) showed that this strain grows nearly twice as fast in the presence of Fe(III)-NTA as in the presence of Fe(III)-citrate, implying that the reduction kinetics of ferric complexes may depend on the specific microbe species and/or the growth conditions. Gescher et al. (17) found that expression of CymA, a cytoplasmic membrane-associated c-type cytochrome of S. oneidensis MR-1, in Escherichia coli converts E. coli into a dissimilatory Fe(III)-reducing bacterium. In intact cells, the Fe(III)-reducing activity was limited to Fe(III)-NTA as an electron acceptor. However, biochemical analysis indicated that the tetraheme c-type cytochrome CymA exhibits reductase activity with Fe(III)-NTA and Fe(III)-citrate, as well as with anthraquinone-2,6-disulfonate (AQDS), a humic acid analogue. The in vitro specific activities of Fe(III)-citrate reductase and AQDS reductase of E. coli spheroplasts were 10 and 30 times higher, respectively, than the specific activities observed in intact cells, suggesting that access of chelated and insoluble forms of Fe(III) and AQDS is restricted in whole cells of E. coli.

Recently, two outer membrane decaheme c-type cytochromes, MtrC and OmcA, of S. oneidensis MR-1 were purified and shown to have ferric reductase activity (55). Purified MtrC and OmcA or the related cytochrome complexes have been shown to reduce different metals (5, 41, 42, 47, 57), and the rates of enzymatic reduction of soluble metal complexes are much higher than the corresponding rates for metal oxide solids or solid nanoparticles (47, 56, 57, 64). So far, the reduction kinetics with metal complexes have not been systematically investigated and compared. Systematic investigation and comparison of MtrC- and OmcA-mediated reduction kinetics of different metal complexes should help us understand the underlying mechanism(s) by which cytochromes accomplish electron transfer to metals. In this work, we determined the kinetics of reduction of a series of Fe(III) complexes with citrate, NTA, and EDTA by reduced MtrC and OmcA using a stopped-flow technique coupled with theoretical calculations. These ligands, particularly citrate and NTA, have previously been investigated in DMRB studies (5, 21, 41) and have significant geological and environmental consequences (7, 19). The objectives of this work were (i) to ascertain the direct reduction of Fe(III) complexes by reduced MtrC and OmcA; (ii) to determine the experimental rates of reduction of Fe(III)-ligand (citrate, NTA, and EDTA) complexes and the characteristics of the reduction kinetics; and (iii) to delineate the relationship between the measured kinetic rates and the thermodynamic and structural parameters of the complexes, such as composition, charge, size, reaction free energy, and reaction activation energy. In this work computational chemistry methods were used to aid in interpretation of abiotic factors controlling electron transfer.

MATERIALS AND METHODS

Chemicals and media.

All chemicals were purchased from Sigma Chemical Co. unless noted otherwise. Growth media were purchased from BD Diagnostics. Ferric chloride hexahydrate (100%) was purchased from Baker. Stock solutions of 6 mM ferric ion-citrate, -NTA, and -EDTA complexes were prepared by dissolving the desired amounts of the solid chemicals in 100 mM HEPES buffer and adjusting the pHs of the solutions to 7.0 using a small amount of 1 M NaOH or nitric acid. Working solutions (300 μM) of ferric complexes with the ligands indicated above were prepared by dilution of stock solutions into 100 mM HEPES buffer (pH 7.0) immediately before measurement. The stock solutions were stored in amber glass bottles at 4°C.

Preparation of reduced cytochromes.

Recombinant MtrC and OmcA were expressed and purified as described previously (55). The cytochromes were prepared using a concentration of 10 μM (100 μM heme) in a buffer containing 100 mM HEPES buffer (pH 7.0), 50 mM NaCl, 10% glycerol, and 1% (wt/vol) n-octyl-β-d-glucopyranoside and purged with O₂-free N₂ gas.

Spectroscopic and stopped-flow kinetic measurement.

Cytochromes were reduced by dithionite by gradually adding microliter quantities of 100 μM sodium dithionite solutions in 100 mM bicarbonate buffer (pH 8) to the cytochrome solutions in an N₂ atmosphere while the UV-visible absorption spectra were observed to ensure that cytochromes were completely reduced with only a negligible excess of sodium dithionite present in the solution. The reduction of the ferric complexes was indirectly observed by monitoring the oxidation of a cytochrome reflected by the decrease in absorbance at 552 nm, corresponding to the absorption maximum of the reduced cytochrome, after known volumes of the cytochrome were rapidly mixed with a ferric ion-ligand complex solution using a BioLogic SF-4 stopped-flow system integrated with a BioLogic MOS 250 spectrometer. Separate experiments confirmed that the formation of ferrous iron quantitatively correlated with the oxidation of the cytochromes by ferrozine analysis of ferrous ion (18) produced during the reaction. All the instruments were housed in the same environmental chamber (O₂ level, <1 ppm; Innovative Technologies, Inc.). All working solutions were placed in the chamber and purged with dry N₂ right before measurement. Tests showed that any residual oxygen had little influence on the oxidation of the cytochromes in the reaction vessels.

Fe(III) and Fe(II) speciation calculations.

The equilibrium speciation of Fe(III) and Fe(II) complexes was calculated using the MINTEQA2 software (1) with the most current, critically reviewed thermodynamic stability constants for the ferric and ferrous complexes (Table 1). The same set of thermodynamic constants was used for calculation of redox potentials and reaction free energies under experimental conditions.

TABLE 1.

Relevant speciation reactions for calculating ferric speciation and reaction free energy at 25°C

Reaction	Log K (I = 0)a	Reference
Fe(III) + e− → Fe(II)	13.00	43
Fe(III) + 2citrate3− → Fe(III)-(citrate)23−	19.12	31
Fe(II) + citrate3− → Fe(II)-citrate−	5.89	43
Fe(II) + 2citrate3− → Fe(II)-(citrate)24−	7.80	46
Fe(III) + H2O + NTA3− → Fe(III)OH-NTA− + H+	13.25	43
Fe(II) + NTA3− → Fe(II)-NTA−	10.18	43
Fe(II) + H2O + NTA3− → Fe(II)OH-NTA2− + H+	1.07	43
Fe(III) + EDTA4− → Fe(III)-EDTA−	27.66	43
Fe(II) + EDTA4− → Fe(II)-EDTA2−	16.01	43

^aI, ionic strength of the solution.

Kinetic data analysis.

The redox reaction can be expressed as the coupling of Fe(III)/Fe(II) and reduced (re-Cyt) and oxidized (ox-Cyt) cytochrome redox pairs:

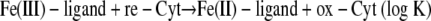(1)

The rate of the redox reaction is then expressed as follows:

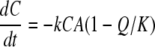(2)

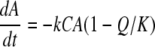(3)

where k is the rate constant, A and C are the Fe(III) and cytochrome (electron equivalent) concentrations, respectively, Q is the ion activity product of the redox reaction, and K is the equilibrium constant.

Because there is enough free energy driving the redox reaction, the affinity term can be neglected in equations 2 and 3. Equations 2 and 3 can then be analytically solved as follows:

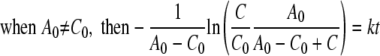(4)

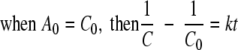(5)

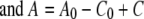(6)

where A₀ and C₀ are the initial Fe(III) and reduced cytochrome concentrations, respectively, and t is time. By calculating the left side of equation 4 or 5 using data from experimental measurements and plotting it against time, the second-order rate constant (k) was determined by the slope in the plot.

Molecular structure and reaction activation energy computations.

Molecular structure optimization, reorganization energy, and electron transfer activation energy calculations were performed using methods described elsewhere (48-51). Briefly, density functional theory (DFT) using B3LYP, in combination with the 6-31G* basis set for H, C, N, and O and the Ahlrichs VTZ basis set for Fe, was used to optimize the structures of the Fe-ligand complexes. The energetic terms, including redox potentials and internal reorganization energies, were determined using B3LYP with the cc-pVTZ-(f) and Ahlrichs VTZ basis sets. The effects of the aqueous environment on redox potentials were accounted for with the dielectric continuum solvation “conductor-like screening model” (COSMO). All calculations were performed using NWCHEM, the software package for computational chemistry on massively parallel computers developed at the Pacific Northwest National Laboratory.

RESULTS

Reduction of ferric complexes by reduced cytochromes.

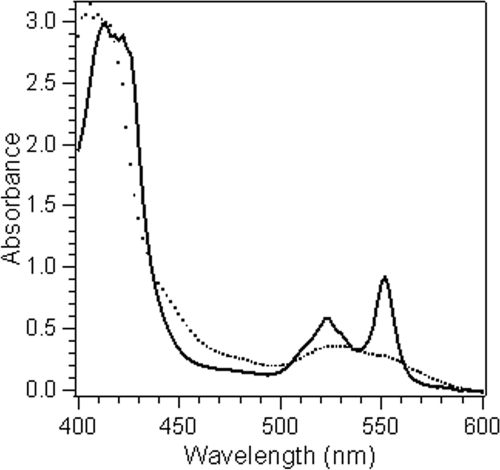
The chemical reduction of both MtrC and OmcA when sodium dithionite was added was instantaneous, as indicated by the spectral changes. In air and in the absence of a reductant, both cytochromes exist in the oxidized form with a characteristic absorption peak at 408 nm (peak α) and a much weaker peak at ∼530 nm (Fig. 1). Addition of a sodium dithionite solution resulted in a shift of the α peak toward 420 nm and appearance of sharp absorption peaks at 522 and 552 nm (peaks β and γ, respectively). During a typical experiment (≤30 min), the solutions of the reduced cytochromes in the absence of an Fe(III) complex or other oxidant remained stable in sealed, anaerobic spectrometer cuvettes under an N₂ atmosphere.

FIG. 1.

Absorption spectra of OmcA (10 μM) in 100 μM HEPES buffer (pH 7.0) in the oxidized form (dotted line) and the reduced form (solid line).

Mixing the reduced cytochrome and Fe(III)-ligand solutions resulted in rapid disappearance of the cytochrome β and γ peaks and shift of the α peak back to 408 nm, indicating that there was oxidation of the cytochrome and, indirectly, reduction of the ferric ion complexes. Real-time analysis of the ferrous concentration was not feasible because of a lack of a proper detection method at the time scale of the reaction. However, the results of ferrozine analysis at the end of the reaction confirmed that there was quantitative production of ferrous ions by the reduced cytochromes. Therefore, observation of spectral changes as an indication of the redox state of the cytochrome provided a valid method for quantification of ferric ion reduction using the stopped-flow technique.

Reduction kinetics.

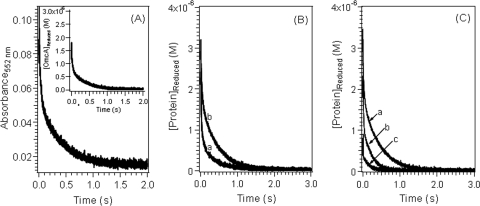
Stopped-flow kinetic curves for the reduction of ferric complexes with citrate, NTA, and EDTA by reduced MtrC or OmcA showed that the reaction was initially very fast and then slowly reached completion within a few hundred milliseconds to a few seconds. A typical stopped-flow kinetic curve is shown for Fe(III)-citrate reduction by OmcA in Fig. 2A. Comparison of the absorption spectra at the end of the reaction (not shown) with the absorption spectra of the oxidized forms (Fig. 1) confirmed that the redox reaction reached completion.

FIG. 2.

Variation of the concentration of reduced cytochromes as a function of time during the reduction of Fe(III) complexes at pH 7.0. (A) Fe(III)-citrate reaction with OmcA. The starting concentrations were as follows: Fe(III), 2 × 10⁻⁴ M; citrate, 3 × 10⁻⁴ M; and OmcA, 3.3 × 10⁻⁶ M. The inset shows the corresponding concentration dependence. (B) Reduction of Fe(III)-citrate complex at [Fe(III)]/[OmcA] ratios of 6:1 by MtrC (line a) and OmcA (line b). The starting concentrations were as follows: Fe(III), 2 × 10⁻⁴ M; citrate, 2 × 10⁻³ M; and MtrC or OmcA, 3.3 × 10⁻⁵ M. (C) Reduction of Fe(III) complex with citrate (line a), NTA (line b), and EDTA (line c) by reduced OmcA. The starting concentrations were as follows: Fe(III), 2 × 10⁻⁴ M; citrate, NTA, or EDTA, 2 × 10⁻³ M; and OmcA, 3.3 × 10⁻⁵ M.

At a given time the absorbance measured at 552 nm (A_t) is the sum of the absorbance of the oxidized cytochrome and the absorbance of the reduced cytochrome since the absorbance of Fe(II)/Fe(III) at this wavelength is negligible,

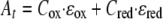(7)

where C_ox and C_red are the concentrations of oxidized and reduced cytochrome, respectively, and ɛ_ox and ɛ_red are the molar absorption coefficients of the oxidized and reduced cytochromes, respectively. Using ɛ_ox and ɛ_red, the observed absorbance at 552 nm, and the initial cytochrome concentration at time zero (C₀), the concentration of reduced cytochrome at time t (C_t) was calculated using the following equation after baseline correction,

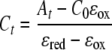(8)

The concentration profile as a function of reaction time closely resembles the profile of the absorbance variations in the original stopped-flow trace (Fig. 2A, inset).

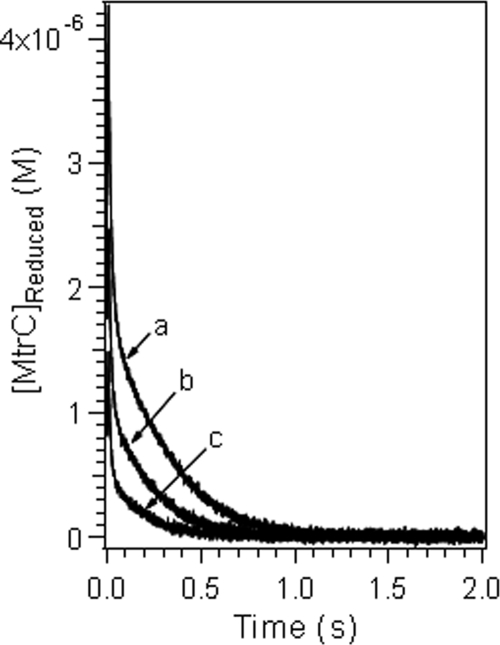
As shown in Fig. 2, the decrease in the reduced cytochrome concentration during ferric reduction occurred in two stages: a fast stage that was completed in a subsecond time frame, followed immediately by a second, slower stage. The extent and duration of the reaction at each stage varied as a function of the cytochrome as well as the ferric ion-to-cytochrome concentration ratio. The reduction of each Fe(III) complex by MtrC was faster than its reduction by OmcA (Fig. 2B). This is in general agreement with previous reports indicating that MtrC reduces U(VI) and Tc(VII) faster and is more electroactive than OmcA (41, 42, 62, 63). For each cytochrome, the reaction rate decreased in the order Fe(III)-EDTA > Fe(III)-NTA > Fe(III)-citrate (Fig. 2C), and increasing the ratio of the ferric complex concentration to the cytochrome concentration increased the apparent reaction rate (Fig. 3). For the reaction of MtrC with Fe(III)-NTA and Fe(III)-EDTA complexes with lower Fe-to-cytochrome concentration ratios, stopped-flow kinetic profiles were also recorded (data not shown). The general characteristics of the stopped-flow curves remained the same as those obtained with higher ferric ion concentrations except that the relative extent of the reaction via the fast reaction pathway decreased.

FIG. 3.

Variation of the concentration of reduced cytochrome as a function of time during the reduction of an Fe(III) complex with NTA at different [Fe(III)]/[OmcA] ratios, including 3:1 (line a), 6:1 (line b), and 12:1 (line c). The initial solution conditions were as follows: for line a, 1.5 × 10⁻⁴ M Fe(III), 2.25 × 10⁻⁴ M NTA, and 5.0 × 10⁻⁵ M OmcA (pH 7.0); for line b, 2 × 10⁻⁴ M Fe(III), 3 × 10⁻⁴ M NTA, and 3.3 × 10⁻⁵ M OmcA (pH 7.0); and for line c, 2.4 × 10⁻⁴ M Fe(III), 3.6 × 10⁻⁴ M NTA, and 2 × 10⁻⁵ M OmcA (pH 7.0).

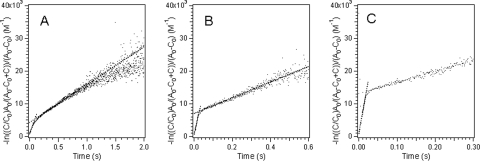
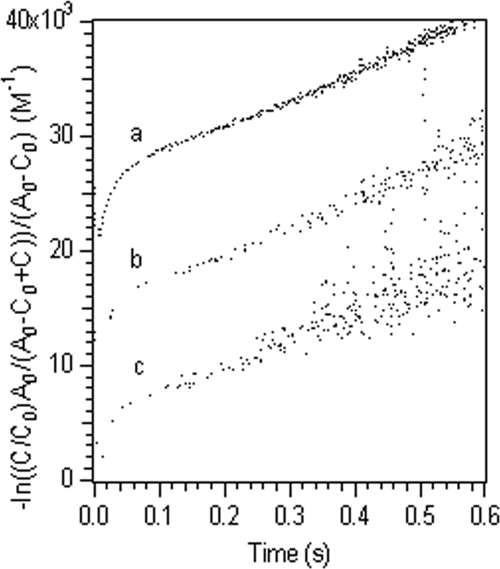
Analysis of the stopped-flow kinetic curves using equation 4 resulted in two straight lines, indicating that there were two reaction rates (Fig. 4). The approximately linear plots for all the experimental data indicated that two parallel second-order bimolecular reactions between the ferric complexes and the cytochrome provided an adequate description for these kinetic reactions (Fig. 4 and Table 2). For the reactions between Fe(III)-NTA or Fe(III)-EDTA complexes and MtrC, a predominant fraction of each reaction proceeded through the fast reaction pathway and the contribution of the slow reaction pathway was negligible. The appropriateness of the two parallel second-order reaction kinetics was further confirmed by the fact that for reactions conducted with different ferric iron-to-cytochrome ratios the calculated second-order rate constant remained constant even though the apparent reaction was proportionally faster at higher ferric iron concentrations (Fig. 5). The calculated second-order reaction rate constants ranged from 0.872 μM⁻¹ s⁻¹ for the fast reaction between MtrC and the Fe(III)-EDTA complex to 0.012 μM⁻¹ s⁻¹ for the slow reaction between OmcA and the Fe(III)-citrate complex (Table 2).

FIG. 4.

Fitted kinetic data for the reduction of an Fe(III) complex with citrate (A), NTA (B), or EDTA (C) by reduced OmcA with parallel second-order reactions.

TABLE 2.

Kinetic parameters for S. oneidensis outer membrane c-type cytochromes MtrC and OmcA at 25°C

Complex	Ferric ion/ligand ratio	Second-order reaction rate constants for MtrC (μM−1 s−1)		Second-order reaction rate constants for OmcA (μM−1 s−1)
		Fast reaction	Slow reaction	Fast reaction	Slow reaction
Fe-citrate	1.5:1	0.2752 ± 0.0062 (74)b	0.0112 ± 0.0003 (26)	0.0373 ± 0.0088 (30)	0.0117 ± 0.0008 (70)
	10:1	0.3362 ± 0.0678 (78)	0.0113 ± 0.0013 (22)	0.0429 ± 0.0058 (40)	0.0111 ± 0.0006 (60)
	Avga	0.3057 ± 0.0545	0.0113 ± 0.0008	0.0401 ± 0.0073	0.0114 ± 0.0007
Fe-NTA	1.5:1	0.2786 ± 0.0049 (86)	0.0656 ± 0.0035 (14)	0.1757 ± 0.0168 (53)	0.0224 ± 0.0016 (47)
	10:1	0.2760 ± 0.0269 (100)	NDc	0.2373 ± 0.0061 (62)	0.0237 ± 0.0005 (38)
	Avga	0.2773 ± 0.0173	ND	0.2065 ± 0.0356	0.0231 ± 0.0013
Fe-EDTA	1.5:1a	0.7207 ± 0.1589 (100)	ND	0.6388 ± 0.0272 (82)	0.0272 ± 0.0053 (18)
	10:1	0.8721 ± 0.0698 (100)	ND	0.6033 ± 0.0328 (86)	0.0151 ± 0.0061 (14)
	Avga	0.7964 ± 0.1376	ND	0.6246 ± 0.0283	0.0285 ± 0.0069

^aThe data are the statistical averages of rate constants at all three [Fe]/[cytochrome] ratios, 150:5, 200:3.3, and 240:2.

^bThe numbers in parentheses are the percentages of measurements for which the ratio of [Fe] to [cytochrome] was 3:1 at an Fe(III) concentration of 1.5 × 10⁻⁴ M.

^cND, not determined.

FIG. 5.

Fitted kinetic data for the reduction of an Fe(III) complex with NTA at different [Fe(III)]/[OmcA] ratios at pH 7.0, including 3:1 (plot a), 6:1 (plot b), and 12:1 (plot c). The initial solution conditions were as follows: for plot a, 1.5 × 10⁻⁴ M Fe(III), 2.25 × 10⁻⁴ M NTA, and 5.0 × 10⁻⁵ M OmcA; for plot b, 2 × 10⁻⁴ M Fe(III), 3 × 10⁻⁴ M NTA, and 3.3 × 10⁻⁵ M OmcA; and for plot c, 2.4 × 10⁻⁴ M Fe(III), 3.6 × 10⁻⁴ M NTA, and 2 × 10⁻⁵ M OmcA.

By defining the intersection point of the two fitted straight lines (Fig. 4) as the turning point from the fast reaction to the slow reaction, the extent of reaction at the fast stage was calculated from the corresponding cytochrome concentration at the turning point (Table 2), and the reminder of the reaction was assumed to proceed via the slow reaction. Except for the reduction of ferric iron-citrate complexes with OmcA, all other reactions proceeded to a larger extent via the fast pathway, although the exact extent of the reaction varied.

Fe(III) speciation and structures of the major complexes.

Equilibrium speciation calculations showed that at a ferric ion-to-ligand ratio of 1:1.5, three Fe(III) species [Fe-(citrate)₂³⁻ (69%), Fe(OH)²⁺ (20%), and Fe-(citrate)⁰ (11%)] were present in the citrate system and two Fe(III) species were present in both the NTA [FeOH-NTA⁻ (92%) and Fe(OH)₂-NTA²⁻ (8%)] and EDTA [FeOH-EDTA²⁻ (15%) and Fe-EDTA⁻ (85%)] systems at pH 7. In each of the three ligand systems, one complex [Fe-(citrate)₂³⁻, FeOH-NTA⁻, and Fe-EDTA⁻] dominated Fe(III) speciation. Increasing the ferric ion-to-ligand ratio to 1:10 resulted in the presence of only Fe-(citrate)₂³⁻ in the citrate system and predicted that three Fe(III) species [FeOH-NTA⁻ (65%), Fe-(NTA)₂³⁻ (27%), and Fe(OH)₂-NTA²⁻ (8%)] would be present in the NTA system and two species [FeOH-EDTA²⁻ (17%) and Fe-EDTA⁻ (83%)] would be present in the EDTA system. Again, Fe-(citrate)₂³⁻, FeOH-NTA⁻, and Fe-EDTA⁻ were the dominant Fe(III) complexes in the three ligand systems.

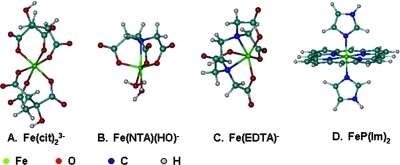
Commonly, the structure of an aqueous metal complex is inferred from the structure of the complex based on crystalline solid and/or other spectroscopic information. Direct determination of the structure of an aqueous metal complex by using X-ray absorption spectra is feasible only for relatively pure complexes at high concentrations. For the complexes in the present work, preliminary extended X-ray absorption fine-structure (EXAFS) results for solutions at relevant ferric ion concentrations indicated that determination of the structure using EXAFS was impossible (data not shown). Therefore, the structures of the dominant ferric complexes in this work were the structures energetically most favorable as calculated at the DFT level (Fig. 6) and further augmented by X-ray diffraction analysis and/or EXAFS data for crystal structures, if available.

FIG. 6.

Computated structures of the dominant ferric-ligand complexes. (A) Fe-(citrate)₂³⁻. (B) FeOH-NTA⁻. (C) Fe-EDTA⁻. (D) bis(Imidazole) iron-porphyrin complex [FeP(im)₂].

For Fe-(citrate)₂³⁻, the structure was optimized with coordination by three carboxylate oxygens from each of the two citrate ligands (Fig. 6A). The ferric coordination in this structure differs from that determined for a compositionally similar compound, (NH₄)₅[Fe-(citrate)₂]·2H₂O, by single-crystal X-ray diffraction in the presence of ammonia solutions (16). In the latter compound, the α-hydroxyl oxygen replaces the third carboxylate oxygen in coordination in both citrate groups. However, it was noted that in (NH₄)₅[Fe-(citrate)₂]·2H₂O, the [Fe-(citrate)₂]⁵⁻ group has a charge of −5; i.e., the α-hydroxyl group in both citrate ligands are deprotonated. In the present complex, Fe-(citrate)₂³⁻, the α-hydroxyl group in both citrate ligands remained protonated. This was likely the cause of the differences in coordination by the carboxylate oxygens instead of the hydroxyl oxygens.

In Fe(OH)-NTA⁻, the ferric ion is coordinated by the NTA nitrogen, three oxygens from each of the NTA carboxylate groups, a hydroxyl oxygen, and a water (Fig. 6B). The structure is close to that of a structurally similar compound, [Fe-(NTA)Cl₂]²⁻, that was synthesized in pyridine (60). The structure of Fe(III)-EDTA⁻ has been determined using single crystals by X-ray diffraction (30) and using solutions by Fe K-edge X-ray absorption spectra (54). The ferric ion is coordinated by two nitrogens and an oxygen of each of the four carboxylate groups of EDTA, as well as a water molecule. This structure is the same as the structure calculated in our work except for a solvent water molecule (Fig. 6C). Because no molecular structure information has been reported for MtrC and OmcA and a DFT calculation for such a large molecule is not feasible, both cytochromes were modeled simply using a bis(imidazole) iron-porphyrin complex, [FeP(im)₂] (Fig. 6D). This heme model serves as a surrogate for the cytochromes and represents an electron donor that is common to all reactions considered.

DISCUSSION

The present results indicate that the reduction of ferric complexes with citrate, NTA, and EDTA by both MtrC and OmcA is generally fast. The reduction reaction proceeds in a “biphasic” manner, with a large part of the reaction occurring in the fast stage. The experimental rate constants (Table 2) showed that there are distinct differences between MtrC and OmcA, as well as among different ferric complexes. The rate constants, which range from 0.872 μM⁻¹ s⁻¹ for the reaction between MtrC and Fe(III)-EDTA to 0.012 μM⁻¹ s⁻¹ for the reaction between OmcA and the Fe(III)-citrate complex, are similar to or higher than the rate constants observed previously for the reduction of ferric complexes with other cytochromes (3, 40, 45). For the three dominant ferric complexes, Fe-(citrate)₂³⁻, FeOH-NTA⁻, and Fe-EDTA⁻, the order for the reduction rates with both cytochromes is as follows: Fe-EDTA⁻ > FeOH-NTA⁻ > Fe-(citrate)₂³⁻.

The biphasic reduction kinetics is attributed to the properties of cytochromes.

Biphasic kinetics is observed for reactions between the cytochromes and the ferric complexes. The fact that this kinetic behavior is observed in the ferric-citrate system when only a single species [Fe-(citrate)₂³⁻] is present in the solution suggests that the observed kinetic behavior is due to the properties of cytochromes. The exact mechanism responsible for this biphasic kinetic behavior is the subject of on-going investigations, but it might involve the presence of heme groups with different redox potentials and/or different reaction sites on the protein surface.

For multiheme cytochromes, it is well known that the redox potentials of the different heme groups can vary as a function of the local environment (8). For example, the redox potentials of the 10 hemes from MtrC range from −100 to −400 mV (22), and the redox potentials for OmcA from Shewanella frigidimarina range from −180 to −400 mV (10), although it is impossible to determine individual potentials for hemes in either protein in the absence of detailed structural information. The redox potentials of the 10 hemes of the cytochromes mentioned above do not appear to be evenly distributed over the entire range. Instead, they often overlap and appear as groups or “clusters” (22, 62, 63). For example, the normalized redox titration data for the OmcA cytochrome from S. frigidimarina could be fitted with two Nernst curves centered at −243 and −324 mV, with spectral distributions of 30 and 70% (10). Similar grouping behavior of the heme redox potentials was also displayed using the differential conductance spectra for both MtrC and OmcA from S. oneidensis (62, 63). Therefore, one plausible interpretation of the biphasic behavior is that the ferric complex reacts with two groups of hemes with different redox potentials within a single cytochrome molecule and that reaction with the group with the more favorable redox potential is faster and reaction with the group with the less favorable redox potential is slower.

Another possible cause of the biphasic kinetics is the presence of multiple types of reaction sites on the cytochromes that have different accessibilities to the ferric complexes. Reaction sites that are less accessible to the substrate likely react more slowly. It is known that there may be conformational differences between cytochromes with different oxidation states (27), and the electron transfer rate may also vary as a function of cytochrome conformation. While there is no experimental evidence that this occurs in the current system, biphasic kinetics due to site heterogeneity has been observed for reactions between other cytochromes and metal complexes or redox partners (9, 25). For example, in the reaction between rat cytochrome P-4501A1 and 7-ethoxycoumarin or aminopyrine, the observed biphasic behavior was explained by the presence of two substrate binding sites for the substrates on the cytochrome (25). In a study involving the reduction of metalloprotein Cu(330) in Rhus vernicifera laccase by Cr(II), it was also found that reaction site heterogeneity in the cytochrome resulted in biphasic reaction kinetics, and it was concluded that major conformational changes in the cytochrome accompanied the electron transfer (9).

Properties of Fe(III)-ligand structure impact the reduction kinetics.

The small variation in the rate constants at different ferric ion-to-ligand ratios suggests that for each ligand the reaction occurs primarily between the protein and a single ferric complex. It is plausible to assume that this complex is the dominant species in the solution since the ligand exchange reactions for ferric complexes with multidentate chelating ligands are much slower than the redox reactions in this work (15, 20). These complexes are Fe-(citrate)₂³⁻, Fe(OH)-NTA⁻, and Fe(III)-EDTA⁻ for the ligand systems. These complexes differ in charge and molecular size. Considering that the reduced cytochromes are likely negatively charged (27), it is not surprising that Fe-(citrate)₂³⁻ reacted slowest due to its high negative charge, which exerts a larger repulsion force when reactants approach each other.

The molecular size of the complex is also an important factor since large ligands can act as spacers that increase the Fe-Fe electron transfer distance (26). While precise data for the molecular sizes of our Fe(III) complexes in aqueous solution are not available, it is reasonable to use the molecular weight to estimate molecular size. The high molecular weight of Fe-(citrate)₂³⁻ (380.2) compared with Fe(OH)-NTA⁻ (210.1) and Fe(III)-EDTA⁻ (291.2) also points to the lowest reaction rate for Fe-(citrate)₂³⁻, which is partially consistent with the trend of the experimental data (Table 2). In addition, as shown in the structures of the complexes (Fig. 6), the ferric ion in Fe-(citrate)₂³⁻ is fully enclosed by the two citrate ligands, while in both Fe(OH)-NTA⁻ and Fe(III)-EDTA⁻ the ferric ion appears to be more exposed on the side opposite the ligand. Hence, the charge, size, and the geometry of the complexes appear to disfavor facile reduction of Fe-(citrate)₂³⁻ by the cytochromes.

The complexes show slight variation in reaction free energies.

While there is no general relationship between the thermodynamics of chemical reactions and the corresponding reaction rates, some correlations are often found for reactions for a set of reactants. One of the most common correlations is the linear free-energy relationship, in which the reaction rate is proportional to the thermodynamic driving force or reaction free energy (6). For the redox reactions between Fe(III) complexes and a given cytochrome, the overall reaction free energy (ΔG) can be evaluated by using the experimental redox potentials of the half-reactions

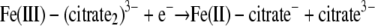(9)

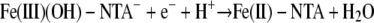(10)

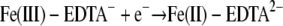(11)

and the redox potential of the cytochromes (4)

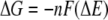(12)

where n is the number of electrons transferred, F is the Faraday constant, and ΔE is the redox potential difference between the reduction potentials of the ferric complexes and the cytochromes. Note that the experimental redox potential depends on the standard redox potential of the Fe(III)/Fe(II) redox couple, the speciation of Fe(III), Fe(II), and the ligand, and the solution pH. Using the standard Fe(III)/Fe(II) redox potential, known stability constants of the Fe(III)/Fe(II) complexes (Table 1), and the initial ferric and ligand concentrations, the redox potentials under the experimental conditions for the half-reactions (equations 9 to 11) were calculated (Table 3). The experimental conditions (e.g., reactant concentrations and solution pH) have a large impact on the calculated redox potentials. The standard redox potentials varied from −0.014 V for Fe-(citrate₂)³⁻ to 0.080 V for Fe-EDTA⁻ to 0.587 V for Fe(OH)-NTA⁻, spanning a range greater than 0.6 V. After the experimental conditions were taken into account, the range of the redox potentials decreased significantly to ca. 0.13 V. Since the ΔG for redox reactions is proportional to the redox potential difference between the ferric complexes and the cytochromes (equation 12), for a given cytochrome the relatively small redox potential differences among the ferric complexes mean that the differences in the reaction free energy among the reactions between the cytochrome and each of the three ferric complexes are small. Therefore, the reaction free energy is unlikely to be the major factor influencing the reaction rate. The differences were small, and the predicted trend for the reaction rate based on the reaction free energy was citrate > NTA > EDTA, which is inconsistent with experimental data obtained in the stopped-flow experiment. This suggests that factors other than reaction free energy influence electron transfer kinetics.

TABLE 3.

Redox potentials for Fe(III) aqueous complex species^a

Reaction	Log K (I = 0)b	E0 (V)	E (V)
Overall redox reactions
Fe(III)-(citrate2)3− + e− → Fe(II)-citrate− + citrate3−	−0.23	−0.014	0.212
Fe(III)OH-NTA− + e− + H+ → Fe(II)-NTA + H2O	9.93	0.587	0.174
Fe(III)-EDTA− + e− → Fe(II)-EDTA2−	0.35	0.080	0.080
Electron transfer reactions
Fe(III)-(citrate2)3− + e− → Fe(II)-(citrate2)4−	1.68	0.099	0.099
Fe(III)OH-NTA− + e− → Fe(II)OH-NTA2−	0.82	0.049	0.049
Fe(III)-EDTA− + e− → Fe(II)-EDTA2−	1.35	0.080	0.080

^aThe standard redox potential (E₀) was calculated from log K, and E is the redox potential under experimental condition.

^bI, ionic strength of the solution.

Reorganization and reaction activation energies play a critical role in the reduction kinetics.

For kinetic reactions, one of the most important factors that influence the reaction rate is the activation energy at the electron transfer step. Experimental determination of the activation energy for the current reactions is not practical. However, a recent development in computational chemistry has allowed reasonably accurate estimation of this parameter from the molecular structures based on Marcus theory (4, 39, 40, 51-53). According to Marcus theory, the diabatic activation energy (ΔG*) is related to the reorganization energy (λ) and reaction free energy (ΔG⁰) in the following way:

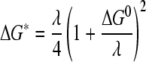(13)

Assuming that there is nonadiabatic electron transfer behavior, which is common in biological systems, the probability of electron transfer in the precursor complex upon thermal activation is related to the electronic coupling matrix element (40). Using a DFT approach very similar to that used by Rosso and Rustad (51), we estimated the rates for the following three electron transfer reactions:

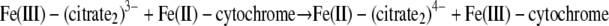(14)

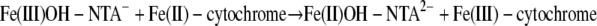(15)

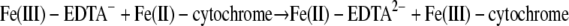(16)

Our DFT calculations provided estimates of the internal reorganization energies for the Fe(III) complexes (the component pertaining to nuclear rearrangement within the precursor complex). A previously published value for a bishistidine heme group (0.08 eV) was used as a representative value for the heme component in the cytochromes (58). The external reorganization energies were computed using Marcus' continuum expression (39) using cavity radii based on the energy-minimized DFT structures. Electronic coupling matrix elements and their distance dependence were obtained from previous studies (29). Values for the equilibrium constant for the formation of the precursor complex were estimated using previously described methods (51) by incorporating electrostatic work corrections for the formation of the precursor and successor complexes using an ionic strength of 0.2 M, which approximated the experimental conditions. This approach yielded a molecular-scale physical electron transfer model that is constrained in its entirety except for the optimal electron transfer distance (51), a quantity that requires significant effort to compute from first principles. Therefore, a single distance value common to all three reactions (equations 14 to 16), which characterizes the cytochrome contribution to separation of the donor and acceptor, is used as the sole fitting parameter in the model. We found that an electron transfer distance of 6.3 ± 0.2 Å, in conjunction with the physical quantities described above, yielded calculated second-order rate constants in excellent agreement with observations (Table 4).

TABLE 4.

Calculated activated energies for electron transfer reactions

Reaction	λ (V)	k12,Calc (μM−1 s−1)a	ke,omcA (μM−1 s−1)b
Fe(III)-(citrate2)3− + Fe(II)-cytochrome → Fe(II)-(citrate2)4− + Fe(III)-cytochrome	1.64	6.6 ± 10−3	3.7 ± 10−2
Fe(III)OH-NTA− + Fe(II)-cytochrome → Fe(II)OH-NTA2− + Fe(III)-cytochrome	1.41	3.5 ± 10−1	1.8 ± 10−1
Fe(III)-EDTA− + Fe(II)-cytochrome → Fe(II)-EDTA2− + Fe(III)-cytochrome	1.31	5.6 ± 10−1	6.4 ± 10−1

^ak_12,Calc is the calculated nonadiabatic rate constant.

^bk_e,omcA is the experimental rate constant of the fast reaction for OmcA.

The calculated reaction rates reproduced the following experimental trend: Fe-EDTA > Fe-NTA > Fe-citrate. Analysis of the model allowed us to conclude that this trend was derived largely from the differences in the reorganization energies predicted for the electron transfer reactions (Table 4). The largest activation energy was associated with the citrate complex, and progressively smaller activation energies were associated with the NTA and EDTA complexes. Larger reorganization energies led to larger activation energies for electron transfer under our conditions, where λ was more than ΔG⁰.

The reorganization energy is the energy required to distort the equilibrium configuration (i.e., nuclear positions) of the reactants into the equilibrium configuration of the products (40, 48), after which electron transfer, a Frank-Condon process, occurs. In solution, the total reorganization energy includes both the internal reorganization energy to distort the bonds of the reactant molecules and the external reorganization energy to rearrange the solvent environment. Thus, the reorganization energy critically depends on the stoichiometry, size, charge, and structural properties of the reactants. Therefore, for metal ion systems where multiple complexes are present, determination of the specific donor and acceptor species becomes critical. For different donor-acceptor pairs, both the Gibbs free energy under the experimental conditions (the driving force of the reaction) and the reorganization energy vary, and, as indicated in equation 13, it is their combined effect that determines the reaction rate. In the present system, the reaction free energies fall within a narrow range, and thus the reaction rate is determined primarily by the reorganization energies.

Implications.

The present results indicated that there is facile reduction of ferric complexes by the outer membrane cytochromes of S. oneidensis MR-1. This is consistent with efficient respiration-linked electron transfer by these bacteria to metal ions that exist as aqueous complexes or as metal oxide solids. The observed variation in the rate of reduction of ferric complexes by MtrC and OmcA suggests that for reduction of some metal complexes by microbial cytochromes, the reorganization energy of participating metal species plays an important role. Dissimilatory reduction of iron, manganese, and other metals is believed to have occurred ever since the inception of life on earth, and it continues to influence the formation and transformation of minerals in nature. Ligands, from simple inorganic anions to large chelating agents with biological origins, are an integral part of the mineral evolution process. For a given metal ion, the nature of the ligand in the metal complexes may determine the rate of dissimilatory metal reduction reactions and thus affect the relative concentrations of the metal ions with different oxidation states. This, in turn, may lead to the formation of different minerals or mineral phases. The present results also suggest that for contaminated sediments where radioactive metals are codisposed with organic chelating agents, any effective bioremediation strategy should take into consideration the ligand complexation effect.