Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2008 Oct 31.
Published in final edited form as: Environ Sci Technol. 2008 May 15;42(10):3648–3654. doi: 10.1021/es702494z

Geostatistical Modeling of the Spatial Distribution of Soil Dioxins in the Vicinity of an Incinerator. 1. Theory and Application to Midland, Michigan

Pierre Goovaerts 1,*, Hoa T Trinh, Avery Demond 2, Alfred Franzblau 3, David Garabrant 3, Brenda Gillespie 4, James Lepkowski 5, Peter Adriaens 2
PMCID: PMC2577050  NIHMSID: NIHMS68146  PMID: 18546703

Abstract

Deposition of pollutants around point sources of contamination, such as incinerators, can display complex spatial patterns depending on prevailing weather conditions, the local topography and the characteristics of the source. Deterministic dispersion models often fail to capture the complexity observed in the field, resulting in uncertain predictions that might hamper subsequent decision-making, such as delineation of areas targeted for additional sampling or remediation. This paper describes a geostatistical simulation-based methodology that combines the detailed process-based modeling of atmospheric deposition from an incinerator with the probabilistic modeling of residual variability of field samples. The approach is used to delineate areas with high level of dioxin TEQDF-WHO98 (Toxic Equivalents) around an incinerator, accounting for 53 field data and the output of the EPA Industrial Source Complex (ISC3) dispersion model. The dispersion model explains 43.7% of the variance in soil TEQ data, while the regression residuals are spatially correlated with a range of 776 meters. One hundred realizations of soil TEQ values are simulated on a grid with a 50 meter spacing. The benefit of stochastic simulation over spatial interpolation is twofold: 1) maps of simulated point TEQ values can easily be aggregated to the geography that is the most relevant for decision making (e.g. census block, ZIP codes); and 2) the uncertainty at the larger scale is simply modeled by the empirical distribution of block-averaged simulated values. Incorporating the output of the atmospheric deposition model as spatial trend yields a more realistic prediction of the spatial distribution of TEQ value than lognormal kriging using only the field data, in particular in sparsely sampled areas away from the incinerator. The geostatistical model provided guidance for the study design (census block-based population sampling) of the University of Michigan Dioxin Exposure Study (UMDES), focused on quantifying exposure pathways to dioxins from industrial sources, relative to background exposures.

Introduction

Deposition of polychlorinated dibenzo-p-dioxins (PCDD) and polychlorinated dibenzofurans (PCDF) near emission sources such as incinerators, can display complex spatial patterns depending on prevailing weather conditions (e.g. wind direction, wet and dry deposition), the local topography and the characteristics of the source (1). Failure to accurately capture this complexity during site characterization can lead to misidentifying populations at risk (2) from exposure to environmental intake concentrations due to inhalation of surrounding air, unintended ingestion of and dermal contact with soil, and cultivated crops or other vegetation. The information available for site characterization impacted by incinerators typically includes air and soil measurements collected near the source, complemented by data about the source and its environment—such as meteorological data, wind speed and direction, the characteristics of the stack, and exhaust emissions (e.g. 3–6).

Often, the datasets of PCDD/F concentrations in soil tend to be small (e.g. reviewed in 5) such that, even with the help of advanced geostatistical methods (7,8), they do not suffice for a detailed modeling of the spatial distribution of contaminants. For example, Williams and Ogston (2002) applied ordinary kriging to 83 soil data to create smooth maps of arsenic and copper concentrations around a waste incinerator (2). Using ordinary kriging with 73 soil samples, Fowles et al (2005) mapped soil TCDD concentrations in the vicinity of a point source of production of the herbicide 2-4-5,T (6). Lorber et al. (2000) used a similar approach to map the soil TEQ concentrations around a municipal soil waste incinerator (3). These studies have the same weaknesses: 1) important information, such as proximity to the incinerator, and the predominant wind direction, was ignored in the interpolation procedure; and 2) the reliability of the estimated concentrations was not reported in most studies. In particular, the presence of a point source of pollution creates spatial trends in the data that invalidate the assumption of stationarity underlying ordinary kriging (7). There are several geostatistical alternatives to ordinary kriging. For example, global spatial trend models accounting for distance to the source and wind direction can be built first, followed by kriging of the residuals (9). More recently, Saito and Goovaerts (2001) developed a variant of kriging with a trend whereby information about the location of the pollutant source and transport is incorporated directly into the kriging system (10).

Distance to the source of pollution, and wind direction are only a few of the parameters that influence the dispersion of pollutants around an incinerator (1). Deterministic dispersion models, such as EPA’s nonreactive Gaussian Industrial Source Complex (ISC3) air quality dispersion model (11), allows one to take into account a wide range of parameters that pertain to meteorological conditions (e.g. ambient temperature, stability class, rural and urban mixing heights, precipitation rate), the local topography, and the characteristics of the source (e.g. emission rate, stack height and diameter, stack temperature and exit velocity, particle diameter). Unfortunately, these parameters are often unavailable for historical pollution events which are often the most consequential. The level of detail in the model output can also provide a false sense of confidence in the model accuracy (2). Results depend on the specification of appropriate local characteristics and their uncertainty is often overlooked in the interpretation phase. Typically, uncertainties in this regard are addressed using sensitivity analysis on the effect of key model inputs on simulation results (4). These authors indicated the sensitivity of the model to dry deposition flux (particle size distribution), particularly when local emission impacts need to be resolved.

A promising avenue of research is the combination of detailed process-based modeling of atmospheric deposition and monitoring data within a probabilistic framework in order to incorporate and propagate the uncertainty attached to the different pieces of information. Such data merging has been accomplished in several air quality mapping studies (12,13). For example, error-in-variable external drift kriging was used to combine annual average NO2 concentrations with regional dispersion model output (12). The studies were, however, conducted mainly at a regional level requiring the estimation of exposure over spatial supports much larger than the measurement support.

This paper describes a geostatistical methodology to combine field data with the predictions of a physical dispersion model. The approach generates a set of equally-probable maps of the spatial distribution of pollutants which can be post-processed to compute the probability that target thresholds are exceeded locally or on average over polygons of various size (i.e. census units). The methodology is illustrated using TEQ field data and a dispersion model created for the incinerator in Midland, Michigan. Results are compared to the univariate lognormal kriging approach.

Materials and Methods

Study Site

The study area is the vicinity of the Dow Chemical Company facility in Midland, Michigan; see Figure 1a. Since the 1940s, areas North-East of the Dow facility have been exposed to the deposition of dioxins resulting from incinerator outfall. Two types of incinerator facilities were used to dispose of solid wastes contaminated with halogenated compounds, including dioxins. During high temperature incineration, so-called de novo chemical synthesis processes take place resulting in the formation of polychlorinated dibenzo-p-dioxins (PCDD) and dibenzofurans (PCDF) as by-products which are then dispersed from the smoke stack. Whereas prior to 1970 incineration was fairly inefficient resulting in the formation, dispersion and deposition of higher concentrations of these by-products, modernization of the facilities since 2000 to a high efficiency (99.9999% destruction of dioxins) incinerator resulted in significant source reduction of emissions. With a prevailing N.E. wind direction, the emission plume impacted the downwind communities. It is assumed that the measured elevated soil dioxin concentrations, ranging from 1–500 ppt (ng/g soil), are largely the result from emission plume deposition prior to the 1980s.

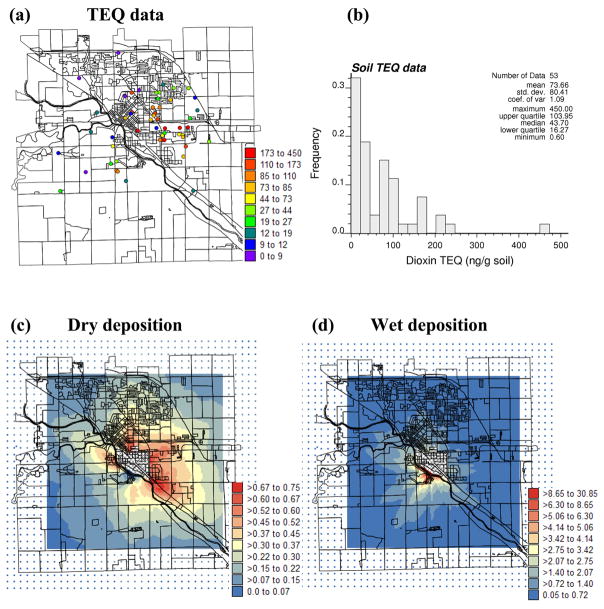
Figure 1.

Figure 1

Open in a new tab

Location map of 53 TEQ data (a) and the corresponding histogram (b). Bottom maps show the grids of 5-year dry (c) and wet deposition (d) values predicted by the dispersion model (units= μg/m2). The outlines of census blocks are displayed in background and the central hatched area denotes the plant property.

Field Data

Up to 265 georeferenced soil TEQ concentrations were measured in Midland area over various sampling campaigns between 1983 and 1998 (14). Discrepancies among databases, as well as the preferential nature of some of the sampling campaigns (e.g. along roads), led us to question the reliability and representativeness of the larger database. The present study was thus based on a smaller set of 53 observations that was used in a previous spatial characterization of dioxin contamination at the site (i.e. map produced by Thiessen polygons) by the company Exponent. These data, which were collected mainly in 1996–1998 (8 samples were taken in 1984), also displayed the highest correlation with the output of the dispersion model. Figure 1a shows the location of those samples using census blocks as the background layer. The need for census block-based information was driven by the study objective to conduct population-based sampling design. Census block shape files for Midland, Bay City and Saginaw were projected to NAD83 Michigan Georef. No air sampling data were available for the period modeled (1987–1991). However, a stack test conducted by EPA in 1992 for the Midland incinerator reported a concentration of 0.00919 TEQ (ng/dscm) with emission of Dioxins and Furans (15).

Air Dispersion Modeling and Correlation to Soil TEQ Concentration

Air concentrations values, as well as total deposition flux values (both dry and wet), were predicted at the nodes of a receptor grid using the short term (ST) version of the EPA Industrial Source Complex (ISC3) dispersion model (11) for the period 1987–1991. ISCST3 is a Gaussian plume model, which accepts a variety of source geometries and emission schedules, predicting ambient air concentration and surface deposition fluxes at receptor points. The exposure assessment grid consists of four nested receptor grids that get coarser further away from the plant property line: 50 m (around the plant property and up to 1,000 m), 100 m (1,000 to 5,000 m range), and 500 m (5,000 to 10,000 m range). The deposition model was run using hourly meteorological data (e.g. wind speed, ambient temperature, precipitation rate) available for 1987–1991 and the set of input parameters reported in Table S1 (Supporting Information). To assess the impact of key model inputs on the simulation results, a sensitivity analysis was conducted and is described in Note S1 and Table S2 (Supporting Information).

Geostatistical Analysis

The uncertainty about the spatial distribution of soil dioxin TEQ was modeled using sequential Gaussian simulation (described in Note S2, Supporting Information) that proceeds in three steps: 1) normal score transform of the data; 2) simulation of attribute values in the normal space; and 3) back-transform of simulated normal scores into simulated values for the original variable. The following methodology was implemented:

  1. The 53 soil TEQ concentrations were normal score transformed to correct for the strongly positively skewed sample histogram. In the absence of information about preferential sampling, no declustering weights were used for this dataset.

  2. The 53 transformed data were regressed against the deposition (wet and dry) values predicted using the numerical dispersion model (base case scenario). This regression model was used to predict the TEQ concentration and standard error at the nodes of the 261×261 simulation grid centered on the incinerator. The grid, which has a 50 m spacing, does not include any node within the boundary of the plant.

  3. The spatial variability of regression residuals was modeled using the semivariogram.

  4. Sequential Gaussian simulation was used to simulate the spatial distribution of TEQ values conditionally to the 53 soil TEQ data, the trend model inferred from the calibration of the deposition data (step 2) and the pattern of correlation modeled in step 3. One hundred realizations were generated over the 261×261 simulation grid.

  5. Point simulated values were averaged within each census block to yield a simulated block value (upscaling). This averaging is repeated for each realization, yielding a set of 100 simulated values for each census block. The following three statistics were derived from the distribution of 100 simulated block TEQ values: mean, variance and proportion of block values that exceeds a threshold of 90 ppt which is the soil generic residential Direct Contact Criterion (DCC) used by the Department of Environmental Quality for Midland, Michigan (16).

To illustrate the benefit of incorporating the output of the atmospheric deposition model as spatial trend in the geostatistical modeling, TEQ values were interpolated at the nodes of the simulation grid using lognormal ordinary kriging (described in Note S3, Supporting Information). Universal kriging was not used since it causes a lot of artifacts in the maps (e.g. negative estimates), in particular in extrapolation situations.

The procedure SAS GLM (17) was used for the regression, while the normal score transform was conducted using the program nscore in the public domain software library, GSLIB (18). Sequential Gaussian simulation with local means and lognormal kriging were implemented by modifying the FORTRAN source code Sgsim and kt3d in GSLIB. Aggregation within census blocks and mapping were accomplished using the commercial product, TerraSeer STIS (Space-Time Intelligence System) (19).

Results and Discussion

Air Dispersion Model

Figure 1b shows the histogram of 53 soil TEQ data. Concentrations range between 0.60 ppt and 450 ppt, with a mean value of 73.7 ppt. Five-year dry and wet deposition values predicted by the dispersion model are mapped in Figure 1c–d. These two variables display contrasting spatial patterns: higher dry deposition is observed downwind on the North-eastern side of the plant, while important wet deposition is predicted on the South-western side of the plant due to different prevailing wind directions during precipitation events. The predicted values for wet deposition are two orders of magnitude larger than for dry deposition. The deposition pathway tends to be dependent on seasonal (e.g. 5) and geographic (e.g. 20) climatologic characteristics. For example, measurements in the Midwest (21,22) showed the ratio between dry/wet deposition of dioxins and furans to be 6:1 (geometric average) and 5:1 (weighted average). On the contrary, findings in the Houston area indicated that wet deposition is a more efficient way of removing PCDDs/Fs from air (23). Schroder et al. (1997) assessed the relative importance of wet, dry particle and gaseous deposition of PCDD/Fs to a bare soil, and found that dry particle-bound deposition accounted for 15% of the total flux of all congeners (24). In addition, more than two-thirds of the deposition was due to large particles. Deposition patterns tend to be dominated by the higher chlorinated congeners, in particular OCDD, which may account for 20–40% of the PCDD/F flux (20). On the other hand, the TEQ of deposited dioxins appears to be dominated by 2,3,4,7,8-PeCDF, contributing between 20–40% of the total flux. To demonstrate the geostatistical methodology, the focus in this paper is on total soil TEQ, despite differences in fate and transport behavior between the various contributing congeners.

Regression Model with Soil Concentrations

The output of the air dispersion model ISCST3 (base case Scenario 1) was regressed against the available soil TEQ concentrations (Figure S1a–b, Supporting Information). The strongest correlation was observed for dry deposition: r=0.641. Wet deposition has a significantly smaller correlation (p=0.0224) with soil data: r=0.344. These observations are despite the fact that wet deposition is often observed to be a more important mechanism than dry deposition for PCDD/F. The result is likely due to the fact that most soil samples were collected close to (within 3 km of) the incinerator, where dry particle deposition is likely more important (4,25). These two mechanisms, as well as their interaction, were used as explanatory variables in a linear regression model using normal score TEQ values as the dependent variable. Air concentration is strongly correlated with dry deposition (r=0.97), hence this variable was not included in the final regression model. This model explains 43.7% of the total variance in soil TEQ concentrations. No significant increase in the proportion of variance explained was observed in the sensitivity analysis (described in Note S2, Supporting Information). Thus, the residual variability in soil concentrations needs to be treated in an uncertainty-based spatial distribution framework.

Geostatistical Model for Soil TEQ Distributions

The geostatistical model was initiated by applying the regression model to the 261×261 exposure assessment grid, yielding the trend model displayed in Figure 2a. The joint contribution of dry and wet depositions generates a continuous ring of high trend values around the plant. Figure 2b shows the map of the regression standard errors which are the smallest for the prediction of the average normal score value of zero, as expected. Because of the proportional effect, standard errors are particularly large on the South-western side of the plant where the highest TEQ concentrations, and also the largest contribution of wet deposition, were predicted (compare Figures 1d and 2b). This uncertainty was combined with the residual kriging variance in the simulation procedure (Eq. S2).

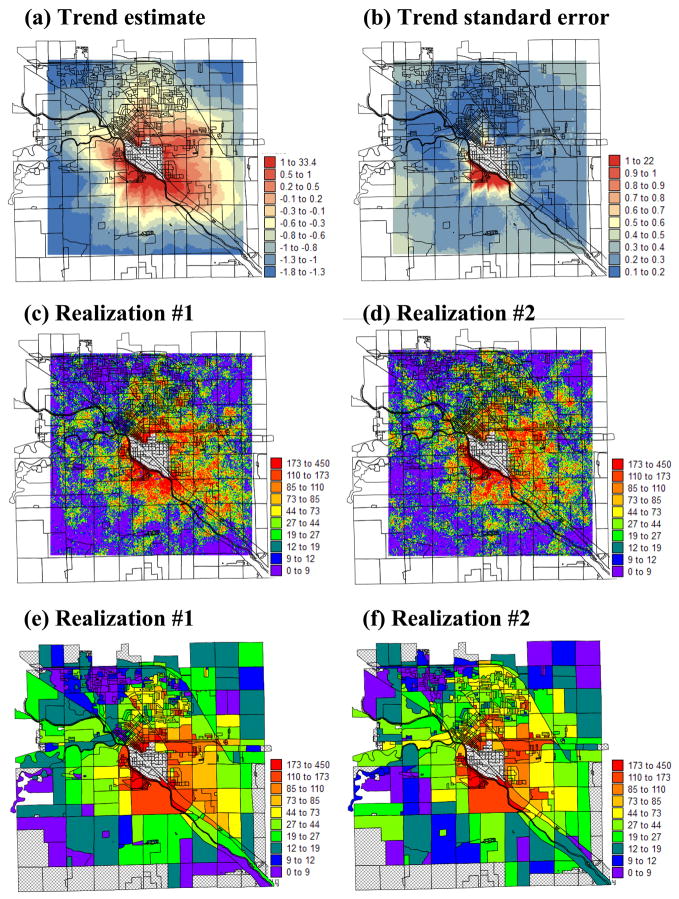
Figure 2.

Figure 2

Open in a new tab

TEQ normal score estimate (a) and associated standard error (b) computed at the nodes of the simulation grid using linear regression. Two realizations of the spatial distribution of TEQ values (c,d) generated by sequential Gaussian simulation, and the results of the averaging to the census block level (e,f). The central hatched area denotes the plant property.

The spatial trend in TEQ data causes the sampled concentrations to be increasingly different as their separation distance increases. This spatial pattern translates into an unbounded experimental semivariogram that never reaches a sill (Figure S1c, Supporting Information). Similar behaviors were observed for other sites with point source of pollution (10,26,27). Once the spatial trend is subtracted, the semivariogram of regression residuals (Figure S1d, Supporting Information) reaches a sill at an estimated distance of 776 meters, which is known as the distance of autocorrelation. This result indicates the presence of spatially structured variability that operates over short distance and cannot be explained by the atmospheric deposition model. In the New Zealand study on soil TCDD, the semivariogram of soil concentrations had a range of autocorrelation of 689 meters along the main axis of the plume and 240 meters in the perpendicular direction (6).

Figure 2c–d shows two realizations of the spatial distribution of TEQ values generated using sequential Gaussian simulation. As expected, the largest TEQ values are found close to the plant property line. Differences between realizations illustrate the uncertainty attached to the exact TEQ value at those locations. Spatial features, such as specific strings or clusters of large values, are deemed certain if seen on most of the simulated maps. Conversely, a feature is deemed uncertain if seen only on a few simulated maps (7,28,29). For example, the extent of the plume on the South-western side of the plant is much wider on the simulated map #1 relatively to realization #2, which illustrates the uncertainty attached to this prediction. Point-simulated values are then averaged to the level of census blocks which represent our decision support (see Figure 2e–f). Although averaging smoothes the spatial variability in the simulated values, substantial differences are still observed among the first two realizations. In particular, simulated TEQ values at the census block level are larger on the Southwestern side of the plant for the first realization.

The information contained in the set of 100 realizations is summarized in Figure 3. The maps of the mean and standard deviation of the point (Figure 3a–c) and census block-level (Figure 3b–d) distributions of 100 simulated TEQ values reflect the impact of the trend model as follows. The uncertainty about TEQ values, as measured by differences among realizations, is the largest on the South-western side of the plant where the regression standard errors are the largest. Field information (availability of soil data) does not attenuate this uncertainty since fewer soil samples were collected on this side of the plant. The maps of standard deviations support the preliminary conclusions inferred from the visual, and necessarily subjective, comparison of the set of two realizations displayed in Figure 2.

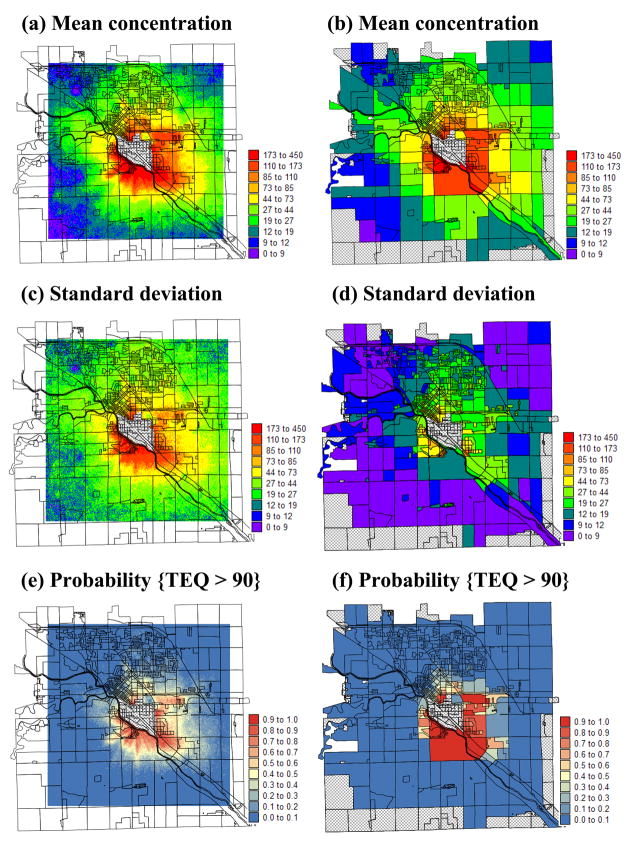
Figure 3.

Figure 3

Open in a new tab

Summary statistics for the distribution of 100 TEQ values simulated at the nodes of a 50 m grid (left) or at the level of census blocks (right): mean (a,b), standard deviation (c,d) and probability that the TEQ concentration exceeds 90 ng/g (e,f). Hatched polygons denote census blocks outside the simulation area.

For decision-making, the uncertainty about TEQ concentrations should be supplemented by a measure of the likelihood that the soil generic residential Direct Contact Criterion (DCC) of 90 ppt (proposed by Michigan) is exceeded (29,30). This likelihood or probability is easily computed at the point or census block level by counting, for each grid node or census block, the proportion of 100 simulated TEQ values that are larger than 90 ppt. By mimicking the spatial distribution of average simulated values, the probability maps (Figure 3e–f) indicate a large probability of exceeding the DCC threshold of 90 ppt on the Southern and eastern part of the plant. Among the 130 census blocks with an average simulated TEQ value greater than 90 ppt, the probability of exceedence ranges from 0.41 to 1. For example, one of the 130 census blocks with an average TEQ value barely above the DCC (simulated average=90.52 ppt) has a simulated value below the DCC for 59 out of 100 realizations, leading to the 0.41 probability of exceedence. This information is critical for decision-making, such as delineation of hazardous areas or selection of locations where additional measurements should be collected. Typically, these probabilities are compared to thresholds p1 and p2 defining tolerable risks for classifying a site as safe (probability of exceedence < p1) or hazardous (probability of exceedence > p2), while probabilities in the range [p1, p2] indicate sites whose classification is uncertain (29,30). Adopting the pair of probability thresholds p1=0.2 and p2=0.8 used in earlier studies (7,29,30), less than half (54 over 130) the census blocks with a simulated average above 90 ppt should be classified as hazardous with certainty.

Simple kriging with local means offers a straightforward way to combine field data with the output of an air dispersion model, while accounting for the spatial correlation in the residual variability. If the dispersion model accounts for all the spatial structure displayed by the data, then the residual kriging estimate will be zero and the mean of simulated values will return the trend estimate. Lognormal kriging (31), which ignores the spatial trend information provided by the air dispersion model, produces smooth maps with unrealistically large concentrations away from the incinerator (e.g. SE corner) where no field data are available (Figure S2b, Supporting Information). The uncertainty, as measured by the lognormal kriging standard error, tends also be larger than the uncertainty modeled by the differences among simulated TEQ values (Figures S2c–d, Supporting Information).

The main benefit of the proposed stochastic simulation approach over point kriging is the availability of a model of uncertainty that is scalable. In particular, the uncertainty modeled at the scale of the data (i.e. soil cores) can be up-scaled to the level of the decision units, which are census blocks in this study. Information critical for decision making, such as the probability of exceeding the DCC threshold or a measure of the uncertainty about predicted TEQ values, can be easily retrieved from the set of simulated maps. These statistics provided guidance for the collection of new human and soil data in the study area. In the companion paper, the new soil data are used to assess the accuracy and precision of the model created using sequential Gaussian simulation. These new data will also be combined with 53 original soil TEQ data, leading to updated models of the spatial distribution of TEQ values.

Supplementary Material

Supporting inf. Supporting Information Available.

Characteristics of the modeled incinerator and input parameters used in ISCST3, sensitivity analysis of the deposition model ISCST3, description of sequential Gaussian simulation and lognormal kriging algorithms, scatterplots of soil TEQ normal scores versus 5-year dry and wet deposition, omnidirectional semivariograms of soil TEQ normal scores before and after subtracting the trend modeled from deposition data, results of lognormal kriging. This material is available free of charge via the internet at http://pubs.acs.org.

Acknowledgments

Financial support for this study comes from the Dow Chemical Company through an unrestricted grant to the University of Michigan. The authors acknowledge Ms. Sharyn Vantine for her continued assistance; Scott Swan for preparing the census shape files used in this study and Drs. Linda Birnbaum, Ron Hites, Paolo Boffetta and Marie Haring Sweeney for their guidance as members of our Scientific Advisory Board. The first author’s contribution was partially funded by grant R44-CA105819-02 from the National Cancer Institute. The views stated in this publication are those of the author and do not necessarily represent the official views of the NCI.

Footnotes

Brief

This paper describes a geostatistical simulation-based methodology that combines the detailed process-based modeling of atmospheric deposition from an incinerator with the probabilistic modeling of residual field variability.

Literature Cited

  • 1.Floret N, Viel JF, Lucot E, Dudermel PM, Cahn JY, Badot PM, Mauny F. Dispersion modeling as a dioxin exposure indicator in the vicinity of a municipal soil waste incinerator: a validation study. Environ Sci Technol. 2006;40:2149–2155. doi: 10.1021/es052309u. [DOI] [PubMed] [Google Scholar]
  • 2.Williams FLR, Ogston SA. Identifying populations at risk from environmental contamination from point sources. Occupational and Environmental Medicine. 2002;59:2–8. doi: 10.1136/oem.59.1.2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Lorber M, Eschenroeder A, Robinson R. Testing the USA EPA’s ISCST-Version 3 model on dioxins: a comparison of predicted and observed air and soil concentrations. Atm Environ. 2000;34:3995–4010. [Google Scholar]
  • 4.Lohman K, Seigneur C. Atmospheric fate and transport of dioxins: local impacts. Chemosphere. 2001;45:161–171. doi: 10.1016/s0045-6535(00)00559-2. [DOI] [PubMed] [Google Scholar]
  • 5.Oh JE, Choi SD, Lee SJ, Chang YS. Influence of a municipal solid waste incinerator on ambient air and soil PCDD/F levels. Chemosphere. 2006;64:579–587. doi: 10.1016/j.chemosphere.2005.11.012. [DOI] [PubMed] [Google Scholar]
  • 6.Fowles J, Gallagher L, Baker V, Phillips D, Marriott F, Stevenson C, Noonan M. A Study of 2,3,7,8-Tetrachlorodibenzo-p-dioxin (TCDD) Exposures in Paritutu, New Zealand. [Accessed July 2, 2007];A Report to the New Zealand Ministry of Health. 2005 February; Available: http://www.moh.govt.nz/dioxins.
  • 7.Goovaerts P. Geostatistics for Natural Resources Evaluation. Oxford University Press; New York: 1997. [Google Scholar]
  • 8.Chiles JP, Delfiner P. Geostatistics: Modeling Spatial Uncertainty. JW Wiley and Sons; New York: 1999. [Google Scholar]
  • 9.Mohammadi J, Van Meirvenne M, Goovaerts P. Mapping cadmium concentration and the risk of exceeding a local sanitation threshold using indicator geostatistics. In: Soares A, Gomez-Hernandez J, Froidevaux R, editors. geoENV I - Geostatistics for Environmental Applications. Kluwer Academic Publishers; Dordrecht: 1997. pp. 327–337. [Google Scholar]
  • 10.Saito H, Goovaerts P. Accounting for source location and transport direction into geostatistical prediction of contaminants. Environ Sci Technol. 2001;35:4823–4829. doi: 10.1021/es010580f. [DOI] [PubMed] [Google Scholar]
  • 11.U.S. EPA. User’s Guide for the Industrial Source Complex (ISC3) Dispersion Models. U.S. EPA; Research Triangle, NC: 1995. EPA-454/B-95-003a. [Google Scholar]
  • 12.van de Kassteele J, Velders GJM. Uncertainty assessment of local NO2 concentrations derived from error-in-variable external drift kriging and its relationship to the 2010 air quality standard. Atmospheric Environment. 2006;40:2583–2595. [Google Scholar]
  • 13.Genikhovich E, Filatova E, Ziv A. A method for mapping the air pollution in cities with the combined use of measured and calculated concentrations. International Journal of Environment and Pollution. 2003;18:56–63. [Google Scholar]
  • 14.Michigan Department of Environmental Quality. [Accessed July 2, 2007];2005 Available: http://www.deq.state.mi.us/documents/deq-whm-hw-dow-2005-06-10-midland-summary-map.pdf.
  • 15.U.S. EPA. [Accessed July 2, 2007];Source Data for Hazardous Waste Combustors. Available: http://www.epa.gov/epaoswer/hazwaste/combust/finalmact/source.htm#Michigan.
  • 16.DEQ. Dioxin Contamination in the Midland Area. U.S. EPA: Research Triangle, NC; 2004. [Accessed July 2, 2007]. Available http://www.deq.state.mi.us/documents/deq-whm-hwrp-dowfactsfinal.pdf. [Google Scholar]
  • 17.SAS Institute Inc. SAS/STAT User’s Guide, Version 6. 4. Vol. 2. SAS Institute Inc.; Cary, NC: 1989. [Google Scholar]
  • 18.Deutsch CV, Journel AG. GSLIB: Geostatistical Software Library and User Guide. Oxford University Press; New York: 1998. [Google Scholar]
  • 19.AvRuskin GA, Jacquez GM, Meliker JR, Slotnick MJ, Kaufmann AM, Nriagu JO. Visualization and exploratory analysis of epidemiologic data using a novel space time information system. International Journal of Health Geographics. 2004;3:26. doi: 10.1186/1476-072X-3-26. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Lohmann R, Jones KC. Dioxins and furans in air and deposition: A review of levels, behaviour and processes. Science of the Total Environment. 1998;219:53–81. doi: 10.1016/s0048-9697(98)00237-x. [DOI] [PubMed] [Google Scholar]
  • 21.Eizter BD, Hites RA. Atmospheric transport and deposition of polychlorinated dibenzo-p-dioxins and dibenzofurans. Environ Sci Technol. 1989;23:1389–1395. doi: 10.1021/es00008a031. [DOI] [PubMed] [Google Scholar]
  • 22.Koester CJ, Hites RA. Wet and dry deposition of chlorinated dioxins and furans. Environ Sci Technol. 1992;26:1375– 1382. [Google Scholar]
  • 23.Correa OE, Raun L, Rifai HS, Suarez MP, Holsen T, Koenig L. Depositional flux of polychlorinated dibenzo-p-dioxins and polychlorinated dibenzofurans in an urban setting. Chemosphere. 2006;64:1550–1561. doi: 10.1016/j.chemosphere.2005.11.020. [DOI] [PubMed] [Google Scholar]
  • 24.Schroder J, Welsch-Pausch K, McLachlan MS. Measurements of atmospheric deposition of polychlorinated dibenzo-p-dioxins PCDDs and dibenzofurans PCDFs to a soil. Atmos Environ. 1997;31:2983–2989. [Google Scholar]
  • 25.Yoshida K, Ikeda S, Nakanishi J, Tsuzuki N. Validation of modeling approach to evaluate congener-specific concentrations of polychlorinated dibenzo-p-dioxins and dibenzofurans in air and soil near a solid waste incinerator. Chemosphere. 2001;45:1209–1217. doi: 10.1016/s0045-6535(00)00587-7. [DOI] [PubMed] [Google Scholar]
  • 26.Aboal JR, Real C, Fernandez JA, Carballeira A. Mapping the results of extensive surveys: The case of atmospheric biomonitoring and terrestrial mosses. Science of the Total Environment. 2006;356:256–274. doi: 10.1016/j.scitotenv.2005.04.025. [DOI] [PubMed] [Google Scholar]
  • 27.Nopmongcol U, Khamwichit W, Fraser MP, Allen DT. Estimates of heterogeneous formation of secondary organic aerosol during a wood smoke episode in Houston, Texas. Atmos Environ. 2007;41:3057–3070. [Google Scholar]
  • 28.Goovaerts P. Geostatistical modelling of uncertainty in soil science. Geoderma. 2001;103:3–26. [Google Scholar]
  • 29.Saisana M, Dubois G, Chaloulakou A, Spyrellis N. Classification criteria and probability risk maps: Limitations and perspectives. Environ Sci Technol. 2004;38:1275–1281. doi: 10.1021/es034652+. [DOI] [PubMed] [Google Scholar]
  • 30.Van Meirvenne M, Goovaerts P. Evaluating the probability of exceeding a site-specific soil cadmium contamination threshold. Geoderma. 2001;102:75–100. [Google Scholar]
  • 31.Saito H, Goovaerts P. Geostatistical interpolation of positively skewed and censored data in a dioxin contaminated site. Environ Sci Technol. 2000;34:4228–4235. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting inf. Supporting Information Available.

Characteristics of the modeled incinerator and input parameters used in ISCST3, sensitivity analysis of the deposition model ISCST3, description of sequential Gaussian simulation and lognormal kriging algorithms, scatterplots of soil TEQ normal scores versus 5-year dry and wet deposition, omnidirectional semivariograms of soil TEQ normal scores before and after subtracting the trend modeled from deposition data, results of lognormal kriging. This material is available free of charge via the internet at http://pubs.acs.org.

NIHMS68146-supplement-Supporting_inf.doc (1.9MB, doc)

RESOURCES