Robust Nonrigid Multimodal Image Registration using Local Frequency Maps

Abstract

Automatic multi-modal image registration is central to numerous tasks in medical imaging today and has a vast range of applications e.g., image guidance, atlas construction, etc. In this paper, we present a novel multi-modal 3D non-rigid registration algorithm where in 3D images to be registered are represented by their corresponding local frequency maps efficiently computed using the Riesz transform as opposed to the popularly used Gabor filters. The non-rigid registration between these local frequency maps is formulated in a statistically robust framework involving the minimization of the integral squared error a.k.a. L₂E (L₂ error). This error is expressed as the squared difference between the true density of the residual (which is the squared difference between the non-rigidly transformed reference and the target local frequency representations) and a Gaussian or mixture of Gaussians density approximation of the same. The non-rigid transformation is expressed in a B-spline basis to achieve the desired smoothness in the transformation as well as computational efficiency.

The key contributions of this work are (i) the use of Riesz transform to achieve better efficiency in computing the local frequency representation in comparison to Gabor filter-based approaches, (ii) new mathematical model for local-frequency based non-rigid registration, (iii) analytic computation of the gradient of the robust non-rigid registration cost function to achieve efficient and accurate registration. The proposed non-rigid L₂E-based registration is a significant extension of research reported in literature to date. We present experimental results for registering several real data sets with synthetic and real non-rigid misalignments.

1 Introduction

Image registration is a central algorithm to many image processing tasks and has a vast range of applications including, but not limited to, medical image analysis, remote sensing, optical imaging, etc. In this section, we will briefly review existing algorithms reported in literature for achieving multi-modal registration. We will point out their limitations and hence motivate the need for a new and efficient computational algorithm for achieving our goal.

1.1 Previous work

Image registration methods in literature to date may be classified into feature-based and “direct” methods. Most feature-based methods are limited to determining the registration at the feature locations and require an interpolation at other locations. If however, the transformation/registration between the images is a global transformation e.g., rigid, affine etc. then, there is no need for an interpolation step. However, in the case of a non-rigid transformation, it is necessary to interpolate. Also, the accuracy of the registration is dependent on the accuracy of the feature detector.

Several feature-based methods involve detecting surfaces landmarks [1], edges, ridges etc. (see [2] for references). Most of these assume a known correspondence with the exception of the work in Chui et.al., [1]. Work reported in Irani et.al., [3] uses the energy (squared magnitude) in the directional derivative image as a representation scheme for matching achieved using the SSD cost function. Recently, Liu et.al., [4] reported the use of local frequency in a robust statistical framework using the integral squared error a.k.a., L₂E. The primary advantage of L₂E over other robust estimators in literature is that there are no tuning parameters in it. The idea of using local phase was also exploited by Mellor et. al., [5], who used mutual information (MI) to match local-phase representation of images and estimated the non-rigid registration between them. However, robustness to significant non-overlap in the field of view (FOV) of the scanners was not addressed. For more on feature-based methods, we refer the reader to the survey by Maintz et.al., [2].

In the context of “direct” methods, the primary matching techniques for intra-modality registration involve the use of normalized cross-correlation, modified SSD, and (normalized) mutual information (MI). Recently, Roche et.al., [6] developed a correlation ratio based algorithm for registering MR scans with ultra-sound images. The results presented were quite impressive however, the issue of robustness to variations in the FOVs of the scanners was not adequately addressed. Direct methods such as, variants of optical flow-based registration that accommodate for varying illumination maybe used for inter-modality registration and we refer the reader to [7, 8] for such methods. Guimond et. al., [9] reported a multi-modal brain warping technique that uses Thirion’s Demons algorithm [10] with an adaptive intensity correction. The technique however was not tested for robustness with respect to significant non-overlap in the FOVs.

A popular “direct” approach is based on the concept of maximizing mutual information (MI) pioneered by Viola and Wells [11] and Collignon et al., [12] and modified in Studholme et al., [13]. Reported registration experiments in these works are quite impressive for the case of rigid motion. In [14], Studholme et.al., presented a normalized MI scheme for matching multi-modal image pairs misaligned by a rigid motion. Normalized MI was shown to cope with image pairs not having exactly the same FOV, an important and practical problem. The problem of being able to handle non-rigid deformations in the MI framework is a very active area of research and some recent papers reporting results on this problem are [5, 15–19]. Computational efficiency and accuracy (in the event of significant non-overlaps) are issues of concern in all the MI-based non-rigid registration methods.

1.2 Overview of Proposed Registration Method

In this paper, we develop a multi-modal registration technique which is based on a local frequency representation of the image data. A local frequency image representation can be obtained by filtering the image with Gabor filters and then computing the gradient of the phase of the filtered images. As an alternative to the Gabor filter, we use the Riesz transform (see section (2), which is computationally more efficient. Once, we compute this local frequency representation for each of the two (source and target) images to be registered, we are ready to find the registration transformation which will best match these representations. Several matching criteria may be defined and we developed a statistically robust measure called the L₂E defined as the squared difference between the true density of the residual — defined as the squared difference between the transformed source and the target local frequency representations — and a Gaussian density approximation of the same. This matching criteria is minimized over a class of smooth transformations expressed in a B-spline basis. The algorithm we have developed is well suited for situations where the source and target images have FOVs with large non-overlapping regions (which is quite common in practise). This formulation leads to a nonlinear cost function whose optimization yields the desired non-rigid registration. Several experiments with synthetic and real 3D data sets are presented to depict the performance of our algorithm.

Rest of the paper is organized as follows: in section 2.1, we present the local frequency computation using the Riesz transform and section 2.2 contains the details of our model for matching the local frequency representations. In section 2.3, we present the numerical algorithm and section 3 contains the experimental results on 2D/3D medical image data sets. Finally, we conclude in section 4.

2 Proposed Registration Method

2.1 Computing Local Frequency using Riesz Transform

For multi-modal image registration, the relation between the brightness of the corresponding pixels is usually complicated: multiple intensity values in one modality image may map into single intensity in another modality; image feature existing in one image may not have correspondence in the other image, etc. However, multi-modal image data, acquired either with different sensors, or with the same sensor, mainly differ in the low frequency components. High frequency components, on the other hand, normally correspond to the physical structure of the object being imaged, and thus are good at expressing the commonality existing within the multi-sensor image pair. In the local frequency representation on which our algorithm is based, edges and ridges will have high values (since they are associated with high frequency components) and will be the dominant features for the matching stage.

In 1-D case, the local (instantaneous) frequency is well defined as the rate of change in phase of analytical signal obtained by Hilbert transform. However, the estimation of local frequency for higher dimensional images is still an important and open problem in the field of signal processing and computer vision. Quadrature filters are widely used as an approach to computing local phase and frequency in an image.

In this work, we present a novel formulation for computing the local-frequency using the Riesz transform which can be regarded as a generalization of the Hilbert transform in higher dimension. The key feature of this formulation is the fact that unlike the Gabor filter based technique, we do not need a bank of filters for computing the local frequency representation. A 3-D generalization of the Hilbert transform may be obtained by the vector sum of 3 Riesz transforms:

$$H_3\left(I\right)={\mathcal{F}}^{-1}\left[\left(\sum _{k=1}^3\frac{-i{u}_k}{\mid u\mid }ek\right)\mathcal{F}\left[I\right]\right]$$ (1)

where I(x, y, z) is the given 3D image and u = (u₁, u₂, u₃)^T is the spatial frequency vector, e_k is the unit vector in the direction of the k^th coordinate axis, and F is the Fourier transform operator. This may be rewritten as:

$$H_3\left(I\right)={\mathcal{F}}^{-1}\left[\frac{\mathcal{F}\left[\nabla I\right]}{\mid u\mid }\right]$$ (2)

After some detailed analysis [20], it is possible to show that the righthand side of equation (2) can be approximated as:

$$\frac{\nabla I}{\sqrt{{\omega }_1^2(x,y,z)+{\omega }_2^2(x,y,z)+{\omega }_3^2(x,y,z)}}=\frac{\nabla I(x,y,z)}{\mid \omega (x,y,z)\mid }$$ (3)

where ω_k(x, y, z) is the k^th component of the local frequency. The frequency magnitude may therefore be estimated as:

$$\mid \omega (x,y,z)\mid \approx \frac{\mid \nabla I(x,y,z)\mid }{\mid H_3\left(I\right)(x,y,z)\mid }$$ (4)

where H₃ is computed using (1). In order to make this approximation less sensitive to noise, we use a smoothing operator on both the computation of the ▽I and H₃. It should be remarked that a precise computation of ▽I is crucial for the correct approximation of |ω|; the best results are obtained when this computation is performed in the frequency domain.

In this way, the estimation of |ω| requires one forward 3-D Fourier transform and 6 inverse 3-D Fourier transforms, plus 2 separable 3-D convolutions. This can be done in O(NlogN) time, where N is the number of voxels in the image. In comparison, the Gabor filter bank requires O(4Nm³k) time — where, m3 is the convolution kernel size and k is the number of filters. In our implementation m3 >> logN. Additional advantages of our approach accrue in the form of storage savings since, there is a large storage requirement in the Gabor filter-based approach described in Liu et al., [4] to keep the responses of a large filter bank at each lattice point for computing the max. local freq. response. No such filterbanks are used in our approach for computing the local frequency response.

Our current implementation uses FFTW³ package which is a very efficient implementation. Even for 3D volumes (210 × 210 × 120), the computation can be done in 1 minute, under a Linux system running on a PC equipped with a 2.6GHZ Pentium4. Figure (1) illustrates two examples of computed local frequency in 2D for two T1 and T2 slices obtained from BrainWeb [21]. Note the richness of the structure in the representation.

Fig. 1.

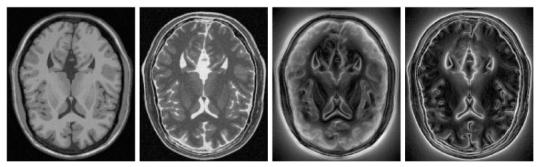
Left: a pair of T1 and T2 images; Right: their corresponding local frequency maps

2.2 Matching Local Frequency Representations

Let I₁ and I₂ be two images to be registered, and assume the deformation field from I₁ to I₂ is u = u(x), i.e. the point x in I₁ corresponds to the x + u(x) in I₂. Denote by F₁ and F₂ the local frequency representations corresponding to I₁ and I₂ respectively. The corresponding local frequency constraint is given by

$$(\mathbf{I}+\mathbf{J}{\left(\mathbf{u}\right)}^{\mathbf{T}}){\mathbf{F}}_1(\mathbf{x}+\mathbf{u}\left(\mathbf{x}\right))={\mathbf{F}}_2\left(\mathbf{x}\right)+∊\left(\mathbf{x}\right)$$ (5)

where J(u) is the Jacobian matrix of deformation field.

Note the above equation holds for the vector-valued frequency representation. However, experiments show that the vector-valued representation is much more sensitive to the noise than the magnitude of frequency and the Jacobian matrix term makes the numerical optimization computationally expensive. Applying Mirsky’s theorem from matrix perturbation theory [22] which states $\sqrt{{\sum }_i{({\tilde{\sigma }}_i-{\sigma }_i)}^2}\le \Vert \mathbf{J}{\left(\mathbf{u}\right)}^{\mathbf{T}}{\Vert }_F$ where ${\tilde{\sigma }}_i-{\sigma }_i$ is the difference in the singular values between the perturbed matrix (I + J(u)^T) and I, and imposing the regularization condition that J(u) is small, we can approximate the $\Vert (\mathbf{I}+\mathbf{J}{\left(\mathbf{u}\right)}^{\mathbf{T}})\mathbf{F}\left(\mathbf{x}\right)\Vert \text{by}\Vert \mathbf{F}\left(\mathbf{x}\right)\Vert$ to get the following simplified form:

$$\Vert {\mathbf{F}}_1(\mathbf{x}+\mathbf{u}\left(\mathbf{x}\right))\Vert =\Vert {\mathbf{F}}_2\left(\mathbf{x}\right)\Vert +∊\left(\mathbf{x}\right)$$ (6)

where ||·|| gives the magnitude of local frequency.

Instead of the popular SSD approach, we develop a statistical robust matching criterion based on the minimization of the integral squared error(ISE) or simply L₂E between a Gaussian model and the true density function of the residual. Traditionally, the L₂E criterion originates in the derivation of the nonparametric least squares Cross-validation algorithm for choosing the bandwidth h for the kernel estimate of a density and has been employed as the goodness-of-fit criterion in nonparametric density estimation. Recently, Scott [23] exploited the applicability of L₂E to parametric problems and demonstrated its robustness behavior and nice properties of practical importance.

In the parametric case, given the r.v. ∊ from (6) with unknown density g(∊), for which we introduce the Gaussian model f(∊|θ), we may write the L₂E estimator as

$${\widehat{\theta }}_{L_{2}E}=\arg \underset{\theta }{\min }\int {[f(∊\mid \theta )-g\left(∊\right)]}^{2}dx$$ (7)

Simply expand above equation and notice the fact that $\int g{\left(∊\right)}^{2}dx$ does not depend on θ and $\int f(∊\mid \theta )g\left(∊\right)dx=E_g\left[f(∊\mid \theta )\right]$ is the so called expected height of the density which can be approximated by the estimator $\frac{1}{n}{\sum }_{i=1}^{n}f({∊}_i\mid \theta )$, hence the proposed estimator minimizing the L₂ distance will be

$${\widehat{\theta }}_{L_{2}E}=\arg \underset{\theta }{\min }[\int f{(∊\mid \theta )}^{2}dx-\frac{2}{n}\sum _{i=1}^{n}f({∊}_i\mid \theta )].$$ (8)

For Gaussian distributions, we have closed form for the integral in the bracketed quantity in (8) and hence can avoid numerical integration which is a practical limitation not only in computation time but also in accuracy. Thus, we get the following criterion L₂E(u, σ) from (8) for our case,

$$\frac{1}{2\sqrt{\pi \sigma }}-\frac{2}{N}\sum _{i=1}^N\exp \{-\frac{{(\Vert {\mathbf{F}}_1(\mathbf{x}+\mathbf{u}\left(\mathbf{x}\right))\Vert -\Vert {\mathbf{F}}_2\left(\mathbf{x}\right)\Vert )}^2}{2{\sigma }^2}\}$$ (9)

Equation (9) differs from the standard SSD approach in that the quadratic error terms are replaced by robust potentials (in this case, inverted Gaussians), so that the large errors are not unduly overweighed, but rather are treated as outliers and given small weight.

Generally, a regularization term is needed for nonrigid registration problem to impose the local consistency or smoothness on the deformation field u. In case u is assumed to be differentiable, this regularization term could be defined as a certain norm of its Jacobian J(u). For simplicity, the Frobenius norm of Jacobian of deformation field $\Vert \mathbf{J}\left(\mathbf{u}\right)\Vert \frac{2}{\mathbf{F}}$ is used here. Altogether, the proposed non-rigid image registration method is expressed by the following optimization problem:

$$\widehat{\theta }=\arg \underset{\theta =[\mathbf{u},\sigma ]}{\min }{L}_{2}E(\mathbf{u},\sigma )+\lambda \Vert \mathbf{J}\left(\mathbf{u}\right){\Vert }_{\mathbf{F}}^2$$ (10)

where λ is the Lagrange multiplier and σ is the parameter controlling the shape of the residual distribution modelled by a zero mean Gaussian ϕ(x|0, σ). Unlike other robust estimators, this shape parameter σ need not be set by the user, but rather it is automatically adjusted during the numerical optimization. Deformation field u, in this work, is expressed for computational efficiency, by a B-Spline model controlled by a small number of displacement estimates which lie on a coarser control grid.

2.3 Numerical Implementation

The numerical implementation is achieved using nonlinear optimization techniques to solve equation (10). In our current implementation, we handle the minimization over σ and u separately. At each step, the σ is the minimizer of the L₂ distance between the true density and model density of residual distribution given fixed u. A zero vector is used as the initial guess for u. In each iteration, we evaluate the gradient of $E\left(\mathbf{u}\right)=L_{2}E(\mathbf{u},\sigma )+\lambda \Vert \mathbf{J}\left(\mathbf{u}\right)\Vert \frac{2}{\mathbf{F}}$ with respect to each of the parameters in u using analytical formulae which can be computed in laboratory frame:

$${\nabla }_{\mathbf{u}}{L}_{2}E=\frac{2}{N\ast {\sigma }^2}\sum _{i=1}^N\{\mathit{exp}\{-\frac{{\mathbf{D}}_i^2}{2{\sigma }^2}\}{\mathbf{D}}_i{\mathbf{G}}_i\}$$ (11)

$${\nabla }_{\sigma }{L}_{2}E=-\frac{1}{2\sqrt{\pi {\sigma }^2}}-\frac{2}{N}\sum _{i=1}^N\{\exp \{-\frac{{\mathbf{D}}_i^2}{2{\sigma }^2}\}\frac{{\mathbf{D}}_i^2}{{\sigma }^3}\}$$ (12)

where

$${\mathbf{D}}_i=\Vert {\mathbf{F}}_1({\mathbf{x}}_{\mathbf{i}}+\mathbf{u}\left({\mathbf{x}}_{\mathbf{i}}\right))\Vert -\Vert {\mathbf{F}}_2\left({\mathbf{x}}_{\mathbf{i}}\right)\Vert$$

is the frequency magnitude error at pixel i,

$${\mathbf{G}}_i=(\nabla \Vert {\mathbf{F}}_1\Vert )({\mathbf{x}}_{\mathbf{i}}+\mathbf{u}\left({\mathbf{x}}_{\mathbf{i}}\right))$$

is the spatial gradient of (||F₁||). Then, a block diagonal matrix is computed as approximation of Hessian matrix by leaving out the second-derivative terms and observing that the overall Hessian matrix is sparse multi-banded block-diagonal. Finally, a preconditioned gradient descent technique is used to update the parameter estimates. In this step, an accurate line search derived by Taylor approximation is performed.

The numerical optimization approach is outlined as follows:

• - Set i = 0 and give an initial guess for deformation field u₀;

• - Gaussian fitting: σ_i = arg min L₂E(u_i σ), this step involves a quasi-Newton nonlinear optimization;

• - Update deformation estimates: u_i+1 = u_i+△u, this step involves a preconditioned gradient descent method close to that used by [7];

• - Iterate: i = i + 1

• - Stopping criteria: $\Vert \Delta \mathbf{u}\Vert \approx 0$

3 Experimental Results

In this section we present three sets of experiments. The first set constitutes of a 2-D example to depict the robustness of L₂E. The second set contains experiments with 2-D MR T1- and T2- weighted data obtained from the Montreal Neurological Institute database [21]. The data sets were artificially misaligned by known non-rigid transformations and our algorithm was used to estimate the transformation. The third set of experiments was conducted with 3-D real data for which no ground truth was available.

3.1 Robustness Property of the L₂E Measure

In this section, we demonstrate the robustness property of L₂E and, hence, justify the use of the L₂E measure in the registration context.

In order to depict the robustness property of L₂E, we designed a series of experiments as follows: with a 2-D MR slice as the source image, the target image is obtained by applying a known nonrigid transformation to the source image. Instead of matching the original source image and transformed image, we cut more than 1/3 of the source image (to simulate the affect of significant non-overlap in the FOVs), and use it and the transformed image as the input to the registration algorithms. Figure 2 depicts an example of this experiment. In spite of missing more than 33% of one of the two images being registered, our algorithm yields a low average error of 1.32 and a standard deviation of 0.97 in the estimated deformation field over the uncut region. The error here is defined by the magnitude of the vector difference between ground truth and estimated deformation fields. For comparison purposes, we also tested the MI and the SSD method on the same data set in this experimental setup. The nonrigid mutual information registration algorithm was implemented following the approach presented in [24]. And in both the MI and SSD method, the nonrigid deformations are modeled by B-Splines with the same configuration as in our method. However, both the MI and the SSD method fail to give acceptable results due to the significant non-overlap between the data sets.

Fig. 2.

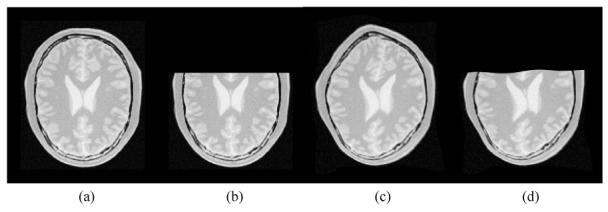
Depiction of the robustness property of the L₂E measure. From left to right: (a): a 2-D MR slice of size 257 × 221; (b): the source image obtained from (a) by cutting the top third of image; (c): transformed (a) serving as the target; (d) warped source image with the estimated deformation.

3.2 Inter-modality Registration

For problem of inter-modality registration, we tested our algorithm on two MR-T1 and -T2 2D image slices from the BrainWeb site [21] of size 181 × 217. These 2 images are originally aligned with each other and are shown in Figure (1) as well as their corresponding local frequency maps computed via the application of the Riesz transform described earlier. In this experiment, a set of synthetic nonrigid deformation fields were generated using four kinds of kernerl-based spline representations: cubic B-spline, elastic body spline, thin-plate spline and volume spline. In each case, we produced 15 randomized deformations where the possible values of each direction in deformation vary from -15 to 15 in pixels. The left half of Table 1 shows the statistics of the difference between the ground truth and estimated deformation fields. For purpose of comparison, in this setup we also tested the nonrigid mutual information registration algorithm which was used in the previous experiment. As shown in the right half of Table 1, MI-based nonrigid registration produces almost same accuracy in the results as our method for this fully overlapped data sets. However, the strength of our technique does not lie in registering image pairs that are full overlapped. Instead, it lies in registering data pairs with significant non-overlap, as shown in Figure 2. Figure 3 shows plots of the estimated B-Spline deformation along with the ground truth as well as the cumulative distribution of the estimated error. Note that the error distribution is mostly concentrated in the small error range indicating the accuracy of our method.

Table 1.

Statistics of the errors between ground truth displacement fields and estimated deformation fields obtained using our method and the MI method on pairs of T1-T2 MR images.

	Our Method			MI Method
Statistics (in pixels)	mean	std. dev.	median	mean	std. dev.	median
Thin Plate Spline	2.03	1.83	1.33	2.02	1.81	1.31
Elastic Body Spline	1.98	1.87	1.28	1.99	1.87	1.27
Volume Spline	2.13	2.03	1.53	2.12	2.04	1.52
Cubic B-Spline	1.29	1.18	0.79	1.27	1.17	0.79

Fig. 3.

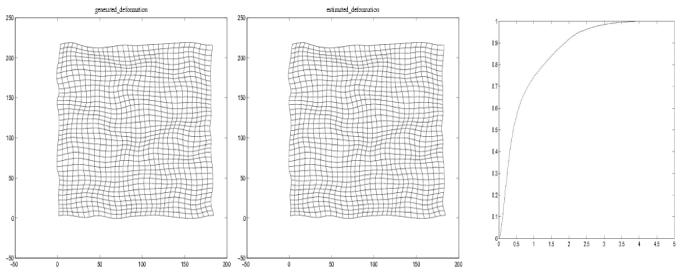
From left to right: the ground truth deformation field; the estimated deformation field; the cumulative distribution of the estimated error in pixels.

3.3 3D Data Example

To conclude our experimental section, we show results on a 3D example for which no ground truth deformations are available. The data we used in our experiments is a pair of MR images of brains from different rats. The source image is (46.875 × 46.875 × 46.875) micron resolution with the field of view (2.4 × 1.2 × 1.2cm), while the target is 3D diffusion-weighted image with (52.734 × 52.734 × 52.734) micron resolution with the field of view (2.7 × 1.35 × 1.35cm). Both the images have the same acquisition matrix (256 × 512 × 256).

Figure 4 shows the registration results for the dataset. As is visually evident, the misalignment has been fully compensated for after the application of the estimated deformation. The registration was performed on reduced volumes (128 × 128 × 180) which took around 10 minutes to obtain the results illustrated in figure 4 with the control knots placed every 16 × 16 × 16 voxels by running our C++ program on a 2.6GHZ Pentium PC. Validation of non-rigid registration on real data with the aid of segmentations and landmarks obtained manually from a group of trained anatomists are the goals of our ongoing work.

Fig. 4.

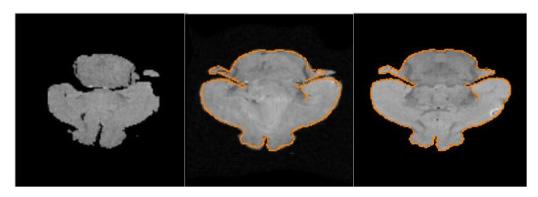
Nonrigid registration of an MR-T1 & MR-DWI mouse brain scan. Left to Right: an arbitrary slice from the source image, a slice of the transformed source overlayed with the corresponding slice of the edge map of the target image and the target image slice.

4 Conclusions

In this paper, we presented a novel algorithm for non-rigid 3D multi-modal registration. The algorithm used the local frequency representation of the input data and applied a robust matching criteria to estimate the non-rigid deformation between the data. The key contributions of this paper lie in, (i) efficient computation of the local frequency representations using the Riesz transform, (ii) a new mathematical model for local-frequency based non-rigid registration, and (iii) the efficient estimation of 3D non-rigid registration between multi-modal data sets possibly in the presence of significant non-overlapping between the data. To the best of our knowledge, these features are unique to our method. Also the robust framework used here namely, the L₂E measure, has the advantage of providing an automatic dynamic adjustment of the control parameter of the estimator’s influence function. This makes the L₂E estimator robust with respect to initializations. Finally, we presented several real data (with synthetic and real non-rigid misalignments) experiments depicting the performance of our algorithm.