Particle verification for single-particle, reference-based reconstruction using multivariate data analysis and classification

Abstract

As collection of electron microscopy data for single-particle reconstruction becomes more efficient, due to electronic image capture, one of the principal limiting steps in a reconstruction remains particle verification, which is especially costly in terms of user input. Recently, some algorithms have been developed to window particles automatically, but the resulting particle sets typically need to be verified manually. Here we describe a procedure to speed up verification of windowed particles using multivariate data analysis and classification. In this procedure, the particle set is subjected to multi-reference alignment before the verification. The aligned particles are first binned according to orientation and are binned further by K-means classification. Rather than selection of particles individually, an entire class of particles can be selected, with an option to remove outliers. Since particles in the same class present the same view, distinction between good and bad images becomes more straightforward. We have also developed a graphical interface, written in Python/Tkinter, to facilitate this implementation of particle-verification. For the demonstration of the particle-verification scheme presented here, electron micrographs of ribosomes are used.

INTRODUCTION

Cryo-electron microscopy combined with single-particle reconstruction (see Frank, 2006) is a powerful method for visualizing biological macromolecules. With use of the transmission electron microscope, it is possible for an idealized homogeneous specimen under ideal conditions of imaging to yield an atomic-resolution reconstruction from as few as 10,000 projections of a structure (Henderson, 1995). However, real specimens are imperfect in terms of homogeneity; imaging is affected by instrument instabilities; and reconstructions are degraded computationally by interpolation and alignment errors. For real, non-ideal specimens and imaging conditions, typically tens of thousands of images are required even to reach intermediate resolutions (in the 10- to 20-Å range).

Initially, when single-particle methods were introduced, small particle sets, on the order of hundreds of particles, were selected manually and individually from digitized micrographs. Thus, particle selection and verification were done in a single step. With the introduction of automated particle selection procedures, to cope with the requirement for much larger data sets, came the need for some form of quality verification. In the following, we will differentiate between the windowing and verification steps, avoiding the term “particle picking,” which lumps both steps together.

Considerable effort has been expended to try to automate particle-windowing (reviewed in Zhu et al., 2004). However, even with the best implementations, reliability is not perfect. That is, a certain proportion of real particles -- “real” as judged by a human observer -- is always excluded, while a portion of non-particles is included. Thus, the second step, particle verification, is normally necessary, in which the output of the automated particle windowing is evaluated for quality-control purposes; this step is typically a manual process.

In a typical implementation of manual particle verification, a set of windowed particles is displayed as a montage. Each candidate image derived from the particle-windowing step can either be confirmed and saved, by a mouse click for example, or it can be skipped and thus rejected and discarded. This mouse-click operation is repeated for each image among the tens of thousands of particles that were obtained in the automated particle-windowing step. This process is quite tedious and, if the goal is high-throughput image-processing, it can be severely rate-limiting.

An implementation of particle-verification using multivariate data analysis (MDA) and classification has been described previously (Roseman, 2004). Here we present an extension of that scheme. whereby, groups of particles are verified collectively, rather than the individual verification of particles. The programs affords further control allowing removal of outliers.

MATERIALS

Grids containing E. coli 70S ribosomes were generated as described previously (Vestergaard et al., 2001). Micrographs were collected under low-dose conditions on an FEI Tecnai F20 at a nominal magnification of 49,700, with defocus values ranging from 1.1 to 3.1 µm underfocus, and digitized on a Z/I scanner (Huntsville, AL) at a step size of 14 µm, corresponding to a pixel size of 2.82 Å. The reference structure was a 70S ribosome with a UAA stop codon in the A site and fMet-Phe-Thr-Ile-tRNAIle in the P-site (Rawat et al., 2003). Using lfc_pick.spi (Rath & Frank, 2004; Suppl. Fig. 1), we windowed 115,221 from 76 micrographs. Batch files, Python scripts, and documentation are provided on the SPIDER Techniques WWW page (http://www.wadsworth.org/spider_doc/spider/docs/techniques.html).

RESULTS

MDA and classification have been used previously for particle verification (Roseman, 2004). In that study, the specimen analyzed was keyhole limpet hemocyanin, a molecule that adopts few orientations of the grid. As a generalization of the procedure, it is deemed desirable to account for specimens that present many more orientations in a continuous range, e.g., the ribosome (Penczek et al., 1994; Shaikh et al., submitted). One option would be to use more classes in a single-step classification, but in practice, overrepresented views tend to dominate inordinately many classes, leaving underrepresented views and non-particles to distribute among too few remaining classes. Instead, we developed a procedure comprising two steps of classification. First, we bin the windowed images by orientation, or in other words, according to which reference projection the windowed images were assigned during multi-reference alignment. Then, the particles associated with a particular reference projection are run through principal component analysis. The particles are then binned further by K-means classification.

Prior to this classification, particle images were windowed using locally normalized fast correlation (Roseman, 2003) (“lfc”), implemented in the SPIDER batch file lfc_pick.spi (Rath & Frank, 2004; Suppl. Fig. 1). Here, in order to describe the performance of the algorithms, we will categorize the output windowed images dichotomously into “real particles” -- i.e., images of the molecule of interest -- and “nonparticles.” We further categorize non-particles into two sub-categories: junk and noise (Lata et al., 1995). “Junk”s images include particle fragments, contaminants, or other material with a density higher than background. Noise images lack any distinct features above background.

Using the procedure lfc_pick.spi, we rank the cross-correlation peaks between a projection of the reference and the micrograph from highest to lowest. With the default settings of lfc_pick.spi, coordinates of peaks in the cross-correlation map of the micrograph are recorded for subsequent windowing, unless they violate proximity criteria; that is, peaks are windowed in the order of ranking until there is no more room left in the micrograph. Typically in the end, there are more areas windowed than there are real particles in the micrograph. Windowed images output by lfc_pick.spi with the highest cross-correlation coefficient (CCC) value often tend to be “junk” while the lowest-ranked images typically contain only noise (Suppl. Fig. 1). These windowed images are then subjected to projection-matching.

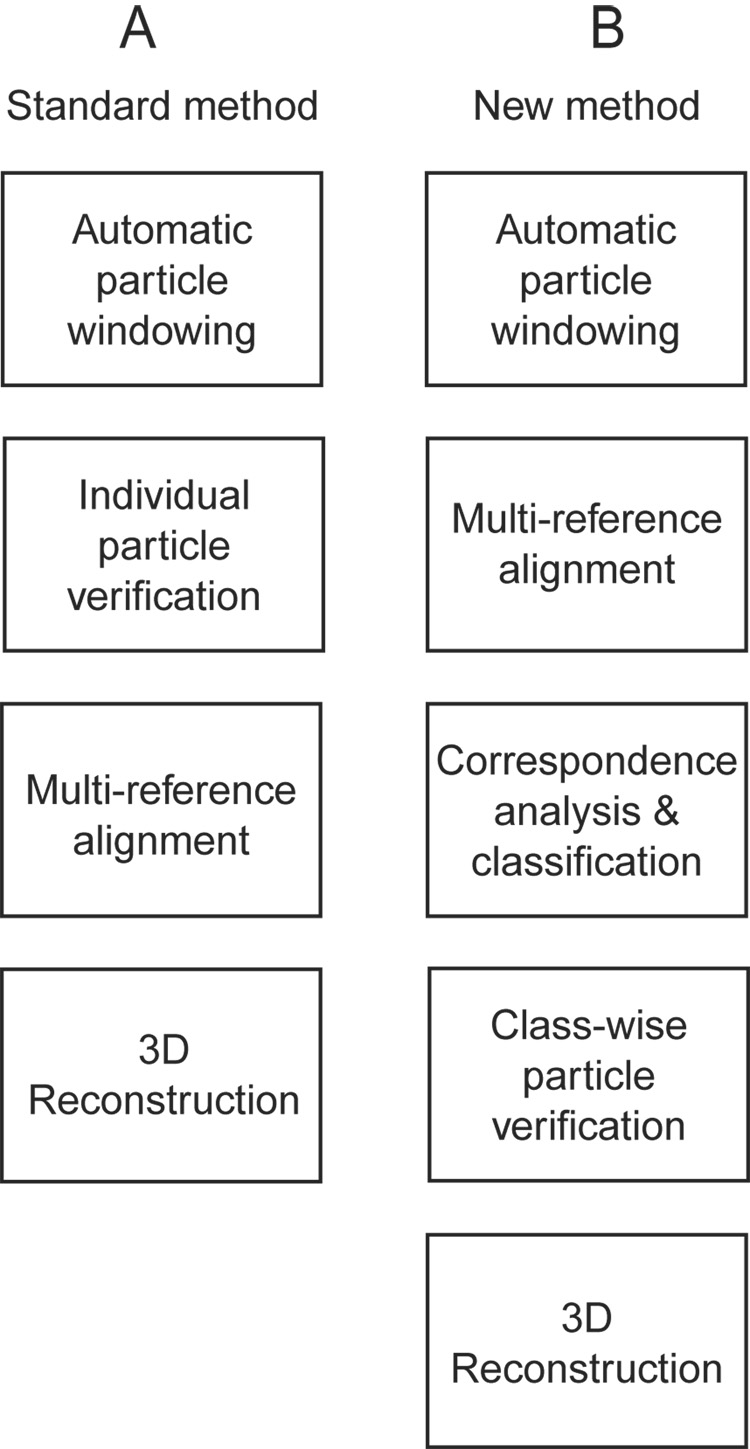
A flowchart for standard projection matching is shown schematically in Figure 1A, and, in the modified form described here, in Figure 1B. The first step of classification, the multi-reference alignment, minimizes the variation in the binned images that is due to orientation; that type of variation is not relevant for the purpose of quality control. Instead, upon K-means classification following multi-reference alignment, the variation is due mainly to the differences between real particles and non-particles. Another potential source of irrelevant variation is difference in defocus. To eliminate or minimize this source of variability, before classification, images are low-pass filtered to the spatial frequency of the first phase reversal of the contrast transfer function for the most strongly underfocused image.

Figure 1.

Flowcharts for two projection-matching schemes. (A) In the standard method, particles are verified individually, and then particles are aligned. (B) In our modified method, particles are aligned first and then verified using classification.

Verification modes

Whole classes and highest ccc modes

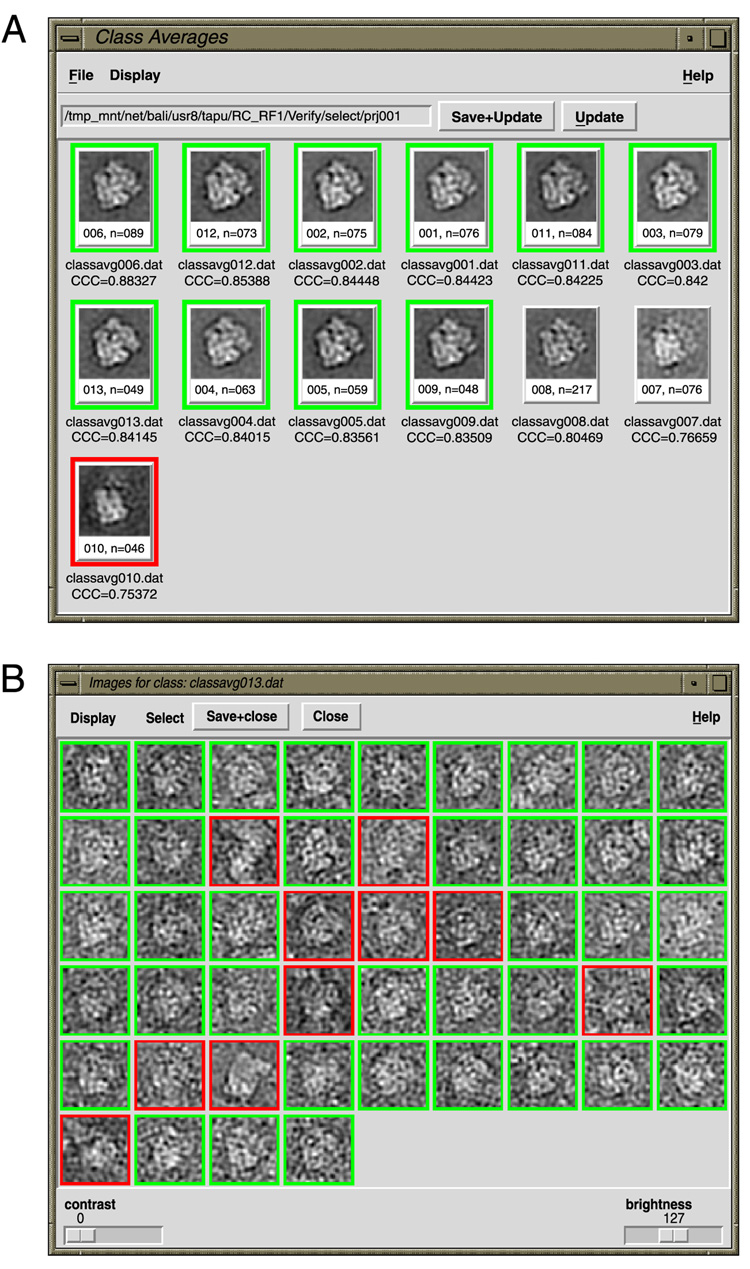
In the simplest mode of classification-based verification, the user selects the desired class averages (Fig. 2A) and thereby selects the windowed images corresponding to those classes (Roseman, 2004). Figure 2A shows a montage of class averages from an E. coli 70S ribosome data set (see Materials section). In this example, the CCC between each class average and the corresponding reference projection was calculated. In the montage, the class averages are ordered from lowest CCC to highest. The number of classes was determined from the number of images classified; here, we used a ratio of one class per 75 images.

Figure 2.

Examples of classification. (A) Montage of class averages for one reference projection. Underneath the average is the class number, followed by the number of images in that class. (B) Montage of individual particles belonging to class #013 above. (C) Montage of the 52 particles with the highest CCC of 217 particles total from class #008 above. The individual images here have been low-pass filtered and are sorted from lowest correlation coefficient to highest.

When the quality of a class is in doubt, a montage of the individual windowed images in that particular class can be viewed. Figure 2B shows an example of a montage of a class containing mostly real particles. Since the particles are aligned and correspond to the same orientation, it is straightforward to discern real particles from non-particles. Note that there are a few non-particles or questionable particles in this class. Outliers will be addressed below. This selection step is then repeated for each reference projection; for an asymmetric object, a choice of quasi-equivalent spacings of 15° between adjacent projections, for example, corresponds to a total of 83 reference projections. Following a few internal book-keeping steps, the verified particles are piped to the 3D reconstruction procedure. This mode will be referred to below as the “whole classes” mode. Since a single mouse operation will select a set of, on average, 75 particles, this mode will be very fast, taking ~1.5 hr for our test data set (Table 1).

Table 1.

Comparison of user-interaction time and error rates for various modes of particle verification.

MODE	TIME	TRUE+	TRUE−	FALSE+	FALSE−
“By hand”	15 hrs	63846	51375	0	0
“Truncated lfc”	1 hr	6s3846	27046	24329	0
“Whole classes”	1.5 hrs	51319	38798	12577	12527
“Highest ccc”	4.5 hrs	41824	43661	7714	22022
“Scatter plot”	10 min	38304	39217	12158	25542

For “whole classes,” TRUE+ means that 51319 particles verified were among the 63846 verified manually. The 38798 TRUE− were excluded and were also excluded manually. The 12577 FALSE+ were included but were excluded manually. The 12527 FALSE− were excluded but were included manually. Verification times are approximate.

Figure 2C shows part of a montage of a class which contains images of predominantly noise. That the average (class #008 in Fig. 2A) looks reasonably normal illustrates the risk posed by reference bias. In this particular montage of class averages, the classes with the lowest correlation values contain non-particle images, like class #008, but in general, the correlation coefficient serves only as a rough guide to quality. Numerical parameterization of class quality will be discussed further below.

Given the observation that there are non-particles still contained in classes of real particles, we deemed it desirable to offer the user more control over the choice of retained particles. In one method, the user selects those particles that have the highest correlation coefficients for each class. The images are arranged in the montage ordered from lowest to highest correlation, so this selection amounts simply to clicking on the first particle to be kept (denoted in Fig. 2B with a “1”). This mode will be referred to below as the “highest ccc” mode. This mode requires only a single mouse operation more than was required for the “whole classes” mode after loading the individual-image montage, so it will also be quite fast, taking ~4.5 hr for our test data set (Table 1).

Scatter plot mode

In a general sense, the time-saving steps entailing classification that we have devised involve the “chunking” of data, such that ensembles of comparable images are evaluated collectively. The more image data that can be displayed simultaneously, the faster this verification can proceed. Above, we represented a class by its average image, and it was possible to evaluate one orientation class – or reference projection – at a time. In contrast, in the “scatter plot” mode that is introduced next, we represent each class as a point in two dimensions, and thus can display representations for all classes and reference projections simultaneously.

First, we needed to parameterize the classes by a pair of suitable metrics. One obvious metric to use is the CCC between the class average and the reference projection. Another promising metric is the standard deviation of the class variance map (SDVAR). The rationale behind the choice of SDVAR was that in an ideal good class, there should be little variation among the individual images constituting this class, and thus the class variance map should be flat, i.e., with a low value for its standard deviation. In addition, a good class would be expected to have a high CCC. The converse would be true of an extremely bad class, i.e., a bad class would be expected to have both a low CCC and a high SDVAR.

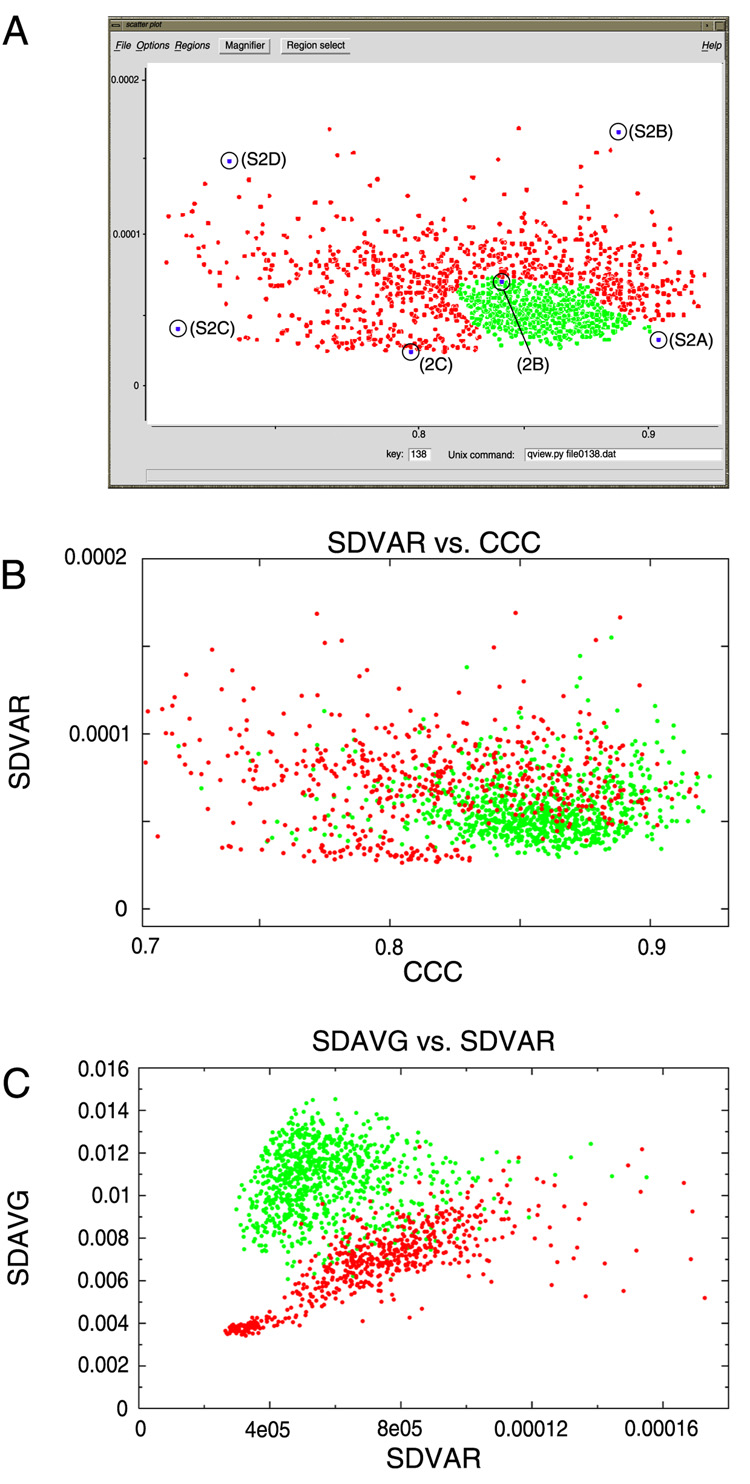
We wrote a Python/Tkinter utility, named scatter.py, designed to select points representing classes within a user-defined region of a 2D plot (Fig. 3A). The boundary of the region containing good classes is determined by viewing montages of individual particles from selected classes in the 2D plot; the user opens the montage by clicking on the corresponding point. The boundary enclosing the good classes and excluding the bad classes defines a polygon, inside which reside the classes that are to be retained. Only on the order of tens of classes need to be opened to define the encapsulating polygon; thus, this mode of verification is extremely fast, taking only ~10 min for our data set (Table 1).

Figure 3.

Scatter plot examples. (A) x-axis is cross-correlation coefficient (CCC). y-axis is standard deviation of the class variance (SDVAR). Selected classes are displayed in green. The boundary between retained and excluded classes was determined by clicking on selected points and opening the montage of individual particles. Labels for circled points refer to the figure for the corresponding montage of particles, e.g., (S2D) for Supplementary Figure 2D. (B) Comparison of the retained classes as selected by the “whole classes” mode. (C) Same classes as in B redisplayed, with the SDVAR as abscissa and the standard deviation of the average (SDAVG) as ordinate.

Since the same classes had been verified above using the “whole classes” mode, we could compare classes chosen using that method with those picked using the “scatter plot” mode. Retained (“good”) and excluded (“bad”) classes from the “whole classes” mode are depicted in Fig. 3B using the same axes: SDVAR and CCC. The points assume roughly the form of a comet, with the good classes -- those with high CCC and low SDVAR -- forming the head, and the bad classes forming the tail. There is overlap in the plot between the retained and excluded classes, meaning that some bad classes will have been retained in the selection in Figure 3A.

While verifying classes, one pattern that we observed was that class averages of good classes tended to have averages showing a bright particle on a dark background, whereas bad classes tended to have averages with a flat density, with little differentiation between particle and background (see Fig. 2A). We parameterized this characteristic using the standard deviation of the average (SDAVG). For the particular data set under analysis, this combination of parameters was shown to be powerful (Fig. 3C). However, for another data set in which evaluation by SDAVG and SDVAR was tested, the separation between good and bad classes was not pronounced (D.J. Taylor & J.S.L., unpublished results).

Python interface

In the verification modes above, the degree of control is quantized. The user can select entire classes, or with additional intervention, can select the particles with the highest correlation coefficients from a class. There were existing Python/Tkinter tools (Baxter et al., 2007) to display contents of a class (classavg.py), and there were separate tools to select particles (montage.py), so we combined those functions and customized them to work in conjunction with the various classification-based verification schemes (Fig. 4), into a utility called verifybyview.py. With this utility, the user can work according to the “whole classes” mode and simply select class averages, or alternatively can deselect individual outliers from an otherwise good class.

Figure 4.

Python/Tkinter interface, verifybyview.py. (A) Class montage. (B) Individual particle montage from class #13, containing the same particles as in Fig. 2B. In both cases here, images are sorted from highest CCC to lowest CCC.

Reliability of the various verification modes

Before the development of the classification-based verification methods, particles for the E. coli ribosome data set had been verified using the standard method, i.e., individually, by hand. Of the 115,221 particles windowed automatically, 63,846 were selected. This mode will be referred to as the “by hand” mode. We used this hand-selected particle set as the initial gold standard to which the results of the classification-based methods would be compared. The rationale for considering visual selection the gold standard is that such characteristics as cohesion, size, and shape of molecule are readily recognized by the expert human eye, and that this performance has yet to be matched by a computational automated procedure.

As an intentionally lenient particle set, we devised a particle set as follows. Since lfc_pick.spi ranks the windowed images by CCC, we manually picked the real particle with the highest CCC and the real particle with the lowest CCC for each micrograph, and we kept all particles in between. From this particle set, only the high-correlation junk images and lowest-correlation noise images will have been excluded. This set, by definition, had all 63,846 of the “by hand” set, plus interspersed non-particles, to bring the total number to 88,175. The mode that gave rise to this particle set will be referred to as the “truncated lfc” mode.

Using the “by hand” particle set as a gold standard, we could examine the error rates for the various modes (Table 1). Likely the most insidious of the types of errors is the false-positives, i.e., non-particles retained as real particles. False-positives will at best contribute noise to the reconstruction, and will at worst contribute to reference bias; they may also prevent a stable, converged refinement. False-negatives -- i.e., good particles that have been erroneously excluded -- are less worrisome. At worst, the signal-to-noise is lessened; in the best case, the particle number is not the limiting factor in the quality of the reconstruction. The simplest classification-based mode, “whole classes,” yielded more false-positives than did the more sophisticated “highest ccc” variant; however, it was three times faster. The false-positive rate for “truncated lfc” was obviously poor. For the “scatter plot” mode, the number of false-positives was comparable to that for the “whole classes” mode, but the number of true-positives was lower than in the latter.

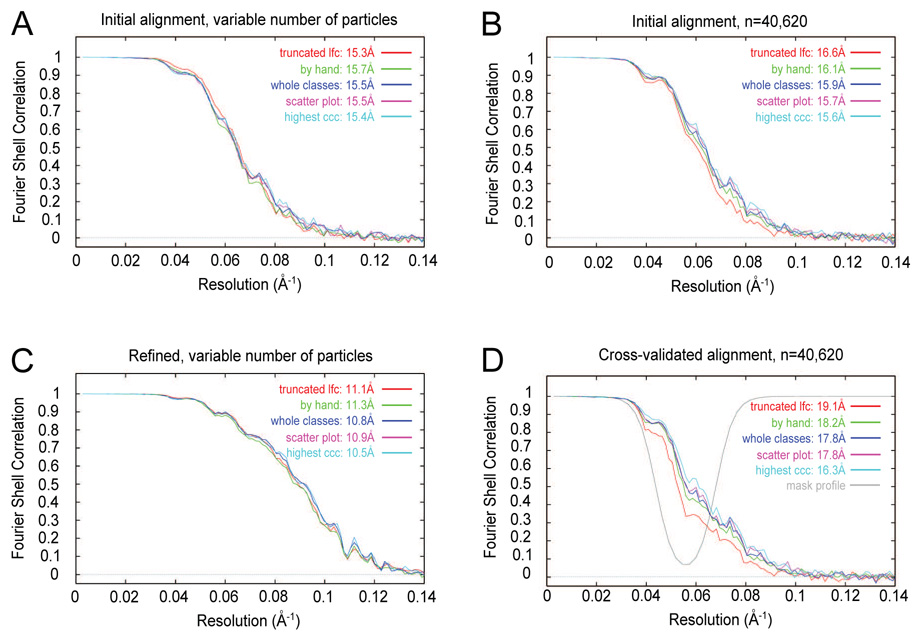
To evaluate the effect of the trade-off between false positives and false negatives, we examined Fourier shell correlation (FSC) curves, adopting the hypothesis that the best particle sets would yield the best resolution curves. Instead, all particle sets showed approximately the same behavior (Fig. 5A). Surprisingly, the “truncated lfc” particle set, which was known to contain the highest fraction of non-particles (28%), showed slightly better FSC values at intermediate resolutions, 1/30Å⁻¹ to 1/17Å⁻¹, than the other curves.

Figure 5.

Fourier shell correlation curves for various particle-verification modes. Following the name of each particle set is the nominal resolution according to the 0.5 FSC criterion. (A) FSC curves for complete particle sets from a single iteration of alignment. The number of particles in each set is listed in Table 1. (B) FSC curves for a fixed number of particles (40,620) used for each particle set. (C) FSC curves for complete particle sets after six iterations of orientation refinement. (D) FSC curves for a fixed number of particles after cross-validated alignment.

The “truncated lfc” particle set comprised the largest particle set, so, supposing that raw particle number reinforces the resolution curve in addition to particle quality, we limited the particle set to a fixed size (40,620) by randomly selecting particles, with a constant number of images for a given defocus group for all of the particle sets. Even though the FSC curves did not overlap (Fig. 5B), the differences were small.

The observation that a particle set with many non-particles could yield a reasonable-looking resolution curve was reminiscent of the effect of reference bias. To test for bias, we performed two experiments. In the case of alignment of pure noise, agreement between the two half-sets used to compute the FSC worsened during the process of refinement (Shaikh et al., 2003). Thus, for our test ribosome images, we refined the orientation parameters for six iterations (Penczek et al., 1994; Shaikh et al., submitted), using all windowed images for each particle set, i.e., not a fixed number. The resolution curves for the particle sets were again similar (Fig. 5C). In contrast to the noise-only case, when there is a mix of real particles and non-particles, it appears that signal from the real particles is sufficient to enable to alignment of the non-particles.

A second test for the presence of reference bias entailed to computation of cross-validated resolution curves (Shaikh et al., 2003). Briefly, we excised a spherical shell from the Fourier transform of the reference, re-ran the alignment, calculated reconstructions, and computed resolution curves. If there were real data in the excised region of the Fourier transforms of the half-sets used to compute the FSC, there would be correlation in the excised region of the FSC. Whereas if only noise were present, there would be no significant correlation in the excised region of the FSC. Rather than mask with a spherical shell with a sharp edge, we used a spherical shell with a soft edge for the mask profile (Fig. 5D, gray), in order to minimize potential alignment artifacts. Use of a soft edge did not show an appreciable difference from a sharp edge in the corresponding resolution curves (data not shown). Use of a fixed number of images did give rise to a better separation of FSC curves than did use of the original, variable number of images (data not shown). Upon cross-validation, the “highest ccc” mode, which required the most user interaction of the classification-based methods tested here, yielded the best FSC curve (Fig. 5D). The “truncated lfc” mode yielded the worst FSC curve. The “by hand” mode was similar in FSC quality to the “scatter plot” and “whole classes” modes. There was a general correlation between user interaction required and strength of the cross-validated FSC.

Effects of false positives

Above, we asserted that the inclusion of false positives is the most insidious type of error in particle-verification. The “by hand” particle set did not show the best behavior out of the five particle sets, so to obtain a better gold standard for “good” particles, we took the intersection of the three particle sets that required the most human interaction: “by hand,” “whole classes,” and “highest ccc.” In all, 38,033 particles were found to be common to these particle sets. Similarly, 39,456 unanimously “bad” particles were identified from those three particle sets. Cross-validated FSC curves best distinguished the behavior of good and bad particle sets above, so additional cross-validation tests were carried out using known numbers of good and bad particles from these new gold standards.

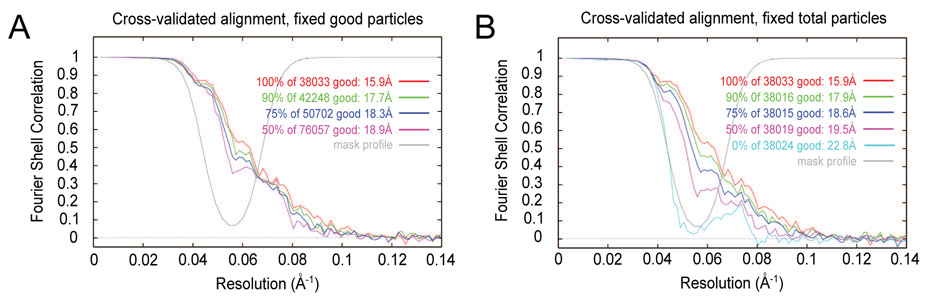
First, we calculated reconstructions and cross-validated FSC curves when using all of the good particles mixed with varying numbers of bad particles, such that the final percentages of good particles were 100%, 90%, 75%, and 50%. The hypothesis had been that the behavior of the cross-validated FSC was largely determined by the total number of good particles (Shaikh et al., 2003). Instead, the presence of bad particles eroded the FSC (Fig. 6A), with a difference in FSC value, between 100% good to 50% good, of approximately 0.15.

Figure 6.

Fourier shell correlation curves using known numbers of good and bad particles. “Good” and “bad” particles were identified from the intersection of the included and excluded particles, respectively, from the particle sets “by hand,” “highest ccc,” and “first good.” The mixtures of good and bad particles are such that the proportion of good particles was 100%, 90%, 75%, or 50%. Following the name of each particle set is the nominal resolution according to the 0.5 FSC criterion. (A) All 38,033 good particles were included with varying numbers of added bad particles. (B) A roughly constant number of total particles was included for each. Slices of three of these reconstructions are shown in Supplementary Figure 3.

Second, since the separation among the particle sets' FSC curves increased when a constant number of windowed images was used (Fig. 5B vs. Fig. 5D), we calculated cross-validated FSC curves upon decreasing the number of good particles while increasing the number of bad particles, such that the number of total windowed images was constant (constant aside from small rounding errors when subsets were drawn). The percentages of good particles were set to be the same as in the experiment above: 100%, 90%, 75%, and 50% (Fig. 6B). An additional FSC from a pair of reconstructions with only bad particles was also calculated. Slice series of three of these reconstructions -- containing 100%, 50%, and 0% good particles – are included in Supplementary Figure 3. Use of a fixed number of images yielded an even larger drop in the cross-validated FSC than in the case with a variable number of images, with a difference between 100% good and 50% good of about 0.25. We propose that one test for the presence of false positives is a cross-validated FSC between half-set reconstructions with a fixed number of images.

DISCUSSION

Rather than attempt to develop a more foolproof particle-picking protocol, we addressed the less ambitious goal of improving manual verification techniques. The simplest verification scheme presented here, the “whole classes” method, shows a false-positive rate of approximately 10%. This rate is somewhat higher than, but similar to, the rate that was reported earlier in a study using MDA and classification (Roseman, 2004). In addition, reliability can be improved with the introduction of additional levels of control, using the “highest ccc” method (Table 1) or the Python/Tkinter utility verifybyview.py (Fig. 4).

The underlying assumption in the use of classification for particle verification is that the real particles will be separated from the non-particles. The ribosome exceeds 2 MDa in molecular mass, has distinctive features, and has high contrast due to its RNA content, so the above assumption tends to hold. Also, our test data set had a large fraction of the windowed images (>1/3) deemed real particles. If the above characteristics do not apply however – if the molecule has low molecular weight, smooth features, low contrast, or a small fraction of windowed images as real particles – that assumption may be invalidated. In this case, the particle verification simply defaults to the fully manual mode.

Further room for improvement lies in the classification method used. K-means classification was used here, because its implementation in SPIDER (command CL KM) works robustly on large image sets, in contrast to Diday's method (SPIDER command CL CLA), and allows straightforward control over the number of classes requested (as opposed to hierarchical classification, SPIDER command CL HC). This verification scheme is not intended to be dependent on any one classification method. Classification algorithms implemented outside of SPIDER, such as self-organized maps (Pascual et al., 2000), may prove useful, as well. The more accurately the classification process separates particles from non-particles, the less intervention would be required on the part of the user. There are large, unexplored areas from computer vision and other fields which may lend themselves to this application.

The notion of “error rate” in particle-picking begs the question of what the “correct” particle set is. It is assumed that the manually verified particle set is to be the gold standard, but that is not necessarily be the case. For the particle sets used in Figure 6 for instance, the gold standard was found to be not precisely the hand-picked particle set but rather the intersection of that particle set with those from two other verification modes. While manually verifying ribosomes, a human user looks for appropriately sized structures with textural features distinguishable from contaminants. Subjectivity is inherent in these decisions, and thus different users will select different particles sets from the same starting set (Zhu et al., 2004). A valuable additional visual cue is that the particles are aligned for the verification step, adding to those cues otherwise used in manual verification.

Given the danger of reference bias, namely, that images of non-particles can give rise to an averaged image that looks like that of a real particle (Fig. 2A, Fig. 2C), there is a danger that a user will include non-particles in a reconstruction, with adverse effects. The best test for particle-set reliability used here proved to be the cross-validated FSC (Fig. 5D, Fig. 6). In the evaluation of a single particle set, a large difference between the normal FSC and the cross-validated FSC may be indicative of aberrant behavior, for example, the “truncated lfc” curves in Figure 5B and Figure 5D. When comparing two or more particle sets, normalization of the number of particles provided even greater sensitivity (Fig. 5D, Fig. 6B). However, one caveat of the cross-validation test, as presented here, is that it operates on collective particle sets, as opposed to individual particles.

Additional checks downstream from the initial verification step may be desirable. One check is to exclude particles with the lowest CCC values. However, a CCC cutoff is generally not effective by itself, since real particle images recorded close to focus may be excluded; thus any such cutoff should be implemented conservatively. Another check would be to exclude aberrant particles during orientation refinement; we are developing an implementation of such a feature. Rather than try to devise a single algorithm that can distinguish real particles from non-particles, it may be more practical to run particle sets through a gauntlet of algorithms in series, with each removing non-particles by one of a set of complementary methods.

Supplementary Material

01. Supplementary Figure 1.

Three galleries of windowed images produced from SPIDER batch file lfc_pick.spi. This batch file windows images successively according to the rank of the locally normalized cross-correlation peaks. (A) Highest-correlation images. In this implementation, contaminants tend to show the highest correlations. (B) Images with intermediate-to-low correlations. Here, there appears to be a transition from some real particles to non-particles. (C) The lowest-correlation images from this micrograph. There is a very low percentage of potential real particles in this regime. The batch file lfc_pick.spi is described at the site http://www.wadsworth.org/spider_doc/spider/docs/techs/recon/newprogs/lfc_pick.spi and parameters therein are described at http://www.wadsworth.org/spider_doc/spider/docs/partpick.html#LFC

02. Supplementary Figure 2.

Representative particle montages from the scatter plot shown in Figure 3A. Particles are sorted from lowest correlation to highest correlation. After the last row in the particle montage is the class average. A few of the lowest-correlation particles have been omitted to display only complete rows of images. (A) From a class at the lower right of the scatter plot, i.e., with a high CCC and low SDVAR. Almost all of the images were judged to contain real particles. (B) From a class at the upper right of the scatter plot, i.e., with a high CCC and high SDVAR. There are some real particles, but some contaminants also. (C) From a class at the lower left of the scatter plot, i.e., with a low CCC and low SDVAR. There are few likely real particles, and the images have relatively flat density profiles. (D) From a class at the upper right of the scatter plot, i.e., with a low CCC and high SDVAR. There are few candidate real particles, while the density profiles are uneven.

03. Supplementary Figure 3.

Slices through three of the reconstructions, each containing approximately 38,000 particles, whose FSC curves were plotted in Figure 6B. (A) 100% of the particles "good." (B) 50% of the particles "good." (C) 0% of the particles "good." Window dimension is 366.6 Angstroms. As a result of reference bias, gross features are similar, even when no real particles are present. Slight differences in appearance are due primarily to excision of spatial-frequency terms at intermediate-resolution during the course of cross-validated alignment. See main text for details.