Evolutionary origins of human apoptosis and genome-stability gene networks

Abstract

Apoptosis is essential for complex multicellular organisms and its failure is associated with genome instability and cancer. Interactions between apoptosis and genome-maintenance mechanisms have been extensively documented and include transactivation-independent and -dependent functions, in which the tumor-suppressor protein p53 works as a ‘molecular node’ in the DNA-damage response. Although apoptosis and genome stability have been identified as ancient pathways in eukaryote phylogeny, the biological evolution underlying the emergence of an integrated system remains largely unknown. Here, using computational methods, we reconstruct the evolutionary scenario that linked apoptosis with genome stability pathways in a functional human gene/protein association network. We found that the entanglement of DNA repair, chromosome stability and apoptosis gene networks appears with the caspase gene family and the antiapoptotic gene BCL2. Also, several critical nodes that entangle apoptosis and genome stability are cancer genes (e.g. ATM, BRCA1, BRCA2, MLH1, MSH2, MSH6 and TP53), although their orthologs have arisen in different points of evolution. Our results demonstrate how genome stability and apoptosis were co-opted during evolution recruiting genes that merge both systems. We also provide several examples to exploit this evolutionary platform, where we have judiciously extended information on gene essentiality inferred from model organisms to human.

INTRODUCTION

The concept of apoptosis is associated with the maintenance of tissue homeostasis (1). The programmed cell death (PCD) in the perspective of multicellular organisms guarantees the substitution of old and/or dysfunctional cells, which are impaired by the accumulation of cellular damages due to environmental insults, as well as participates directly in tissue development (2). According to KEGG (3), a reference pathway database, there are up to 100 genes coordinately working in apoptosis. Removing one of these components affects several others and it may impair the whole pathway. In complex metazoan organisms, a defective apoptosis is associated with organogenesis disorders and also uncontrolled cell growth, which is typically found in neoplastic diseases (4). In the perspective of a cancer cell, suppressed apoptosis is a requirement in order to enhance cell fitness (5). In some extent, it is thought that apoptosis is related to genome instability in the sense that mutation prone clones, containing aberrant genetic content (i.e. high number of chromosome aberrations and DNA point-mutations), need a defective apoptosis to escape cell death (6–8).

Genome-maintenance mechanisms are intimately linked to apoptotic components, as indicates the high number of proteins that interact with the tumor-suppressor protein p53. In fact, this protein interacts with the four major DNA repair mechanisms: nucleotide excision repair (NER), base excision repair (BER), mismatch repair (MMR) and recombinational repair (RER)—homologous recombinational repair (HRR) and nonhomologous end-joining (NHEJ). Concerning NER and MMR, p53 can act in both transactivation-independent and -dependent manner (9). Furthermore, several DNA repair proteins can stimulate apoptosis in response to DNA lesions, as for example the BER-associated protein poly(ADP-ribose) polymerase-1 (PARP1) (10) and the MMR proteins MSH2, MSH6 and MLH1 (11). Indeed, the overlapping among apoptosis and DNA repair genes renders difficult a precise definition of functional boundaries among all systems, which is a characteristic of complex biological networks (12).

On the other hand, apoptosis and genome-stability networks have different evolutionary roots. For instance, the core machinery of eukaryotic repair systems seems to be conserved among the three domains of life, although an expressive number of eukaryotic proteins have no counterpart in archaea or bacteria (13). Likewise, metazoan apoptosis contains several components that can be identified in ancient organisms such as prokaryotes and unicellular eukaryotes. However, many molecular sources in the eukaryotic apoptosis network might have been inherited from prokaryotes by horizontal gene transfer (HGT) in different events, being exapted to new functions to form apoptosis network (14).

Notwithstanding the components of these two networks having been extensively identified in eukaryote phylogeny (15,16), few data are available about the evolutionary scenario that functionally linked apoptosis to genome-stability gene network (5,17,18). One approach to assess the role of each component in a given interacting network is through comparative genomics. Using well-studied models, as yeast and mouse, comparative genomics provides powerful tools to draw evolutionary inferences for poorly studied organisms (16).

In a previous paper we characterized the entanglement among apoptosis and genome-stability pathways in a human protein–protein-association network (19). Here, we extend this characterization to build a platform to transfer functional information from several organisms to human. The idea is based on the consensus that each component of a gene/protein interaction network in the present living organisms has its origin at some point of the evolution. Thus the scenario that gives rise to the present network can be tracked-down by searching the root of each component in a given species tree.

Our goal here is to create an orthology map across a species tree for the human apoptosis and genome-stability gene/protein-association network in order to transfer to humans the information described for other eukaryotes. We searched for orthologs [i.e. homologous genes derived from a single ancestral gene in the last common ancestor (LCA) of compared species (20)] among 35 fully sequenced eukaryotic genomes. Likely orthology was inferred from orthologous groups using STRING database (21,22), and for each set of orthologs we found the most parsimonious scenario on the eukaryote phylogeny (23). To verify this orthology data, we reconstructed the entire analysis using Inparanoid database as a different data source, and essentially obtained the same results (see Supplementary materials). As further network characterizations, we estimated gene plasticity by measuring gene abundance and distribution of each orthologous groups among the extant species, and considered essentiality data available for yeast and mouse orthologs. Both plasticity and essentiality information were transferred to the human gene network. As a result we obtained a gene network where it is possible to discriminate ancient, less plastic and more essential regions from earlier, more plastic and less essential ones. Furthermore, the many cancer genes identified in this gene network are located in the earlier, more plastic and less essential region. We anticipate that our analyses can be applied to study the origins of a broad range of neoplastic diseases.

MATERIALS AND METHODS

Human gene/protein-association network

The protein–protein interaction network associating 180 human genes of apoptosis and genome-stability pathways has been extensively described in Ref. (19). Briefly, the network is generated using the database STRING (24) with input options ‘databases’,’experiments’ and 0.700 confidence level. STRING integrates different curated, public databases containing information on direct and indirect functional protein–protein associations. Each protein is identified according to both gene HUGO ID (25) and Ensembl Peptide ID (26) (Supplementary Table S1). The results from the search are saved in data files describing links between two genes and then handled in Medusa software (27).

Parsimony analysis: inferring evolutionary roots of human apoptosis and genome-stability genes

The parsimony analysis is divided into two major steps in order to construct parsimonious scenarios for individual sets of orthologous, given a species tree. We first built a consensus phylogeny for the eukaryotes listed in STRING database (22). The eukaryote phylogeny is based on a manual integration of a variety of phylogenies (28–33). We determined the presence of homologs among the organisms in the species tree for the 180 genes of apoptosis and genome-stability networks. Likely homology was inferred using the orthology information from the eukaryotic clusters of orthologous groups of proteins (KOGs) (21), which was retrieved through the orthology assignments in the STRING server; STRING has augmented the KOG orthology information by adding additional species (currently 35 eukaryotes) and creating more groups (NOGs, nonsupervised orthologous groups) as well as giving direct association among the three-domain phylogeny. In total, 142 eukaryotic orthologous groups were identified (Supplementary Table S1). To benchmark the analysis, we retrieved the orthologous groups for same set of genes using Inparanoid database, as discussed later.

The second major step is the reconstruction of the evolutionary scenario for each individual set of orthologous genes. This problem has been previously formulated as follows (23): given a species tree and a set of orthologs with a particular phyletic pattern, find the most parsimonious mapping for the set of orthologs on the tree. Precisely, concerning our problem, this question can be restated as: for each orthologous group associated with the human apoptosis and genome-stability genes, find its earliest ortholog in the eukaryote phylogeny.

The incongruence of any evolutionary scenario is resolved according to the gain/penalty approach (23), where the most parsimonious scenario of presence/absence of all the genes at all ancestral nodes of the tree is obtained by using an inconsistency function defined as

1

where λ is the number of gene losses, γ is the number of gene gains and g is the gain penalty. For each different scenario a function S is calculated and the most parsimonious scenario is chosen as the one that yields the minimum value of S. The relative costs of the evolutionary events consider two cost units for gene birth or gene acquisition (i.e. g = 2), and one cost unit for gene loss. This ratio is proposed by Mirkin and coworkers (23). Subsequently, other works validate the 2:1 ratio in prokaryotes (34,35) which thereafter has been used in similar analysis in eukaryotes and prokaryotes (36–38). Further details and the corresponding evolutionary scenario for all orthologous groups are presented in Supplementary Figures S14–S49 and also provided in spreadsheet format (Supplementary Table S3).

To verify the robustness of our orthology analysis we compared each gene evolutionary scenario with a corresponding one obtained using a different data source. In this case, we reconstructed the entire evolutionary analysis considering the Inparanoid database (39). In contrast to KOG algorithm, Inparanoid is designed to find orthologs and in-paralogs between two species and to separate in-paralogs from out-paralogs. KOG and Inparanoid orthology analysis lead to roughly the same conclusions. We present and discuss these results in Supplementary Material Online (Supplementary Figures S3–S6, S50–S94 and Table S4).

Diversity analysis of orthologous groups

An orthologous group (OG) corresponds to a set of genes from different extant species that have a common gene ancestor. To obtain a quantitative expression of the orthologous distribution (i.e. distribution of the items of an orthologous group), we have measured the information content of two different databases (STRING and Inparanoid) using Shannon Information Theory (7,40–43) defined as follows. Consider n as the number of selected OGs, each one representing an orthologous groups. Each OG is labeled by α (α = 1, …, n) and has N_α items (orthologous genes), distributed among M possible organisms. Consequently, for a given OG we can define s(i,α) as being the number of items of a given organism i, (i = 1, …, M), whose sum for a given α adds up to N_α The probability p(i,α) that, among the N_α items of the α-OG, a randomly chosen one belongs to the organism i is written as

2

such that ∑i p(i, α) = 1. The normalized Shannon information function H_α is defined as

3

where we have divided by ln(M) in order to normalize the quantities, guaranteeing that 0 ≤ H_α ≤ 1. Observe that if there is one gene per organism, N_α = M, p(i,α) = 1/M, and H_α = 1. In fact, H_α reflects the spread of the distribution s(i,α), i.e. it measures the diversity that exists in the αth OG. H_α near 0 indicates poor diversity, while a H_α close to 1 suggests high diversity. As a complementary quantity, we also estimate the abundance D_α in the αth OG by simply obtaining the ratio between the number of items (orthologous genes) and the number of organisms.

Transference of functional information from yeast and mouse to human gene/protein-association network

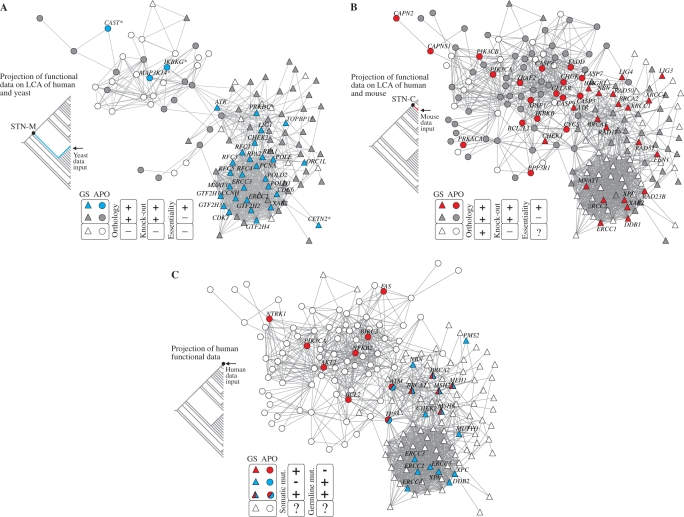
To predict developmental essentiality of a human gene, we used the mammalian phenotype information of the corresponding mouse orthologs. In this analysis, a gene is defined as ‘essential’ for organism development if a knock-out of a mouse ortholog confers embryonic or perinatal lethality (44). We obtained the mouse phenotype data from the curated knock-out collection available in Mouse Genome Database (MGD) (http://www.informatics.jax.org) (45). To predict cellular essentiality of a human gene, we used the phenotype information of the corresponding yeast orthologs. In this analysis, a human gene is defined as ‘essential’ at cellular level if a knock-out of its ortholog confers lethality to yeast. The yeast knock-out data were obtained from the Saccharomyces SGD project ‘Saccharomyces Genome Database’ (http://www.yeastgenome.org/) (46). Human and yeast orthology is also verified using as data source the Inparanoid database (47) and is provided in Supplementary Table S1. In this analysis, six essential genes, out of 32, were not listed as orthologs when using Inparanoid (these genes are presented in Figure 5A with an asterisk besides their names).

Figure 5.

Integrating evolutionary and functional data. (A) Projection of yeast lethality data onto human apoptosis and genome-stability gene network: essential (blue GNNs) and nonessential yeast orthologs (grey GNNs) according to SGD database (46). The graph presents all orthologs inferred in the LCA of yeast and human (i.e. rooted or present in STN-M). White GNNs correspond to genes present in the branch but absent in yeast, as predicted in the parsimony analysis (see ‘Materials and Methods’ section). Asterisks identify six GNNs whose orthology are predicted by orthologous groups but not confirmed in the Inparanoid database (47). (B) Projection of mouse lethality data onto human apoptosis and genome-stability gene network: essential (red GNNs) and nonessential (grey GNNs) mouse orthologs according to MGD database (45). The graph presents only GNNs whose orthologs are inferred in the LCA of mouse and human (i.e. rooted or present in STN-C). GNNs that lack knock-out data in MGD database are indicated as white GNNs (mainly in ρ module). (C) Projection of genes causally implicated in human cancer—CAN genes—according to Cancer Gene Census (48). Colors indicate whether the gene is somatically mutated in cancer (red GNNs) or mutated in germline predisposing to cancer (blue GNNs) or both. White GNNs indicate genes not mentioned in the Cancer Gene Census.

Human gene mutation statistics

The data for the analysis of CAN genes is obtained from Cancer Gene Census (48). Both germline-mutated and somatic-mutated CAN genes are retrieved and then crossed with the list of 180 genes of our study. We identified 25 CAN genes placed in our network-based model of apoptosis and genome stability (Supplementary Table S1).

Genotype statistics of germline CAN genes located on ρ module is further analyzed in the XP mutation database (http://www.xpmutations.org). The representativeness of the sample was tested against a second database [Human gene Mutation Database—HGMD (49)] which is regarded as a reference mutation database for (published) gene lesions responsible for human inherited diseases. Table 1 shows as equivalent the samples obtained here from HGMD and XP database. However, the former contains limited gene information comparing to the latter (50). Indeed, we could successfully retrieve the zygosity information only accessing the XP database.

Table 1.

Allelic distribution of CAN genes placed in ρ module according to XP mutation database (Panel A). Sample representativeness compared to a second databases (Panel B)

Panel A	Number of Genotypes (%)a			Total genotypes	(Panel B) Entriesb
CAN gene	null/non-null	non-null/non-null	null/null		XP database	HGMD
ERCC2	20 (43.5)	26 (56.5)	0 (0.0)	46	76c	48
ERCC3	3 (60.0)	2 (40.0)	0 (0.0)	5	8	11
ERCC4	0 (0.0)	7 (100.0)	0 (0.0)	7	18d	17
ERCC5	0 (0.0)	5 (100.0)	0 (0.0)	5	10	12
XPA	6 (6.0)	94 (94.0)	0 (0.0)	100	128e	25
XPC	0 (0.0)	13 (100.0)	0 (0.0)	13	28f	42
DDB2	0 (0.0)	5 (100.0)	0 (0.0)	5	8g	8
Σ	29 (16.0)	153 (84.1)	0 (0.0)	182	276	163

^aData obtained from XP mutations database (http://www.xpmutations.org) is compiled according to the absence (null) or presence (non-null) of CAN gene alleles. Null/non-null genotypes are only heterozygous, while non-null/non-null genotypes include heterozygous and homozygous.

^bThe number of allelic records present in XP mutations database is compared to a second human inherited mutation database [Human gene Mutation Database — HGMD (49)] in order to attest the sample representativeness.

^cOne allele is duplicated in the database (the XP1BR entry).

^dThree alleles have no mutation data (XP80TO, XP81TO and XP89TO entries).

^eOne allele had no zygosity information (XP10OS entry).

^fFour alleles have no zygosity information (XP6BR, XP4BR, XP3BE and XP22BE entries). Polymorphisms are not considered in the analyses.

^gOne allele is duplicated (XP25PV entry).

RESULTS

Apoptosis and genome-stability gene set

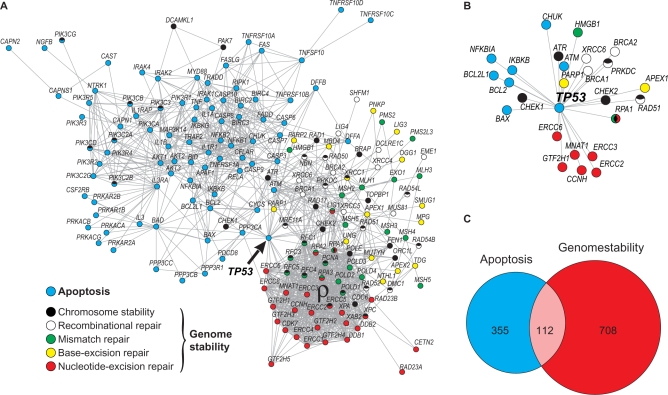
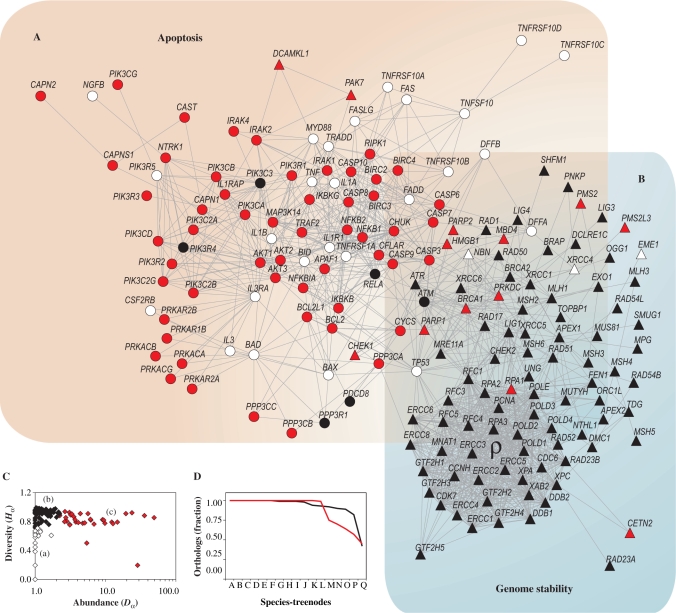
Our analysis begins with a list of 180 genes participating in human apoptosis and genome-stability functions as previously defined (19) and provided as supplementary material online (Supplementary Table S1). To define this gene set we have characterized several genome-maintenance mechanisms as well as the interactions among their components. In Figure 1A we reproduce these interactions to illustrate the links between apoptosis and genome-stability gene networks, which are collectively referred to as the genome-maintenance gene network. Each node corresponds to a gene-network node (GNN), while the lines represent direct (physical) and/or indirect (functional) associations according to STRING database for human. They are derived from high-quality systematic protein–protein interaction mapping (22). Note the position of TP53 gene in the network topology connecting apoptosis to 18 genome-stability components (Figure 1A, arrow, and Figure 1B). This functional overlap is further emphasized in Figure 1C for the complete network, which shows the number of links distributed for each gene set. Although apoptosis and genome stability have equivalent number of components in this network (i.e. 86:100), the connectivity of the latter is almost 2-fold, as indicated by the Venn diagram. Such difference arises mainly due to the large number of associations among NER, MMR and chromosome stability components, yielding a highly connected gene module (Figure 1A, ρ).

Figure 1.

Human apoptosis and genome-stability gene network. (A) Graph of interactions among genes involved in apoptosis and DNA repair pathways, as previously characterized in Castro et al. (19). Different pathways are represented in different colors. Network nodes with more than one color represent genes participating in more than one pathway. Gene IDs of each pathway are provided in Supplementary Table S1. (B) Magnification of TP53 gene position of in the network topology. It highlights the functional overlap of TP53, linking apoptosis to several genome-stability components. (C) Venn diagram showing the distribution of links between apoptosis and genome-stability pathways. The overlapped area corresponds to those links connecting both systems. The large number of associations among NER, MMR and chromosome-stability components is designed as ρ module.

Construction of parsimonious evolutionary scenarios

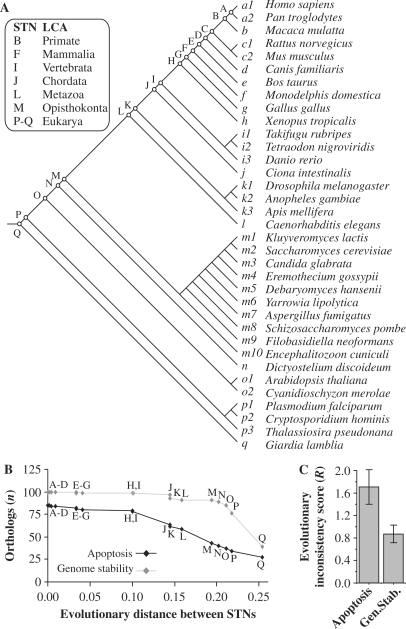
In order to infer the ancestral states of human apoptosis and genome-stability genes we considered eukaryotic clusters of orthologous groups of proteins (KOGs) (21), using the orthology assignments in the STRING server (22). In total, apoptosis and genome-stability genes are distributed in 142 KOGs and for each one of these orthologous groups we found the most parsimonious mapping onto the eukaryote phylogeny. In Figure 2A we present the topology of the species tree used in this analysis (28–33), which is arranged in 17 subdivisions (monophyletic groups) based upon phylogenetic relationships. Every species-tree node (STN) is labeled according to the ascending subtree, and is referred to as the LCA of this subset.

Figure 2.

Inferring evolutionary roots of human apoptosis and genome-stability genes. (A) Eukaryote species tree topology used in the parsimony analysis. The phylogenic relationship among these 35 eukaryotes is based on a manual integration of a variety of phylogenies (28–33). STNs and the corresponding LCA are indicated. (B) Distribution of apoptotic and of genome-stability orthologs according to the roots inferred in the species tree and plotted as a function of the divergence between STNs (based on branch-length estimates). In Supplementary Material Online we exemplified the parsimony analysis. The evolutionary distances were computed using three protein families regarded as very conserved among distant taxa and described as able to reconstruct the three-domain phylogeny: 40S ribosomal proteins, translation initiation factor 5A proteins and Flap structure-specific endonuclease 1 proteins (73). All proteins used in the analysis are aligned in Supplementary Figures S10–S12. The distances are expressed as the fraction of sites that differ between the branches in a multiple alignment, which is an approximation of the branch-length that separates STNs. (C) Divergence between KOG and Inparanoid-derived scenarios. For apoptosis genes, R = 1.709 STNs ±0.224 (SE) and for genome-stability genes R = 0.807 STNs ±0.202 (SE). It means that for each root inferred in our analyses, the estimated error for apoptosis is approximately two STNs up and down from the rooting point in the species tree, while for genome stability the error is approximately one STN up and down.

To give a quantitative view of the evolutionary roots inferred for the 180 human genes studied here, we plotted the number of human apoptotic and genome-stability orthologs in each STN (Figure 2B). Accordingly, this distribution suggests a sequential enlargement of the network, with a progressive increase of apoptosis. In contrast, genome-stability orthologs are mainly rooted in STN-P (at the base of eukaryote species tree), suggesting that orthologs involved in apoptosis are more recent. Furthermore, in order to assess the robustness of our orthology analysis we reconstructed the entire evolutionary scenarios using Inparanoid database as a different data source, and essentially obtained the same results. In contrast to KOG algorithm, Inparanoid is designed to find orthologs and in-paralogs between two species and to separate in-paralogs from out-paralogs (39). We used this second approach to construct the evolutionary inconsistence score (R) that estimates the divergence between the two scenarios (i.e. ΔSTN). We present and discuss these results in Supplementary Material Online (Supplementary Figures S3–S6, S50–S94 and Supplementary Table S4). Briefly, for apoptosis genes, R = 1.709 STNs ±0.224 (SE) and for genome-stability genes R = 0.807 STNs ±0.202 (SE) (Figure 2C). It means that for each root inferred in our analyses, the estimated error for apoptosis is approximately two STNs up and down from the rooting point in the species tree, while for genome stability the error is approximately one STN up and down.

In order to test a phylogeny where Caenorhabditis elegans is not at the root of the metazoa we included Nematostella vectensis, which thus changes the base of metazoa (Supplementary Figure S9). We chose this organism because (i) Nematostella is a cnidarian; (ii) the idea that the cnidarians are at the base of metazoa is less controversial than the nematodes; and (iii) switching a taxon like this goes some way to testing the effect of the phylogeny used. The result after this process is that the roots of the human genes remain almost the same (the complete analysis is available at Supplementary Table S5) and further discussed at supplements (section 1.4: the deep root of metazoans).

From species-tree nodes to gene-network nodes

To assess the details of the evolutionary scenario described earlier in the context of known and predicted gene functions, we used the network-based model presented in Figure 1A (19).

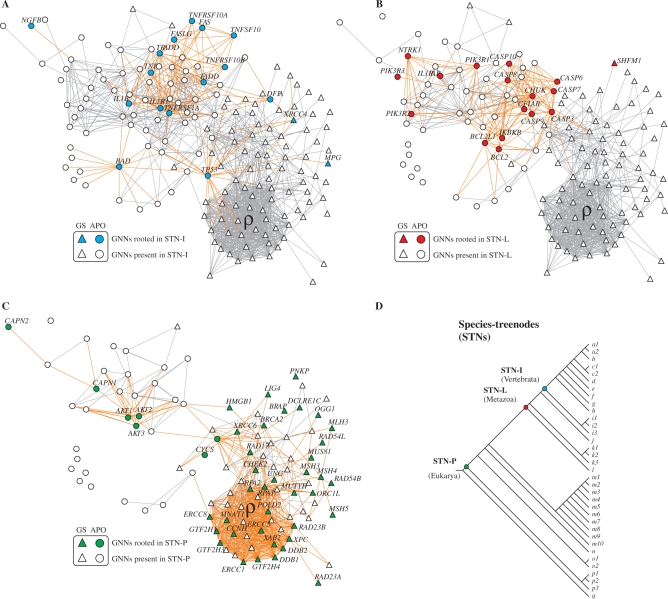
Starting from the complete network graph we generated three relevant orthology projections to characterize the functional differences between apoptosis and genome stability (Figure 3A–C). In these graphs we highlighted the nodes according to the roots inferred in the species tree (Figure 3D). Note that here each gene-network node (GNN) represents an ortholog of a gene in the human apoptosis and genome-stability gene network.

Figure 3.

From STNs to gene-network nodes (GNNs). Orthology projection of genes rooted in STN-I (A), STN-L (B) and STN-P(C). Roots of an ortholog: color nodes; presence of an ortholog: white nodes. The location of these three STNs in the species tree is indicated (D). In Supplementary Material Online we provide further examples of this orthology projection approach (Supplementary Figure S2) and compared with Inparanoid evolutionary scenarios as a different orthology data source (Supplementary Figures S3–S6).

The orthology information regarding other STNs is provided in Supplementary Table S1. As quantitatively showed in Figures 2B–D, the more recent STNs concentrate apoptosis roots (round GNNs in Figure 3A and B). However, there is a qualitative difference: observe the pooled origins inferred for several components of apoptosis extrinsic (Figure 3A) and intrinsic (Figure 3B) pathways.

To analyze this result it is important to consider the biochemical signature of apoptosis, that is, the caspase activation, which is triggered by either intrinsic or extrinsic apoptosis pathways. The intrinsic pathway is associated with mitochondrial outer membrane permeabilization and cytochrome c (CYCS) release in response primarily to developmental cues or cellular damage. It triggers apoptosis through the Bcl-2 gene family and the initiator protease caspase-9. In contrast, the extrinsic pathway is characterized by the ligation of cell surface receptors via specific death ligands, as the TNF gene product, to generate catalytically active caspase-8 (51,52). The protein encoded by TNF gene is a multifunctional proinflammatory cytokine that belongs to the tumor necrosis factor (TNF) superfamily, which also includes the ligands FAS (FASLG) and TRAIL (TNFSF10). These ligands bind to several members of TNF-receptor superfamily (e.g. TNFRSF1A, TNFRSF10A, TNFRSF10B and FAS receptors) and are involved in the regulation of a wide spectrum of biological processes, such as immune surveillance, innate immunity, haematopoiesis and tumor regression [for review, see (53)].

Accordingly, it is noticeable that the components of intrinsic pathway are rooted mainly in STN-L or earlier (e.g. CYCS is deeply rooted in eukaryote species tree—Figure 3C). In contrast, the subsequent enlargement of the network graph is provided mainly by orthologs of the extrinsic pathway, whose ligands and receptors are rooted in STN-I projection, or later (e.g. IL1A, IL3RA, IL3 and TNFRSF10D genes are observed only in mammals, that is, STN-F and later, evinced by comparing STN-I projection versus complete human network; details of these orthologs are presented in the explicit parsimony analysis—Supplementary Figures S46, S48 and S49).

In STN-P projection (Figure 3C), however, only a small fraction of genes belongs to apoptosis. Instead, this graph is remarkable by the large presence of genome-stability components (triangular GNNs), as quantitatively addressed in Figure 2B.

Taking all results together, this evolutionary scenario of genome-maintenance mechanisms is marked by three major functional increments: the first is the evolution of genome-stability gene network, whose components originate in the basal position of this species tree [STN-P, inconsistency between datasets R = 0.63 STNs ±0.22 (SE)]; the second is the appearance of several apoptotic intrinsic components, rooted near metazoan divergence [STN-L, inconsistency between datasets R = 1.23 STNs ±0.23 (SE)]; the third consists of the network enrichment with several apoptotic extrinsic members and happens near chordate-vertebrata root [STN-I, inconsistency between datasets R = 0.35 STNs ±0.16 (SE)]. The network core of apoptosis and genome-stability systems are rooted in this tree before the divergence of metazoans, while GNNs placed in the periphery of the networks represent more recent evolutionary innovations. Therefore, the striking feature of these graphs is the increasing association between apoptosis and genome-stability functions with the emergence of an entangled gene network, which is fully consistent with the evolutionary strategy used in eukarya of adding complexity to existing core systems (54,55). (Inparanoid database essentially produces the same evolutionary scenario; please see Supplementary Figure S6.)

Also, additional evidence of the ancestral roots of genome stability can be inferred considering the likely origin of the ancestral eukaryotic KOGs by identifying their closest prokaryotic orthologous groups (COGs). The KOG-to-COG correspondence is presented in Supplementary Figure S8, and shows that 77.0% of the genome-stability orthologs have identifiable prokaryotic orthologous groups, against 39.5% for apoptotic orthologous genes.

Despite the several organisms that have been considered, the construction of the gene network is directed to human. Therefore, the interpretation of the evolutionary scenarios is ultimately linked with the characterization the human gene network. It means that we cannot infer that the gene network in the actual organism at the root of the eukaryotes was smaller. As we have stated in the introduction section, our goal is to create an orthology map across the species tree in order to transfer to human the information described for other eukaryotes. This is a one-way strategy, which is explored in the subsequent sections.

Plasticity analysis

Genetic plasticity may be understood as the ability of a functional gene network to tolerate changes in its components. There are different sources for such changes (gene duplication, gene loss, mutations and horizontal gene transfers), with different causes and effects. These changes in the genome may or may not be naturally selected, depending on the effect they have either on cell fitness or organism viability, in the case of complex organisms. The result of such an evolutionary dynamics is genetic variability among organisms of the same species or, ultimately, speciation. Gene networks are not equally plastic and hence do not equally respond to these variation pressures: depending on the gene, its function, influence on other genes, and their relevance, some changes are more likely to be tolerated or selected than others.

Focusing in networks in general, one may expect that gene networks that are more tolerant to variation will present a larger variability inside a species and among species. Focusing now on individual genes, organisms should be more tolerant to drastic changes (e.g. gene knock-out) when the change is performed on genes located at a more plastic network. These two characteristics, the gene variability among different genomes and the organism response to knock-out of single genes, allow two independent measures to estimate gene network plasticity. One possible plasticity measure is estimating the number and the distribution of orthologs among different organisms. A second, independent plasticity measure may be obtained by assessing cell lethality data. In what follows we present and discuss these two plasticity measures.

Diversity and abundance analysis

We evaluated the diversity and abundance of the orthologous groups to estimate the plasticity of each gene in our human apoptosis and genome-stability gene network (precise definition in the Materials and methods section and further exemplified in Supplementary Material Online).

The network graph presented in Figure 4A and B incorporates diversity and abundance statistics, allowing the discrimination in three distinct classes of genes based on the distribution of diversity as a function of abundance (Figure 4C). The first class (a) refers to genes placed in orthologous groups with low diversity and low abundance (Figure 4A and B, white GNNs; Figure 4C, white diamonds). It means that few organisms present these orthologs, and the associated orthologous groups have few components. This implies a very recent origin for these GNNs, since (i) all are present in humans, the end of our species tree; and (ii) they are not present in many extant species. For example, TP53 and FAS have their origins at STN-I, as shown in Figures S38 and S40 in Supplementary Material Online. This class of genes must then be located at region of the network that is plastic enough to accept new genes. The second (b) refers to genes placed in orthologous groups with high diversity and low abundance (Figure 4A and B, black GNNs; Figure 4C, black diamonds), indicating a small number of genes per organism, but present in many different species. These genes are located in the most ancient region of the network. It implies poorly plastic genes, highly conserved among species. The last class (c) refer to those genes placed in orthologous groups with high diversity and high abundance (Figure 4A and B, red GNNs; Figure 4C, red diamonds), which clearly requires high plasticity. Note that both red and white GNNs (plastic GNNs) are segregated from the black GNNs (poorly plastic) in the network. This segregation should be expected since plasticity must be a characteristic of a set of interacting genes rather than a characteristic of an individual gene. Figure 4D supports these finding by showing the relative presence of the three classes of genes in the STNs: the more recent genes in the network emerge at the highly plastic regions of the network, while the more ancient ones are located at the poorly plastic regions.

Figure 4.

Plasticity analysis of orthologous groups. (A and B) Diversity H_α and abundance D_α of orthologous groups are overlaid on apoptosis and genome-stability gene network according to the categories defined in C. (C) Distribution of H_α as a function of D_α: (a) orthologous groups with low diversity and low abundance (white); (b) orthologous groups with high diversity and low abundance (black); (c) orthologous groups with high diversity and high abundance (red). (D) Fraction of orthologous groups present in the STNs: orthologous groups with low diversity and low abundance (white dashed line); orthologous groups with high diversity and low abundance (black solid line); and orthologous groups with high diversity and high abundance (red solid line). In Supplementary Material Online we provide examples of the diversity analysis.

Observe that this inhomogeneous distribution of white, red and black GNNs in the network graph reflects also in the function performed by the genes. While white and red GNNs are clearly populating apoptosis network, black GNNs are placed mainly in genome stability. This result suggests a high evolutionary conservation of genome-stability orthologs (i.e. class b, orthologs present in many organisms and with few variants), contrasting with apoptosis GNNs that concentrate the plasticity of the network (i.e. class c orthologs with many variants per organisms).

Essentiality in Saccharomyces cerevisiae

A second, independent plasticity measure is obtained by assessing cell lethality data. Here we considered the eukaryotic model Saccharomyces cerevisiae available in the Saccharomyces Genome Database (SGD) (46). We transferred this information to the STN representing the LCA of yeast and human (i.e. STN-M), which is then projected on the corresponding human network topology. The yeast results are showed in Figure 5A. Observe that essential genes are concentrated in a specific portion of the network (blue GNNs) corresponding to the lower plasticity area showed in Figure 4 (black GNNs there). Furthermore, likely orthology inferred in the LCA of yeast and human indicates that yeast have lost several genes in the course of its evolution, but mainly apoptotic genes (white GNNs in Figure 5A). Such loss, together with the presence of essential genes overlaid on genome-stability area (blue triangular GNNs), indicates that our evolutionary scenario is consistent with the plasticity measures shown in Figure 4: the lost genes are represented by plastic GNNs (red and white symbols in Figure 4).

Lethality in Mus musculus

In order to complement this lethality measure with a complex multicellular eukaryotic model, we assessed Mus musculus lethality data in Mouse Genome Database—MGD (45). The phenotypic statistics in MGD database consider lethal any allele that causes death anytime after fertilization and before the postnatal day 2; thus, knock-out alleles may indicate ‘developmental lethality’ or ‘essentiality’ to embryonic stem cells. Evidence of mouse lethality is obtained according to the frequency expected by Mendelian genetics (i.e. zygosity and allelic distribution observed in the offspring): any significant deviation from the expected frequency for the knock-out allele indicates lethality. Therefore, from the putative 178 Mus musculus orthologs identified in our analysis, we find 124 genes for which knock-out data are available (Supplementary Table S1). While the majority produced viable phenotypes, 39 knock-out alleles have been associated with embryonic-perinatal lethality. The data are then transferred to the STN representing the LCA of mouse and human (i.e. STN-C) and then projected on the corresponding human network topology (Figure 5B). This data projection shows a homogeneous distribution of lethal alleles among nonlethal ones (red and grey GNNs, respectively), and a concentration on the genomic stability network of genes lacking knock-out data (white GNNs). Figure 5B highlights the essentiality of apoptosis and genome-stability gene network to the organism development. However, except for those genes without knock-out information (mainly placed in ρ module), mouse statistics indicate that the vast majority of knock-out alleles are nonessential at cellular level, given that even after gene disruption the cellular expansion is still viable. Such reading complements the results found for yeast, since what is nonessential to yeast is also nonessential to mouse at cellular level. A pictorial consequence of the complementarity of the results for yeast and mice is that the set of blue symbols in Figure 5A almost do not overlap with red symbols in Figure 5B.

Correlating plasticity and cancer statistics

The most systematical, available data about the functional impairment of human genome-maintenance mechanisms comes from cancer statistics. According to a global human disease network described by Goh et al. (44), from the 180 genes listed in our genome-maintenance gene network, 51 are associated with some human disorder. From these, >50% are implicated in cancer. As an application for the plasticity estimates presented in the previous sections, we now consider cancer statistics data.

Genes causally implicated in cancer are collectively identified as cancer genes—CAN genes (48), and share a common feature: while they are potentially lethal to organism due to disruption of tissue architecture, mutations in these genes that lead to cancer are not lethal to the cell. These mutations are of two types: somatic or germline. While the first arise after organism development and in few cells, the second are inherited—present before conception—and thus continue afterwards in every cell. In fact, germline mutations in CAN genes cause cancer predisposition, not cancer per se, contrasting with somatic mutations that are to a large extent the primary cause of cancers (56).

Mutations that lead to cancer increase cell fitness (5,57), implying that the gene network may tolerate (and the cell may even benefit from) this genetic change (58). Consequently it is reasonable to expect that CAN genes are located on plastic gene networks.

We assessed the cancer statistics available in the Cancer Gene Census at the Cancer Genome Project—CGP (http://www.sanger.ac.uk/genetics/CGP). The graph of Figure 5C shows the projection of mutations causally implicated in human cancer retrieved from that census. Observe that CAN genes have a polarized distribution in the network topology. Those presenting exclusively somatic mutations are associated with apoptotic functions (red GNNs), and are at the plastic portion of the network, while those presenting exclusively germline ones are associated with genome stability (blue GNNs), at the poorly plastic region. Conversely, CAN genes that show both mutation types are at an in-between and overlap apoptosis and genome-stability networks.

The location of the germline mutations poses a challenge to our evolutionary scenario. How can we explain germline mutations in these human genes, given that they are located at a poorly plastic region? Also, care should be taken in order to consider these results together with yeast and mouse due to differences among statistical data. For instance, CAN gene statistics comes mainly from epidemiological data and shows exclusively genes in which mutations that are causally implicated in oncogenesis have been described at least in two independent reports, showing mutations in primary patient material (48). According to CGP census, the underlying rationale for interpreting a mutated gene as causal in cancer development is that the number and pattern of mutations in the gene are likely to have been selected because they confer a growth advantage on the cell population from which the cancer has developed (48). Also, in contrast to mouse and yeast knock-out alleles, CAN gene may have a range of mutations, from a single nucleotide substitution to a complete transcript disruption (i.e. null alleles is the most severe situation, equivalent to mouse and yeast knock-out data).

In order to circumvent such data limitations and improve the analysis we further investigated the human statistics assessing the genotypic profile of several CAN gene loci. We attempt to obtain the proportion of null and non-null alleles in human following the strategy used in mouse to infer lethality according to the expected frequency in a Mendelian distribution. We focus the analysis in the set of CAN genes placed in ρ module, collectively represented in the same locus-specific mutation database—XP mutation database (http://www.xpmutations.org). These CAN genes are also associated with the same DNA repair function (nucleotide-excision repair) and are related to three rare autosomal recessive human clinical disorders (Xeroderma pigmentosum, Cockayne Syndrome and Trichothiodystrophy), which may turns reliable the obtaining of a representative sample (XP database is a repository of XP mutations identified in patients worldwide). We retrieved 182 mutated genotypes available in that database, which is then pooled according to the zygosity and the presence of null and nonnull alleles (Table 1, Panel A). Sample number is also compared to a second database in order to attest the representativeness of the database (Table 1, Panel B) (see Supplementary Material Online for further details). Given the data, in case null/null patients exist in some extent in human population, it would be a strong argument against the essentiality of genes located at the poorly plastic region of the network. As is pointed in Table 1, this is not the case. There is a total absence of null alleles in homozygous. Therefore, considering equivalent criteria among human, mouse and yeast to infer lethality, the data is consistent with lethality of germline CAN genes in the network projection, allowing the less-plastic area to be regarded as essential in human.

DISCUSSION

We presented an orthology map in order to locate the eukaryotic genes in the human apoptosis and genome-stability gene/protein-association network. According to our scenario, apoptosis and genome stability have different origins in the evolution, in spite of the complex interaction between both systems observed in human gene network (see Figure 6 for a summary). The genome-stability network seems to have emerged earlier in eukaryotic evolution.

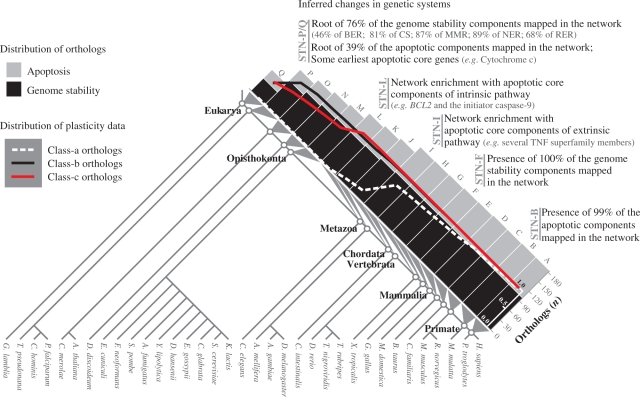
Figure 6.

Summary of the inferred changes in genetic systems. The histograms show the distribution of 180 human orthologs according to the roots inferred in the eukaryote species tree (for details, see Figures 2 and 3). STNs and the corresponding LCA are indicated. Inset graph shows the presence fraction of orthologs of each STNs (for details, see Figure 4D). Diverse important events related to the roots of sets of genes are pointed along the STNs. Chromosome stability (CS).

Our results are consistent with several scenarios described by different authors. For instance, the position of genome stability in the base of eukaryotic species tree is highly consistence with the DNA repair functions described in prokaryotes [DNA repair in Escherichia coli is extensively recognized and has served as a paradigm for the investigation of other organisms: NER (59), BER (60), MMR (61) and RER (62)]. Also, the root of BCL2 in the base of LCA of metazoans is consistent with the identified pro-survival functioning of Bcl-2 protein family members in C. elegans (63,64). Likewise, the position of caspases and in the base of LCA of metazoans has been previously described (14), which is consistent with the origins of intrinsic pathway components that predate TNF-like cytokines (65). These TNF extrinsic pathway core components has been described across vertebrates (47) and corroborate our scenario, in line with the mammalian-like functioning of extrinsic apoptosis pathway described in Danio rerio and the absence of TNF and TNF receptor superfamily members in C. elegans (52).

However, the novelty here is that our results describe the genome-maintenance mechanisms as a whole, in a network-based model, to produce a unique evolutionary scenario. This point of view allows investigating the sequential events that led to the entanglement of apoptosis and genome-stability gene networks.

In the course of human genome-maintenance network evolution, three major functional increments are remarkable as is summarized in Figure 6. The first is associated to the base of the species tree and comprises genome-stability genes. The second evolves gradually, especially near the metazoan origin, with many gene components added to apoptosis intrinsic pathway, such as BCL2 and the caspase gene family members. The third continues the apoptosis enrichment with the addition of several extrinsic components, such as TNF superfamily members.

Furthermore, as the macroevolutionary perspective of these conclusions must be considered together with the estimated evolutionary error (i.e. two species tree nodes up and down from the rooting point in the species tree), it is conceivable that some genes are actually not as recent as one might think. Nevertheless, our conclusions do point that in the course of human genome-maintenance gene network evolution there must have been a dramatic increase in the number of apoptotic components, contrasting with the early origin of genome-stability genes. We identified the expansion of apoptotic components in both KOG and Inparanoid-derived data.

This numerical expansion of apoptotic components could be related to the origin of other cell functions. Such assumption may be illustrated by the TP53 appearance at the transition to later evolutionary scenarios: p53 protein regulates not only apoptosis, but it is also a key regulator of cellular senescence, defined as a permanent cell cycle arrest (66). Senescence is an alternative tumor suppressor mechanism, where damaged cells are prevented from dividing (67). If the senescence has functionally emerged with TP53 gene, this second tumor-suppressor mechanism may have relaxed the selective pressure on apoptosis, increasing its tolerance against nonadaptive processes (e.g. genetic drift, mutation and recombination) and favoring its evolution. Our results are consistent with the emergence of both major mechanisms of tumor control during metazoan evolution, although in what regards senescence more genes should be taken into account to draw a safe conclusion.

Likewise, TP53 can exemplify the evolution of genome-stability gene network. Acting as a transcription factor, p53 protein is able to modulate all DNA-repair processes (9,68). Such DNA-repair gene response to p53 protein is in line with evidences showing that even conserved gene functions are subject to substantial evolution at the regulatory level (69).

The plasticity analysis pointed the genes that during evolution suffered less duplication, such that they are poorly abundant and widely distributed among extant species. The results locate these more conserved genes mainly on the genome-stability network, which is also the more ancient portion of the network. In contrast, certain pairs of genes known to function together in human are placed in different distribution and abundance (e.g. ATM and BRCA1, MUS81 and EME1, PCNA and RPA1, RPA1 and RPA2—Figure 4). Analyzing together, it may indicate that the enlargement of the network can also occur through the addition of new nodes that eventually evolve to work together with ancient ones.

Lethality measures were performed in two complementary ways: one assessing knock-out data on yeast genes and the second regarding essentiality in mice. These two measures are complementary for the following reasons: yeast is a unicellular organism and lethality concerns only cell viability, while mouse is a multicellular animal, with a complex ontogeny. In this later case, a viable embryo implies survival after egg implantation and a relevant cell expansion. As a consequence, when an organism is labeled as viable, certainly the cell is viable and so is the organism. However, when the organism is not viable, the experimental procedure does not always discriminate whether the problem occurred at cell or at organism level. In summary, lethality data on unicellular organisms as yeast give sound information on what genes are essential for cell viability, while on multicellular organisms as mice the sound information is on what genes are not essential at cell level. Transferring cell essentiality information from mice and yeast to the human apoptosis and genome-stability gene network revealed that essential genes at cell level are mostly located at the more ancestral region of the network.

The integration of the information on ancestrality, plasticity and essentiality poses challenging questions. We found that the more ancient, less plastic and more essential genes are located on the genome stability, while the apoptosis network comprises the more recent, more plastic and less essential genes. Genome stability is required to guarantee the information transference from a parental genome to its offspring and thus provides one of the essential ingredients for natural selection to act: memory. It is not surprising that genome-stability network is rooted as early as possible in the species tree. It is also reasonable that such a crucial function is performed by highly conserved genes, where gene duplication is not favored due to the high possibility of disrupting a very essential pathway, yielding a poorly plastic network. Ancestrality, plasticity and essentiality have been pointed as correlated features in typical prokaryotes (70). On the other hand, in multicellular organisms with a more complex ontogeny, such as Mus musculus, the available literature reports not having found these correlations (71,72). Here we find cell gene essentiality to be correlated with ancestrality and plasticity in both unicellular and complex multicellular organisms. The point is that here we discriminate cell lethality from organism lethality: by isolating data from essential genes for cell survival from essential genes for organism viability, the correlation between cell essentiality, ancestrality and plasticity emerges and follows the same trends as in unicellular organisms.

A test for this putative evolutionary scenario for the human genome-maintenance network is given by the location of the human CAN genes. In more complex organisms natural selection acts at two different levels (organism fitness and cell fitness), what may stem conflicting selective pressures: while a fast proliferating cell clone is naturally selected in a unicellular organism, a fast proliferating cell clone in a complex organism may represent a tumor that may end up by killing the organism. In complex organisms, apoptosis and genome-stability networks work also as tissue-maintenance mechanisms, favoring natural selection acting at the organism level. As disruption of such a mechanism may favor natural selection acting at cell level, it stands to reason that many CAN genes are located at the plastic, less cell-essential region of the genome-maintenance network.

Specifically, concerning human functional data, at least two questions emerge from the evolutionary analysis of cancer statistics: (i) why the distribution of CAN genes is polarized between the two major segments described in the evolutionary scenario? and (ii) why CAN genes implicated in both types of cancers (somatic and germline) overlap apoptosis and genome-stability networks? While additional work will be needed to fully characterize the relevance of these results, it is clear for us that this evolutionary perspective may bring further insights in understanding cancer and its origins.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Brazilian Agencies FAPERGS, CAPES and CNPq (grant 140947/2006-0, partially). Funding for open access charge: grant 40947/2006-0.

Conflict of interest statement. None declared.