The Design of a Next Generation Force Field: The X-POL Potential

Abstract

An electronic structure-based polarization method, called the X-POL potential, has been described for the purpose of constructing an empirical force field for modeling polypeptides. In the X-POL potential, the internal, bonded interactions are fully represented by an electronic structure theory augmented with some empirical torsional terms. Non-bonded interactions are modeled by an iterative, combined quantum mechanical and molecular mechanical method, in which the molecular mechanical partial charges are derived from the molecular wave functions of the individual fragments. In this paper, the feasibility of such an electronic structure force field is illustrated by small model compounds. A method has been developed for separating a polypeptide chain into peptide units and its parameterization procedure in the X-POL potential is documented and tested on glycine dipeptide. We envision that the next generation of force fields for biomolecular polymer simulations will be developed based on electronic structure theory, which can adequately define and treat many-body polarization and charge delocalization effects.

1. Introduction

Molecular mechanics or force fields, employing empirical potential energy functions,¹ play a central role in computer simulations, which ultimately determine the accuracy of computational results.² Although remarkable success has been achieved in molecular dynamics and Monte Carlo simulations of liquids, solutions and biopolymers, thanks to the development and careful validation of several force fields,^3–8 there are also a number of deficiencies in the current generation of force fields. First, the choice of the energy terms and the associated degrees of freedom are arbitrary in defining a force field.⁹ As a result, different force fields often have seemingly very different parameters (for example, partial charges), but the computed dynamic and thermodynamic properties can be similar. Secondly, by and large, most force fields make use of the harmonic approximation to bond stretch and angle bending, and there is a lack of consideration of the coupling among different energy terms. Of course, a number of force fields do include anharmonicity and cross terms,^7,8,10,11 but there is no systematic way of improving the functional form and its performance because little is known about their effects in biomolecular simulations. Empirical force fields can be developed by parametrizing against observed vibrational frequencies.^1,9,11 Thirdly, the treatment of many-body polarization effects suffers from difficulties in choosing the functional form and empirical parameters.^8,12–21,29 Just as atomic partial charges, there is no rigorous definition of atomic (or group) polarizabilities, nor is it measurable experimentally. There are many ways of describing molecular polarization, which of course is a well-defined quantity. Fourthly, charge transfer effects are ignored in all empirical force fields and there is no obvious way of including these effects.^22–25 Although the energy contributions are typically small in most applications, charge transfer can be important in certain situations.^23,24 Finally, the form of the empirical potentials is not appropriate for modeling chemical reactions involving bond formation and bond breaking or regions significantly away from the adiabatic ground state. Although specialized potentials26(a) or general functional forms26(b) can be developed to treat specific processes, they are restricted to applications to that particular case only. In view of these difficulties, it is of interest to consider alternative approaches to design a force field for biomolecular simulation and modeling that takes these effects into account. It is our hope that the present paper may contribute to this goal.

Combined quantum mechanical and molecular mechanical (QM/MM) potentials,^27–30 in principle, provide a reasonable solution to all the deficiencies mentioned above, at least for the region that is explicitly treated by quantum mechanics. The internal energy terms used in the force field as well as electrostatic interactions are described by the quantum chemical method used to represent the “QM” region. There is no ambiguity in the functional form, nor in the selection of internal degrees of freedom. Molecular polarization and charge transfer are naturally represented by electronic structure theory. And, of course, such a method can be used to model chemical reactions.³¹ Ten years ago, we described a method for treating many-body polarization effects in fluid simulations by combined QM/MM techniques.³² This method takes an different approach to treat polarization and electronic effects which do not have the problems in the classical polarizable force fields noted above.^8,12–21,29 We had envisioned developing an electronic structure based polarization force field, which hereafter is called the X-POL potential, for biomolecular simulations that naturally includes molecular polarization. In paper 1, we outlined the general principles and formalisms of this approach,³² and in the second paper, we demonstrated the feasibility of carrying out fluid simulations with such a polarizable potential function for liquid water.³³ This approach was also applied to liquid HF.³⁴ In this paper, we develop the theory for constructing a force field to treat polypeptides on the basis of the X-POL potential.

We emphasize that the goal here is the development of a molecular-orbital based force field, which is empirical and contains parameters; these parameters shall be optimized to reproduce the properties of a set of target molecular systems following the same philosophy in developing and validating molecular mechanics force fields. Yet, the fundamental elements including the bonded and electrostatic “terms” are determined by electronic structure theory. We do not aim at developing a linear scaling method for a fully solvated protein system,^35–37 although such a treatment is esthetically appealing and the X-POL potential can be developed into a quantum model for biopolymers. This indeed is the approach undertaken in ab initio molecular dynamics and Car-Parrinello molecular dynamics which have been successfully used in numerous applications.^38–40 However, these studies are limited to small systems with relatively short simulations. It would be difficult in the near future to extend the method to much larger systems such as a solvated protein or nucleic acid. Semiempirical models overcome the problem computational costs,^41–44 but they are considered inaccurate for general applications. Some time ago, Head-Gordon estimated that a Hartree-Fock (HF) or density functional theory (DFT) calculation of a protein of about 10000 atoms would only be remotely feasible with the assumption of 100-fold increase in computer speed and a true linear scaling in molecular size.³⁷ Such calculations in a single energy evaluation are interesting, which still represent a daunting task today. However, it is necessary to perform statistical mechanical simulations to obtain ensemble averages in order to compare the computed results with experiments. The need to repeat energy and gradients evaluations for millions of times is the computation bottleneck in electronic structure methods for condensed phase systems.

Clearly, the only possibility that HF or DFT methods can be used as a reliable force field in biomolecular simulations is to introduce approximations, keeping in mind that it is necessary to be able to evaluate the energy and gradients for a given configuration within a few seconds of time. To this end, an X-POL potential, which was also called the molecular-orbital derived empirical potential for liquids (MODEL),³² has been constructed for simulations of liquid water and hydrogen fluoride,^33,34 in which three approximations were made: (a) the wavefunction of the entire system is constructed as a Hartree product of the antisymmetric wavefunctions of individual molecules, (b) the interactions between any pair of residues are evaluated by combined QM/MM techniques, and (c) the electronic structure of individual molecules are treated by a semiempirical HF method. In this method, the electronic structure of each solvent molecule or amino acid residue in a polypeptide is influenced and polarized by the electrostatic field generated from the rest of the system, which in turn affects the wavefunctions of other molecules. Consequently, the total energy of the system is determined self-consistently. Clearly, many-body polarization effects are naturally described by electronic structure theory. The main advantage of this approach is that the treatment of molecular polarization as well as other energy components can be systematically improved by using ab initio HF, DFT or advanced techniques such as perturbation, multiconfiguration, and couple cluster theories.

The X-POL potential also differs from combined QM/MM approaches that treat the induced dipoles classically in the MM region.^{28,29,45–50} The difficulties and uncertainty of representing polarization in classical force field^8,12–21,29 still exists in these coupled QM/MM-pol methods, whereas the X-POL potential treats the entire system equally. Furthermore, charge transfer effects can easily be included in the X-POL potential, which would be exceedingly difficult in the classical treatment. The X-POL force field is designed as a quantum mechanical model for biomolecular simulations.

In what follows, we first review the X-POL potential for treatment of liquid systems without covalent-bond connection between molecules. Then, in section 3, we introduce the new theory for treating polypeptides in which covalent bonding connections between residues must be separated. Section 4 presents the algorithm and computational details, and Section 5 highlights the results and parameterization process. Finally, we summarize the major findings of this study and future perspectives.

2. Theoretical Background

For completeness, this section reviews the method presented in refs. ³² and ³³. The next section contains the new methodology developed in the present work. We first consider a system consisting of N molecules that are not covalently connected in a primary unit cell with periodic boundary conditions along with nearest image convention. For the sake of brevity, we assume this is a simple liquid system with identical solvent molecules such as liquid water; obviously there is no restriction for solutions and mixed solvents in the method presented below.³³ To focus our discussion, we assume that the readers are familiar with combined QM/MM methods. We make the first assumption that the wavefunction of the liquid system (Φ) is represented by a Hartree product of the antisymmetric wavefunctions of the individual molecules{Ψ_I;I = 1,…,N}:

$$\mathrm{\Phi }=\prod _{I=1}^N{\mathrm{\psi }}_I$$ (1)

where the individual molecular wavefunction is written as a Slater determinant of M doubly occupied molecular orbitals (MOs), {ϕ_i(I)} with 2M electrons in each molecule. As usual, the MOs are linear combinations of an atomic orbital basis set, {χ_μ}, spanning over the entire molecule, which are subjected to the orthonormal constraint:

$${\mathrm{\Lambda }}_{ij}(I)={\displaystyle \sum _{\mu \nu }{c}_{i\mu }}(I)c_{j\nu }(I)S_{\mu \nu }(I)-{\delta }_{ij}=0$$ (2)

where S_μν(I) is the overlap integral between atomic orbitals χ_μ and χ_ν in molecule I.

The assumption made in eq (1) neglects the exchange correlation interactions between molecules, thus, the entire system does not satisfy the Pauli exclusion principle, but this approximation is quite reasonable in the spirit of a force field development. To account for the short-range exchange repulsion and the long-range dispersion interactions, we use an empirical function to parametrically model these effects, and we adopt the popular Lennard-Jones potential:

$$E_{IJ}^{\nu dW}={\displaystyle \sum _{\alpha =1}^A{\displaystyle \sum _{\beta =1}^{B}4{\epsilon }_{\alpha \beta }}}\left[{\left(\frac{{\sigma }_{\alpha \beta }}{R_{\alpha \beta }}\right)}^{12}-{\left(\frac{{\sigma }_{\alpha \beta }}{R_{\alpha \beta }}\right)}^6\right]$$ (3)

where A and B are the number of atoms in molecules I and J, which are the same in this discussion, and the parameters ε_αβ and σ_αβ can be derived using the combining rules such that ε_αβ = (ε_αε_β)^1/2 and σ_αβ = (σ_α + σ_β)/2. ε and σ are atomic empirical parameters that are considered to have the same meaning and treatment as in a typical MM force field, and they depend on the specific functional type.

The Hamitonian of the system can be written as:

$$\widehat{H}={\displaystyle \sum _{I=1}^N{\widehat{H}}_I^o+\frac{1}{2}}{\displaystyle \sum _{I=1}^N{\displaystyle \sum _{J\ne 1}^N{\widehat{H}}_{IJ}}}$$ (4)

where ${\widehat{H}}_I^o$ is the electronic Hamiltonian of an isolated molecule in the gas phase, and ${\widehat{H}}_{IJ}$ describe the interactions between molecules I and J. The interaction Hamitonian can be expressed by eq (5):

$${\widehat{H}}_{IJ}({\mathrm{\psi }}_J)=-{\displaystyle \sum _{i=1}^{2M}{V}_i({\mathrm{\psi }}_J)}+{\displaystyle \sum _{\alpha =1}^A[Z_{\alpha }(I)V_{\alpha }({\mathrm{\psi }}_J)+E_{IJ}^{\nu dW}]}$$ (5)

Here, Z_α(I) is the nucleus charge of atom α in molecule I, V_t (Ψ_J) is the electrostatic potential of molecular J at either the electronic (t = i) or nuclear (t = α) positions of molecule I. The electrostatic potential due to molecule J is defined as follows:

$$V_t({\mathrm{\psi }}_J)=-{\displaystyle \int }\frac{d\mathbf{r}{\rho }_J(\mathbf{r})}{|{\mathbf{r}}_t-\mathbf{r}|}+{\displaystyle \sum _{\beta =1}^B\frac{Z_{\beta }(J)}{|{\mathbf{r}}_t-{\mathbf{R}}_{\beta }(J)|}}$$ (6)

where ρ_J (r) is the electron density of molecule J, derived from the molecular wavefunction, ρ_J (r) =|Ψ_J (r)|².

The total potential energy of the system is

$$E_{tot}=<\mathrm{\Phi }|\widehat{H}|\mathrm{\Phi }>-{\displaystyle \sum _{I=1}^N{E}_I^o}$$ (7)

where $E_I^o=<{\mathrm{\psi }}_I^o|{\widehat{H}}_I^o|{\mathrm{\psi }}_I^o>$ is the energy of molecule I in the gas phase with the wavefunction ${\mathrm{\psi }}_I^o,$ which has a constant value and is used here purely for setting the zero of energy of the condensed phase system corresponding to that of infinitely separated or non-interacting species.

In principle, eq (7) can be determined by standard HF theory with or without optimization of the instantaneous molecular wavefunction Ψ_I in the presence of all other molecules. Of course, the method above is not restricted to HF theory and can be equivalently written in the form of DFT or any other electronic structure methods. For exampled, Wesolowski and coworkers have used a frozen density functional method for large systems without optimization of the electron density of individual fragments.^51,52 The fragmental molecular orbital method developed by Kitaura and coworkers allows for fully optimization of the wave function.⁵³

Without further approximation, it is necessary to compute the two-electron integrals arising from different molecules, which would be too expensive for a force field. Fortunately, this problem can be adequately treated by a combined QM/MM approach, which is the second assumption of the X-POL potential. Here, the electronic integral in eq (6) is expressed as a multipole expansion on molecule J. The two-electron two-center Coulomb integrals can also be evaluated in exactly the same way as that described by Dewar and Thiel in semiempirical NDDO methods.⁵⁴ Alternatively, if we only use the monopole term, i.e., partial atomic charges, the interaction Hamiltonian can be simplified to

$${\widehat{H}}_{IJ}({\mathrm{\psi }}_J)=-{\displaystyle \sum _{i=1}^{2M}{\displaystyle \sum _{\beta =1}^B\frac{e·q_{\beta }({\mathrm{\psi }}_J)}{|{\mathbf{r}}_i-{\mathbf{R}}_{\beta }(J)|}}}+{\displaystyle \sum _{\alpha =1}^A{\displaystyle \sum _{\beta =1}^B\frac{Z_{\alpha }(I)q_{\beta }({\mathrm{\psi }}_J)}{R_{\alpha \beta }}}}+E_{IJ}^{\nu dW}$$ (8)

where q_β (Ψ_J) is the partial atomic charge on atom β of molecule J, fitted to reproduce the electrostatic potential of eq (6) from the wavefunction Ψ_J, and R_αβ is the distance between two atoms. Previously, we have shown that intermolecular interactions can be adequately described simply by scaling the Mulliken population charges in the simulation of liquid water.³³ In developing an X-POL force field for biopolymers, it is desirable to include at least the dipolar expansion terms.

With this treatment of the potential energy of eq (7) is variationally optimized to obtain the ground state potential energy of the system.

Recently, Gascon et al.⁵⁵ described a self-consistent space-domain decomposition method for computing electrostatic potentials of proteins. The method reported in that work appears to be the same as that described above except that Morokuma’s ONIOM and the 6-31G(d) basis set were used.^56,57 These authors do not appear to be aware of the method reported in references 32–34. Soon after the publication of ref 32, Field also described a similar implementation making use of both the AM1 and HF/STO-3G method.⁵⁸

3. The Electronic-Structure Polarization Force Field for Proteins

For biomolecular systems such as proteins and nucleic acids, the division of the entire system into individual molecular fragments is not obvious because each residue is covalently connected to its neighbors.^29,59–64 In this case, it is necessary to decide the basic unit for the “molecular partition” and to consider the effects of charge delocalization between neighboring fragments. In this section, we present a novel procedure for constructing a force field based on molecular orbital theory, for energy minimization and dynamics simulations of proteins.

3.1. Quantum Mechanical Model

Before we begin constructing the X-POL force field, a critical decision must be made on the choice of a specific quantum mechanical model to represent the system. Of course, it would be ideal to use an accurate electronic structure theory such as CCSD(T) or a well-tested DFT model along with a large basis set. However, these methods are not practical in the foreseeable future, and it is not clear if DFT methods can yield accurate results without rigorous treatment of dispersion interactions. The most practical choice is semiempirical quantum mechanical models coupled with proper parameterizations, such as the self-consistent extended Huckel theory (SC-EHT),^66–67 and the formalisms based on the neglect diatomic differential overlap (NDDO) approximation.⁴¹ The recent parameterization of the self-consistent charge density functional tight-binding (SCC-DFTB) model,^68,69 yielded promising results; however, the procedure and the use of tabulated electronic integrals make it difficult for force field development. It would be of interest to improve the atomic parameters in the SC-EHT method. We find that the general formalisms used in the MNDO,⁷⁰ AM1⁴² and PM3⁴³ models are most appealing because the theory is well-defined and has been extensively tested. The semiempirical formalisms contain atomic parameters, and the total number of parameters are no more than those associated with a given atom type in the current empirical force fields.

We anticipate that the semiemipirical parameters will be fully optimized for each functional group in the amino acid residues, keeping in mind that we are interested in developing a force field rather than a “general” QM model. The parameterization will necessarily include optimizations of the molecular geometries (including radial distribution functions), energies (such as heats of formation), electronic structural properties (such as molecular dipoles, electron affinities, and ionization potentials), spectroscopic data (for example, vibrational frequencies, NMR chemical shifts), and condensed phase properties (such as heats of vaporization, density, diffusion constants, relaxation time, and solvation free energies) among others for a set of selected compounds representing different functionalities. Of course, the X-POL force field can be systematically improved by increasing the level of the QM theory employed. It is expected that the parameterization process will become less dependent on fitting against experimental data (or high-level QM results) as the level of the QM model increase. In this paper, our focus is on the theory for constructing a polypeptide chain represented by a QM model. We adopt the Austin Model 1 (AM1)⁴² method without further optimization for specific functional groups, except the boundary atoms discussed below.

3.2. System Partition and Boundary Definition

We consider a system of polypeptide of N residues, which is divided into N subunits or fragments. The interactions among different subunits are determined through a combined QM/MM algorithm. It would be natural to use the formal chemical structure of each amino acid residue as the “QM” subunit; however, it is more appropriate to keep intact the resonance delocalization in a peptide bond in electronic structure calculations. Thus, we adopt the “peptide unit” convention defined in the IUPAC nomenclature, (Pure Appl. Chem., 1974, 40, 291–308. http://www.chem.qmul.ac.uk/iupac/misc/ppep1.html) which consists of the −CHR−CO−NH− atoms. For our computational purpose, which will become clear below, we make the sequence separation across the C_α atoms of adjacent residues, as illustrated in Figure 1. Thus, the Ith peptide unit contains the atoms $-{\mathrm{C}}_{\alpha }^I{\mathrm{R}}^I-\text{CO}-\text{NH}-{\mathrm{C}}_{\alpha }^{I+1}\mathrm{H}-,\text{in which}\text{NH}-{\mathrm{C}}_{\alpha }^{I+1}\mathrm{H}$ belong to the (I+1)th amino acid residue. In our definition, the C_α atoms are equally shared by adjacent peptide units. In the following, we follow the IUPAC recommendation to simply refer the “peptide unit” as a “residue” when no ambiguity arises.

Figure 1.

Definition of peptide units and the division of the C_α boundary atom. Two quantum mechanical fragments are highlighted in green and red, corresponding to residues I−1 and I.

In this partition scheme, each residue (peptide unit) shares two C_α atoms with the neighboring residues, except the N- and C-termini. We call these atoms as the boundary atoms (Figure 1). With the use of a semiempirical QM model, the boundary carbon atom has the standard valence s and p orbitals and four valence electrons. Adopting the generalized hybrid orbital (GHO) approach for the treatment of a QM-MM boundary in combined QM/MM calculations,^59,60 we make the same transformation of the sp atomic orbitals (AOs) on the boundary atom into a set of four orthonormal hybrid orbitals (HOs), on the basis of the local geometry about the C_α atom:

$$\left(\begin{array}{l}{\eta }_1^I\hfill \\ {\eta }_2^I\hfill \\ {\eta }_3^I\hfill \\ {\eta }_4^I\hfill \end{array}\right)={[{\mathbf{T}}_{\mathrm{B}}(I)]}^{-1}\left(\begin{array}{l}{s}_1^I\hfill \\ p_x^I\hfill \\ p_y^I\hfill \\ p_z^I\hfill \end{array}\right)$$ (9)

where the superscript I specifies that the orbitals are located on atom C_α(I), and the subscript B indicates that the transformation matrix has dimensions of (4 × 4) for the boundary atom. The transformation matrix in eq (9) is defined by the geometry of the four atoms bounded to the boundary atom and their local coordinates and its expression has been given in ref. 60. We note that the hybrid orbitals are orthonormal by construction, and they are also orthogonal to all other AO basis functions due to the NDDO approximation. In ab initio HF theory, the HOs need to be orthogonalized to the rest of the basis functions and procedures have been described previously.^61,63

In defining the HOs in eq (9), the transformation matrix, T_B(I), is constructed in such a way that the orientations of the four HOs are pointing sequentially towards the carbonyl carbon, the C_β(I) (or H_α2 for glycine) atom of the sidechain, the amino nitrogen of the (I−1)th peptide unit, and the H_α atom (Figure 2). Therefore, there are two boundary atoms and four boundary hybrid orbitals in the Ith residue in the present QM partition; the first two hybrid orbitals, ${\eta }_1^I\text{and}{\eta }_2^I,$ on the C_α(I) atom, and the third and the fourth hybrid orbitals, ${\eta }_3^{I+1}\text{and}{\eta }_4^{I+1},$ on the C_α(I + 1) atom. Assuming that there are N_I atomic orbital basis functions on all other atoms in residue I, we have a total of N_I + 4 basis functions, called active orbitals, that are mixed atomic and hybrid orbitals to form the MOs of the subsystem. We note that, similar to the GHO method,^59–62 the remaining four hybrid orbitals, two from C_α(I) and two from C_α(I + 1), will also be used in constructing the Fock matrix, but they are not variationally optimized in self-consistent field (SCF) calculations of residue I.

Figure 2.

Assignment and sequence of hybrid orbitals on the boundary atom. Hybrid orbitals in red and green belong to different QM fragments.

3.3. Potential Energy Surface and Procedure

In optimizing the antisymmetric wavefunction Ψ_I, of residue I, we note that this QM subunit is embedded in the electric field of classical partial charges (or multipoles if higher order of density expansion is used) of the rest of the system, although they are also treated quantum-mechanically. Thus, in principle, the computational procedure is identical to that used in the GHO method for combined QM/MM systems,^59,60 except that two “active” hybrid orbitals from each boundary atom participate in the SCF optimization. Specifically, if the density matrix for residue I is P^H(I), which has dimensions of [N_I + 4] × [N_I + 4], the total interaction energy between residue I and the rest of the system is

$$\begin{array}{cc}{E}_I=\hfill & {\displaystyle \sum _{\mu \nu }{P}_{\mu \nu }^{\mathrm{H}}(I)H_{\mu \nu }^{\mathrm{H}}(I)+1/2{\displaystyle \sum _{\mu \nu }{\displaystyle \sum _{\lambda \sigma }{P}_{\mu \nu }^{\mathrm{H}}}(I)P_{\mu \nu }^{\mathrm{H}}(I)W^{\mathrm{H}}(\mu \nu ,\lambda \sigma )}+}\hfill \\ & +E_{IP}^{nuc}+E_I^{nuc}-E_I^o\hfill \end{array}$$ (10)

where the superscript H indicates that all matrix elements are given in the mixed AO and HO basis, $H_{\mu \nu }^{\mathrm{H}}(I)$ is an element of the “effective” one-electron integral matrix that include the interaction Hamiltonian of eq (8), W^H (μν,λσ) is the usual two-electron integrals including both Coulomb, (μν,λσ), and exchange, (μλ,νσ), terms, and $E_I^{nuc}\text{and}{E}_{IP}^{nuc}$ are the nuclear Coulombic energies within residue I and that with the rest of the protein system, respectively. The effective Hamiltonian matrix element $H_{\mu \nu }^{\mathrm{H}}(I)$ is given below:^59,60

$$\begin{array}{ll}{H}_{\mu \nu }^{\mathrm{H}}(I)=\hfill & H_{\mu \nu }^{\mathrm{o},\mathrm{H}}(I)+J_{\mu \nu }^{\mathrm{H}}(I)+\frac{1}{2}{\displaystyle \sum _{i,j=3}^4{P}_{{\eta }_i{\eta }_j}^{\mathrm{H}}(I)W^{\mathrm{H}}(\mu \nu ,{\eta }_i^I{\eta }_j^I)}+\hfill \\ \hfill & +\frac{1}{2}{\displaystyle \sum _{i,j=1}^2{P}_{{\eta }_i{\eta }_j}^{\mathrm{H}}(I+1)W^{\mathrm{H}}(\mu \nu ,{\eta }_i^{I+1}{\eta }_j^{I+1})}\hfill \end{array}$$ (11)

where η_i specifies the boundary auxiliary orbitals from residues (I) and (I+1) that are not optimized in the SCF for residue I, $H_{\mu \nu }^{\mathrm{o},\mathrm{H}}(I)$ is the standard one-electron matrix for residue I, $J_{\mu \nu }^{\mathrm{H}}(I)$ is the “QM/MM” one-electron integral due to the first term of eq (8) summed over all other residues other than I, and $P_{{\eta }_i{\eta }_j}^{\mathrm{H}}(I)\text{and}{P}_{{\eta }_i{\eta }_j}^{\mathrm{H}}(I+1)$ are the populations of the auxiliary hybrid orbitals specified by eq (11).

The total potential energy of the entire system is

$$E_{tot}=\frac{1}{2}{\displaystyle \sum _{I=1}^N{E}_I}$$ (12)

We further define the interaction energy between residues I and J by^32,33

$$E_{IJ}=\frac{1}{2}[<{\mathrm{\psi }}_I|{\widehat{H}}_{IJ}|{\mathrm{\psi }}_I>+<{\mathrm{\psi }}_J|{\widehat{H}}_{JI}|{\mathrm{\psi }}_J>]$$ (13)

This is necessary to ensure that E_IJ = E_JI because in combined QM/MM calculations the two integrals in the bracket parentheses may not be identical.

Although the wavefunction of eq (1) can be variationally optimized for all residues simultaneous in each SCF cycle, it is more convenient to sequentially optimize the wavefunction of each residue, by keeping the partial charges (derived from the corresponding wavefunctions) of the rest of the system fixed. Thus, we have a double iterative SCF procedure: (1) the SCF optimization of the wave function of each residue, and (2) the SCF optimization of the mutual polarization of the entire system. Specifically, after the individual wavefunctions for all residues are converged, which constitute one iterative cycle in the “system” SCF, we check the convergence of the total energy of the system in eq (11). This is repeated until the total energy is converged to a given tolerance. This double-SCF procedure has been used previously in our treatment of liquid water in Monte Carlo simulations; typically less than 5 system iterations are sufficient to achieve convergence.³³

4. Computational Details

The computational procedure of the X-POL force field follows roughly the same approaches outlined in references 32 and 33. However, there are several new aspects that need be defined here. It is clear that eq (11) requires the density matrix elements, $\{P_{{\eta }_i{\eta }_j}^{\mathrm{H}}(I);I=1,\cdots ,N\},$ for the auxiliary orbitals on the two boundary atoms in each residue during SCF optimizations. In the original GHO method developed for QM/MM calculations, the density is obtained by transferring the partial atomic charge on the boundary carbon from the MM force field, to the three auxiliary orbitals, plus the density of one electron.⁵⁹ In the X-POL potential, there are two hybrid orbitals from each boundary atom and the nuclear charges are not adjusted as in QM/MM calculations; however, the major difference here is that these auxiliary orbitals are also active orbitals in the neighboring residues, which are fully optimized in SCF calculations. Consequently, the “auxiliary” densities are no longer invariant, but they are dynamically changing due to the change of molecular geometry and instantaneous charge polarizations. Furthermore, these optimized densities provide the necessary input for the auxiliary orbitals in the neighboring residues.

The next critical issue is to define an appropriate procedure for determining the partial charges for all other residues in eq (8) when the wavefunction of residue I is being optimized. A number of possibilities are available, including Mulliken population charges,⁷¹ electrostatic potential fitted charges,⁷² and the class IV (CM2) charges proposed by Cramer and Truhlar.^73–76 A good charge mapping procedure will ensure that “QM/MM” interactions be accurately determined in comparison with experimental data – through parameterization of the force field. However, special care must be taken in any charge mapping procedure such that the charge density to be used as the auxiliary density is appropriately neutralized by the atomic charges in the subunit where these “auxiliary orbitals” reside and are “active”. This can be done by imposing a charge constraint if electrostatic potential fitting procedure is used. In the present study, which is aimed at demonstrating the feasibility of the X-POL force field, we adopt the Mulliken population analysis, which properly divides the charge population between the “auxiliary orbitals” (note that they are “active orbitals” in the fragment where they are determined) and the rest of the QM subunit. Clearly, in future development of a reliable force field, both the “classical” representation of the electrostatic potential from a given wavefunction in terms of multipole expansions and the specific method for obtaining these multipoles shall be a primary focus of study.

Thirdly, in the X-POL treatment, short-range exchange repulsion and long-range dispersion forces are represented by the traditional Lennard-Jones potential. Obviously, these are empirical terms that must be properly optimized against experimental and high-level ab initio results on bimolecular interactions and liquid properties including density. We have demonstrated in Monte Carlo simulations of liquid water using the X-POL approach that the van der Waals parameters in the Lennard-Jones potential can be similarly adjusted as in the development of empirical potentials, e.g., the TIP3P and TIP4P models. In the present study, we employ the corresponding parameters in the CHARMM22 force field without further modification. Note that it might be tempting to use “pure” electronic structure methods to determine the repulsive and dispersive energies; however, this would be futile in force field development if computational speed is taken into consideration.

We present an algorithm for optimization of the individual molecular wavefunction with the GHO boundary treatment.⁵⁹ The convergence of the entire system is achieved by an iterative SCF procedure outline below.

1. Determine the transformation matrices {T_t (I);I = 1,…,N} for the interconversion between the AOs and a set of mixed AOs and HOs, ${\mathbf{C}}_{\mathrm{I}}^{\text{HO}}={\mathbf{T}}_{\mathbf{t}}{(I)}^{-1}{\mathbf{C}}_I^{\text{AO}},$ where the subscript “t” specifies that the matrix has dimensions of [N_I + 8] × [N_I + 8]. Compute the [N_I + 4] × [N_I + 4]-dimensional density matrix, {P^H (I);I = 1,…,N} using the active HOs for each residue.

2. For each residue, perform SCF optimization sequentially, beginning from residue I = 1.

3. For residue I, expand P^H (I) into full dimension by adding the auxiliary density matrix elements, and transform it into the AO basis ${\mathbf{P}}_{\mathbf{t}}^{\text{AO}}(I)={[{\mathbf{T}}_{\mathbf{t}}{(I)}^{-1}]}^{+}{\mathbf{P}}_{\mathbf{t}}^{\text{HO}}(I)[{\mathbf{T}}_{\mathbf{t}}{(I)}^{-1}].$ Construct the full Fock matrix ${\mathbf{F}}_{\mathbf{t}}^{\text{AO}}(I)$ in AO basis, including QM/MM interaction terms. Transform ${\mathbf{F}}_t^{\text{AO}}(I)\text{into HO basis},{\mathbf{F}}_{\mathbf{t}}^{\text{HO}}(I)={[{\mathbf{T}}_{\mathbf{t}}(I)]}^{+}{\mathbf{F}}_{\mathbf{t}}^{\text{AO}}(I)[{\mathbf{T}}_{\mathbf{t}}(I)].$ Remove the columns and rows corresponding to the auxiliary hybrid orbitals to yield the “active” Fock matrix F^AO(I), which is of [N_I + 4] × [N_I + 4]-dimension. Diagonalize F^AO(I) and compute the energy and new density matrix P^H (I).

4. Test convergence. If not satisfied, go to step (c). If convergence is met, compute new partial charges from the optimized wave function and set the densities of the active HOs as auxiliary densities for other SCF optimizations. Incrementing I by one until I = N, and then, go to step (c).

5. Compute the total energy, and test convergence. If not satisfied, go to step (b).

We point out that the matrices transformations in step (c) are quite simple because it only involves orbitals on the boundary atoms (a total of 8 orbitals). Thus, it takes a negligible amount of computer time. As can be seen from the algorithm above, the Fock matrix construction and diagonalization are performed for each individual residues, and there are a total of N separate SCF calculations of the size of each residue in each system iteraction. In our experience on the simulation of liquid water, the total number of system iterations does not increase, perhaps by one or two cycles, with increased system size. Thus, the total computational time is linear scaling by $S\times N\times O(N_{\text{max}}^3),$ where S is the number of iterations in system SCF, and $O(N_{\text{max}}^3)$ is the computing efforts for the largest residue. The difference beween electronic structure calculations for a molecule of the size of ${\displaystyle {\sum }_I^N{N}_I}$ orbitals and that of N separate calculations of the size of N_max is obvious because the former would scale as $O({[{\displaystyle {\sum }_I^N{N}_I}]}^3)$ due at least to diagonalization.

5. Results and Discussion

To illustrate the feasibility of the X-POL force field, we present test cases to illustrate the procedure for optimizing parameters associated with the boundary atoms, and an application to a tetrapeptide model interacting with a single water molecule. Here, we have assumed that the semiempirical AM1 model is adequate for treating the individual residues; obviously, the AM1 model itself is not satisfactory for constructing a force field for protein simulations. However, there is little doubt that they can be parameterized to accurately treat specific functional groups and interactions. The parameterization of the NDDO-based semiempirical QM model for different functional groups and atom types shall be left for future exploration.

5.1. Parameterization of Boundary Atoms

To parameterize the semiempirical force field for the boundary carbon atom and to assess its performance, we consider three model compounds; propane, 2-methyl-propane (isobutene), and 2,2-dimethyl-propane (neopentane). In each case, a single boundary atom is defined at the C₂ atom position, and two fragmental QM subunits are treated. We aim at the selection of a minimum number of model compounds in the parameterization process to achieve transferability by satisfying key quantum chemical requirements.⁵³ These include (1) the balance of electronegativity, (2) the properties of chemical bonding, and (3) the conformational potential energy profiles involving the boundary atom. Our experience in the development of the GHO methods, at the semiempirical level,^59,60 semiempirical SCC-DFTB treatment,⁶² ab initio HF level,61(a)^,62 and DFT method,61(b) show that if the electron-withdrawing power and the formation of the chemical bonds are adequately balanced with the QM model that the boundary atom mimics, the empirical parameters for the boundary atoms are fully transferable, just as all other standard semiempirical parameters or basis sets.

Taking the three criteria listed above into consideration, we found that we only need to modestly modify the parameters of the original AM1 Hamiltonian for carbon. We focused on the one-center core integrals U_ss and U_pp and the resonance integrals β_s and β_p, the latter of which are closely related to chemical bonding (see below). We slightly decreased these values to obtain the best overall results, but it is closer that of the original AM1 value. Note that in the full parameterization process of the X-POL potential, the balance with all other atoms will also be consistently considered. The parameters for the boundary carbon atom are listed in Table 1 along with the standard AM1 values and those used in the GHO model.⁵⁹

Table 1.

Modified parameters for the carbon boundary atom in the present MODpol force field along with the original AM1 values and those used in the GHO model. All values are given in eV.

Parameters	AM1	GHO	MODpol
βs	−15.715783	−5.500524	−12,85205
βp	−7.719283	−14.666638	−5,680080
Uss	−52.028658	−52.028658	−49,774256
Upp	−39.614239	−38.703112	−39,573436

The semiempirical parameters for the resonance integrals, β_s and β_p, are most directly responsible for chemical bonding and molecular geometry. The optimized parameters in table show that the X-POL potential has very similar values compared with the original AM1 parameters. This is in contrast to the GHO method,⁵⁹ which does not have the double self-consistent field treatment to optimize the auxiliary hybrid orbital densities. The bond lengths and selected bond angles of propane, 2-methyl-propane and 2,2-dimethyl-propane, optimized using the X-POL potential and the AM1 method are given in Table 2 (see Scheme 1 for atom assignment). The key parameters to be examined are the bond lengths and bond angles associated with the boundary atom, C_B, which is placed at the C2 position in all three cases. The present comparison is best made with the values optimized using the AM1 model, rather than the experimental or high-level ab initio results, because the main purpose is to evaluate the possibility to parameterize the boundary atom to reproduce the results from the QM model used to describe the QM subunits. For the nine C_B-C bonds and three C_B-H bonds in these three model compounds, the average unsigned error is 0.004 and 0.003 Å, respectively. The agreement with the AM1 results is good. Bond angles see somewhat greater variations mainly because the way that the hybrid orbitals are defined. In the original GHO approach, the hybrid orbital pointing towards the QM fragment is defined based on the local (instantaneous) geometry of the other (MM) three bonds connected to the boundary atom.⁵⁹ The remaining three auxiliary hybrid orbitals are created by using Schmidt orthorgonalization and equal hybridization.⁶⁰ In the present application, we have adopted the same definition and partitioning scheme for the hybrid orbitals, but of course, all hybrid orbitals should be treated equally based on the respective local geometry followed by a Lowdin-type orthorgonalization. The latter approach would resolve the slight imbalance caused by the hybridization method. Nevertheless, the optimized bond angles are still reasonable for the present test purposes.

Table 1.

Optimized bond lengths (Å) and bond angles (degrees) using the X-POL potential and the full AM1 method.

	propane		2-methylpropane		2,2-dimentylpropane
bond	AM1	X-POL	AM1	X-POL	AM1	X-POL
CB-C1	1,516	1,523	1,523	1,524	1,527	1,523
CB-C3	1,516	1,526	1,523	1,524	1,527	1,526
CB-C4(H)	1,118	1,123	1,523	1,524	1,527	1,523
CB-C5(H)	1,118	1,120	1,121	1,118	1,527	1,519
H11-C1	1,114	1,115	1,114	1,115	1,114	1,115
H12-C1	1,114	1,113	1,114	1,114	1,114	1,114
H13-C1	1,114	1,113	1,114	1,113	1,114	1,114
H31-C3	1,114	1,115	1,114	1,114	1,114	1,114
H32-C3	1,114	1,113	1,114	1,115	1,114	1,115
H33-C3	1,114	1,113	1,114	1,114	1,114	1,114
H41-C2			1,114	1,113	1,114	1,114
H42-C4			1,114	1,115	1,114	1,115
H43-C4			1,114	1,113	1,114	1,114
H51-C5					1,114	1,115
H52-C5					1,114	1,114
H53-C5					1,114	1,114
angle
C1- CB-C3	111,87	107,25	110,78	114,75	109,5	114,6
C1- CB-C4			110,96	107,34	109,5	107,2
C1- CB-C5					109,5	106,5
C3- CB-C4			110.78	107,25	109,5	107,3
C3- CB-C5					109,5	106,7
C4- CB-C5					109,5	114,7

Scheme 1.

Atom numbers assigned to the three alkanes which are separated into two quantum mechanical fragments across a boundary atom C_B.

On the other hand, the fundamental criterion necessary to ensure transferability of these atomic parameters for boundary atoms is the balance of the electron-withdrawing power of the boundary atom with that of the QM model that it mimics (AM1 in the present case). Therefore, the boundary atom must have the same electronegativity as that of an “AM1 carbon” atom so that there is no charge transfer between two identical groups. The most relevant parameters in the semiempirical theory are the one-center U_ss and U_pp terms, which are optimized in connection with the resonance integral parameters (as they are not independent in energy calculations). We found that it is possible to achieve this goal by only optimizing these four parameters listed in Table 1. This is illustrated by the computed Mulliken population charges for the three alkane model compounds. It perhaps should be emphasized here that the Mulliken population⁷¹ is in fact the best charge analysis to examine the balance of the electron-withdrawing abilities of different elements or between atoms of the same type but they are treated differently (AM1 vs. GHO).

Ideally, there is no net charge transfer between two neighboring groups across the boundary atom in the X-POL potential, although slight variation is inevitable since the boundary atom is, after all, an approximation to the original QM method. Propane is used as the primary target in the parameterization and the goal is to have as little charge transfer as possible between two fragments via C_B. Table 3 shows that the sum of the total charges of the two QM fragments are nearly the same (0.080 a.u.) both from AM1 and the X-POL calculations and the partial charge on the boundary carbon only differ by 0.001 a.u (Scheme 1). To remove the effect of the hydrogen atoms on the C_B atom, which have not been reparameterized, we examine the second symmetric system, neopentane. The unrestrained AM1 calculation yields a total net charge of 0.030 a.u. for two methyl groups, which may be compared to values of 0.026 and 0.027 a.u. from the X-POL potential. Importantly, the two fragments are reasonably balanced. The small different among the individual methyl groups is again due to the definition of the hybrid orbitals for the boundary atom, which are not completely equivalent. For isobutene, the difference between the two QM fragments is 0.060 a.u. more positive for one methyl group and an H_B than two methyl groups from full AM1 calculations, whereas the difference is 0.059 a.u. The agreement between AM1 and X-POL partial charges on the C_B atom is also good, which shows the absolute amount of charge imbalance between the boundary atom and the standard carbon.

Table 3.

Mulliken population charges (a.u.) obtained using the X-POL potential and the full AM1 method.

	propane		2-methylpropane		2,2-dimentylpropane
bond	AM1	X-POL	AM1	X-POL	AM1	X-POL
CB	−0,160	−0,159	−0,111	−0,107	−0,060	−0,054
C1	−0,210 (0.004)	−0,230 (0.003)	−0,206 (0.010)	−0,223 (0.012)	−0,202 (0.015)	−0,230 (0.013)
H11	0,071	0,072	0,072	0,072	0,072	0,072
H12	0,071	0,084	0,07203	0,085	0,072	0,086
H13	0,071	0,077	0,072	0,078	0,072	0,086
C3	−0,210 (0.004)	−0,235 (−0.003)	−0,206 (0.010)	−0,223 (−0.001)	−0,202 (0.015)	−0,230 (0.007)
H31	0,071	0,072	0,072	0,085	0,072	0,085
H32	0,071	0,083	0,072	0,073	0,072	0,072
H33	0,071	0,077	0,072	0,077	0,072	0,086
C4 (H)	0,076	0,076	−0,206 (0.010)	−0,242 (0.012)	−0,202 (0.015)	−0,236 (0.013)
H41			0,072	0,084	0,072	0,085
H42			0,072	0,073	0,072	0,073
H43			0,072	0,084	0,072	0,085
C5 (H)	0,076	0,083	0,081	0,084	−0,202 (0.015)	−0,225 (0.020)
H51					0,072	0,072
H52					0,072	0,086
H53					0,072	0,086

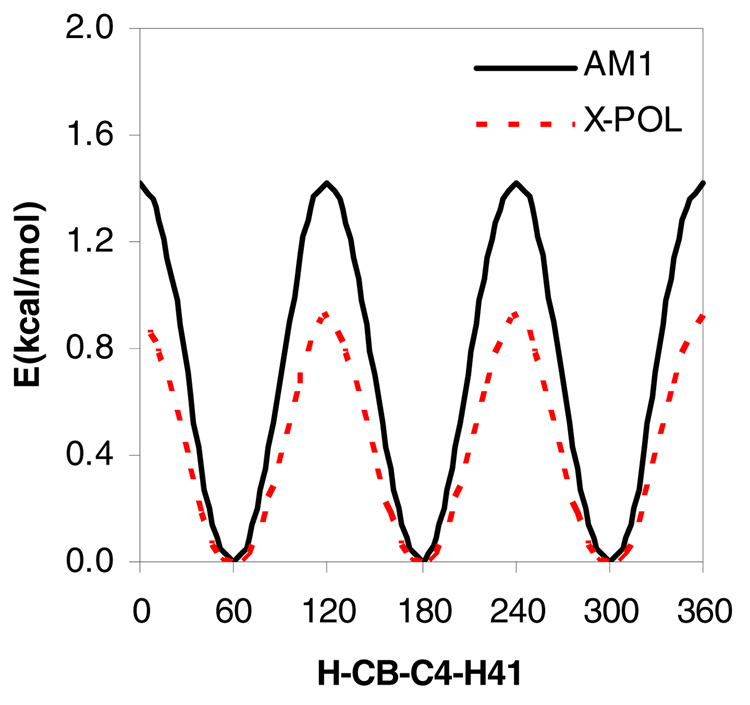
The torsional potential energy profiles for isobutene about a C-C dihedral are illustrated in Figure 3. The torsional energy from the X-POL potential has contributions from “pure” QM, QM/MM, and “pure” MM (van-der Waals) terms, and the computed barrier height is about 0.5 kcal/mol lower than the full AM1 energy. This trend has been observed in the GHO boundary approach,⁵⁹ and this difference is easily corrected by adjusting the semiempirical method or by including a classical torsional term. The latter scenario is probably a simple choice for constructing an empirical force field, and this would be the only internal bonding terms required in the X-POL potential.

Figure 3.

Torsional potential energy profiles for 2-methylpropane (isobutene) about the H22-CB-C4-H41 dihedral angle from AM1 and X-POL optimizations. Energies are in kcal/mol and dihedral angles in degrees.

5.2. Glycine and Glycine-dipeptide

To examine the possibility that the X-POL potential can be applied to proteins, we optimized the structures of glycine and glycine dipeptide, which are compared with the full original AM1 calculations. Note that the main goal here is to show that the boundary parameters optimized above are transferable to polypeptides and the development of the X-POL potential will involve full optimization of the QM model itself for different functional groups. Listed in Table 4 are computed partial atomic charges for glycine when the boundary atom is placed on the C_α atom with the first hybrid orbital pointed either towards the carbonyl carbon (C_α-C) or towards the amino nitrogen (C_α-N), as the current definition of the hybrid orbitals still does not yield exactly equivalent hybridizations. The results are compared with the AM1 values, while geometrical parameters are presented in Figure 4.

Table 4.

Mulliken population charges (a.u.) for glycine obtained using the X-POL potential and the full AM1 method.

Atom	AM1	X-POL
		Cα-C	Cα-N
N	−0,349	−0,350	−0,348
HT1	0,157	0,128	0,126
HT2	0,151	0,180	0,160
Hα1	0,122	0,108	0,120
Cα	−0,047	−0,056	−0,067
Hα2	0,085	0,126	0,120
C	0,302	0,266	0,283
OT1	−0,342	−0,374	−0,355
OT2	−0,314	−0,282	−0,291
HO2	0,236	0,254	0,252

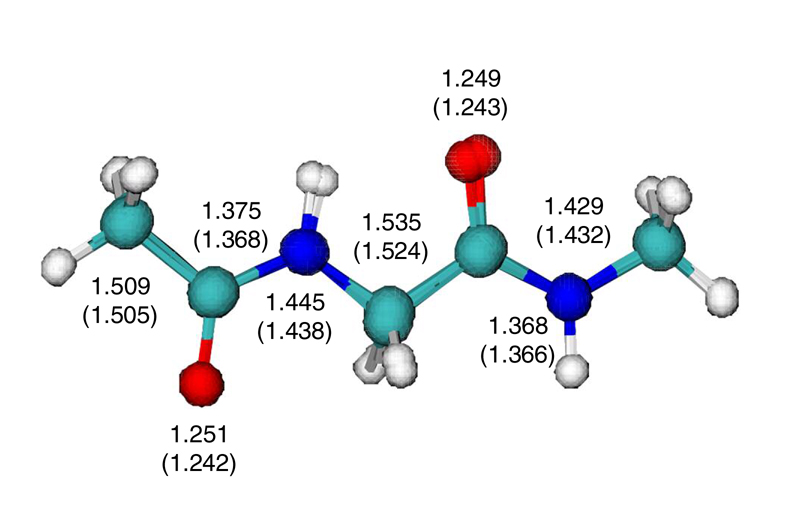
Figure 4.

Superposition of the optimized structures using the AM1 and the X-POL potentials for glycine dipeptide. Bond lengths in angstroms are given for the X-POL potential and for the AM1 model in parentheses.

Overall the partial charges show reasonable transferability. The amino group has a total net partial charge of −0.041 a.u. from AM1, whereas it is −0.042 and −0.062 a.u. from the X-POL potential when the hybrid orbitals are defined based on the C_α-C vector and the C_α-N vector, respectively. For the carboxyl group, the total net charges are −0.136, −0.111 and −0.118 a.u. from AM1, X-POL (C_α-C bond) and X-POL (C_α-N bond), respectively. The difference is only about 0.02 a.u. for such a strong electron-withdrawing group. Overall, there is little charge transfer between the two QM fragments for both partition schemes in comparison with the AM1 partial charges.

The optimized structure of glycine dipeptide for the extended conformation is illustrated in Figure 4 along with some selected bond lengths from the X-POL and AM1 potentials. Overall, the structural agreement is excellent with root-mean-square difference of 0.007 Å for bonds shown in Figure 4. The combined group charges are given in Table 5 and the trend of charge polarization is adequately retained in the X-POL potential and the charge delocalization across the boundary atom is also good.

Table 5.

Mulliken population charges (a.u.) for glycine dipeptide obtained using the X-POL potential and the full AM1 method.

atom/group	AM1	X-POL
		Cα-C	Cα-N
CH3	0.060	0.060	0.058
CO	−0.067	−0.091	−0.094
NH	−0.130	−0.132	−0.142
Hα1	0.111	0.096	0.108
CB	−0.039	−0.002	−0.013
Hα2	0.111	0.128	0.121
CO	−0.085	−0.133	−0.111
NH	−0.147	−0.123	−0.124
CH3	0.185	0.195	0.197

6. Summary

An electronic structure-based polarization potential, which is called the X-POL potential, has been described for the purpose of constructing an empirical force field for modeling polypeptides. The X-POL potential takes an entirely different philosophical approach towards the development of a force field and the treatment of electronic polarization and charge delocalization. The internal, bonded interactions are fully represented by an electronic structure theory augmented with some empirical torsional terms. Non-bonded interactions are modeled by an iterative, combined quantum mechanical and molecular mechanical method, in which the molecular mechanical partial charges are derived from the molecular wave functions of the individual fragments. In this paper, the X-POL potential is illustrated by making use of the neglect of diatomic differential overlap (NDDO) approximation and the AM1 model as the quantum mechanical method, without further parameterization for specific functional groups. The main purpose of this study is to demonstrate the feasibility of such an electronic structure force field, and to develop a practical and well-defined method for separating a polypeptide chain into peptide units. The boundary is treated following the ideas of the generalized hybrid orbital (GHO) technique developed for the treatment of QM and MM boundaries, and extended to bridge two QM regions in the X-POL potential. The parameterization procedure and philosophy for the boundary treatment between QM fragments in the X-POL potential is documented and tested by a number of simple compounds.

The X-POL model presented here is an empirical force field, although it is based on quantum mechanical formalisms. If one finds that a particular QM model used or the approximations made are inadequate to treat certain properties, for example, the torsional potential energy profile about a single bond rotation, one can include a purely empirical energy term such as the sine and cosine function series in the current force fields. Although this might be deemed ad hoc, the method is nevertheless systematic in that one can always seek for a better, more accurate QM representation of the individual residues such that these empirical functional terms can be eliminated.

In two forthcoming papers, we describe the analytical energy gradient techniques for the X-POL potential and an application to a solvated protein. The exact treatment and construction of individual force fields in the future may differ from the method presented here, but the general direction seems to be clear. We envision that the next generation of force fields for biomolecular polymer simulations will be developed based on electronic structure theory, which is one way of properly define and treat many-body polarization and charge delocalization effects.