Description of microcolumnar ensembles in association cortex and their disruption in Alzheimer and Lewy body dementias

Abstract

The cortex of the brain is organized into clear horizontal layers, laminae, which subserve much of the connectional anatomy of the brain. We hypothesize that there is also a vertical anatomical organization that might subserve local interactions of neuronal functional units, in accord with longstanding electrophysiological observations. We develop and apply a general quantitative method, inspired by analogous methods in condensed matter physics, to examine the anatomical organization of the cortex in human brain. We find, in addition to obvious laminae, anatomical evidence for tightly packed microcolumnar ensembles containing approximately 11 neurons, with a periodicity of about 80 μm. We examine the structural integrity of this new architectural feature in two common dementing illnesses, Alzheimer disease and dementia with Lewy bodies. In Alzheimer disease, there is a dramatic, nearly complete loss of microcolumnar ensemble organization. The relative degree of loss of microcolumnar ensembles is directly proportional to the number of neurofibrillary tangles, but not related to the amount of amyloid-β deposition. In dementia with Lewy bodies, a similar disruption of microcolumnar ensemble architecture occurs despite minimal neuronal loss. These observations show that quantitative analysis of complex cortical architecture can be applied to analyze the anatomical basis of brain disorders.

Anatomical investigations into the organization of cortical structure have relied on tools similar to those used by the great neuroanatomists of the 19th and early 20th centuries—namely, an appreciation of neuronal size and packing density in lamina, supplemented by information from electrophysiology and tract tracing experiments (1–9). These studies have revealed a somewhat dichotomous view of cortical architecture: an anatomical appreciation of a classic six-layered organization of neocortex and a neurophysiological recognition that functional units frequently reflect a vertical pattern of organization. We hypothesize that neuronal anatomical organization is more complex than simple laminae: We postulate the presence of anatomical units organized perpendicular to the pial surface in the same fashion as the functionally defined columns and develop a method to assess, using quantitative tools, cytoarchitectural patterns in human brain. Using this method, we detect a cytoarchitectural feature that we call a “microcolumnar ensemble” in high order association cortex in human brain.

As an example of the utility of this method, we examined the cytoarchitecture in two neuropathological disorders. Alzheimer disease is a common, severe dementia associated with the development of amyloid-β (Aβ) containing senile plaques in the neuropil, intraneuronal, phosphotau-containing neurofibrillary tangles, and prominent overall neuronal loss. Dementia with diffuse Lewy bodies presents with a clinical syndrome that is quite similar to Alzheimer disease, but it is neuropathologically distinct. Although dementia with Lewy bodies frequently has diffuse Aβ deposits, unlike Alzheimer disease there is only modest neuronal loss, and the characteristic neuropathological alteration is the presence of scattered neuronal inclusions (“Lewy bodies”) in the deep layers of cortex (10). The underlying pathophysiology of dementia with Lewy bodies is completely unknown and even whether Lewy bodies themselves contribute to the dementia is still controversial. We find a marked loss of microcolumnar ensemble architecture in both Alzheimer and Lewy body diseases, suggesting a commonality in the neuropathological underpinnings of dementia in these conditions.

Methods

Tissue.

Brain tissue from 22 Alzheimer disease cases, 5 dementia with Lewy bodies cases, and 11 neuropathologically normal (control) cases was provided by the Massachusetts Alzheimer's Disease Research Center Brain Bank (courtesy of E. T. Hedley-Whyte). The neuropathological diagnoses conform to established criteria (10, 11). None of the control cases met criteria for Alzheimer disease or dementia with Lewy bodies. All brains were fixed in metaperiodate-lysine-paraformaldehyde within 36 h after death. By using a freezing sledge microtome, 50-μm-thick sections were obtained from blocks containing the superior temporal sulcus (STS) region. The geometry of the 50-μm-thick tissue slices under consideration is such that the two greater lengths span along the pial surface and into the brain (ending at the boundary between the gray and white matter), respectively.

Previous studies of a detailed map of Alzheimer-related pathologies have shown that, although there are no cortical areas consistently free of both amyloid deposits and neurofibrillary change, there is hierarchical vulnerability among areas (13). Because Alzheimer dementia and dementia with Lewy bodies affect clinically memory and cognitive skills that are thought to be subserved by neural systems involving high order association cortex, using the multimodal association cortex is key to our study design. The cortex in the inferior bank of the STS was selected for several reasons: (i) It represents a high order association cortex (12) and has been extensively characterized in Alzheimer disease and dementia with Lewy bodies (14, 15), (ii) the STS is one of only three areas in the primate brain that receives input from all sensory modalities (12), and (iii) it is well demarcated anatomically and shows little brain-to-brain variability as opposed to other potential high order association areas. Our previous studies of the STS area suggest a striking uniformity in neuron cell number across age in control groups, and a graded loss of neurons in Alzheimer disease (14–17). The fact that the STS can be identified with gross anatomical cues rather than depending on cytoarchitectonic boundaries is particularly important in Alzheimer disease, where the very cell packing and density patterns that define cytoarchitectonic boundaries are disrupted.

Sections were stained by using the Nissl method. Neuronal counts were performed following the stereologic optical dissector procedure (14), which consists of bringing the tissue slice under an optical microscope that is connected to a computer screen. By manual selection, the positions of neurons on the screen are recorded automatically and stored in the computer. The positions of neurons were located in the inferior bank of the STS, approximately 1 cm medial to the crown of the gyrus. The location of each neuron was identified in an area of length 700–1,400 μm along the pial surface and depth of the full thickness of the gray matter. The location of the pial surface, gray-white matter junction and of each neuron was recorded by the Bioquant Image Analysis System (R & M Biometrics, Nashville, TN).

Quantitative Method for Cytoarchitectural Analysis.

We present a method to study neuronal architecture. We label all n neurons in the entire sample with index i, where i = 1, 2, … n. For a given neuron i we calculate the local neuron density field ρ_i(x, y) in the following way. We place a square lattice grid over the sample with the lattice origin (0,0) at a neuron i and the x axis parallel to the pial surface. Each grid cell is a square of an edge Δ. If we denote the center of a grid cell by (x, y) and count the number of neurons n_i(x, y) inside the cell, this cell will contribute to the local neuron density field at (x, y), n_i(x, y)/Δ². By considering all grid cells, we obtain the final local neuron density field ρ_i(x, y) = n_i(x, y)/Δ², which is calculated with respect to the particular neuron i at the center of the grid. We repeat the whole process for every neuron i ∈ {1, 2, … , n} in the sample and finally calculate the average neuron density field g(x, y) as an average over all local density fields ρ_i(x, y), i ∈ {1, 2, … , n}, g(x, y) Σ_i=1ⁿρ_i(x, y)/n.

Note that Δ is the parameter of the method. We evaluate Δ such that the statistical error due to local inhomogeneities of the neuronal density is minimal, and at the same time the resolution large enough to be able to detect the microcolumnar structure. We can estimate the upper limit of the statistical error for a completely random sample, where the position of any selected neuron is independent of positions of other neurons. For such a random sample, the average number of neurons in the grid cell with coordinates (x, y) is given by the Poisson formula 〈n_i(x, y)〉 = Δ²g(x, y) [note that g(x, y) represents the local neuronal density]. The standard deviation of the number of neurons in the cell for the Poisson distribution is 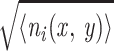= Δ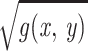. The standard deviation of the local density ρ_i(x, y) is then Δ² times smaller. Because g(x, y) is the averaged value of the local densities over n independent neurons serving as the origin of the grid, we can use the central limit theorem to find its variance and conclude that the standard deviation of g(x, y) is 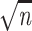times smaller and thus equal to 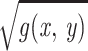/(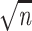Δ). The relative error σ of g(x, y) is hence (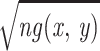Δ)⁻¹. Taking into account that g(x, y) ≈ 600 neurons/mm² and the total number of neurons analyzed is n ≈ 20,000, we find that σ ≈ 0.3/Δ if Δ is measured in micrometers. To be able to detect a 3% change of g(x, y) between two neighboring grid cells at a distance Δ, we should select Δ = 10 μm.

The quantity g(x, y) defined above is the analog of the density correlation function used in condensed matter and statistical physics to describe the structure of anisotropic liquids, which is obtained experimentally as a Fourier transform of the angular intensity of the scattered neutron or x-ray beam (18). The analogy to neutron or x-ray scattering stems from the fact that we compute contributions to the image from the neighborhood of every neuron in the cortex, similarly to the way that neutrons or X-rays are scattered from every atom of the liquid.

Results

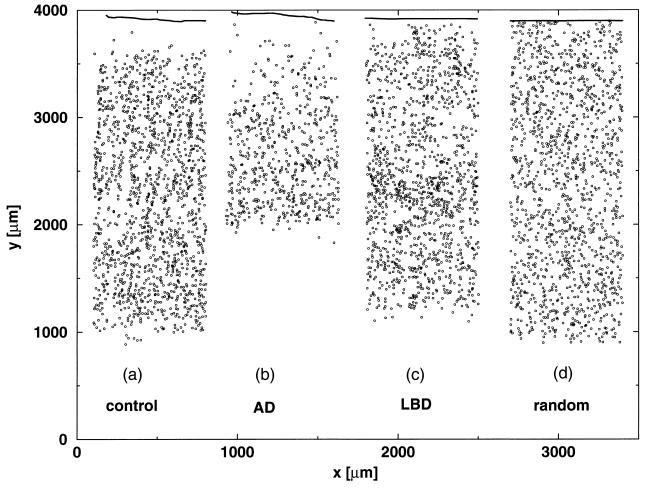
A typical pattern of neuron distribution in the cortex bordering the STS region is presented in Fig. 1a. Each dot represents the location of a recorded neuron, where the data span all of the laminae in a 50-μm-thick tissue, starting from the pial surface and ending at the junction of the gray and white matter. In Fig. 1b, we show the Alzheimer disease cortex of a similar width. In Fig. 1c, we show the cortex of dementia with diffuse Lewy bodies. In Fig. 1d, we show a strip of randomly scattered dots, representing neurons, the size of the strip and the number of dots the same as the number of neurons in the control case in Fig. 1a. Solely by inspection of Fig. 1a, it is difficult to conclude whether neurons are distributed randomly or organized in some way. It is impossible to compare the neuronal organizations of Fig. 1 a, b, c, and d without a quantitative approach.

Figure 1.

(a) Typical example of distribution of neurons in a tissue sample of a normal STS cortex. We count neurons (dots) in 50-μm-thick STS cortex slices of a length l parallel to the pial surface (solid line) by the depth of the cortex h; l varies from 700 to 2,000 μm. The depth of cortex h is 3.0 mm. (b) Same as a, but for Alzheimer disease cortex. The depth of cortex h is 2.5 mm. (c) Same as a, but for cortex of dementia with Lewy bodies. The depth of cortex h is 3.1 mm. (d) Same as a, but for a random placement of the same number of dots as illustrated in a.

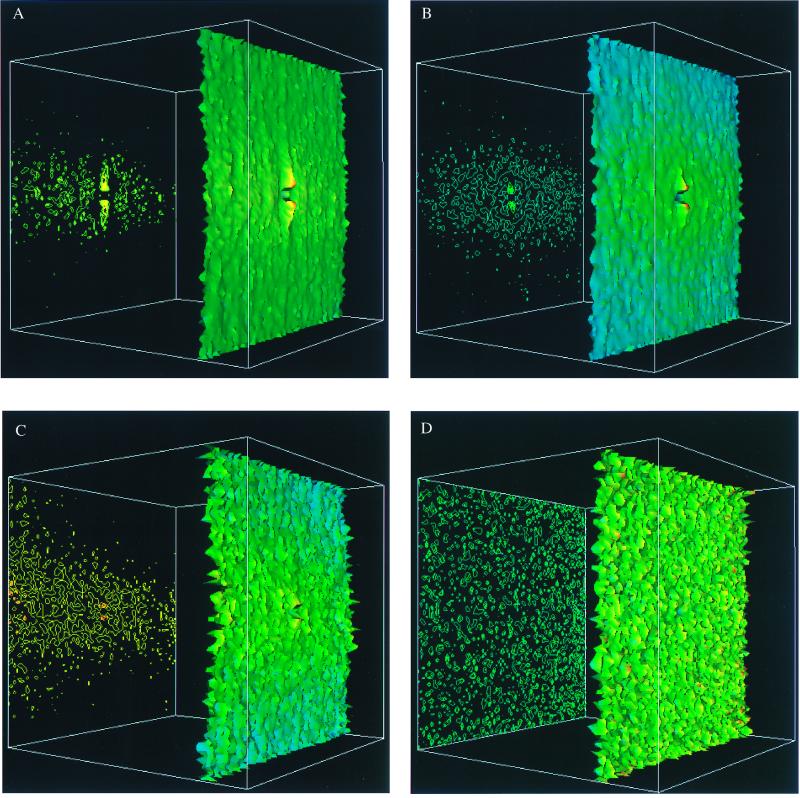
We collect the locations of all neurons (a total of n = 22,007 neurons) in a series of 700-μm-wide strips in the lower bank of the STS regions of 11 healthy elderly individuals (the total length of the cortex 11.9 mm). We calculate g(x, y) over all of the neurons in the tissue slice, where the x coordinate is parallel and the y coordinate is perpendicular to the pial surface. After applying our method to each case individually, we then average over all of the cases. Fig. 2A shows a three-dimensional color representation of g(x, y) in the STS region for the whole population of control brains. Fig. 2A is consistent with the following results: (i) a small region of radius of ≈10 μm of very low density exists in the center of the figure, indicating an excluded volume effect—i.e., the centers of two nerve cells cannot be closer than about 10 μm. This distance corresponds to a typical diameter of a neuron. (ii) The laminar structure is represented by the horizontal strip of predominantly yellow color of about 300-μm-width decaying in the y direction to low-density peripheral regions indicated by mostly green colors. (iii) Narrow regions of higher density are clearly seen as “ridges” in the vertical direction. The vertical column of high density is surrounded on both sides by two parallel low density regions of similar width.

Figure 2.

Three-dimensional color surface representations (right) and the corresponding contour maps (left) of the neuron density g(x, y) in a population of brain STS association cortex, calculated by using the method described in the text. The corners of the grid have coordinates (±400 μm, ±400 μm). The height of the surface is in an absolute scale for all of the figures whereas the color code is normalized for each figure separately such that the maximal value of g(x, y) corresponds to red and the minimal value of g(x, y) to blue. A shows g(x, y) in control brain STS association cortex, averaged over the population of 11 different cases (n = 22,007 neurons). The average density is 660 neurons/mm², the minimal density is 434 neurons/mm², and the maximal density is 845 neurons/mm². B shows g(x, y) in Alzheimer disease STS cortex averaged over the population of 22 cases (n = 19,391 neurons). The average density is 488 neurons/mm², the minimal density is 381 neurons/mm², and the maximal density is 669 neurons/mm². C shows g(x, y) in STS cortex of dementia with Lewy bodies, averaged over a population of five different cases (n = 6,751 neurons). The average density is 693 neurons/mm², the minimal density is 480 neurons/mm², and the maximal density is 948 neurons/mm². D shows g(x, y) computed from a random distribution of positions as in Fig. 1d. The average density is 513 neurons/mm², the minimal density is 258 neurons/mm², and the maximal density is 696 neurons/mm².

Our quantitative results as well as this computer image suggest both the presence of the well established laminar organization as well as a structure of alternating columns, perpendicular to the pial surface, with a typical spacing of about 80 μm. In the control brain, we define a microcolumnar ensemble quantitatively to be the vertical ensemble of neurons with a density larger than the average density (660 neurons/mm²). This region is 50 μm wide and 310 μm high (area 15,500 μm²). Averaging the density of neurons over this region and multiplying it by the area, we estimate that the microcolumnar ensemble contains approximately 11 neurons.

Next, we apply our method to examine the neuronal architecture of STS cortex in Alzheimer disease and examine whether loss of microcolumnar ensembles in individual patients is related to either neurofibrillary tangles or Aβ deposits. We collect a total of 19,391 neurons from 22 cases (the total length of the cortex 18.2 mm) with a clinical history of dementia and neuropathological diagnosis of Alzheimer disease (11). The average overall loss of neuronal density is about 30% whereas the total loss of neurons approaches 50% (14). The overall neuronal loss reflects both the decreased density and decreased cortical depth, due to atrophy. One consequence of this is that laminar structure is sometimes more pronounced in Alzheimer disease, as spared lamina stand out in contrast to depleted vulnerable lamina. This effect can be noticed in Fig. 2B, which shows the density profile, obtained analogously to Fig. 2A. Although the microcolumnar ensembles are visible in control cases (Fig. 2A), no visible columnar structure can be detected in the Alzheimer disease cases (Fig. 2B). Further analysis shows that, in marked contrast to the control brains, in Alzheimer disease, the region in which neurons achieve the density of a microcolumn (660 neurons/mm²) becomes shorter and thinner, covering an area of just 10 μm wide and 70 μm high (area 700 μm²). This represents a loss of over 95% of the area normally occupied by this unique architectural component of the cortex.

We reason that a microcolumnar ensemble with a substantially lower density than average would be dysfunctional. We therefore compare the percent of the total rectangular regions that have a given number of neurons per 50 μm by 310 μm area with independent assessments of total Aβ deposition or neurofibrillary tangle number, previously published from these same cases (14). For example, we compare the percentage of the cortex that achieves a density of at least 8 neurons per 15,500 μm². This represents approximately one standard deviation below the mean number of neurons observed in a microcolumnar ensemble in a control brain, and so accounts for the majority (68.3) of all microcolumnar ensembles in a control brain. The percent area in which this density is achieved varies quite closely with the total number of neurons in the region (P < 0.007). Intriguingly, there is also an inverse correlation (P < 0.05) between the number of regions that achieves this minimal density and the number of neurofibrillary tangles assessed with PHF-1 immunostaining and stereological techniques (14). No relationship between disruption of microcolumnar ensembles and deposition of Aβ can be detected (P = 0.86). Comparable results are obtained by using various “cut-offs” for the number of neurons per microcolumnar ensemble. These results are surprising because neurofibrillary tangles have previously been thought to primarily affect horizontal laminae in cortex (19). Our current results suggest that one important consequence of neurofibrillary tangle formation is disruption of microcolumnar ensembles. By contrast, Aβ deposition does not appear to be responsible for cytoarchitectural alterations, although it remains possible that downstream influences of Aβ deposits ultimately impact cortical structural organization.

As an additional example of the utility of this technique, we study cytoarchitectural changes in cases of dementia with Lewy bodies. The cases we chose have some diffuse Aβ deposits but no neurofibrillary change and do not meet CERAD criteria (11) for Alzheimer disease. The total number of 6,751 neurons in the STS segments studied in 5 cases of dementia with diffuse Lewy bodies (the total length of the cortex 3.5 mm) is about 15 less than in the comparable region of controls, but this difference does not reach statistical significance. Similarly, the density of control cases is 660 neurons/mm², of cases of dementia with Lewy bodies 693 neurons/mm², and of Alzheimer disease cases only 488 neurons/mm². We apply our quantitative analysis of neuronal geometric distribution to cases of dementia with Lewy bodies. No microcolumnar structure is evident as a result of the combined analysis of 6,751 neurons from the 5 cases (Fig. 2C) or in 4 of the 5 cases when analyzed individually.

For comparison, we apply our method to randomly shuffled neurons in the cortex (as are “neurons” in Fig. 1d). The corresponding density map is presented in Fig. 2D. The results in Fig. 2D looks very different from the density maps in Fig. 2 A–C, which correspond to neurons in the cortex, indicating that the distribution of neurons in the real cortex is far from random. The summarized results are presented in the Table 1.

Table 1.

Summarized results

	Control	Alzheimer disease	Lewy body dementias
Number of cases	11	22	5
Length of cortex	11.9 mm	18.2 mm	3.5 mm
Number of neurons	22.007	19.391	6.751
Average density	660/mm2	488/mm2	693/mm2
Width of microcolumns	50 μm	10 μm	—
Height of microcolumns	310 μm	70 μm	—

Discussion

We examine the neuronal architecture in the STS region because the STS region is a heteromodal association cortex with extraordinarily diverse, and for the most part reciprocal, connections with multiple primary sensory and first-order association areas including auditory, visual, somatosensory, and olfactory, as well as strong reciprocal projections with limbic cortices and the striatum (9, 12, 20–24). The ventral portion and the dorsal portions of the STS region are strongly interconnected, but these subregions have distinct projection patterns (25). For example, the dorsal area connects strongly to the temporal vision area (area MT) and the “where” dorsal stream of visual information, whereas the ventral portion of the STS region has strong connections with area IT and related areas which provide the “what ” ventral stream of visual connections (26). Lesion and functional imaging studies have implicated the STS region in higher order visual function including face recognition and even autobiographical memory (27–31). Thus, from an anatomical and functional perspective, there is little doubt that the STS region is in a unique position to subserve the highest order integrative neural systems in humans.

We examine the cortical architecture of this region with a quantitative method of architectural analysis and demonstrate a structural unit in the STS cortex. The cortical structural element is an array perpendicular to the pial surface of roughly 11 neurons with periodicity of 80 microns, which we call a microcolumnar ensemble. These neurons are anatomically closely packed, presumably to allow focused interactions so that ascending projections can be in intimate contact with neurons within the ensemble. This apparent “columnarity” is in accord with qualitative impressions of temporal cortex (32).

Previous studies using a variety of techniques have revealed structures that may be related to microcolumnar ensembles. The size and shape of these anatomically defined microcolumnar ensembles resembles the size and shape of “neuronal domains,” which are functionally defined 50-μm-wide by 200-μm-tall regions, recognized by using optical recordings of neuronal populations labeled with calcium-sensitive indicators (33). Computer-assisted analysis led Buxhoeveden et al. to conclude that there were structures of size 34 μm wide by 400 μm tall in layer III of the Tpt area in both nonhuman primates and humans (2). The exact relationship between the microcolumnar ensembles we describe here and these other anatomical and functional units remains to be determined.

When applied to the population of Alzheimer disease brains, our quantitative analysis reveals a feature of Alzheimer disease neuropathology, a disruption of microcolumnar ensembles. A similar degree of disruption of microcolumnar ensembles is found in dementia with Lewy bodies, where the understanding of the cause of the disease and the neuropathological manifestations are still in their infancy. Our result is intriguing: Although the loss of neurons in dementia with Lewy bodies is substantially less than in Alzheimer disease, we find a similar disruption of microcolumnar ensembles in both cases.

In Alzheimer disease, we find in addition that the density of neurons in microcolumnar ensembles is strongly related to the density of neurofibrillary tangles but not to the amount of Aβ deposition. It does not appear that neurofibrillary tangles are themselves arrayed in individual microcolumnar ensembles (8), but, nonetheless, neurofibrillary tangles clearly alter the precise architecture of neurons in the cortex. These results support the possibility that extracellular deposition of Aβ is not by itself sufficient to cause neuronal alterations, a view recently advanced on the basis of molecular studies (34). This result is also in accord with observations of APP overexpressing transgenic mice (35, 36) in which Aβ deposition does not lead to cortical neuronal death.

The above results indirectly imply that the disruption of the observed microcolumnar ensembles contributes to cognitive impairment. We believe that application of quantitative measures of cortical organization may prove useful in analysis of other psychiatric and neurological disorders of brain dysfunction, such as schizophrenia and dyslexia, where structural alterations are not apparent with conventional techniques. To enhance the widespread use of the method of quantitative architectural analysis, we provide public access to the software: http://polymer.bu.edu/alzheimers.

Abbreviations

Aβ

amyloid-β

STS

superior temporal sulcus